Research on dynamic wind tunnel test technology of rotor airfoil
-
摘要: 旋翼翼型的设计优化及性能确定亟须建立并发展翼型动态风洞试验技术。通过动力学仿真与结构优化设计，基于FL–11低速风洞研制出旋翼翼型两自由度动态试验装置，可实现俯仰/沉浮单自由或两自由度耦合运动，最高振荡频率达到5 Hz；基于FL–20连续式跨声速风洞研制出旋翼翼型高频高速动态试验装置，最高振荡频率达到17 Hz，试验最高雷诺数为5 × 106，模拟参数包线满足真实直升机参数要求；基于FL–14低速风洞研制出大尺度旋翼翼型动态试验装置，翼型模型弦长为800 mm，试验最高雷诺数达到4 × 106。完善了旋翼翼型动态试验精准测试相关技术，并开展了验证性试验，试验数据规律合理、量值可靠，表明试验系统及相关测试技术具有较高的可靠性，可为旋翼翼型动态气动特性试验评估提供重要的设备平台和技术支撑。Abstract: It is urgent to establish and develop the dynamic wind tunnel test technology for rotor airfoil design optimization and performance determination. Through dynamic simulation and structural optimization design, based on the FL–11 low-speed wind tunnel, a two degree of freedom dynamic test device for rotor airfoil is developed. It can not only complete the single degree of freedom dynamic motion of pitch and plunge, but also realize the coupling operation of pitch/plunge, with the highest oscillation frequency of 5 Hz. Based on the FL–20 continuous transonic wind tunnel, a set of high-frequency and high-speed oscillation test device for rotor airfoil is developed, with the maximum pitch oscillation frequency exceeding 17 Hz and the maximum test Reynolds number exceeding 5 × 106. The simulated parameter envelope meets the parameter requirements of the real helicopter. A large-scale rotor airfoil dynamic test device is developed based on the FL–14 low-speed wind tunnel, with the airfoil model chord length of 800 mm and the maximum test Reynolds number of 4 × 106. The accurate measuring and testing technique of the rotor airfoil dynamic test is developed, and the verification test is carried out. The results show that the dynamic test data of the rotor airfoil are reasonable and reliable, which indicates that the test system and related test technology have high reliability. It can provide important technical support for the research of rotor airfoil dynamic stall.
-
Keywords:
- rotor /
- airfoil /
- dynamic /
- wind tunnel test /
- plunging oscillation
-
0 引 言
旋翼翼型动态失速是一种非定常[1]、非线性[2]气动现象，其机理十分复杂。动态失速的发生通常被视为直升机飞行的“硬边界”[3]，精确预测翼型动态失速特性有利于进行旋翼气动优化设计[4]、气动弹性响应和气动导数计算等[5-7]。翼型动态风洞试验数据是改进和发展CFD数值模拟技术的标准依据和支撑基础[8]。旋翼翼型动态试验主要利用正弦振荡的翼型模型在自由来流中模拟桨叶段的俯仰/沉浮运动[9]。
美、俄等国家持续利用风洞试验完成高性能旋翼翼型研发工作。除精准的静态试验能力外，还在风洞中建立了专门研究直升机旋翼翼型动态气动特性的试验装置和技术[10-13]。旋翼翼型试验技术通常须达到或超过真实直升机的减缩频率（约0.030～0.200），国外主要研究机构的试验装置或研究都符合这一要求[14-15]。另外，来流马赫数通常要求接近真实直升机桨叶马赫数，侧重研究后行桨叶大迎角分离的来流马赫数一般约0.3～0.4，而侧重研究前行桨叶激波诱导失速的来流马赫数一般要达到0.7～0.8[16]。目前国际上对旋翼翼型动态失速的研究仍在不断深入。在试验技术研究方面，主要集中在以天平测力、快速响应压敏漆（fast-response pressure sensitive paint）和传感器测压等试验手段准确预测判定翼型的动态气动力和边界层转捩特性[17-19]、精细测试动态失速细节流动结构变化[20-24]，采用三维数字图像互相关技术（DIC）等非接触测量手段测量流固耦合模型的位移变形[25]，以及采用新技术抑制动态失速[26-28]等方面。
中国空气动力研究与发展中心（以下简称气动中心）[29]、西北工业大学[30-32]、南京航空航天大学[1,33]、上海交通大学[5]等在旋翼翼型动态失速研究方面开展了一些工作，由模拟翼型俯仰单自由度振荡向模拟俯仰/沉浮/摆振多自由度振荡发展[33]，由模拟定常来流向模拟非定常来流发展[34]。总的来说，我国在旋翼翼型动态风洞试验技术研究上起步较晚，关注固定翼翼型多，关注旋翼翼型少，技术发展水平明显落后于国外。很长一段时间内，我国没有成熟的旋翼翼型动态试验装置和技术可用，航空工业直升机设计研究所林永峰等[35]只能在俄罗斯TsAGI SVS–2风洞进行CH–9.5旋翼翼型动态失速特性试验。
分析国内外现状，差距集中体现在以下2个方面：1）国内现有试验装置模拟参数不足以覆盖旋翼翼型动态失速范围，试验装置能力不能完全满足旋翼翼型动态失速研究需要。2）测试试验技术不能满足数据高精准度要求，动态试验结果受到测试手段、同步采集、模型变形等多个因素影响，国内对这些因素尚未开展系统研究，难以对动态试验数据精准度给出明确的评价结论。以上差距直接带来的问题是：国内开展的旋翼翼型试验较少且模拟参数不足，获得的试验数据不能支撑旋翼翼型的设计和评估，也难以给数值模拟方法的改进提供基础，在开展自主翼型动态设计[36]时缺少较为丰富和全面的风洞试验数据作为支撑。
旋翼翼型的设计优化及性能确定亟须发展旋翼翼型动态风洞试验技术。本文在低速和高速风洞中设计研制了3套旋翼翼型动态试验装置并建立了精准测试方法：其在 FL–11低速风洞（闭口式）中具备旋翼翼型两自由度动态试验能力，为更全面精准地模拟旋翼翼型动态过程奠定了技术基础；其在 FL–20连续式跨声速风洞中具备高频高速动态试验能力，为精确重构旋翼翼型非定常气动力（需要更高雷诺数和更高阶气动导数）提供了技术条件；其在FL–14低速风洞（开口式）中具备大尺度旋翼翼型动态试验能力，为研究旋翼翼型缩比模型的尺度效应提供了技术支撑。
表1列出了国内外主要气动研究机构的动态试验模拟能力。气动中心的动态试验装置驱动能力和模拟参数包线满足真实直升机参数要求（以我国某型直升机典型前飞工况为例，在满足减缩频率相似和马赫数相似的前提下，需要能够模拟的第一阶振荡频率为12 Hz。目前气动中心研制的高频高速动态试验装置在10°振幅时的振荡频率为17 Hz，可以满足该试验条件）。
表 1 国内外主要气动研究机构动态试验模拟能力对比表Table 1 Comparison of dynamic test simulation capabilities of major international aerodynamic research institutes风洞名称 模型尺度（弦长）/m 来流马赫数 雷诺数/(105) 振荡幅值 振荡频率/Hz 运动自由度 美国NASA结冰风洞[37] 0.40 0.40（最大） 37 10° 5.0 俯仰 德国荷兰DNW TWG[12] 0.30 0.30～0.50 35 4°～7° 6.6 俯仰 法国ONERA F2[38] 0.50 0.16（常用） 19 10° 5.0 俯仰 俄罗斯TsAGI SVS−2[35] 0.18 0.30～0.60 25 5° 15.0 俯仰 中国南京航空航天大学
非定常风洞[33]0.30 0.10（最大） 7 10° （俯仰）
100 mm （沉浮）4.0（俯仰）
2.0（沉浮）俯仰/沉浮 中国西北工业大学 NF−3[39] 0.70 0.20（最大） 32 15° （俯仰）
100 mm （沉浮）5.0（俯仰）
3.0（沉浮）俯仰/沉浮 中国西北工业大学 NF−6[31] 0.20 0.30 14 10° 8.0 俯仰 中国气动中心 FL−11[40] 0.40 0.20～0.32 30 20° （俯仰）
150 mm （沉浮）6.0（俯仰）
5.0（沉浮）俯仰/沉浮 中国气动中心 FL−14[29] 0.80 0.25（最大） 40 30° 4.0 俯仰 中国气动中心 FL−20[41-42] 0.21 0.20～0.60 50 10° 17.0 俯仰 1 旋翼翼型动态试验装置研制
为解决动态装置仿真优化设计、动力驱动同步控制、大尺寸及高频高速振荡装置抑振等关键技术难题，本文在低速和高速风洞中设计研制了3套旋翼翼型动态试验装置，以提升旋翼翼型动态气动特性测试能力。
1.1 两自由度动态试验装置
旋翼翼型两自由度动态试验装置（基于气动中心FL–11低速风洞）主要用于准确模拟旋翼桨叶片段的复杂运动，以研究耦合振荡翼型动态气动特性。
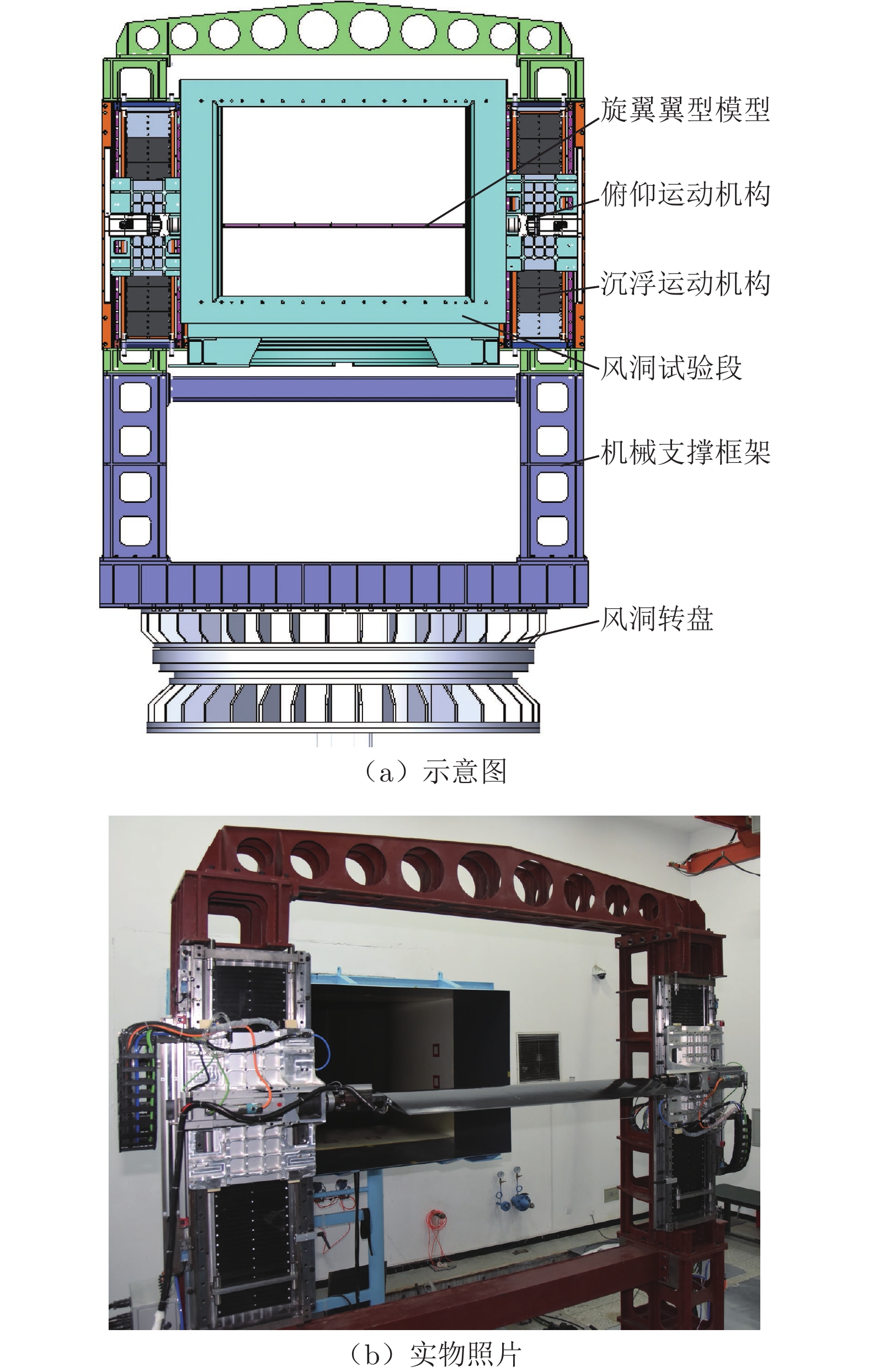
模型采用横跨安装方式，如图1所示。装置主要由俯仰运动机构、沉浮运动机构和机械支撑框架等构成。其中俯仰运动机构由伺服电机、行星减速器和支座等构成，可实现模型俯仰运动；沉浮运动机构由大功率、大推力、高动态的直线电机和滑轨支座等构成，可实现模型沉浮运动。俯仰运动机构整体安装在直线电机上，随沉浮机构一起上下运动，可实现模型俯仰/沉浮耦合运动。由于沉浮机构的运动惯量较大，为避免滑落，在直线电机的两端安装缓冲器和气压式制动器以防止“飞车失控”。
![]()
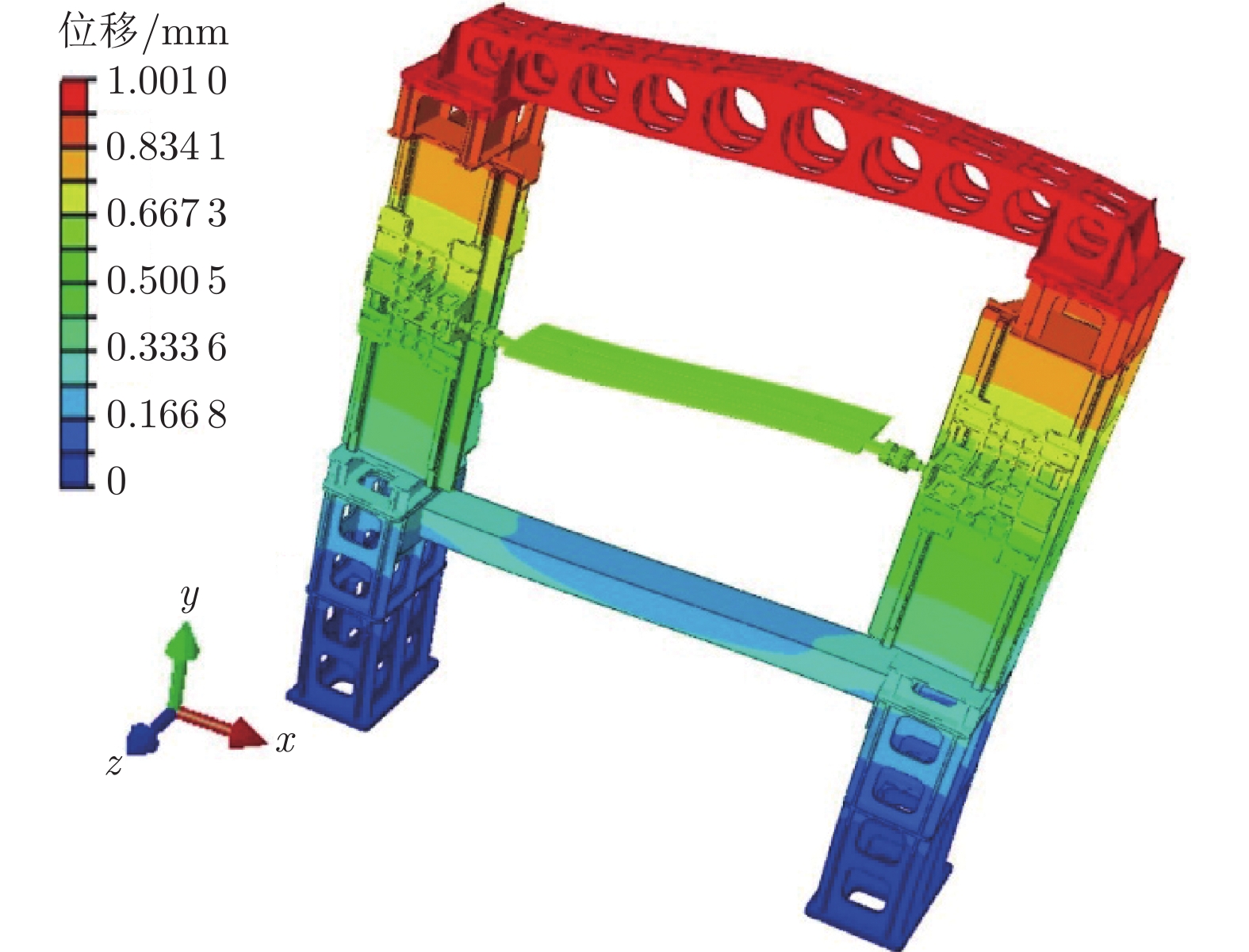
图 1 低速风洞两自由度动态试验装置Fig. 1 Dynamic test device of two degree of freedom in low speed wind tunnel在俯仰/沉浮运动和气动力的耦合影响下，模型及支撑系统将产生较大幅度的振动。当振动频率与装置的固有频率重合时，还会产生剧烈的共振现象，严重影响试验的质量和安全。本文在满足强度、刚度和动态性能要求的前提下，对装置结构进行了优化设计。采用有限元法对装置进行了计算，得到其前五阶固有频率，如表2所示。基于LANCZOS方法对装置进行了模态分析，得到其第一阶模态振型如图2所示。可以看到，第一阶固有频率为18.5 Hz（大于装置的最高振荡频率5 Hz，且远离装置的外载频率），可避免装置结构在振荡过程中发生共振。
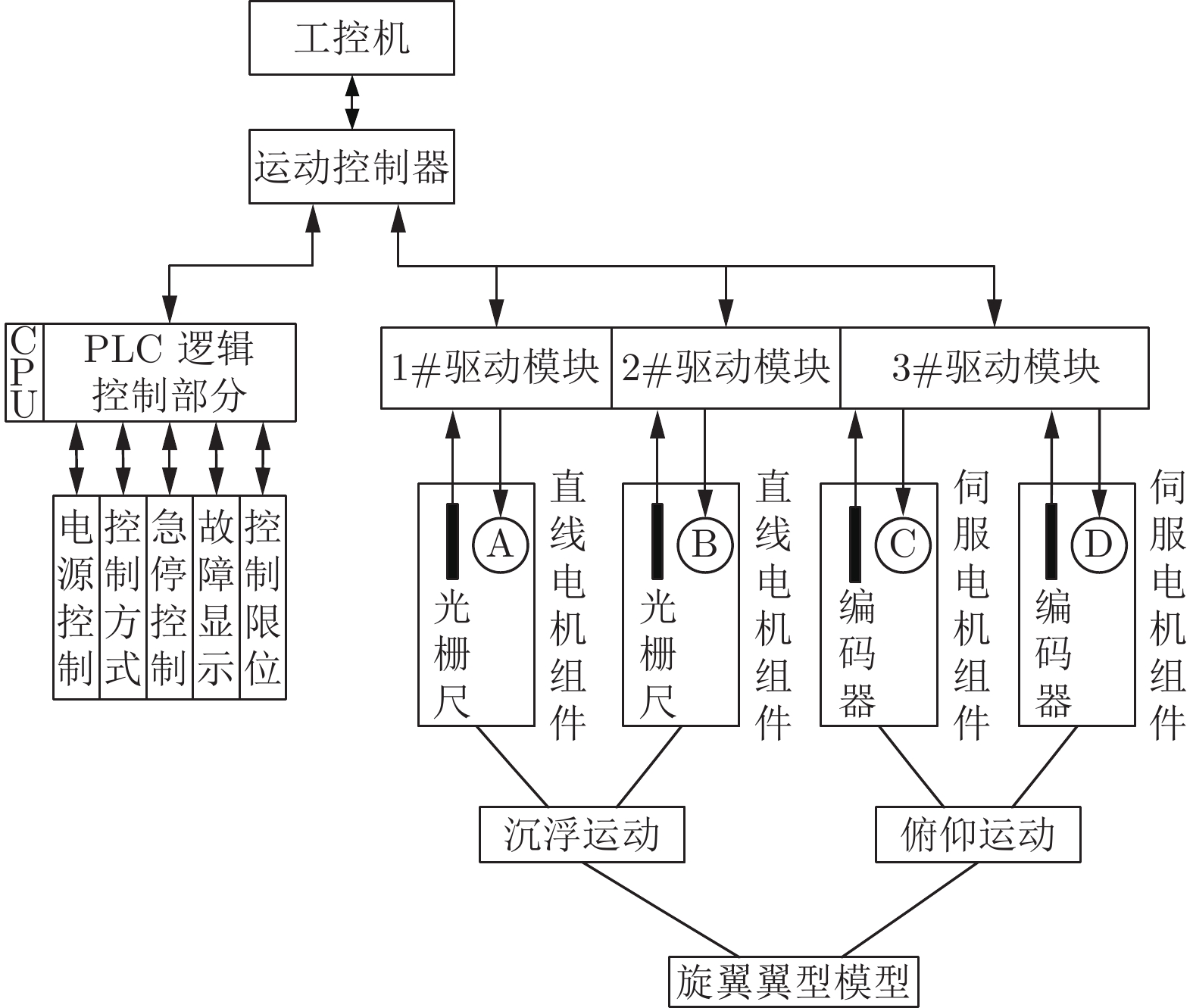
表 2 装置前五阶固有频率Table 2 The first five order inherent frequency阶数 固有频率/Hz 1 18.5 2 20.3 3 24.9 4 48.0 5 65.3 控制系统结构如图3所示。软硬件设计实现了功能层次化和结构模块化，并具有功能扩充能力。选用SIMOTION D运动控制器和S120伺服驱动来实现直线电机和伺服电机的运动控制，配置工控机及控制软件来实现人机对话。系统可设置相应的速度、角度、位移、频率和相位差等运动参数，还可反馈系统的运行状态及电流、位置等实际值。1FN3直线电机导轨和光栅尺均垂直安装，光栅尺输出CLIQ信号反馈给S120伺服驱动，1FT7伺服电机（CLIQ信号输出）编码器信号直接进入S120伺服驱动。高精度多轴运动控制中心、动态性能优异的直线电机、伺服电机、光栅尺、绝对值编码器构成装置的全闭环运动控制系统，有效地保证了整个测试系统的控制精度；同时，还利用基于龙门轴锁定增益补偿算法的同步控制技术提升了电机同步精度，利用基于主从轴同步运动的电子凸轮技术实现了振幅和频率的无级调节。装置运行性能测试结果表明：俯仰角度精度和同步精度≤3′，沉浮位移精度和同步精度≤1 mm。
![]()
图 3 低速风洞动态试验装置控制系统结构Fig. 3 Control system structure of low speed wind tunnel dynamic test device1.2 高频高速动态试验装置
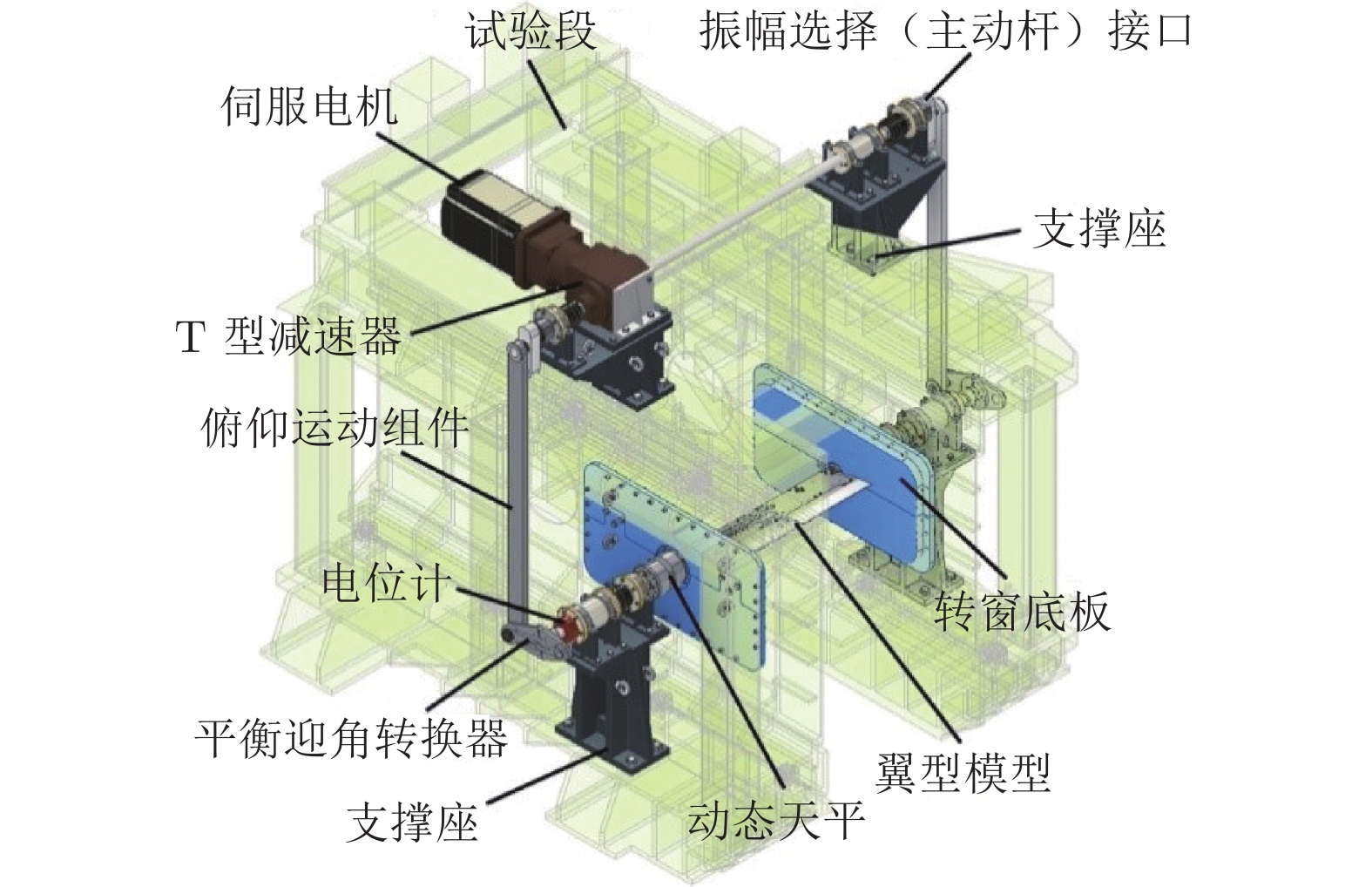
旋翼翼型高频高速动态试验装置（基于气动中心FL–20连续式跨声速风洞，如图4所示）主要用于研究高马赫数和高减缩频率下振荡翼型的动态气动特性，可使模拟的来流参数和非定常运动参数更加接近真实直升机旋翼的实际运行工况。
![]()
图 4 旋翼翼型高频高速动态试验装置Fig. 4 High frequency and high speed rotor airfoil dynamic test device装置主要由俯仰运动组件、天平（或假天平）及支撑座等构成。翼型模型横跨式安装，通过两端天平、联轴器与俯仰运动组件连接，采用双端驱动，两侧传动轴具有对称的结构，两台天平左右对称布置。俯仰运动组件由激励器、膜片联轴器和轴承等构成。激励器由伺服电机、减速器和曲柄摇杆机构等组成，伺服电机为永磁同步伺服电机，减速器为两端同步输出的T型高精度减速器，曲柄摇杆机构采用无急回特性构型设计。通过改变减速器输出轴连接的主动杆拨盘方式，实现模型振幅调节；通过改变伺服电机的转速，实现模型振荡频率调节；通过改变翼型装置从动杆连接方式，实现俯仰平衡迎角调节。装置可实现俯仰单自由度运动，可在来流马赫数（Ma）为0.6、压力为2 atm（1 atm ≈ 101.325 kPa）下稳定运行。
控制系统采用上位机和下位机的控制方式，两者之间通过TCP/IP通讯。上位机采用工业控制计算机，在上位机上通过NI LabView编写人机界面，实现系统零位、控制参数、运动角度和速度、运动振幅和频率等参数的设置。下位机采用SIMOTION运动控制器，实现对伺服驱动系统的控制。
1.3 大尺度旋翼翼型动态试验装置
大尺度旋翼翼型动态试验装置（基于气动中心FL–14低速风洞）主要用于研究较大弦长的旋翼翼型动态气动特性，能够以较小的缩比模拟更大尺度的直升机旋翼桨叶。
该试验装置为Π形结构，如图5所示，在两端支撑立柱上安装低转速、大扭矩伺服电机，配合专用变频器直接驱动横梁及安装在横梁上的翼型模型做正弦振荡。为确保伺服电机驱动能力满足要求，对翼型模型和横梁整体进行了动力学仿真设计，仿真结果如图6所示。两台伺服电机同步可输出的扭矩为3000 N·m，转速为150 r/min，满足试验要求。
![]()
图 5 大尺度旋翼翼型动态试验装置示意图Fig. 5 Schematic diagram of dynamic test device for large scale airfoil model翼型横梁跨度较大（约4.6 m），翼型最大厚度约72 mm，强度符合要求（安全系数4.4）。但其刚度不足，翼型与横梁在驱动力、气动力、惯性力和重力的交互作用下易产生上下振动，发生变形（最大变形26 mm）。为减小横梁与翼型在动态试验时的变形，避免振动发散，采取上下随动拉张线的办法抑振（图7）。张线经滑轮组转向后吊挂砝码，经验证，抑振效果明显。
![]()
图 7 FL–14低速风洞旋翼翼型动态试验张线抑振Fig. 7 Vibration suppression of rotor airfoil dynamic test in FL–14 low-speed wind tunnel经测试，基于FL–11低速风洞研制的旋翼翼型两自由度动态试验装置的最高沉浮频率为5 Hz，最大沉浮振幅为150 mm（根据常规直升机旋翼桨叶一般的挥舞和弯曲变形幅值折算），试验雷诺数（Rec，以弦长c为参考长度）达3 × 106；基于FL–20连续式跨声速风洞研制的高频高速动态试验装置的最高频率为17 Hz，试验雷诺数达5 × 106；基于FL–14低速风洞研制的大尺度旋翼翼型动态试验装置的模型弦长为800 mm，试验雷诺数达4 × 106。3套旋翼翼型动态试验装置的详细技术指标如表3所示。其中，α为翼型俯仰振荡迎角，h为翼型转动中心垂直方向位置，α1为俯仰振荡幅度，h1为沉浮振荡幅度，fpi为俯仰振荡频率，fpl为沉浮振荡频率，α0为平衡迎角。
表 3 旋翼翼型动态试验装置技术指标Table 3 Technical specifications of rotor airfoil dynamic test device风洞 测试内容 技术指标 FL−11 α −180°～180°，精度0.01°，在线连续可调 h −150～150 mm，精度0.01 mm，在线连续可调 α1 ≤30°，精度0.05°，在线连续可调 h1 ≤150 mm，精度0.05 mm，在线连续可调 fpi、fpl 俯仰0.1～6.0 Hz，沉浮0.1～5.0 Hz，
精度优于0.01 Hz，在线连续可调Rec 3 × 106 FL−20 α1 3°、5°、8°、10°，精度优于0.1° α0 −5°、0°、5°、10°，精度优于0.1° fpi 0.2～17.0 Hz，精度优于0.05 Hz Ma 0.2～0.6 Rec 5 × 106（压力2 atm） FL−14 α −180°～180°，精度0.01°，在线连续可调 α1 ≤30°，精度0.05°，在线连续可调 fpi 0.1～4.0 Hz，精度优于0.01 Hz，在线连续可调 Rec 4 × 106 2 旋翼翼型动态试验精准测试技术
2.1 基于智能算法的动态试验模型结构设计优化
为追求更高的模拟运动参数和气动测量精度，需要在满足模型结构强度、刚度、固有频率和稳定性等前提下，通过优化设计使模型质量尽可能轻。本文在实现模型精密加工的前提下（模型加工后，采用三坐标仪检测模型外形，前缘的测量值和数模值平均误差小于0.02 mm），着重在模型结构优化设计等方面拓展尝试。
首先，建立有限元分析模型，分析模型质量、强度、刚度、固有频率和稳定性情况；其次，运用径向基神经网络（Radial Basis Functions, RBF）模型和全局优化、梯度优化两种智能算法组合对翼型模型法兰、前横梁厚度和复合材料铺层厚度等进行优化；再次，利用NSGA–Ⅱ多目标优化算法对蒙皮复合材料铺层角度进行优化，获得Pareto最优解集；最后，选择最合适优化结果制作翼型模型，对模型进行模态分析。
1）初始模型
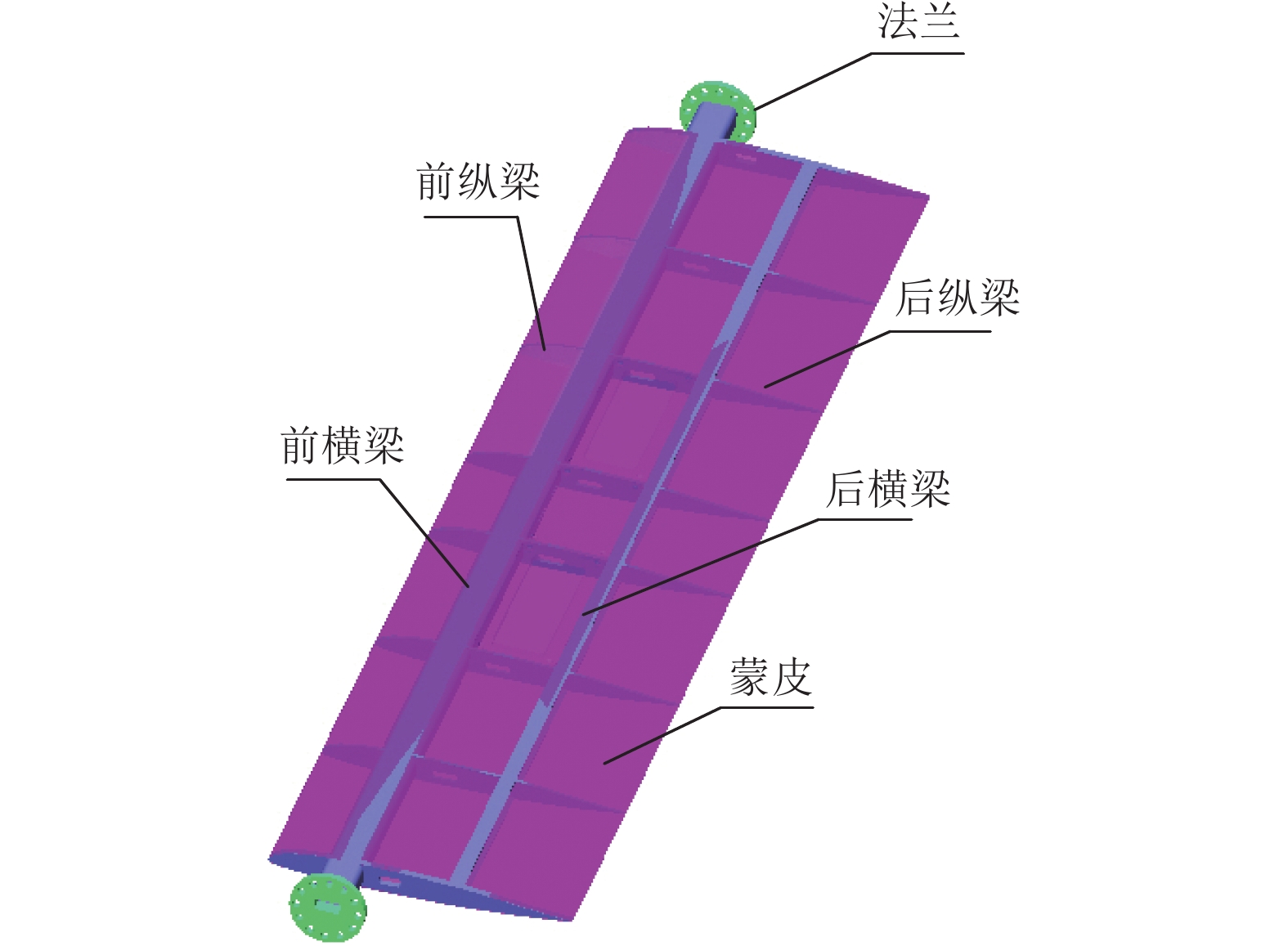
翼型模型（图8）由前横梁（厚8.0 mm）、后横梁（厚4.8 mm）、前纵梁（厚4.4 mm）、后纵梁（厚4.4 mm）、蒙皮（厚2.4 mm）和法兰（厚12.0 mm）等构成。模型质量为15.67 kg。前横梁和法兰材料为7075铝合金，其余均为T800碳纤维增强复合材料。前、后纵梁共有8组。蒙皮由12层T800碳纤维增强复合材料铺设组成，每层厚度为0.2 mm；铺层角度包括0°、±45°、90°。
为确保计算精度，采用4节点四边形网格划分各个部件，有限元模型共划分57833个网格，如图9所示。
2）优化算法
本文采用的代理模型为RBF模型。RBF是基于人脑细胞对外界反应的局部性原理提出的，有很强的函数逼近能力，可以生成高精度的近似模型。RBF模型由输入层、隐含层和输出层组成，径向基函数Y(X)的基本形式为：
$$ Y(X)=\sum_{1}^{m} \beta_{1} \phi(r_{i}, C) $$ (1) 式中：
$r_{i}(X)=\left\|X-X_{i}\right\|$ 是${X}$ 与第$ i $ 个样本点$X_{i}$ 在设计空间上的距离，$\left\|X-X_{i}\right\|$ 为矩阵的欧拉范数；$C$ 为控制参数；$ \beta _{1}$ 为基函数ϕ(ri, C)的加权系数；$ m $ 为基函数个数。本文采用全局优化算法和梯度优化算法进行组合优化，在计算初期采用多岛遗传算法（MIGA）进行全域搜索，避免计算陷入局部最优的困境，然后将全局优化得到的结果作为序列二次规划算法（SQP）的初值，保证计算收敛，得到最优解。
3）优化结果
优化结果如表4所示，优化设计使得模型质量下降34.05%，受载最大等效应力减小9.91%，最大位移减小23.06%，第一阶固有频率提高12.80%，失效指标（复合材料的主要性能）提高56.18%，大幅提高了材料安全裕度。
表 4 翼型模型结构优化结果Table 4 Optimization results of airfoil model structure优化目标 质量/kg 受载最大
等效应力/N最大位移
/mm第一阶固有
频率/Hz失效
指标初始值 12.567 252.15 7.46 56.10 0.728 优化值 8.288 227.16 5.74 63.28 0.319 变化值 4.279 25.34 1.72 7.18 0.409 变化率 34.05 9.91 23.06 12.80 56.18 2.2 动态气动载荷测试
旋翼翼型动态气动载荷测试主要包括升力、阻力和俯仰力矩3个纵向分量的测试，综合采用脉动压力传感器测量技术和双天平动态同步测力技术获取纵向分量随迎角和位移的变化曲线。双天平动态同步测力为直接测试方式，可直接得到翼型模型整体的3个纵向分量，并对动态失速后的三维流动结构引起的翼型模型整体载荷变化有所感应，但其精准度受双天平组合、翼型模型端面和支撑杆等影响，特别是运动翼型端面需与风洞洞壁之间留有缝隙，该缝隙对气动载荷有一定影响，且其影响量随着振荡频率和振幅的变化而变化。脉动压力传感器测量为间接方式，通过对测试所得的翼型模型表面压力分布积分获取3个纵向分量，其精准度受翼型端面、支撑杆等影响较小，但受到测压点数量及测压管道等影响，且积分获取的阻力为压差阻力，不包括摩擦阻力。测压管道（从翼型模型表面测压孔至动态压力传感器之间的压力传递管道）的长度、内径等对运动翼型实时迎角与同步采集的压力之间的相位偏差存在影响，模型高速运动时捕获不到峰值，致使精准度降低。针对上述影响因素，可研究确定最佳测压管路参数，基于频响函数进行脉动压力数据修正[43]。对于测力与测压两种方式，可先以静态试验数据作为标准，考核测力与测压两种方式测试结果精准度，再对比分析动态试验数据的精准度，综合给出精准度较高的动态试验结果。
2.2.1 脉动压力传感器测量
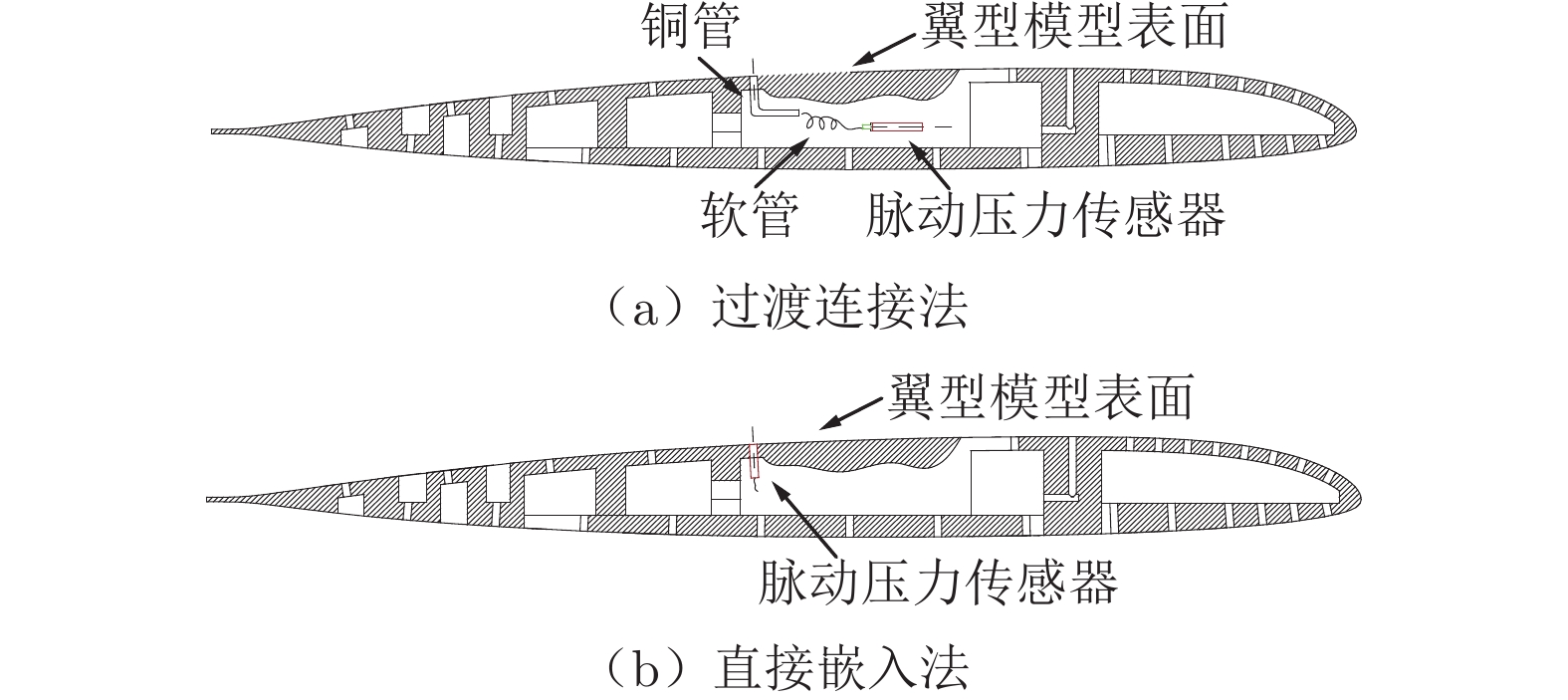
动态测压管路的设计对翼型表面脉动压力测量的精准度有直接的影响。选取翼型中间段布置测压剖面（通常位于模型中心剖面或者关于中心剖面对称），布置若干个测压孔。测压孔在前缘附近较密，在后缘附近较疏，在吸力面比在压力面更密。动态试验模型间接测压通道为由测压孔、测压过渡铜管和测压软管等组成的过渡通道，如图10（a）所示。测压孔垂直于当地型面，其出口按当地型面修型。测压铜管与测压孔用胶粘接牢固无间隙。传感器置于模型内部，通过软管与测压铜管相连。值得注意的是，若关注高频部分的压力信号（例如进行边界层转捩测试），应采用脉动压力传感器直接嵌入翼型表面的方式，如图10（b）所示。部分无法直接嵌入的传感器采用软管和铜管过渡连接，但其信号会存在高频信号畸变，需进行基于频响函数的脉动压力管路修正[43]。
![]()
图 10 旋翼翼型动态风洞试验传感器安装布置示意图Fig. 10 Installation layout of sensors for dynamic wind tunnel test of rotor airfoil低速风洞试验测压元件采用ENDVECO 8510B系列差压式脉动压力传感器，量程为1 psi（1 psi≈6895 Pa）。单个传感器需连接4根电缆，并引入参考压软管及测量端压力软管。压力传感器的参考压（即外界大气压）由多个传感器共用的参考压软管输入。高速风洞测压元件采用频响高、精度高、尺寸小的Kulite XCE–062系列绝压式脉动压力传感器，量程为25 psi。
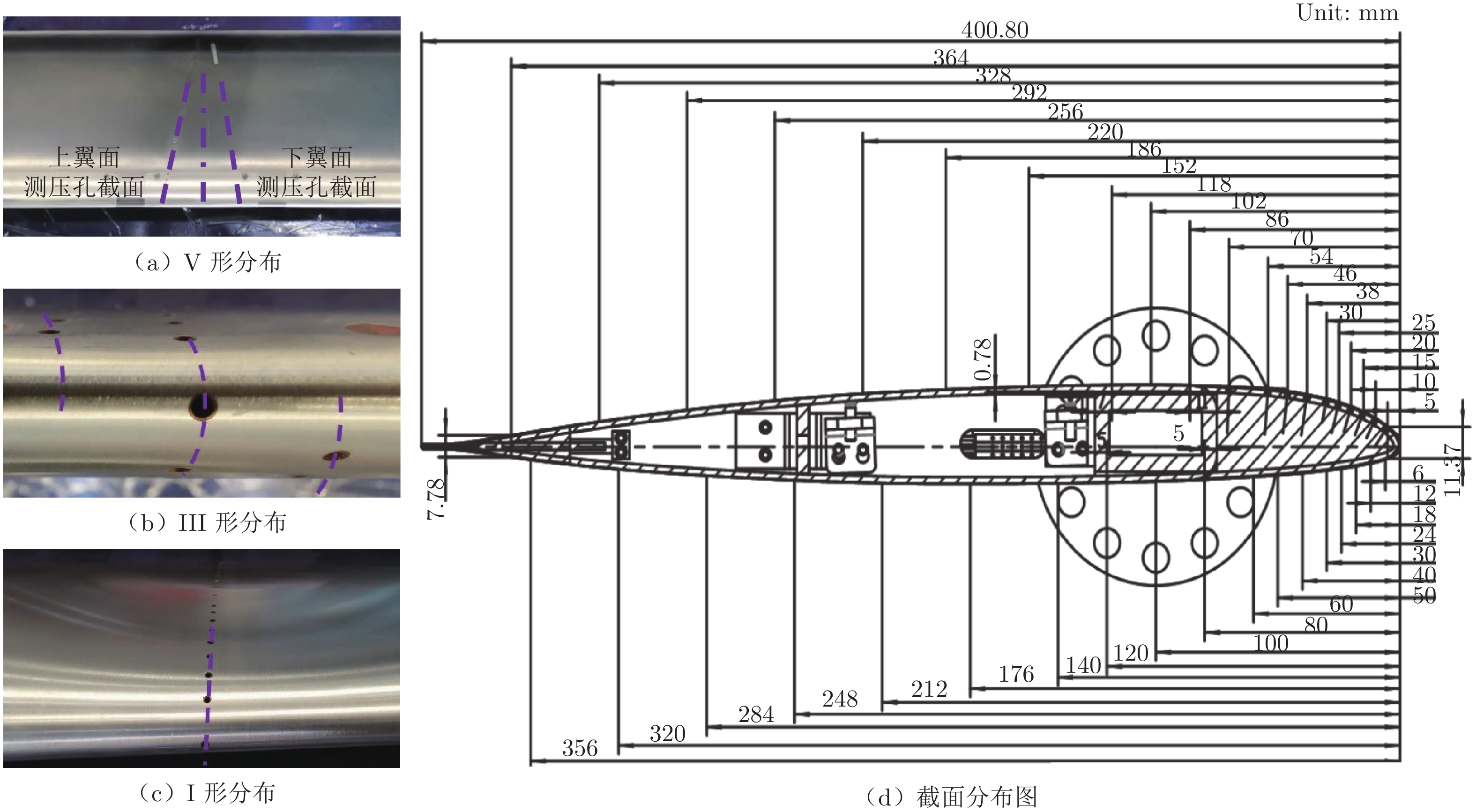
针对不同试验对象进行脉动压力测量管路优化设计，测压孔位置分布设计有3种：Ⅴ形、Ⅲ形和Ⅰ形方案，如图11所示。吸力面测压剖面和压力面测压剖面组合构成Ⅴ形积分测量剖面，测压点从前缘开始分别沿上下翼面呈Ⅴ形布置，Ⅴ形夹角24°（与中线夹角各12°），Ⅴ形两条线端距离20 mm，以保证后缘测压孔加工的便利性。Ⅴ形方案充分利用有限空间布置更多的传感器，且可减小上一测压孔对下一测压孔的影响，多用于高速风洞试验，可有效削减洞壁干扰带来的三维效应。Ⅲ形方案多用于小尺度模型低速风洞试验，由中间测压剖面和分别距离中间测压剖面3%弦长距离的两侧测压剖面组成，可以增加动态压力测量孔的数量，提高压力积分精度。Ⅰ形方案多用于大尺度（弦长400 mm以上）模型低速风洞试验，布置在翼型模型的正中间剖面位置。
脉动压力信号畸变会引起幅值、相位和频谱等产生误差。幅值误差直接影响脉动量的大小，导致动载荷误差；在对多个测点压力积分求解宏观气动力/力矩时，相位误差会使分析结果产生致命错误；频谱误差会导致某些频段幅值放大，某些频段缩小，导致载荷谱失真。研究分析管路特征参数对脉动压力信号的影响规律，并对管路长度、内径、规格和限制器规格等进行了优化设计。最终优选内径1.5 mm、外径2.0 mm的金属铜管（长10 cm）与内径1.7 mm、外径2.2 mm的PVC软管（长15 cm）的混合管路；不关注高频脉动信号时，可采用压扁管限制器对高频脉动信号进行过滤。
2.2.2 分体式并联双天平动态同步测力
目前的翼型动态风洞试验通常采用单端驱动和单天平测量方式，以往试验经验表明，在高频振荡时单端驱动会引起翼型模型非对称大变形。针对这一问题，本文采用两端驱动、双天平同步测试[42]的风洞试验结构布局，提出了一种分体式并联双天平动态同步测力方案，即构型相同的双天平分体以并联的方式分别从两端支撑试验模型，组合完成模型气动力/力矩的测量，单个天平可承受5500 N升力、1300 N阻力、250 N·m俯仰力矩。
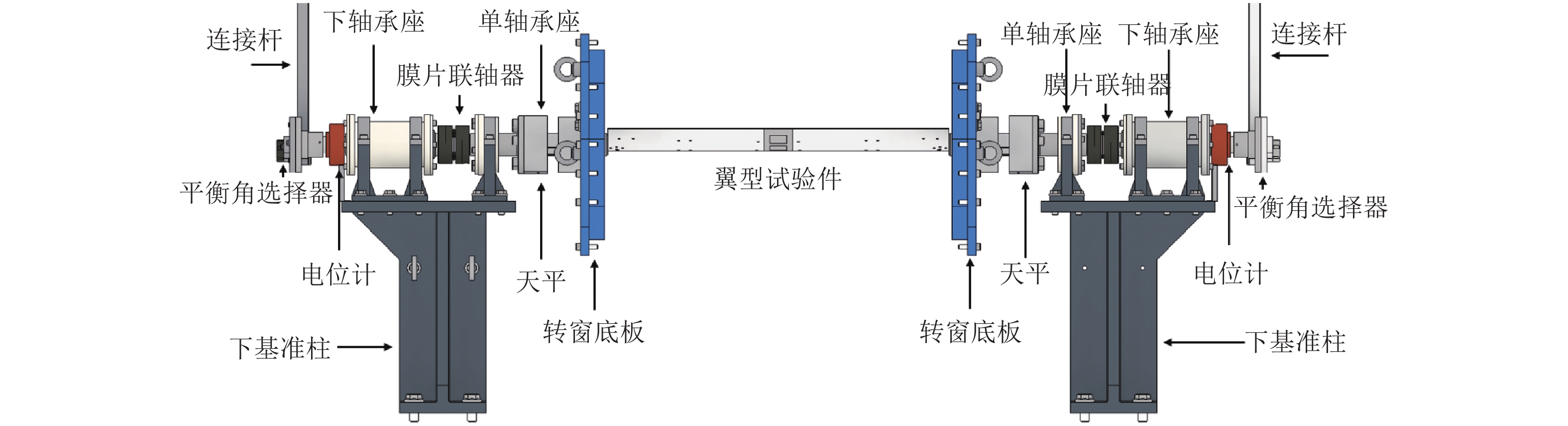
高速风洞旋翼翼型双天平动态同步测力装置包括转窗底板、传动轴、双天平、轴承、膜片联轴器和平衡迎角选择器等。天平置于传动轴法兰和模型法兰之间，膜片联轴器、轴承位于天平和驱动机构之间，转窗底板与天平连接。天平固定端与浮动端为半刚性连接，当受到气动载荷和惯性载荷后，翼型变形引起的位移通过天平、从动杆传导到连杆机构上，会使连杆的圆周运动不能稳定在一个平面上，导致运动机构失稳，天平测量的精准度无法保证。为了满足试验需求，对天平进行了隔振与解耦设计，消除了失稳对天平的影响。如图12所示，在装置中设计了轴承和膜片联轴器，使得从俯仰运动组件传递来的动力只有扭矩，将翼型固接的天平解耦，翼型振荡产生的载荷均传递到天平上，同时翼型穿过转窗底板，仅与天平接触，确保天平测量的精准度。
![]()
图 12 高速风洞动态天平与翼型连接方式Fig. 12 Connection between dynamic balance and airfoil in high speed wind tunnel低速风洞翼型动态试验天平的固定端与俯仰电机减速器输出接口之间用法兰连接、螺钉拉紧；天平的浮动端与模型间也采用法兰连接，如图13所示，模型端部和侧壁之间采用随动密封。天平浮动端面与模型端面之间装有蝶形弹簧，使天平具有轴向自由度，可沿着旋转轴线作微量平移。天平测量元件为三柱梁组合弹性元件，可测量5个分量。天平测量电桥为惠斯顿全桥电路，选用常温应变计，共6个电桥。
![]()
图 13 低速风洞翼型动态试验天平安装连接图Fig. 13 Installation and connection diagram of airfoil dynamic test balance in low speed wind tunnel2.3 数据同步采集及处理
要提高动态试验数据精准度，必须解决表面动态压力分布及天平载荷实时测量、来流速压高精度测量以及动态位移实时精确测量等关键问题。为了准确分析翼型动态气动载荷，需要实现翼型动态气动载荷和模型的角度、位移、起始相位、速压等信号同步采集。为了研究不同起始相位下的翼型动态气动载荷，数据采集系统还需具备任意相位信号触发采集功能。
2.3.1 PXI总线同步采集系统
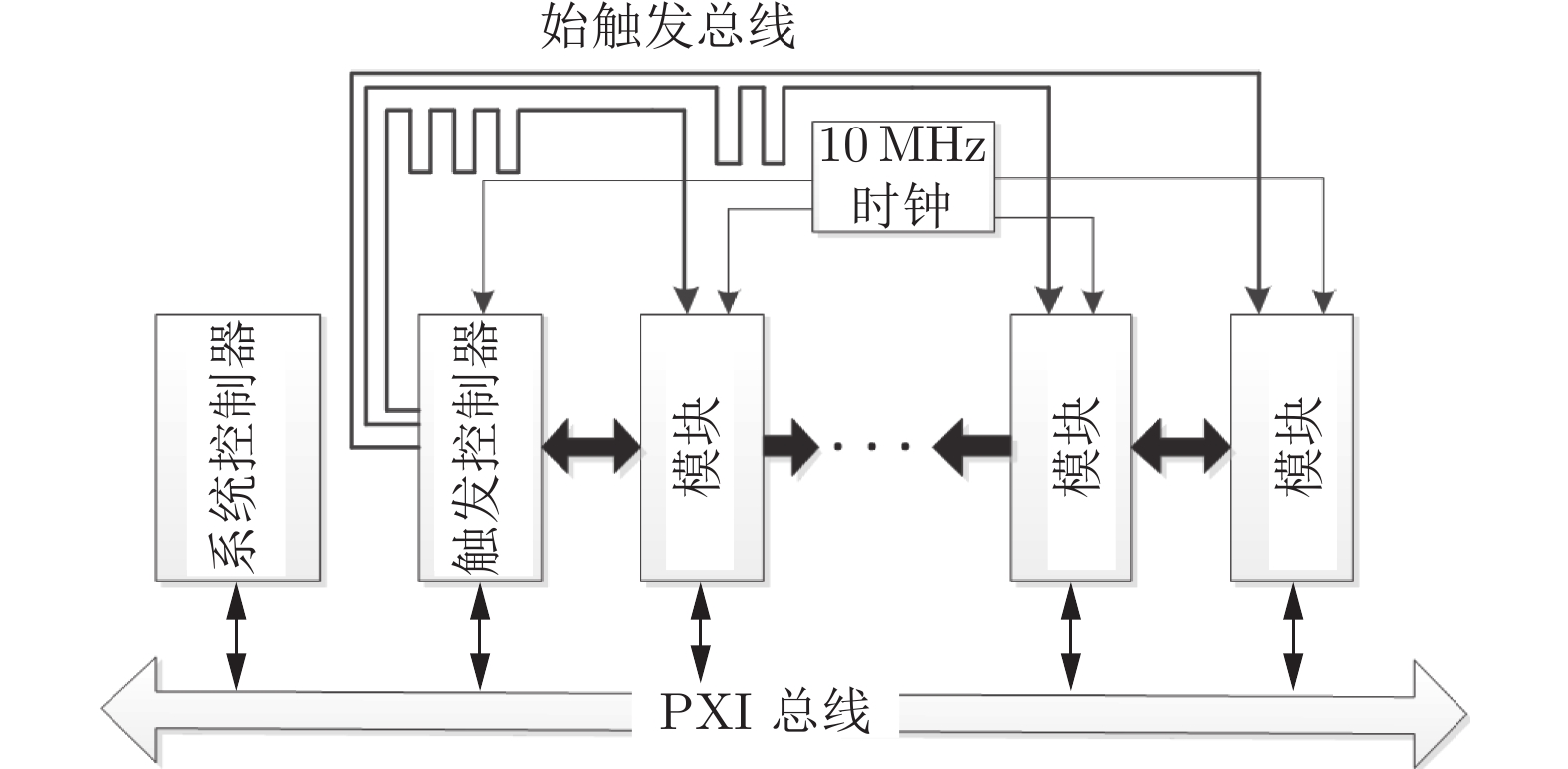
数据采集系统采用PXI总线的多通道同步数据采集平台。SCXI–1143信号调理模块安装在SCXI–1001机箱内，完成信号的耦合、放大和滤波；调理后的信号通过线缆传输至高精度数据采集模块PXI–6123，PXI–6123安装在PXI–1045机箱内，通过机箱背板星形总线共享采样时钟和开始触发信号，实现各通道数据同步采集，如图14所示。使用安装在PXI–1045机箱内的远程控制卡PXI–8336实现信号传输。通过MXI远程控制套件和光纤将PXI–1045机箱与测量分析工作站相连，实现远程控制和数据传输。数据采集系统结构如图15所示。
2.3.2 动态信号同步采集
动态试验角度和位移信号是重要的试验参数，采集时要与对应的动态压力、天平载荷同步记录。角度和位移信号采用电位计和光栅尺测量，与传感器和天平信号一起接入动态数据采集系统。PXI总线同步采集系统可将任一模拟输入信号或脉冲信号作为开始采集触发信号，因此，将角度或位移传感器信号作为触发信号，实现动态参数同步采集，并严格保证试验数据的对应关系。传感器和天平信号经增益放大器放大、可编程8阶巴特沃斯低通滤波处理。
2.3.3 数据采集软件
数据采集软件基于LabWindows/CVI软件平台编写开发。通过调用DAQmx数据采集驱动程序，实现对PXI数据采集卡的控制和数据采集。数据采集软件运行于测量分析工作站中，实现数据采集、传输、存储、显示等功能。参数配置主要有以下功能：
1）设置通道参数（放大倍数，同步方式，滤波频率）；
2）采样频率在采集卡的允许范围内可选；
3）采样数据长度根据需要可选；
4）数据采集文件存储格式兼容后续处理；
5）采集数据的曲线显示设置与曲线显示；
6）数据采集和保存。
2.3.4 数据处理
试验的气动系数按照风轴系给出。风轴系定义为：原点为翼型模型对称剖面弦线1/4位置，x轴沿来流反方向，y轴垂直向上，z轴按照右手法则确定。俯仰和沉浮振荡运动方程为：
$$ \alpha(t)=\alpha_{0}+\alpha_{1} \sin (2 \pi t+\varPhi) $$ (2) $$ h(t)=h_{1} \sin (2 \pi z f t) $$ (3) 式中：t为振荡时间，α(t)为翼型俯仰振荡实时迎角，h(t)为翼型转动中心实时垂直方向位置，f为振荡频率，Ф为俯仰和沉浮振荡运动相位差。不同振荡频率下，每个周期对翼型的迎角、沉浮位移、脉动压力和天平载荷均采样256个点，共采集16个周期，去掉前后各半周期，用15个完整周期数据进行平均。将平均后1个周期数据进行六阶最小二乘多项式拟合，按等相位角输出80个点。对翼型表面压力分布进行光顺处理后，采用式（4）～（8）进行压力系数计算和压力积分，获取翼型升力系数和俯仰力矩系数等。
$$ C_{pi}=\dfrac{p_{i}-p_{∞}}{\dfrac{1}{2} \rho v^{2}}=\dfrac{p_{i}-p_{∞}}{q_{∞}}=\dfrac{p_{i}-p_{∞}}{p_{0}-p_{∞}} $$ (4) $$ C_{N}=\int_{0}^{1} C_{p,\rm{l}} \rm{d} \bar{x}-\int_{0}^{1} C_{p,\rm{u}} \rm{d} \bar{x} $$ (5) $$ {C_C} = \int_{{{\bar y}_{\rm{l},\max }}}^{{{\bar y}_{\rm{u},\max }}} {{C_{p{,\rm{be}}}}{{\rm{d}}}\bar y - } \int_{{{\bar y}_{\rm{l},\max }}}^{{{\bar y}_{\rm{u},\max }}} {{C_{p{,\rm{af}}}}{{\rm{d}}}\bar y} $$ (6) $$ C_{L}=C_{N} \cos \alpha-C_{C} \sin \alpha $$ (7) $$ \begin{split}{C_m} =& \int_0^1 {({{C_{p{,\rm{l}}}} - {C_{p{,\rm{u}}}}} )( {0.25 - \bar x} )} {\rm{d}}\bar x +\\& \int_{{{\bar y}_{\rm{l},\max }}}^{{{\bar y}_{\rm{u},\max }}} {{C_{p{,\rm{be}}}}\bar y{\rm{d}}\bar y - \int_{{{\bar y}_{\rm{l},\max }}}^{{{\bar y}_{\rm{u},\max }}} {{C_{p{,\rm{af}}}}\bar y{\rm{d}}\bar y} } \end{split} $$ (8) 式中：Cpi为测压点压力系数；pi为测压点静压；p0、p∞、ρ、v、q∞分别为来流总压、静压、密度、速度、动压；CN为法向力系数；CC为轴向力系数；Cp,u、Cp,l分别为翼型上、下表面压力系数；Cp,be、Cp,af分别为翼型最大厚度之前和最大厚度之后的压力系数；
$ \bar{x}=x / c $ 、$ \bar{y}=y / c $ 分别为x、y坐标相对于弦长c的无量纲量；$\bar{y}_{\operatorname{u,max}}$ 、$\bar{y}_{\operatorname{l,max}}$ 分别为翼型上、下表面最大纵坐标相对于弦长c的无量纲量；CL为翼型的升力系数；Cm为翼型绕1/4弦点的俯仰力矩系数。在翼型动态风洞试验中，天平不仅采集翼型气动载荷，还采集翼型与天平本身的惯性载荷，该数据应从试验数据中扣除。设(Fy, Fx, Mz)表示翼型所受到的纵向气动载荷，其中，Fy为升力，Fx为阻力，Mz为俯仰力矩，(Fy1, Fx1, Mz1)、(Fy2, Fx2, Mz2)分别表示天平1、2测量的纵向气动载荷。动态双天平测力数据处理流程包括初读数的扣除、天平公式计算、力矩中心转换、气动系数转换、数据轴系转换、双天平数据使用等，即：
1）试验前对天平进行校准，得到天平的校准系数，进一步处理确定天平载荷数据。
2）设置装置运动参数，在翼型振荡、风洞无来流条件下进行初读数测量，得到初始纵向气动载荷(Fy0, Fx0, Mz0)，以排除试验模型重量和惯性载荷的影响。
3）天平测量振荡翼型的气动载荷，得到Fy1、Fy2、Fx1、Fx2、Mz1、Mz2等。
4）去除惯性载荷的影响，得到翼型动态气动载荷为：
$$ {F_y} = {F_{y1}} + {F_{y2}} - {F_{y0}} $$ (9) $$ {F_x} = {F_{x1}} + {F_{x2}} - {F_{x0}} $$ (10) $$ {M_z} = {M_{z1}} - {M_{z2}} - {M_{z0}} $$ (11) 2.4 模型位移实时测量
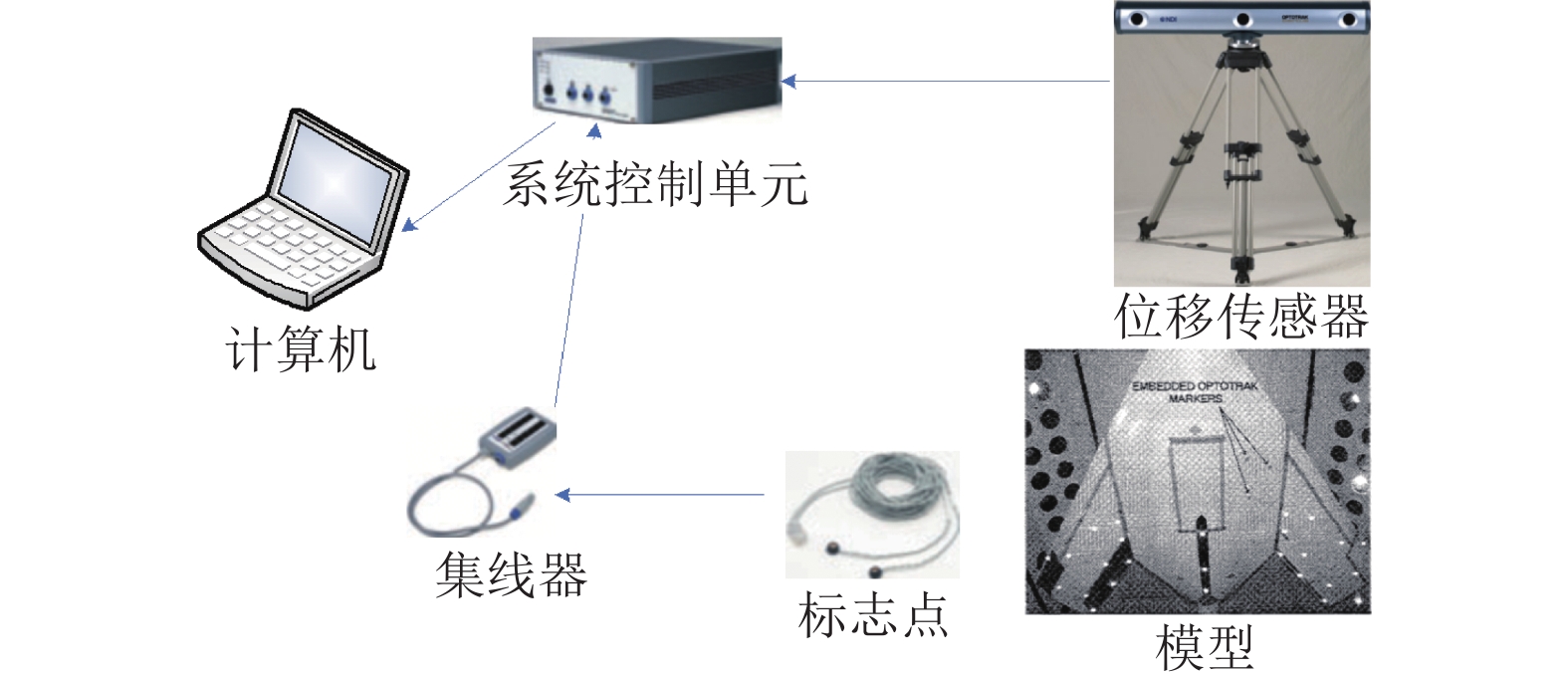
翼型模型在动态运动过程中，由于机构间隙和结构变形等原因，在较大气动载荷和自身惯性载荷下，会产生一定的位移偏差，后端电位计或光栅尺测试位移方式也会造成位移测量偏差。为解决以上问题，本文采用基于线阵CCD的OptotrakTM光学非接触测量技术对气动测量剖面的当地实时位移进行测量。OptotrakTM系统主要由位移传感器、系统控制单元（SCU）、标志点（marker）和集线器（strober）等组成，如图16所示。标志点（本文采用主动发光二极管）最大发光频率为4600 Hz，系统最高采样频率为4600/(N+2) Hz（N为标志点个数）。通过两两垂直的3个线阵CCD重构三维空间，捕捉标志点的空间位置坐标。测量模型整体位移时，在模型刚性较好的位置粘贴不少于3个标志点构建模型刚体，与PXI总线同步采集系统通过主从站方式共享同一采集时钟，实现同步采集。模型俯仰角度和沉浮位移采用2种方式获取：1）利用位移翼型两端的电位计（GL–100）和光栅尺（LC185）测量，其测量值为名义值；2）利用OptotrakTM系统测量模型标志点（图17）数据，其测量值为实测值。对比2种方式测量的结果，获得模型真实角度和位移数据，并对电位计和光栅尺数据进行修正。
![]()
图 17 旋翼翼型动态振荡位移变形测量试验照片Fig. 17 Test photo of oscillation displacement and deformation measurement for rotor airfoil先后开展了模型位移姿态（俯仰角度和沉浮位移）静态测量、俯仰/沉浮单自由度振荡测量、俯仰/沉浮耦合振荡测量等试验内容。表5给出了位移姿态静态测量精准度结果，可以看到，位移姿态的名义值与实测值较为一致，二者偏差基本可忽略，这表明该旋翼翼型动态试验装置具有较高的控制精准度。
表 5 静态测量精准度结果Table 5 Results of static measurement俯仰角度 沉浮位移 名义值/(°) 实测值/(°) 名义值/mm 实测值/mm −5 −4.957 −30 −29.946 5 5.046 −15 −15.054 10 9.985 15 15.001 20 20.038 30 29.932 表6给出了俯仰–沉浮两自由度耦合振荡（f = 1.0 Hz）方式下，有风/无风及不同风速下的实测结果。有风后，模型存在一定风载变形，模型中心区域位移实测值与名义值偏差有所增大，受惯性力和风载耦合影响，俯仰和沉浮两自由度耦合振荡时位移偏差达到2 mm。基于OptotrakTM光学非接触测量技术可以弥补传统接触式测量技术的不足，能够更准确地测量翼型模型的实际角度和位移数据，为下一步开展旋翼翼型动态试验结果的不确定性分析提供数据支撑。
表 6 俯仰–沉浮两自由度耦合振荡动态测量结果Table 6 Dynamic measurement results of pitching and plunging coupled oscillation俯仰角度 沉浮位移 名义值/(°) 实测值/(°) 名义值/mm 实测值/mm 5 4.951
（无吹风）30 30.930
（无吹风）4.964
（吹风，v=34 m/s）31.940
（吹风，v=34 m/s）4.947
（吹风，v=45 m/s）32.882
（吹风，v=45 m/s）3 风洞验证试验结果分析
基于CRA309旋翼翼型模型，在FL–11低速风洞、FL–14低速风洞和FL–20连续式跨声速风洞中开展了验证试验。
3.1 FL–11低速风洞典型试验结果
3.1.1 俯仰–沉浮耦合振荡试验结果
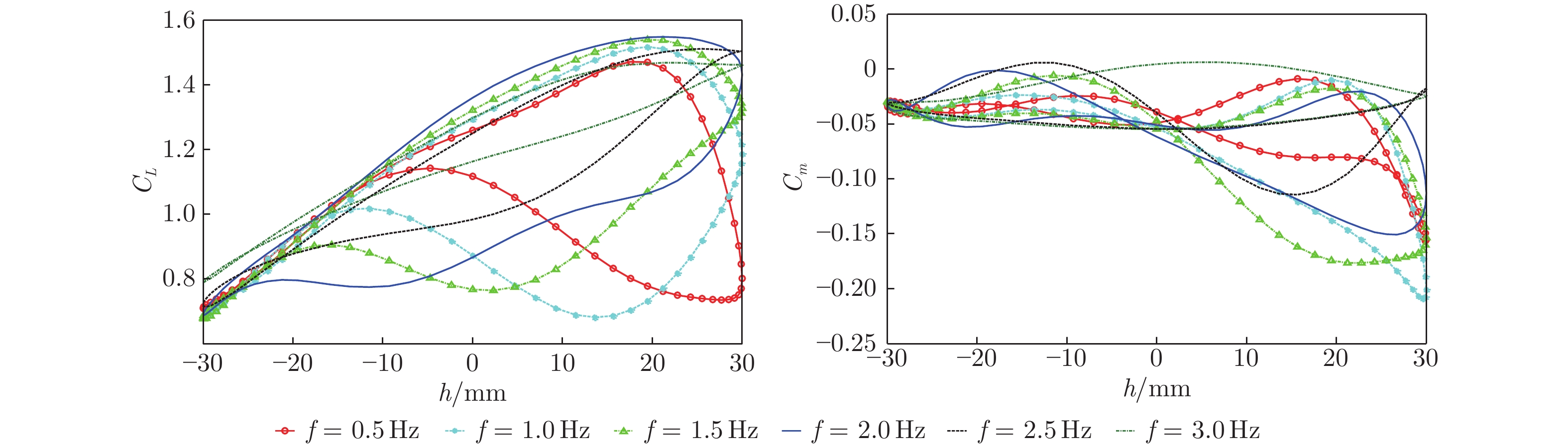
图18为v = 34 m/s、Rec = 9.3 × 105、α0 = 10°、α1 = 5°、h1 = 30 mm、fpi = fpl时，不同振荡频率（0.5～3.0 Hz，对应减缩频率k = πf'c/v = 0.018～0.111，其中f'为旋转频率）下的耦合试验结果。可以看出，随着振荡频率增大，升力系数和力矩系数在上升沿和下降沿之间的变化幅度逐渐减小。
![]()
图 18 耦合振荡试验频率影响结果对比Fig. 18 Comparison of frequency influence results of coupled oscillation test3.1.2 同步测力测压试验结果
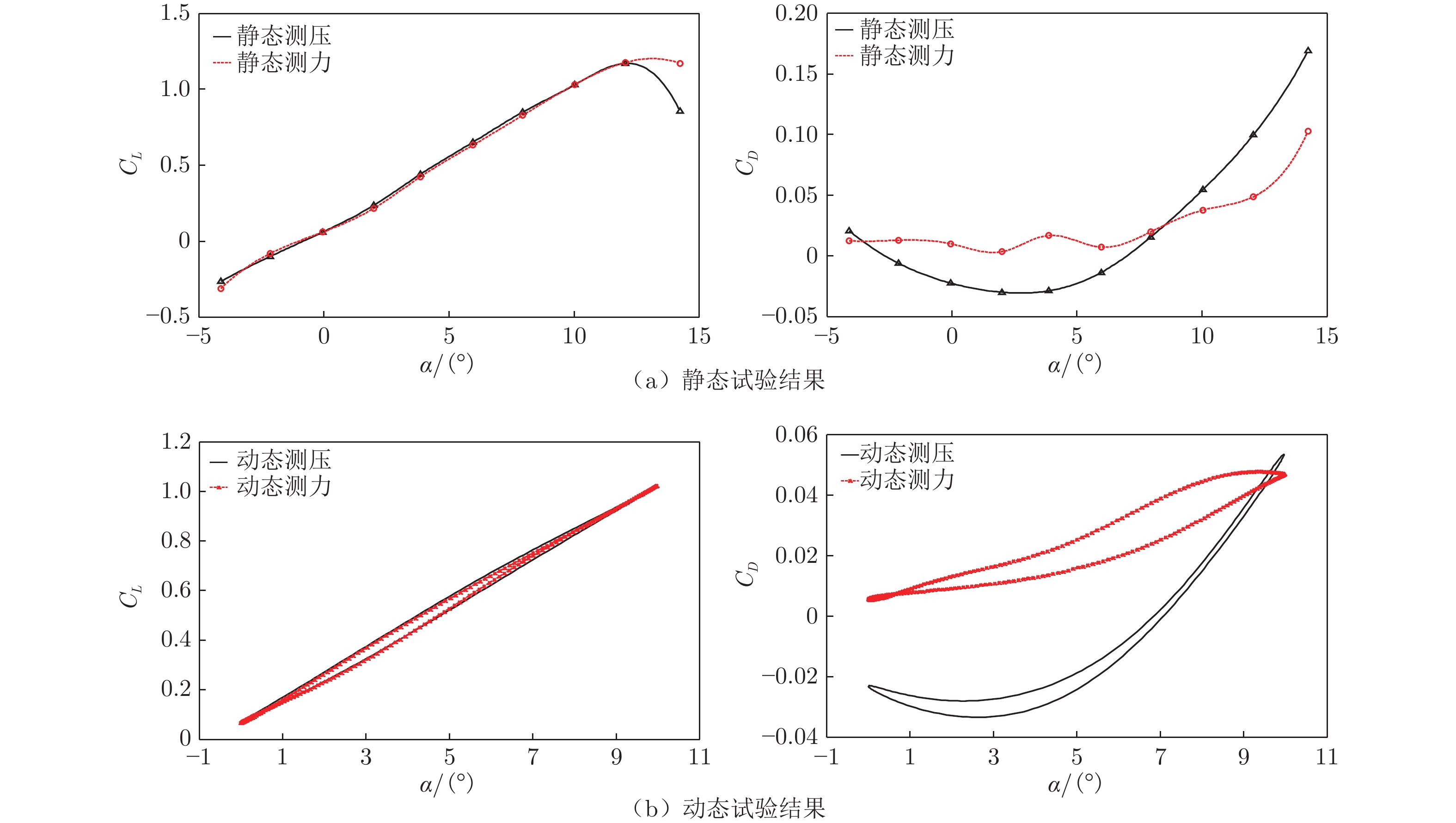
采用双天平两端同步动态测力方式测量翼型的气动载荷，并实现测力测压同步采集，典型试验结果如图19所示（v = 34 m/s、α0 = 5°、α1 = 5°、f = 2 Hz），其中CD为阻力系数。可以看出，测力、测压两种试验手段获得的翼型静态和动态CL～α曲线在失速之前一致性良好，可互相验证和补充。由于测压手段积分得到的CD～α曲线只包含压差阻力，在部分工况下，曲线在小迎角范围（约7°以内）会出现了“负阻力”现象。通过测力手段获得的阻力系数包含了压差阻力和摩擦阻力，则不会出现“负阻力”现象，测量值较为合理。试验综合评估考核了脉动压力测量、双天平测力两种动态数据给定方法，结果表明试验系统及相关测试技术具有较高的可靠性。
![]()
图 19 旋翼翼型静态/动态风洞试验测力结果和测压结果对比Fig. 19 Comparison of static and dynamic wind tunnel test results of rotor airfoil3.2 FL–14低速风洞典型试验结果
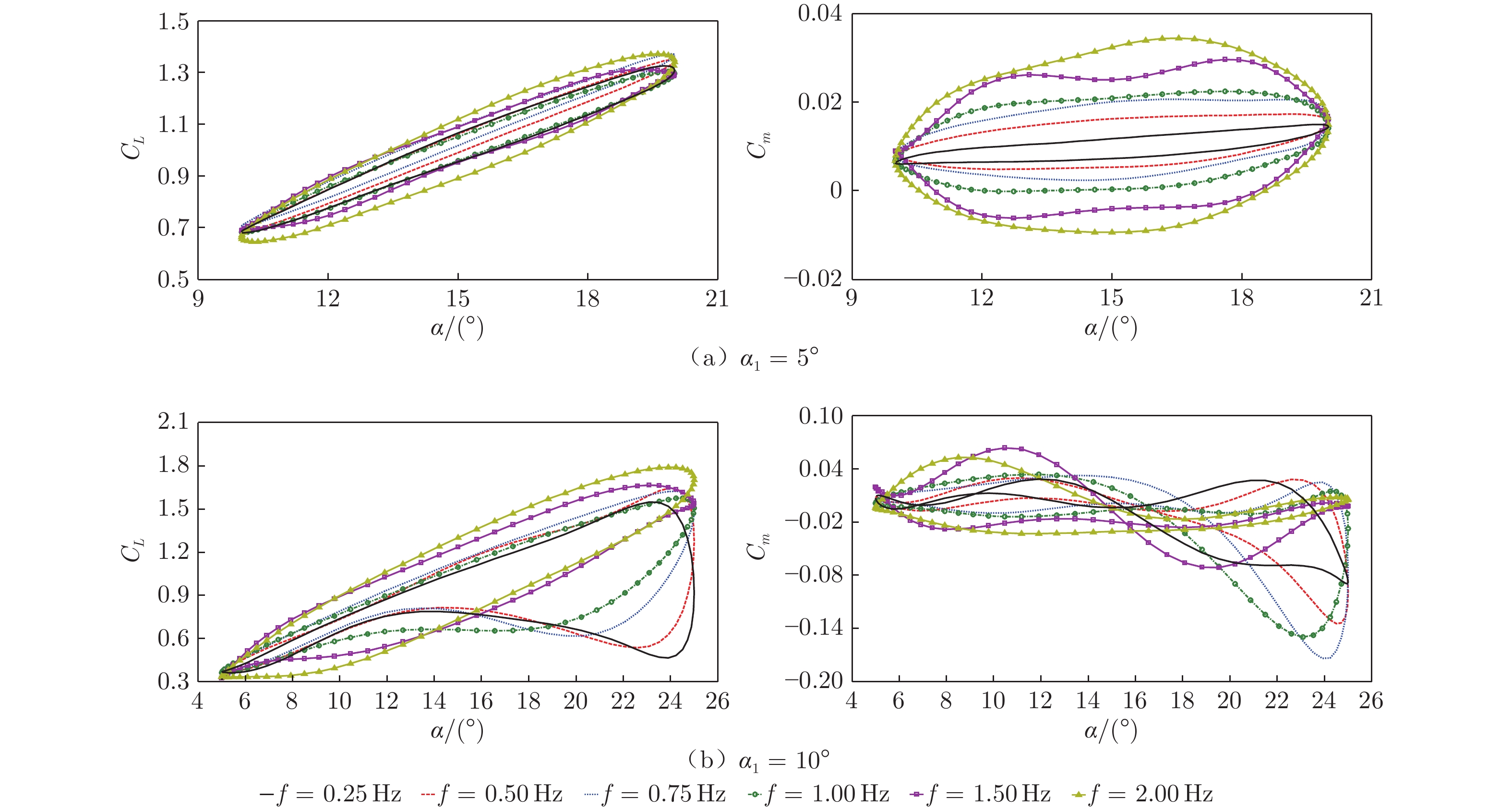
Ma = 0.1、α0 = 15°、变振荡频率（f = 0.25～2.00 Hz，对应k = 0.018～0.148）的试验结果如图20所示。当α1 = 5°时，CL～α、Cm～α迟滞环面积随振荡频率增大而增大；当α1 = 10°时，迟滞环面积及最大升力系数较α1 = 5°时明显增大。
![]()
图 20 变振荡频率的翼型气动曲线Fig. 20 Aerodynamic curve of airfoil with varying oscillation frequency3.3 FL–20连续式跨声速风洞典型试验结果
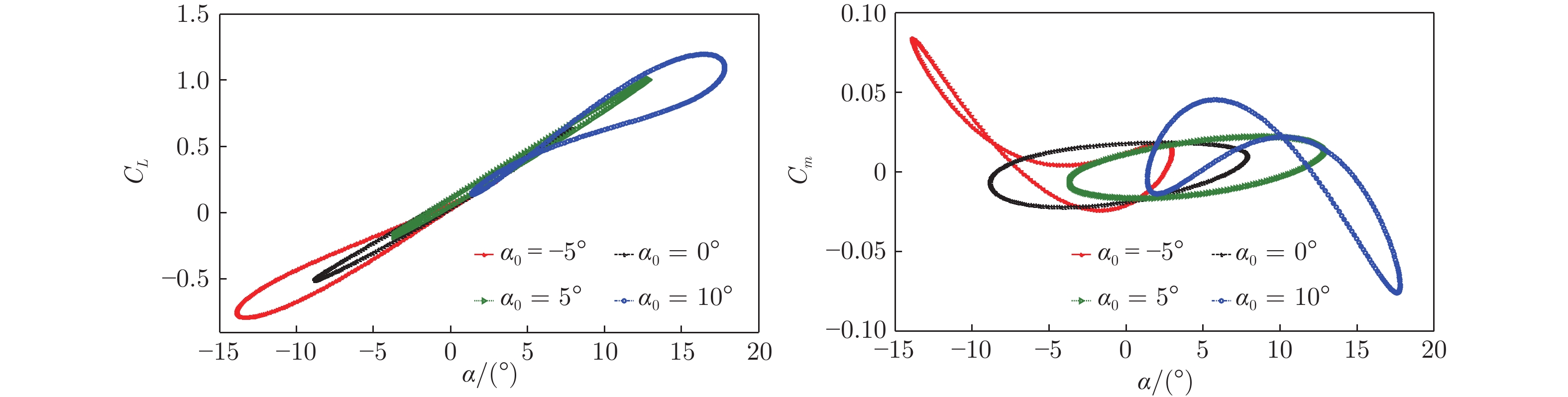
在Ma = 0.3、α1 = 8°、f = 10 Hz（对应k = 0.065）工况下，变平衡迎角（α0 = –5°、0°、5°、10°）试验结果如图21所示。可以看到，CL～α、Cm～α曲线基本以平衡迎角为中点形成迟滞环，随着平衡迎角的增大，翼型的最大升力系数和力矩负峰值均有增大的趋势。迟滞环面积在α0 = 10°时最大，在α0 = –5°时次之。
![]()
图 21 不同平衡迎角下振荡翼型气动曲线Fig. 21 Aerodynamic curves of oscillating airfoil at different balanced angles of attack在Ma = 0.2、α1 = 10°、α0 = 0°工况下，新研制的高频高速动态试验装置的最高振荡频率可达17 Hz（图22（a）），在国际同类试验装置中处于先进水平。为使风洞试验模拟的马赫数和雷诺数接近或达到真实直升机桨叶的相似参数水平，需要在较高马赫数下开展增压试验。在风洞压力2 atm、Ma = 0.6、α1 = 8°、α0 = 5°、f = 10 Hz工况下，雷诺数为5 × 106（图22（b）），达到了真实直升机动态失速桨叶雷诺数范围。
![]()
图 22 高频高速动态试验装置运动能力考核试验结果Fig. 22 Test results of motion ability assessment of high frequency and high speed dynamic test device4 结论与展望
1）基于FL–11低速风洞研制了旋翼翼型俯仰/沉浮两自由度动态试验装置，可实现俯仰/沉浮单自由度或两自由度耦合运动，振荡频率为0～5 Hz，最高试验雷诺数达到3 × 106。
2）基于FL–20连续跨声速风洞研制了旋翼翼型高频高速动态试验装置，最大振荡频率达到17 Hz，最大振幅为10°，最高来流马赫数为0.6，最高试验雷诺数达到5 × 106。
3）基于FL–14低速风洞研制了一套大尺度旋翼翼型动态试验装置，翼型模型弦长为800 mm，最高试验雷诺数达到4 × 106。
4）完善了旋翼翼型动态试验精准测试相关技术，并开展了验证性试验，试验数据规律合理、量值可靠，表明试验系统及相关测试技术具有较高的可靠性。此外，还发展了动态试验模型设计优化、双天平动态测力、同步控制采集参数、动态数据过滤光滑、模型实时位移测量等关键技术。
5）本文研制的 3 套旋翼翼型动态试验装置模拟的参数包线达到了真实直升机的参数要求，可为旋翼翼型动态失速问题研究提供技术支撑，为建立直升机旋翼翼型设计评估技术体系和实现高性能自主翼型研发提供可靠的设备平台和技术保障。
未来还可在以下几个方面开展工作：研制旋翼翼型高阶振荡试验装置，继续完善针对旋翼翼型高阶动态特性的高精准度测试技术，开展翼型小振幅极限环振荡下的非线性气动弹性影响研究，获得旋翼翼型高阶振荡气动阻尼特性，为旋翼桨叶动力学分析和考虑动态特性的翼型气动优化设计提供数据支撑。
-
![]()
图 1 低速风洞两自由度动态试验装置
Fig. 1 Dynamic test device of two degree of freedom in low speed wind tunnel
![]()
图 3 低速风洞动态试验装置控制系统结构
Fig. 3 Control system structure of low speed wind tunnel dynamic test device
![]()
图 4 旋翼翼型高频高速动态试验装置
Fig. 4 High frequency and high speed rotor airfoil dynamic test device
![]()
图 5 大尺度旋翼翼型动态试验装置示意图
Fig. 5 Schematic diagram of dynamic test device for large scale airfoil model
![]()
图 7 FL–14低速风洞旋翼翼型动态试验张线抑振
Fig. 7 Vibration suppression of rotor airfoil dynamic test in FL–14 low-speed wind tunnel
![]()
图 10 旋翼翼型动态风洞试验传感器安装布置示意图
Fig. 10 Installation layout of sensors for dynamic wind tunnel test of rotor airfoil
![]()
图 12 高速风洞动态天平与翼型连接方式
Fig. 12 Connection between dynamic balance and airfoil in high speed wind tunnel
![]()
图 13 低速风洞翼型动态试验天平安装连接图
Fig. 13 Installation and connection diagram of airfoil dynamic test balance in low speed wind tunnel
![]()
图 17 旋翼翼型动态振荡位移变形测量试验照片
Fig. 17 Test photo of oscillation displacement and deformation measurement for rotor airfoil
![]()
图 18 耦合振荡试验频率影响结果对比
Fig. 18 Comparison of frequency influence results of coupled oscillation test
![]()
图 19 旋翼翼型静态/动态风洞试验测力结果和测压结果对比
Fig. 19 Comparison of static and dynamic wind tunnel test results of rotor airfoil
![]()
图 20 变振荡频率的翼型气动曲线
Fig. 20 Aerodynamic curve of airfoil with varying oscillation frequency
![]()
图 21 不同平衡迎角下振荡翼型气动曲线
Fig. 21 Aerodynamic curves of oscillating airfoil at different balanced angles of attack
![]()
图 22 高频高速动态试验装置运动能力考核试验结果
Fig. 22 Test results of motion ability assessment of high frequency and high speed dynamic test device
表 1 国内外主要气动研究机构动态试验模拟能力对比表
Table 1 Comparison of dynamic test simulation capabilities of major international aerodynamic research institutes
风洞名称 模型尺度（弦长）/m 来流马赫数 雷诺数/(105) 振荡幅值 振荡频率/Hz 运动自由度 美国NASA结冰风洞[37] 0.40 0.40（最大） 37 10° 5.0 俯仰 德国荷兰DNW TWG[12] 0.30 0.30～0.50 35 4°～7° 6.6 俯仰 法国ONERA F2[38] 0.50 0.16（常用） 19 10° 5.0 俯仰 俄罗斯TsAGI SVS−2[35] 0.18 0.30～0.60 25 5° 15.0 俯仰 中国南京航空航天大学
非定常风洞[33]0.30 0.10（最大） 7 10° （俯仰）
100 mm （沉浮）4.0（俯仰）
2.0（沉浮）俯仰/沉浮 中国西北工业大学 NF−3[39] 0.70 0.20（最大） 32 15° （俯仰）
100 mm （沉浮）5.0（俯仰）
3.0（沉浮）俯仰/沉浮 中国西北工业大学 NF−6[31] 0.20 0.30 14 10° 8.0 俯仰 中国气动中心 FL−11[40] 0.40 0.20～0.32 30 20° （俯仰）
150 mm （沉浮）6.0（俯仰）
5.0（沉浮）俯仰/沉浮 中国气动中心 FL−14[29] 0.80 0.25（最大） 40 30° 4.0 俯仰 中国气动中心 FL−20[41-42] 0.21 0.20～0.60 50 10° 17.0 俯仰 
下载: 导出CSV
表 2 装置前五阶固有频率
Table 2 The first five order inherent frequency
阶数 固有频率/Hz 1 18.5 2 20.3 3 24.9 4 48.0 5 65.3
下载: 导出CSV
表 3 旋翼翼型动态试验装置技术指标
Table 3 Technical specifications of rotor airfoil dynamic test device
风洞 测试内容 技术指标 FL−11 α −180°～180°，精度0.01°，在线连续可调 h −150～150 mm，精度0.01 mm，在线连续可调 α1 ≤30°，精度0.05°，在线连续可调 h1 ≤150 mm，精度0.05 mm，在线连续可调 fpi、fpl 俯仰0.1～6.0 Hz，沉浮0.1～5.0 Hz，
精度优于0.01 Hz，在线连续可调Rec 3 × 106 FL−20 α1 3°、5°、8°、10°，精度优于0.1° α0 −5°、0°、5°、10°，精度优于0.1° fpi 0.2～17.0 Hz，精度优于0.05 Hz Ma 0.2～0.6 Rec 5 × 106（压力2 atm） FL−14 α −180°～180°，精度0.01°，在线连续可调 α1 ≤30°，精度0.05°，在线连续可调 fpi 0.1～4.0 Hz，精度优于0.01 Hz，在线连续可调 Rec 4 × 106
下载: 导出CSV
表 4 翼型模型结构优化结果
Table 4 Optimization results of airfoil model structure
优化目标 质量/kg 受载最大
等效应力/N最大位移
/mm第一阶固有
频率/Hz失效
指标初始值 12.567 252.15 7.46 56.10 0.728 优化值 8.288 227.16 5.74 63.28 0.319 变化值 4.279 25.34 1.72 7.18 0.409 变化率 34.05 9.91 23.06 12.80 56.18
下载: 导出CSV
表 5 静态测量精准度结果
Table 5 Results of static measurement
俯仰角度 沉浮位移 名义值/(°) 实测值/(°) 名义值/mm 实测值/mm −5 −4.957 −30 −29.946 5 5.046 −15 −15.054 10 9.985 15 15.001 20 20.038 30 29.932
下载: 导出CSV
表 6 俯仰–沉浮两自由度耦合振荡动态测量结果
Table 6 Dynamic measurement results of pitching and plunging coupled oscillation
俯仰角度 沉浮位移 名义值/(°) 实测值/(°) 名义值/mm 实测值/mm 5 4.951
（无吹风）30 30.930
（无吹风）4.964
（吹风，v=34 m/s）31.940
（吹风，v=34 m/s）4.947
（吹风，v=45 m/s）32.882
（吹风，v=45 m/s）
下载: 导出CSV
-
[1] 史勇杰, 厉聪聪, 徐国华. 基于合成射流的旋翼翼型动态失速控制研究[J]. 南京航空航天大学学报, 2020, 52(2): 270–279. SHI Y J, LI C C, XU G H. Rotor airfoil dynamic stall control based on synthetic jet[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2020, 52(2): 270–279.
[2] NEGI P S, HANIFI A, HENNINGSON D S. Unsteady response of natural laminar flow airfoil undergoing small-amplitude pitch oscillations[J]. AIAA Journal, 2021, 59(8): 2868–2877. doi: 10.2514/1.J059743
[3] 马奕扬, 招启军, 赵国庆. 基于后缘小翼的旋翼翼型动态失速控制分析[J]. 航空学报, 2017, 38(3): 127–137. MA Y Y, ZHAO Q J, ZHAO G Q. Dynamic stall control of rotor airfoil via trailing-edge flap[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 127–137.
[4] 喻伯平, 李高华, 谢亮, 等. 基于代理模型的旋翼翼型动态失速优化设计[J]. 浙江大学学报(工学版), 2020, 54(4): 833–842. YU B P, LI G H, XIE L, et al. Dynamic stall optimization design of rotor airfoil based on surrogate model[J]. Journal of Zhejiang University (Engineering Science), 2020, 54(4): 833–842.
[5] QIU Z, WANG F X. Aeroelastic responses of airfoil under dynamic stall forced to oscillate by cyclic pitch input[J]. Journal of Sound and Vibration, 2020, 479: 115366. doi: 10.1016/j.jsv.2020.115366
[6] 戴玉婷, 严慧, 王林鹏. 基于非线性气动力的失速颤振计算与试验研究[J]. 工程力学, 2020, 37(8): 230–236. DOI: 10.6052/j.issn.1000-4750.2019.03.0141 DAI Y T, YAN H, WANG L P. Calculation and experi-mental study of stall flutter based on nonlinear aero-dynamics[J]. Engineering Mechanics, 2020, 37(8): 230–236. doi: 10.6052/j.issn.1000-4750.2019.03.0141
[7] 张庆, 叶正寅. NACA0012翼型跨声速强迫运动非定常气动力模型[J]. 哈尔滨工程大学学报, 2020, 41(11): 1683–1688. ZHANG Q, YE Z Y. Unsteady aerodynamic model of NACA0012 associated with forced oscillations and trans-lations in transonic flight[J]. Journal of Harbin Engineering University, 2020, 41(11): 1683–1688.
[8] 朱呈勇, 王同光. 振荡翼型和振荡来流下的动态失速数值研究[J]. 太阳能学报, 2019, 40(9): 2433–2440. ZHU C Y, WANG T G. Numerical investigation into dynamic stall under pitch oscillation and oscillating free-stream[J]. Acta Energiae Solaris Sinica, 2019, 40(9): 2433–2440.
[9] RAZAVI DEHKORDI M H, SOLTANI M R, DAVARI A R. Statistical analysis on the effect of reduced frequency on the aerodynamic behavior of an airfoil in dynamic physical motions[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 535: 122450. doi: 10.1016/j.physa.2019.122450
[10] CARR L W, CHANDRASEKHARA M S. Compressibility effects on dynamic stall[J]. Progress in Aerospace Sciences, 1996, 32(6): 523–573. doi: 10.1016/0376-0421(95)00009-7
[11] CARR L W. Progress in analysis and prediction of dynamic stall[J]. Journal of Aircraft, 1988, 25(1): 6–17. doi: 10.2514/3.45534
[12] RICHTER K, KOCH S, GARDNER A D, et al. Experi-mental investigation of unsteady transition on a pitching rotor blade airfoil[J]. Journal of the American Helicopter Society, 2014, 59(1): 1–12. doi: 10.4050/jahs.59.012001
[13] GARDNER A D, WOLF C C, RAFFEL M. Review of measurement techniques for unsteady helicopter rotor flows[J]. Progress in Aerospace Sciences, 2019, 111: 100566. doi: 10.1016/j.paerosci.2019.100566
[14] HILLENHERMS C. Experimental investigation of a super-critical airfoil oscillating in pitch at transonic flow[M]. Aachen: Shaker Verlag GmbH, 2003.
[15] MERZ C B, WOLF C C, RICHTER K, et al. Experimental investigation of dynamic stall on a pitching rotor blade tip[C]//Proc of the New Results in Numerical and Experi-mental Fluid Mechanics X. 2016. doi: 10.1007/978-3-319-27279-5_30
[16] AL-JABURI K, FESZTY D, NITZSCHE F. A methodology for simulating 2D shock-induced dynamic stall at flight test-based fluctuating freestream[J]. Chinese Journal of Aero-nautics, 2019, 32(10): 2223–2238. doi: 10.1016/j.cja.2019.05.009
[17] HILLENHERMS C, SCHRÖDER W, LIMBERG W. Experi-mental investigation of a pitching airfoil in transonic flow[J]. Aerospace Science and Technology, 2004, 8(7): 583–590. doi: 10.1016/j.ast.2004.07.001
[18] GARDNER A D, KLEIN C, SACHS W E, et al. Investi-gation of three-dimensional dynamic stall on an airfoil using fast-response pressure-sensitive paint[J]. Experiments in Fluids, 2014, 55(9): 1–14. doi: 10.1007/s00348-014-1807-4
[19] GARDNER A D, RICHTER K. Transition determination on a periodic pitching airfoil using phase averaging of pressure data[C]// Proc of the New Results in Numerical and Experimental Fluid Mechanics X, 2016. doi: 10.1007/978-3-319-27279-5_26
[20] RAFFEL M, KOMPENHANS J, WERNERT P. Investi-gation of the unsteady flow velocity field above an airfoil pitching under deep dynamic stall conditions[J]. Experi-ments in Fluids, 1995, 19(2): 103–111. doi: 10.1007/BF00193856
[21] WANG Q, ZHAO Q J. Experiments on unsteady vortex flowfield of typical rotor airfoils under dynamic stall conditions[J]. Chinese Journal of Aeronautics, 2016, 29(2): 358–374. doi: 10.1016/j.cja.2016.02.013
[22] DAVARI A R. Wake structure and similar behavior of wake profiles downstream of a plunging airfoil[J]. Chinese Journal of Aeronautics, 2017, 30(4): 1281–1293. doi: 10.1016/j.cja.2017.05.007
[23] LI Z Y, FENG L H, KARBASIAN H R, et al. Experimental and numerical investigation of three-dimensional vortex structures of a pitching airfoil at a transitional Reynolds number[J]. Chinese Journal of Aeronautics, 2019, 32(10): 2254–2266. doi: 10.1016/j.cja.2019.04.015
[24] WEI B B, GAO Y W, LI D. Physics of dynamic stall vortex during pitching oscillation of dynamic airfoil[J]. Interna-tional Journal of Aeronautical and Space Sciences, 2021, 22(6): 1263–1277. doi: 10.1007/s42405-021-00389-5
[25] WOOD J N, BREUER M, DE NAYER G. Experimental investigations on the dynamic behavior of a 2-DOF airfoil in the transitional Re number regime based on digital-image correlation measurements[J]. Journal of Fluids and Struc-tures, 2020, 96: 103052. doi: 10.1016/j.jfluidstructs.2020.103052
[26] LI G Q, ZHANG W G, JIANG Y B, et al. Experimental investigation of dynamic stall flow control for wind turbine airfoils using a plasma actuator[J]. Energy, 2019, 185: 90–101. doi: 10.1016/j.energy.2019.07.017
[27] GARDNER A D, RICHTER K, MAI H, et al. Experimental investigation of air jets to control shock-induced dynamic stall[J]. Journal of the American Helicopter Society, 2014, 59(2): 1–11. doi: 10.4050/jahs.59.022003
[28] ZANOTTI A, GIBERTINI G. Experimental assessment of an active L-shaped tab for dynamic stall control[J]. Journal of Fluids and Structures, 2018, 77: 151–169. doi: 10.1016/j.jfluidstructs.2017.11.010
[29] 张卫国, 武杰, 兰波, 等. 旋翼翼型低速风洞静、动态试验技术研究[C]// 中国力学大会论文集. 2015. ZHANG W G, Wu J, Lan B, et al. Experimental techniques for low speed static and dynamic test of rotor airfoil[C]// Proc of the Chinese Mechanics Conference. 2015.
[30] GAO Y W, ZHU Q L, WANG L. Measurement of unsteady transition on a pitching airfoil using dynamic pressure sensors[J]. Journal of Mechanical Science and Technology, 2016, 30(10): 4571–4578. doi: 10.1007/s12206-016-0928-5
[31] 王莹, 高超, 吕哲. 跨声速风洞翼型动态失速试验系统研制[J]. 科学技术与工程, 2018, 18(32): 95–103. DOI: 10.3969/j.issn.1671-1815.2018.32.016 WANG Y, GAO C, LÜ Z. The development of airfoil dynamic stall experiment system in a transonic wind tunnel[J]. Science Technology and Engineering, 2018, 18(32): 95–103. doi: 10.3969/j.issn.1671-1815.2018.32.016
[32] 许和勇, 邢世龙, 叶正寅, 等. 基于充气前缘技术的旋翼翼型动态失速抑制[J]. 航空学报, 2017, 38(6): 86–98. XU H Y, XING S L, YE Z Y, et al. Dynamic stall suppression for rotor airfoil based on inflatable leading edge technology[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(6): 86–98.
[33] 史志伟. 非定常自由来流对模型动态气动特性影响的实验研究[D]. 南京: 南京航空航天大学, 2006. SHI Z W. Experimental research of oscillating free-stream effects on dynamic characteristics of wind tunnel models[D]. Nanjing: Nanjing University of Aeronautics and Astronau-tics, 2006.
[34] WANG Q, ZHAO Q J. Unsteady aerodynamic charac-teristics investigation of rotor airfoil under variational freestream velocity[J]. Aerospace Science and Technology, 2016, 58: 82–91. doi: 10.1016/j.ast.2016.08.001
[35] 林永峰, 黄建萍, 黄水林, 等. 直升机旋翼翼型动态失速特性试验研究[J]. 航空科学技术, 2012, 23(4): 25–28. LIN Y F, HUANG J P, HUANG S L, et al. Experimental investigation of rotor airfoil dynamic stall characteristics[J]. Aeronautical Science & Technology, 2012, 23(4): 25–28.
[36] WANG Q, ZHAO Q J, WU Q. Aerodynamic shape optimization for alleviating dynamic stall characteristics of helicopter rotor airfoil[J]. Chinese Journal of Aeronautics, 2015, 28(2): 346–356. doi: 10.1016/j.cja.2014.12.033
[37] REINERT T, FLEMMING R J, NARDUCCI R, et al. Oscillating airfoil icing tests in the NASA Glenn research center icing research tunnel[C]//Proc of the SAE Technical Paper Series, 400 Commonwealth Drive. 2011. doi: 10.4271/2011-38-0016
[38] PAPE A L, PAILHAS G, DAVID F, et al. Extensive wind tunnel tests measurements of dynamic stall phenomenon for the OA209 airfoil including 3D effects[C]//Proc of the 33st European Rotor Forum. 2007.
[39] 惠增宏, 谭森林, 高永卫, 等. 一种低速旋翼翼型动态试验驱动机构: 中国, CN109752164B[P]. 2019-11-01. HUI Z H, TAN S L, GAO Y W, et al. Low-speed rotor-wing type dynamic test driving mechanism: China, CN10975-2164B[P]. 2019-11-01.
[40] 张卫国, 李国强, 孔鹏, 等. 一种翼型两自由度动态风洞试验装置: 中国, CN108844711A[P]. 2018-11-20. ZHANG W G, LI G Q, KONG P, et al. Airfoil profile two-freedom dynamic wind tunnel testing device: China, CN108844711A[P]. 2018-11-20.
[41] 张卫国, 李国强, 康洪铭, 等. 一种翼型高速风洞动态试验装置: 中国, CN109632249A[P]. 2019-04-16. ZHANG W G, LI G Q, KANG H M, et al. Airfoil high speed wind tunnel dynamic test device: China, CN-109632249A[P]. 2019-04-16.
[42] 李国强, 赵亮亮, 张卫国, 等. 一种翼型高速风洞双天平动态测力装置及方法: 中国, CN109682568A[P]. 2019-04-26. LI G Q, ZHAO L L, ZHANG W G, et al. Airfoil high-speed wind-tunnel double-balance dynamic force measuring device and method: China, CN109682568A[P]. 2019-04-26.
[43] WANG X, WANG X N, REN X B, et al. Effects of tube system and data correction for fluctuating pressure test in wind tunnel[J]. Chinese Journal of Aeronautics, 2018, 31(4): 710–718. doi: 10.1016/j.cja.2018.01.021
-
期刊类型引用(1)
1. 李国强，赵鑫海，易仕和，宋奎辉，赵光银. 旋翼动态失速与反流流动控制研究进展. 实验流体力学. 2023(04): 29-47 . 
本站查看
其他类型引用(0)
计量
- 文章访问数: 366
- HTML全文浏览量: 305
- PDF下载量: 89
- 被引次数: 1
