Free oscillation dynamic derivative test technology of a short-blunt shape vehicle
-
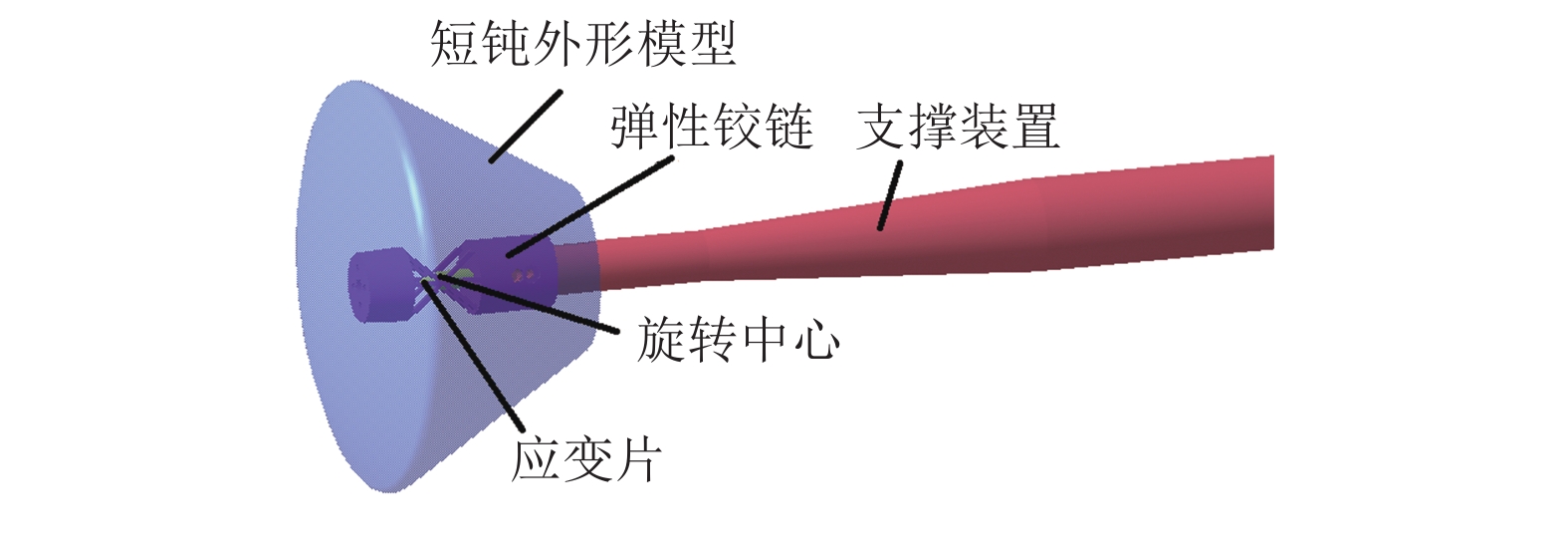
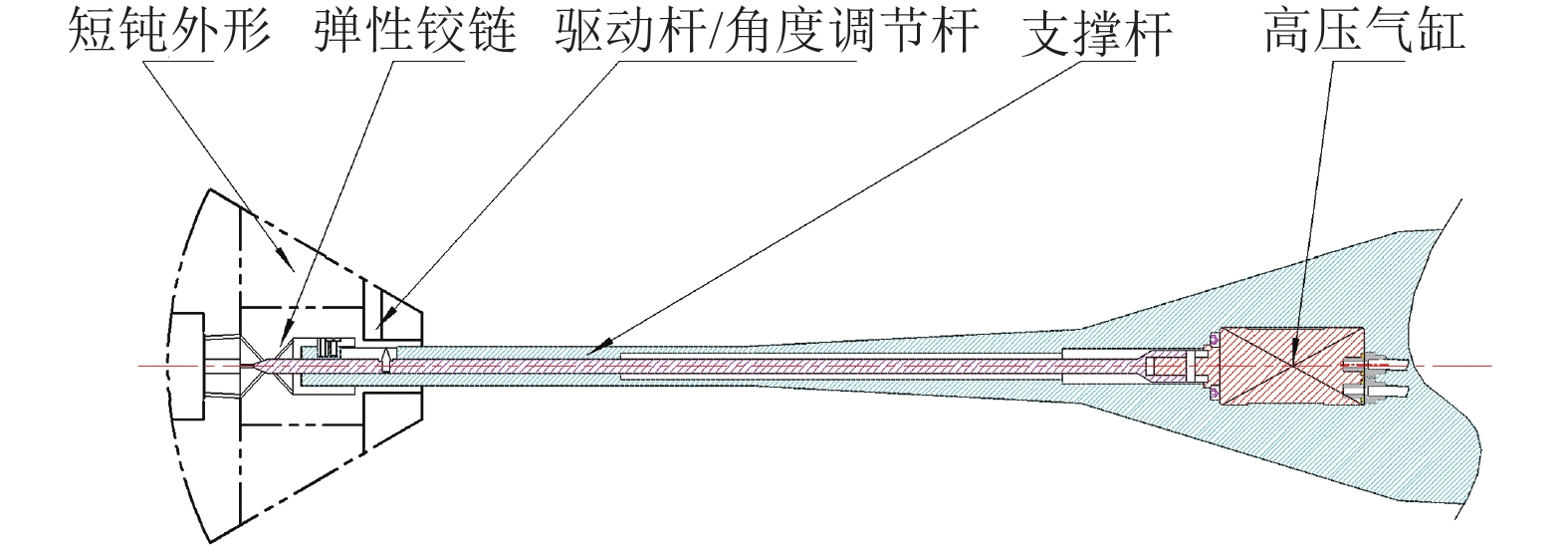
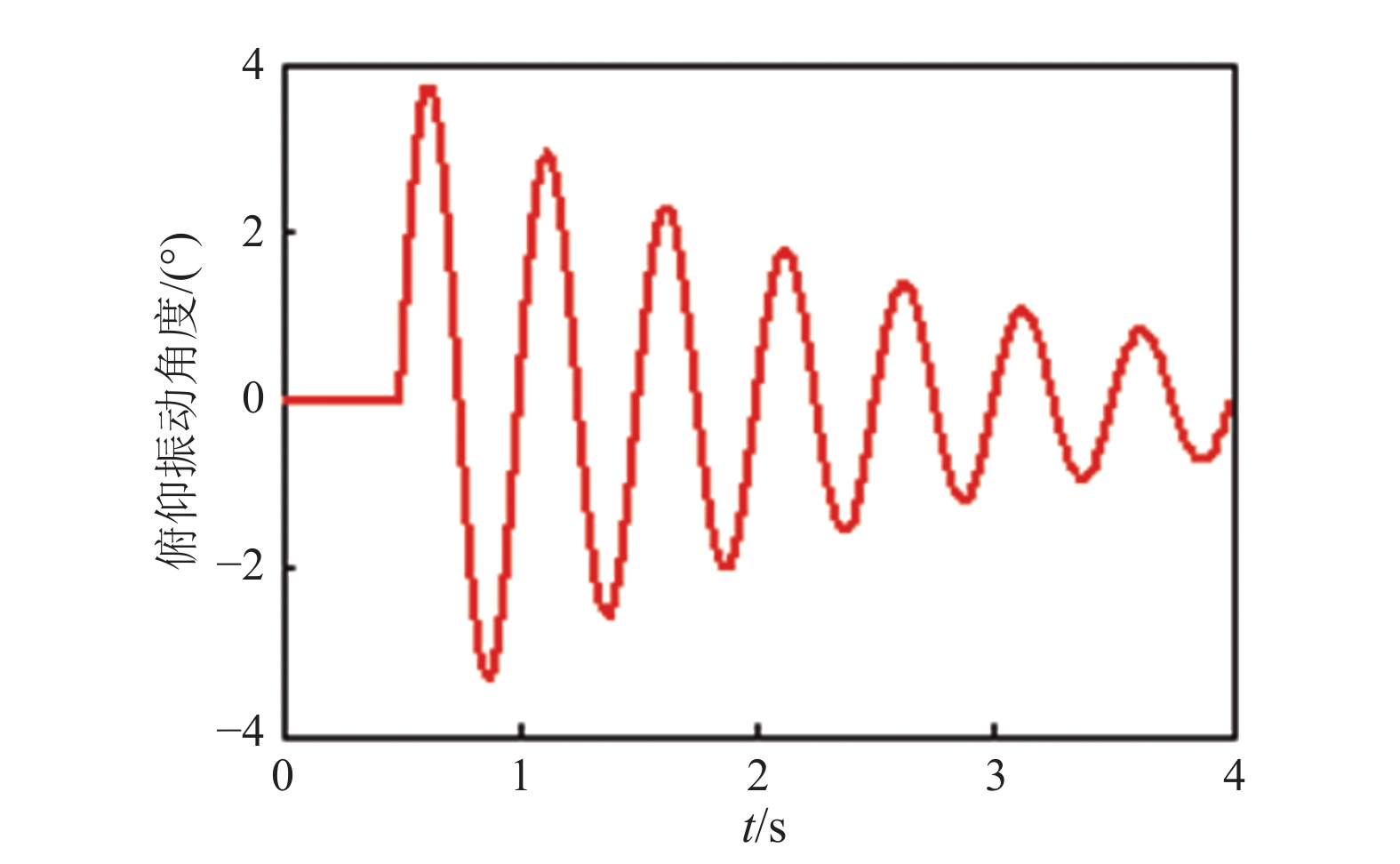
摘要: 为研究短钝外形飞行器的动稳定特性，基于自由振动动导数试验方法在1.2 m量级亚跨超声速风洞中建立了动导数测量试验技术。通过新设计的弹性铰链和轴承铰链解决了短钝外形飞行器弹性支撑和低频振动模拟问题。利用新建立的试验装置研究了马赫数、迎角、减缩频率对动稳定特性的影响。在短钝外形飞行器气动力特点下，新设计的弹性铰链能够满足模型支撑和振动需要，轴承铰链的支撑方式可以在风洞中模拟接近实际减缩频率的振动。在亚跨超声速风洞中完成了某短钝外形飞行器俯仰动导数的测量，获取了俯仰动不稳定状态点，为此类飞行器的动稳定特性研究提供了试验基础。Abstract: In order to study the dynamic stability characteristics of the short-blunt shape vehicle, the free oscillation dynamic derivative test method is used to establish the dynamic derivative measurement test technology in the 1.2 m trisonic wind tunnel. The newly designed elastic hinges and bearing hinges solve the problem of elastic support and low-frequency oscillation simulation of the short-blunt shape vehicle, and the newly established test device is used to study the influence of the Mach number, angle of attack, reduced frequency, and shape on dynamic stability characteristics. The newly designed elastic hinge can meet the model support and oscillation requirement under the aerodynamic characteristic condition of the short-blunt shape vehicle in the wind tunnel, and the bearing hinge support can simulate the oscillation frequency close to the actual reduced frequency in the wind tunnel. In the trisonic wind tunnel, the measurement of the pitch derivative of a short-blunt shaped vehicle was completed, and the unstable state points of the pitching were obtained, which provides experimental support for future research on the dynamic stability characteristics of this type of vehicle.
-
0 引言
流体壁面剪应力的精确测量是流体力学领域的难题[1]。随着MEMS技术的发展，硅基[2-3]和柔性聚合物基[4]的壁面剪应力微传感器研究发展受到重视，而传感器标定是其测量的基础和前提。根据不同应用需求初步形成了不同类型的动、静态壁面剪应力标定方法和装置[5-9]。本文介绍了平板流动、管道流动和旋转流动等静态标定方法，以及平面波振动、阶梯圆盘旋转运动等动态标定方法，介绍了工作原理和典型结构装置，可为壁面剪应力传感器标定方法的选定提供参考。
1 壁面剪应力静态标定方法
壁面剪应力传感器的静态标定需要施加稳定已知量值的剪应力，读取对应输出。采用流体力学经典模型，通过测量其他物理量从而换算得到对应壁面剪应力值是常用方法。由于之前长期缺乏有效的流体壁面剪应力传感器，相关标定研究不系统，尚未形成统一的标准[10-11]。
目前，常见标定方法主要有平板模型标定法、管道流动标定法[12]和旋转运动标定法[13]。
1.1 平板模型标定法
早在20世纪上叶就有学者和机构对平板模型边界层进行了大量理论和实验研究，并得到平板表面层流和湍流边界层壁面剪应力的理论计算模型。
在空气中，均匀来流绕过一个厚度很薄的平板时，如果平板迎角为0，可以应用普朗特边界层微分方程解决粘性流动问题，平板边界层如图 1所示[14]。
理论上，由于平板绕流压强顺流不变，即
(1) 式中：μ表示流体的动力粘度，ν表示流体的运动粘度，U∞表示平板前端均匀来流流速，x表示距平板前缘的距离。
随着来流速度增大，雷诺数也将增大。当平板表面雷诺数大于临界雷诺数，绕流场可能由层流状态转变为湍流[15]，如图 2所示。
通过动量积分方程可以得到湍流边界层中壁面剪应力的计算公式：
(2) 式中：xt为湍流边界层前沿到测量点的距离，ρ为空气密度，δ2为动量厚度，可通过下式计算得到：
(3) 通过确定测量点到转捩位置的距离xt，就可以得到来流速度U∞与剪应力τ的函数关系。
由于平板表面发生转捩的位置不易测得，常常采用强制转捩的方法获得全湍流状态的平板边界层。Tani对转捩带粗糙体高度进行了研究，并得出粗糙体的极限高度计算公式[16]：
(4) 式中：k′ crit为粗糙体的极限高度。
平板模型标定法能产生数百帕量级的壁面剪应力，标定精度受风洞 (或水道) 来流速度测量误差、测试点距前缘距离测量误差及环境温度测量误差等因素的影响。然而，平板边界层的流场状态不易控制，可结合实验方法 (如升华法、油流法等) 初步判断平板表面流动转捩与分离情况。
1.2 管道流动标定法
管道流动因其运动受到管壁约束，管道内的流动参数 (如流量、温度和壁面静压等) 较易测量，也是常见的剪应力标定方法。
1.2.1 管道流动动量损失标定法
当方形管道的宽高比较大时[17]，入口处来流稳定的通道内流体运动可近似为二维流动。管道内流体的动量平衡与壁面剪应力作用相关[18]。通过测量管壁沿程压力损失，可以得到壁面剪应力的大小，标定装置如图 3所示。
定义pinlet/poutlet为管道内入口处压力和出口处压力的比值。对于压力比pinlet/poutlet≤1.1，可忽略管道内流体的压缩性，完全发展的不可压缩层流管道内的压力分布是线性的，剪应力表达式可以简单表示为：
(5) 式中：h为管道高度，
马赫数大于0.3的流动问题要考虑流体压缩性。对于压力比pinlet/poutlet≥1.1，管道内压力分布不再是线性变化[19]。通过非线性压力Π=p(x)/poutlet与非线性距离X之间的关系，代入公式 (5) 可以得到大压力比下的管道剪应力计算公式：
(6) 式中:Lc为管道的长度，poutlet为管道出口处的压力，X为沿管道方向x位置与管道长度Lc的比值。常数a和b能够从Π2=aX+b的曲线计算得到[20]。
1997年，美国麻省理工学院研发了一种基于动量损失原理的空气介质剪应力标定装置[21]，量程0~1Pa，如图 5所示。在微型气槽内壁面开凿压力检测孔，由于流体在槽腔运动产生摩擦阻力引起流体动量的损失，导致沿气流运动方向有着不同的壁面压力分布，换算可得压差中点剪应力值。此外，还考虑了空气压缩性，给出了不同压差范围的剪应力计算方法并用此装置对自主研发的浮动元件式剪应力传感器进行了标定。
2002年，美国凯斯西储大学Patel等在研究壁面剪应力传感器时采用了此原理搭建起一套小型的扁平管道标定装置，并对浮动式剪应力传感器进行了标定，标定最大剪应力达到80Pa[18]。
2015年，中国空气动力研究与发展中心李建强等研究建立了管道流动动量损失原理的空气介质剪应力标定装置，增设了精密温控系统，可实现从环境温度到55℃的温度控制[22]。
2014年，中国船舶科学研究中心建立了水介质的动量损失管流标定装置，并利用LDV、PIV等对MEMS热膜剪应力传感器进行了测试标定[7]。
1.2.2 微型层流管道标定法
流体在通过极低雷诺数的微型扁薄矩形水道 (具有较大宽高比w/h)，可获得可控的槽内纯剪切流[23]，如图 6所示。
当管道内的流场形态为均匀层流时，其速度剖面曲线为二次曲线，管道体积流量Q与流动中心处最大流速相关，根据二维定常流动流体壁面剪应力的定义式[24]，可以导出管道内壁面剪应力与体积流量之间的关系：
(7) 因矩形通道横截面宽度w无法实现远大于截面高度h，在剪应力计算时引入矩形通道的形状修正因子
(8) 式中：Dh为水力学半径，
Φ(n) 为矩形通道的修正因子，该修正因子的引入可降低扁薄矩形水道侧壁对中心流速的影响效应[17],
(9) 2005年，美国加州理工学院的Xu Y.等人根据该流动原理搭建起适用于MEMS剪应力传感器标定的微型管道测试平台，管道高度仅0.3mm，并实现对传感器0~5Pa范围内的剪应力标定[23]。
2009年，中国西北工业大学依此原理建立了微型扁薄标定水槽。2014年，李雁冰等根据该装置原理，对恒流驱动的热膜剪应力传感器进行了水下标定实验[25]，并给出标定模型。王雷涛、严宇超等增加了溢流系统和温度控制系统，并对系统误差进行了分析。
1.3 旋转运动标定法
平板模型和管道流动标定装置均需要有气源或者水压动力源作为介质流动的动力，尤其搭建专门风洞较为困难，因此有研究者采用圆盘或者圆筒的旋转运动带动周边流场流动从而形成一定的壁面剪切应力。
2004年，美国国家航空航天局 (NASA) Zuckerwar等采用旋转圆轮建立了标定装置[26]，如图 8所示。1个电机速度可控的圆形旋转轮和1个与其同轴心的固定圆弧槽，传感器平齐安装在槽上且靠近轮的边缘。当旋转圆轮与传感器之间的间隙h极小时，圆轮与圆弧槽间的流体形成简单库艾特流动，产生的剪应力为：
(10) 式中：r为轮子半径，ω为电机带动的旋转轮的转速，通过调节转速的大小可以获得需要的剪应力。
Zuckerwar通过对圆轮的精确安装，控制圆轮和同轴圆弧槽之间的缝隙最小达50μm，实现最大发生剪应力达到234.49Pa。
1992年，美国麻省理工学院的Shajii J[27]等采用锥板式[28-30]的剪应力标定装置对浮动式剪应力传感器标定进行过相关研究，如图 9(a)所示。2006年，韩国浦项科技大学机械工程系的Kim[31]等采用2个平行放置的圆盘建立了壁面剪应力标定装置，如图 9(b)所示，并对热膜剪应力传感器实现0~0.8Pa范围内的标定。另外，美国加州理工学院的Brown G. L.[32]等采用圆筒式粘度计[33-34]的构造，如图 9(c)所示，搭建了剪应力标定装置。2012年，日本名古屋大学的Terashima O.[35]等对圆筒剪应力发生装置进行了改进，将外圆筒改为平板，如图 9(d)所示，更便于传感器的安装。
![]()
图 9 (a) 锥板式标定装置原理图; (b) 静态标定的圆盘示意图; (c) 圆筒式旋转黏度计测量原理; (d) 旋转圆筒-平板标定法示意图Fig. 9 (a) Cone-plate wall shear stress calibration device. (b) Disk static calibration device.(c) Coaxial cylinder viscometers measurement device. (d) Rotating cylinder-plat wall shear stress calibration device旋转运动剪应力标定装置的搭建较为简单，但要保证产生剪应力的精度，对旋转装置偏心度要求较高，且若要产生较大范围的剪应力，圆盘或圆筒的直径和旋转速度要求很大。通常，此类方法仅用于0~2Pa范围内的剪应力标定。此外，该标定方法流场状态复杂，主要是利用其平均效应。
2 动态剪应力标定方法
动态剪应力标定需要加载一个周期性变化的剪应力。通常动态标定是为了研究传感器在中频或者高频激励下的响应情况，因此需要动态标定装置能产生较高频率的激励信号。
2.1 平波管标定方法
平波管实现动态测量原理为用扬声器产生声波，声波驱动流体产生动态剪应力信号，利用麦克风测量产生信号的频率实现对剪应力传感器的动态测量。管道尾部加入消声装置以消除回声对测量的影响。
2000年，美国佛罗里达大学的Chandrasekaran等建立了以平面声波驱动的动态剪应力标定装置，如图 10所示，该装置可产生最大0.1Pa，频率范围100Hz到20kHz的动态剪应力信号，如图 11所示。利用该装置对带有隔热空腔的硅基热敏传感器进行了动态测试[9]。
![]()
图 10 佛罗里达大学动态标定装置示意图Fig. 10 Dynamic wall shear stress calibration device designed by university of Florida![]()
图 11 佛罗里达大学动态标定装置在恒定振幅激励下的频率响应Fig. 11 Plot of the frequency response of the PWT for constant voltage amplitude of speaker excitation2001年，美国麻省理工学院的Sheplak等采用相同原理的平波管动态标定装置，并对浮动式剪应力传感器动态性能进行了标定测试[11]。
平面声波将引起振荡的压力梯度，通过测量压力波动，可以换算得到壁面动态变化的剪应力[11]：
(11) 式中：p′为压力波动的幅值。
2.2 圆盘动态标定法
2006年，韩国浦项科技大学机械工程系的Kim等在研究静态圆盘旋转标定法的同时对转动圆盘进行了改造，采用阶梯式转动圆盘，得到最高激励频率400Hz动态变化的剪应力，其结构如图 12所示。阶梯厚度为δh，2个圆盘的间隙的改变为
3 结论
介绍了国内外流体壁面剪应力标定方法及其原理和装置。通过对比分析，可以得到以下几点启示：
(1) 采用平板模型标定方法可以依托现成风洞或者水道，可以获得较大发生范围的剪应力 (从0帕到上百帕)，实验系统可以适配多种类型的剪应力传感器；
(2) 微型管道流槽标定是一种紧凑便捷的专用标定装置，截面尺寸及雷诺数很小，水槽高度经常在毫米级以下 (百微米量级)。发生的剪应力范围通常在10Pa以内；
(3) 动量损失剪应力标定装置也属于专用定制，使用比较方便，剪应力发生范围极大 (可达上百帕)；
(4) 旋转运动标定方法的装置较易搭建，对机械装置及装配等精度要求较高，发生的剪应力范围较小，其流场状态复杂，主要取用平均效应；
(5) 动态标定方法中研究及使用较多的是平波管法。
综上，可根据各类流体壁面剪应力传感器的工作要求、尺寸、安装条件 (贴附面为平面或曲面、安装高度等) 和应用环境的不同，选用不同的标定方法或装置。
目前，不同标定方法流场状态及品质影响，误差和不确定度及精度分析等研究较少，尚需关注。
-
![]()
图 7 轴承铰链低频振动信号模拟
Fig. 7 Simulation of low frequency oscillation signal of bearing hinge
![]()
图 12 典型俯仰振动发散曲线和收敛曲线
Fig. 12 Typical pitch oscillation divergence curve and convergence curve
![]()
图 14 减缩频率对俯仰动导数的影响
Fig. 14 The effect of reducing frequency on pitch dynamic derivative
表 1 典型的短钝外形模型风洞试验载荷
Table 1 Typical wind tunnel test load of short-blunt shape model
单元 轴向力
X/N法向力
Y/N俯仰力矩
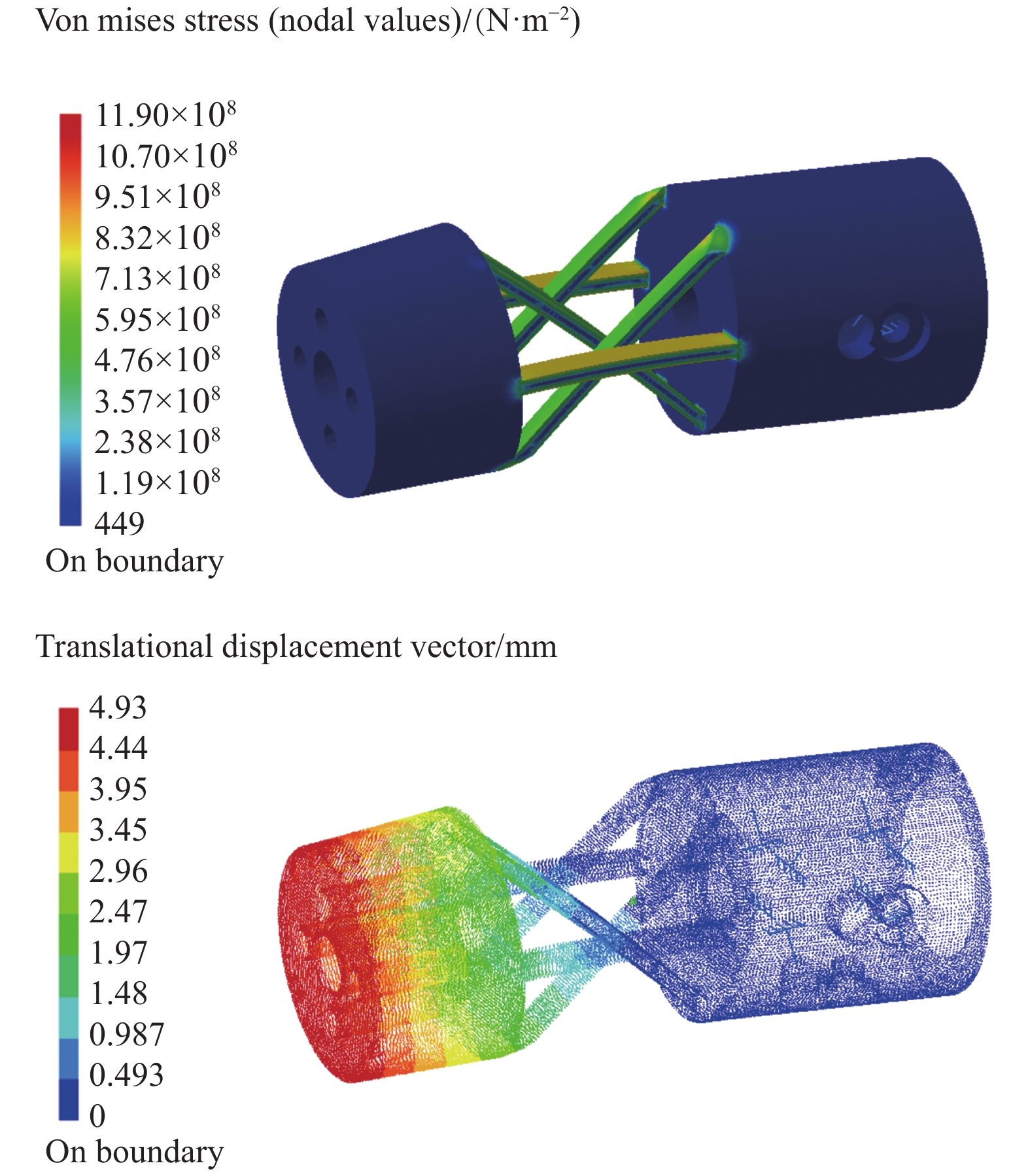
Mz / (N·m)最大载荷 3000 100 6 
下载: 导出CSV
表 2 不同梁厚度下的刚度、应力、变形角
Table 2 Stiffness, stress and deformation angle under different beam thickness
梁厚度/
mm刚度/
（N·m·rad–1）最大应力/
MPa最大理论变形角/（°） δ 16.06 2317.0 21.69 δ+0.25 30.64 1608.0 11.29 δ+0.50 54.46 1158.0 6.68 δ+0.75 77.48 917.4 4.44 δ+1.00 110.99 650.7 2.92 δ+1.25 221.56 434.4 1.55
下载: 导出CSV
表 3 三次重复性试验结果
Table 3 Results of three repeated tests
试验理论迎角 0° 2° 5° 8° 10° Test 1 –0.3936 –0.3355 –0.3936 –0.4126 –0.5197 Test 2 –0.3415 –0.3768 –0.4115 –0.3575 –0.5685 Test 3 –0.3858 –0.3526 –0.3795 –0.3988 –0.5865 均值 –0.3736 –0.3550 –0.3949 –0.3896 –0.5582 标准差 0.0281 0.0208 0.0160 0.0287 0.0346
下载: 导出CSV
-
[1] WAY D W, POWELL R W, CHEN A, et al. Mars science laboratory: entry, descent, and landing system performance[C]//Proc of the 2007 IEEE Aerospace Conference. 2007. doi: 10.1109/AERO.2007.352821
[2] REICHENAU D E A. Aerodynamic characteristics of disk-gap-band parachutes in the wake of Viking entry forebodies at Mach numbers from 0.2 to 2.6[R]. AEDC-TR-72-78, 1972. doi: 10.21236/ad0746291
[3] Petrick D, Davis B, Peregino P, et al. An experimental approach to determine the flight dynamics of NASA's Mars Science Lab Capsule[R]. ARL-TR-6790, 2017.
[4] EDQUIST K T, HOLLIS B R. Mars science laboratory heatshield aerothermodynamics: design and reconstruction [R]. AIAA 2013-2781, 2013. doi: 10.2514/6.2013-2781
[5] ALKANDRY H, BOYD I, REED E, et al. Numerical study of hypersonic wind tunnel experiments for Mars entry aeroshells[R]. AIAA 2009-3918, 2009. doi: 10.2514/6.2009-3918
[6] YOSHINAGA T,TATE A,WATANABE M,et al. Orbital re-entry experiment vehicle ground and flight dynamic test results comparison[J]. Journal of Spacecraft and Rockets,1996,33(5):635-642. doi: 10.2514/3.26813
[7] 赵梦熊. 载人飞船返回舱的再入气动环境[J]. 气动实验与测量控制,1995,9(4):1-7. ZHAO M X. The aerodynamic and aerothermodynamic circumstances of capsule type re-entry vehicle[J]. Aerodynamic Experiment and Measurement & Control,1995,9(4):1-7.
[8] 赵梦熊. 载人飞船返回舱的动稳定性[J]. 气动实验与测量控制,1995,9(2):1-8. ZHAO M X. The dynamic stability characteristics of capsule type Re-entry vehicles[J]. Aerodynamic Experiment and Measurement & Control,1995,9(2):1-8.
[9] 方方. 神舟飞船返回舱气动设计综述[J]. 航天器工程,2004,13(1):124-131. doi: 10.2514/3.26813 [10] 马洋,张青斌,丰志伟. 大气环境对火星探测器气动特性影响分析[J]. 航天返回与遥感,2016,37(2):18-25. DOI: 10.3969/j.issn.1009-8518.2016.02.003 MA Y,ZHANG Q B,FENG Z W. Influence of atmosphere condition on aerodynamic characteristics of Mars probe[J]. Spacecraft Recovery & Remote Sensing,2016,37(2):18-25. doi: 10.3969/j.issn.1009-8518.2016.02.003
[11] 何开锋,和争春. 飞船返回舱跨声速全局稳定性研究[J]. 飞行力学,1999,17(3):34-38. DOI: 10.3969/j.issn.1002-0853.1999.03.007 HE K F,HE Z C. The global stability analysis of reentry capsule transonic flight[J]. Flight Dynamics,1999,17(3):34-38. doi: 10.3969/j.issn.1002-0853.1999.03.007
[12] 宋玉辉,陈农,秦永明. 亚跨超声速返回舱动稳定特性[J]. 航天返回与遥感,2014,35(2):31-38. DOI: 10.3969/j.issn.1009-8518.2014.02.005 SONG Y H,CHEN N,QIN Y M. Sub-, trans- and super-sonic dynamic stability characteristics for reentry capsule[J]. Spacecraft Recovery & Remote Sensing,2014,35(2):31-38. doi: 10.3969/j.issn.1009-8518.2014.02.005
[13] 刘伟,赵海洋,杨小亮. 返回舱动态稳定性分析及被动控制方法研究[J]. 中国科学G辑,2010,40(9):1156-1164. LIU W,ZHAO H Y,YANG X L. Analysis of dynamic stability and research of passive control method for capsule[J]. Science in China (Series G),2010,40(9):1156-1164.
[14] 张涵信,袁先旭,叶友达,等. 飞船返回舱俯仰振荡的动态稳定性研究[J]. 空气动力学学报,2002,20(3):247-259. DOI: 10.3969/j.issn.0258-1825.2002.03.001 ZHANG H X,YUAN X X,YE Y D,et al. Research on the dynamic stability of an orbital reentry vehicle in pitching[J]. Acta Aerodynamica Sinica,2002,20(3):247-259. doi: 10.3969/j.issn.0258-1825.2002.03.001
[15] 杨在山. 载人飞船返回舱的气动特性分析与外形设计[J]. 气动实验与测量控制,1996,10(4):12-18. YANG Z S. The configuration and aerodynamic characteristics of manned re-entry capsules[J]. Aerodynamic Experiment and Measurement & Control,1996,10(4):12-18.
[16] 贾区耀, 陈农, 杨益农, 等. 返回舱跨声速动稳定特性[C]//近代空气动力学研讨会论文集. 2005: 182-187. [17] 梁杰,李志辉,李齐,等. 返回舱再入跨流域气动及配平特性数值研究[J]. 空气动力学学报,2018,36(5):848-855. DOI: 10.7638/kqdlxxb-2018.0128 LIANG J,LI Z H,LI Q,et al. Numerical simulation of aerodynamic and trim characteristics across different flow regimes for reentry module[J]. Acta Aerodynamica Sinica,2018,36(5):848-855. doi: 10.7638/kqdlxxb-2018.0128
[18] 宋威,艾邦成,蒋增辉,等. 返回舱跨声速自由飞行的静动稳定性[J]. 实验流体力学,2019,33(4):89-94. DOI: 10.11729/syltlx20180083 SONG W,AI B C,JIANG Z H,et al. Free flight static and dynamic aerodynamic characteristics for re-entry capsule at transonic speed[J]. Journal of Experiments in Fluid Mechanics,2019,33(4):89-94. doi: 10.11729/syltlx20180083
[19] 周伟江. 返回舱自由振动跨声速非定常流场数值模拟[J]. 空气动力学学报,2000,18(1):46-51. DOI: 10.3969/j.issn.0258-1825.2000.01.007 ZHOU W J. Numerical simulation of unsteady transonic flow around a free oscillating reentry vehicle[J]. Acta Aerodynamica Sinica,2000,18(1):46-51. doi: 10.3969/j.issn.0258-1825.2000.01.007
[20] 胡静,宋玉辉,陈农,等. 返回舱动稳定特性风洞试验的影响参数[J]. 航天返回与遥感,2013,34(5):14-19. DOI: 10.3969/j.issn.1009-8518.2013.05.003 HU J,SONG Y H,CHEN N,et al. Study of key parameters for dynamic stability of reentry capsule[J]. Spacecraft Recovery & Remote Sensing,2013,34(5):14-19. doi: 10.3969/j.issn.1009-8518.2013.05.003
[21] 范洁川. 风洞试验手册[M]. 北京: 航空工业出版社, 2002: 430-440. [22] USELTEM B L, WALLACE A R. Damping-in-pitch and drag characteristics of the Viking configuration at Mach numbers from 1.6 through 3[R]. AEDC-TR-72-56, 1972.
[23] USELTON B L, SHADOW T O, MANSFIELD A C. Damping in pitch derivatives of 120 and 140 degree blunted cones at Mach numbers of 0.3 through 3[R]. AEDC-TR-70-49, 1972.
-
期刊类型引用(5)
1. 陈纪仲，田海平，丁俊飞，马国祯，陈怡纯. 壁湍流摩阻时空信号无接触测量实验研究. 实验流体力学. 2024(04): 66-74 . 
本站查看
2. 高南，刘玄鹤. 实用化壁面切应力测量技术的综述与展望. 空气动力学学报. 2023(03): 1-24 . 百度学术
3. 刘丹. 免标定壁面剪应力测量技术研究. 科技创新与应用. 2023(34): 188-192 . 百度学术
4. 陆连山，李栋. 利用双参数非线性拟合求解湍流边界层壁面摩擦速度. 西北工业大学学报. 2020(02): 253-260 . 百度学术
5. Xuanhe Liu，Zhuoyue Li，Nan Gao. An improved wall shear stress measurement technique using sandwiched hot-film sensors. Theoretical & Applied Mechanics Letters. 2018(02): 137-141 . 必应学术
其他类型引用(4)
计量
- 文章访问数: 808
- HTML全文浏览量: 350
- PDF下载量: 62
- 被引次数: 9
