0   引言

高超声速边界层转捩对飞行器的气动力/热有直接影响，进而关系到飞行器热防护材料的布置。但是，导致高超声速边界层转捩的因素繁多，研究人员对部分转捩机理仍不清楚^[1-2]。地面风洞实验是开展高超声速边界层转捩研究的主要手段之一，但是可用于三维高超声速边界层测量的实验技术仍极为缺乏，且已有测量技术的动态扰动解析频率普遍较低。针对以上问题，研究人员发展了一套非介入式的光学测量系统——聚焦激光差分干涉仪(Focused Laser Differential Interferometry, FLDI)，用于对流场的密度脉动进行解析。

FLDI是一种基于光的折射和干涉原理发展而来的测量技术，具有光学测量响应频率高的优点。通过合理布置光路, 可以将FLDI测量系统的探头体积降低到一个较小的值，使其具有较高的空间分辨率。作为非介入式流场测量技术，FLDI不会破坏流场结构，所测得的量通过简单的后处理即可直接换算出流场密度脉动信息。此外，FLDI适用范围广，对于极端流场(如高焓风洞)的测量不存在探头损坏的风险。

国外对于光学测量技术的研究起步较早，早在20世纪70年代，Smeets在ISL(German-French Re-search Institute Sanit-Louis)就首次发展出FLDI测量技术并将其用于风洞来流和桌面台架式喷流平台的密度脉动测量^[3-6]。Parziale在2012年复现了FLDI技术^[7-9]，用于加州理工大学T5风洞高超声速来流环境中尖锥模型边界层不稳定波的测量研究以及T5风洞高超声速来流密度扰动的测量^[10-11]。2014年，Fulghum首次在FLDI技术中使用Sanderson棱镜取代Wollaston棱镜，用于高超声速风洞中的密度脉动测量^[12]。2015年，Schmidt和Shepherd提出了一种对任意密度脉动场中装备Wollaston棱镜的FLDI测量系统输出量的数值计算方法^[13]，并通过数值分析和实验对比验证了FLDI测量技术的有效性。2016年，Jewell和Parziale等搭建了双测点FLDI系统^[14]并对尖锥模型边界层不稳定波群的互相关性进行了研究分析。同年Settles和Fulghum对装备Sanderson棱镜的FLDI测量技术进一步进行理论和实验分析^[15]，发现Sanderson棱镜比Wollaston棱镜更小的分光角使得FLDI的测点体积更小，空间分辨率更高；并且，由于是对S方向偏振光和P方向偏振光的光强分别进行探测, 可以通过信号的相干性将有效信号从非相干的噪声中剥离出来。

本文介绍了国内首次独立发展的FLDI测量系统。在详细讲述FLDI测量原理的基础上，展示了测量实验中所用到的风洞、尖锥模型、FLDI等设备，并对FLDI测量系统的探头尺寸进行标定。在马赫数为8的常规高超声速风洞单位雷诺数10⁷/m的来流中，运用FLDI测量系统对7°半锥角尖锥模型边界层进行第二模态不稳定波探测，将测量结果与PCB数据进行对比，并对FLDI测量系统进行误差分析，验证了FLDI测量系统在高超声速边界层测量中的优良性能。

1   FLDI测量原理

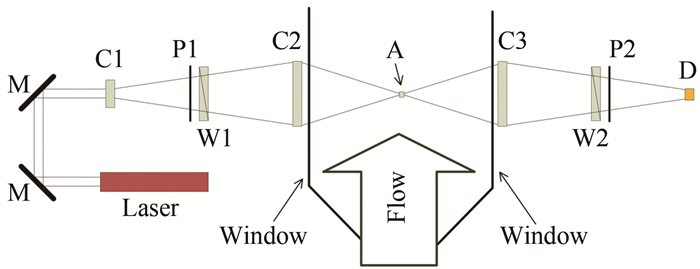
FLDI是基于光的折射和干涉的光学测量技术，主要分为发射光路和接收光路两部分，原理如图 1所示。聚焦区域A左边的部分为发射光路，右边的部分为接收光路。

图  1  FLDI原理图

Fig.  1  Schematic diagram of the FLDI technique

下载: 全尺寸图片 幻灯片

(1) 发射光路。由激光器发射一束相位相同、偏振方向一致的平行激光束(为合理布置光学器件占用空间，通过反射镜M适当改变该平行激光束的路线), 平行激光束穿过凹透镜C1后形成发散的锥形光束, 而后通过偏振片P1得到偏振方向完全一致的发散激光束。之后Wollaston棱镜W1将光束分为光强相等、偏振方向相互垂直、频率幅值相位相等且具有一定分离角的两束发散激光束。接着光束经过凸透镜C2汇聚在聚焦区域A处形成两个分离的焦点，聚焦区域A即FLDI测量探头所在的敏感区域。

(2) 接收光路。由凸透镜C3将经过聚焦区域的发散光速进行再聚合，之后通过Wollaston棱镜W2将两束具有一定分离角的激光束进行合并，通过偏振片P2过滤得到偏振方向一致的聚焦激光束。在光束焦点位置放置光电接收器D将光强信息转换为电压信号。

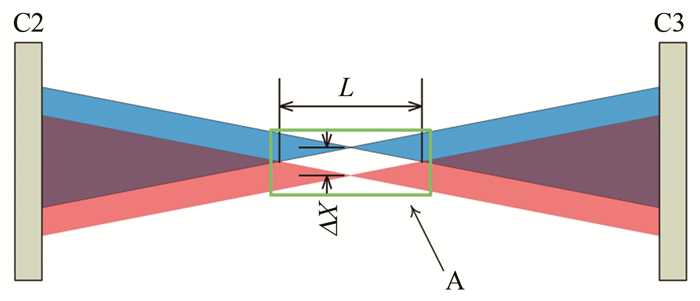
如图 2所示，由于Wollaston棱镜的分光作用，激光束在聚焦区域A内所走过的路径并不相同，由此形成一个菱形敏感区域。而在聚焦区域A之外的地方，两束光所走过的路径几乎重合，流场的密度变化会同时改变两束光的光程，因此不会改变FLDI系统的干涉光强，故聚焦区域A以外的流场密度脉动不会被FLDI系统捕获，即对测量信号没有影响。图中C2、C3为聚焦凸透镜，A为聚焦区域，即FLDI测点区域，蓝色和红色部分分别是分离的两束光线，L为两束光分离路径的长度，ΔX为焦点的分离距离。ΔX也是FLDI测量探头的等效直径，即测点垂直于流向的空间分辨率。

图  2  FLDI测点菱形区域A

Fig.  2  Rhombus FLDI measuring region A

下载: 全尺寸图片 幻灯片

气体的折光率和其密度成线性关系，由Gladstone-Dale公式给出：

其中，n为折光率，ρ为密度，K为空气的Gladstone-dale常数。当光的传播介质是空气时，K=0.000 225 7 m³/kg。

由公式(1)可知，聚焦区域流体的密度差引起空气折光率的不同，从而导致两束光线存在光程差，如公式(2)所示:

其中, ΔOPL为两束光的光程差，n₁、n₂为两个分离焦点处空气的折光率，OPL(Optical Path Length)为激光走过聚焦区域A的光程长度。

光程差进而引起相位差，如公式(3)、(4)所示：

其中，Δφ为两束光的相位差，λ₀为激光波长，和分别是两个分离焦点处空气的密度。

在光路还原的过程中，两束光的相位差会造成干涉，从而引起光强的变化(公式(5))。

其中，I₁=I₂=I₀为单个聚焦点光强，I_d为接收光路光强，l₁·l₂为两束偏振光单位矢量的点积。

光电探测器电压与光强的关系表示为公式(6)：

其中，V是光电接收器的输出电压，I为激光光强，R为二极管敏感度，R_L为负载电阻。

综上，可以得出流场密度脉动和传感器电信号之间的关系，如公式(7)所示：

其中，Δρ为两分离焦点处的空气密度差，ρ_L为测点平均密度，V₀=2I₀RR_L。

由此，可实时测量FLDI系统聚焦区域A所在位置的流场密度梯度，通过时域分析可得到该区域的密度脉动，通过频域分析可以得到该区域密度脉动的频谱特征。

2   实验设备

2.1   风洞

本文通过FLDI测量技术对第二模态波的探测是基于马赫数为8的常规高超声速风洞开展的。

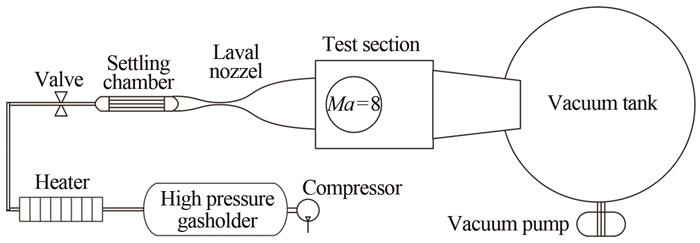
常规高超声速风洞主要由压气机、高压气罐、加热器、稳定段、Laval喷管、实验段、真空罐、真空泵等部分组成(如图 3所示)。实验前，阀门关闭，压气机往高压气罐内充入高压气体，真空泵将真空罐抽成接近真空的低压状态。待高压气罐和真空罐内气体压力温度状态稳定到预定值后打开阀门，同时启动加热器，风洞开始运行。高压气体通过加热器后形成高温高压气流，该气流经过主截止阀后进入稳定段，并在Laval喷管前形成均匀稳定的气流，经过Laval喷管后气流加速到马赫数8，在实验段中模拟高超声速来流的实验环境。

图  3  常规高超声速风洞原理图

Fig.  3  Schematic diagram of conventional hypersonic wind tunnel

下载: 全尺寸图片 幻灯片

2.2   FLDI测量设备

根据FLDI原理图搭建一套FLDI测量设备(图 4和5)，其中激光器Laser选用波长为632 nm的He-Ne激光器，凹透镜C1焦距为30 mm，凸透镜C2焦距为400 mm，Wollaston棱镜半分离角为2弧分。光电接收器响应频率为10 MHz, 数据采集系统响应频率为3 MHz。

图  4  FLDI发射光路

Fig.  4  FLDI light path(emitting part)

下载: 全尺寸图片 幻灯片

图  5  FLDI接收光路

Fig.  5  FLDI light path(receiving part)

下载: 全尺寸图片 幻灯片

本文搭建的FLDI测量系统聚焦区域A(图 2所示)沿被测流场流向的宽度ΔX为^[13]：

f为凸透镜C2的焦距，σ为Wollaston棱镜的分离角)；聚焦区域A垂直于被测流场流向的长度L则需要通过光路敏感性测试获得。

2.3   尖锥模型

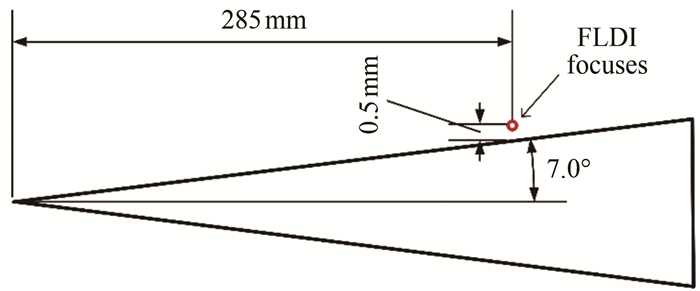
实验模型为7°半锥角尖锥标模(图 6)，FLDI测点位置(聚焦区域A的中心点)距离尖锥头部轴向距离为285 mm，距离尖锥表面0.5 mm(图 7)。实验来流速度为马赫数8，来流单位雷诺数为10⁷/m。根据实验测量及数值模拟经验预测，该来流条件下，尖锥表面位于FLDI测点位置处的边界层厚度约为1 mm，处于转捩过程的线性增长区域。预计本文搭建的FLDI测量系统可以探测到边界层第二模态不稳定波及其谐波。

图  6  7°半锥角尖锥和FLDI测点

Fig.  6  7° half-angle sharp cone and the measuring point

下载: 全尺寸图片 幻灯片

图  7  FLDI测点位置示意图

Fig.  7  Sketch of the FLDI measuring point position

下载: 全尺寸图片 幻灯片

3   FLDI敏感性测试

如图 2所示，L的大小决定了FLDI系统测点区域的长度。理论上，FLDI测点区域的中心位置最为敏感，远离中心点处的敏感性会越来越小。当敏感性下降到高斯分布的特征值以下，即可认为到达光路的非测量区域。

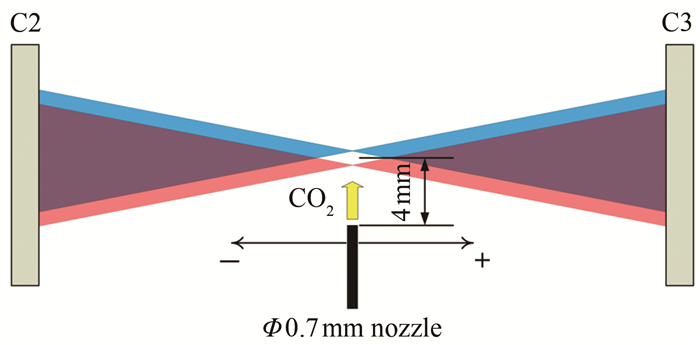
通过直径0.7 mm的小喷管喷射出的CO₂气流对光路敏感性进行探测(图 8)。小喷管与光线同高度，出口距离光线4 mm。将小喷管沿着光路移动，记录下小喷管在不同位置时传感器的信号，通过CO₂气流对光路造成的光程差来表征测量区域的敏感性。两束光的光程差Δφ由公式(9)、(10)给出：

图  8  FLDI敏感性测试原理

Fig.  8  Schematic diagram of the FLDI sensibility test

下载: 全尺寸图片 幻灯片

根据测试得出RMS(Δφ)和CO₂小喷管距离光路中心距离的散点图(图 9)，将数据点进行高斯曲线拟合。敏感性低于最大值的1/e²时认为到达光路的非测试区域。由此得到FLDI测量区域的L值为0.3 m。

图  9  FLDI敏感性测试结果

Fig.  9  Result of the FLDI sensitivity test

下载: 全尺寸图片 幻灯片

4   实验结果

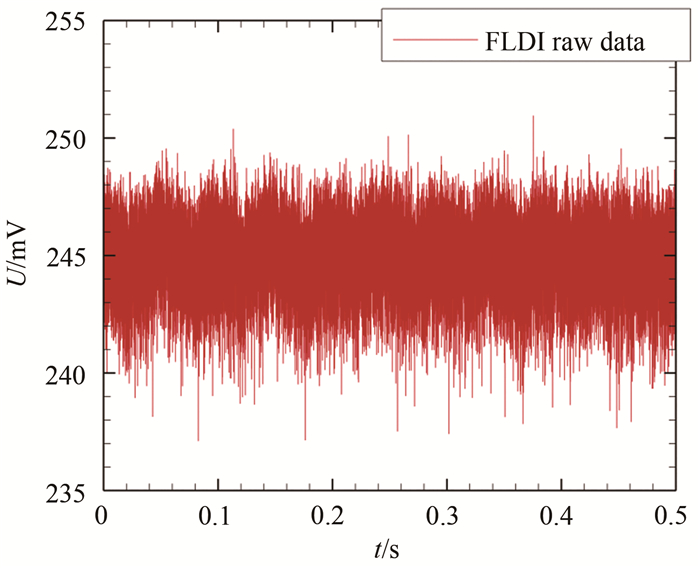
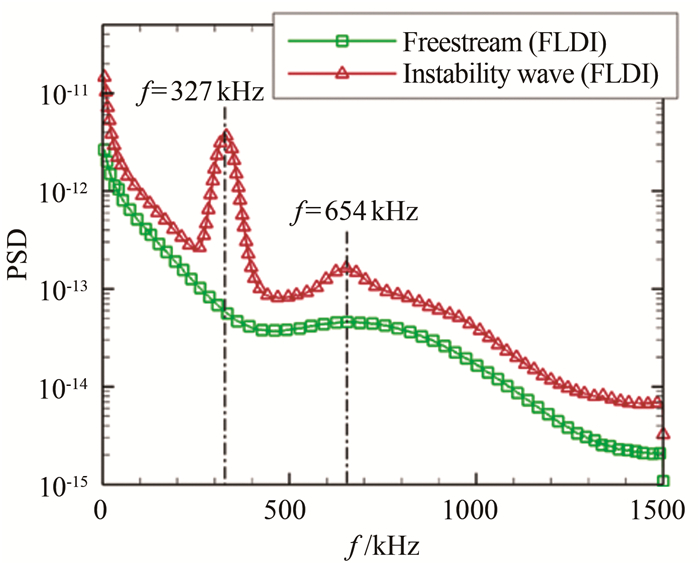
通过FLDI测量技术对总压4.4 MPa、总温730 K、马赫数8、单位雷诺数10⁷/m的高超声速自由来流及该流动下的尖锥边界层进行测量，对原始电信号(图 10)进行功率谱密度分析，结果如图 11所示。FLDI成功捕获到频率在327 kHz的第二模态不稳定波以及654 kHz第二模态不稳定波谐波。此外，对比FLDI测得的自由来流的信号功率谱和边界层内FLDI测点位置的信号功率谱可知，FLDI具有较高的信噪比。受限于数据采集系统的3 MHz采样频率，本次实验FLDI可以有效解析到1.5 MHz的密度脉动。

图  10  FLDI边界层测量原始数据

Fig.  10  FLDI raw data of boundary layer measurement

下载: 全尺寸图片 幻灯片

图  11  FLDI测得边界层第二模态不稳定波

Fig.  11  Second mode instability wave in boundary layer captured by FLDI

下载: 全尺寸图片 幻灯片

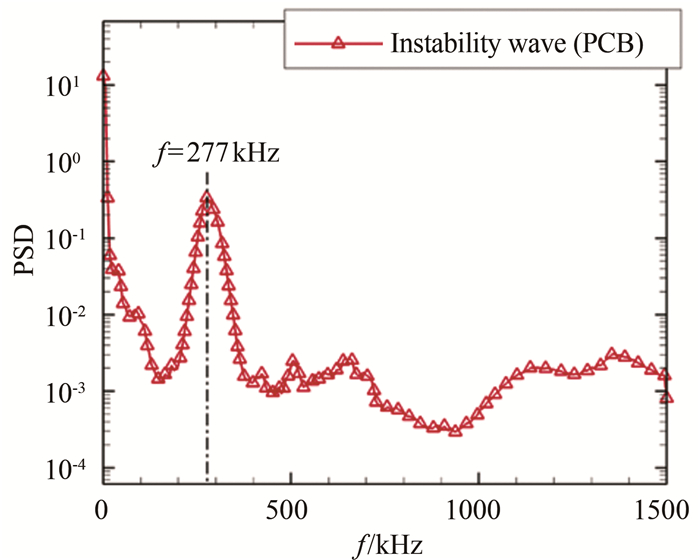
图 12为FLDI测点位置下方PCB传感器测得的边界层第二模态不稳定波。PCB探测到的第二模态不稳定波频率为277 kHz，未探测到明显的第二模态不稳定波的谐波。此外，PCB无法直接探测风洞自由来流扰动。

图  12  PCB测得的边界层第二模态不稳定波

Fig.  12  Second mode instability wave in boundary layer detected by PCB sensor

下载: 全尺寸图片 幻灯片

通过FLDI和PCB数据频谱分析对比，不难看出FLDI测得的信号频谱更加光滑，更加符合真实情况。此外，FLDI探测到的第二模态不稳定波的频率要比PCB所探测到的第二模态不稳定波的频率高50 kHz。在测量过程中，FLDI测点并不在PCB传感器的正上方，而是在PCB传感器测点上游约5 mm的位置，FLDI测得的是边界层内部空间点的密度脉动，PCB测得的是尖锥表面压力脉动。测点位置的不同，以及密度脉动和压力脉动的换算关系，导致两种测量方法存在偏差。此外，风洞运行时模型的振动也对测量结果有不利影响。对于FLDI和PCB测得第二模态不稳定波的频率不同的现象，后续还需通过实验对比和线性理论分析加深对该现象的理解。

5   误差分析

FLDI的系统误差可以通过误差传递原理评估。测得的原始电信号通过公式(7)推导得出Δρ/ρ_L，将此求解过程中的变量误差作为误差函数的输入参数，可计算得出FLDI的误差范围^[16-17]。

公式(7)中光路敏感区域长度L是通过光路敏感性测试所得，引入误差较大，假定其相对误差为20%。平均密度ρ_L是通过数值模拟获得，不妨假定其相对误差为5%。测得电压值V/V₀与人工调整的设备状态有关，存在一定的误差，假设其相对误差为10%。激光波长λ₀的误差由激光器的性能和工况决定，其相对误差不超过1%，可以忽略不计。空气的Gladstone-dale常数K的相对误差较小，也可以忽略不计。由此推导得出通过公式(7)计算的Δρ/ρ_L的相对误差约为23%。结合数据分析中选取截断信号的截断误差和数据后处理引入的误差，假设该部分相对误差为15%，得到FLDI的系统误差约为27%。

FLDI测试中，电气噪声和机械振动会给测量系统引入随机误差。通过在无振动的环境下测量均匀密度气体可以得到由电器噪声引入的随机误差信号。在风洞启动前近似认为气体密度均匀，此时测得的一段信号作为电气噪声。通过分析对比，电气噪声引起的随机误差相对于信号较小，可以忽略。风洞运行时的机械振动所引入的误差在此次实验中无法从测量信号中剥离出来。但是机械振动一般频率较低(低于10 kHz)，经过滤波处理可以有效地抑制机械振动引起的随机误差。

6   总结与讨论

本文搭建了一套FLDI测量系统，通过对尖锥模型高超声速边界层第二模态波的探测, 验证了该测量系统的有效性及其性能特点。得到以下主要结论：

(1) FLDI测量系统具有极高的响应频率。当接收光路长度小于3 m时，光路的响应频率可以高达100 MHz。系统的响应频率瓶颈在于数据采集系统和光电传感器的响应频率。

(2) FLDI光路中光学器件的参数和布置决定了测量敏感区域的大小，通常测量敏感区域的ΔX值一般在1 mm以下，通过合理设计光路可以将敏感区域积分路径L的值降低到10 mm。因此，FLDI测量系统具有较高的空间分辨率。

(3) 作为一种非介入式的测量工具，FLDI测量系统不会破坏所测流场的结构，其测得的流场数据更加直接准确。此外，FLDI在极端流场的实验测量中不存在探头损毁的风险，适用范围广，为高焓风洞等特殊流场下的实验研究提供了一个行之有效的工具。

(4) 鉴于FLDI测量系统的性能特点，其适用于高超声速边界层转捩以及感受性等问题的研究，为深入认识高超声速边界层转捩机制提供了有效手段。