Formation of confined free film in the window on a vertical perforated plate
-
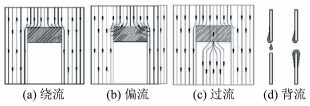
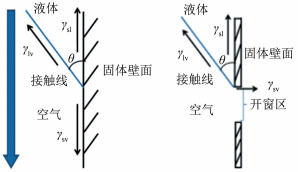
摘要: 液膜是常见的气液接触方式之一,依据单或双自由面可分为壁面膜和自由膜。不同于传统液膜研究,板上开窗或开孔后会同时存在这2种液膜。实验采用了6种液体(Ka数52~3000)和10余种不同尺寸的矩形窗(9~1152mm2),观察了垂直板上下降液膜通过开窗区产生的自由膜流动行为。结果表明,在表面张力、惯性力、重力及黏性力的共同作用下,液体通过开窗区的方式有绕流、过流、偏流和"背流"4种主要形式。随着流量的增加,过流又可以有液滴、液柱、液膜以及它们的组合等丰富流型,同时窗内自由膜在表面张力主导下易受扰动而聚并、破碎,流型呈现多样性和动态性。当流量达到临界值时,窗口内会形成完整稳定的受限自由液膜,呈现板上壁面膜与窗口内受限自由膜交替共存的特殊液膜——孪生液膜。本文关联了临界Re数、Ka数和无量纲几何参数Nx,给出了成膜条件的经验判别式。孪生液膜具有的特殊波列结构、成膜过程的迟滞现象以及2种液膜和固体壁间相互作用引起的多重干扰等,都体现出与传统的壁面液膜和自由液膜不同的流动性质。实验结果将有助于工业过程中开窗和开孔的几何优化,强化传递过程,并进一步丰富传统的液膜研究领域。Abstract: Liquid film is a common contact way between gas/liquid and can be divided into wall-bounded film and free film according to the film formation process and the number of free surfaces. When a plate is perforated, both kinds of films exist. This paper describes some experimental observations of free-surface flows arising when a thin liquid film flows through the window on a vertical perforated plate. Dozens of rectangular windows (9~1152mm2) and six fluids (Ka from 52 to 3000) were used to investigate the flow mechanisms. Several typical flow patterns including pass-around flow, pass-through flow, bias flow and back-side flow are well defined under such a flow condition. Here a special focus is given to the window region, where various free-surface flow patterns composed of droplets, columns, sheets and their combinations were observed with increasing flow rate. Meantime, free film in the window is surface tension dominated and susceptible to disturbance, resulting in coalescence or break of liquid columns and films. At a critical flow rate, liquid film is able to full fill the window, forming a stable complete confined free film. Mutual influence between confined free film in the window region and wall-bounded film around shows special wavy trains, which is also called "twin liquid film". Based on experimental data and scaling analysis, an empirical equation which relates Reynolds number Re, Kapitza number Ka and a dimensionless length Nx is proposed to characterize the film formation conditions. It is found that critical film formation Reynolds number increases with Kapitz number and window size. And hysteresis phenomenon is manifested by obviously different flow transition Re for confined free film formation and breaking. The results can help window geometry optimization industrial processes to improve local heat and mass transfer. It can also enrich the traditional film flow investigations.
-
Keywords:
- twin-liquid film /
- flow transition /
- film formation /
- perforated plate
-
0 引言
二维细长结构是桥梁和建筑结构中常见的构件形式,如桥梁的主梁、桥墩、斜拉索、吊杆,输电系统的导线,建筑中的吊杆和立柱等,这类结构的风荷载和风致振动及控制问题是设计中需要重点考虑的问题。在其抗风研究中,二维节段模型风洞试验是最常用的方法之一。为了保证模型周围的流动为二维流动,模型两端设置端板或补偿模型[1-4]是常用和必要的手段。
研究发现节段模型的端部状态对结构尾流形态、旋涡脱落频率及风压分布具有十分明显的影响[5-12]。A. Slaouti和J.H.Gerrard发现圆柱模型自由端形成的旋涡对距离端部3~4倍直径范围有影响[5]。D.Gerich等研究了不同端部状态对旋涡脱落频率的影响,发现在端板边界层的影响范围内旋涡脱落频率减小10%~15%[6]。P.K. Stansby发现即使长细比达到20,圆形断面结构的背风压也会受到端部效应的影响,设置端板可以消除端部效应[7]。B.E.Lee对比了有无端板情况下矩形断面的风压分布,认为是否设置端板对有尖锐棱角结构测试结果的影响不明显[8]。E.D.Obasaju在研究中发现当采用小尺寸的端板时背风面吸力的绝对值比无端板时减小,采用较大尺寸的端板时,背风面吸力的绝对值比无端板时增大[9]。N. Toy等发现端板间距离增大到15倍的方柱宽度后,中间位置的背风压不再随长细比的改变而变化[10]。Y. Kubo等研究了不同端板对矩形断面阻力系数和背风压的影响,发现随着端板尺寸增大,阻力系数和背风压系数绝对值逐渐增大并趋于某一数值[11]。白桦研究了不同端板对2种桥梁端面气动特性的影响[12]。
上述研究中,缺乏针对不同风迎角下端板尺寸影响的研究,当风迎角改变后,现有结论是否可行有待验证。另外,当端板尺寸不足时,试验造成多大的误差,以及如何对端板不足的试验结果进行修正,也是普遍关心的基本试验技术问题。本研究以此为出发点,通过风洞试验,针对最常见的3种宽高比的断面,分析了不同风迎角下端板尺寸对风压系数、阻力系数及斯托罗哈数St的影响,根据不同端板下模型的测试结果,为类似结构试验时端板的设计以及端板不足时的数据修正提供依据。
1 风洞试验介绍
1.1 试验模型及测点布置
试验在石家庄铁道大学风工程研究中心STU-1风洞的高速试验段内进行,该试验段宽2.2m,高2.0m,长5.0m,最大风速大于80.0m/s,模型区在40和65m/s时的湍流度不大于0.16%[13]。
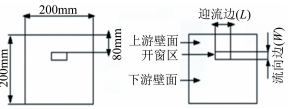
试验模型采用刚性测压模型,考虑了桥梁节段模型中常见的3种矩形断面,其宽高比B/H分别为1、5和10。3种断面模型的长度均为1.7m,保证该长度的模型范围内的流场不会受到风洞两侧洞壁边界层的影响。在模型上轴向布置了6圈测压孔,从端部向中间依次标注为A、B、C、D、E和F。模型安装和各圈测压孔轴向布置如图 1所示。B/H=1的模型边长为100mm,每边布置了7个测压孔,风迎角α=45°时阻塞度为7.1%。B/H=5的模型宽450mm,高为90mm,每圈布置了44个测压孔,其中宽度方向布置了15个测压孔,高度方向布置了7个测压孔,风迎角α=10°时阻塞度为8.3%。B/H=10的模型宽为450mm,高45mm,每圈布置了60个测压孔,其中宽度方向布置了23个测压孔,高度方向布置了7个测压孔,风迎角α=10°时阻塞度为6.1%。3种断面测压孔周向布置如图 2所示。测压孔编号原则:将迎风侧中间测点标注为1号测点,其余编号沿着逆时针方向增大。试验风速为16.5m/s。
1.2 参数定义
定义Sd为沿逆时针方向各测点离开1号测点的模型表面无量纲距离,如公式(1) 所示:

(1) 式中:Li为测点i到1号测点的模型表面距离;S为模型断面的周长。
风压系数Cp表达式为:

(2) 式中:Cp, i为测点i的平均风压系数;pi为作用在测点i处的风压;ρ为空气密度;U为来流平均风速。
阻力系数CD表达式为:

(3) 式中:CD为平均阻力系数;N为模型周向测点数;Li为第i个测压点代表的长度;θi为第i个测压点所在表面与来流的夹角;H为模型高度。
升力系数CL表达式为:

(4) 式中:CL为平均升力系数;B为模型宽度。
斯托罗哈数表达式为:

(5) 式中:f为旋涡脱落频率。
端板的大小用无量纲尺寸表示。B/H=1模型的端板为圆形,直径分别为2L、3L、4L、5L和6L(L为模型断面对角线的长度)。B/H=5和B/H=10模型采用矩形断面的端板,用bxhy的形式表示,其中b表示端板宽度方向,x为端板宽度与模型高度H的比值,h表示端板高度方向,y为端板高度与模型高度H的比值,如b9h2表示端板宽度为模型高度的9倍,端板高度为模型高度的2倍。
下文中为了便于比较,在分析端板大小对试验结果影响的基础上,认为端板的继续增大对结果影响很小时的试验结果为理论值。定义B/H=1模型端板尺寸为6L时中间位置的测试结果为该模型的理论值;定义B/H=5模型端板尺寸为b11h11时中间位置的测试结果为该模型的理论值;定义B/H=10模型端板尺寸为b22h12时中间位置的测试结果为该模型的理论值。
下文中的气动力系数根据文献[14]的研究结果,采用Maskell的方法进行了修正。
2 端板尺寸对气动力的影响
2.1 端板尺寸对B/H=1模型气动力的影响
将各圈测点的压力进行积分得到各圈的气动力,并计算出阻力、升力系数,分析阻力、升力系数随端板尺寸的变化规律。
B/H=1模型各圈的气动力系数随端板尺寸的变化规律如图 3所示。未设置端板时,各圈气动力系数具有明显差异,设置端板后,各圈气动力间的差异明显减小。以阻力系数为例,未设置端板时阻力系数的最大值出现在A圈为1.592,最小值出现在F圈为1.209。设置4L的端板后,阻力系数最大值出现在A圈为1.649,最小值出现在F圈为1.584。设置4L的端板后,各圈与理论值的最大误差为2.3%,认为端部效应被抑制。
B/H=1模型不同风迎角下的F圈气动力系数随端板尺寸的变化规律如图 4所示。随着端板尺寸的增大,阻力系数逐渐增大并趋于理论值。升力系数的变化与风迎角有关,风迎角小于10°时,随着端板尺寸的增大升力系数绝对值逐渐增大,例如风迎角α=10°时,无端板时为-0.425,设置6L的端板后为-0.630;风迎角大于20°时,随着端板尺寸的增大,升力系数绝对值逐渐减小,例如风迎角α=25°时,无端板时为-0.376,设置6L的端板后为-0.082。
能够有效消除端部效应的最小端板尺寸与风迎角有关,风迎角较大时,所需的端板尺寸也相应增大,如当风迎角小于10°时,采用3L的端板后的阻力系数测试结果与理论值间的误差小于5%;当风迎角大于25°,端板尺寸到达5L之后,测试结果与理论值的误差小于5%。
2.2 端板尺寸对B/H=5模型气动力的影响
B/H=5模型不同风迎角下的F圈气动力系数随端板宽度的变化规律如图 5所示(端板高度为6倍模型高度)。风迎角小于2°时,是否设置端板对F圈阻力系数的影响不是十分明显,与理论值最大误差为6.6%。风迎角大于2°时,随着端板尺寸的增大,阻力系数逐渐增大并趋于理论值;升力系数绝对值呈增大的趋势。当端板宽度增大到9倍模型高度时,各风迎角下的阻力系数、升力系数与理论值的误差在5%以内,认为不受端部效应的影响。
B/H=5模型不同风迎角下的F圈气动力系数随端板高度的变化规律如图 6所示(端板宽度为9倍模型高度)。当风迎角α < 2°时,是否设置端板对阻力系数的影响不是十分明显,阻力系数的最大误差为4.9%;风迎角α>4°时,随着端板高度的增大阻力系数逐渐趋近于理论值。升力系数的变化规律与阻力系数类似,随着端板高度的增加,升力系数的绝对值逐渐增大并趋于理论值。
2.3 端板尺寸对B/H=10模型气动力的影响
B/H=10模型不同风迎角下的F圈气动力系数随端板宽度的变化规律如图 7所示(端板高度为12倍模型高度)。风迎角较大时,端板宽度的改变对阻力系数有一定的影响,例如α=10°时无端板时的阻力系数为2.007,理论值为2.300,两者之间的误差为12.7%,当风迎角α < 8°时,端板宽度的改变对阻力系数的影响不明显。端板宽度的改变对升力系数的影响与之类似。
B/H=10模型气动力系数随端板高度的变化如图 8所示(端板宽度为18倍模型高度)。风迎角较小时,端板尺寸的改变对阻力、升力系数的影响不明显,风迎角较大时,端板尺寸的改变对气动力系数才有一定的影响。
3 端板尺寸对风压分布的影响
3.1 端板尺寸对B/H=1模型风压分布的影响
风迎角a=0°和45°情况下,B/H=1模型的风压系数随端板尺寸的变化如图 9所示。设置端板后,模型迎风面风压分布的变化较小,背风面的变化较为明显。风迎角α=0°且无端板时,模型侧面与背面的风压系数绝对值偏小,设置端板后,即使尺寸很小,也会使风压分布有较大的改善。风迎角增大后,模型端部形成的旋涡增大,因此端板尺寸也需要相应增大才能保证尾流的风压不受端部效应的影响。
3.2 端板尺寸对B/H =5模型风压分布的影响
风迎角a=10°情况下,B/H=5模型风压系数随端板尺寸的变化如图 10所示。随着端板宽度、高度的增大,B/H=5模型背风面和上表面风压系数的绝对值逐渐增大。另外,随着端板尺寸的增大,模型下表面再附点的位置向前移动。
3.3 端板尺寸对B/H =10模型风压分布的影响
风迎角a=10°情况下,B/H=10模型风压系数随端板尺寸的变化如图 11所示。对于B/H=10模型,端板尺寸的改变对背风面、上表面的风压系数有一定的影响,对下表面再附点的影响可以忽略。
4 端板尺寸对斯托罗哈数的影响
为了说明端板尺寸对模型周围流场的影响,对脉动升力的功率谱进行分析,进而得到端板尺寸对St的影响。
4.1 端板尺寸对B/H=1模型斯托罗哈数的影响
风迎角α =45°时,B/H=1模型各圈St随端板尺寸的变化规律如图 12所示。无端板时各圈均未发现周期脱落的旋涡,说明端部影响模型周围的流动状态,随着端板尺寸的增大,各圈的流动状态逐渐变得一致。采用5L和6L的端板后,各圈间的St基本相等,与其他研究人员的结果[15-16]一致,说明端部效应被消除。
4.2 端板尺寸对B/H=5模型斯托罗哈数的影响
风迎角α =10°时,B/H=5模型St随端板尺寸的变化规律如图 13所示。当端板宽度增大到9H、高度增大到6H后,St不再发生明显改变。
4.3 端板尺寸对B/H=10模型斯托罗哈数的影响
风迎角α =10°时,B/H=10模型St随端板尺寸的变化如图 14所示。无端板情况下,在D、E、F 3圈处出现规则的旋涡脱落,其范围较B/H=1、B/H=5模型要大,说明模型宽高比增大后,模型端部效应的影响范围减小。端板宽度增大到16H后,端板高度增大到10H后,St不再发生改变。
随着模型宽高比的增大,端板尺寸的增大对模型中间位置气动力系数的影响逐渐减小,说明端部效应对中间位置的影响逐渐减弱。
5 结论
通过风洞试验,研究了端板尺寸对桥梁节段模型中最常见的3种宽高比的二维矩形断面风压系数、阻力系数和斯托罗哈数St的影响,得到如下结论:
(1) 模型端部效应不仅对端部有影响,对中间位置的风压分布影响也不容忽视,设置端板是获得较准确试验结果的必要条件。
(2) 消除端部效应的最小端板尺寸与风迎角有关,随着风迎角的增大,所需的端板尺寸也相应增大。
(3) 模型的端部效应对St有明显影响。
-
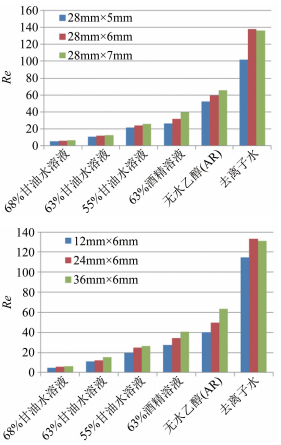
表 1 实验流体的物理性质
Table 1 Physical properties of the liquids used
Ka 密度
ρ/(kg·m-3)黏度
μ/(N·s·m-2)表面张力
σ/(N·m-1)68%甘油水溶液 52.7 1160 0.0175 0.058 63%甘油水溶液 127 1150 0.0090 0.057 55%甘油水溶液 295 1110 0.0046 0.055 63%酒精溶液 406 880 0.0014 0.037 无水乙醇 670 790 0.0027 0.030 去离子水 2.93×103 1000 0.00098 0.072 表中: 
-
[1] 胡军, 胡国辉, 孙德军.沿平板下落薄膜流动的研究综述[J].力学进展, 2005, 35(2):161-169. DOI: 10.6052/1000-0992-2005-2-J2004-109 Hu J, Hu G H, Sun D J. A review on thin films falling along an inclined plate[J]. Advances in Mechanics, 2005, 35(2):161-169. DOI: 10.6052/1000-0992-2005-2-J2004-109
[2] Batchelor G K, Moffatt H K, Worster M. Perspectives in fluid dynamics:a collective introduction to current research[M]. Cambridge:Cambridge University Press, 2002.
[3] Kapitza P. Dynamic stability of the pendulum with vibrating suspension point[J]. Soviet Physics-JETP, 1951, 21(5):588-597. https://www.mendeley.com/research-papers/dynamic-stability-pendulum-vibrating-suspension-point/
[4] Wasden F K, Dukler A E. A numerical study of mass transfer in free falling wavy films[J]. American Institute of Chemical Engineers Journal, 1990, 36(9):1379-1390. DOI: 10.1002/(ISSN)1547-5905
[5] Alekseenko S, Nakoryakov V E, Pokusaev B G. Wave flow of liquid films[M]. New York:Begell House, 1994.
[6] Chang H-H, Demekhin E A. Complex wave dynamics on thin films[M]. Elsevier, 2002.
[7] Kalliadasis S, Ruyer-Quil C, Scheid B, et al. Falling liquid films[M]. Springer Science & Business Media, 2011.
[8] Squire H B. Investigation of the instability of a moving liquid film[J]. British Journal of Applied Physics, 1953, 4(6):167-169. DOI: 10.1088/0508-3443/4/6/302
[9] Brown D. A study of the behaviour of a thin sheet of moving liquid[J]. Journal of Fluid Mechanics, 1961, 10(2):297-305. DOI: 10.1017/S002211206100024X
[10] Lin S, Roberts G. Waves in a viscous liquid curtain[J]. Journal of Fluid Mechanics, 1981, 112:443-458. DOI: 10.1017/S0022112081000505
[11] Lin S P. Breakup of liquid sheets and jets[M]. England:Cambridge University Press Cambridge, England, 2003.
[12] Sirignano W A, Mehring C. Review of theory of distortion and disintegration of liquid streams[J]. Progress in Energy & Combustion Science, 2000, 26(4):609-655. http://www.academia.edu/21244677/Review_of_theory_of_distortion_and_disintegration_of_liquid_streams
[13] Pritchard W. Instability and chaotic behaviour in a free-surface flow[J]. Journal of Fluid Mechanics, 1986, 165:1-60. DOI: 10.1017/S0022112086002987
[14] Mackowiak J. Fluid dynamics of packed columns[M]. London, New York:Springer, 2010.
[15] Fair J R, Seibert A F, Behrens M, et al. Structured packing performance experimental evaluation of two predictive models[J]. Industrial & Engineering Chemistry Research, 2000, 39(6):1788-1796. https://www.researchgate.net/publication/231394040_Structured_Packing_PerformanceExperimental_Evaluation_of_Two_Predictive_Models
[16] Pavlenko A, Pecherkin N, Chekhovich V, et al. Hydrodynamics in falling liquid films on surfaces with complex geometry[J]. Microgravity Science and Technology, 2009, 21(1):207-213. DOI: 10.1007/s12217-009-9157-1
[17] Yao Y, Pavlenko A, Volodin O. Effects of layers and holes on performance of wire mesh packing[J]. Journal of Engineering Thermophysics, 2015, 24(3):222-236. DOI: 10.1134/S1810232815030042
[18] Kolev N, Kralev B, Kolev D. Gas side controlled mass transfer in a new packing with stamped horizontal lamellae operating at extremely low liquid loads[J]. Chemical Engineering and Processing:Process Intensification, 2013, 63:44-49. DOI: 10.1016/j.cep.2012.07.004
[19] 戴干策, 胡剑光, 于建国, 等. 适应粘性吸收剂的有壁与无壁液膜交替的规整填料: 中国, 201210234334. 6. 2013-07-10. Dai G C, Hu J G, Yu J G, et al. Wall liquid film and wall-free liquid film alternate structured filler adapting to viscous absorbent:China, 201210234334.6. 2013-07-10.
[20] Hu J, Liu J, Yu J, et al. CO2 absorption into highly concentrated dea solution flowing over a vertical plate with rectangular windows[J]. International Journal of Greenhouse Gas Control, 2013, 19:13-18. DOI: 10.1016/j.ijggc.2013.08.007
[21] 胡剑光, 刘佳特, 袁猛, 等.新型垂直板规整填料流体力学及传质性能[J].化工学报, 2014, 65(1):116-122. http://www.cnki.com.cn/Article/CJFDTOTAL-HGSZ201401019.htm Hu J G, Liu J T, Yuan M, et al. Hydrodynamics and mass transfer characteristics of a novel vertical-sheet structured packing[J]. Journal of Chemical Industry and Engineering, 2014, 65(1):116-122. http://www.cnki.com.cn/Article/CJFDTOTAL-HGSZ201401019.htm
[22] 王良生, 戴干策.圆盘反应器成膜性的持液量研究[J].化学反应工程与工艺, 2000, 16(2):127-135. http://www.cnki.com.cn/Article/CJFDTOTAL-HXFY200002005.htm Wang L S, Dai G C. A study of film forming and hold-up in a rotating disc-ring reactor[J]. Chemical Reaction Engineering and Technology, 2000, 16(2):127-135. http://www.cnki.com.cn/Article/CJFDTOTAL-HXFY200002005.htm
[23] 邓斌, 戴干策.圆盘反应器液膜表面更新数值模拟[J].化工学报, 2015, 66(4):1407-1416. DOI: 10.11949/j.issn.0438-1157.20141688 Deng B, Dai G C. Numerical simulation of surface renewal frequency on vertically rotating disc[J]. Journal of Chemical Industry and Engineering, 2015, 66(4):1407-1416. DOI: 10.11949/j.issn.0438-1157.20141688
[24] Hu J, Yang X, Dai G. Numerical investigation on hydrodynamics of vertically confined free film[J]. The Canadian Journal of Chemical Engineering, 2016, 94(2):340-348. DOI: 10.1002/cjce.v94.2
[25] Oliver J F, Huh C, Mason S G. Resistance to spreading of liquids by sharp edges[J]. Journal of Colloid and Interface Science, 1977, 59(3):568-581. DOI: 10.1016/0021-9797(77)90052-2
[26] Brunet P, Flesselles J-M, Limat L. Dynamics of a circular array of liquid columns[J]. The European Physical Journal B, 2007, 55(3):297-322. DOI: 10.1140/epjb/e2007-00057-y
[27] Schmuki P, Laso M. On the stability of rivulet flow[J]. Journal of Fluid Mechanics, 1990, 215:125-143. DOI: 10.1017/S0022112090002580
[28] Ruan B, Jacobi A M, Li L. Effects of a countercurrent gas flow on falling-film mode transitions between horizontal tubes[J]. Experimental Thermal and Fluid Science, 2009, 33(8):1216-1225. DOI: 10.1016/j.expthermflusci.2009.07.009
-
期刊类型引用(18)
1. 韩笑,高创,郑怡彤,刘小兵. 切角凹槽矩形截面桥塔的气动特性试验研究. 石家庄铁道大学学报(自然科学版). 2024(01): 9-15+23 .  百度学术
百度学术
2. 白桦,刘博祥,姬乃川,李加武. 节段模型二元端板合理尺寸估算方法. 振动与冲击. 2023(02): 312-320 .  百度学术
百度学术
3. 王仰雪,刘庆宽,靖洪淼,李震,孙一飞. 倾斜栏杆对流线型箱梁涡激振动性能影响的试验研究. 振动与冲击. 2023(06): 232-239+254 .  百度学术
百度学术
4. 于畅,仇法梅,田学东,杨群,刘小兵. 圆角矩形柱平均气动力特性的雷诺数效应试验研究. 石家庄铁道大学学报(自然科学版). 2023(02): 29-34 .  百度学术
百度学术
5. 杨群,于畅,刘小兵,刘庆宽. 不同圆角率的方形断面斯特罗哈数的雷诺数效应研究. 振动与冲击. 2023(11): 223-231 .  百度学术
百度学术
6. 刘庆宽,王仰雪,孙一飞,李震,韩原,靖洪淼. 栏杆高度对流线型箱梁涡振性能影响的试验研究. 湖南大学学报(自然科学版). 2023(07): 140-150 .  百度学术
百度学术
7. 刘路路,杨皓然,邹云峰,何旭辉,韩艳,陈志强. 公铁同层双幅非对称主梁气动干扰特性研究. 铁道科学与工程学报. 2023(10): 3861-3872 .  百度学术
百度学术
8. 杨群,于畅,于文文,刘小兵. 圆角方柱气动特性的风洞试验研究. 振动与冲击. 2023(24): 59-68 .  百度学术
百度学术
9. 韩振,李波,甄伟,杨庆山,田玉基. 宽厚比为5的超高层建筑风荷载特性研究. 哈尔滨工程大学学报. 2022(02): 196-202 .  百度学术
百度学术
10. 张庆华,马文勇,杨杰,张彦,周帅伟. 不同风倾角下典型等边角钢静风力风洞试验研究. 振动工程学报. 2022(02): 277-283 .  百度学术
百度学术
11. 白桦,王涵,姬乃川,李加武. 节段模型长宽比对风洞测力试验及计算分析的影响. 中国公路学报. 2022(08): 202-212 .  百度学术
百度学术
12. 杨群,刘庆宽,韩瑞,刘小兵. 不同圆角率的方形断面气动特性的雷诺数效应. 振动与冲击. 2020(04): 150-156 .  百度学术
百度学术
13. 沈国辉,姚剑锋,郭勇,邢月龙,楼文娟. 直径30 cm圆柱的气动力参数和绕流特性研究. 振动与冲击. 2020(06): 22-28 .  百度学术
百度学术
14. 温青,池俊豪,华旭刚,王修勇,孙洪鑫. 端部条件和展弦比对矩形断面节段模型气动力特征的影响. 实验流体力学. 2020(04): 36-43 .  本站查看
本站查看
15. 任若松,梁新华,刘小兵,马文勇,刘庆宽. 准流线型桥梁断面气动力特性的雷诺数效应研究. 工程力学. 2020(S1): 139-144+167 .  百度学术
百度学术
16. 李海飞,梁新华,孙一飞,崔会敏,刘庆宽. 流线型桥梁断面表面脉动风荷载特性研究. 工程力学. 2020(S1): 242-248+260 .  百度学术
百度学术
17. 马文勇,汪冠亚,郑熙,陈铁,李智,张程远,方平治. 端部状态对斜置圆柱气动力分布的影响. 实验流体力学. 2019(02): 43-50 .  本站查看
本站查看
34. 杨群,刘庆宽,孙亚松,刘小兵. 圆角方形断面气动特性试验. 振动.测试与诊断. 2020(01): 140-147+208 .  百度学术
百度学术
其他类型引用(16)







 下载:
下载: