Effects of end condition on aerodynamic force distribution on a skewed circular cylinder
-
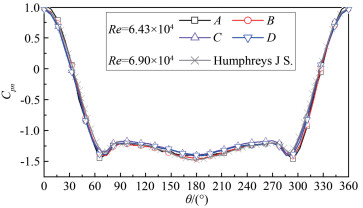
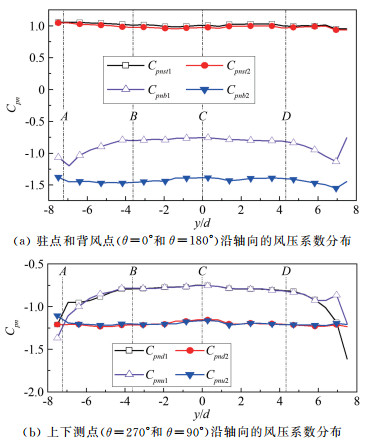
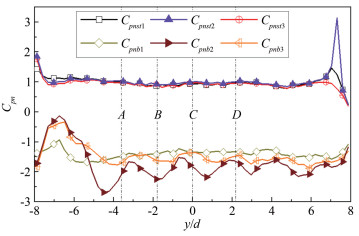
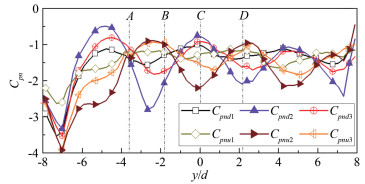
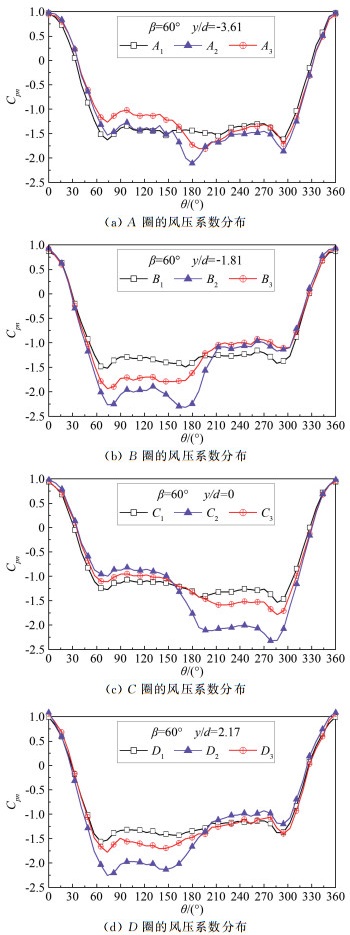
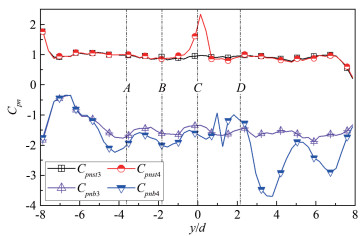
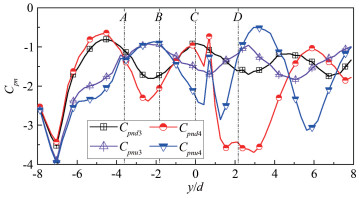
摘要: 在有限长度圆柱气动力测试风洞试验中,端部状态的变化对气动力有很大影响。在雷诺数为6.43×104时,通过刚性模型风洞测压试验对3种端部状态下的斜置圆柱气动力特性进行研究,基于平均风压系数沿斜置圆柱的轴向和周向分布规律,分析端部状态对斜置圆柱气动力测试结果的影响。结果表明:斜置圆柱表面风压沿轴向可分为近上游端部区、中间区和近下游端部区;由于马蹄涡的存在,在近上游端部区的背风面,风压沿轴向有一个突变,端部状态对马蹄涡强度有很大影响;在中间区,背风面风压沿轴向出现交替变化,可能是由于在近上游端部区形成的旋涡受到轴向流作用向中间区流动导致的,端部状态对交替风压变化的幅度和阻力系数有很大影响;当下游端部封闭时,近下游端部区的迎风面和背风面风压都会出现突变,且迎风面的突变幅度更大,下游端板对近下游端部区迎风面的风压分布影响更大。Abstract: The change of the end conditions has significant influences on the aerodynamic forces when a finite length cylinder is tested in the wind tunnel for its aerodynamic forces. In the present study, the characteristics of aerodynamic forces on an oblique cylinder with various end conditions at Reynolds number of 6.43×104 are studied through a rigid model pressure test in a wind tunnel. Using the wind pressure distribution along the length of the cylinder, the effects of end conditions on aerodynamic forces on the oblique circular cylinder are revealed. The results show that the wind pressure on the oblique cylinder could be classified into three states along the length of the cylinder, that the state near the upstream end plate, the state at the middle and the state near the downstream end plate. The wind pressure on the leeward near upstream end plate has a significant variation (convex) due to the existence of the horseshoe vortex. The existence of the end plates significantly influences the strength of the horseshoe vortex. At the middle state, the wind pressure on the leeward varies alternately along the length, which is probably induced by the motion of the horseshoe vortex through the axial flow. The end conditions also influence the amplitude of the alternative wind pressure at the leeward and the local drag coefficient on the cylinder. Near the downstream end plate state, wind pressure on the windward and leeward varies sharply when the downstream end plate is closed. The downstream end plate has a more significant influence on the wind pressure distribution at the windward than at the leeward.
-
0 引 言
目前世界上在用的大尺寸航空声学风洞有20余座,分布在美国、德国、意大利、日本和韩国等多个国家[1-4]。5.5 m × 4.0 m航空声学风洞背景噪声和湍流度指标均达到世界先进水平[5-6]。该风洞闭口试验段用于容纳试验模型开展闭口试验,是风洞回路的关键部段。本文主要针对该航空声学风洞闭口试验段总体结构方案、定位与锁紧、提升机构、可更换下壁板和开度可调侧壁板等进行了详细研究,并对加工和装配过程中的加工变形控制技术和装配精度保证等技术进行了介绍。
1 设计指标及功能要求[7]
1)试验段尺寸为5.5 m(宽) × 4 m(高) × 14 m(长)。
2)试验段为闭口,风速为8~130 m/s。
3)闭口试验段模型区中心湍流度 ≤ 0.05%。
4)轴向静压梯度设计指标L|dCp/dx| ≤ 0.003 (轴向静压梯度dCp/dx指试验段静压沿中心轴向变化,L为模型区长度)。
5)满足风洞开、闭口试验状态快速切换要求。
6)满足腹撑、尾撑、半模、地效试验活动地板(单带)等试验配套需求。
2 总体技术方案
根据闭口试验段研制指标和功能需求,将闭口试验段设计为可移动部段,放弃了传统的轨道运输方案(轨道运输方案会使消声室地面轨道错综复杂,导致换向和消声室大门密封困难及试验效率低等问题)。采用气浮驱动技术,以满足开口和闭口试验工况快速切换[8-9]要求。气垫运输路径采用压光水泥地面(水平度 ≤ 0.5%,平面度 ≤ 0.5%),在闭口试验段长期停放位置预埋钢板。
为降低该风洞在开口状态下的射流噪声,采用不同形式的声学喷口。不同形式的声学喷口具有不同的出口形状,由开口试验状态切换到闭口试验状态时,若直接将闭口试验段入口与声学喷口出口对接,对接处的过渡与密封处理极其困难,将影响低湍流度试验性能指标。因此,在方案设计时,在闭口试验段前部向上游增加了声学喷口长度,切换试验状态时,将声学喷口拆除,闭口试验段入口直接与收缩段出口对接。
考虑到风洞模型、尾撑变角度机构重量和尺寸较大,为方便其进出闭口试验段,在试验段顶部设置进出通道,并在试验段上框架设计了电动执行的提升平移机构。采用带行走机构、可沿导轨轴向移动的可更换下壁板,能够兼顾常规试验与地效试验等特种试验,使闭口试验段具有高适应性的功能扩展能力。侧壁板采用“铰链+推杆”的方案实现扩散角可调,为优化闭口试验段轴向静压梯度提供了技术支撑。基于上述功能需求和总体方案,结合试验段内表面高精度要求、大跨距支腿对试验段的高刚性要求,以及试验段装配精度要求[10-13],对闭口试验段采用了“框架+壁板”的结构形式。
3 闭口试验段设计
闭口试验段主要包括支腿、框架、壁板、上下转盘和提升平移机构等,如图1所示。闭口试验段外形尺寸16.15 m(长) × 8.1 m(宽) × 12.15 m(高),中心轴线标高8 m,总重187 t。试验段整体采用框架结构,选取刚度较大的工字钢及箱型梁作为主要承力构件。壁板装配在框架上,形成15 m(长) × 5.5 m(宽) × 4 m(高)的气流通道;下壁板为可更换结构形式,通过轮式机构驱动,可顺利进出试验段。试验段共有4组支腿,用于支撑上部洞体结构,支腿下部均为π形结构,用以安装气垫模块。上、下转盘分别安装于上、下壁板,上、下转盘同轴且可随壁板移动。提升平移机构位于试验段顶部,可将上、中壁板提起,并平移到试验段后方。
3.1 有限元分析
为了保证闭口试验段各精度指标的实现和运行安全,采用有限元方法对其结构强度、刚度及模态进行了分析[14]。
重点针对闭口试验段框架静力学和动力学进行分析。在对应支撑处施加4个壁板的重力、气动载荷、提升装置及转盘等载荷后,计算得到主体结构等效应力 < 100 MPa,应力集中处最大应力为131 MPa(图2),可以通过工艺倒角加以改善。最大变形为2.79 mm(位于框架上横梁处,图3),满足强度设计要求(安全裕度≥ 1.5)和刚度要求(≤ 3 mm)。前六阶模态振型及固有频率如图4所示。试验段气流平稳,压力脉动极小,不会激发闭口试验段的共振。在实际运行中,试验段的振动状态良好。
3.2 定位和锁紧
闭口试验段采用气浮驱动,重复定位精度不高,若不进行精准定位,对流场品质影响很大。同时,闭口试验段利用气浮驱动就位后,须与风洞洞体或地基进行定位和锁紧,以防风洞运行过程中闭口试验段在气动力作用下移位,降低风洞流场品质,影响风洞安全运行。在设计中采取了如下措施:在闭口试验段前、后支腿支座不同侧面位置分别设置一组导向轮和垂直定位装置,在对应支腿就位位置的预埋钢板上设置与风洞轴线平行的Y形导向槽;在闭口试验段入口端中心标高位置两侧设置导向销,位置与收缩段出口段两侧的弹性滚轮导向装置对应;在闭口试验段入口两侧设置转销连接机构,用于闭口试验段入口法兰与收缩段出口法兰的快速连接,两法兰之间充气密封,确保试验段流场达标。
具体定位过程为:通过气垫运输使闭口试验段支腿上的导向轮进入Y形导向槽,经Y形导向槽沿气流反向由粗略到精准导向,再将闭口试验段两侧的导向销插入收缩段出口两侧的弹性滚轮导向装置,进行高精度导向;当两法兰面接触后,插入支腿位置的垂直定位装置,防止闭口试验段气垫泄压后位置移动,然后进行气垫泄压。依靠弹性滚轮装置弹性下降至风洞安装位置,此时以转销机构锁紧连接法兰面,充气密封。闭口试验段移出与上述相反。
3.3 提升平移机构的设计
提升平移机构用于将闭口试验段上中壁板(长5.5 m ,宽 5.3 m,重14 t)提升600 mm后,再沿试验段轴线方向后移5500 mm,为腹撑支杆、尾撑变角度机构、模型等提供安装通道。其关键技术主要有2个方面的挑战:
1)实现提升及平移功能。
2)提升重量重,提升过程中螺旋升降机丝杆受压,存在失稳风险。
主要解决措施为:
1)为实现提升及平移功能,提升平移机构由提升平台和平移机构组成。提升平台通过一组4台机械同步的螺旋升降机实现对上中壁板的提升功能;平移机构采用两侧对称丝杆螺母副驱动、直线导轨副导向,并控制两侧伺服电机实现同步驱动。
2)提升平移机构原设计方案如图5所示,提升框架与上中壁板固连为一体,由4台螺旋升降机同步驱动。螺旋升降机丝杆在提升过程中受压力作用,其外载荷为提升框架和上中壁板重量之和,受载偏大,存在失稳风险。经优化后,提升平移机构如图6所示:提升机构只提升上中壁板部分,提升载荷减小(约8 t);螺旋升降机丝杆只受拉力作用,不存在失稳风险;4组提升支腿均有轴承导向装置,横向稳定性增加,极大提高了机构刚度,满足设计要求。
3.4 可更换下壁板及开度可调侧壁板的设计
为满足可更换地效试验活动地板(单带)的设计要求,重点考虑了更换的便捷性与重复性定位精度,采用如图7所示的行走轮式可更换下壁板,由电机驱动沿布置在下框架上的钢轨移动。如图8所示,壁板前端设置一对导向销,用于壁板就位过程中的导向,以此确保横向定位精度。壁板两侧各设2个插销定位机构(图9),用于确保壁板轴向定位精度。同时,将壁板与试验段框架连为一体,共同承受气动载荷,以确保壁板在试验状态不松动。更换壁板时,将壁板更换车与试验段出口对齐,松开侧向插销,壁板通过行走机构自试验段框架运行至壁板更换车上,完成下壁板更换。
为满足闭口试验段轴向静压梯度调节需要,试验段出口宽度尺寸可调,可调范围为5.50~5.74 m。侧壁板前端通过铰链固定在过渡段上,后端通过2组手动推杆驱动侧壁板绕前端铰链转动,实现试验段出口宽度尺寸的调节(图10)。侧壁板尺寸大(13.5 m× 4 m × 0.336 m,长 × 宽 × 厚),质量重(>10 t),为避免在开度调节时侧壁板产生非均匀变形,设计中做如下处理:
1)在侧壁板下均匀布置多组滑动支座,壁板重量通过支座均匀作用于下方主纵梁,侧壁板与支座接触面为不锈钢/聚四氟乙烯摩擦副。经计算,该摩擦副产生的摩擦力对侧壁板变形影响极小。
2)通过控制侧壁板高度,使侧壁板上端与上框架和主纵梁间留有一定间隙,避免侧壁板开度调节时发生卡滞。
4 制造和装配
闭口试验段结构复杂,制造和装配精度要求高,因此解决制造和装配过程工艺问题十分重要。主要从加工变形控制技术和装配精度保证措施2个方面进行说明。
4.1 焊接变形控制技术
闭口试验段焊接加工件多为大尺寸薄壁件,在焊接过程中容易产生变形,若焊接工艺采取不当,将导致加工余量无法满足要求。对上述结构件主要采取焊前预防、焊接过程控制、焊后校正等手段控制焊接变形[15]。以如下3类结构件为例:
1) 壁板类焊接
以上壁板(6 m × 5.5 m × 12 mm,长 × 宽 × 厚,筋为槽钢)为例(图11),焊缝全部集中在底板上表面,底板下表面需切削加工。该结构件焊接主要控制角变形,解决措施为在壁板下表面装焊相同大小的底板。焊接时,同时从底板中心向两侧对称装焊各肋板。采用对称的逆向分段焊接法焊接各肋板,将整个焊缝分成若干分段,每一段的焊接方向皆与焊接总方向相反。
2) 箱型梁焊接
左右主纵梁均为细长箱形结构,在焊接过程中应严格控制焊接产生的扭曲和角变形。图12为主纵梁焊接的场景。焊接时,在顶板与底板表面装焊防变形底板;从中间向两端分别装焊除底座外的各肋板、档板,通过分析施焊后可能产生变形的大小及方向,在焊接前使被焊件发生大小相同、方向相反的变形,以抵消或补偿焊接导致的变形(反变形措施)。
3) 框架焊接
上框架结构(13.25 m × 7.7 m × 0.25 m,长 × 宽 × 高,如图13所示)刚性较差,焊接时容易产生扭曲变形和角变形。焊接时,先装焊各横梁和纵梁,回火后按接口部位采用镗削方式加工至满足装配焊接要求。将各横梁与纵梁的装配位置整体焊接在一个大底板上定位,并对结构刚性差的部位使用拉筋进行加固,防止焊接变形和后续的热处理变形。
4.2 装配精度保证措施
闭口试验段尺寸大、装配零件多、装配精度要求高。按照从下到上、从外到内的顺序,依次装配两侧主纵梁、下壁板、侧框架、左右侧壁板、上壁板和上框架。
闭口试验段安装主要有2个关键指标要求:1)上下转盘同轴度≤Φ0.3 mm;2)壁板的平面度≤5 mm、平行度≤5 mm、对称度≤2 mm。实践证明,为保证上下转盘同轴度要求,在保证主纵梁加工质量的前提下,在装配环节应避免两侧主纵梁发生扭转、倾斜等现象。计算表明主纵梁安装精度对上下转盘同轴度安装指标的实现起决定性作用,应该在安装前通过理论计算,确定出其安装精度范围,避免安装后期指标不达标而重新调整。闭口试验段内型面的平面度、平行度、对称度及对角偏差等要求较高,而内腔型面共由14块壁板组成(上、下各由5块壁板组成,左、右各由2块壁板组成),各壁板尺寸大、刚度不一,壁板之间须互相协调才能达到型面要求。因此,闭口试验段壁板装配应根据不同的壁板形式,确定不同的调整方式,如采用拉(顶)杆使壁板产生强制变形以满足平面度要求,增加壁板间的连接装置使壁板阶差满足要求等[16]。通过采用上述方法,该闭口试验段各安装指标均达到要求。
5 结 论
1)经试验表明:闭口试验段在最高风速130 m/s的工况下能够安全稳定运行。试验段的加工精度满足试验要求,各风速工况下模型中心区气流湍流度< 0.05%;在常用风速条件下,调节扩散角尺寸,轴向静压梯度满足了设计指标(≤0.003)的要求。
2)闭口试验段高精度定位和可移动的功能特点,满足了腹撑、尾撑、半模、地效、活动地板(单带)等试验功能的需求。
3)闭口试验段的定位与锁紧、提升机构等设计方案对同类型风洞的闭口试验段研制具有一定借鉴意义。
-
[1] Sarpkaya T. A critical review of the intrinsic nature of vortex-induced vibrations[J]. Journal of Fluids and Structures, 2004, 19(4):389-447. DOI: 10.1016/j.jfluidstructs.2004.02.005
[2] Stansby P K. The effects of end plates on the base pressure coefficient of a circular cylinder[J]. Aeronautical Journal, 1974, 78:36-37. https://www.researchgate.net/publication/285353239_The_effects_of_end_plates_on_the_base_pressure_coefficient_of_a_circular_cylinder?_sg=P7GV4ls58QYc4Hw9DIoV_okPNY0HGf_qoF6FQsJNyU-1RYTtjYyPlTMKJdnOslzRDTxFVXUvi-bKf8Q4bVz3NQ
[3] Fox T A, West G S. On the use of end plates with circular cylinders[J]. Experiments in Fluids, 1990, 9(4):237-239. DOI: 10.1007/BF00190426
[4] Inagaki A, Mino Y, Iwamoto M, et al. Aspect ratio and end wall effects on the surface pressure coefficient of a circular cylinder[J]. Journal of Fluid Science and Technology, 2014, 9(3):JFST0062-JFST0062. DOI: 10.1299/jfst.2014jfst0062
[5] 郑云飞, 刘庆宽, 马文勇, 等.端部状态对斜拉索节段模型气动特性的影响[J].工程力学, 2017, 34(S1):192-196. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx2017z1033 Zheng Y F, Liu Q K, Ma W Y, et al. Influence of end conditions on aerodynamic force of section models for stay-cables[J]. Engineering Mechanics, 2017, 34(S1):192-196. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gclx2017z1033
[6] Shirakashi M, Hasegawa A, Wakiya S. Effect of the secondary flow on Karman vortex shedding from a yawed cylinder[J]. Bulletin of JSME, 1986, 29(250):1124-1128. DOI: 10.1299/jsme1958.29.1124
[7] Matsumoto M. Vortex shedding of bluff bodies:a review[J]. Journal of Fluids and Structures, 1999, 13(7-8):791-811. DOI: 10.1006/jfls.1999.0249
[8] Hayashi T, Kawamura T. Non-uniformity in a flow around a yawed circular cylinder[J]. Flow Measurement and Instrumentation, 1995, 6(1):33-39. https://www.researchgate.net/publication/245218732_Non-uniformity_in_a_flow_around_a_yawed_circular_cylinder
[9] 顾明, 杜晓庆.不同风向角下斜拉桥拉索模型测压试验研究[J].振动与冲击, 2005, 24(6):5-8, 20. DOI: 10.3969/j.issn.1000-3835.2005.06.002 Gu M, Du X Q. Testing study on wind pressures on a stayed cable model under different wind angles[J]. Journal of vibration and shock, 2005, 24(6):5-8, 20. DOI: 10.3969/j.issn.1000-3835.2005.06.002
[10] 李寿英, 顾明.斜、直圆柱绕流的CFD模拟[J].空气动力学学报, 2005, 23(2):222-227. DOI: 10.3969/j.issn.0258-1825.2005.02.017 Li S Y, Gu M. Numerical simulation for flow around perpendicular and oblique circular cylinders[J]. Acta Aerodynamica Sinica, 2005, 23(2):222-227. DOI: 10.3969/j.issn.0258-1825.2005.02.017
[11] Ma W Y, Liu Q K, Du X Q, et al. Aerodynamic forces and galloping instability for a skewed elliptical cylinder in a flow at the critical Reynolds number[J]. Fluid Dynamics Research, 2017, 49(4):045509. DOI: 10.1088/1873-7005/aa7704
[12] 马文勇, 刘庆宽, 刘小兵, 等.风洞试验中测压管路信号畸变及修正研究[J].实验流体力学, 2013, 27(4):71-77. DOI: 10.3969/j.issn.1672-9897.2013.04.013 Ma W Y, Liu X K, Liu X B, et al. Study on correction and distortioneffects caused by tubing systems of pressure measurements in wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(4):71-77. DOI: 10.3969/j.issn.1672-9897.2013.04.013
[13] Zdravkovich M M. Flow around circular cylinder[M]. Oxford:Oxford University Press, 1997.
[14] Humphreys J S. On a circular cylinder in a steady wind at transition Reynolds numbers[J]. Journal of Fluid Mechanics, 1960, 9(4):603-612. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=S0022112060001341
[15] 郑云飞, 刘庆宽, 马文勇, 等.端板对二维矩形风洞试验模型气动特性的影响[J].实验流体力学, 2017, 31(3):38-45. http://www.syltlx.com/CN/abstract/abstract11022.shtml Zheng Y F, Liu Q K, Ma W Y, et al. Effects of end plates on aerodynamic force of rectangular prisms in wind tunnel test[J]. Journal of Experiments in Fluid Mechanics, 2017, 31(3):38-45. http://www.syltlx.com/CN/abstract/abstract11022.shtml
[16] ESDU. Mean forces, pressures and flow field velocities for circular cylindrical structures: Single cylinder with two-dimensional flow, ESDU 80025[R]. London, UK: Engineering Sciences Data Unit, 1980.
[17] 梁辉, 姜胜耀, 段日强.有限长倾斜圆柱绕流的展向特性研究[C]//第十四届全国反应堆热工流体学术会议暨中核核反应堆热工水力技术重点实验室2015年度学术年会论文集. 2015. Liang H, Jiang S Y, Duan R Q. Spanwise Characteristics of flow crossing a yawed circular cylinder[C]//Proc of the 14th National Symposium on reactor thermal fluid. 2015.
[18] Hayashi T, Yoshino F, Waka R, et al. Pressure distribution on the surface of a yawed circular cylinder (the effect of end-plates on the spanwise pressure distribution)[J]. Transactions of the Japan Society of Mechanical Engineers Series B. 1992, 58(545):71-78. DOI: 10.1299/kikaib.58.71







 下载:
下载: