Development and application of the measurement system for thrust vectoring tests at 2.4m×2.4m transonic wind tunnel
-
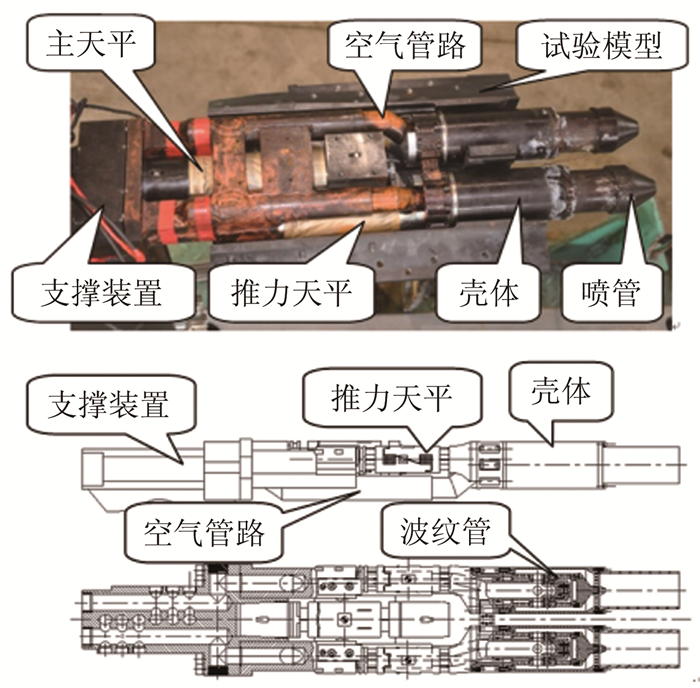
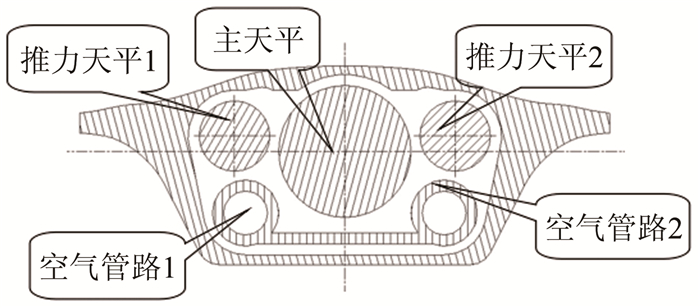
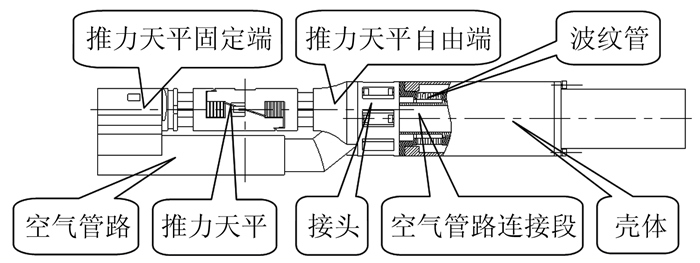
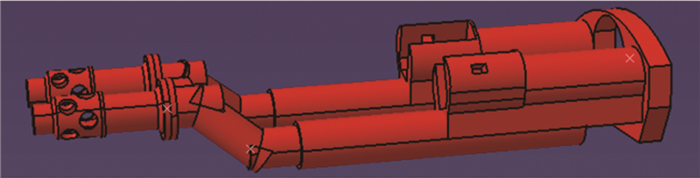
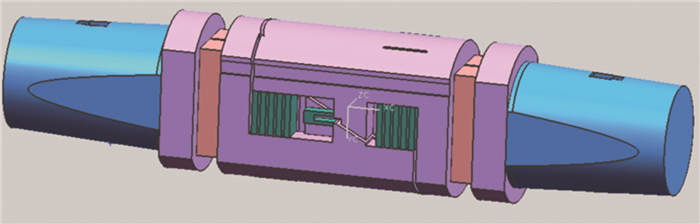
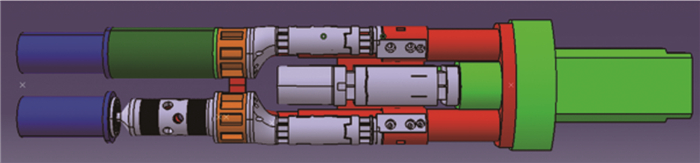
摘要: 推力矢量控制（TVC）技术能实现飞行器过失速机动飞行，使飞行器突破失速障、增强机敏性，在改善起降性能、巡航性能等方面具有重要作用。在2.4m跨声速风洞推力矢量试验中，采用3台六分量应变天平和2个独立的空气桥系统来实现飞机模型气动力和2个尾喷管转向喷流推进特性同时分别测量。推力矢量试验模型扁平外形使测力系统的布局及结构设计受到较大限制，狭小的模型内部需布置3台六分量天平、2套独立的空气桥系统及管路、支撑系统、压力测量系统等，采用传统方式无法完成如此复杂的系统设计，更无法完成高压条件下空气桥系统与测力天平的匹配设计。在测力系统的研制中，采用了一体化设计理念和刚度匹配设计方法，结合ANSYS有限元软件较好地解决了系统各部件的布局及结构优化等问题。天平校准结果和风洞试验结果证明测力系统满足推力矢量试验需求。Abstract: The thrust vectoring control (TVC) technology enables aircraft to fly in post-stall maneuver, which is very important for breaking through obstacle stall, enhancing mobility and improving take-off/landing and cruise performance. For TVC test at 2.4m×2.4m transonic wind tunnel, three six-component strain-gauge balances and two separate air systems are applied to respectively measure the performance of the whole model and nozzles at the same time. The thrust vector test model is flat, so that the layout and structure design of the measurement system is constrained. In the small internal model, it is very difficult to set up three six-component balances, two separate air bridge systems and pipeline, a supporting system, a pressure measurement system and so on. The complex system design cannot be realized by traditional methods and neither can the matching design of the air bridge system and the force balance under the condition of high pressure be accomplished. In the development of the measurement system, the integrated design concept and the stiffness matching design method are adopted. Combined with ANSYS finite element software, the layout and structure optimization of each component of the system have been solved. The results of balance calibration and wind tunnel test prove that the measurement system meets the requirement of thrust vector test.
-
Keywords:
- thrust vector /
- wind tunnel balance /
- finite element /
- calibration
-
0 引言
翼型是飞机机翼、尾翼等空气动力部件的核心要素, 在研制新翼型的过程中必须采用风洞实验验证其各项气动力特性。翼型的升力和阻力是其气动力特性至关重要的气动参数, 一般来说, 翼型阻力比升力小一个数量级, 精确测量阻力相对更加困难, 发展实用可靠的翼型阻力精细测量技术具有十分重要的工程应用价值。
在风洞实验中, 一般采用尾迹积分法测量翼型阻力, 即在翼型下游某截面安装尾耙, 通过测量该截面的总压、静压获得该截面的动量损失, 再对动量损失进行积分获得翼型阻力。尾耙的高度和安装位置等因素对翼型阻力测量存在一定影响:(1)尾耙的安装位置会直接影响阻力测量的精度。如果尾耙安装位置离翼型太近, 尾耙会对翼型绕流产生干扰, 改变翼型压力分布, 而且尾迹区动量损失曲线形状会过于"尖瘦", 对其进行积分计算阻力时会带来较大误差; 如果尾耙安装位置离翼型过远, 虽然动量损失曲线足够"肥胖"光滑, 但其一部分可能会超出尾耙测点区域, 也会给积分带来较大误差, 影响阻力测量精度。对于低速风洞, 尾耙一般安装于翼型下游0.5~1倍弦长处; 而对于高速风洞, 由于尾耙对翼型的扰动增大, 位置一般更靠后一些。(2)尾耙的高度以能捕获整个翼型尾迹为原则, 一般都大于1倍翼型弦长。对于翼型大迎角实验和高速实验, 其尾迹区的宽度较大, 尾耙高度宜选择大一些(可能需3倍弦长以上)。而在满足强度和刚度的条件下, 尾耙的其他尺寸应尽量小一些, 以减少对流场的干扰。
Taylor[1]、Bollay[2]和Goett[3]等最早研究发现尾迹截面的位置对阻力测量的影响, 当尾迹截面距离翼型后缘过近会导致计算误差较大; Vinh[4]通过数值模拟研究在大气中采用尾迹积分法计算单个翼型阻力时发现, 一般在翼型下游4~5倍弦长以后, 尾迹积分的位置对阻力计算结果几乎无影响。周瑞兴等[5]进行了尾迹法测量阻力的研究, 设计了头部15°倒角的总压探头, 保证了在流线有很大偏角时仍能测得比较准确的总压值; 焦予秦、支真莉[6-7]改进了低速风洞中以尾迹动量损失积分法测量翼型阻力的积分公式, 加入了压差影响和气流偏角影响, 得到了更好的高升力构型的阻力测量结果。以上工作均是针对低速实验进行研究, 对于跨声速实验, 周伟等[8]以数值模拟方法研究了风洞中尾耙的轴向安装位置对阻力测量的影响, 得出了"尾耙安装于翼型下游2倍弦长之后的测量值比较可靠"的结论。
在西北工业大学NF-6增压连续式跨声速翼型风洞中, 大多采用安装于翼型下游1.35倍弦长处的尾耙测量阻力。研究结果表明, 此处尾耙离翼型较近, 影响阻力测量结果。在文献的基础上, 根据风洞实际结构, 在翼型下游2.90倍弦长处的风洞侧壁上加工槽缝、安装尾耙进行实验, 对比分析了离模型较近及离模型足够远的尾耙阻力测量结果。另外, 对常用尾耙的多次实验结果分析发现, 在较大迎角或较大马赫数下, 尾耙高度不足以完全覆盖动量损失范围。需基于测得的动量损失曲线得到合适的尾耙高度, 且考虑尾耙位置后移需要更大的尾耙高度, 设计新的尾耙进行实验。
本文采用2个不同高度的尾耙, 在西北工业大学NF-6跨声速风洞实验段的2个轴向安装位置进行同一翼型实验, 通过对比分析同一尾耙高度、不同安装位置以及同一安装位置、不同尾耙高度的阻力实验数据, 获得不同实验条件下合适的尾耙高度及安装位置的组合, 改进NF-6风洞阻力测量精度。
1 实验风洞和模型
实验在西北工业大学NF-6增压连续式跨声速翼型风洞二元实验段进行。实验段尺寸为0.8 m×0.4 m×3 m (高×宽×长), 上下壁为开孔壁, 左右壁为实壁[9]。实验模型为OA309旋翼翼型(弦长c=200 mm), 展长为400 mm。图 1为翼型和尾耙在风洞中的安装照片。
2 阻力测量方法和尾耙
实验中, 以尾耙测量尾迹横截面的动量损失。尾耙上布置总压探针和静压探针。总压探针测量其前端所在的风洞横截面位置的总压(一般总压沿垂直于上下壁面的方向是变化的); 静压探针数量较少, 一般取其测得的平均值作为该横截面上的静压值。
实验中使用2种不同高度的尾耙。A尾耙竖向高度为270 mm(总压探针测量范围为260 mm), B尾耙竖向高度为500 mm(总压探针测量范围为480 mm); A、B尾耙的其他外形尺寸一致。尾耙的2个轴向安装位置分别为1位置和2位置。尾耙安装在1位置时, 总压探针前端距翼型前缘距离为470 mm, 即总压探针前端距离翼型后缘1.35 c(弦长c＝200 mm); 尾耙安装在2位置时, 总压探针前端距离翼型后缘2.90 c。
A尾耙的几何数据如图 2所示。尾耙上共有53根总压探针, 编号为1~53, 上下两端探针分布较疏、中间较密, 探针之间的距离为5 mm×17+4 mm×20+5 mm×17;4根静压探针均布, 编号为54~57。B尾耙探针分布和A尾耙类似:总压探针共103根(5 mm×32+4 mm×40+5 mm×32); 4根静压探针均布。
如图 3所示, 取控制体0截面-Ⅰ截面。0截面在翼型远前方, 此处气流未受翼型扰动, 来流静压和总压分别为p∞、p0; Ⅰ截面在翼型下游无限远, 此处气流静压已恢复至来流静压p∞, 总压为p0, 1, 根据动量定理可得翼型阻力Q[10]:
![]()
图 3 风洞中动量法测翼型阻力原理图Fig. 3 Principles for drag measurement with momentum method in wind tunnel
(1) 式中, ρ为气体密度, v∞为来流速度, v1为Ⅰ截面气流速度, y为纵坐标方向。
由于Ⅰ截面在翼型下游无限远处, 尾迹范围无限大, 不可能在该处安装尾耙测量阻力, 因此, 在翼型下游适当位置取Ⅱ截面安装尾耙。假设尾耙测量截面尾迹内的静压已保持为常数, 并且气流在Ⅰ截面-Ⅱ截面之间没有能量损失, 则尾耙测量截面尾迹内的总压也为p0, 1; 而在尾迹之外, 认为气流没有能量损失, 因此总压p0保持不变。定义Ⅱ截面尾耙处气流总压、静压分别为p0, w、pw。
对于高速风洞实验, 风洞中各截面的气流密度并不相同。在Ⅱ截面处, 对式(1)进行推导可得翼型阻力系数CD为[6, 10-12]:
(2) 式中, CD, wt为空风洞时风洞本身流动损失引起的阻力系数, h为尾耙高度, lm为Ⅱ截面处的无量纲单位高度上的动量损失(Momentum loss), 即:
(3) 式中, γ为气体比热比(空气中γ＝1.4)。
3 实验结果分析
3.1 尾耙不同安装位置对阻力测量的影响
将A尾耙分别安装在1和2位置进行实验。图 4给出了马赫数Ma＝0.50和0.80条件下A尾耙在1、2位置的阻力系数。可以看出:迎角α较小时, A尾耙在1、2位置的阻力系数差别不大; 随着迎角α增大(无论是较大的负迎角还是正迎角), 1位置的阻力系数大于2位置的阻力系数。
![]()
图 4 A尾耙在1、2位置处的阻力系数Fig. 4 Drag coefficient for wake rake A at installation position 1 and 2在Ma=0.50和0.80条件下, A尾耙在1、2位置的动量损失曲线如图 5和6所示。从图 5可以看出, 当迎角大于±10°, 2位置的尾迹动量损失范围超出了尾耙测量范围, 尾耙高度明显不够, 这样积分得到的阻力系数是不真实的; 从图 6可以看出, 2位置的尾迹动量损失范围超出尾耙测量范围的正迎角提前到9°, 负迎角提前到-8°, 说明随着马赫数增大, 同一迎角状态下尾迹动量损失范围扩大, 所需的尾耙高度更大。A尾耙安装在2位置, 其高度不足以覆盖尾迹范围, 测得的阻力系数值小于真实值, 这是2位置的阻力系数小于1位置的主要原因; 另外, 由于A尾耙在1位置时离翼型较近, 翼型扰动相对较大, 对阻力测量结果也会产生一定影响。
![]()
图 5 A尾耙在1、2位置的动量损失曲线(Ma=0.50)Fig. 5 The momentum loss curve for wake rake A at installation position 1 and 2 (Ma=0.50)![]()
图 6 A尾耙在1、2位置的动量损失曲线(Ma=0.80)Fig. 6 The momentum loss curve for wake rake A at installation position 1 and 2 (Ma=0.80)从动量损失曲线图还可以看出, 在小迎角条件下, 对尾迹动量损失曲线积分求阻力时, 2位置的积分计算结果更为精确, 因为1位置的动量损失曲线比2位置更为尖瘦。对比图 5和6的-2°和0°的动量损失曲线, 可以看出:1位置的尾迹中心区动量损失变化十分剧烈, 竖向范围较小, 尾迹中心区总压探针相对较少, 积分求阻力可能会产生一定误差; 而尾耙后移至2位置时, 相同状态下动量损失的峰值减小、竖向范围扩大, 尾迹中心区的总压探针增多, 积分结果更为精确。
3.2 不同尾耙高度对阻力测量的影响
上节实验结果验证了尾耙安装在1位置时过于靠近翼型, 阻力系数测量结果不精确; 当尾耙后移至2位置时, A尾耙的高度不够。本节以尾耙高度更高的B尾耙在2位置进行实验。
图 7给出了Ma=0.50、0.70条件下, A、B尾耙在2位置的阻力系数, 图 8和9为Ma=0.50、0.70条件下A、B尾耙在2位置的动量损失曲线。
![]()
图 7 A、B尾耙在2位置的阻力系数Fig. 7 Drag coefficients for wake rake A and B in installation position 2![]()
图 8 A、B尾耙在2位置的动量损失曲线(Ma=0.50)Fig. 8 The momentum loss curve for wake rake A and B in installation position 2 (Ma=0.50)![]()
图 9 A、B尾耙在2位置的动量损失曲线(Ma=0.70)Fig. 9 The momentum loss curve for wake rake A and B at installation position 2 (Ma=0.70)从图 7可以看出, 整体上, B尾耙的阻力系数略大于A尾耙, 这是因为B尾耙竖向高度较大, 洞壁干扰和堵塞干扰等相应增大, 尾耙本身对阻力测量结果造成较大影响。在大迎角时, 2位置的B尾耙的阻力系数比A尾耙大得多, 除因B尾耙高度较大造成的影响外, 根据图 8和9可以看出, 主要原因是此时A尾耙的高度并未完全覆盖尾迹动量损失范围, 计算所得的阻力系数是不正确的, 比B尾耙测得的阻力系数小是合理的。
另外, 从图 8和9还可以看出:B尾耙的动量损失曲线光滑性较差(尤其是迎角较小时), 积分求得的阻力系数可能存在一定误差; 随着迎角和马赫数增大, 曲线变得更为光滑, 积分所得的阻力系数误差随之减小。
4 结论
本文对西北工业大学NF-6增压连续式跨声速风洞翼型阻力测量精度改进方法进行了研究, 对比分析了2种尾耙高度和安装位置对阻力测量结果的影响, 得出以下结论:
(1) 当实验迎角和马赫数较小时, 采用较小高度的A尾耙(高270 mm)安装于2位置(尾耙总压探针前端距离翼型后缘2.90倍弦长)进行实验比较合适。
(2) 当实验迎角或实验马赫数较大时, 应考虑采用B尾耙(高500 mm)安装于2位置(尾耙总压探针前端距离翼型后缘2.90倍弦长)进行实验。
-
表 1 天平设计载荷
Table 1 Design load of balance
名称 Y
/NMz
/(N·m)X
/NMx
/(N·m)Z
/NMy
/(N·m)全机天平 15000 1000 1200 480 2200 500 推力天平 1200 200 800 50 1200 200 
下载: 导出CSV
表 2 全机天平计算应变
Table 2 The calculated strain of primary balance
名称 Y Mz X Mx Z My 贴片处应变(×10-6) 445 480 390 270 170 340
下载: 导出CSV
表 3 推力天平的计算应变
Table 3 The calculated strain of thrust balance
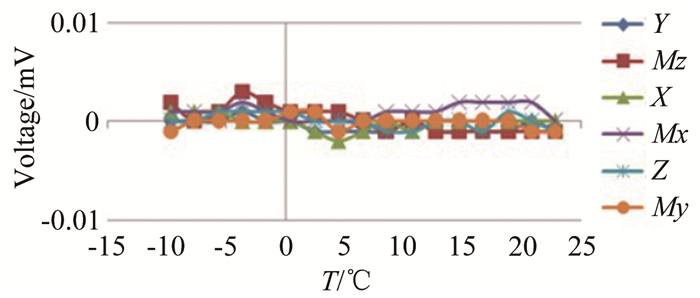
应变(×10-6) Y Mz X Mx Z My 推力天平 205 560 270 175 207 558 推力天平带空气桥系统 0MPa 204 440 268 141 204 478 1MPa 198 400 267 140 203 442 2MPa 191 370 266 137 201 402
下载: 导出CSV
表 4 全机天平校准结果
Table 4 Calibration result of the primary balance
Y Mz X Mx Z My 校准不确定度/% 0.08 0.09 0.11 0.15 0.10 0.12
下载: 导出CSV
表 5 推力天平1校准结果
Table 5 Calibration result of the thrust balance 1
校准不确定度/% Y Mz X Mx Z My 推力天平 0.03 0.02 0.06 0.20 0.05 0.05 推力天平带空气桥系统 0MPa 0.30 0.20 0.10 0.90 0.14 0.19 1MPa 0.35 0.30 0.11 1.00 0.20 0.24 2MPa 0.50 0.45 0.11 1.50 0.30 0.30 60g/s 0.32 0.16 0.12 0.91 0.20 0.21 100g/s 0.50 0.22 0.20 1.00 0.23 0.30 200g/s 0.60 0.33 0.27 0.89 0.30 0.34
下载: 导出CSV
-
[1] 曲东才.推力矢量控制技术发展及关键技术分析[J].航空科学技术, 2002, (3):30-33. http://www.cqvip.com/QK/97819X/200203/6318569.html Qu D C. Development for thrust vector control technology and analysis for critical technology[J]. Acronantical Science and Technology, 2002, (3):30-33. http://www.cqvip.com/QK/97819X/200203/6318569.html
[2] 贾毅, 郑芳, 黄浩, 等.低速风洞推力矢量试验技术研究[J].实验流体力学, 2014, 28(6):92-97. http://www.syltlx.com/CN/abstract/abstract10796.shtml Jia Y, Zheng F, Huang H, et al. Research on vectoring thrust test technology in low-speed wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(6):92-97. http://www.syltlx.com/CN/abstract/abstract10796.shtml
[3] Smith C L, Riddle T R. Jet effects testing considerations for the next-generation long-range strike aircraft[R]. AIAA-2008-1621, 2008. DOI: 10.2514/6.2008-1621
[4] Crose J, Mack T, Marx D. NASA/MFSC nozzle test bed[R]. AIAA-89-2871, 1989. DOI: 10.2514/6.1989-2871
[5] 付尧明, 王强, 额日其太, 等.矢量喷管六分量测力试验台的研制[J].流体力学实验与测量, 2002, 16(1):87-93. http://d.wanfangdata.com.cn/Periodical/ltlxsyycl200201014 Fu Y M, Wang Q, Eriqitai, et al. Development of the six-component force-measuring balance for thrust-vectoring nozzle testing[J]. Experiments and Measurements in Fluid Mechanics, 2002, 16(1):87-93. http://d.wanfangdata.com.cn/Periodical/ltlxsyycl200201014
[6] 贺伟, 童泽润, 李宏斌.单模块超燃发动机推力测量天平研制[J].航空动力学报, 2010, 25(10):2285-2289. http://www.cnki.com.cn/Article/CJFDTOTAL-DJZD201402033.htm He W, Tong Z R, Li H B. Investigation of thrust balance for the single module scramjet[J]. Journal of Aerospace Power, 2010, 25(10):2285-2289. http://www.cnki.com.cn/Article/CJFDTOTAL-DJZD201402033.htm
[7] 章荣平, 王勋年, 黄勇, 等.低速风洞全模TPS试验空气桥的设计与优化[J].实验流体力学, 2012, 26(6):48-52. http://www.syltlx.com/CN/abstract/abstract10476.shtml Zhang R P, Wang X N, Huang Y, et al. Design and optimization of the air bridge for low speed full-span TPS test[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(6):48-52. http://www.syltlx.com/CN/abstract/abstract10476.shtml
[8] 王超, 林俊.天平与波纹管系统结构设计与有限元分析[J].实验流体力学, 2013, 27(3):77-92. http://www.syltlx.com/CN/abstract/abstract10437.shtml Wang C, Lin J. Structure design and finite element analysis on system of balance and bellows[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(3):77-92. http://www.syltlx.com/CN/abstract/abstract10437.shtml
[9] 刘岩, 段玫, 张道伟.波纹管应力分析研究进展[J].管道技术与设备, 2006, (4):31-33. http://www.cqvip.com/QK/97879X/200604/22690496.html Liu Y, Duan M, Zhang D W. Development of stress analysis of bellows[J]. Pipeline Technique and Equipment, 2006, (4):31-33. http://www.cqvip.com/QK/97879X/200604/22690496.html
[10] 哈力旦·木沙, 买买提依明·艾尼.机械密封焊接金属波纹管膜片结构的有限元分析[J].新疆大学学报(自然科学版), 2007, 24(4):490-494. http://www.doc88.com/p-340625080328.html Halidan Musha, Mamaitiming Aini. FEM analysis of metal welded bellow wave of mechanical seal[J]. Journal of Xinjiang University (Natural Science Edition), 2007, 24(4):490-494. http://www.doc88.com/p-340625080328.html
[11] 刘高计, 谌满荣, 于卫青.风洞应变天平优化设计方法研究[J].弹箭与制导学报, 2006, 26(2):94-97. http://d.wanfangdata.com.cn/Periodical/djyzdxb200602033 Liu G J, Chen M R, Yu W Q. The research of optimum design method of strain-gauge balance in wind-tunnel[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2006, 26(2):94-97. http://d.wanfangdata.com.cn/Periodical/djyzdxb200602033
[12] Braman K B, Schweikhard W G, Yechout T R. Thrust modeling:A simplified in-flight thrust and airflow prediction technique for flight test performance measurements[R]. AIAA-83-2751, 1983. https://www.researchgate.net/publication/268462374_Thrust_modeling_-_A_simplified_in-flight_thrust_and_airflow_prediction_technique_for_flight_test_performance_measurements
[13] Wong K C. Derivation of the data reduction equations for the calibration of the six-component thrust stand in the CE-22 advanced nozzle test facility[R]. NASA/TM 2003-212326. https://www.researchgate.net/publication/24293133_Derivation_of_the_Data_Reduction_Equations_for_the_Calibration_of_the_Six-Component_Thrust_Stand_in_the_CE-22_Advanced_Nozzle_Test_Facility
[14] Booth D, Ulbrich N. Calibration and data analysis of the MC-130 air balance[C]. 8th International Symposium on Strain-Gauge Balances, Ameron Hotel Flora, Lucerne, Switzerland, 2012. DOI: 10.2514/6.2013-545
-
期刊类型引用(18)
1. 韩笑，高创，郑怡彤，刘小兵. 切角凹槽矩形截面桥塔的气动特性试验研究. 石家庄铁道大学学报(自然科学版). 2024(01): 9-15+23 . 
百度学术
2. 白桦，刘博祥，姬乃川，李加武. 节段模型二元端板合理尺寸估算方法. 振动与冲击. 2023(02): 312-320 . 百度学术
3. 王仰雪，刘庆宽，靖洪淼，李震，孙一飞. 倾斜栏杆对流线型箱梁涡激振动性能影响的试验研究. 振动与冲击. 2023(06): 232-239+254 . 百度学术
4. 于畅，仇法梅，田学东，杨群，刘小兵. 圆角矩形柱平均气动力特性的雷诺数效应试验研究. 石家庄铁道大学学报(自然科学版). 2023(02): 29-34 . 百度学术
5. 杨群，于畅，刘小兵，刘庆宽. 不同圆角率的方形断面斯特罗哈数的雷诺数效应研究. 振动与冲击. 2023(11): 223-231 . 百度学术
6. 刘庆宽，王仰雪，孙一飞，李震，韩原，靖洪淼. 栏杆高度对流线型箱梁涡振性能影响的试验研究. 湖南大学学报(自然科学版). 2023(07): 140-150 . 百度学术
7. 刘路路，杨皓然，邹云峰，何旭辉，韩艳，陈志强. 公铁同层双幅非对称主梁气动干扰特性研究. 铁道科学与工程学报. 2023(10): 3861-3872 . 百度学术
8. 杨群，于畅，于文文，刘小兵. 圆角方柱气动特性的风洞试验研究. 振动与冲击. 2023(24): 59-68 . 百度学术
9. 韩振，李波，甄伟，杨庆山，田玉基. 宽厚比为5的超高层建筑风荷载特性研究. 哈尔滨工程大学学报. 2022(02): 196-202 . 百度学术
10. 张庆华，马文勇，杨杰，张彦，周帅伟. 不同风倾角下典型等边角钢静风力风洞试验研究. 振动工程学报. 2022(02): 277-283 . 百度学术
11. 白桦，王涵，姬乃川，李加武. 节段模型长宽比对风洞测力试验及计算分析的影响. 中国公路学报. 2022(08): 202-212 . 百度学术
12. 杨群，刘庆宽，韩瑞，刘小兵. 不同圆角率的方形断面气动特性的雷诺数效应. 振动与冲击. 2020(04): 150-156 . 百度学术
13. 沈国辉，姚剑锋，郭勇，邢月龙，楼文娟. 直径30 cm圆柱的气动力参数和绕流特性研究. 振动与冲击. 2020(06): 22-28 . 百度学术
14. 温青，池俊豪，华旭刚，王修勇，孙洪鑫. 端部条件和展弦比对矩形断面节段模型气动力特征的影响. 实验流体力学. 2020(04): 36-43 . 本站查看
15. 任若松，梁新华，刘小兵，马文勇，刘庆宽. 准流线型桥梁断面气动力特性的雷诺数效应研究. 工程力学. 2020(S1): 139-144+167 . 百度学术
16. 李海飞，梁新华，孙一飞，崔会敏，刘庆宽. 流线型桥梁断面表面脉动风荷载特性研究. 工程力学. 2020(S1): 242-248+260 . 百度学术
17. 马文勇，汪冠亚，郑熙，陈铁，李智，张程远，方平治. 端部状态对斜置圆柱气动力分布的影响. 实验流体力学. 2019(02): 43-50 . 本站查看
34. 杨群，刘庆宽，孙亚松，刘小兵. 圆角方形断面气动特性试验. 振动.测试与诊断. 2020(01): 140-147+208 . 百度学术
其他类型引用(16)
计量
- 文章访问数: 174
- HTML全文浏览量: 88
- PDF下载量: 14
- 被引次数: 34
