Deformation and breakup behaviors of a drop in ambient liquid under impact
-
摘要: 采用基于液-液体系的坠落实验装置对冲击作用下单个液滴在环境液体中的变形破碎行为进行了实验研究。针对高速摄影捕捉到的5种液滴典型变形破碎模式进行了定量化考察和规律性分析。结果表明,液滴初始直径、液滴与环境液体的密度比和粘度比、界面张力系数以及坠落高度等实验参数相互组合可以得到相似的实验结果,其中We数是区分液滴变形破碎模式的关键参数。进一步研究液滴变形破碎模式与无量纲参数的依赖关系发现,在1 < We < 700、0.001 < Oh < 0.005的实验条件范围内,液滴变形破碎模式与Oh数无明显依赖关系,而在We数相近情况下,液滴变形破碎模式呈现明显的相似性。Abstract: In this study, we carry out an experimental investigation of the behaviors as well as the mechanism of the liquid-liquid drop deformation and breakup process following an impact. With high speed photography, five distinct deformation and breakup modes are captured, for which the key factors that dominate the transition are quantitatively analyzed. The results show that similar deformation behaviors may occur for a proper combination of drop sizes, density ratios between drop and ambient fluid, interfacial tensions and free falling heights. Two non-dimensional parameters, i.e. Weber number (We) and Ohnesorge number (Oh), are calculated to estimate these effects. It is found that, similar deformation behaviors may have a strong correlation with the Weber number. After a further survey of the test range of present study (1 < We < 700, 0.001 < Oh < 0.005), it can be concluded that the deformation and breakup pattern is barely affected by the Ohnesorge number, whereas exhibits a strong dependence on the Weber number.
-
0 引言
直升机在波浪水面稳定漂浮、抗沉、人员应急撤离等能力是其漂浮特性的综合体现。漂浮特性优良是直升机水上迫降/降落的先决条件,也是直升机具备稳定漂浮以保证机内乘员应急逃生、机体装置顺利回收的必要条件。对于任何跨海飞行的直升机而言,都必须开展全面的水上迫降漂浮特性能力分析和验证研究,以确定直升机的稳定漂浮海况条件和极限倾覆边界[1]。
自20世纪50年代开始,国外就针对直升机水上迫降、漂浮性能开展了深入的理论和试验研究,并大量采用了加装应急浮囊系统及优化应急浮囊结构布局的方式来提升直升机的水面漂浮性能。1954年,英国Saunders-Roe有限公司(现英国地效飞行器有限公司)首次利用模型试验研究了结构选型、缩尺比例对直升机水上迫降性能的影响,并基于研究结论首次提出了适用于直升机水上迫降及漂浮特性研究的模型制作要求和试验流程[2]。基于已有的试验手段,该公司于1968年通过模型试验对贝尔206A直升机在恶劣海况下的漂浮特性展开了研究。结果表明,即使在波陡比为1:12~1:10的临界破碎波状态,直升机仍具有较好的稳定漂浮能力而不发生倾覆[3]。英国韦斯特兰公司基于EH101直升机开展了系统的自动漂浮充气系统设计和模型试验研究,研究结果表明:在4级海况条件下,加装应急漂浮系统的EH101直升机在前后浮筒打开后,能快速以最佳角度承受海浪直立漂浮,具备了优良的漂浮性能[4]。美国海军利用水池模型试验,对安装应急漂浮系统的“超海妖”直升机模型进行了5级海况条件下的稳定性和耐波性能力验证研究[5]。大量试验数据和研究经验为国外的直升机着水及漂浮特性试验研究技术奠定了坚实的基础。
随着应急浮囊在直升机领域的不断应用,我国在21世纪初也开始将加装应急浮囊直升机的水面冲击特性、着水后运动特性、漂浮特性等作为研究重点。中国直升机设计研究所采用模型试验方法,对某机型在静水、规则波条件下的着水安全范围进行了研究[6]。中国船舶科学研究中心、中国特种飞行器研究所结合直升机的结构特点,采用时域数值计算方法对直升机在随机波中的横向漂浮稳定性进行了计算分析[7-8]。黄鑫锋分别采用理论分析和数值模拟方法对直升机横倾稳定性和应急气囊对直升机运动响应影响特性进行了研究,并验证了分析方法的准确性[9]。
国外在研究直升机的漂浮特性时,往往采用带漂浮装置的大缩比模型,模型的材料属性、内部(含浮囊)舱壁划分、布局构造、应急出口位置和分布等均与实机进行了近似模拟。试验时,基于静水、规则波和不规则波水面条件对直升机的静稳定性、动态运动响应、倾覆边界和漂浮时间进行研究。其研究结果能为实机迫降和应急撤离程序编制(如有效运营海况范围、应急出口布局合理性、迫降时舱门的抛投可行性以及有利漂浮姿态范围等)提供有利依据。国内在直升机漂浮特性的试验研究方面开展的工作较少,在直升机的漂浮特性试验方法和影响参数研究方面尚未形成体系,也无相关技术条款对其进行规范和要求,与国外的差距较大。针对我国直升机漂浮特性试验技术方面的技术瓶颈,本文以某直升机背景机型为研究对象,开展了系列变试验参数的规则波模型水池试验,重点考察直升机在水面漂浮过程中的运动规律和纠偏能力;基于模型运动情况,初步探索了浮囊强度、约束条件和浪向对直升机漂浮特性的影响,并提出适用于直升机漂浮特性的模型试验方法和试验建议。研究结果可为同类机型的漂浮能力测试和应急漂浮系统能力验证提供参考。
1 试验设计
1.1 试验装置
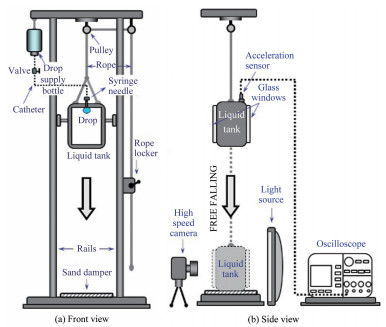
试验在中国特种飞行器研究所高速水动力航空科技重点实验室开展。试验方案如图 2所示,整个试验装置安装在试验支架下部,漂浮试验所需的附属保护装置固定于模型上,模型的首部和尾部导航片安装于支架底板的导航杆上,安装时应保证导航片的中心线沿竖直方向,以限制模型偏航运动,安装完成后,将附属装置穿入导航片中。
需说明的是,限定浪向和偏移的漂浮特性试验通常可实现模型四自由度运动,当需要开展全放开的六自由度运动和限定浪向的五自由度运动时,应将模型及其上的附属保护装置从试验支架上释放,并利用附属装置对模型的初始浪向和运动安全性进行保护。
为保证试验过程中对模型运动姿态的实时监控,在直升机模型内部安装有微型数据采集系统、惯性测量单元、磁罗盘、传感器等测试仪器。其中,微型数据采集系统用于数据采集和记录,惯性测量单元用于模型运动姿态的测量,磁罗盘用于监测模型运动过程的航向变化情况,传感器用于测试模型的加速度变化参数。
1.2 试验程序
整个试验过程主要有如下3个步骤:
(1) 试验状态调试及准备。在平静水面条件下,调整模型初始状态,确保模型纵向与波浪传播方向符合试验状态要求,并对机身内部安装的测试仪器进行初始数据监测和状态归零。
(2) 水面条件模拟及漂浮试验。在试验水域利用造波机制造指定参数的波浪。在不同波浪参数、约束条件和初始浪向条件下,测量直升机漂浮过程的横摇角、加速度变化情况。其中,横摇角记为φ,机头加速度记为AfZ,机身中部加速度记为AcZ。
(3) 水面及模型状态恢复。在完成对应状态的模型试验后,关闭造波机、收回模型,利用消波板消除水面余波。同时,对采集到的数据进行回收分析,确保数据可行后,恢复模型状态准备后续试验。
1.3 相似准则
直升机在迫降后的水面漂浮过程中,主要受到水流的阻碍和扰动作用。为此,直升机模型严格按照水面航行体的模拟相似条件(几何相似、运动相似及动力相似)和弗洛德数(Fr)相似准则进行缩比[10],模型与实机的比例关系如表 1所示。
表 1 比例关系(λ表示模型的缩放比例)Table 1 The proportional relationship (λ is the scale of the model)名称 模型值 模型缩放比例 实机尺寸 长度 L λ λL 力 F λ3 λ3F 惯性矩 I λ5 λ5I 质量 m λ3 λ3m 时间 t 

速度 V 

线加速度 a 1 a 角速度 w 

1.4 试验状态
试验时,模型的重量、重心、惯性距等参数需基于实机参数按相似准则进行换算。规则波波浪参数根据实机的使用海域要求并结合试验设备的工作能力综合选取。根据CAA在2005年提出的直升机迫降试验建议,对于规则波试验,波陡应不高于1/10,且在指定波高内,波长的数量应不低于10个。具体参数的选取方法详见文献[10-12]。本次试验选取的波浪参数为:波高0.25 m、波长3~17 m。
整个漂浮特性试验共包含直升机刚性浮囊模型五自由度横浪规则波试验、直升机柔性浮囊模型五自由度横浪规则波试验和六自由度自由漂浮规则波试验等3项内容。
2 数据分析
直升机在水面自由漂浮时,航向会发生一定程度变化,图 3给出了加装柔性浮囊构型直升机的航向变化曲线。从图中可以看出,随着时间增长,直升机的航向变化较大;漂浮时间在28 s之前,直升机的遭遇浪向为横浪;其后浪向角β改变,并始终处于105°~160°范围内。为对试验数据进行有效整理和对比分析,基于船舶理论浪向规定,将发生浪向改变后的试验数据按照不同波浪类别进行划分,如图 4所示,并以此为依据开展后续试验数据分析。分析时主要基于各参数的双幅值运动参数进行处理。
3 试验结果及分析
3.1 直升机在规则波中的运动
基于耐波性分析原理,航行体在规则波面的摇荡运动可分解为横摇、升沉和纵摇3种运动状态。因直升机水面漂浮特性重点关注的是其横向稳定和平衡漂浮能力,故本文将研究重点确定为对横摇角度及相应加速度的变化规律分析。
图 5给出了规则波条件下,直升机的横摇角φ、机头加速度AfZ、机身中部加速度AcZ随时间的变化曲线。由图可知,直升机在规则波面中的运动呈现出显著的周期性变化规律,即因规则波扰动的影响,直升机做持续的强迫摇荡运动。
3.2 浮囊刚度对直升机漂浮特性的影响分析
图 6给出了加装不同刚度浮囊结构时,五自由度直升机模型在规则波横浪条件下的漂浮特性试验曲线,曲线表征了各响应参数双幅值随波长的变化情况。其中,图形纵坐标为单位模型长度对应的响应参数测试值。
从图中曲线可以看出,所选择的波长范围内,横摇角、加速度双幅值均呈现出显著的类线性变化趋势,即各参数幅值均随着波长增加而不断减小。
对不同浮囊材料而言,安装不同刚度的浮囊结构时,横摇、加速度随波长的变化曲线均存在一定差异,且刚性浮囊构型的曲线数值大于柔性浮囊构型的对应数值。从2种浮囊构型的曲线相差量来看,机头加速度AfZ、机身中部加速度AcZ和横摇角φ依次增加。具体地,机头加速度AfZ受浮囊刚度影响不大,机身中部加速度AcZ仅在波长较大时会受到浮囊刚性强度的影响,而横摇角φ受浮囊刚度影响的范围最广,除最大波长处两者数值相当外,在整个波长范围内两者的横摇角曲线差异显著。
造成这种差异的原因主要有两个方面:一方面,当直升机漂浮于水面时,刚性浮囊构型的吃水相对柔性浮囊结构更浅,机体表面受到的水动阻力也更小,在波浪水面条件下,更容易出现水面扰动引起的横向和纵向移动;另一方面,因刚性浮囊直升机机身干舷较高(水面以上的净面积较大),故更易遭受风、浪峰的冲击产生侧倾压力,摇荡运动会更为剧烈。
此外,从试验过程的模型偏转情况来看,当使用刚性浮囊构型时,直升机的航向角受波浪及外部环境影响较小,当直升机受到扰动,其航向变化缓慢且幅度较小,改变值通常可控制在10°以内。因此可认为直升机的“打横”(机身侧向迎浪)纠正能力较差。
3.3 约束度对直升机漂浮特性的影响分析
图 7给出了柔性浮囊构型的直升机分别在五自由度和六自由度规则波横浪条件下的漂浮特性试验曲线。
在所选择的波长范围内,横摇角φ、加速度双幅值随波长的变化情况与前文所述规律一致——呈现出类线性的减小趋势。
但对柔性浮囊构型的直升机而言,当分别采用不同约束条件开展试验时,相同浪向下的机头加速度AfZ双幅值相差不大。但自由度的增加会引起横摇角在小波长范围、机身中部加速度AcZ在全波长范围内的减小,说明约束度的全放开能一定程度减小上述参数的变化量。当采用五自由度模型试验代替自由漂浮特性试验时,附属装置会对直升机的真实运动特性造成不利干扰,基于该试验所得到的直升机漂浮运动能力将更为保守。
3.4 浪向对直升机漂浮特性的影响分析
图 8给出了加装柔性浮囊构型直升机在自由漂浮特性试验条件下不同浪向的试验曲线。
加装柔性浮囊构型的直升机在水面自由漂浮时,其航向会发生显著变化。当受到轻微波浪或外力干扰即发生较大幅度的偏航,以摆脱最不利的“打横”状态(机身侧向迎浪)。
当直升机处于不同浪向时,模型的运动响应数值均存在一定差异:其中,横摇角φ双幅值变化最为明显,在横浪条件下,横摇角φ双幅值最大,并随着浪向改变,该值大幅减小;但对机头加速度AfZ和机身中部加速度AcZ而言,浪向的变化并不会引起该参数的大幅改变,主要表现为小波长范围内横浪状态的机头加速度AfZ略大于其他浪向,其他浪向状态的机身中部加速度AcZ略大于横浪情况。随后,当波长继续增大,不论是机头加速度AfZ还是机身中部加速度AcZ,在其他浪向的幅值均大于横浪状态的对应数值。
综上所述,对不同浪向而言,运动响应的极值跨度较大,其中以横浪时的变化范围最大,其他浪向角时跨度较小,即横浪条件下直升机的摇荡最为剧烈。
4 结论
本文基于规则波水面条件,对不同浮囊刚度、试验约束条件和浪向范围的直升机漂浮响应特性进行了研究,通过分析各项试验数据,可得出如下结论:
(1) 直升机在水面漂浮时,横摇角、加速度双幅值均随着波长增加而不断减小——波长越长,运动幅度越小。
(2) 浮囊刚度对直升机的水面漂浮特性会产生较大影响。相同浪向条件下,加装刚性浮囊的直升机响应参数双幅值明显大于柔性浮囊构型。在开展模型试验时,建议以实机浮囊参数为基准,开展相应的模型材料、结构布局等效模拟设计,以确保基于模型的漂浮特性试验结果能真实反映直升机的响应特性。
(3) 从直升机的波浪运动特性来看,安装刚性浮囊的直升机航向变化能力较弱,无法自行掌控航向偏移而避开侧向迎浪,因而更易发生倾覆。为此,建议优先选择柔性浮囊作为漂浮逃生的迫降装置。
(4) 从基于不同约束度的试验结果来看,利用加约束的简化试验方式并不能很好地反映直升机的真实漂浮状态,且所得结论较为保守。为此,在试验条件允许的情况下,建议以完全自由漂浮状态开展类似试验。
(5) 直升机加装柔性浮囊自由漂浮时,不同浪向的运动响应呈现出较大差异。其中,初始的横浪状态横摇角双幅值、加速度双幅值最大,且浪向角变化越明显,运动响应数值减少越多。试验时,可将横浪作为直升机的水面漂浮最不利航向角,开展极限漂浮能力研究。
-
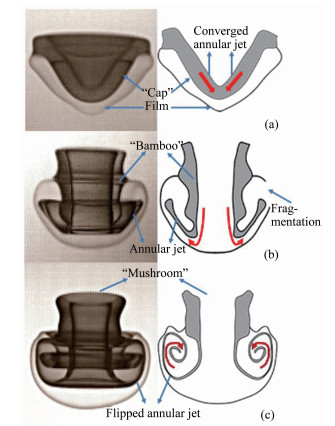
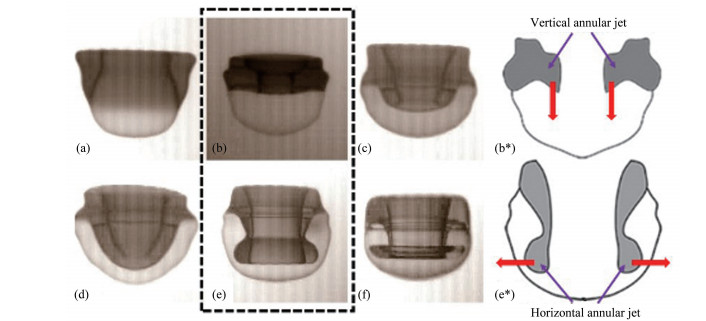
图 8 液滴变形破碎模式之间的转变过程图像,上行:(a)袋状模式,(b)过渡模式,(c)帽状模式,(b*)过渡模式剖视图;下行:(d)帽状模式,(e)过渡模式,(f)竹节状模式,(e*)过渡模式剖视图
Fig. 8 Transition between drop deformation and breakup modes, upper row: (a) bag mode, (b) transition mode, (c) cap mode, (b*) cross-sectional view of transition mode; lower row: (d) cap mode, (e) transition mode, (f) bamboo mode, (e*) Cross-sectional view of transition mode
表 1 液滴与环境液体的相关物性参数
Table 1 Related properties of drop and ambient fluid
Fluid type Density
/(g·cm-3)Viscosity
/(mPa·s)Interface tension coefficient
/(mN·m-1)Drop 1050~1630 0.6~2.4 14.49~25.01 Ambient fluid 1015~1035 2.8~4.6 表 2 液滴5种典型变形破碎模式所对应的实验条件
Table 2 Typical experimental conditions for five modes of drop deformation and breakup
Mode Fig.3 d0/mm ρd/ρa μd/μa σ/(mN·m-1) h/m A 7.2 1.129 0.705 25.01 0.3 B 6.0 1.170 0.296 16.50 0.8 C 6.0 1.170 0.296 16.50 1.5 D 4.3 1.523 0.202 15.49 0.6 E 4.7 1.567 0.142 14.69 1.3 Deformation Fig.5 d0/mm ρd/ρa μd/μa σ/(mN·m-1) h/m a1 6.0 1.170 0.296 16.50 0.60 a2 5.3 1.287 0.447 18.97 0.30 a3 5.0 1.434 0.352 18.62 0.15 b1 6.0 1.170 0.296 16.50 1.50 b2 6.2 1.344 0.417 18.63 0.50 b3 5.3 1.287 0.447 18.97 0.80 c1 4.3 1.523 0.202 15.49 0.60 c2 4.1 1.502 0.212 16.11 0.90 c3 4.2 1.563 0.161 14.69 0.60 -
[1] Lane W R. Shatter of drops in streams of air[J]. Ind Eng Chem, 1951, 43(6):1312-1317. DOI: 10.1021/ie50498a022
[2] Hinze J O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes[J]. AIChE Journal, 1955, 1(3):289-295. DOI: 10.1002/(ISSN)1547-5905
[3] Hanson A R, Domich E G, Adams H S. Shock tube investigation of the breakup of drops by air blasts[J]. Phys Fluids, 1963, 6(8):1070-1080. DOI: 10.1063/1.1706864
[4] Simpkins P G, Bales E L.Water-drop response to sudden acce-lerations[J]. J Fluid Mech, 1972, 55(4):629-639. DOI: 10.1017/S0022112072002058
[5] Krzeczkowski S A. Measurement of liquid droplet disintegration mechanisms[J]. Int J Multiphase Flow, 1980, 6(3):227-239. DOI: 10.1016/0301-9322(80)90013-0
[6] Wierzba A, Takayama K. Experimental investigation of the aerodynamic breakup of liquid drops[J]. AIAA Journal, 1988, 26(11):1329-1335. DOI: 10.2514/3.10044
[7] Yoshida T, Takayama K. Interaction of liquid droplets with planar shock waves[J]. Trans ASME J Fluids Engng, 1990, 112(4):481-486. DOI: 10.1115/1.2909431
[8] Wierzba A. Deformation and breakup of liquid drops in a gas stream at nearly critical Weber numbers[J]. Experiments in Fluids, 1990, 9(1):59-64. DOI: 10.1007%2FBF00575336
[9] Hsiang L P, Faeth G M. Near-limit drop deformation and secondary breakup[J]. Int J Multiphase Flow, 1992, 18(5):635-652. DOI: 10.1016/0301-9322(92)90036-G
[10] Hsiang L P, Faeth G M. Drop properties after secondary breakup[J]. Int J Multiphase Flow, 1993, 19(5):721-735. DOI: 10.1016/0301-9322(93)90039-W
[11] Liu Z, Reitz R D. An analysis of the distorsion and breakup mechanisms of high speed liquid drops[J]. Int J Multiphase Flow, 1997, 23(4):631-650. DOI: 10.1016/S0301-9322(96)00086-9
[12] Joseph D D, Belanger J, Beavers G S. Breakup of a liquid drop suddenly exposed to a high-speed airstream[J]. Int J Multiphase Flow, 1999, 25(6):1263-1303. https://www.researchgate.net/publication/222457588_Breakup_of_a_liquid_drop_suddenly_exposed_to_a_high-speed_airstream
[13] Lee C H, Reitz R D. An experomental study of the effect of gas density on the distortion and breakup mechanism of drops in high speed gas stream[J]. Int J Multiphase Flow, 2000, 26(2):229-244. DOI: 10.1016/S0301-9322(99)00020-8
[14] Joseph D D, Beavers G S, Funada T. Rayleigh-Taylor instability of viscoelastic drops at high Weber numbers[J]. J Fluid Mech, 2002, 453:109-132. https://www.researchgate.net/publication/231787206_Rayleigh-Taylor_instability_of_viscoelastic_drops_at_high_Weber_numbers
[15] Theofanous T G, Li G J, Dinh T N. Aerobreakup in rarefied supersonic gas flows[J]. Trans ASME J Fluids Engng, 2004, 126(4):516-527. DOI: 10.1115/1.1777234
[16] Theofanous T G, Li G J, Dinh T N, et al. Aerobreakup in disturbed subsonic and supersonic flow fields[J]. J Fluid Mech, 2007, 593:131-170. https://www.researchgate.net/profile/Guangjun_Li2/publication/232005867_Aerobreakup_in_disturbed_subsonic_and_supersonic_flow_fields/links/564216c908aebaaea1f8b869.pdf?origin=publication_detail
[17] Theofanous T G, Li G. On the physics of aerobreakup[J]. Phys Fluids, 2008, 20(5):052103. DOI: 10.1063/1.2907989
[18] Pilch M, Erdman C A. Use of breakup time data and velocity history data to predict the maximum size of stable fragments for acceleration-induced breakup of a liquid drop[J]. Int J Multiphase Flow, 1987, 13(6):741-757. DOI: 10.1016/0301-9322(87)90063-2
[19] Gelfand B E. Droplet breakup phenomena in flows with velocity lag[J]. Progress in Energy and Combustion Science, 1996, 22(3):201-265. DOI: 10.1016/S0360-1285(96)00005-6
[20] Guildenbecher D R, Lopez-Rivera C, Sojka P E. Secondary ato-mization[J]. Experiments in Fluids, 2009, 46(3):371-402. DOI: 10.1007/s00348-008-0593-2
[21] Majithia A K, Hall S, Harper L, et al. Droplet breakup quantification and processes in constant and pulsed air flows[C]//Proceedings of the 22nd Conference on Liquid Atomization and Spray Systems (ILASS-Europe), Como Lake, Italy, 2008.
[22] Kulkarni V, Sojka P E. Bag breakup of low viscosity drops in the presence of a continuous air jet[J]. Phys Fluids, 2014, 26(7):072103. DOI: 10.1063/1.4887817
[23] Mohit J, Surya P R, Gaurav T, et al. Secondary breakup of a drop at moderate Weber numbers[J]. Proceedings of the Royal Society A, 2015, 147:20140930. https://www.researchgate.net/publication/276177709_Secondary_breakup_of_a_drop_at_moderate_Weber_numbers
[24] Patel P D, Theofanous T G. Hydrodynamic fragmentation of drops[J]. J Fluid Mech, 1981, 103:307-323. http://www.osti.gov/scitech/biblio/5273464
[25] Hsiang L P, Faeth G M. Drop deformation and breakup due to shock wave and steady disturbances[J]. Int J Multiphase Flow, 1995, 21(4):545-560. DOI: 10.1016/0301-9322(94)00095-2
[26] Landeau M, Deguen R, Olson P. Experiments on the fragmentation of a buoyant liquid volume in another liquid[J]. J Fluid Mech, 2014, 749:478-518. DOI: 10.1017/jfm.2014.202
[27] 熊燃华, 许明, 李耀发, 等.液-液两相介质中液滴在冲击作用下的演变过程[J].中国科学:物理学力学天文学, 2010, 40(6):773-780. http://phys.scichina.com:8083/sciG/EN/Y2010/V40/I6/773 Xiong R H, Xu M, Li Y F, et al. The deformation and breakup of a drop-in-liquid under an impact loading[J]. Science China Phys, Mech and Astron, 2010, 40(6):773-780. http://phys.scichina.com:8083/sciG/EN/Y2010/V40/I6/773
[28] Andreas J M, Hauser E A, Tucker W B. Boundary tension by pendant drops[J]. J Phys Chem, 1938, 42(8):1001-1019. http://www.researchgate.net/publication/231423689_Boundary_Tension_by_Pendant_Drops
-
期刊类型引用(8)
1. 李存标,史明涛. 从现代实验技术的发展和数据处理方法的应用到科学发现. 气动研究与试验. 2023(04): 31-51 .  百度学术
百度学术
2. 李强,万兵兵,杨凯,朱涛. 高超声速尖锥边界层压力脉动和热流脉动特性试验. 航空学报. 2022(02): 240-248 .  百度学术
百度学术
3. 刘是成,姜应磊,董昊. 高超声速圆锥边界层不稳定性及转捩实验研究. 实验流体力学. 2022(02): 122-130 .  本站查看
本站查看
4. 熊有德,余涛,薛涛,吴杰. 聚焦激光差分干涉法测量超/高超声速流动的进展. 实验流体力学. 2022(02): 9-20 .  本站查看
本站查看
5. 郭栋梁,侯超,朱臣,熊文楠,陈爽,许晓斌,杨华,黄永安. 飞行器表面气动载荷的柔性智能蒙皮多参量测量. 实验流体力学. 2022(02): 146-154 .  本站查看
本站查看
6. 刘姝怡,陈坚强,袁先旭,熊有德,吴杰. 6°攻角尖锥高超声速边界层高频不稳定波实验研究. 实验流体力学. 2021(06): 1-7 .  本站查看
本站查看
7. 袁湘江,沙心国,时晓天,高军. 高超声速流动中噪声与湍流度的关系. 航空学报. 2020(11): 224-232 .  百度学术
百度学术
8. 杨凯,朱涛,王雄,陶伯万,朱新新,王辉,杨庆涛. 原子层热电堆热流传感器研制及其性能测试. 实验流体力学. 2020(06): 86-91 .  本站查看
本站查看
其他类型引用(4)







 下载:
下载: