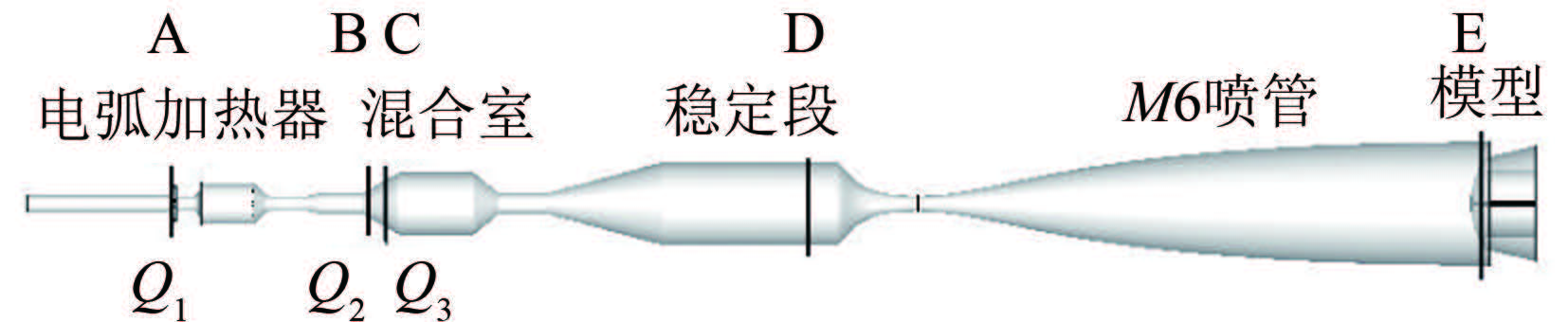
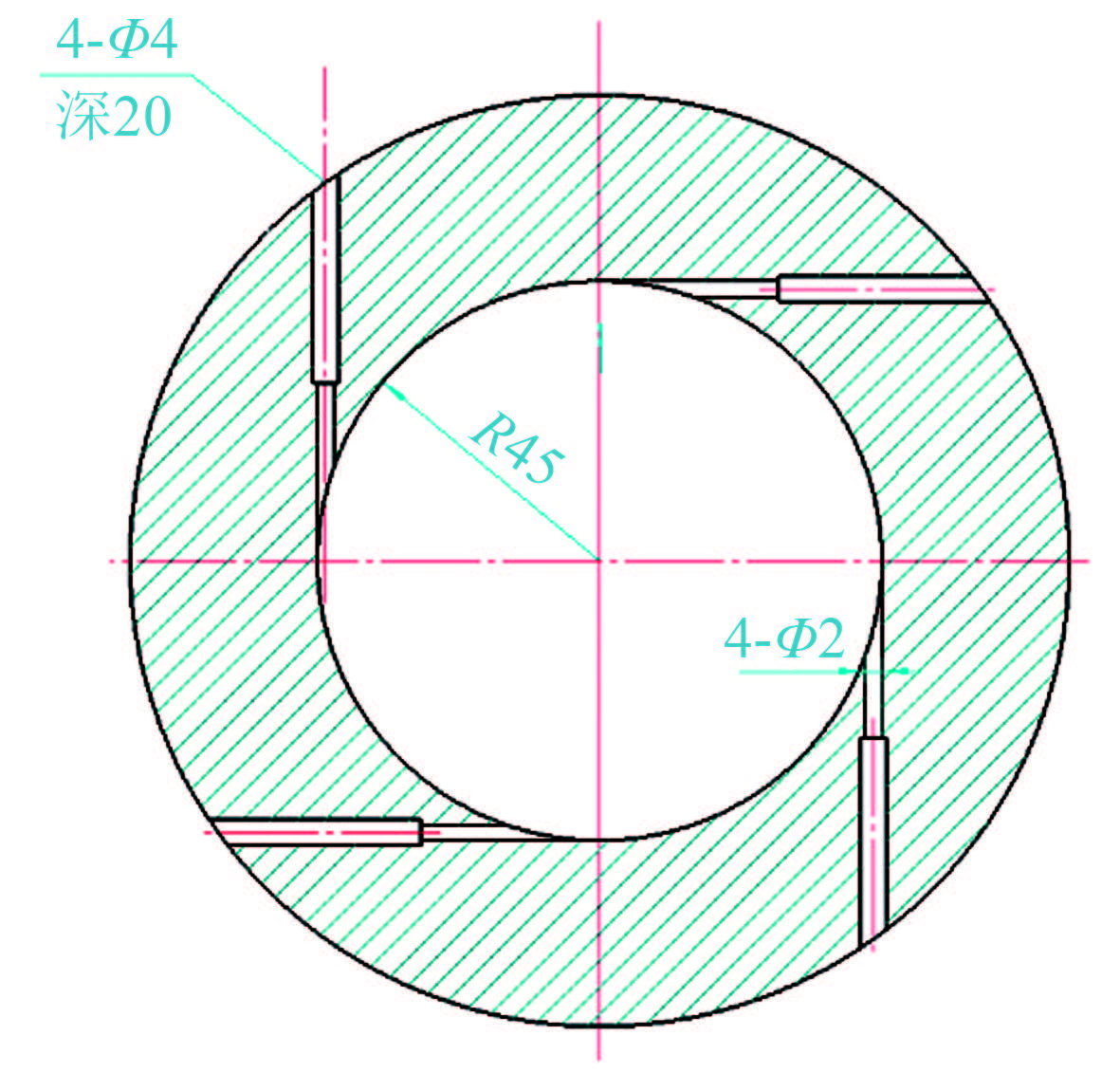
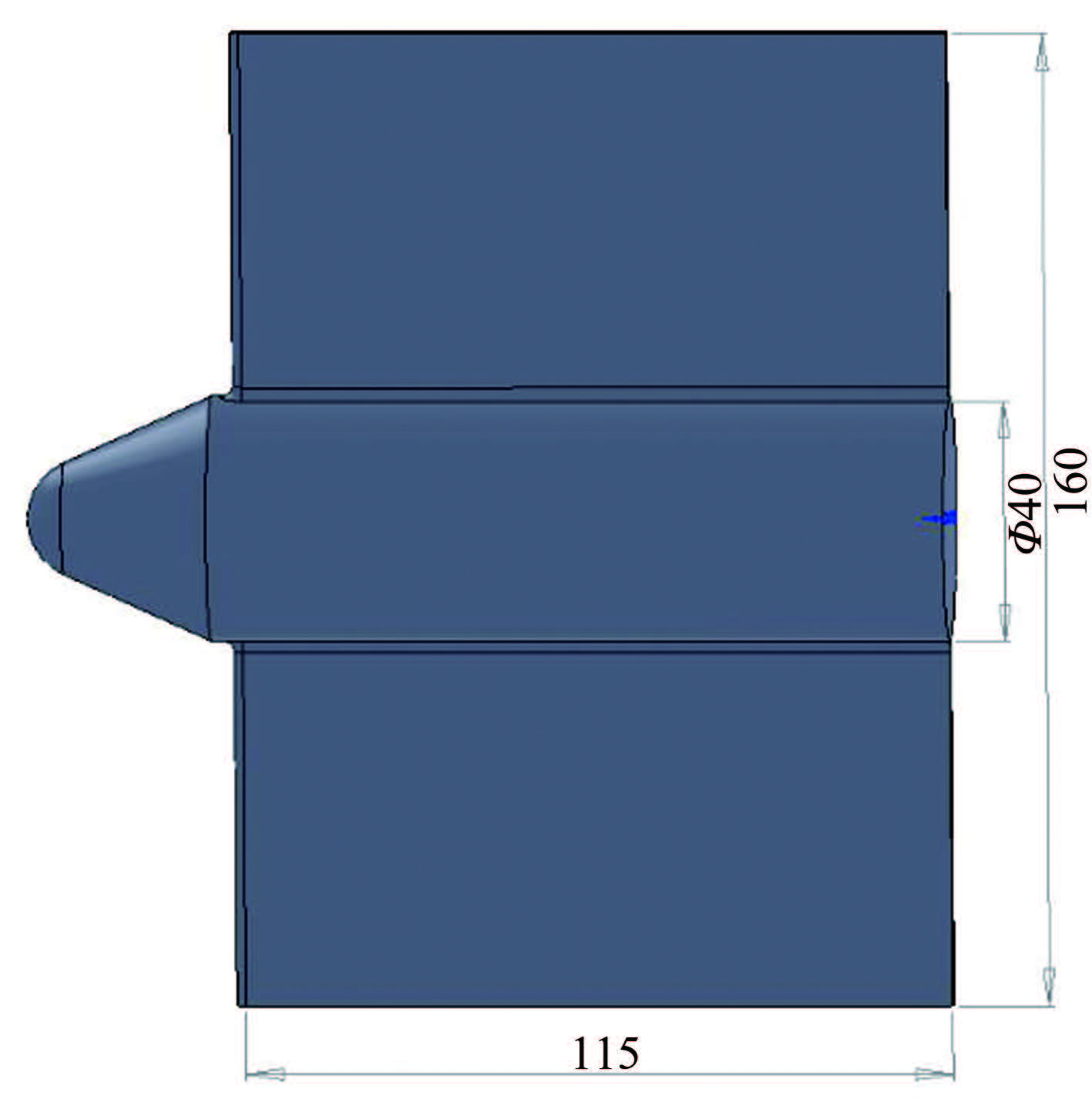
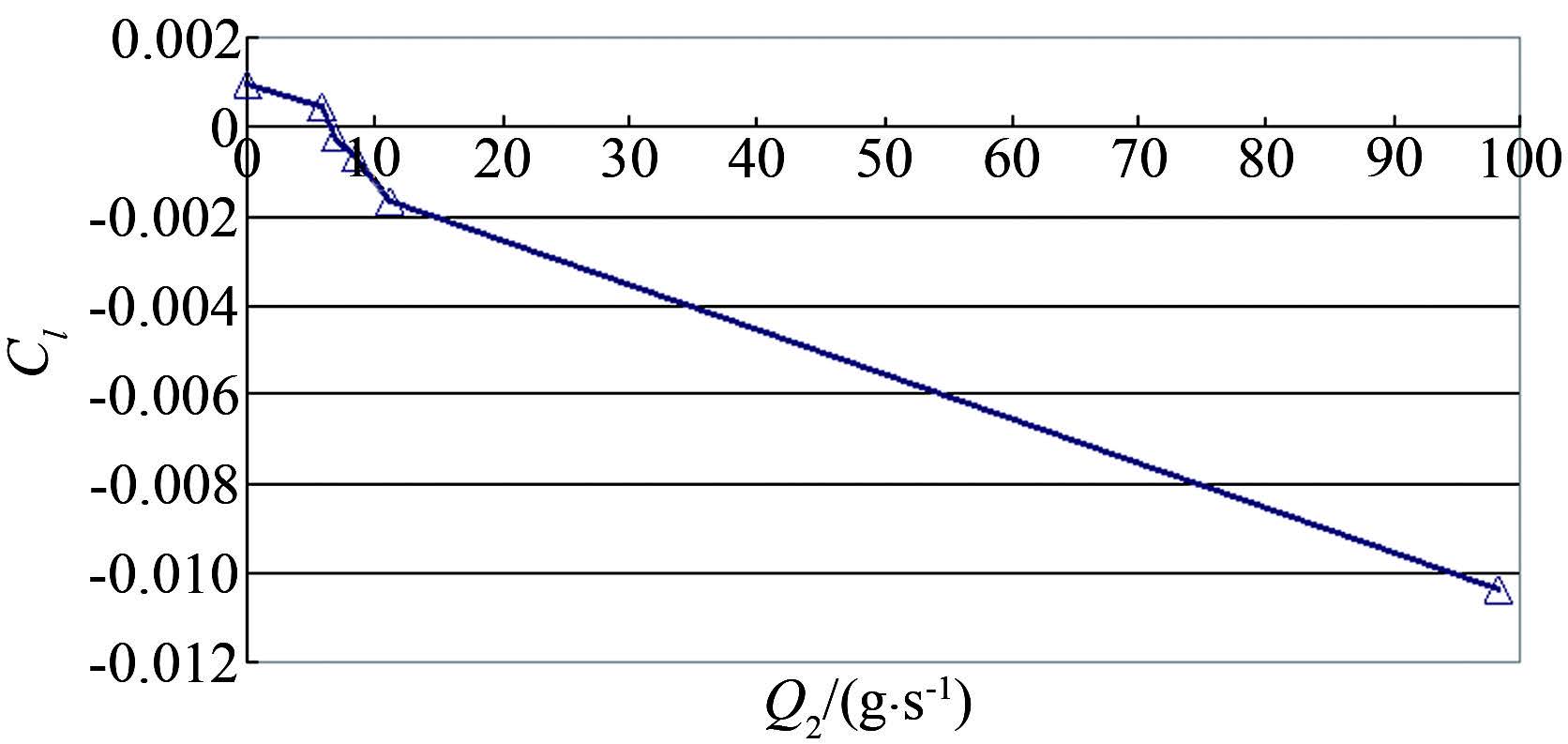
Investigation on the flow rotation effect and elimination in hypersonic wind tunnel
-
摘要: 风洞实验需要高品质的来流,但部分高超声速风洞由于加热器特性可能导致流场中存在气流旋转,为了消除或减小旋转,提出了在风洞稳定段前加入反向旋转气流来抵消气流旋转的思路。为验证该思路及了解高超声速流场中旋转程度总体效应,设计了一种带翼模型和高精度滚转力矩天平。在Φ0.3m高超声速低密度风洞中进行了M6、总压约2×105Pa、氮气常温时(电弧加热器不通电)多种进气条件下的滚转力矩测量实验,结果表明流场中存在旋转,滚转力矩系数Cl最大为1.657×10-3,采用约2%总流量的反向气流可达到滚转力矩系数降低2个数量级的效果,为提高风洞流场品质提供了较为有效的解决措施。Abstract: Wind tunnel experiments require high quality flow field,but in some hypersonic wind tunnel,the inlet flow may be rotated for preventing the local overheating of the heater.In order to eliminate the rotation,a reverse rotating flow is added into the main stream before the stability section of the wind tunnel.A wing model and a high precision roll balance were designed to study the total effect of the flow rotation in the hypersonic wind tunnel.The rolling moment measurements are carried out in the Φ0.3m hypersonic low density wind tunnel of CARDC under the test conditions of Mach 6, stagnation pressure of about 2×105Pa and room temperature nitrogen.The results show the rotation exits and the maximum rolling moment coefficient is 1.657×10-3;Reverse flow of about 2% total flow flux can reduce the rolling moment coefficient by 2 orders of magnitude. It is proved to be an effective solution for improving the quality of the wind tunnel flow field.
-
Keywords:
- hypersonic wind tunnel /
- flow rotation /
- rotation moment
-
0 引言
翼型是飞机机翼、尾翼等空气动力部件的核心要素, 在研制新翼型的过程中必须采用风洞实验验证其各项气动力特性。翼型的升力和阻力是其气动力特性至关重要的气动参数, 一般来说, 翼型阻力比升力小一个数量级, 精确测量阻力相对更加困难, 发展实用可靠的翼型阻力精细测量技术具有十分重要的工程应用价值。
在风洞实验中, 一般采用尾迹积分法测量翼型阻力, 即在翼型下游某截面安装尾耙, 通过测量该截面的总压、静压获得该截面的动量损失, 再对动量损失进行积分获得翼型阻力。尾耙的高度和安装位置等因素对翼型阻力测量存在一定影响:(1)尾耙的安装位置会直接影响阻力测量的精度。如果尾耙安装位置离翼型太近, 尾耙会对翼型绕流产生干扰, 改变翼型压力分布, 而且尾迹区动量损失曲线形状会过于"尖瘦", 对其进行积分计算阻力时会带来较大误差; 如果尾耙安装位置离翼型过远, 虽然动量损失曲线足够"肥胖"光滑, 但其一部分可能会超出尾耙测点区域, 也会给积分带来较大误差, 影响阻力测量精度。对于低速风洞, 尾耙一般安装于翼型下游0.5~1倍弦长处; 而对于高速风洞, 由于尾耙对翼型的扰动增大, 位置一般更靠后一些。(2)尾耙的高度以能捕获整个翼型尾迹为原则, 一般都大于1倍翼型弦长。对于翼型大迎角实验和高速实验, 其尾迹区的宽度较大, 尾耙高度宜选择大一些(可能需3倍弦长以上)。而在满足强度和刚度的条件下, 尾耙的其他尺寸应尽量小一些, 以减少对流场的干扰。
Taylor[1]、Bollay[2]和Goett[3]等最早研究发现尾迹截面的位置对阻力测量的影响, 当尾迹截面距离翼型后缘过近会导致计算误差较大; Vinh[4]通过数值模拟研究在大气中采用尾迹积分法计算单个翼型阻力时发现, 一般在翼型下游4~5倍弦长以后, 尾迹积分的位置对阻力计算结果几乎无影响。周瑞兴等[5]进行了尾迹法测量阻力的研究, 设计了头部15°倒角的总压探头, 保证了在流线有很大偏角时仍能测得比较准确的总压值; 焦予秦、支真莉[6-7]改进了低速风洞中以尾迹动量损失积分法测量翼型阻力的积分公式, 加入了压差影响和气流偏角影响, 得到了更好的高升力构型的阻力测量结果。以上工作均是针对低速实验进行研究, 对于跨声速实验, 周伟等[8]以数值模拟方法研究了风洞中尾耙的轴向安装位置对阻力测量的影响, 得出了"尾耙安装于翼型下游2倍弦长之后的测量值比较可靠"的结论。
在西北工业大学NF-6增压连续式跨声速翼型风洞中, 大多采用安装于翼型下游1.35倍弦长处的尾耙测量阻力。研究结果表明, 此处尾耙离翼型较近, 影响阻力测量结果。在文献的基础上, 根据风洞实际结构, 在翼型下游2.90倍弦长处的风洞侧壁上加工槽缝、安装尾耙进行实验, 对比分析了离模型较近及离模型足够远的尾耙阻力测量结果。另外, 对常用尾耙的多次实验结果分析发现, 在较大迎角或较大马赫数下, 尾耙高度不足以完全覆盖动量损失范围。需基于测得的动量损失曲线得到合适的尾耙高度, 且考虑尾耙位置后移需要更大的尾耙高度, 设计新的尾耙进行实验。
本文采用2个不同高度的尾耙, 在西北工业大学NF-6跨声速风洞实验段的2个轴向安装位置进行同一翼型实验, 通过对比分析同一尾耙高度、不同安装位置以及同一安装位置、不同尾耙高度的阻力实验数据, 获得不同实验条件下合适的尾耙高度及安装位置的组合, 改进NF-6风洞阻力测量精度。
1 实验风洞和模型
实验在西北工业大学NF-6增压连续式跨声速翼型风洞二元实验段进行。实验段尺寸为0.8 m×0.4 m×3 m (高×宽×长), 上下壁为开孔壁, 左右壁为实壁[9]。实验模型为OA309旋翼翼型(弦长c=200 mm), 展长为400 mm。图 1为翼型和尾耙在风洞中的安装照片。
2 阻力测量方法和尾耙
实验中, 以尾耙测量尾迹横截面的动量损失。尾耙上布置总压探针和静压探针。总压探针测量其前端所在的风洞横截面位置的总压(一般总压沿垂直于上下壁面的方向是变化的); 静压探针数量较少, 一般取其测得的平均值作为该横截面上的静压值。
实验中使用2种不同高度的尾耙。A尾耙竖向高度为270 mm(总压探针测量范围为260 mm), B尾耙竖向高度为500 mm(总压探针测量范围为480 mm); A、B尾耙的其他外形尺寸一致。尾耙的2个轴向安装位置分别为1位置和2位置。尾耙安装在1位置时, 总压探针前端距翼型前缘距离为470 mm, 即总压探针前端距离翼型后缘1.35 c(弦长c=200 mm); 尾耙安装在2位置时, 总压探针前端距离翼型后缘2.90 c。
A尾耙的几何数据如图 2所示。尾耙上共有53根总压探针, 编号为1~53, 上下两端探针分布较疏、中间较密, 探针之间的距离为5 mm×17+4 mm×20+5 mm×17;4根静压探针均布, 编号为54~57。B尾耙探针分布和A尾耙类似:总压探针共103根(5 mm×32+4 mm×40+5 mm×32); 4根静压探针均布。
如图 3所示, 取控制体0截面-Ⅰ截面。0截面在翼型远前方, 此处气流未受翼型扰动, 来流静压和总压分别为p∞、p0; Ⅰ截面在翼型下游无限远, 此处气流静压已恢复至来流静压p∞, 总压为p0, 1, 根据动量定理可得翼型阻力Q[10]:

(1) 式中, ρ为气体密度, v∞为来流速度, v1为Ⅰ截面气流速度, y为纵坐标方向。
由于Ⅰ截面在翼型下游无限远处, 尾迹范围无限大, 不可能在该处安装尾耙测量阻力, 因此, 在翼型下游适当位置取Ⅱ截面安装尾耙。假设尾耙测量截面尾迹内的静压已保持为常数, 并且气流在Ⅰ截面-Ⅱ截面之间没有能量损失, 则尾耙测量截面尾迹内的总压也为p0, 1; 而在尾迹之外, 认为气流没有能量损失, 因此总压p0保持不变。定义Ⅱ截面尾耙处气流总压、静压分别为p0, w、pw。
对于高速风洞实验, 风洞中各截面的气流密度并不相同。在Ⅱ截面处, 对式(1)进行推导可得翼型阻力系数CD为[6, 10-12]:

(2) 式中, CD, wt为空风洞时风洞本身流动损失引起的阻力系数, h为尾耙高度, lm为Ⅱ截面处的无量纲单位高度上的动量损失(Momentum loss), 即:

(3) 式中, γ为气体比热比(空气中γ=1.4)。
3 实验结果分析
3.1 尾耙不同安装位置对阻力测量的影响
将A尾耙分别安装在1和2位置进行实验。图 4给出了马赫数Ma=0.50和0.80条件下A尾耙在1、2位置的阻力系数。可以看出:迎角α较小时, A尾耙在1、2位置的阻力系数差别不大; 随着迎角α增大(无论是较大的负迎角还是正迎角), 1位置的阻力系数大于2位置的阻力系数。
在Ma=0.50和0.80条件下, A尾耙在1、2位置的动量损失曲线如图 5和6所示。从图 5可以看出, 当迎角大于±10°, 2位置的尾迹动量损失范围超出了尾耙测量范围, 尾耙高度明显不够, 这样积分得到的阻力系数是不真实的; 从图 6可以看出, 2位置的尾迹动量损失范围超出尾耙测量范围的正迎角提前到9°, 负迎角提前到-8°, 说明随着马赫数增大, 同一迎角状态下尾迹动量损失范围扩大, 所需的尾耙高度更大。A尾耙安装在2位置, 其高度不足以覆盖尾迹范围, 测得的阻力系数值小于真实值, 这是2位置的阻力系数小于1位置的主要原因; 另外, 由于A尾耙在1位置时离翼型较近, 翼型扰动相对较大, 对阻力测量结果也会产生一定影响。
从动量损失曲线图还可以看出, 在小迎角条件下, 对尾迹动量损失曲线积分求阻力时, 2位置的积分计算结果更为精确, 因为1位置的动量损失曲线比2位置更为尖瘦。对比图 5和6的-2°和0°的动量损失曲线, 可以看出:1位置的尾迹中心区动量损失变化十分剧烈, 竖向范围较小, 尾迹中心区总压探针相对较少, 积分求阻力可能会产生一定误差; 而尾耙后移至2位置时, 相同状态下动量损失的峰值减小、竖向范围扩大, 尾迹中心区的总压探针增多, 积分结果更为精确。
3.2 不同尾耙高度对阻力测量的影响
上节实验结果验证了尾耙安装在1位置时过于靠近翼型, 阻力系数测量结果不精确; 当尾耙后移至2位置时, A尾耙的高度不够。本节以尾耙高度更高的B尾耙在2位置进行实验。
图 7给出了Ma=0.50、0.70条件下, A、B尾耙在2位置的阻力系数, 图 8和9为Ma=0.50、0.70条件下A、B尾耙在2位置的动量损失曲线。
从图 7可以看出, 整体上, B尾耙的阻力系数略大于A尾耙, 这是因为B尾耙竖向高度较大, 洞壁干扰和堵塞干扰等相应增大, 尾耙本身对阻力测量结果造成较大影响。在大迎角时, 2位置的B尾耙的阻力系数比A尾耙大得多, 除因B尾耙高度较大造成的影响外, 根据图 8和9可以看出, 主要原因是此时A尾耙的高度并未完全覆盖尾迹动量损失范围, 计算所得的阻力系数是不正确的, 比B尾耙测得的阻力系数小是合理的。
另外, 从图 8和9还可以看出:B尾耙的动量损失曲线光滑性较差(尤其是迎角较小时), 积分求得的阻力系数可能存在一定误差; 随着迎角和马赫数增大, 曲线变得更为光滑, 积分所得的阻力系数误差随之减小。
4 结论
本文对西北工业大学NF-6增压连续式跨声速风洞翼型阻力测量精度改进方法进行了研究, 对比分析了2种尾耙高度和安装位置对阻力测量结果的影响, 得出以下结论:
(1) 当实验迎角和马赫数较小时, 采用较小高度的A尾耙(高270 mm)安装于2位置(尾耙总压探针前端距离翼型后缘2.90倍弦长)进行实验比较合适。
(2) 当实验迎角或实验马赫数较大时, 应考虑采用B尾耙(高500 mm)安装于2位置(尾耙总压探针前端距离翼型后缘2.90倍弦长)进行实验。
-
表 1 天平静校载荷及精度
Table 1 The calibrated load and prcision of the balance
单元 最大静校载荷/g或g·mm 静校重复性精度/‰ 单元灵敏度/mV/(V·g)或mV/(V·g·mm) 滚转力矩 5000 1 3.4×10-4 法向力 300 9 1.19×10-4 侧向力 300 6 1.46×10-4 表 2 实验状态及结果
Table 2 Experimental states and measured results
状态 总压/MPa 总流量/(kg·s-1) Q1/(kg·s-1) Q2/(kg·s-1) Q3/(kg·s-1) Mx/(g·mm) 原始的Cl 修正后的Cl 1 0.202 - - - - -47.68 -0.000713 0 2 0.197 0.3931 0.2415 0 0.1516 53.738 0.000944 0.001657 3 0.196 0.3929 0.2412 0.0058 0.1459 24.94 0.000445 0.001158 4 0.198 0.3947 0.2435 0.0068 0.1444 -16.6 -0.000283 0.00043 5 0.201 0.3987 0.2441 0.0086 0.146 -42.96 -0.000731 -0.000018 6 0.2 0.3971 0.2415 0.0112 0.1444 -97.89 -0.001655 -0.000942 7 0.204 0.4061 0.2451 0.0982 0.0628 -691.09 -0.010331 -0.009618 -
[1] 李荣先, 李勇, 张会强, 等. 旋风筒内强旋湍流流动的实验研究[J]. 燃烧科学与技术, 1996, 2(2): 135-138. http://www.cnki.com.cn/Article/CJFDTOTAL-RSKX602.005.htm 吴国江, 王峻晔, 郑文德, 等. 旋风筒内旋转气流的测量及分析[J]. 上海交通大学学报, 1998, 32(7): 66-69. http://www.cnki.com.cn/Article/CJFDTOTAL-RSKX602.005.htm
[2] Rhode D L, Lilley D G, Mclaughlin D K. Mean flowfields in axisymmetric combustor geometries with swirl[J]. AIAA Journal, 1983, (4): 593-600. http://www.cnki.com.cn/Article/CJFDTOTAL-SHJT807.015.htm 唐明, 朱惠龄, 严传俊, 等. 模型燃烧室中三元旋转流场的实验研究[C]//高等学校工程热物理学术会议论文集, 1986. http://www.cnki.com.cn/Article/CJFDTOTAL-SHJT807.015.htm
[3] Paschereitc O, Gutmark E, Weisenstein W. Coherent structures in swirling flows and their role in acoustic combustion control[J]. Physics of Fluids, 1999, 11: 2667-2678. http://cn.bing.com/academic/profile?id=2225660524&encoded=0&v=paper_preview&mkt=zh-cn
[4] 蒋忠东, 赵忠良, 王树民, 等. 高超声速风洞小滚转力矩测量技术研究[J]. 航空学报, 2001, 22(6): 488-490. [5] 白葵, 冯明溪, 付光明. 小不对称再入体滚转气动力测量技术[J]. 流体力学实验与测量, 2002, 9: 16(3): 64-67. DOI: 10.1063/1.870128
[6] Li R X, Li Y, Zhang H Q, et al. Experimental study of strongly swirling flows in a cyclone section[J]. Journal of Combustion Science and Technology, 1996, 2(2): 135-138. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB200106001.htm Wu G J, Wang J Y, Zheng W D, et al. Measurement and analysis of swirling flow in a cyclone cylinder[J]. Journal of Shanghai Jiaotong University, 1998, 32(7): 66-69. http://www.cnki.com.cn/Article/CJFDTOTAL-HKXB200106001.htm
[7] Jiang Z D, Zhao Z L, Wang S M, et al. Research on the measurement techniques for micro-rolling-moment in a hypersonic wind tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(6): 488-490. http://www.cnki.com.cn/Article/CJFDTOTAL-LTLC200203011.htm Bai K, Feng M X, Fu G M. Experimental technique for rolling aerodynamic of slight asymmetric re-entry body[J]. Experiments and Measurements in Fluid Mechanics, 2002, 16(3): 64-67. http://www.cnki.com.cn/Article/CJFDTOTAL-LTLC200203011.htm
-
期刊类型引用(18)
1. 韩笑,高创,郑怡彤,刘小兵. 切角凹槽矩形截面桥塔的气动特性试验研究. 石家庄铁道大学学报(自然科学版). 2024(01): 9-15+23 .  百度学术
百度学术
2. 白桦,刘博祥,姬乃川,李加武. 节段模型二元端板合理尺寸估算方法. 振动与冲击. 2023(02): 312-320 .  百度学术
百度学术
3. 王仰雪,刘庆宽,靖洪淼,李震,孙一飞. 倾斜栏杆对流线型箱梁涡激振动性能影响的试验研究. 振动与冲击. 2023(06): 232-239+254 .  百度学术
百度学术
4. 于畅,仇法梅,田学东,杨群,刘小兵. 圆角矩形柱平均气动力特性的雷诺数效应试验研究. 石家庄铁道大学学报(自然科学版). 2023(02): 29-34 .  百度学术
百度学术
5. 杨群,于畅,刘小兵,刘庆宽. 不同圆角率的方形断面斯特罗哈数的雷诺数效应研究. 振动与冲击. 2023(11): 223-231 .  百度学术
百度学术
6. 刘庆宽,王仰雪,孙一飞,李震,韩原,靖洪淼. 栏杆高度对流线型箱梁涡振性能影响的试验研究. 湖南大学学报(自然科学版). 2023(07): 140-150 .  百度学术
百度学术
7. 刘路路,杨皓然,邹云峰,何旭辉,韩艳,陈志强. 公铁同层双幅非对称主梁气动干扰特性研究. 铁道科学与工程学报. 2023(10): 3861-3872 .  百度学术
百度学术
8. 杨群,于畅,于文文,刘小兵. 圆角方柱气动特性的风洞试验研究. 振动与冲击. 2023(24): 59-68 .  百度学术
百度学术
9. 韩振,李波,甄伟,杨庆山,田玉基. 宽厚比为5的超高层建筑风荷载特性研究. 哈尔滨工程大学学报. 2022(02): 196-202 .  百度学术
百度学术
10. 张庆华,马文勇,杨杰,张彦,周帅伟. 不同风倾角下典型等边角钢静风力风洞试验研究. 振动工程学报. 2022(02): 277-283 .  百度学术
百度学术
11. 白桦,王涵,姬乃川,李加武. 节段模型长宽比对风洞测力试验及计算分析的影响. 中国公路学报. 2022(08): 202-212 .  百度学术
百度学术
12. 杨群,刘庆宽,韩瑞,刘小兵. 不同圆角率的方形断面气动特性的雷诺数效应. 振动与冲击. 2020(04): 150-156 .  百度学术
百度学术
13. 沈国辉,姚剑锋,郭勇,邢月龙,楼文娟. 直径30 cm圆柱的气动力参数和绕流特性研究. 振动与冲击. 2020(06): 22-28 .  百度学术
百度学术
14. 温青,池俊豪,华旭刚,王修勇,孙洪鑫. 端部条件和展弦比对矩形断面节段模型气动力特征的影响. 实验流体力学. 2020(04): 36-43 .  本站查看
本站查看
15. 任若松,梁新华,刘小兵,马文勇,刘庆宽. 准流线型桥梁断面气动力特性的雷诺数效应研究. 工程力学. 2020(S1): 139-144+167 .  百度学术
百度学术
16. 李海飞,梁新华,孙一飞,崔会敏,刘庆宽. 流线型桥梁断面表面脉动风荷载特性研究. 工程力学. 2020(S1): 242-248+260 .  百度学术
百度学术
17. 马文勇,汪冠亚,郑熙,陈铁,李智,张程远,方平治. 端部状态对斜置圆柱气动力分布的影响. 实验流体力学. 2019(02): 43-50 .  本站查看
本站查看
34. 杨群,刘庆宽,孙亚松,刘小兵. 圆角方形断面气动特性试验. 振动.测试与诊断. 2020(01): 140-147+208 .  百度学术
百度学术
其他类型引用(16)







 下载:
下载: