Experimental study on Rayleigh–Bénard convection during supercritical phase transition of carbon dioxide
-
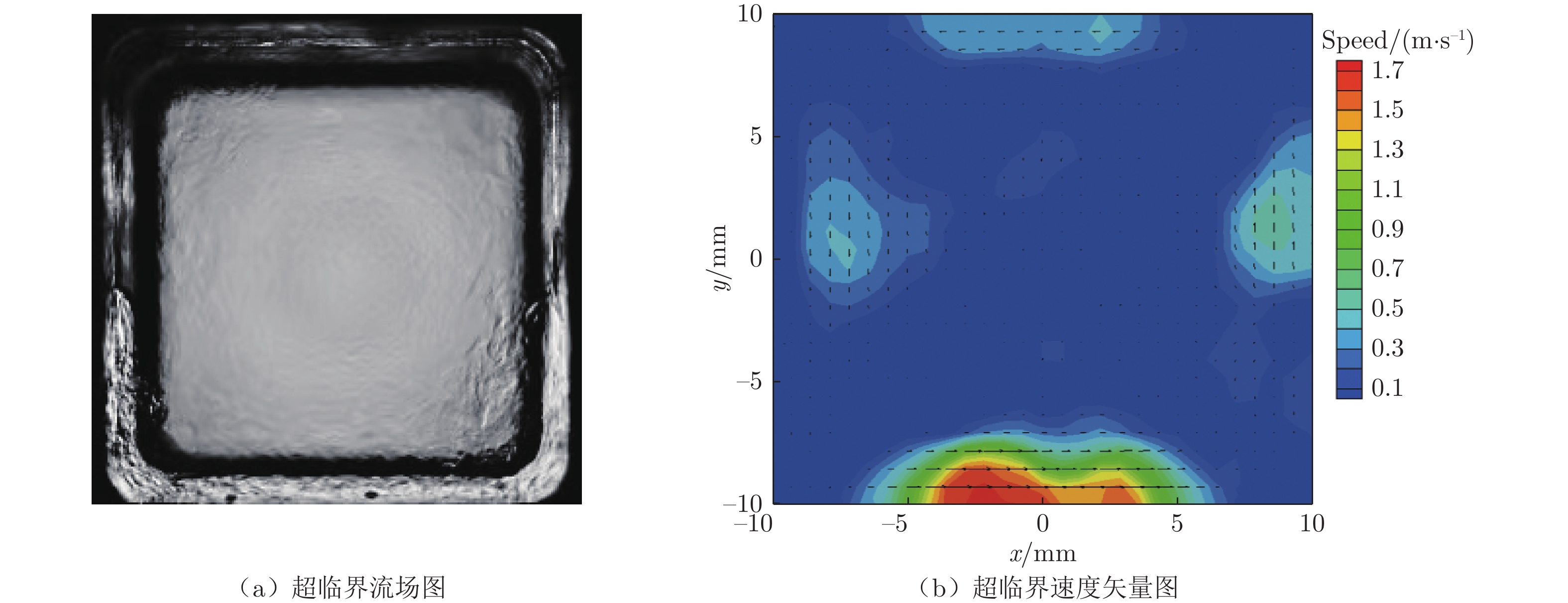
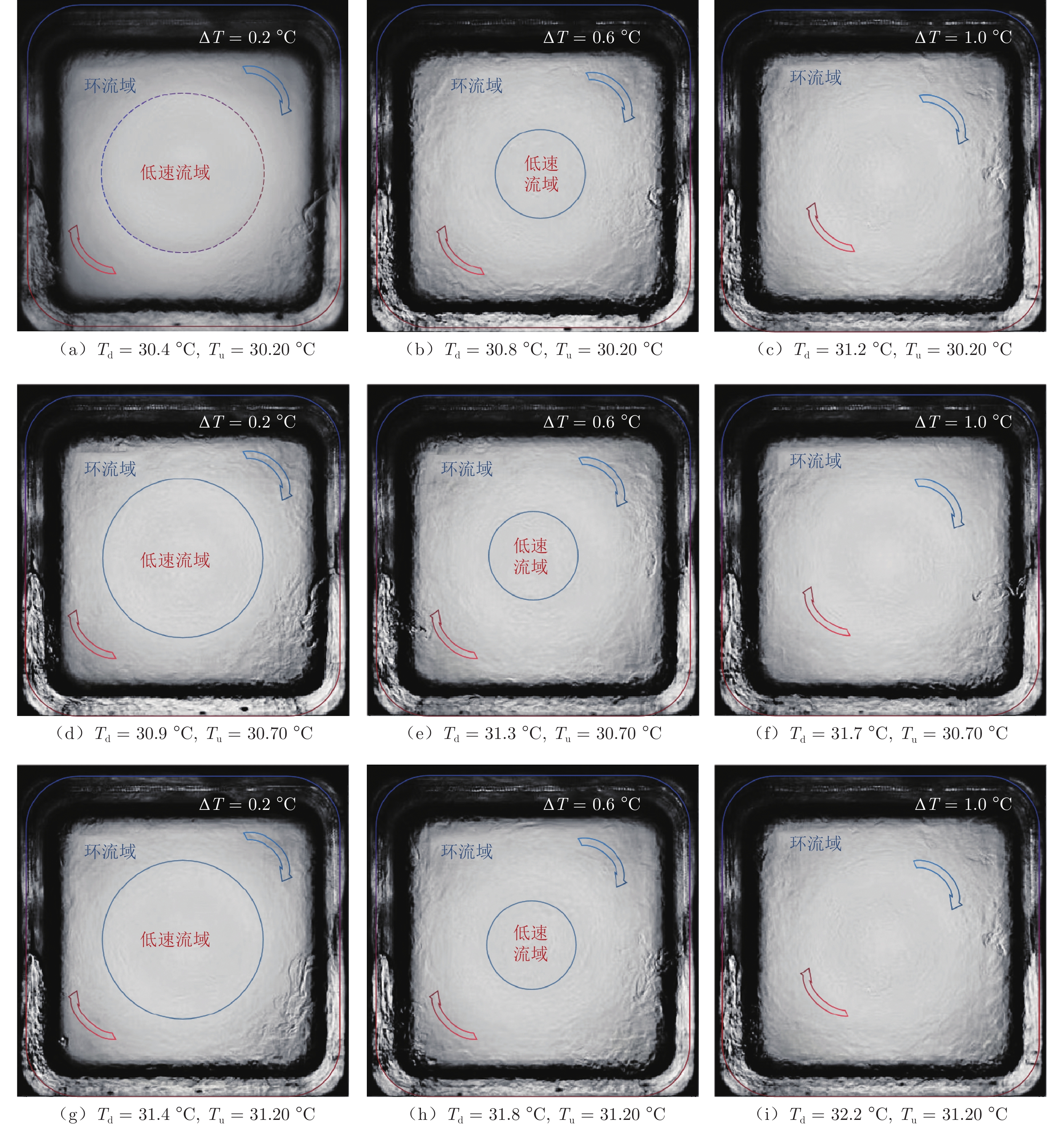
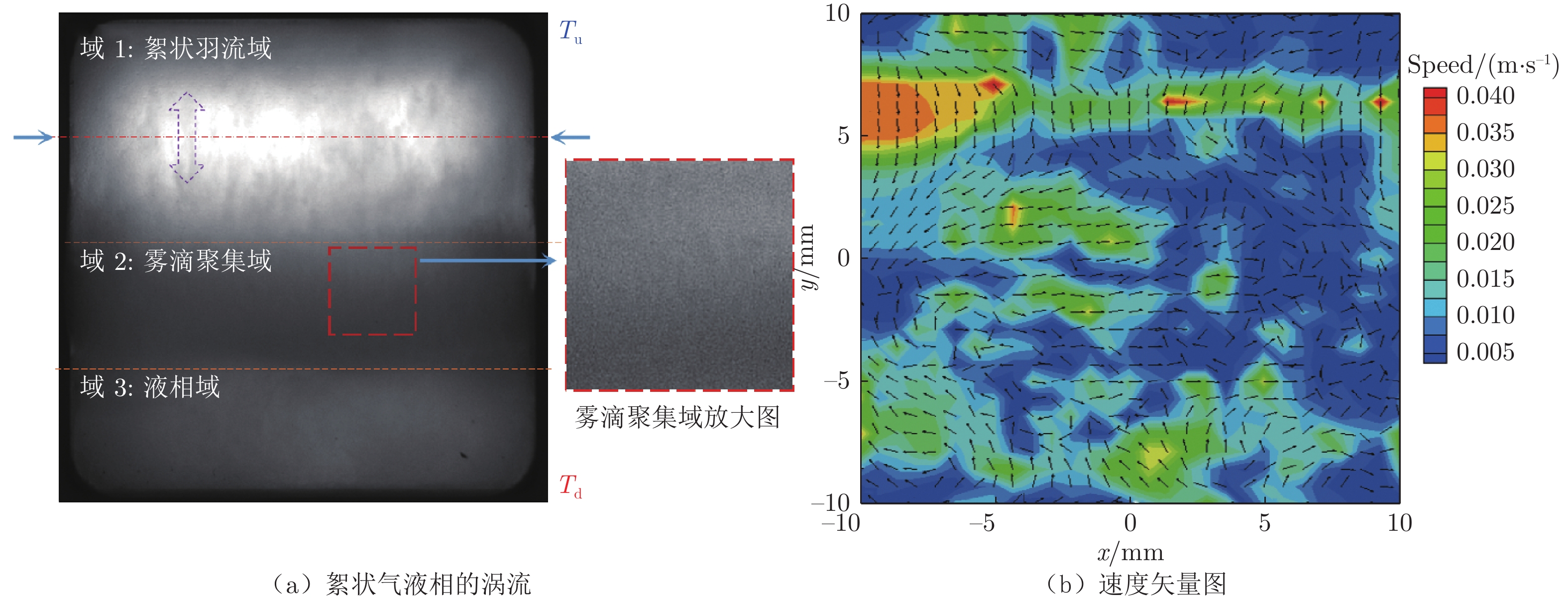
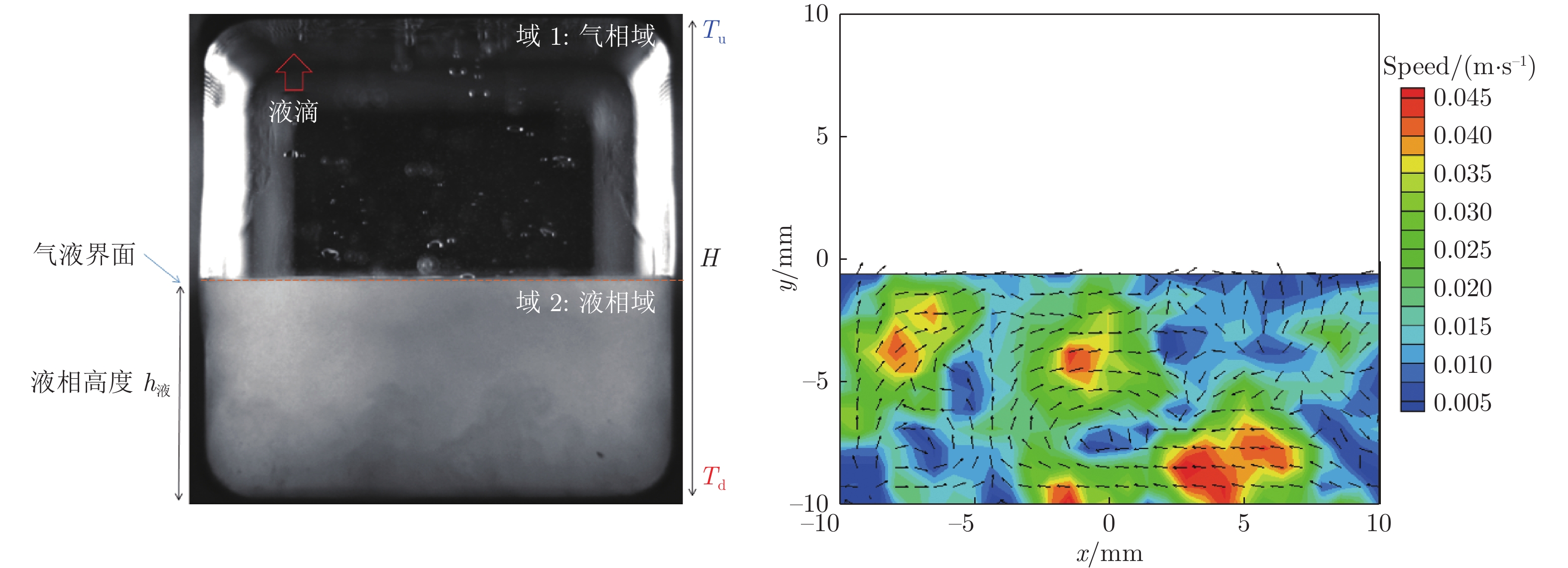
摘要: 超临界流体是一种极端条件下(温度与压力均处于临界点以上)的非常态流体。浮力驱动的超临界流体Rayleigh–Bénard(RB)对流则是一种新的非线性热对流体系,其浮力作用不符合Boussinesq近似,且在温差的作用下物性在临界点附近出现剧烈畸变并伴随着丰富的流动与相变耦合过程。本实验设计了可承载超临界二氧化碳(SCO2)的透明蓝宝石压力容器,建立竖直温度梯度作用下的超临界流体RB对流,观测不同温差作用下的流动结构和超临界相变过程并通过图像互相关算法计算“雾化”液滴的速度场。实验采用铂电阻测温,并精确控制容器上下端的温差,研究SCO2在线性降温过程中多种流态与速度场的演化。在线性降温过程中,SCO2经历超临界流动、跨临界流动和气液两相流动3个典型过程。跨临界流动是相变与浮力热对流的强耦合过程,导致超临界二氧化碳RB对流具有多态的非稳态流动。实验结果表明:超临界RB对流对温差极为敏感,温差越大则超临界域内的对流越剧烈;随着温度的降低,雾化的液滴不断凝聚,形成丰富的多层流动结构,并最终向气液两相流动演化。
-
关键词:
- 超临界流体 /
- Rayleigh–Bénard对流 /
- 相变
Abstract: Supercritical fluid is a kind of special fluid under extreme conditions (temperature and pressure are above the critical point). The Rayleigh–Benard (RB) convection of supercritical fluid driven by buoyancy is a new nonlinear thermal convection system. Its buoyancy does not conform to the Boussinesq approximation. Under the action of temperature difference, the physical properties of RB fluid show severe distortion near the critical point, accompanied by abundant flow and phase transition coupling processes. In this experiment, a transparent sapphire pressure vessel capable of carrying supercritical carbon dioxide (SCO2) was designed to establish RB convection of supercritical fluid under the effect of vertical temperature gradient. The flow structure and supercritical phase transition process under different temperature differences were observed. The velocity field of “atomized” droplets was calculated by image cross-correlation algorithm. In the experiment, platinum resistance temperature measurement was used to accurately control the temperature of the upper and lower ends of the container, and the evolution of various flow modes and velocity fields in the linear cooling process was studied. In the linear cooling process, SCO2 goes through three typical processes: supercritical flow, transcritical flow and gas liquid two-phase flow. The strong coupling of the transcritical phase transition with buoyancy convection results in the heterogeneous unsteady flow of supercritical carbon dioxide RB convection. It shows that the supercritical RB convection is extremely sensitive to temperature difference, and the larger the temperature difference is, the more intense the convection in the supercritical domain is. With the decrease of temperature, the atomized droplets condense to form abundant structure of multi-layer flows, which finally turn to the two-phase flow.-
Keywords:
- supercriticial fluid /
- Rayleigh–Bénard convection /
- phase change
-
0 引 言
雷诺数是风洞试验模拟的重要相似准数之一,它反映了粘性力、惯性力对流体运动的影响,许多流动现象,如:气流的分离和附着,涡的形成、发展与破裂,激波/边界层干扰等都与雷诺数密切相关[1-2]。为了满足大型客机和运输机对风洞试验雷诺数模拟能力的需求,美国建立了数个5m量级大型高速风洞和NTF低温高雷诺数风洞,欧洲建立了ETW低温高雷诺数风洞,使得风洞试验雷诺数的模拟能力达到了107,基本达到飞行雷诺数的量级,这些高雷诺数风洞的建成投产,为美欧在大型客机研制的垄断地位打下了坚实基础。
随着美国在阿富汗战争和伊拉克战争中利用全球鹰和捕食者等高空、长航时无人机在侦查、情报获取和精确打击等方面展现出的巨大军事效益,使得世界各国对高空、长航时无人机研制成为热点。但在该领域空气稀薄,飞行Re低(一般为105量级),气体流动常常处于层流状态,且容易产生分离,从而对翼型的升阻比和发动机的性能等产生较大的影响。因此,在高空低雷诺数条件下,高升阻比翼型、发动机内部旋转部件高性能叶型的气动设计问题日益凸显[3-4]。目前,国内研究此类问题的主要手段大都通过CFD等商业计算软件进行计算研究[5-8],王英锋等[5]通过采用基于叶栅法计算轴流压气机特性的计算程序,对雷诺数对轴流压气机稳定性的影响进行了计算,给出了“随着Re的降低,压气机的稳定性下降”的结论;温泉等[7]通过计算软件对雷诺数效应对小流量多级轴流压缩机的性能进行数值分析,给出了“降低Re会使附面层增厚,增大了叶型损失系数”的结论;唐海龙[8]等通过仿真计算对低雷诺数对发动机性能的影响进行了计算研究,给出了“低雷诺数效应会引起发动机相关部件的效率、流通能力等参数变化,Re越低对流通能力影响越大”的结论。但是其计算结果的准确性与可靠性亟需通过风洞试验的验证。而现阶段国内高速风洞基本都是暂冲式风洞,并不具备模拟高空和低雷诺数的试验条件。
目前,中国空气动力研究与发展中心建成的0.6m×0.6m连续式跨声速风洞(简称0.6m连续式跨声速风洞)的运行总压能够降低至0.15个大气压,使得试验Re的模拟能力达到105量级,该风洞的建成为CFD等商业软件计算结果的准确性与可靠性验证创造了试验条件。但是在低雷诺数条件下,风洞流场品质是否满足相关技术指标要求,直接影响到风洞试验数据的精准度。为此,在开展相关型号验证试验前,需要就雷诺数效应对0.6m连续式跨声速风洞性能的影响进行研究,确保风洞试验数据的准确性和可靠性。
1 风洞简介
0.6m×0.6m连续式跨声速风洞(外形轮廓见图 1)是中国空气动力研究与发展中心高速所于2012年建成的一座连续式跨声速风洞。该风洞采用半挠性壁喷管设计方案实现了马赫数0.2~1.6的连续运行;在风洞回路一拐和二拐之间配置有一台AV90-3型轴流式压缩机作为风洞的主动力系统,其最大功率为3.8MW,最高转速3600r/min,转速控制精度为0.03%,静叶角46°~76°连续可调(见图 2);在试验段驻室与超扩段之间配置有一套E71-3型离心式压缩机用于跨声速范围的驻室抽气,其最大功率为1.5MW,最高转速8570r/min,转速控制精度为0.1%,导叶角60°~105°连续可调(见图 3);在三拐前大开角出口配置有一套管翅式换热器系统,用于高温气体的冷却;在风洞三、四拐之间及驻室配置有一套抽真空系统,用于控制风洞的运行总压及空气露点。为了防止压缩机出现喘振,对轴流式和离心式压缩机分别配置有一套防喘回路。该风洞主要性能指标为:试验段截面尺寸:0.6m×0.6m; 风洞运行总压:p0=(0.15~2.5)×105Pa;总温:T0=(280~323)K;马赫数:Ma=0.2~1.6; Re范围:Rec=(0.1~2.25)106(c=0.06m);总压控制精度:≤0.2%;Ma控制精度:≤0.002。
为了实现雷诺数模拟试验能力,该风洞采用总压与马赫数独立控制的运行策略,利用压缩机转速和中心体控制系统的配套运行实现风洞马赫数的精确控制,利用三、四拐角段之间的中压供气系统和抽真空控制系统配套运行实现风洞总压15~250kPa连续可调,上述运行策略为开展雷诺数效应对风洞性能影响提供了良好的试验平台。
2 雷诺数效应影响研究
风洞试验中,一般通过改变运行总压、运行介质以及介质的比重或温度等方式来扩大Re的模拟能力。0.6m连续式跨声速风洞正是通过降低风洞运行总压来降低试验Re的。为了了解低雷诺数效应对风洞性能的影响,在0.6m连续式跨声速风洞中开展了相关的影响研究。
2.1 对轴流式压缩机性能影响研究
在压缩机热力性能试验中,开展了雷诺数效应对轴流式压缩机性能的影响试验。图 4给出了总压15和96kPa条件下,1000~2500r/min压缩机热力性能试验结果。可以看出,总压96kPa时,压缩机随着流量的减小直接进入喘振区,而总压15kPa时压缩机性能发生了明显变化。与总压96kPa性能相比,压缩机安全运行边界变窄,相同流量条件下,压比减小,且经历较大的失速区后再进入喘振区,说明喘振是压缩机深度失速诱发的结果,而这种现象随着Re的降低越发明显。图 5给出了压缩机叶栅翼型分别在Re为1×105和1×106这2种不同Re条件下翼型上流线分布矢量图的计算结果(参考长度为翼型弦长)。由图 5可见,随着Re的降低,压缩机叶栅附面层厚度增加,尾缘出现了气流分离,使得叶栅损失增大;且Re越低,尾缘处的气流分离区域越大,叶栅的损失也就越大,使得压缩机在相同转速下能有效提供的压比减小,流通能力下降,文献 [9-12]也得出类似结果。图 6给出了相同条件下压缩机喘振边界的理论计算结果,可以看出,计算结果与试验结果规律相似。
2.2 对运行压比的影响
图 7给出了Ma=0.2~0.8时,相同马赫数条件下,Re对流场建立所需压比的对比曲线。由图可以看出,当Rec<5×105(c=0.1$\sqrt{A}$,A代表试验段横截面积),相同马赫数下所需的压比明显增大,说明随着Re的下降,风洞内流道损失明显增大。图 8给出了风洞不同总压状态下第一拐角段的压力损失系数

2.3 对空间流场均匀性的影响
图 9给出了不同运行总压条件下,压缩机出口总压系数均方根偏差随Re的变化曲线。由图可知,随着Re的减小,压缩机出口总压的均匀性分布变差,尤其是当Rec<4×105时(c=0.1$\sqrt{A2}$,A2为二拐出口横截面积),其均匀性变差的趋势更为明显。图 10和11分别在总压100和20kPa状态下,通过Fluent软件对风洞大开角段入口和出口速度分布进行了理论计算。对比可知,总压100kPa时,大开角入口和出口速度分布都比较均匀,而总压20kPa时,大开角段速度分布均匀性变差,在圆变方部段4个角上存在明显的气流分离。造成上述现象的主要原因是由于在低雷诺数条件下,气流的粘性作用增强,惯性作用减弱,抗逆压梯度能力减弱,气流流过拐角部段、压缩机部段以及大开角部段后,气流存在明显的分离,使得风洞管道中气流的总压均匀性遭到破坏,在整个回流管道中循环往复,从而使得风洞空间流场均匀性下降。
2.4 对控制精度的影响
图 12给出了Ma=0.2,总压p0 =20、50、100和250kPa时,风洞总压系数Cp0(

2.5 对模型区马赫数分布均匀性的影响
图 15给出了0.6m连续式跨声速风洞Re对试验段模型区马赫数均方根的影响曲线。由图可知,当Rec<2×105(c=0.1$\sqrt{A}$)时,Re对试验段模型区马赫数均匀性具有显著影响,随着Re的下降,模型区马赫数均方根偏差明显增大。造成这一现象的原因主要有:一是低雷诺数条件下,风洞空间流场的总压和速度场的均匀性分布下降;二是低总压条件下,总压及马赫数的控制精度下降也降低了风洞空间流场的总压和速度场的均匀性。
3 流场校测及标模试验
为了验证低雷诺数下0.6m连续式跨声速风洞试验段模型区流场均匀性的变化情况以及对标模试验数据的影响,在总压20kPa的低Re数条件下,对风洞进行了流场校测试验和标模试验。表 1给出了流场校测结果。图 16~18分别给出了Ma=0.2~0.8,Rec(c=0.1$\sqrt{A}$)对GBM-04A标模CLα、CD0、CMCL的试验结果。由表 1数据可知,尽管0.6m连续式跨声速风洞低雷诺数条件下的总压控制精度、马赫数控制精度及模型区马赫数均方根偏差等流场性能指标都存在一定程度的下降,但该风洞流场指标仍满足国军标1179-91[13]规定要求。由图 16和17可知,当Rec<5×105时,Re对Cα、CD0的影响非常明显,CLα随Re减小而减小,CD0随Re减小而增大,该变化趋势符合Re对CLα、CD0影响规律[14],由图 18可知,低雷诺数条件下对CMCL的影响并不明显。从0.6m连续式跨声速风洞低雷诺数条件下的流场校测和标模试验结果可知,在低雷诺数运行条件下,该风洞仍能够真实、准确反映Re对风洞流场性能和测力试验数据的影响规律,是开展高空低雷诺数飞行器、翼型和发动机等性能研究的理想地面模拟试验平台。
表 1 流场校测结果(p0=20kPa)Table 1 The results of the flow field calibration(p0=20kPa)
Ma平均
总压/kPa总压
控制精度Ma
控制精度模型区
均方根偏差0.2 20.0756 0.07% 0.0030 0.0019 0.3 20.0507 0.08% 0.0024 0.0015 0.4 20.0508 0.07% 0.0016 0.0015 0.5 20.0510 0.10% 0.0015 0.0013 0.6 20.0481 0.08% 0.0018 0.0013 0.7 20.0754 0.07% 0.0010 0.0016 0.8 20.0926 0.10% 0.0014 0.0018 0.9 20.0501 0.08% 0.0014 0.0021 1.0 20.0373 0.08% 0.0011 0.0027 1.1 20.0407 0.10% 0.0009 0.0090 1.2 20.0832 0.09% 0.0013 0.0110 1.3 20.0964 0.09% 0.0018 0.0078 1.4 20.0500 0.10% 0.0010 0.0104 4 结 论
(1) 低雷诺数效应对0.6m连续式跨声速风洞轴流式压缩机性能具有明显影响,当Rec<5×105(c=0.1$\sqrt{A}$)时,压缩机入口流量急剧下降,损失增大、压比减小。
(2) 低雷诺数效应对0.6m连续式跨声速风洞流场性能具有显著影响,当Rec<5×105(c=0.1$\sqrt{A}$)时,风洞总压控制精度、Ma控制精度和模型区马赫数均方根偏差等流场性能指标明显下降。
(3) 0.6m连续式跨声速风洞能够准确反应雷诺数效应对GBM-04A标模测力试验数据的影响规律,当Rec<5×105(c=0.1$\sqrt{A}$)时,Re对Cα、CD0的影响显著。
(4) 低雷诺数条件下,0.6m连续式跨声速风洞仍能够真实、准确反映Re对风洞流场性能和测力试验数据的影响规律,是开展高空低雷诺数飞行器、翼型、发动机等性能研究的理想地面模拟试验平台。
5 下一步工作打算
(1) 开展风洞低压条件下总、静压测量精度以及控制精度的技术研究,进一步提高风洞总压及Ma控制精度以及试验数据的测量精度,为开展低Re数条件下风洞性能研究提供更为准确可靠的试验数据。
(2) 对风洞收缩段型面进行优化改进,提高收缩段收缩型面制安水平,降低由于收缩型面对来流均匀性的影响。
(3) 开展压缩机尾罩及拐角导流片降噪性能研究和外形优化设计,一方面减小经过导流片气流的分离和损失,另一方面降低风洞回路噪声水平。
(4) 联合压缩机研制厂家,开展低Re数条件下压缩机叶栅翼型性能研究,通过翼型优化设计,提高压缩机在低Re数条件下的压缩能力,降低压缩机的损失系数。
-
-
[1] 张庆富, 杨文芳. 超临界CO2的应用技术及发展现状[J]. 毛纺科技, 2011, 39(8): 48–54. DOI: 10.19333/j.mfkj.2011.08.014 ZHANG Q F, YANG W F. Development and application of supercritical CO2[J]. Wool Textile Journal, 2011, 39(8): 48–54. doi: 10.19333/j.mfkj.2011.08.014
[2] 李淑芬, 吴希文, 侯彩霞, 等. 超临界流体技术开发应用现状和前景展望[J]. 现代化工, 2007, 27(2): 1–7, 9. DOI: 10.16606/j.cnki.issn0253-4320.2007.02.001 LI S F, WU X W, HOU C X, et al. Supercritical fluid technology and application[J]. Modern Chemical Industry, 2007, 27(2): 1–7, 9. doi: 10.16606/j.cnki.issn0253-4320.2007.02.001
[3] 王军辉, 郭鹏程, 颜建国, 等. 水平小圆管内超临界二氧化碳对流传热特性的试验研究[J]. 西安理工大学学报, 2018, 34(3): 272–277. DOI: 10.19322/j.cnki.issn.1006-4710.2018.03.004 WANG J H, GUO P C, YAN J G, et al. Experimental studies on convection heat transfer of supercritical carbon dioxide in a horizontal circular mini-tube[J]. Journal of Xi’an University of Technology, 2018, 34(3): 272–277. doi: 10.19322/j.cnki.issn.1006-4710.2018.03.004
[4] 杨俊兰, 马一太, 曾宪阳, 等. 超临界压力下CO2流体的性质研究[J]. 流体机械, 2008, 36(1): 53–57,13. DOI: 10.3969/j.issn.1005-0329.2008.01.014 YANG J L, MA Y T, ZENG X Y, et al. Study on the properties of CO2 fluid at supercritical pressure[J]. Fluid Machinery, 2008, 36(1): 53–57,13. doi: 10.3969/j.issn.1005-0329.2008.01.014
[5] 杨俊兰, 马一太, 李敏霞. 超临界CO2流体及其换热特性分析[J]. 流体机械, 2013, 41(5): 66–71. DOI: 10.3969/j.issn.1005-0329.2013.05.015 YANG J L, MA Y T, LI M X. Analysis of supercritical CO2 fluid and the heat transfer performance[J]. Fluid Machinery, 2013, 41(5): 66–71. doi: 10.3969/j.issn.1005-0329.2013.05.015
[6] 刘旻昀, 黄彦平, 唐佳, 等. 超临界流体物性畸变特性的多尺度研究[J]. 原子能科学技术, 2021, 55(11): 1921–1929. DOI: 10.7538/yzk.2021.youxian.0825 LIU M Y, HUANG Y P, TANG J, et al. Multi-scale study on property distortion mechanism of supercritical fluid[J]. Atomic Energy Science and Technology, 2021, 55(11): 1921–1929. doi: 10.7538/yzk.2021.youxian.0825
[7] 邢凯翔. 超临界二氧化碳布雷顿循环近临界特性研究[D]. 杭州: 浙江大学, 2021. XING K X. Study on near-critical characteristics of supercritical carbon dioxide Brayton cycle[D]. Hangzhou: Zhejiang University, 2021.
[8] 杨富方, 刘航滔, 杨震, 等. 超临界二氧化碳循环工质热物性研究进展[J]. 热力发电, 2020, 49(10): 21–29. DOI: 10.19666/j.rlfd.202006163 YANG F F, LIU H T, YANG Z, et al. Thermophysical properties of working fluid of supercritical carbon dioxide cycle: research progress[J]. Thermal Power Generation, 2020, 49(10): 21–29. doi: 10.19666/j.rlfd.202006163
[9] 王鹏飞, 张尧立, 谢榕顺, 等. 超临界二氧化碳的自然循环流动特性[J]. 厦门大学学报(自然科学版), 2022, 61(1): 80–86. DOI: 10.6043/j.issn.0438-0479.202012004 WANG P F, ZHANG Y L, XIE R S, et al. Characteristics of natural circulation flow of supercritical carbon dioxide[J]. Journal of Xiamen University (Natural Science), 2022, 61(1): 80–86. doi: 10.6043/j.issn.0438-0479.202012004
[10] 杨凤叶, 王珂, 刘彤, 等. 竖直管内超临界二氧化碳局部对流换热研究[J]. 压力容器, 2013, 30(3): 1–4,14. DOI: 10.3969/j.issn.1001-4837.2013.03.001 YANG F Y, WANG K, LIU T, et al. Research of local convection heat transfer of CO2 at supercritical pressures in a vertical tube[J]. Pressure Vessel Technology, 2013, 30(3): 1–4,14. doi: 10.3969/j.issn.1001-4837.2013.03.001
[11] 淮秀兰, SHIGERU Koyama. 微通道内超临界二氧化碳的压降与传热特性[J]. 工程热物理学报, 2004, 25(5): 843–845. DOI: 10.3321/j.issn:0253-231X.2004.05.036 HUAI X L, SHIGERU K. Heat transfer and pressure drop of supercritical carbon dioxide in multi-port channels[J]. Journal of Engineering Thermophysics, 2004, 25(5): 843–845. doi: 10.3321/j.issn:0253-231X.2004.05.036
[12] 周全, 夏克青. Rayleigh–Bénard湍流热对流研究的进展、现状及展望[J]. 力学进展, 2012, 42(3): 231–251. ZHOU Q, XIA K Q. Progress, present situation and prospect of Rayleigh–Bénard turbulent heat convection research[J]. Advances in Mechanics, 2012, 42(3): 231–251.
[13] 郗恒东, 孙超, 夏克青. 湍流热对流中的动力学和传热研究[J]. 物理, 2006, 35(4): 265–268. DOI: 10.3321/j.issn:0379-4148.2006.04.002 XI H D, SUN C, XIA K Q. Flow dynamics and heat transport in turbulent thermal convection[J]. Physics, 2006, 35(4): 265–268. doi: 10.3321/j.issn:0379-4148.2006.04.002
[14] 周全, 孙超, 郗恒东, 等. 湍流热对流中的若干问题[J]. 物理, 2007, 36(9): 657–663. DOI: 10.3321/j.issn:0379-4148.2007.09.001 ZHOU Q, SUN C, XI H D, et al. Various issues in turbulent thermal convection[J]. Physics, 2007, 36(9): 657–663. doi: 10.3321/j.issn:0379-4148.2007.09.001
[15] XI H D, XIA K Q. Flow mode transitions in turbulent thermal convection[J]. Physics of Fluids, 2008, 20(5): 055104. doi: 10.1063/1.2920444
[16] 陈鑫, 郗恒东. 瑞利–伯纳德热湍流中的多湍流态现象[J]. 空气动力学学报, 2022, 40(2): 147–155. DOI: 10.7638/kqdlxxb-2022.0002 CHEN X, XI H D. Multiple flow states in turbulent Rayleigh–Bénard convection[J]. Acta Aerodynamica Sinica, 2022, 40(2): 147–155. doi: 10.7638/kqdlxxb-2022.0002
[17] ACCARY G, BONTOUX P, ZAPPOLI B. Turbulent Rayleigh–Bénard convection in a near-critical fluid by three-dimensional direct numerical simulation[J]. Journal of Fluid Mechanics, 2009, 619: 127–145. doi: 10.1017/s0022112008004175
[18] VALORI V, ELSINGA G E, ROHDE M, et al. Particle image velocimetry measurements of a thermally convective supercritical fluid[J]. Experiments in Fluids, 2019, 60(9): 1–14. doi: 10.1007/s00348-019-2789-z







 下载:
下载: