0   引　言

方腔流动包含流致振荡、声不稳定性和波的相互作用等丰富的流体动力学特征，被进行了广泛研究。方腔流动问题最早被关注，是由于内埋武器弹舱产生的强烈噪声影响了飞行器结构安全和武器精准度^[1-2]。随着航空运输业的发展，飞机起飞和着陆阶段的重要噪声源—低速方腔—也得到了广泛关注^[3-4]。Roshko^[5]报道了不同几何形状方腔的平均流动结构，发现方腔内均存在回流结构。Tracy^[6]和Basley^[7]等研究了马赫数0.20～0.95方腔的流动特性，认为长深比（L/D）小于6的方腔为开式方腔，其前缘剪切层横跨整个方腔并与后缘撞击；长深比大于13时为闭式方腔，剪切层从前缘分离并在方腔底部再附。前人在开式方腔流动中发现了强烈的压力振荡和噪声辐射，认为这是一个复杂的反馈过程。流动的不稳定性导致方腔前缘剪切层内涡卷起，在向下游传播的过程中，涡结构在黏性效应作用下快速增长，涡与方腔后缘撞击后辐射噪声并产生压力扰动前传，从而形成闭环，这一过程被称为“剪切层模态”^[8]。在前人研究结果的基础上，Rossiter^[9]对方腔流动反馈的影响参数进行了探索，给出了一个预测振荡主频率的半经验公式，但该公式未考虑三维参数影响。

Gharib等^[10]研究了水中的方腔流动，发现了一种基于薄边界层的流动模态，即“尾迹模态”。在尾迹模态下，方腔流动的阻力和噪声强度增大，而振荡主频不随速度的增大而改变。Colonius等^[11]在二维直接数值模拟（DNS）中也发现了尾迹模态。Shieh等^[12]数值模拟了具有相同参数的二维和三维方腔流动，在二维情况下观察到了剪切层模态和尾迹模态，而在三维情况下仅观察到剪切层模态。Martin等^[13]研究了低马赫数下三维开式方腔的流动和噪声辐射，发现在剪切层模态下流动表现出部分三维性，在尾迹模态下流动表现出二维性，两种流动模态的噪声辐射有很大不同。

如前所述，方腔剪切层模态的振荡机制主要是一个准二维和自持的过程，因此大部分实验、理论和数值模拟研究工作都集中于探究雷诺数、马赫数和长深比对反馈机制的影响，以降低方腔流致噪声^[14]。Block^[15]、Ahuja^[16]等对方腔宽长比（W/L）的影响进行了研究，前者发现随着方腔宽度减小，辐射噪声强度增大；而后者观察到随着方腔宽度减小，流致振荡强度降低。产生这种差异的原因目前尚不明确，可能是马赫数、雷诺数或边界层厚度对流动结构产生的影响所致。近年来，研究者开始关注三维方腔^[17-18]，但目前大多数研究集中于无限宽度（infinite width）方腔和固定宽度方腔，对方腔宽度影响的研究相对较少，特别是宽长比小于0.5的情况，几乎没有被研究过。

本文采用麦克风阵列、脉动压力传感器和TR-PIV（Time-Resolved Particle Image Velocimetry）等测量设备，开展侧壁约束效应对三维方腔自持振荡和噪声辐射影响的实验研究，对比不同宽长比方腔的辐射噪声强度、频谱特性和指向性，结合方腔内壁面压力分布及流场结构，综合分析减小宽长比对方腔流致振荡及噪声辐射的抑制机理。

1   实验设置及方案

1.1   风洞及模型

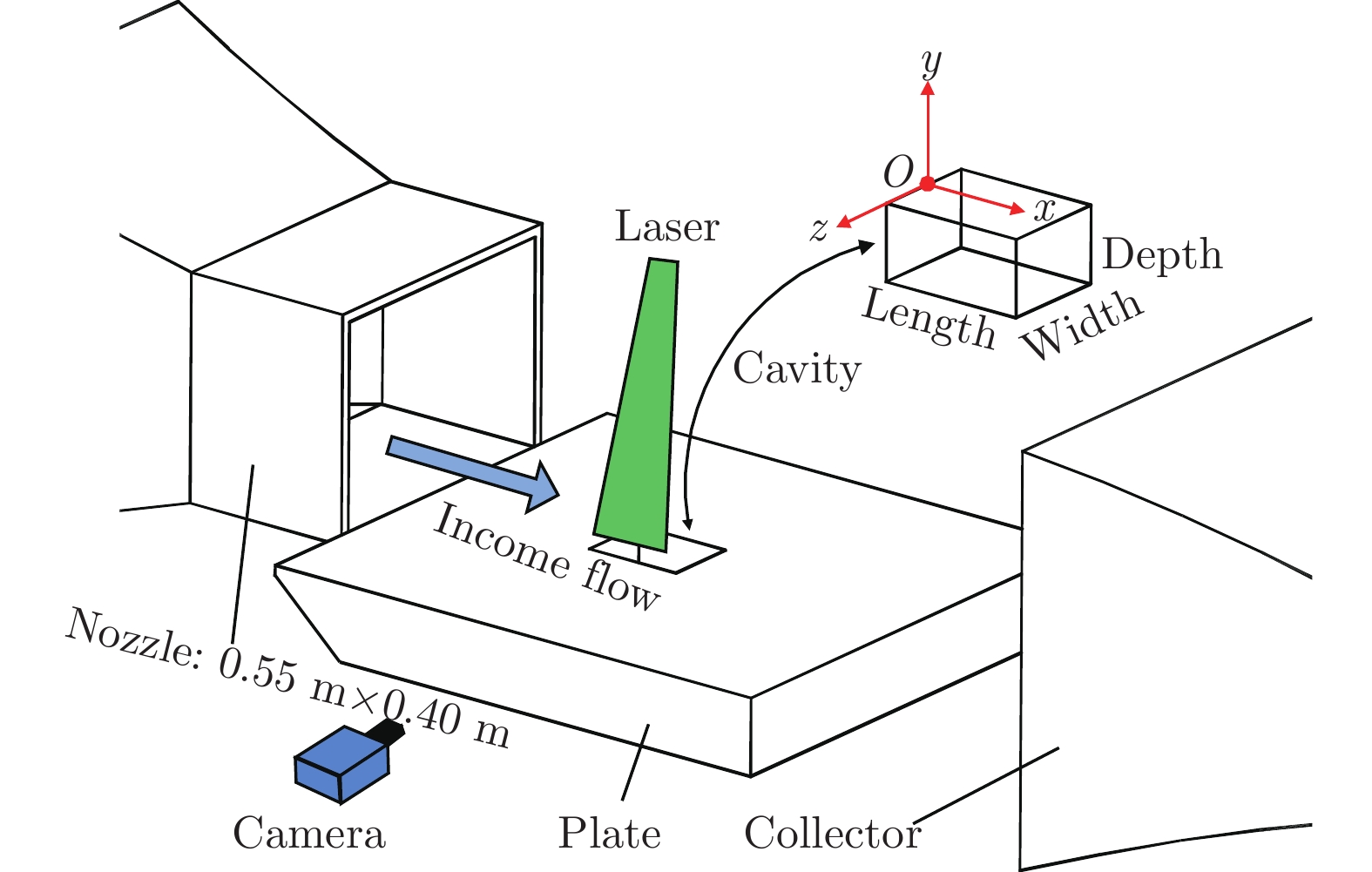
实验在中国空气动力研究与发展中心0.55 m×0.40 m声学风洞中开展，如图1所示。该风洞为回流式低速风洞，配备矩形试验段，40 m/s风速下的来流湍流度小于0.05%，80 m/s风速下的背景噪声小于78 dB（A）。

图  1  声学风洞实验实物图

Fig.  1  CARDC low-speed acoustic wind tunnel

下载: 全尺寸图片 幻灯片

矩形方腔实验模型为有机玻璃材质，通过平板（有机玻璃材质）与风洞试验段出口相连，平板上表面与试验段出口下表面齐平。方腔沿试验段中心线水平安装，方腔上部开口所在平面与平板上表面齐平，前缘距平板前缘200 mm。为便于阐述，以方腔上部开口前缘中心点为原点O建立坐标系，沿流向为x轴正向，y轴与x轴垂直，指向上方，z轴垂直于xOy平面，其正向根据右手定则确定（图2）。

图  2  实验方案示意图

Fig.  2  Test configuration of experiments

下载: 全尺寸图片 幻灯片

实验测量了5个宽度不同的矩形方腔，其x向长度、y向深度均相同（长度L=200 mm，深度D=100 mm）。5个方腔的z向宽度分别为20、40、60、80和100 mm，方腔的宽长比（W/L）在0.1～0.5之间变化。来流马赫数Ma=0.03～0.25。

1.2   测量设备及方案

1.2.1   噪声测量

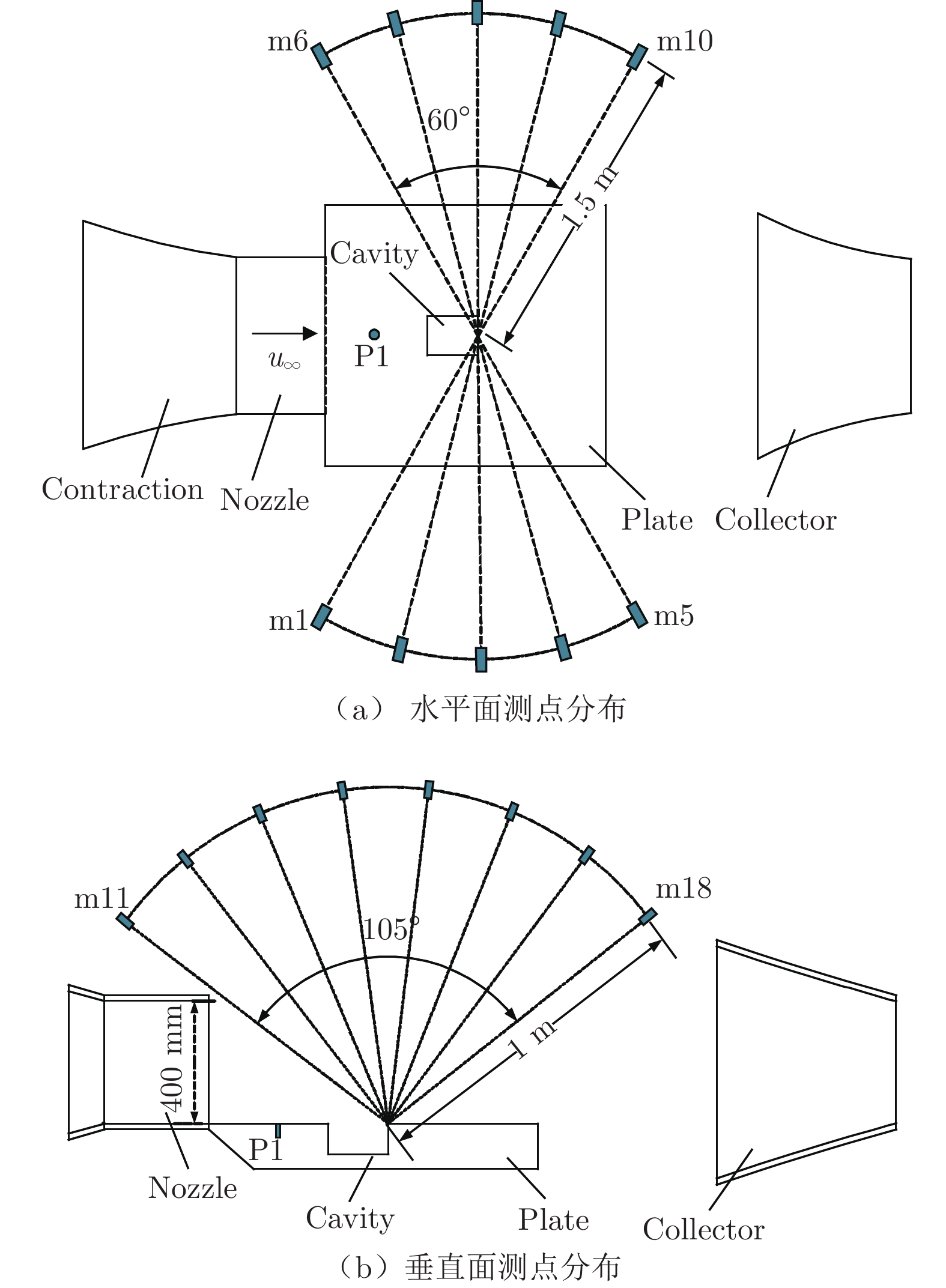
噪声测量使用B&K 4955麦克风，分别在水平面和垂直平面内测量噪声强度和指向性。如图3所示，在y=200 mm水平面内，以方腔上部开口后缘中心点为圆心、1.5 m为半径，左右两侧各均匀布置5个麦克风，彼此夹角15°；在z=0 mm的垂直平面内，以方腔上部开口后缘中心点为圆心、1.0 m为半径，均匀布置8个麦克风，彼此夹角15°。麦克风频率响应范围为20 Hz～40 kHz，声压级（L_SP）测量精度优于0.1 dB，声压级公式为：

图  3  水平面和垂直平面的麦克风阵列布置示意图

Fig.  3  The arrangement of microphone arrays in horizontal and vertical directions

下载: 全尺寸图片 幻灯片

式中：p为波动压力；p_ref为参考声压，p_ref =2×10^–5 Pa。

噪声测量采样频率25.6 kHz，采样时间30 s。对原始数据进行分段处理，使用平均周期图谱法计算功率谱密度^[19]，对每段数据加汉明窗函数^[20]，每个窗口的样本数为25600，重叠50%，频率分辨率为1.56 Hz。由于温度、湿度以及麦克风支撑装置的影响，多次测量时发现：对于垂直平面，噪声测量误差不大于0.2 dB，对于三脚架支撑的水平面，噪声测量误差不大于0.5 dB。

1.2.2   动态压力测量

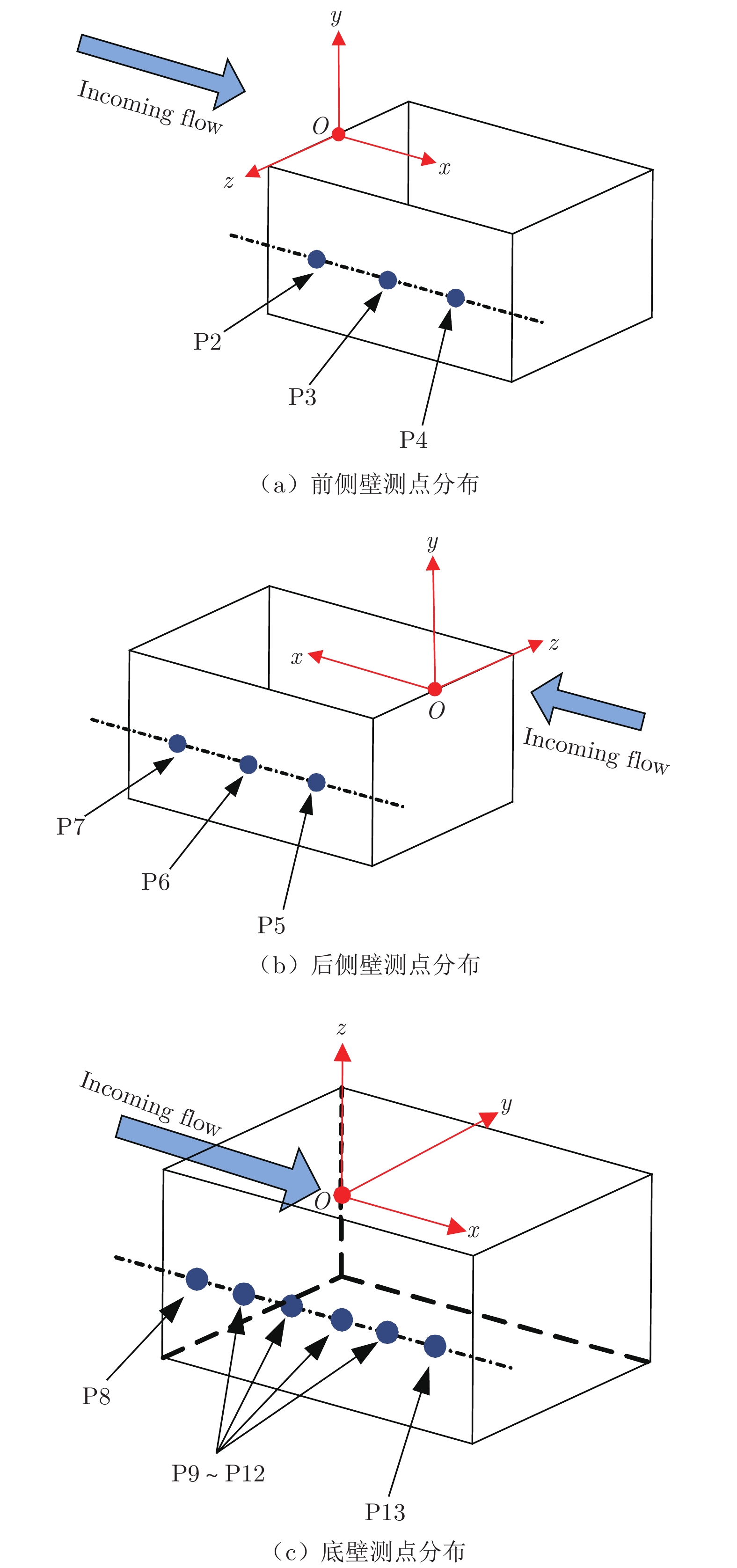
使用13个压阻式脉动压力传感器（以P1～P13表示）测量壁面脉动压力。脉动压力传感器表面直径3.8 mm，最大量程为1 psi（约6.895 kPa），测量精度0.1%。如图3所示，P1安装于方腔上游，距离方腔前缘160 mm。其他12个传感器安装于方腔内壁面，如图4所示，P2～P4安装于左侧壁（迎来流左侧），P5～P7安装于右侧壁，P8～P13安装于底壁。所有传感器均沿其所在壁面水平中心线等距安装，并确保传感器表面与方腔壁面齐平。Roshko^[5]的实验结果表明，即使传感器与腔体壁之间存在间隙，传感器安装于方腔内部对方腔流动也基本无影响。

图  4  方腔内壁面脉动压力传感器布置示意图

Fig.  4  The arrangement of high frequency dynamic pressure sensors on the cavity walls

下载: 全尺寸图片 幻灯片

脉动压力传感器采样频率51.2 Hz，采样周期30 s，数据处理方法与麦克风的数据处理方法相同，脉动压力的功率谱密度采用系综平均法计算^[19]，脉动压力测量结果可以给出方腔内壁面噪声强度和平均压力。

1.2.3   流场测量

使用高频PIV测量流场（见图5）。相机型号为PHOTRON SA-Z，双曝光模式，配备85 mm尼康镜头，变焦比2.2，放大比例3.4 pixel/mm，视场最小分辨率0.3 mm。激光器为Nd:YLF激光器（30 mJ，双脉冲）。示踪粒子为甘油，直径1 μm。采用同步控制器实现激光器和相机同步采集，采样频率1.8 kHz。以PIVTEC–PIVview2C软件进行图像分析，图像处理采用带窗口的迭代多重网格技术。

图  5  PIV测量实物图

Fig.  5  PIV system in the acoustic anechoic room

下载: 全尺寸图片 幻灯片

使用PIV测量了Ma=0.12～0.25范围内5个不同宽长比的方腔中心平面（z=0 mm）的流场。为了比较近壁面流动与中心平面流动的差异，还测量了宽长比为0.5的方腔近壁面（z=40 mm）处的流场。

2   结果与讨论

2.1   噪声结果

2.1.1   方腔振荡及辐射噪声主频率分析

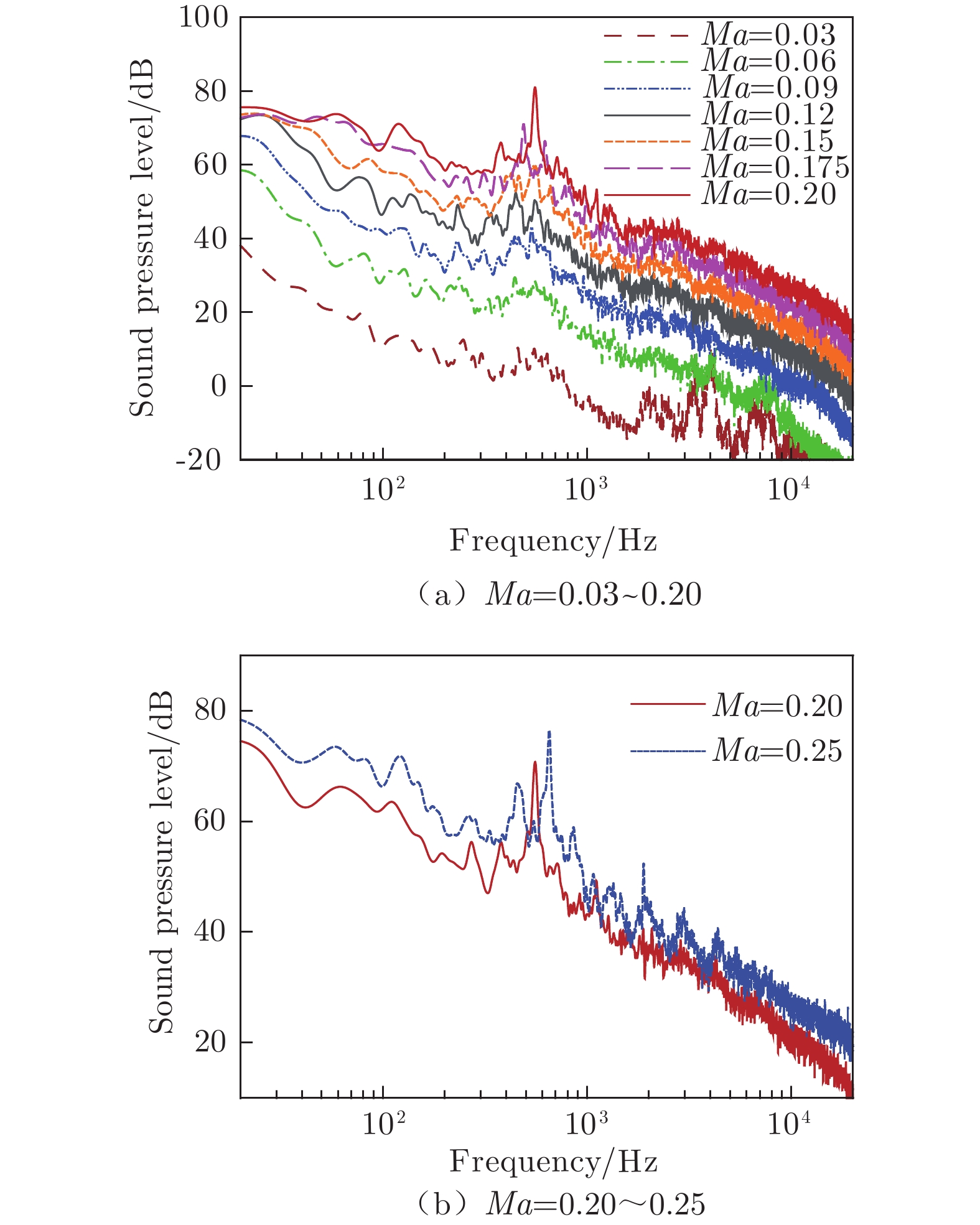
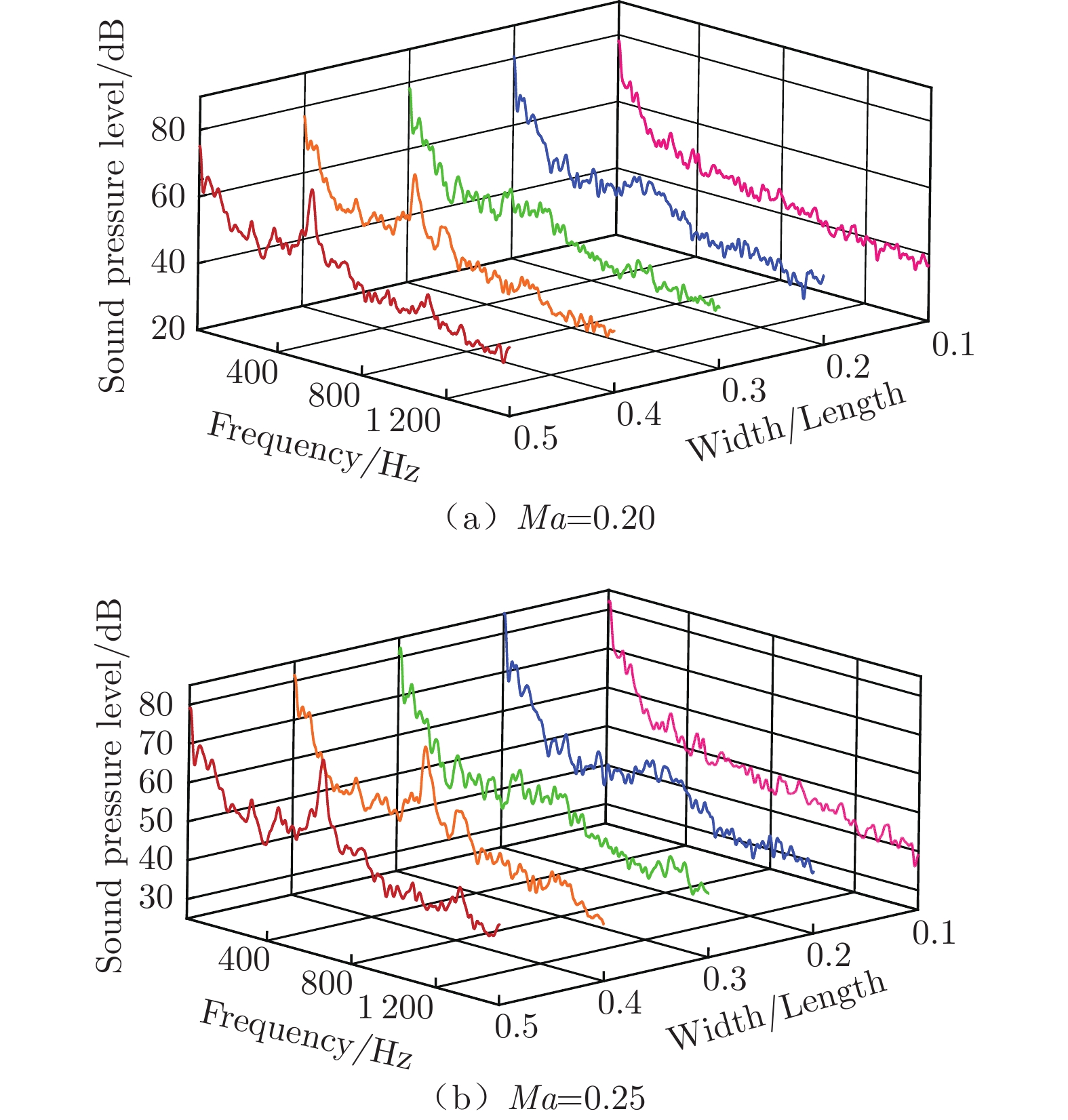
通过测量宽长比为0.5的方腔远场噪声，分析方腔流致振荡及噪声辐射特性。图6给出了马赫数从0.03增大至0.25过程中的方腔噪声频谱特性变化曲线。由图6（a）可知，来流马赫数在0.03～0.09之间时，噪声频谱波动出现于550 Hz附近，但波动幅值较小，没有明显的频率尖峰，这说明方腔流动在较低风速时即开始表现出振荡和不稳定性特征，但尚未形成自持振荡。随着来流马赫数继续增大，远场噪声频谱在550 Hz附近开始出现明显频率尖峰，Ma=0.15时出现3个频率尖峰（400、558和660 Hz），Ma=0.175时出现2个频率尖峰（484和611 Hz），Ma=0.20时，仅有一个550 Hz频率尖峰。噪声频谱峰值反映了方腔流致振荡过程中的脱落涡动力学行为，该过程可视为一个多涡竞争自持振荡形成过程。

图  6  不同风速下的方腔远场噪声频谱特性（W/L=0.5）

Fig.  6  PSD distributions for different wind speeds at W/L=0.5

下载: 全尺寸图片 幻灯片

同时可以看到，在来流马赫数0.03～0.20范围内，频率尖峰中心频率并未随马赫数增大而变化，说明在较低来流马赫数下，方腔流致振荡斯特劳哈尔数（Strouhal number）随来流马赫数不同而不同，对应的流体动力学特征区别明显，这一现象在以往方腔研究中并未引起注意。根据前人研究结果^[21]可知，方腔远场噪声频谱是方腔流动涡结构的表征，前缘剪切层不稳定性导致的涡卷起，随着流动向下游移动，并与方腔后缘撞击，产生噪声辐射。本文认为：在低速条件下，脱落涡与方腔后缘撞击产生的压力扰动不能形成强相干运动，扰动能量不足以建立反馈回路，进一步证明了方腔自持振荡是一个随来流速度逐渐发展的过程。

当来流马赫数为0.20时，方腔噪声尖峰频率为550 Hz；来流马赫数为0.25时，尖峰频率为650 Hz。由图6（b）可以看出，当来流马赫数大于0.20时，方腔辐射噪声尖峰频率随着来流马赫数的增大而增大，符合斯特劳哈尔数相似定理，说明此时方腔能够形成稳定的自持振荡。为预测方腔噪声主频率，Rossiter^[9]提出了一个半经验公式：

式中，Sr_n为振荡模态n对应的斯特劳哈尔数；f_n、L和u_∞为方腔振荡频率、方腔长度和自由来流速度；α为涡运动与声传播的迟滞时间，k为涡对流速度。

式（2）中的经验参数α和k与方腔内流动结构和长深比相关，是通过实验数据拟合确定的^[22]，k的取值范围在0.50~0.75之间，α的取值由长深比决定。对于长深比为2的方腔，k=0.5，α=0.25。用式（2）预测与本文实验相同参数的方腔噪声主频率，得到来流马赫数0.20和0.25时的主频率分别为555 Hz和660 Hz，与实验结果吻合得非常好，此时的方腔振荡模态为Rossiter三阶模态。

2.1.2   侧壁约束效应对方腔噪声的抑制

对于宽长比为0.5的方腔，在来流马赫数为0.20时，方腔流动已经形成自持振荡并辐射出尖频噪声。为研究侧壁约束效应对方腔流致振荡的抑制作用，实验对比了宽长比为0.1、0.2、0.3、0.4和0.5的方腔远场噪声。图7（a）给出了来流马赫数0.20时不同宽长比方腔的远场噪声频谱对比，当宽长比W/L≤0.3时，方腔辐射噪声的频率尖峰明显减弱甚至消除。由图7（b）可以看出，当来流马赫数提高至0.25时也出现了相同现象。

图  7  不同宽长比方腔噪声频谱对比

Fig.  7  PSD comparison for different W/L ratios

下载: 全尺寸图片 幻灯片

图8给出了方腔宽长比为0.3和0.4时的垂直和水平方向的噪声总声压级（OASPL）对比结果。可以看出，减小方腔宽度并不会改变水平方向的噪声总声压级，但会大幅降低垂直方向的方腔上游总声压级，表现出明显的侧壁约束效应；与宽长比0.4的方腔相比，宽长比0.3的方腔上游噪声强度最高能够降低3 dB。对于长深比L/D≥1的方腔，产生的噪声主要是纵波，具有向上游辐射的强烈指向性^[21]，因此，减小宽长比能够显著降低方腔流致振荡辐射噪声总声压级。

图  8  宽长比0.3与0.4的方腔噪声总声压级对比（Ma=0.20）

Fig.  8  OASPL comparison between cases with W/L=0.3 and W/L=0.4 at a wind speed of Ma 0.20

下载: 全尺寸图片 幻灯片

前人对方腔宽度的研究多集中于无限宽度和宽长比≥0.5的单一状态，上述侧壁约束效应尚未被报道。方腔辐射噪声与内部流动结构密切相关，本文认为：当方腔宽长比减小时，由于侧壁的黏性效应，方腔流动的三维性^[23]加强，内部涡结构的强度降低，导致方腔的自持振荡和辐射噪声受到抑制。后文将通过壁面脉动压力和PIV流场测量结果进一步分析噪声抑制机理。

2.2   壁面压力结果

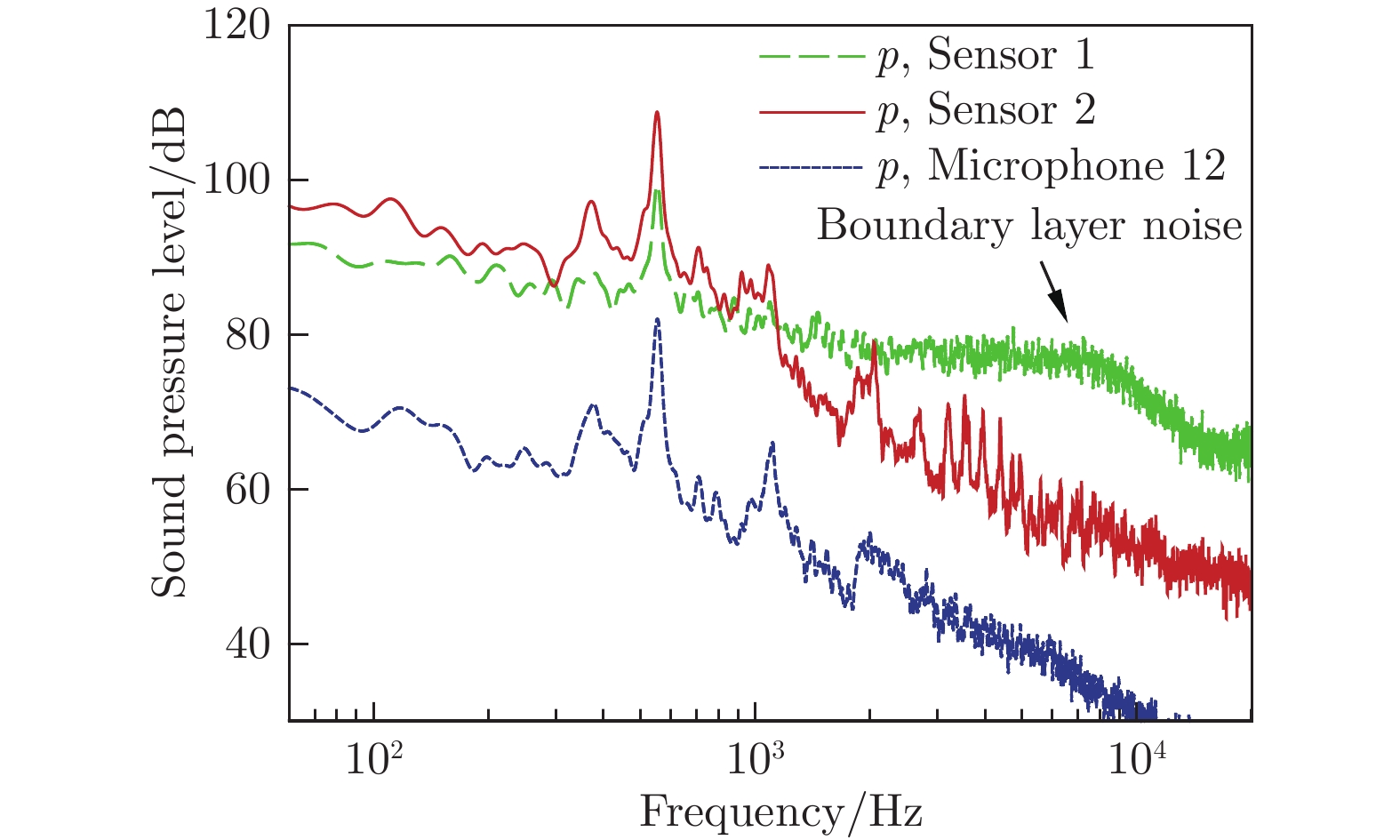
图9给出了来流马赫数0.20、宽长比0.5条件下，方腔前缘及内壁面压力频谱与远场噪声频谱的对比（绿线为前缘测量结果，红线为方腔壁面测量结果，蓝线为远场测量结果）。壁面脉动压力传感器测得的压力频谱和远场噪声频谱具有相同的频域分布及变化趋势。由图9可知，方腔内壁面压力频谱的尖峰强度明显高于方腔前缘，分析认为方腔上游的压力脉动是由方腔内辐射的二次波引起的。方腔前缘压力频谱在高频段能量较高，是由于来流边界层的高频分量注入所导致。方腔内部的压力频谱在高频段存在多个尖峰频率，分析认为是由于内部回流诱导涡对流产生的，在远场传播中快速衰减，不能产生有效的噪声辐射。

图  9  方腔内壁面脉动压力频谱与远场噪声频谱的对比（Ma=0.20，W/L=0.5）

Fig.  9  PSD distributions based on surface pressure fluctuations at local pressure sensors 1 and 2 and at far-field microphone 12 with a wind speed of Ma 0.20 and W/L=0.5

下载: 全尺寸图片 幻灯片

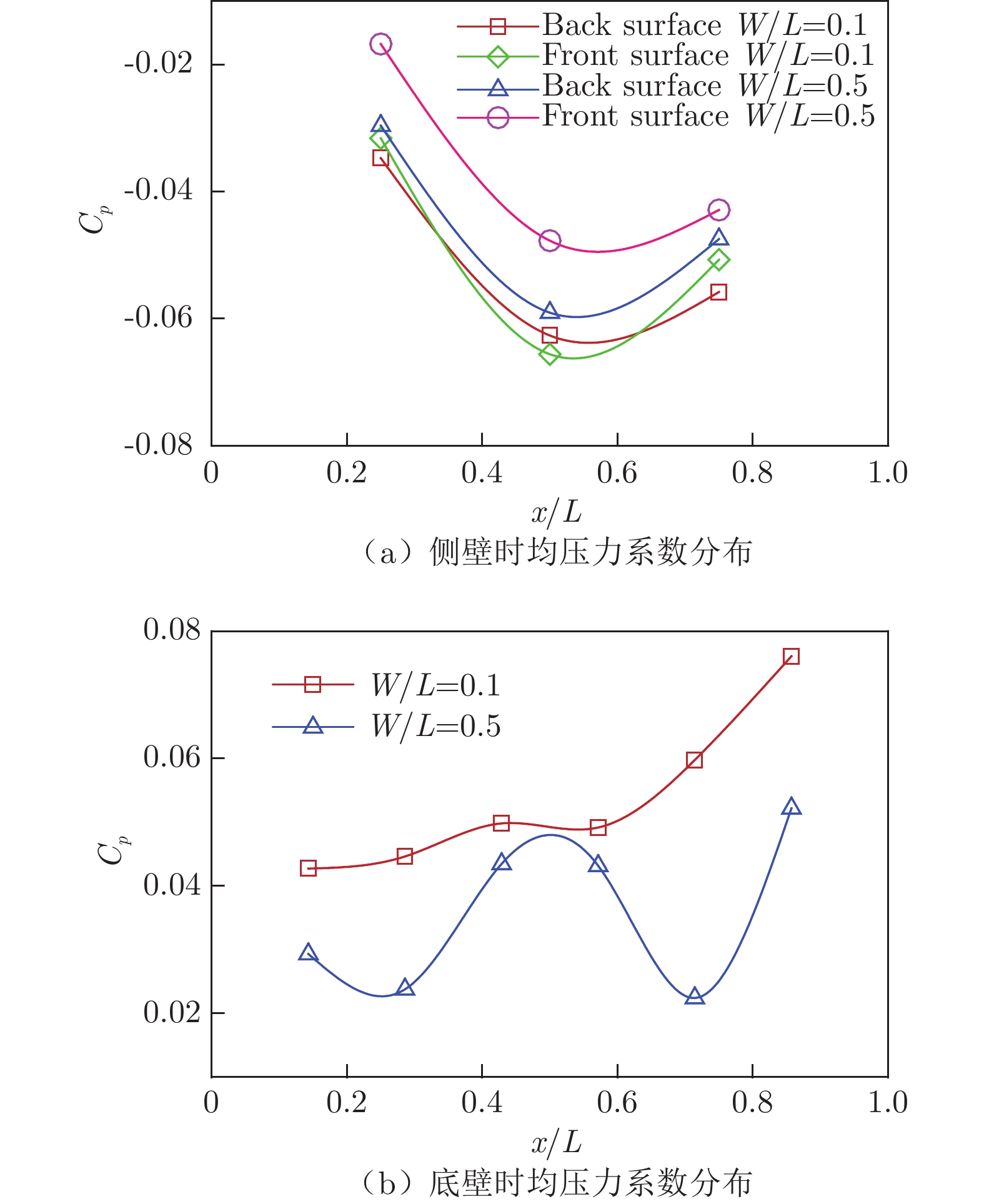
对脉动压力数据进行时间平均，得到各点的平均压力p_mean，进而计算方腔壁面的时均压力系数C_p。图10给出了来流马赫数0.20、宽长比为0.1和0.5的方腔壁面时均压力系数C_p分布对比。图中各点为实验测量值，采用三次曲线对其进行拟合。由图10（a）可以看出，宽长比减小，双侧壁C_p值减小，但沿流向的分布趋势基本不变。图10（b）则显示：底壁的C_p值随宽长比的减小而增大，但沿流向分布发生了明显变化。由于方腔壁面时均压力系数分布与内部流动（特别是主回流涡结构）具有强相关性，因此由壁面压力分布可知，方腔侧壁约束效应改变了内部的流动及涡结构。

图  10  宽长比0.1与0.5的方腔壁面时均压力系数对比（Ma=0.20）

Fig.  10  Comparison of mean pressure coefficients between the cases with W/L=0.5 and W/L=0.1 at Ma 0.20

下载: 全尺寸图片 幻灯片

2.3   流场结果

为进一步研究方腔宽度对流动结构的影响，采用TR-PIV测量了不同宽度方腔内各截面的流场结构。图11为来流马赫数0.20、宽长比0.5时中心平面（z=0 mm）一个流致振荡周期（T₀）内具有代表性的瞬时流线及涡量分布图：方腔前缘初始产生一个小涡结构，随来流向下游移动并逐渐增大，与方腔内的大涡结构融合并注入能量，形成一个更大的回流结构，最后与方腔后缘撞击并辐射噪声，部分涡结构由后缘挤出，同时在方腔内产生诱导涡，完成一个振荡循环。该结果与前人对方腔流动的假设吻合。

图  11  一个振荡周期内方腔瞬时流场变化（Ma=0.20，W/L=0.5）

Fig.  11  Six snapshots of flow pattern in a period T₀ in the central plane at a wind speed of Ma 0.20 and W/L=0.5. The streamlines are shown, while the background denotes the field of spanwise vorticity

下载: 全尺寸图片 幻灯片

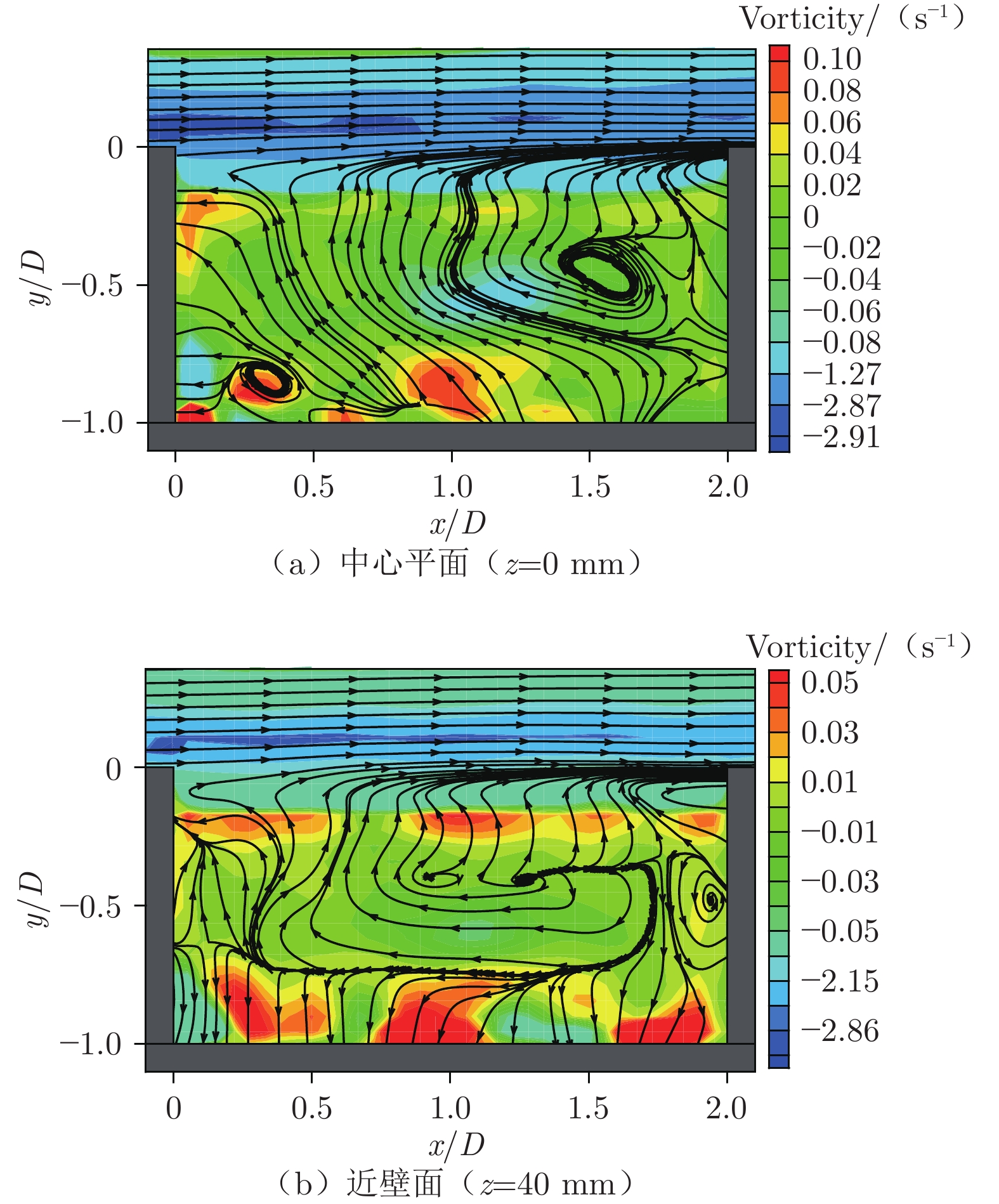
考虑到方腔流动具有三维特性^[23]，对近壁面流场结构进行了测量。图12为来流马赫数0.20、宽长比0.5时中心平面（z=0 mm）和近壁面（z=40 mm）的时均流场对比：中心平面流线分布以二维流动为主，而近壁面流线有着明显的源流动，呈现出较高的三维特性；同时，近壁面的涡量值小于中心平面，回流强度被大幅抑制。

图  12  方腔中心平面和近壁面时均流场分布对比（Ma=0.20，W/L=0.5）

Fig.  12  Mean flow pattern comparison between central plane and near wall plane at the wind speed of Ma 0.20 (W/L=0.5)

下载: 全尺寸图片 幻灯片

通过对比不同宽长比方腔中心平面的流场结构，结合方腔近壁面流动特征，分析方腔侧壁约束效应对辐射噪声的抑制机理。图13为来流马赫数0.20，宽长比0.1、0.2、0.3、0.4和0.5的方腔中心平面（z=0 mm）流场结构。可以看出：随着宽长比减小，方腔内的主回流结构逐渐向上游移动，中心平面流动逐渐表现出类似近壁面的三维流场特征。

图  13  不同宽长比方腔中心平面时均流场对比（Ma=0.20）

Fig.  13  The comparison of mean flow patterns in the central plane for different W/L at the wind speed of Ma 0.20

下载: 全尺寸图片 幻灯片

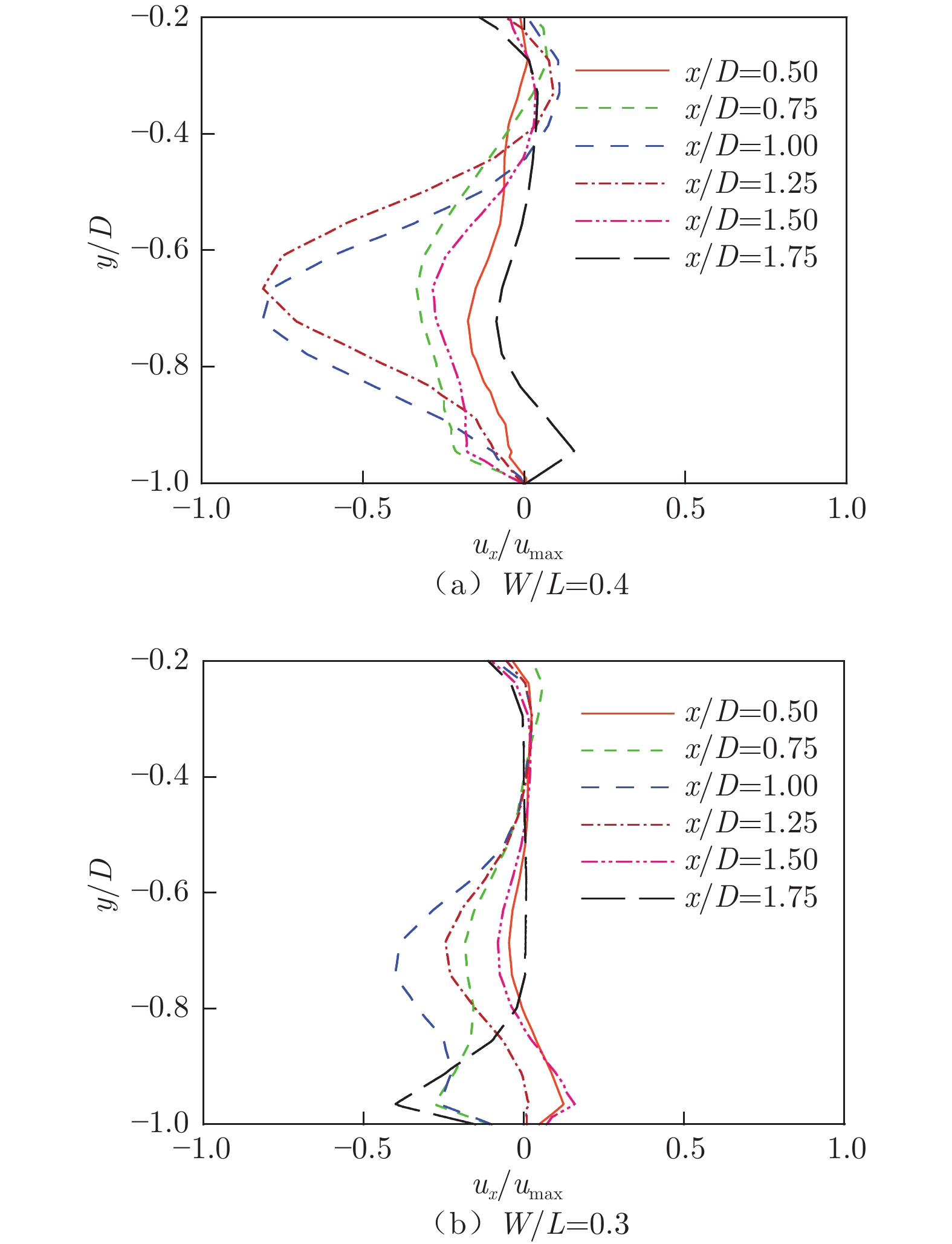
图14给出了宽长比为0.3和0.4的方腔沿流向各截面的无量纲化速度型曲线（图中，u_max为方腔内x方向最大流速，u_x为方腔内当地x方向的实际速度）。可以看出，随着宽长比减小，方腔内回流速度降低，流动涡量减小。

图  14  宽长比0.3和0.4的方腔中心平面流向时均速度型对比（Ma=0.20）

Fig.  14  The mean streamwise velocity profiles inside the cavity for W/L=0.4 and W/L=0.3 in the central plane at a wind speed of Ma 0.20

下载: 全尺寸图片 幻灯片

综上，本文认为：三维方腔侧壁约束效应之所以能够抑制振荡及辐射噪声，是由于方腔宽度减小时，回流涡结构向上游移动、流动呈现三维特性、涡量值减小等多种因素共同作用导致的。此时，涡与方腔后缘撞击强度降低，自持振荡被抑制甚至消除。

3   结　论

1）由于前缘剪切层的不稳定性，来流马赫数大于0.03时，方腔就开始出现压力波动。随着来流马赫数增大，方腔内部通过多涡竞争机制逐渐形成自持振荡。来流马赫数大于0.20时，方腔出现Rossiter三阶模态流致振荡，并辐射出指向方腔上游的尖频噪声，噪声频率变化满足斯特劳哈尔数相似准则。

2）对于自持振荡方腔流动，减小方腔宽长比能够大幅度抑制方腔振荡及辐射的尖频噪声。来流马赫数0.20时，将方腔宽长比由0.4降至0.3，方腔上游噪声总声压级能够降低3 dB以上。

3）方腔壁面压力分布和PIV流场结果表明：减小方腔宽长比，加强侧壁约束效应，能够改变方腔流动结构，增强方腔流动的三维性，降低涡强度；同时，还能够促使方腔内大涡结构向前缘移动，削弱涡与方腔后缘的撞击程度，进而抑制方腔流致振荡和尖频噪声辐射。