Experimental study on time-delay effect of unsteady hydrodynamics of the supercavitating vehicle in water tunnel
-
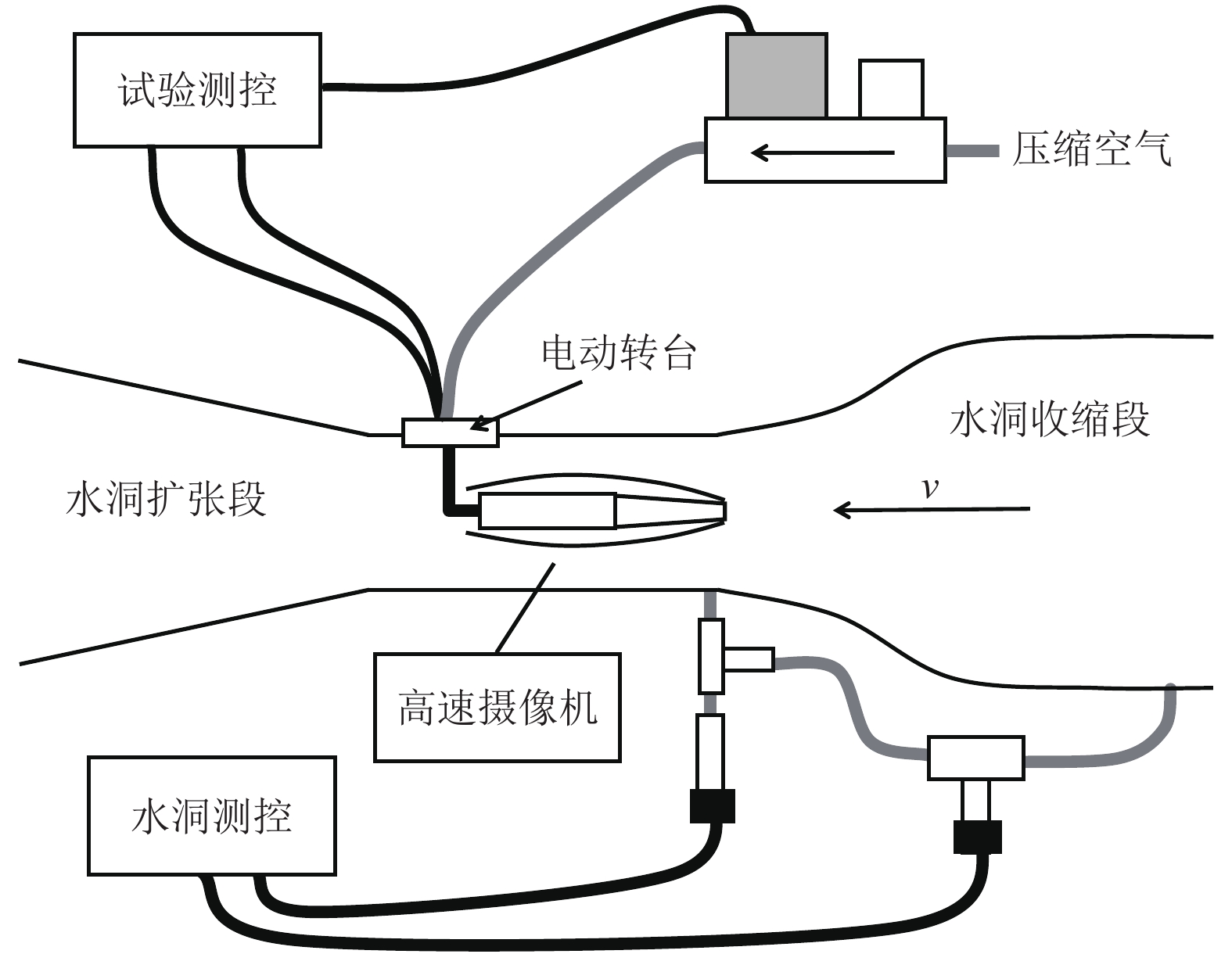
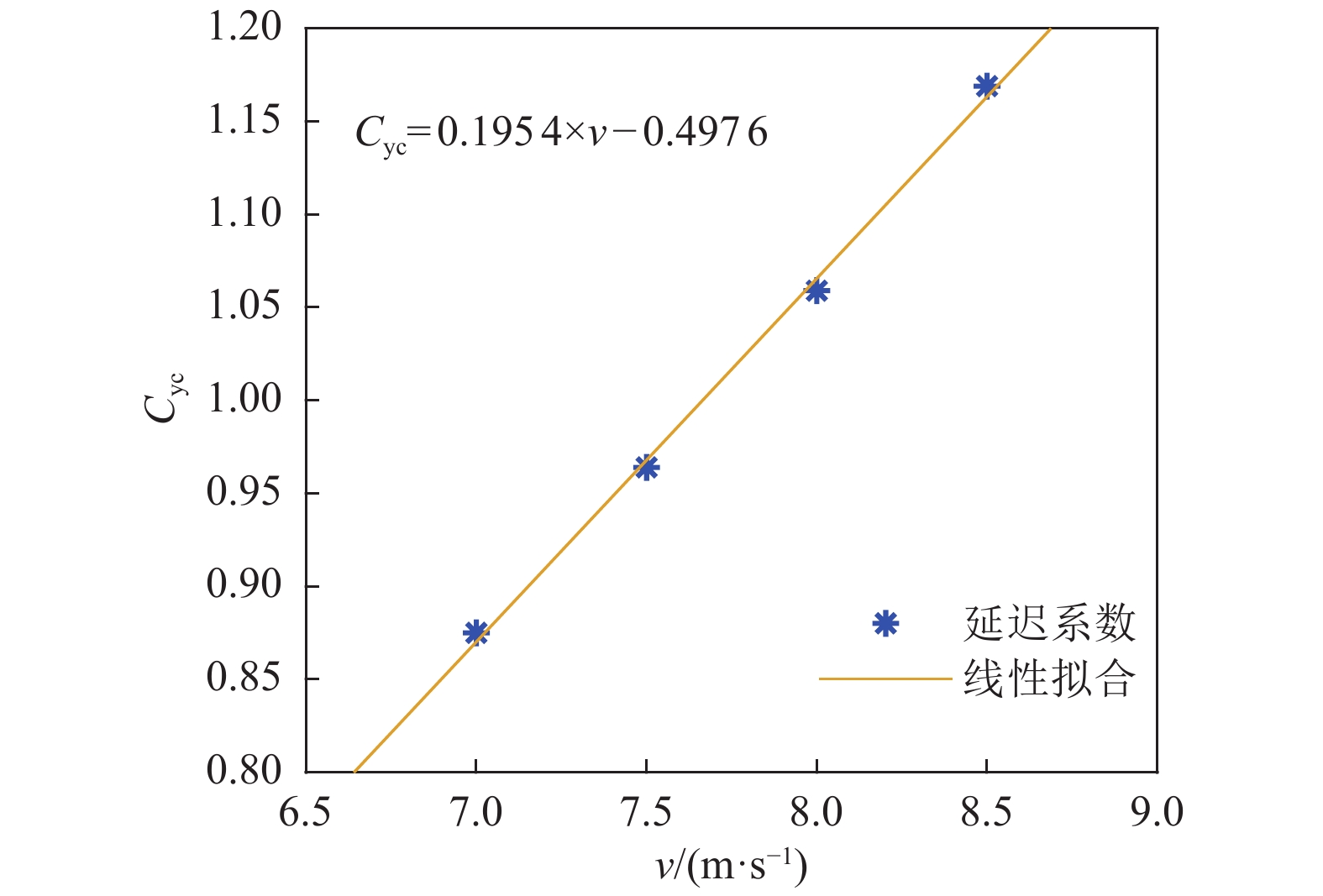
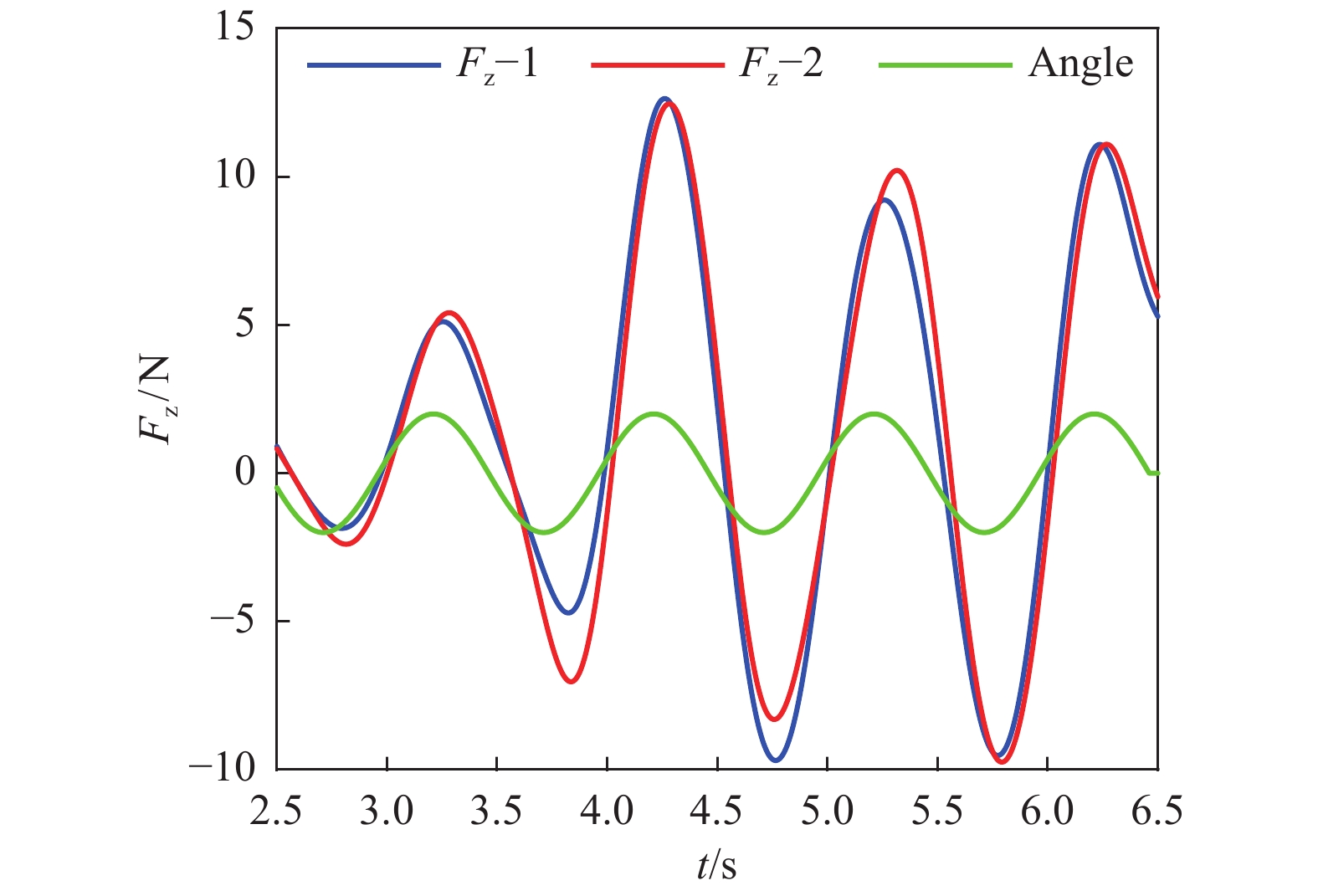
摘要: 空泡延迟效应在机动航行诱发的尾拍振荡中影响显著,是超空泡航行体的重要力学特性,在动力学建模中必须加以考虑。采用人工通气超空泡的试验方法,在西北工业大学高速水洞实验室开展了超空泡航行体连续变攻角测力试验研究,测量攻角与流体动力随时间变化历程来定量分析延迟时间特性。通过试验研究,获得了不同试验条件下变化的延迟时间;无量纲化的延迟系数与水速近似成线性关系,且随预置舵角的增大而增大;在试验采用的摆动频率中,摆动频率较大的工况,延迟系数较小。Abstract: The cavity-delay-effect has a significant impact on the tail slapping induced by maneuvering, and it is an important mechanical characteristic of supercavitating vehicles, which must be considered in dynamic modeling. The experimental method of artificial ventilated supercavitation is used in the laboratory of Northwestern Polytechnical University’s high-speed water tunnel to carry out the continuous variable angle of attack experiment. The delay time is quantitatively analyzed by measuring the changes of attack angle and dynamic force with time. Varying delay times are obtained under different conditions, and the dimensionless time-delay coefficient is approximately linearly related to the water speed. The time-delay coefficient increases with the increase of the preset rudder angle. Among the oscillation frequency used in the experiment, the larger the oscillation frequency is, the smaller the time-delay coefficient is.
-
0 引 言
翼型叶片广泛存在于航空/地面运输工具和民用气动设备中,如飞机增升装置、直升机旋翼、发动机转/静叶片、风力机和风扇叶片等。当气流撞击或流经翼型叶片时,会产生各类空气动力噪声。其中,由外界干扰、翼型表面凹凸等引起的边界层扰动发展至翼型后缘(Trailing Edge, TE)所产生的噪声,称为“翼型后缘噪声”,如图1(a)所示。
研究表明,随着来流马赫数Ma或雷诺数Re的变化,翼型后缘噪声具有不同的频谱特性:
当基于翼型弦长的来流雷诺数足够大时(Re > 106),整个边界层流动在到达翼型后缘之前已成为充分发展的湍流,由此湍流边界层引起的翼型后缘噪声本质上是一种宽频噪声[2]。
当来流雷诺数较小(Re < 106)且湍流度较低时,整个翼型边界层为层流流动,此时边界层扰动在翼型后缘引起的噪声主要为纯音噪声[1],常具有典型“阶梯状”离散频谱特性,如图1(b)所示。这种纯音噪声常产生于以中/低雷诺数运行的小型飞行器、无人机、风力机和轴流风扇中,也是这些小型气动设备的主要噪声源之一。与宽频噪声相比,翼型后缘纯音噪声的离散频率通常高10 dB以上[3],人耳会感知到强烈啸叫,特别令人烦扰。
随着微/小型飞行器和无人机工业的快速发展(2016—2022年,产能每年增长约20.7%[4])、全球中小型风力机迅速扩容(美国市场研究机构Navigant Research预计,从2020年的176.4 MW将增长至2026年的446 MW)以及小型轴流风扇在办公、家用设备中的广泛应用,翼型叶片所引起的纯音噪声已严重影响到人们的工作与生活,甚至威胁到人们的身心健康。2022年6月5日颁布施行的《中华人民共和国噪声污染防治法》对国内工业生产、交通运输和社会生活中的环境噪声作出了严格规定,要求做到还静于民,维护和谐安宁的生活环境。因此,研究中/低雷诺数下翼型后缘纯音噪声的关键物理机制并探索有效的噪声控制策略,对于低噪声翼型叶片设计及小型飞行器、无人机、风力机/风扇等的降噪技术应用具有重要理论价值和指导意义。
自20世纪70年代以来,中/低雷诺数下翼型后缘纯音噪声特性及发声机制一直是研究者关注的热点与研究难点[5-15],研究者还对相关研究工作进行了总结与展望[1, 16]。本文基于现有文献,对中/低雷诺数下翼型后缘纯音噪声产生机理、噪声研究及分析方法、主/被动控制策略等进行更为全面的综述,重点分析现有机理研究中存在的争议问题和尚未涉及的研究内容,尝试提出某些研究新思路、新方法及噪声控制策略,并对未来研究方向进行展望。
1 翼型后缘纯音噪声物理机制研究
1.1 声反馈机制研究
作为声反馈机制研究的先驱,Paterson等[5]通过实验发现:在一定雷诺数和迎角下,压力面边界为层流流动的对称NACA翼型后缘产生的噪声具有阶梯状离散频谱特性,即在中心频率f中心两边存在其他离散频率fn(n为频率阶次),如图1(b)所示。各阶次纯音频率随来流速度v的变化如图2所示。中心频率f中心与v1.5成正比:
$$ f_{中心} = 0.011 v^{1.5} (c\nu)^{−0.5} $$ (1) 式中:c为翼型弦长,ν为运动黏性系数。其他各阶次离散频率fn与v0.8成比例。Paterson等认为,所有离散频率噪声都来源于翼型后缘的旋涡脱落。旋涡脱落产生的噪声通常具有单一频率及相应谐波,而图2中的离散频率与中心频率并非谐波关系。因此,旋涡脱落理论仅能解释中心频率f中心与v1.5的关系,无法解释频谱中的阶梯状离散频率。
Tam[6]认为阶梯状离散频率噪声可能是由翼型后缘尾流中形成的声反馈所导致:尾流脱落涡沿下游增强,产生噪声,声波向上游传播并在翼型后缘引起激振,从而在后缘与附近流场之间形成声反馈回路(Acoustic Feedback-Loop, AFL),如图3(a)所示。Zang等[7]的实验研究也表明可能存在该反馈回路,但上述推论仍然受到诸多质疑(包括Tam等的后续研究[17])。
Langehouse[8]认为,声反馈的形成与边界层中T–S波的发展有关,其反馈回路应在翼型后缘与压力面边界层之间形成:层流中T–S波在后缘引起的噪声向上游传播,在上游边界层不稳定的初始位置,增强了与之相位相同的部分频率的T–S波,再向下游发展至后缘,形成反馈回路,如图3(b)所示。这一声反馈回路模型被其后大量研究所证实。
尽管如此,对于声反馈回路的区间(即反馈发生的初始位置)问题仍存在较大争论。Arbey等[9]认为声反馈回路应在压力边界层内最大速度点与翼型后缘之间;Pröbsting[11]、Jaiswal[12]等则认为声反馈回路可从翼型前缘开始直到翼型后缘,与Goldstein[13]的理论分析也较为一致。无论声反馈区间如何,Kingan等[10]运用该边界层声反馈回路模型,在理论上成功预测了翼型后缘阶梯状离散频率噪声的各阶次频率,证明了采用这种声反馈机制解释离散纯音噪声的合理性。
Desquesnes等[14]研究发现,翼型可能存在压/吸力面边界层双声反馈,其中压力面为主声反馈,吸力面为次声反馈,且噪声强度由翼型后缘处压/吸力面T–S波的相位差决定,如图3(c)所示。Yang等[15]的实验也部分验证了双声反馈T–S波在翼型后缘的相位差对噪声幅值的影响。但近年来的多数研究[12, 18-20]表明,压/吸力面双声反馈可以独立存在,形成各自的后缘噪声特性,噪声幅值与后缘处T–S波的相位差没有直接联系。
在何种情况下可能形成边界层内的T–S波声反馈呢?大量研究认为,引起翼型后缘离散纯音噪声的声反馈与翼型边界层的层流分离泡(laminar separa-tion bubble)密切相关[14, 19-26]。Pröbsting等[26]实验研究了不同雷诺数下NACA 0012翼型压/吸力面的层流分离泡变化及其引起的纯音噪声特性:在一定迎角下,当Re较低时,层流分离泡仅发生于翼型后缘附近的吸力面,此时声反馈发生于吸力边界层与后缘之间,如图4(a)所示;随着Re增大,吸力面分离泡前移,层流分离泡出现于翼型后缘附近的压力面,声反馈主要发生在压力边界层,如图4(b)所示;当Re进一步增大,压/吸力面的分离泡同时前移且尺寸萎缩,压/吸力面边界层的声反馈消失,如图4(c)所示。
Nguyen等[23]对层流分离泡与声反馈之间的关联开展了数值模拟研究,发现声反馈引起的离散纯音噪声的确与分离泡大小和位置相关,且压/吸力面分离泡位置取决于翼型迎角α或来流雷诺数Re。表1为α = 2°时压/吸力面层流分离泡位置随Re的变化情况,表2为Re = 1.8 × 105时压/吸力面层流分离泡位置随α的变化情况。Yakhina等[19]的进一步实验研究发现,形成后缘离散纯音噪声的必要条件是翼型边界层内发生层流分离且分离泡位置应在翼型后缘附近,分离泡在后缘处起到了放大边界层内T–S波的作用。Wu等[20]的数值模拟研究也证实翼型后缘层流分离泡是纯音噪声声反馈形成的必要条件。总体而言,相关研究普遍认为:边界层内T–S波需利用层流分离泡得到快速增长后,才能提供足够能量维持自激振荡的声反馈,进而产生离散频谱纯音噪声。
1.2 涡脱落机制研究
声反馈引起翼型后缘纯音噪声的机制已被大量研究所阐明,尤其是过去10年,声反馈理论和实验研究都取得了较大突破[15, 18-23]。尽管如此,声反馈是否是翼型后缘纯音噪声形成的先决条件仍存在较大争论,因为在部分翼型后缘噪声研究中仅出现了单频纯音噪声,而未出现阶梯状离散频率噪声。
Nash等[27]首先提出了质疑。他们通过实验研究发现:当风洞壁安装吸声声衬后,在所有中/低雷诺数和翼型迎角条件下都仅出现了单频纯音噪声,而未安装吸声声衬时出现了多个由风洞共振引起的噪声峰值频率。Nash等认为阶梯状离散频率噪声极可能是由模型安装方式不同而引起,实际并不存在声反馈。为消除可能出现的安装效应影响,Tam等[17]采用直接数值模拟(DNS)方法研究了中等雷诺数下不同后缘厚度翼型的噪声,也仅出现了单频纯音噪声。他们认为后缘尾流区不稳定性才是纯音噪声的源头,而声反馈并非翼型后缘纯音噪声形成的先决条件。
对于翼型后缘仅出现单频噪声的现象[17, 27],本文作者认为这极可能是整个流场对噪声频率进行选择的结果,并不能由此否认翼型后缘的阶梯状离散频率噪声。翼型后缘噪声频率是如何选择的呢?这就涉及到声反馈机制与涡脱落机制之间的相互竞争问题。Tam等[17]研究的翼型后缘为弱圆弧型(类似钝体后缘),形成的尾流通常会因整体不稳定而出现自激振荡的涡脱落现象,即卡门涡街[28-29]。当边界层T–S波传播至后缘,就会与钝体后缘涡脱落之间形成竞争关系(图5)。若后缘涡脱落能量较强,就可能占据主导地位,从而抑制声反馈发生,导致最终仅出现单频涡脱落纯音噪声。这也可以解释Nash等[27]实验研究中的单频纯音噪声现象。若边界层T–S波在层流分离泡中得到显著增强,使得声反馈能量强于后缘脱落涡振荡能量,则噪声频谱中就可能出现阶梯状离散频率。
对于仅出现单频纯音噪声的现象,McAlpine等[30]认为纯音噪声仅由T–S波在分离泡中的简单增长引起,声反馈并非纯音噪声出现的必要条件;建议可以研究流场中绝对/对流不稳定性,分析整体不稳定性与后缘噪声之间的关联。Johns等[31]基于DNS和绝对不稳定性理论分析认为:虽然后缘附近分离泡内流场仅出现了局部对流不稳定,但声反馈的存在也会导致流场整体不稳定;不过,声反馈所选择的噪声频率与后缘涡脱落频率一致,远低于T–S波的最大增长频率。Sandberg等[32]认为,当边界层激发T–S波后,较大迎角和厚度的翼型单频噪声由整体不稳定的翼型边界层涡脱落决定,零迎角和厚度较小的翼型则是以T–S波频率噪声为主。Khorrami等[33]研究钝体后缘的缝翼时发现,当缝翼和主翼夹角为30°时,缝翼后缘噪声主要来自后缘的涡脱落,与声反馈机制无关。Makiya等[34]研究多段翼噪声时,发现流场内可能存在2种噪声机制的竞争:在较低的雷诺数下,主要是由绝对不稳定引起的涡脱落噪声,无明显离散频谱;当雷诺数高于某临界值时,T–S波声反馈激发的噪声占主导地位,呈现出明显的阶梯状离散特性;当雷诺数介于两者之间时,则上述2种后缘噪声机制都可能存在。
1.3 声反馈机制与涡脱落机制的竞争
总体而言,声反馈和涡脱落已被视为中/低雷诺数下产生翼型后缘纯音噪声的2种主要机制。大量研究已经证实:前者是由边界层内不稳定T–S波在翼型后缘散射噪声并向上游传播而形成的[8-15, 18-23, 24-26, 35-36](T–S波需在层流分离泡中得到显著增强后才能维持自激振荡的声反馈机制);而后者主要是由翼型尾流绝对不稳定性所引发的自激振荡[30-34]。与声反馈机制相比,目前与后缘噪声涡脱落机制相关的研究工作及成果较少,其原因可能是所研究的翼型后缘多为尖后缘且翼型安装迎角较小,因此后缘噪声多以T–S波声反馈机制为主。
但是,当翼型迎角稍大或具有钝体后缘时(实际翼型并非严格的尖后缘),在某些工况下,涡脱落机制(由边界层层流分离或钝体尾流不稳定性引发)很可能与声反馈机制发生竞争,甚至占据主导地位。在这种情况下,基于声反馈机制所采取的噪声控制方法可能效果欠佳,需要寻找新的噪声控制思路。
因此,针对不同形状翼型的边界层流动,这2种噪声机制如何形成、如何相互竞争进而决定后缘噪声特性,已成为目前翼型叶片后缘噪声研究中需要解决的关键问题之一。
2 翼型后缘纯音噪声研究模型与分析方法
目前,研究者主要采用线性稳定性理论分析、风洞实验和数值模拟等方法,在中/低雷诺数范围内进行翼型后缘纯音噪声特性与机理研究。绝大多数的研究针对NACA系列对称翼型(例如NACA 0012、NACA 0018等)开展,部分研究采用了SD7003弯曲翼型(图6)[19, 23]。在一定工况下,这些翼型都出现了阶梯状离散频谱现象。Yakhina等[19]的实验研究表明:SD7003弯曲翼型出现离散频率噪声的迎角和雷诺数区间明显低于NACA系列对称翼型。
2.1 线性稳定性理论分析
基于拟平行流和小扰动假设,求解线性N–S方程,采用线性稳定性理论对翼型边界层内T–S波频率及其沿流向的发展进行分析。小扰动假设的脉动速度u为:
$$ u(x, y, z, t) =\psi(y){\rm{e}}^{{\rm{i}}(\beta x + \gamma z − \omega t)} $$ (2) 式中:ω为小扰动角频率;β、γ分别为小扰动流向和展向波数;ψ为流函数。分析边界层内T–S波沿流向空间的发展情况(空间模态)时,ω和γ通常设为实数并给定相应值;β为需要计算的变量,可表示为β = βr + iβi,其中βi表示沿流线的空间增长率。
通过数值模拟或实验得到流场某一截面的平均速度场后,即可求解线性N–S方程得到小扰动沿流向的空间发展,获得边界层中最不稳定增长频率及各截面的扰动幅值,以确定声反馈发生及选择噪声频率。
对于翼型后缘附近层流分离流动或尾流涡脱落的自激振荡特性,采用绝对/对流不稳定理论进行整体稳定性分析[28-32]。绝对/对流不稳定理论采用时–空模态研究小扰动随空间和时间的变化情况,因此式(2)中的频率ω也为复数,即ω = ωr + iωi。通过求解色散关系式Disp(β, ω, Re) = 0,获得某截面流场对应鞍点的绝对频率ω0r及其增长率ω0i,进而分析层流分离或翼型尾流的绝对/对流不稳定性,判断流场整体不稳定特性,以确定涡脱落发生与选择噪声频率。
线性稳定性理论分析结果常与后文介绍的风洞实验和数值模拟结果进行对比,以确定翼型后缘纯音噪声的声反馈或涡脱落发生机制。
2.2 实验研究与数值模拟
绝大多数实验研究在开口射流声学风洞中进行,极少数实验研究在经过声学处理的闭口风洞中进行[27]。在开口风洞实验中,为保证翼型扰流的二维流场特性,翼型通常安装于与风洞出口侧壁(或上下壁)齐平的两挡板之间。采用远/近场麦克风阵列分别测量噪声指向特性和分布特性,采用粒子图像测速仪(PIV)、热线风速仪(hot-wire anemometer)、壁面压力传感器等测量流场特性,分析噪声与瞬态流场的相关性,确定噪声产生机制。在闭口风洞实验中,为测量远场噪声,常采用可透声不透气的凯夫拉纤维布作为闭口实验段的侧壁[27]。
在以往风洞实验中,壁面声反射和空腔声共振(闭口风洞)、射流边界对声波的折射和多普勒效应(开口风洞)及翼型安装方式等因素常导致同一翼型在不同风洞实验中得到的后缘噪声特性存在较大差异,进而分析得出不同的噪声产生机制,这些实验结果导致的争论持续至今。2022年,Redonnet等[37]在闭口风洞实验中再次证实风洞翼型安装效应的确会导致翼型后缘噪声的不同频谱特性,并推断开口风洞实验中翼型安装方式(通常安装于两挡板之间)可能会形成半空腔结构,也会产生共振。Arcondoulis等[38]在开口风洞实验中采用了无挡板支撑方式,并采用声模态分析方法消除了半共振空腔影响的可能性,但仍然出现了翼型后缘离散纯音噪声。由于翼型后缘T–S波声反馈过程对外界干扰较为敏感,因此,在风洞实验中如何避免外界干扰是相关研究中必须关注的问题。
为消除风洞本体及安装效应对翼型后缘噪声特性的影响,研究者采用DNS[14, 17, 27, 39]、LES[23, 40]等对翼型流场和噪声开展了数值模拟研究。部分数值模拟研究得到了阶梯状离散频谱,间接证实可能存在边界层T–S波声反馈,但大多数数值模拟研究结果中仅出现了单一频率或相应谐波噪声,得出了翼型后缘纯音噪声可能来自于T–S波的简单增长(非反馈)或尾缘涡脱落的结论。在频率分布和噪声强度方面,数值模拟结果与实验结果也存在较大差异。这其中一个重要原因就是数值计算无法完全模拟各风洞中的实验状况,特别是在开/闭口风洞中存在各种声反馈或空腔声共振的情况下。为此,Tank等[41]对中等雷诺数下NACA 0012翼型流场数值模拟结果和实验结果出现差异的原因进行了较为详细的分析。
3 翼型后缘纯音噪声主/被动控制
翼型后缘噪声机理研究的主要目的是寻找有效方法控制噪声、改善环境。目前的翼型后缘纯音噪声控制方法可以归纳为被动模式和主动模式。
被动模式中应用最为广泛也较为有效的控制方法是采用仿生锯齿翼型前/后缘[42-48]。采用前缘锯齿,主要目的是使翼型层流边界层在发展到翼型后缘之前就转捩为充分发展的湍流,从而抑制T–S波声反馈[8, 42]。与前缘锯齿相比,后缘锯齿应用更广且噪声控制效果更好。Chong等[43]研究了不同形状后缘锯齿对控制纯音噪声的作用(图7),认为其噪声控制机理是后缘锯齿触发了转捩,阻止了层流分离泡的出现。没有层流分离泡对T–S波的显著增强,就不会出现声反馈,大大减弱了翼型后缘纯音噪声。
其他关于后缘锯齿噪声控制的研究注重对锯齿后缘结构的优化[44-48]。Hu等[47]的研究表明,与其他形状的后缘锯齿相比,具有仿生羽毛形状的后缘锯齿可以达到更好的噪声控制效果,如图8中的hww锯齿形状。Gelot等[49]认为后缘锯齿降噪机理可分为两个方面:一方面,锯齿降低了转捩区内声波幅值,从而减弱了声能量;另一方面,锯齿增强了声波与T–S波的相位干扰,减弱了声反馈能量。
与翼型后缘锯齿具有相似机理的控制方法还有翼型后缘毛刷[50-51]、多孔材料翼型[52-53]及在翼型后缘安装变形副翼[54]等。Geyer等[52]采用多孔材料制成如图9(a)所示的SD7003翼型,与光滑翼型进行比较,研究发现:SD7003翼型没有出现纯音噪声,且中低频率范围的噪声有所降低;多孔材料具有透气性,若孔隙率较低,高频段噪声反而增强(主要是表面粗糙度增大引起的噪声)。Ai等[54]在翼型后缘安装变形副翼,显著改变了边界层流场特性,可以使得翼型噪声增大或降低。该研究未特别关注翼型后缘纯音噪声,但后缘变形能够改变边界层流场,必然会影响层流流动T–S波声反馈,值得进一步研究。
尽管后缘锯齿、多孔材料翼型等能够降低翼型后缘噪声,但同时也会显著改变翼型前/后缘整体结构,降低部分气动性能(如升力减小),这在一定程度上削弱了降噪带来的收益。与被动控制模式相比,主动控制模式的优点之一是可以根据来流情况对控制进行开闭和调节。在关闭状态下,设计合理的主动控制不会影响翼型气动性能。主动控制模式的缺点在于需外部提供能量,在控制设计时必须加以考虑,否则可能会降低控制效果。
壁面吹/吸气[55-57]和等离子技术[58-60]是目前主要的翼型后缘噪声主动控制方法。在风力机叶片噪声控制研究中,Wolf等[55]采用壁面吸气方式减小边界层厚度和湍流尺度,降低了后缘湍流噪声。针对平板翼型,Szoke等[56]采用壁面垂直或斜向吹/吸气方式降低了翼型后缘湍流噪声(图10)。但是,吹/吸气对中/低雷诺数下的后缘纯音噪声控制效果如何?目前除非常有限的数值计算分析[57]外,尚未见到公开发表的相关实验研究。部分原因可能是目前采用的吹/吸气控制结构比较复杂,而中/低雷诺数翼型叶片尺寸较小,吹/吸气控制较难实施。
等离子体技术因结构简单常用于翼型的流动与噪声控制。Inasawa等[58]使用等离子体在中/低雷诺数下对翼型后缘噪声进行控制,将作动器安装在弦长55%~60%处时,等离子体诱导的射流可以增强边界层稳定性,显著抑制T–S波增长,从而抑制声反馈发生,降低翼型后缘噪声。Inasawa等[59]运用等离子体诱导的扰动对翼型边界层实施干扰(图11):当等离子体扰动频率f1(f1 = 1/T1)接近自然增长T–S波频率时,翼型后缘纯音频率锁定于等离子扰动频率f1,但噪声强度减小;当扰动频率远离自然增长T–S波频率时,翼型边界层发生湍流转捩,后缘纯音噪声被完全抑制,仅呈现出宽频噪声特性。Al-Sadawi等[60]在平板翼型钝体后缘附近分别沿流向(PA1)、横向(PA2)、轴向(PA3)布置等离子体(图12),也成功抑制了钝体后缘的涡脱落噪声。
4 问题与展望
综上所述,尽管中/低雷诺数下翼型后缘纯音噪声产生机制与控制研究已开展了半个世纪,取得了不少成果,但仍有一些关键问题需要回答和解决。
4.1 如何充分利用中/低雷诺数下翼型后缘噪声特性指导低噪声翼型设计?
小型飞行器、风力机等旋转机械的翼型叶片形状各异,叶片迎角展向分布不尽相同,导致其边界层内T–S波的演化及后缘涡脱落都有变化,直接表现为传播至远场的翼型后缘噪声存在差异。现有研究绝大部分都是针对某些翼型(如NACA系列对称翼型)开展,尚未全面认知不同形状翼型的后缘噪声特性,无法提供充分的实验依据来指导低噪声翼型设计。由于翼面压强梯度分布特性与翼型型面密切相关,且对边界层T–S波的发展具有重要影响,本文认为,可以设计一普适翼型,通过调节翼型压/吸力面压强梯度分布,模拟不同形状翼型和迎角下的边界层流动,研究中/低雷诺数下压强梯度变化对翼型后缘噪声的影响规律,再根据低强度或无纯音噪声情况所对应的压强梯度分布特性指导低噪声翼型设计(即反向设计)。
4.2 T–S波声反馈机制如何形成?与涡脱落机制之间如何相互竞争?
大量研究已经证实,声反馈是翼型后缘纯音噪声产生机制之一。但声反馈对外界干扰敏感,其本身形成过程仍存在较大争论(有的甚至得到相反的结论。
1)声反馈机制形成的必要条件问题
近年的多数研究强调:形成声反馈的必要条件是后缘附近存在层流分离泡,使得缓慢增长的T–S波转换为快速增长的无黏K–H波,才能维持自激振荡的声反馈。但若T–S波初始扰动较强(比如存在表面凸起、外界湍流较强等),在没有层流分离泡的情况下能否形成声反馈呢?在现有研究中,翼型边界层内T–S波自然生成,发生声反馈时层流分离泡可能已然形成,无法回答这一问题。
2)声反馈区间问题
声反馈到底是从层流分离位置、不稳定初始位置还是从前缘位置开始,也存在较大争论。自然生成的T–S波一旦形成声反馈,就无法确定T–S波真正的开始位置,也就无法判断边界层内某处测得的扰动是否为声反馈的结果。
3)双声反馈作用问题。关于双声反馈是否独立作用于远场噪声也存在争论。
涡脱落是后缘纯音噪声另一产生机制,与流场绝对不稳定性相关,其噪声频谱特性与声反馈有较大差异。在一定工况下,流场中可能同时存在声反馈和涡脱落机制,但仅呈现出一种噪声特性,这就涉及到两者之间相互竞争及频率选择的问题,这也是目前最具争议性的问题。现有研究采用NACA系列翼型,边界层T–S波自然生成,研究得到的已是声反馈和涡脱落相互竞争之后的结果,对于两者之间如何竞争转换及自身所受影响难以深入探讨,导致现有噪声机理研究常常得出不同的结论。
针对上述问题,本文认为可采用一新的研究思路:人工引入T–S波,结合人为设置的压强梯度变化,首先研究声反馈和涡脱落机制单独作用下的翼型后缘噪声与流场特性,然后改变流动工况,研究两者共同作用下的噪声与流场,分析声反馈和涡脱落分别占主导地位时对另一机制的抑制作用及自身所受到的影响,从而揭示两者之间复杂的竞争机制并确定噪声频率选择准则。
4.3 如何在噪声机理理论分析指导下有效抑制翼型后缘噪声?
关于翼型后缘噪声主动和被动控制方法已经有了大量研究。常用的后缘锯齿和多孔材料等会显著改变翼型表面结构,造成较大的气动性能损失。传统吹/吸气控制结构复杂,不易在中/低雷诺数翼型中实施,等离子体作动器通常安装于翼型表面,易受外界环境(如湿度)影响而导致电离空气失效。
本文认为,可针对不同的噪声产生机制采用不同的噪声控制技术:对以声反馈机制为主的后缘噪声,采用抑制T–S波增长的主动消波技术(active wave cancellation)[61]进行控制。消波技术可采用开/闭环控制,通过引入与T–S波幅值相当、相位相反的控制信号抑制边界层扰动。对以涡脱落机制为主的后缘噪声,可采用内置等离子体吹/吸气控制方式,通过合理布置吹/吸气位置,改变流场整体不稳定性,达到抑制涡脱落发生的效果。
针对4.1节和4.2节提出的问题及解决方案,实验模型可设计为上翼面平坦、下翼面为NACA曲面的平板翼型。下翼面采用转捩带将层流流动转捩为充分发展的湍流;上翼面离前缘一定距离处布置激振器引入小扰动,模拟边界层T–S波。为改变上翼面压强梯度以模拟不同翼型或迎角,可将翼型模型安装于风洞闭口实验段,通过调节上翼面一侧壁面形状,在翼面上形成顺/逆压梯度,如图13所示。为防止闭口实验段产生声波共振,上下壁面可采用张紧的凯夫拉纤维布,达到透声不透气效果。在上壁面设计一支撑架,用以改变上壁面形状。调节支撑架高度H可改变上翼面区域流向速度,形成翼面前段边界层顺压和翼面后段逆压;H越大,顺/逆压梯度越大。调节图13中的距离L可以改变顺压区和逆压区范围。当逆压增大至一定程度时,可在上翼面边界层后段形成层流分离。采用上述调节方式,可以模拟不同形状翼型和迎角下的边界层流动。
通过开展人工诱导T–S波和层流分离泡之间的相互影响研究,可区分T–S波或涡脱落占主导地位的翼型后缘纯音噪声。对于边界层T–S波占主导地位的声反馈噪声,可采用主动T–S波消除技术抑制T–S波增长;对于以涡脱落为主的噪声,可采用改变流场绝对/对流不稳定性的方法进行控制。
5 结 论
本文从噪声产生机理、研究方法和噪声控制策略等方面,总结分析了中/低雷诺数下翼型后缘纯音噪声的研究现状,得到如下结论:
1)声反馈和涡脱落已被公认为翼型后缘纯音噪声的主要产生机制。前者由层流边界层内T–S波在后缘散射噪声并向上游传播,并在边界层与翼型后缘之间形成,产生的噪声常具有“阶梯状”离散频谱特性;后者主要由层流分离泡或尾流绝对不稳定性引起,产生的噪声具有单频特性。与声反馈机制相比,关于涡脱落机制的研究工作与成果较少。
2)声反馈形成条件及其与涡脱落之间的竞争仍是目前翼型叶片后缘噪声研究中亟待解决的关键问题。现有研究中的边界层T–S波自然生成,难以深入探讨2种机制之间的竞争及自身所受影响,需要设计新模型、采用新思路,对声反馈和涡脱落分别进行研究。
3)基于噪声机理研究成果,可以有针对性地采用主动或被动控制方法。对于T–S波占主导地位的声反馈,采用主动T–S波消除技术进行控制;对涡脱落噪声则采用可以改变流动绝对/对流不稳定性的方法进行控制。
-
表 1 试验工况
Table 1 Experimental conditions
工况编号 水流速度
v/(m·s–1)通气流量
Q/SLPM摆动频率
f /Hz摆动幅值
A/(°)预置舵角
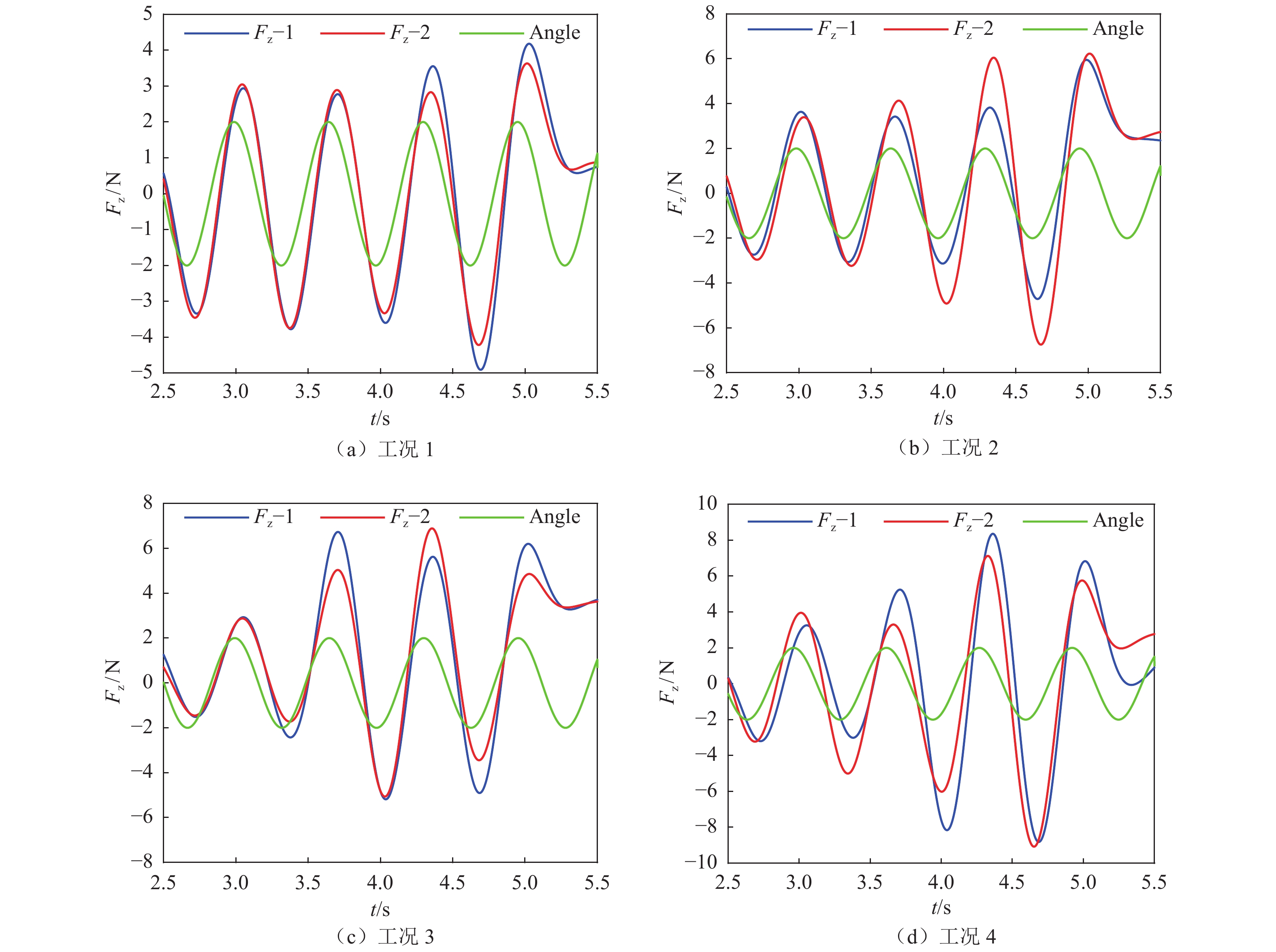
α/(°)1 7.0 80 1.53 2 0 2 7.5 80 1.53 2 0 3 8.0 80 1.53 2 0 4 8.5 80 1.53 2 0 5 8.5 80 1.53 2 10 6 8.5 80 1.53 2 20 7 8.5 80 1.00 2 0 表 2 不同水流速度下延迟时间对比
Table 2 Comparison of delay time at different water velocity
工况
编号水流速度
v/(m·s–1)第1次试验
延迟时间t/s第2次试验
延迟时间t/s平均延迟
时间t'/s延迟
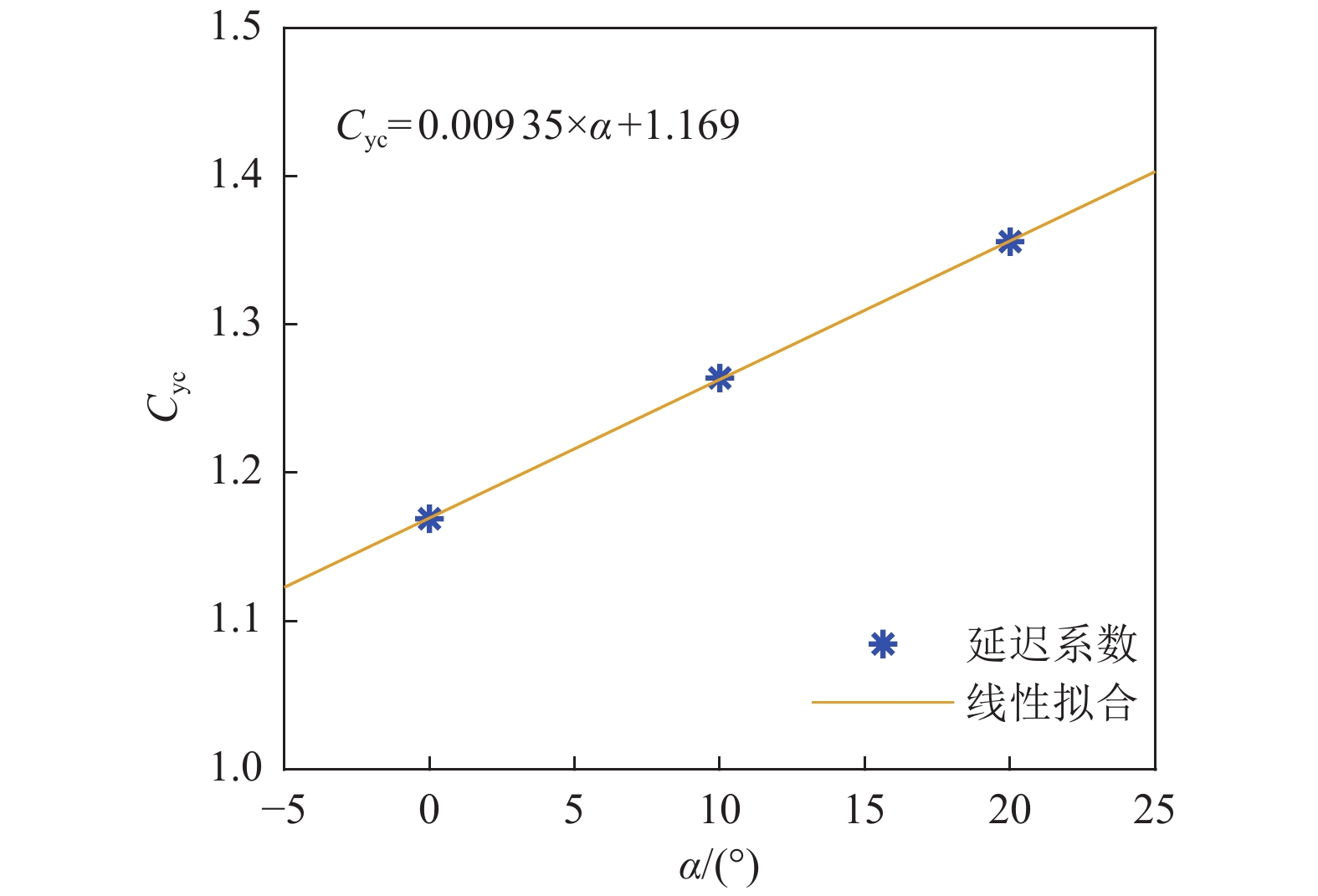
系数Cyc1 7.0 0.0548 0.0532 0.0540 0.875 2 7.5 0.0542 0.0568 0.0555 0.964 3 8.0 0.0571 0.0572 0.0572 1.059 4 8.5 0.0622 0.0566 0.0594 1.169 表 3 空化器不同舵角下的延迟时间对比
Table 3 Comparison of delay time at different rudder angle
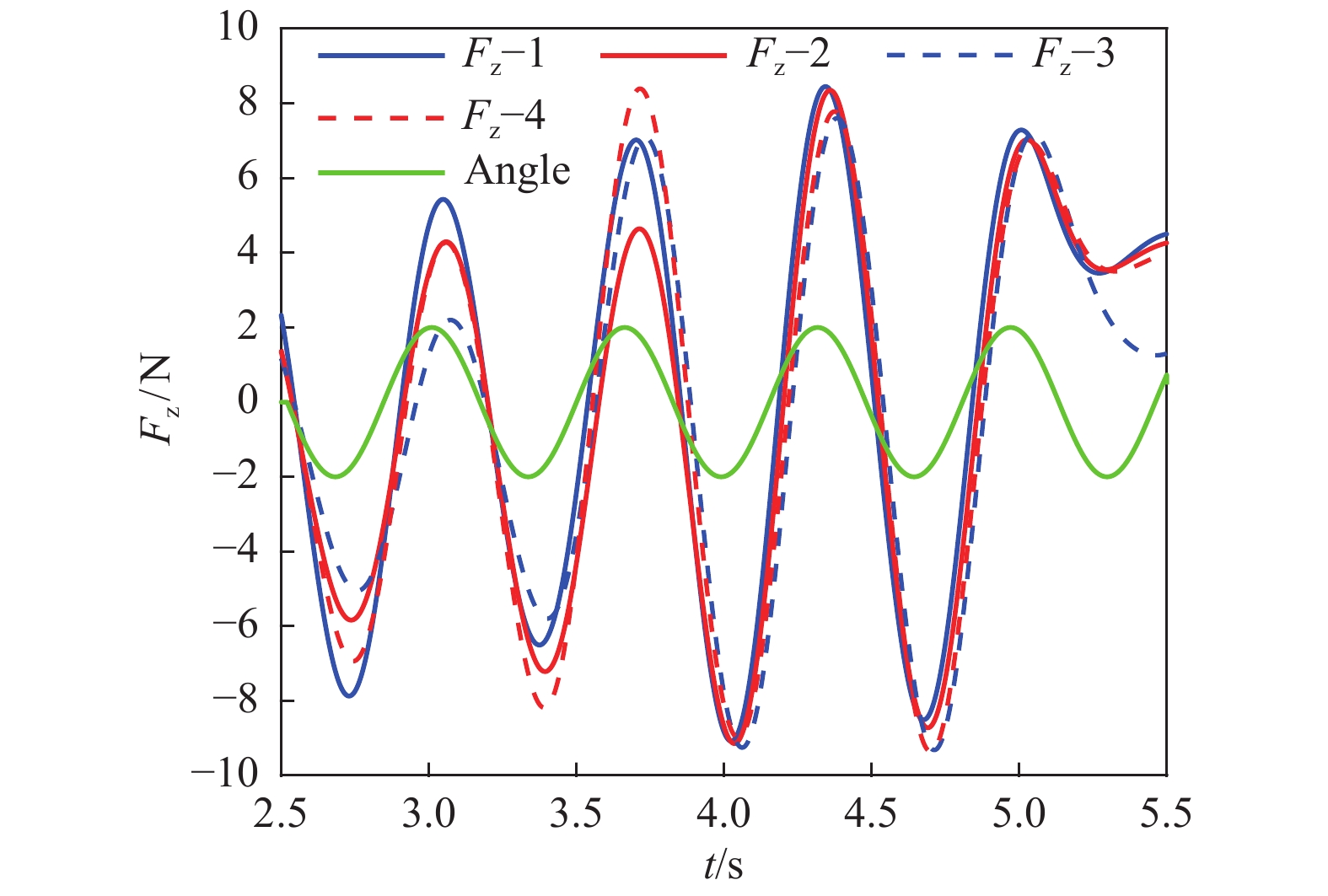
工况编号 舵角α/(°) 第1次试验延迟时间t/s 第2次试验延迟时间t/s 第3次试验延迟时间t/s 第4次试验延迟时间t/s 平均延迟时间t'/s 延迟系数Cyc 4 0 0.0622 0.0566 — — 0.0594 1.169 5 10 0.0656 0.0623 0.0643 0.0646 0.0642 1.264 6 20 0.0668 0.0688 0.0698 0.0702 0.0689 1.356 表 4 不同摆动频率下延迟时间对比
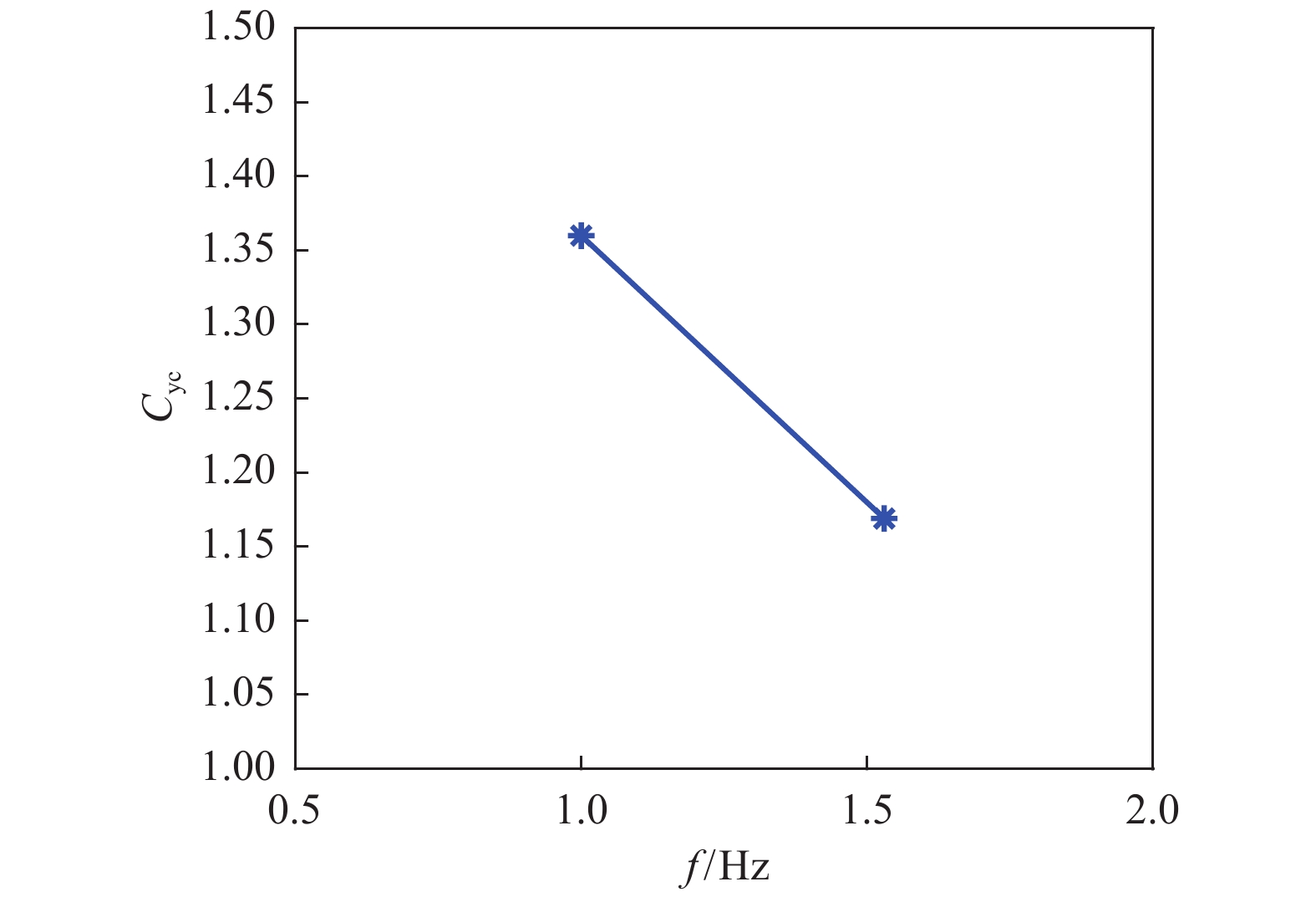
Table 4 Comparison of delay time at different oscillation frequency
工况
编号摆动频率
f /Hz第1次试验
延迟时间t/s第2次试验
延迟时间t/s平均延迟
时间t'/s延迟
系数Cyc4 1.53 0.0622 0.0566 0.0594 1.169 7 1.00 0.0663 0.0718 0.0691 1.360 -
[1] VASIN A D. The principle of independence of the cavity sections expansion (logvinovich's principle) as the basis for investigation on cavitation flows[C]//Proc of the RTO AVT Lecture Series on Super-cavitating Flows. 2001.
[2] KIRSCHNER I N,KRING D C,STOKES A W,et al. Control strategies for supercavitating vehicles[J]. Journal of Vibration and Control,2002,8(2):219-242. doi: 10.1177/107754602023818
[3] KIRSCHNER I N, ROSENTHAL B J, UHLMAN J S. Simplified dynamical systems analysis of supercavitating high-speed bodies[C]// Proceedings of the 5th International Symposium on Cavitation. 2003.
[4] GOEL A. Robust control of supercavitating vehicles in the presence of dynamic and uncertain cavity[D]. Gainesville: University of Florrda, 2005.
[5] 罗凯,李代金,党建军,等. 考虑空泡延迟特性的超空泡航行器运动控制模型[J]. 交通运输工程学报,2010,10(3):41-45. DOI: 10.3969/j.issn.1671-1637.2010.03.007 LUO K,LI D J,DANG J J,et al. Motion control model of supercavitating vehicle considering time-delay effect of supercavi-tation[J]. Journal of Traffic and Transportation Engineering,2010,10(3):41-45. doi: 10.3969/j.issn.1671-1637.2010.03.007
[6] 李代金,罗凯,党建军,等. 超空泡水下航行器空间运动建模与弹道仿真[J]. 兵工学报,2012,33(8):956-961. LI D J,LUO K,DANG J J,et al. Kinematic modeling and trajectory simulation for underwater supercavitating vehicles[J]. Acta Armamen-tarii,2012,33(8):956-961.
[7] 韩云涛,许振,白涛,等. 基于时滞特性的超空泡航行体预测控制[J]. 华中科技大学学报(自然科学版),2020,48(7):52-58. HAN Y T,XU Z,BAI T,et al. Predictive control of supercavitating vehicle based on time delay characteristics[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition),2020,48(7):52-58.
[8] 李东旭. 水下超空泡高速射弹数值分析与试验[J]. 四川兵工学报,2011,32(10):25-29. LI D X. Numerical analysis and experiment on high-speed projectile of underwater supercavity[J]. Journal of Sichuan Ordnance,2011,32(10):25-29.
[9] 何乾坤,魏英杰,尤天庆,等. 空泡摆动对超空泡航行体尾拍影响分析[J]. 北京航空航天大学学报,2012,38(4):509-512, 518. HE Q K,WEI Y J,YOU T Q,et al. Analysis of tail-slaps of supercavitating vehicle influenced by distortion of cavity shape[J]. Journal of Beijing University of Aeronautics and Astronautics,2012,38(4):509-512, 518.
[10] KULKARNI S S,PRATAP R. Studies on the dynamics of a super-cavitating projectile[J]. Applied Mathematical Modelling,2000,24(2):113-129. doi: 10.1016/S0307-904X(99)00028-1
[11] 赵成功,王聪,魏英杰,等. 质心位置对超空泡射弹尾拍运动影响分析[J]. 北京航空航天大学学报,2014,40(12):1754-1760. ZHAO C G,WANG C,WEI Y J,et al. Analysis of the effect of mass center position on tailslap of supercavitating projectile[J]. Journal of Beijing University of Aeronautics and Astronautics,2014,40(12):1754-1760.
[12] 赵成功,王聪,孙铁志,等. 初始扰动对射弹尾拍运动及弹道特性影响分析[J]. 哈尔滨工业大学学报,2016,48(10):71-76. DOI: 10.11918/j.issn.0367-6234.2016.10.010 ZHAO C G,WANG C,SUN T Z,et al. Analysis of tail-slapping and ballistic characteristics of supercavitating projectiles under different initial disturbances[J]. Journal of Harbin Institute of Technology,2016,48(10):71-76. doi: 10.11918/j.issn.0367-6234.2016.10.010
[13] 赵成功. 高速射弹非定常运动多相流场与弹道特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2017. ZHAO C G. Research on multiphase flow and trajectory characteri-stics of unsteady movement of high speed projectile[D]. Harbin: Harbin Institute of Technology, 2017.







 下载:
下载: