Research on the static aero-elastic sensitivity of stiffness of flexible wing
-
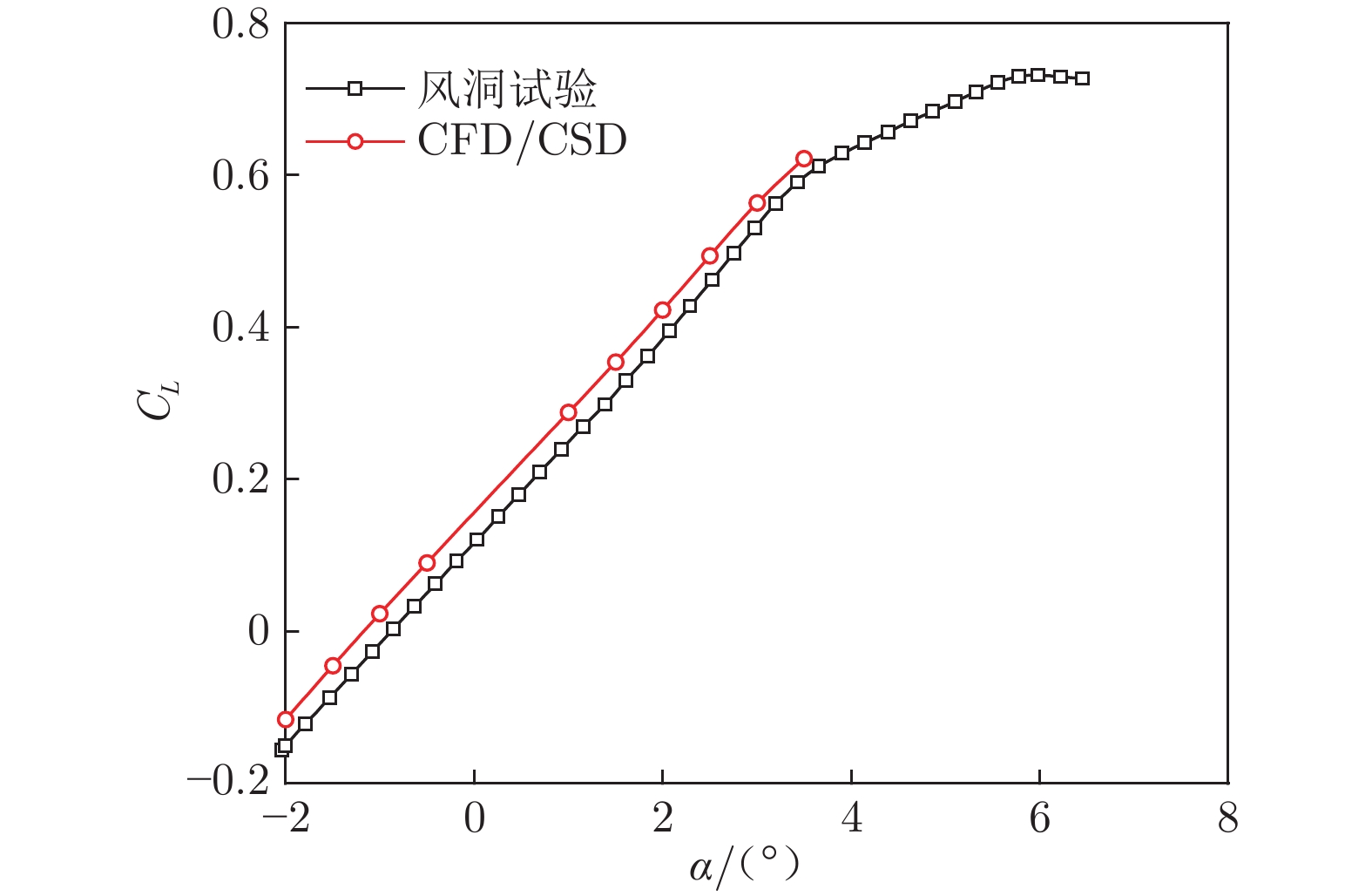
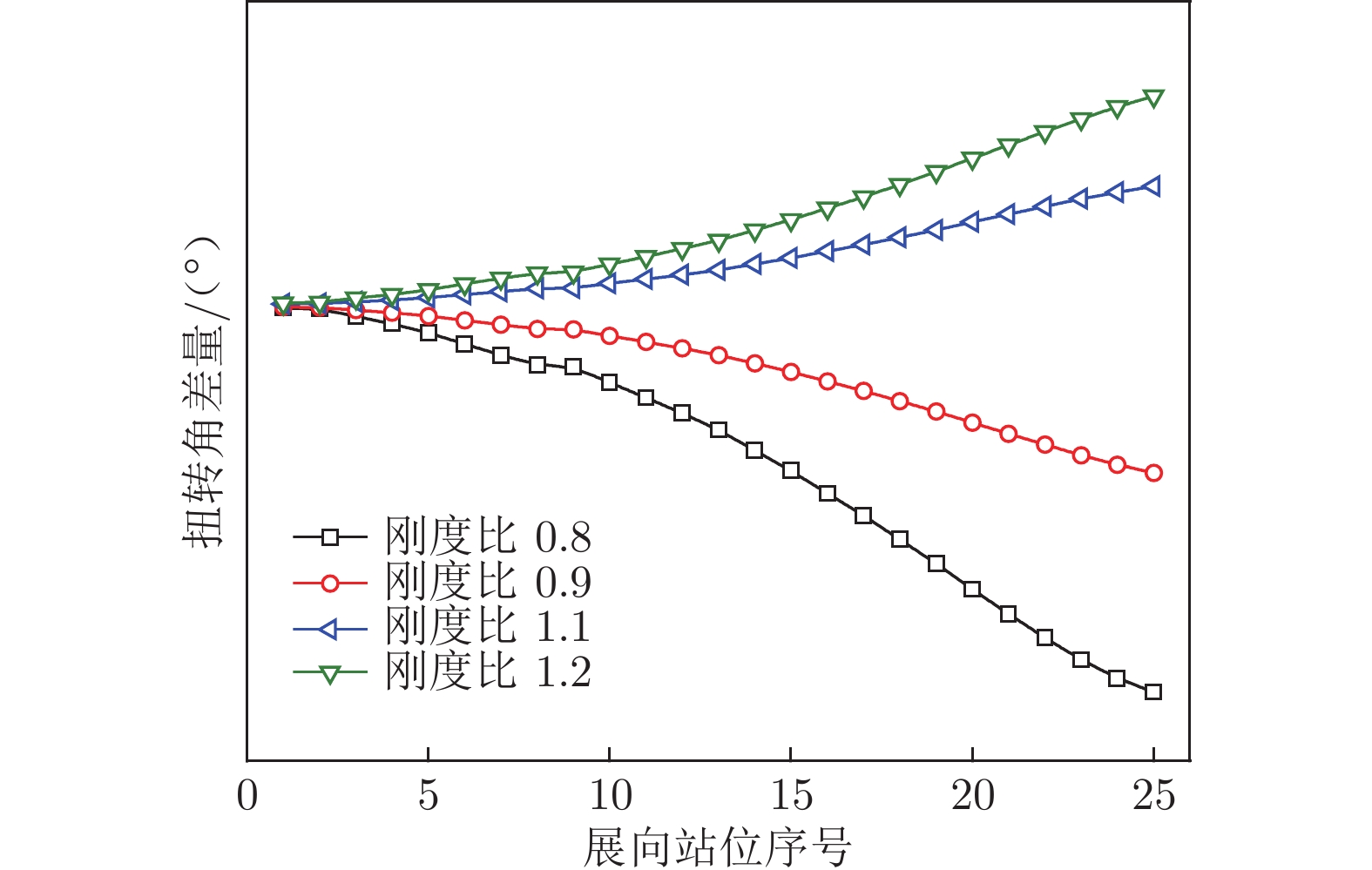
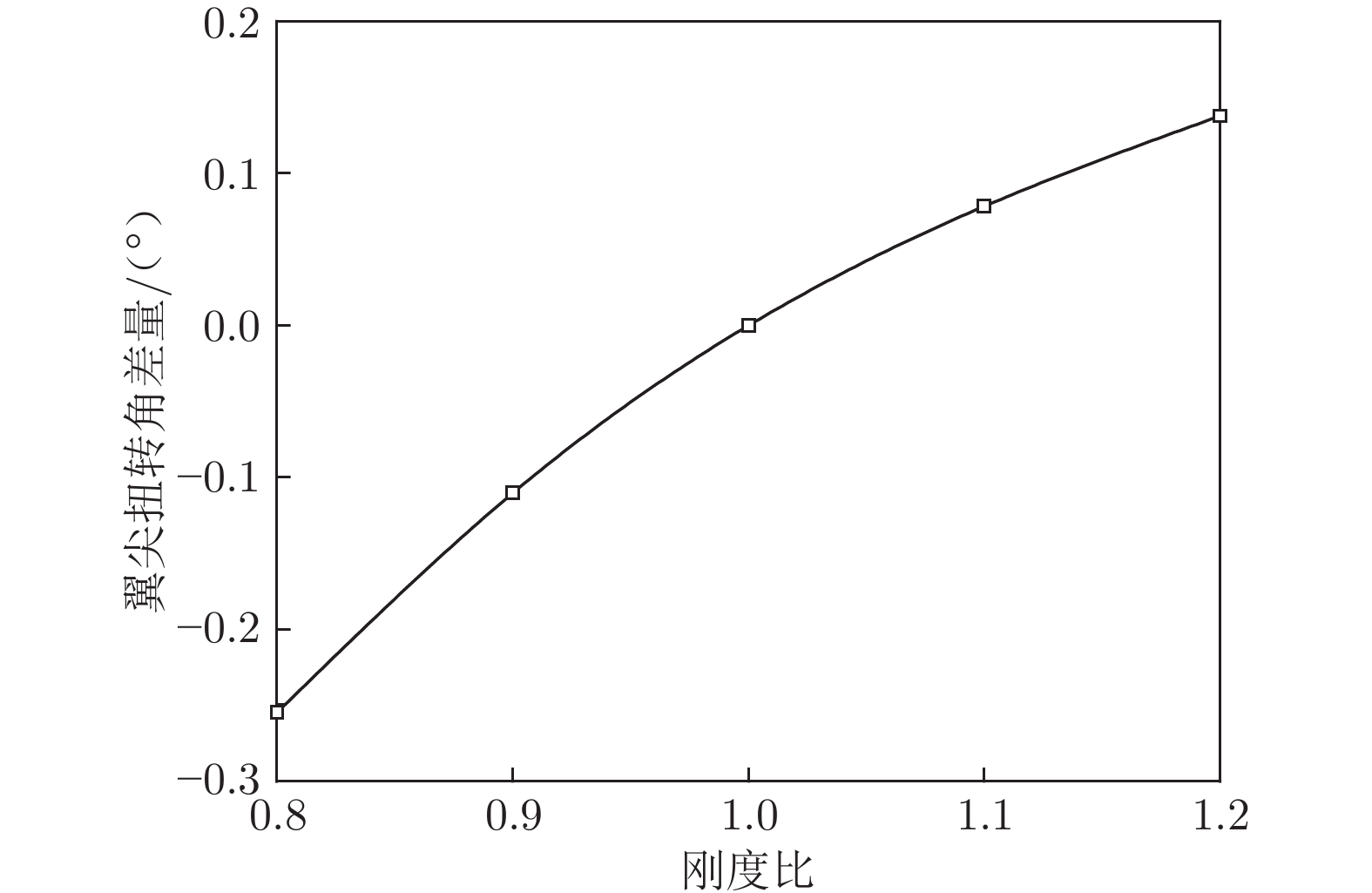
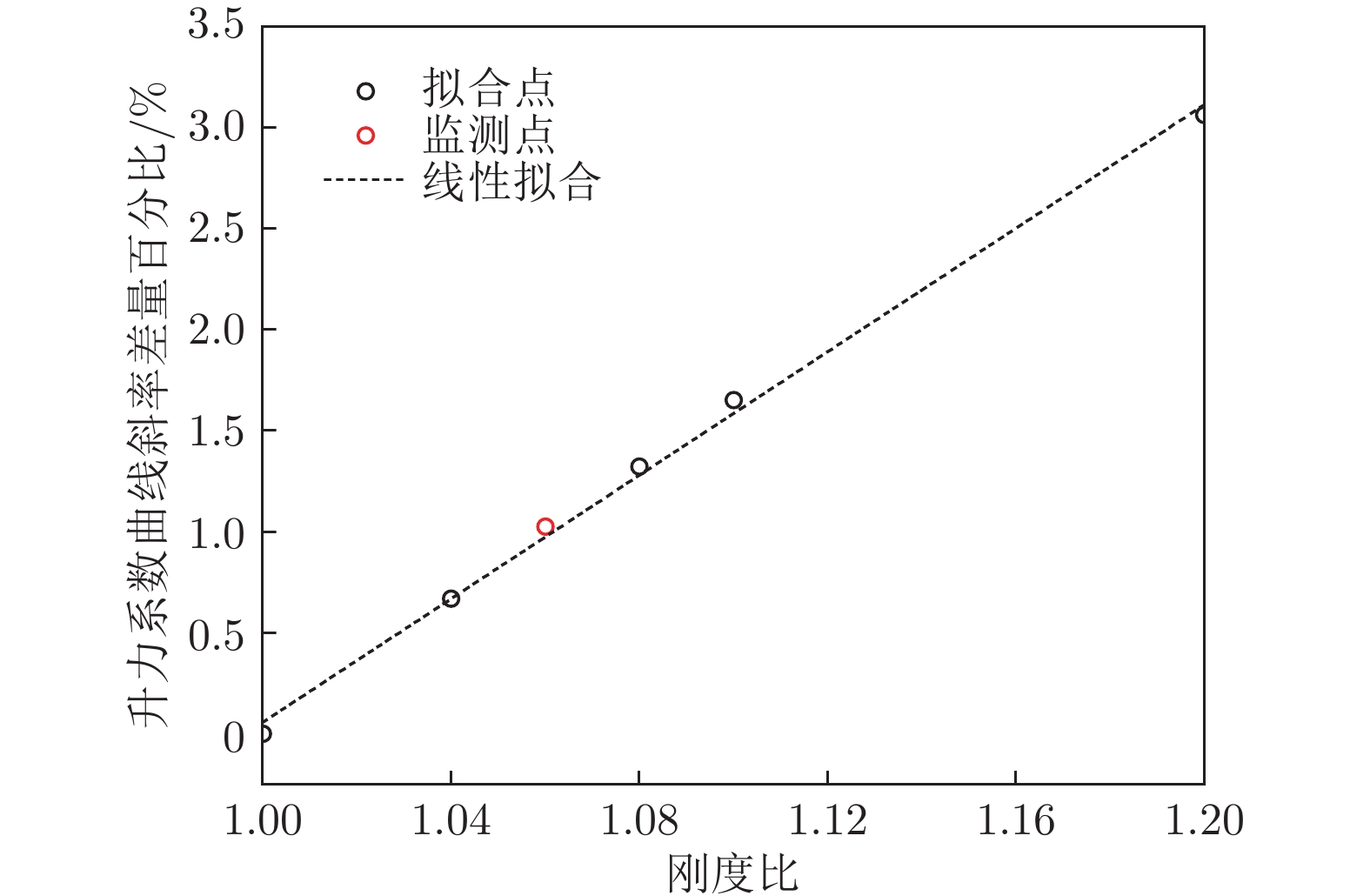
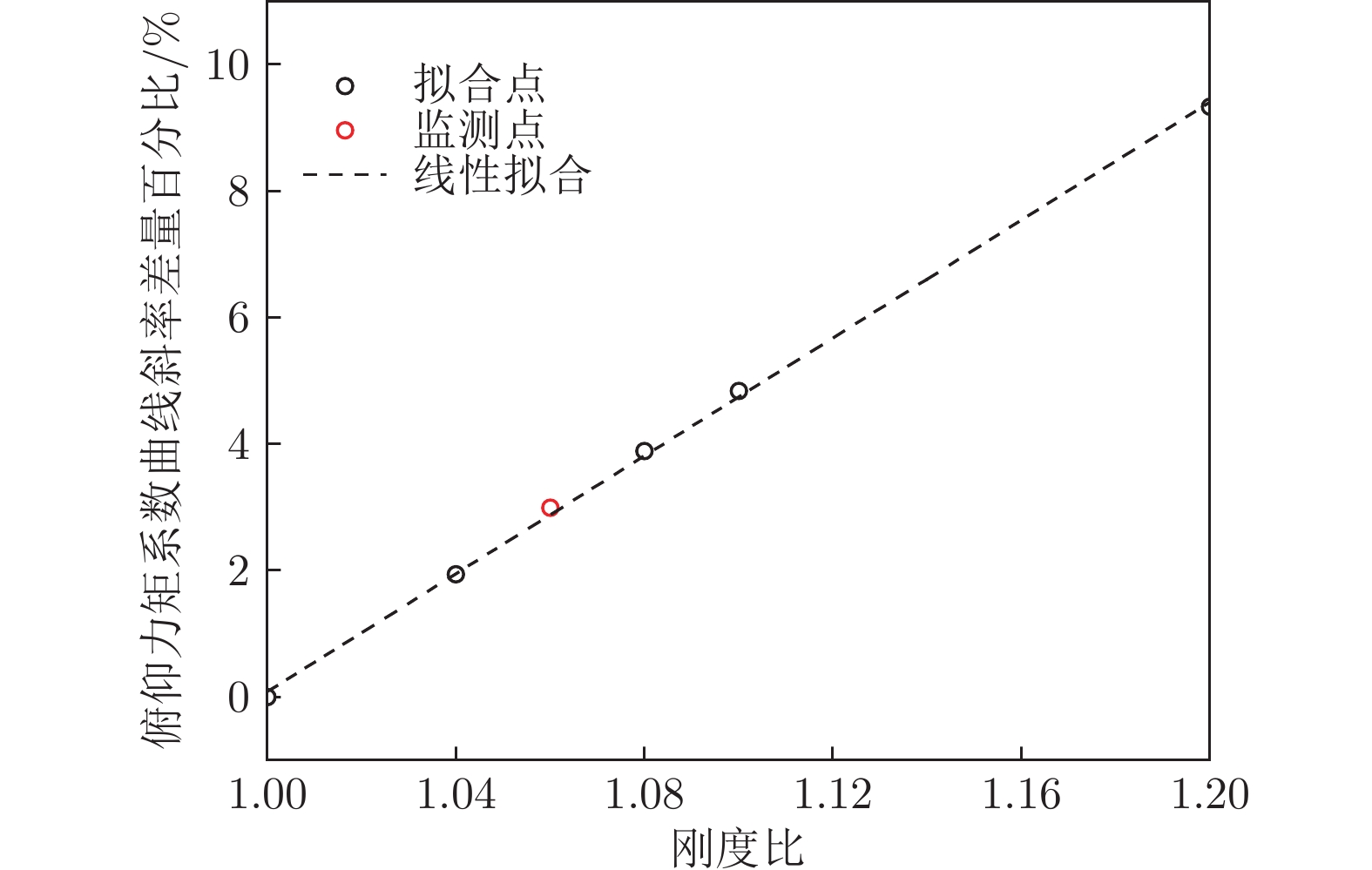
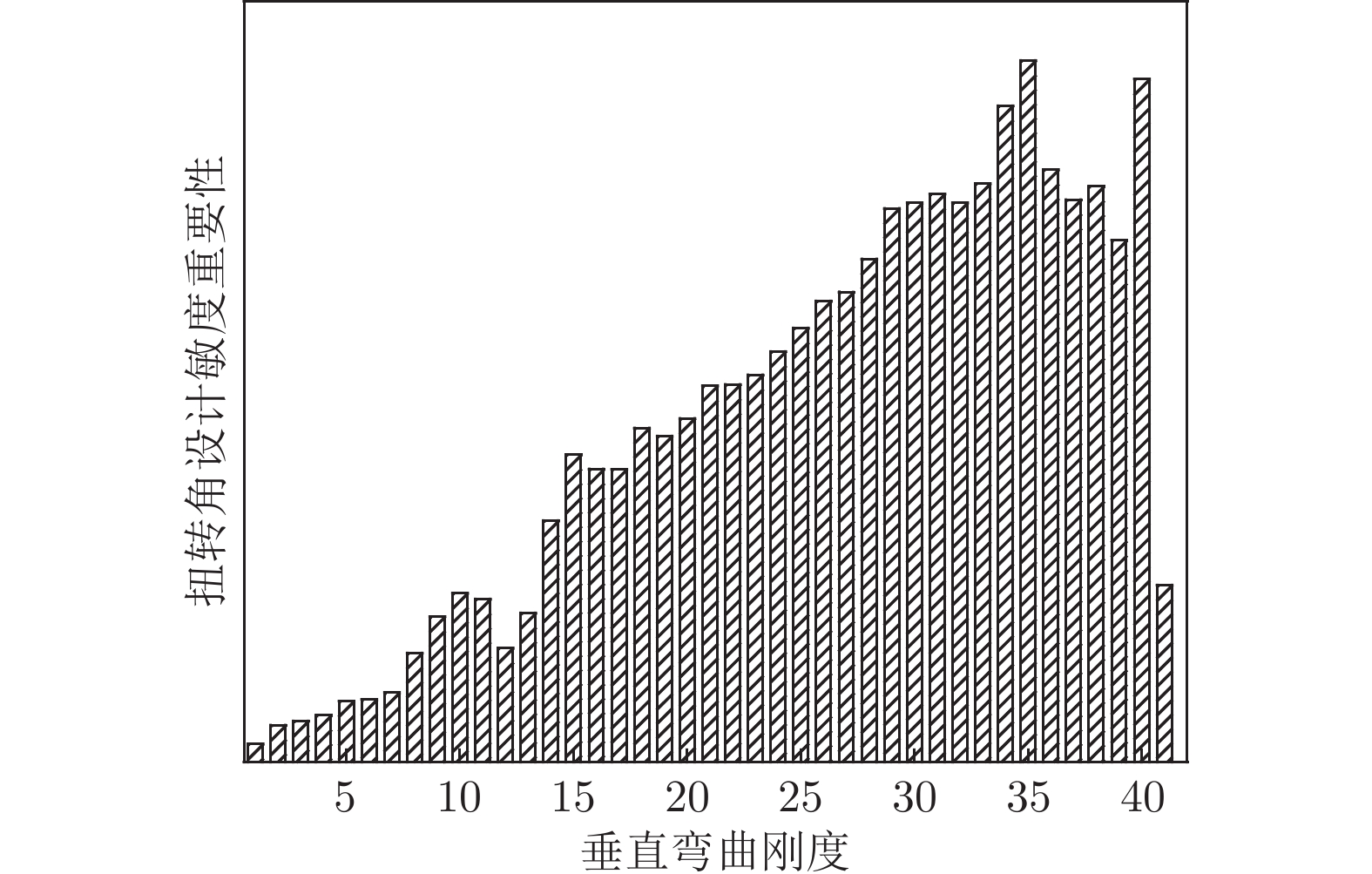
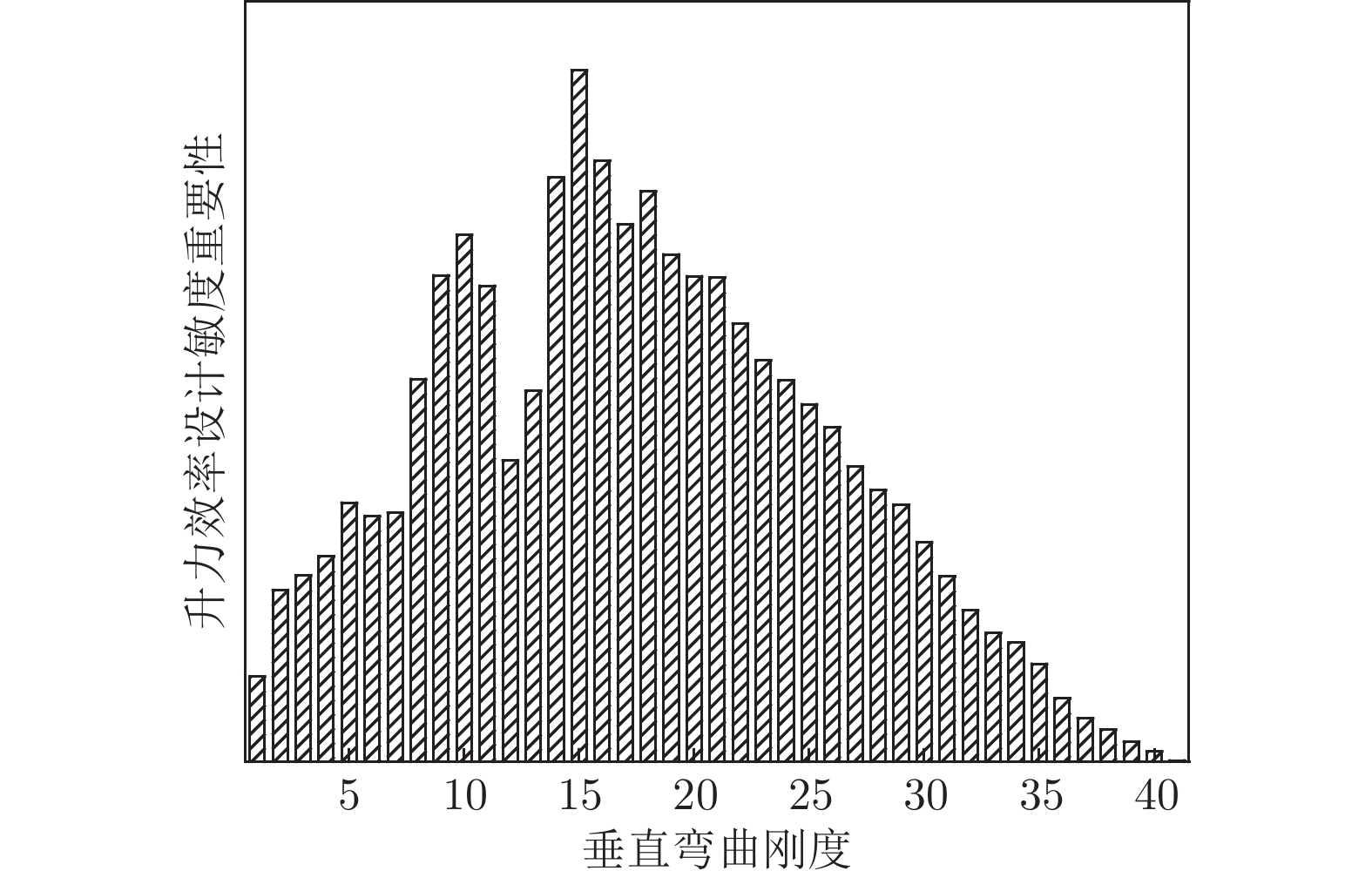
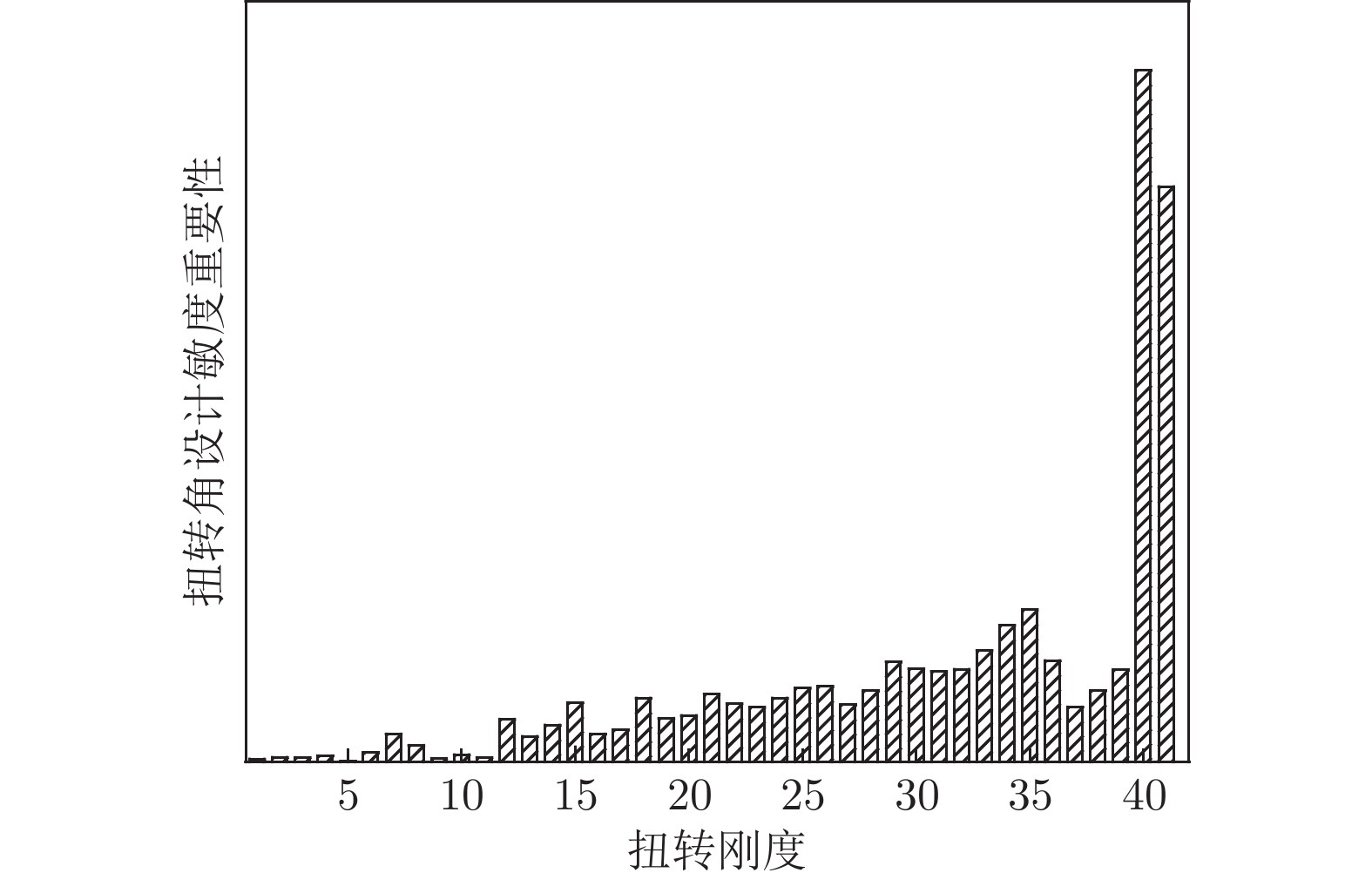
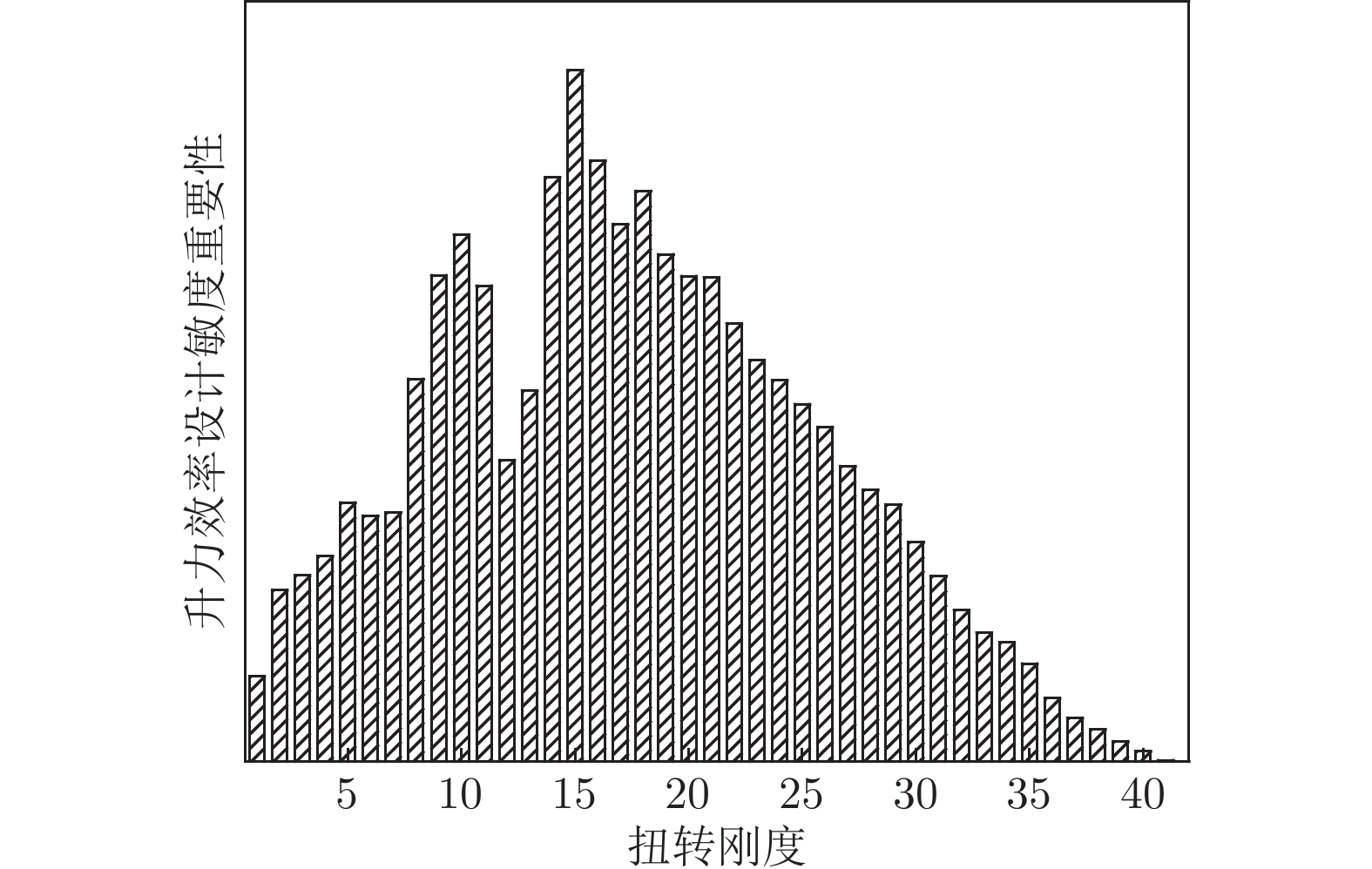
摘要: 为保证大展弦比柔性机翼在巡航飞行时的气动性能够达到设计指标，需要在机翼气动外形设计阶段进行型架设计。机翼刚度对气动载荷有显著影响，是影响静气动弹性的重要因素之一。基于流固耦合方法开展变刚度型架外形设计鲁棒性分析研究，建立以机翼刚度为自变量的全机弹性气动导数评估模型，并以机翼扭转角及升力效率为约束，开展机翼刚度敏度分析。结果表明：垂直弯曲刚度、扭转刚度是影响机翼扭转角及全机升力效率的主要刚度特性；在机翼刚度变化不超过10%时可冻结型架外形；全机弹性气动导数与刚度比呈线性关系。研究结果可用于工程型号设计中的目标刚度静气动弹性评估。Abstract: In order to ensure that the aerodynamic performance of high aspect ratio wing in cruise flight can meet the design targets, it is necessary to carry out the jig shape design in the wing design stage. The wing stiffness has a significant effect on the aerodynamic loads, which is one of the important factors affecting the aeroelastic characteristics. Robustness analysis of jig shape design with various stiffness properties was conducted based on CFD/CSD method. The aerodynamic characteristics evaluation model was established with the stiffness value as the independent variable. The sensitivity analysis of the stiffness was carried out with the wing twist angle and lift efficiency as constraints. The research results, providing support for the static aeroelastic evaluation of wing stiffness in the engineering design, show that the vertical bending stiffness and twist stiffness are the main characteristics that affect the wing twist angle and lift efficiency. The Jig shape can be frozen with the increasing stiffness ratio less than 1.1. And linear relationship between elastic aerodynamic derivatives and stiffness ratio is established.
-
0 引 言
液滴蒸发广泛存在于日常生活和工程应用中，如喷雾冷却[1-2]、农药喷洒[3-4]、喷墨打印[5-6]等。固着液滴在壁面上的蒸发涉及耦合的传热传质过程，包括：液滴和壁面间的导热、液滴内部的传热和气液界面的传质扩散。然而，目前对液滴蒸发的实验研究大都采用高速摄像技术记录液滴蒸发过程接触角、接触直径随时间的变化，用于分析液滴蒸发过程的形态变化，进而分析其传质规律，应用于工程上预测液滴质量蒸发率。此外，也有文献结合实验和理论分析方法研究了表面润湿性对液滴蒸发速率的影响[7-8]，结果表明亲水表面的液滴质量蒸发率更快；还有文献研究了外部对流[9]、液滴内部毛细流[10]和Marangoni流[11]等因素对液滴质量蒸发率的影响。然而，采用高速摄像技术研究液滴蒸发，当进入蒸发后期，液滴尺寸较小时，将产生较大偏差。
相较于液滴蒸发传质特性的研究，对固着液滴蒸发传热特性的研究还较少。事实上，在诸如喷雾冷却等工程应用中，掌握液滴蒸发过程的界面传热特性将对优化喷雾冷却工业设计、强化传热发挥着重要作用。 现有文献对固着液滴蒸发传热特性的研究大都采用数值模拟或理论分析方法。Lee等[12]对液滴在恒温加热表面蒸发的马兰戈尼流动和传热特性进行了数值模拟研究，应用动态网格技术模拟蒸发过程的气液界面行为，并分析了均匀和局部加热方式对蒸发过程中液滴内部流动模式的影响。Gibbons等[13]对超疏水蒸发液滴的热流密度分布进行了理论研究，结果表明局部热流密度在三相接触线处最大。
现有文献对固着液滴蒸发过程界面传热特性的实验研究还较少，主要原因在于传统热电偶测温方式为点测量，并不能获得接触面温度分布；此外，热电偶的存在会对液滴蒸发过程造成影响。也有少量文献采用红外热像仪[14]、热致变色液晶[15]、平面激光诱导荧光技术[16]捕获液滴蒸发过程的温度变化。相较于热电偶测温方式，非接触式测温不易影响液滴蒸发过程的形态变化。而对比上述非接触式测量方法，红外热像仪价格较为昂贵，将其应用于相变传热特性研究时需采用红外透明材料作为基底，此外温度测量还会受工质发射率以及周围环境的影响，标定复杂，若要实现恒定热流密度加热条件，更是十分困难；热致变色液晶的测温范围狭窄（约为20 ℃）；平面激光诱导荧光测温技术成本高。
温敏漆（Temperature Sensitive Paint, TSP）测温依据光猝灭原理，是上世纪八十年代发展起来的一种非接触式、全域测温技术。温敏漆由温敏探针分子与高分子粘合剂配置而成，在一定波长激发光的照射下，探针分子会发射出特定波长的荧光，发光强度与温度有关。通过捕获表面发光强度，进而获得其温度分布。温敏漆测温具有响应快（约为1~10 ms）、价格低、易标定等优点。自温敏漆测温技术被提出以来，学者们将其逐渐应用于气动热场测量，美国西密歇根大学刘天舒教授在这一领域开展了大量的研究工作[17-19]。近年来，有学者将温敏漆测温技术应用于相变传热特性研究。Francom与Kim[20]使用温敏漆测量了脉动热管中的工质温度变化；Hirai等[21]采用温敏漆捕获了过冷水滴在表面凝固过程的接触面温度分布；AL Hashimi等[22]采用温敏漆测温技术研究了池沸腾和流动沸腾中流体与壁面传热的热流密度分布。目前国内的温敏漆测温技术也得到了较快发展。张扣立等[23]总结了近两年在中国空气动力研究与发展中心激波风洞中开展的温敏涂层技术相关研究工作，解决了如发光材料研制、模型建立、数据处理等一系列关键问题，并制作了一套适用于激波风洞试验的高速TSP测量及标定系统。刘旭等[24]总结并推导了基于时间解析温度数据计算热流密度的导热反问题模型，指出对于温敏漆测温可以在涂料设计、物理建模以及计算方法等方面进行完善，提高 TSP的热流测量精度。作者在前期工作中采用温敏漆测温技术研究了液滴蒸发过程的固液接触面温度分布和热流密度分布[25]，以及液滴撞击加热壁面的接触面瞬时热流密度分布[26]。为得到相变传热的热流密度分布，在采用温敏漆测温获得接触面温度分布的同时，现有文献大都采用热电偶测量基底背部温度，并构建一维非稳态导热反问题模型。然而热电偶测温属于点测量，无法获得基底背部的全域温度分布，因此所得到的热流密度分布存在一定偏差。
本文探索了基于双层温敏漆的测温方案用于研究固着液滴蒸发的传热特性，实验捕获液滴与加热基底接触面的温度分布，以及基底背部的温度分布，构建一维非稳态导热反问题模型，掌握液滴蒸发过程的固液接触面处热流密度分布。
1 实验研究
1.1 实验系统
本文采用实验系统如图1所示，系统由三部分组成：实验件、激发光源和图像采集系统。实验件采用透光率大于93%的钠钙玻璃（60 mm长 × 40 mm宽 × 1.2 mm厚）作为基底，在钠钙玻璃的上方通过麦勒棒涂布器[27]涂覆温敏漆，并通过螺旋测微仪测量涂抹前后基底厚度的差值获得温敏漆厚度约为 1-2 μm。温敏漆的上方贴合厚度为10 μm的黑膜，以防止外部光强和液滴内部气泡运动对捕获光强的影响。在钠钙玻璃的下方镀有铟锡氧化物镀层（Indium Tin Oxides，ITO），通过连接直流稳压电源提供恒定热流密度加热，且透明的ITO镀层不会影响对温敏漆发光强度的捕捉。在ITO镀层下方贴合截面面积一半的黑膜，并在黑膜下方涂覆温敏漆。下层温敏漆仅涂覆一半的原因是为了使上层温敏漆的发射光强可以穿透钠钙玻璃未贴合黑膜和温敏漆的区域，被实验件下方的CMOS相机捕获。激发光采用LED光源，由直流稳压电源供电，额定功率1 W，光源布置需保证能同时照射基底上、下两层温敏漆。图像采集系统包括两台12位CMOS相机，帧率为60帧/秒，分辨率为1280 × 960。一台相机布置在实验件上方，用于记录液滴蒸发过程的形态变化。另一台相机布置在实验件下方，同时捕获上、下两层温敏漆的发光强度（需指出的是，对于上层温敏漆，相机实际捕获的是未被下层黑膜遮挡的区域）。液滴蒸发过程中，若液滴形态维持对称，则下方相机能同时捕获液滴固液接触面和基底底部温度分布。在下方相机前放置滤光片，避免激发光源和周围光强的影响。
实验选择正戊烷为工质，液滴初始体积为3 μL，壁面初始温度为55 ℃。
1.2 温敏漆的配置与使用
实验配备温敏漆采用二氯三钌（II）水合物为探针分子，聚丙烯酸为粘合剂，并加入无水乙醇混合后按质量比2∶5∶20配置，并进行充分震荡1~2小时。实验前采用荧光光度计对温敏漆激发光谱及发射光谱进行测定以选择合适波长的激发光源和滤光片，图2所示为温敏漆的激发光谱和发射光谱。根据测定结果，激发光源选取波长460~465 nm，滤光波长为590 nm，虽然滤光波长与温敏漆发射光谱峰值波长并未完全对应，但经温度标定，不会对测量结果造成影响。
![]()
图 2 温敏漆的激发光谱与发射光谱Fig. 2 Excitation spectrum and emission spectrum of temperature sensitive paint温敏漆在使用前需要对其光强-温度关系进行标定，其标定方法如下：先打开LED灯源进行照射10分钟，因为温敏漆的发射光强与激发光有关，所以提前照射10分钟使激发光稳定，之后给ITO镀层通电。实验过程中，在上下表面贴合热电偶用于温度标定，CMOS相机记录不同温度下的温敏漆发光强度，每次记录时间2分钟。温度标定范围为25 ℃至55 ℃，通过调节ITO镀层供电电压改变表面温度。图3所示为本实验系统上、下两层温敏漆的光强-温度标定曲线，图中参考光强取上表面26 ℃时温敏漆的发光光强。
![]()
图 3 温敏漆光强-温度标定曲线Fig. 3 Calibration curve of light intensity temperature of temperature sensitive paint1.3 实验误差分析
实验采用两台相机分别记录液滴接触直径和接触面温度分布随时间的变化。液滴接触直径的测量误差为单个像素点对应长度，即5.2 μm。温敏漆测量误差由相机噪声引起[28]图片灰度值波动计算，绝对误差为2.2 ℃。为减小测量误差，在处理温度数据时采用巴特沃斯滤波器，将温度数据进行滤波处理，其滤波函数如下：
$$ {\left| {T(w)} \right|^2} = \frac{1}{{1 + {{\left(\dfrac{w}{{{w_c}}}\right)}^{2n}}}} $$ (1) 式中：wc为截止频率，n为巴特沃斯滤波器的阶数。通过式（1）将每个像素点的温度沿时间轴滤波，经滤波后测温误差减小为0.7 ℃。图4为某一像素点滤波前、后的温度随时间的变化曲线。
2 热流密度计算模型
基于双层温敏漆测温的实验方案，能同时掌握液滴固液界面和基底底部的瞬时温度分布，进而通过建立非稳态导热的反问题模型，采用数值计算方法，分析获得液滴蒸发过程固液接触面的热流密度分布。为简化计算，模型假设如下：1） 加热基底物理性质不随温度变化。2） 液滴蒸发过程中形态对称。3） 对于钠钙玻璃基底，只考虑沿厚度方向的导热。4）实验系统中黑膜的导热热阻为1 × 10−4 m2∙K/W， 钠钙玻璃的导热热阻为1.904 × 10−2 m2∙K/W，相比钠钙玻璃，黑膜的热阻忽略不计。基于以上假设，本文建立了一维非稳态导热模型，如图5所示。
钠钙玻璃内部温度分布能量守恒方程为：
$$ \rho c\frac{{\partial T}}{{\partial t}} = \lambda \frac{{{\partial ^2}T}}{{\partial {x^2}}} $$ (2) 式中：ρ为钠钙玻璃密度，取2.52 × 103 kg/m3；c为钠钙玻璃比热，取0.8 × 103 J/(kg·K)；λ为钠钙玻璃导热系数，取0.63 W/(m·K)；T为温度；t为时间；x为沿玻璃厚度方向的空间位置。
$$ t = 0,{\text{ }}T = {T_0} $$ (3) 边界条件为：
$$ x = {\text{0}},{{ - }}\lambda \frac{{\partial T}}{{\partial x}} = {q_{{\text{ITO}}}} - h(T - {T_\infty }) $$ (4) $$ x = L,{\text{ }}T = T_{{\text{TSP2}}}^{} $$ (5) 式中：qITO = UI/A是ITO镀层提供的恒定热流密度，U为通电电压，I为通电电流，A为ITO镀层与基底的接触面积；h为基底表面与空气的对流传热系数；T∞为环境温度，TTSP2为上层温敏漆捕获的温度分布。
方程（2~5）采用隐式格式的有限差分法进行数值求解。在基底内部均匀划分N个节点，空间步长Δx = L/（N−1），L为基底厚度1.2 mm。经差分后的方程如下：
$$ Fo(T_{k + 1}^{P + 1} - 2T_k^{P + 1} + T_{k - 1}^{P + 1}) = T_k^{P + 1} - T_k^P $$ (6) $$ t = 0,{\text{ }}T_k^1 = T_0^{} $$ (7) $$ x = 0, - \lambda \frac{{T_2^{P + 1} - T_{\text{1}}^{P + 1}}}{{\Delta x}} = {q_{{\text{ITO}}}} - h(T_{TSP1}^{P + 1} - {T_\infty }) $$ (8) $$ x = L,{\text{ }}{T^{P + 1}} = T_{{\text{TSP2}}}^{P + 1} $$ (9) 式中：Fo = λΔt/（ρcΔx2）为傅里叶数，Δt为时间步长，TTSP1为下层温敏漆捕获的温度分布。上标P为时层序号，下标k为基底内的节点位置。
为方便计算，上述差分方程的系数矩阵列式如下：
$$ \begin{split}&\left( {\begin{array}{*{20}{c}} {1 + 2Fo + 2FoBi}&{ - 2Fo}&0&0&0& \cdots &0&0&0 \\ { - Fo}&{1 + 2Fo}&{ - Fo}&0&0& \cdots &0&0&0 \\ 0&{ - Fo}&{1 + 2Fo}&{ - Fo}&0& \cdots &0&0&0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0&0&0& \cdots &0&{ - Fo}&{1 + 2Fo}&{ - Fo}&0 \\ 0&0&0& \cdots &0&0&{ - Fo}&{1 + 2Fo}&{ - Fo} \\ 0&0&0& \cdots &0&0&0&0&1 \end{array}} \right) \left( {\begin{array}{*{20}{c}} {T_1^{P + 1}} \\ {T_2^{P + 1}} \\ {T_3^{P + 1}} \\ \vdots \\ {T_{N - 2}^{P + 1}} \\ {T_{N - 1}^{P + 1}} \\ {T_N^{P + 1}} \end{array}} \right) =\\& \left( {\begin{array}{*{20}{c}} {T_{\text{1}}^P - 2FoBi{T_\infty } + 2Fo\dfrac{{\Delta x}}{\lambda }{q_{{\text{ITO}}}}} \\ {T_2^P} \\ {T_3^P} \\ \vdots \\ {T_{N - 2}^P} \\ {T_{N - 1}^P} \\ {T_{TSP}^{P + 1}} \end{array}} \right) \end{split}$$ (10) 其中Bi = hΔx/ λ为毕渥数。
由式（10）可以计算出基体内部各节点的瞬时温度，根据能量守恒，由式（11）可以得到液滴蒸发过程中固液接触面的热流密度分布。
$$ {q_{\text{d}}} = - \frac{{\Delta x}}{2}\rho c\frac{{(T_{{\text{TSP2}}}^{P + 1} - T_{{\text{TSP2}}}^P)}}{{\Delta t}} - \lambda \frac{{T_{{\text{TSP2}}}^{P + 1} - T_{N - 1}^{P + 1}}}{{\Delta x}} $$ (11) 3 实验结果及分析
图6所示为正戊烷液滴蒸发过程中不同时刻的俯视形态变化，上、下表面温度分布和固液接触面热流密度分布。首先，温敏漆测温获得的液滴接触线形貌与俯视图捕捉到的一致（即第一列俯视图与第四列热流密度分布图的形貌一致），说明采用温敏漆用以分析液滴蒸发过程中界面温度变化的可行性。低温正戊烷液滴接触加热表面后，热流密度迅速达到最大值（t = 0.12 s）；随着液滴温度的提高，固液接触面处热流密度开始逐渐下降（t = 0.30 s）；之后由于液膜变薄，热流密度会再次增大（t = 2.78 s）。图中还可以看出，液滴接触线处的热流密度最大，这与Gibbons等[13,29]的研究结果一致。由上表面温度分布可以观察到液滴固液接触面处存在明显温度梯度。从获得的热流密度分布图中，可以观测到当t = 0.30 ~2.78 s时液滴内部存在明显对流单元，这与Guggilla等[30]使用红外热像仪捕获到的液滴内部对流单元一致。
![]()
图 6 正戊烷液滴蒸发的俯视图、上表面温度分布图、下表面温度分布图和热流密度分布图Fig. 6 Top view, upper surface temperature distribution, lower surface temperature distribution and heat flux distribution of n-pentane droplet evaporation为分析液滴接触面沿径向温度分布随时间的变化，选取液滴中轴线处的温度分布进行分析，如图7所示。图8（a）为温敏漆捕获上表面的温度分布，液滴接触壁面瞬间，壁面温度还没有明显下降；伴随着液滴铺展，壁面温度开始下降；随液滴即将完全蒸发，其温度又开始逐渐回升（t = 2.78~2.97 s）。图8 （b）为温敏漆捕获下表面温度分布，下表面的温度变化明显滞后于上表面温度变化。
![]()
图 8 液滴接触面径向温度分布随时间变化Fig. 8 Change of radial temperature distribution on droplet contact surface with time图9所示为液滴接触面的径向热流密度分布随时间变化。当液滴接触壁面时（t = 0.12 s）热流密度最大；随液滴的铺展，其热流密度逐渐减小（t = 0.12~1.88 s）；之后，由于液膜变薄，液滴汽化增强，热流密度再次增大。
![]()
图 9 液滴接触面热流密度分布随时间的变化Fig. 9 Variation of Heat Flux Distribution on Droplet Contact Surface with Time结合图9和6可以发现，液滴蒸发过程的最大热流密度处集中于接触线附近，这是因为在接触线附近液滴处于薄液膜蒸发区域，具有更强的换热能力。随液滴蒸发进行，液滴厚度整体变薄，固液接触面的温度分布也更加均匀，因此，接触线处与液滴内部热流密度的差值会逐渐减小，最终趋于一致。
图10为液滴固液接触面中心位置的热流密度和基底上、下表面温度随时间的变化。图中可以看出液滴汽化过程可以分为3个阶段：1）初始加热阶段，热流密度迅速上升，基底上表面温度迅速下降，下表面温度基本维持不变。2）对流单元蒸发阶段，该阶段可从热流密度分布图（图6）看见明显对流单元，热流密度逐渐减小后基本维持不变；基底上表面温度由于持续加热开始略有回升，随液滴汽化，温度逐渐下降；而基底下表面温度持续稳定下降。这是由于基底下表面始终由ITO镀层提供恒定加热热流密度，随液滴蒸发进行，基底下表面温度不断下降。3）薄膜蒸发阶段，该阶段对流单元消失，由于液膜较薄，汽化增强，所以该阶段热流密度先增大，随液滴即将完全蒸发，其热流密度又迅速减小。
![]()
图 10 液滴固液接触面中心位置热流密度，基底上、下表面温度随时间的变化Fig. 10 Change of heat flux at the center of the solid-liquid contact surface of the droplet, and the temperature of the upper and lower surfaces of the substrates with time为验证实验结果的可靠性，本文对液滴汽化的总换热量进行校核。根据式（11）获得的热流密度qd对面积和汽化时间进行二重积分，得到总蒸发换热量QTSP，式（12）为QTSP计算式。
$$ {Q_{TSP}} = \iint {{q_d}dAdt} $$ (12) 为方便计算，计算面积并非实际接触面积，而是与液滴接触线相切的矩形面积。由于无液滴接触区域的热流密度较有液滴接触区域的热流密度小一个数量级以上，故对计算结果造成的影响可以忽略。
液滴汽化的理论换热量用Qth表示，计算式如下：
$$ {Q}_{th}=mr $$ (13) 式中：m为液滴质量，r为汽化潜热。经计算，QTSP为0.69073 J，Qth为0.68687 J，两者偏差仅0.56%，验证了本文方法的可靠性。本文研究成果有助于拓宽相变传热热流密度的实验测量方法。
4 结 论
本文采用双层温敏漆测温方案研究了固着液滴在加热壁面蒸发过程的固液接触面热流密度分布。得到的主要结论如下：
1） 温敏漆捕获的液滴接触线轮廓与俯视图获得的液滴接触线轮廓一致，并通过计算校核液滴换热量，表明本文实验方案的可靠性。
2） 液滴接触加热壁面后，液滴接触线先铺展，随后接触线持续收缩，由于接触线附近为薄液膜蒸发区，因此接触线附近的局部热流密度最大。
3） 液滴汽化过程可以分为三个阶段：初始加热阶段，对流单元蒸发阶段和薄膜蒸发阶段。在初始加热阶段，热流密度迅速上升。在对流单元蒸发阶段，可从热流密度分布图中看见明显对流单元，热流密度逐渐减小后基本维持不变。在薄膜蒸发阶段对流单元消失，由于液膜较薄，汽化增强，所以该阶段热流密度先增大，随液滴即将完全蒸发，其热流密度又迅速减小。
4） 温敏漆测温可以较为准确的测量液滴与加热基底间的温度分布。对比于广泛使用的非接触红外测温方式，温敏漆测温具有基底材料选择广、响应快、分辨率高、成本低等优点。本文研究成果有助于拓宽相变传热特性的实验研究方法。
-
![]()
图 7 弹性机翼的翼尖扭转角差量与刚度比的关系
Fig. 7 Relationship between delta wing-tip twist angle and stiffness ratio
![]()
图 10 俯仰力矩系数曲线斜率与刚度比的关系
Fig. 10 Relationship between slope of pitching moment curve and stiffness
![]()
图 11 刚度特性在扭转角约束中的分布
Fig. 11 Distribution of stiffness characteristics under the constraint of twist angle
![]()
图 12 刚度特性在升力效率约束中的分布
Fig. 12 Distribution of stiffness characteristics under the constraint of lift efficiency
![]()
图 13 垂直弯曲刚度对扭转角的设计敏度重要性
Fig. 13 Design sensitivity importance of vertical bending stiffness to twist angle
![]()
图 14 垂直弯曲刚度对升力效率的设计敏度重要性
Fig. 14 Design sensitivity importance of vertical bending stiffness to lift efficiency
![]()
图 15 扭转刚度对扭转角的设计敏度重要性
Fig. 15 Design sensitivity importance of torsional stiffness to twist angle
-
[1] TILMANN C P, FLICK P M, MARTIN C A, et al. High altitude long endurance technologies for sensor craft[C]// Proc of Novel Vehicle Concepts and Emerging Vehicle Technologies Symposium. 2003.
[2] NGUYEN N, TRINH K, REYNOLDS K, et al. Elastically shaped wing optimization and aircraft concept for improved cruise efficiency[C]//Proc of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine. 2013. doi: 10.2514/6.2013-141
[3] NOLL T E, BROWN J M, PEREZ-DAVIS M E, et al. Investigation of the Helios prototype aircraft mishap: volume I mishap report[R]. VA 23681-2199, 2004.
[4] BHATIA K, WERTHEIMER J. Aeroelastic challenges for a high speed civil transport[C]//Proc of the 34th Structures, Structural Dynamics and Materials Conference. 1993. doi: 10.2514/6.1993-1478
[5] CORMAN J A, SAROJINI D, GHARBI A, et al. Estimating jig shape for an aircraft wing determined through aerodynamic shape optimization with rigid body assumptions[C]//Proc of the AIAA Scitech 2019 Forum. 2019. doi: 10.2514/6.2019-0418
[6] WAN Z Q,LIANG L,YANG C. Method of the jig shape design for a flexible wing[J]. Journal of Aircraft,2014,51(1):327-330. doi: 10.2514/1.C031926
[7] ZINK P S,RAVEH D E,MAVRIS D N. Integrated trim and structural design process for active aeroelastic wing technology[J]. Journal of Aircraft,2003,40(3):523-531. doi: 10.2514/2.3126
[8] BISPLINGHOF R L, ASHLEY H, HALFMAN T L. Aeroelasticity[M]. New York: John Wiley and Sons, Inc. , 1962.
[9] SCHUSTER D M. An inverse method for computation of structural stiffness distributions of aeroelastically optimized wings[R]. AIAA-1993-1540, 1993. doi: 10.2514/6.1993-1540
[10] 刘东岳,万志强,杨超,等. 大展弦比机翼总体刚度的气动弹性优化设计[J]. 航空学报,2011,32(6):1025-1031. LIU D Y,WAN Z Q,YANG C,et al. Aeroelastic optimization design of global stiffness for high aspect ratio wing[J]. Acta Aeronautica et Astronautica Sinica,2011,32(6):1025-1031.
[11] 张建刚,孙仁俊,金鑫. 大展弦比后掠机翼静气弹效应对气动载荷的影响实验与分析[J]. 应用力学学报,2017,34(3):570-575,616. ZHANG J G,SUN R J,JIN X. Test and study of static aeroelastic effects on wing's aerodynamic load[J]. Chinese Journal of Applied Mechanics,2017,34(3):570-575,616.
[12] JAMESON A, SCHMIDT W, TURKEL E. Numerical solution of the Euler equations by finite volume methods using Runge Kutta time stepping schemes[C]//Proc of the 14th Fluid and Plasma Dynamics Conference. 1981. doi: 10.2514/6.1981-1259
[13] MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal,1994,32(8):1598-1605. doi: 10.2514/3.12149
[14] HARDER R L,DESMARAIS R N. Interpolation using surface splines[J]. Journal of Aircraft,1972,9(2):189-191. doi: 10.2514/3.44330
[15] BURG C. A robust unstructured grid movement strategy using three-dimensional torsional springs[C]//Proc of the 34th AIAA Fluid Dynamics Conference and Exhibition. 2004. doi: 10.2514/6.2004-2529
[16] MAO K, XUE F, BAI F, et al. An engineering correction method of static aeroelasticity and Reynolds number effect on wind tunnel pressure distribution[M]//Singapore: Springer Singapore, 2019: 114-134. doi: 10.1007/978-981-13-3305-7_10
[17] ADELMAN H M,HAFTKA R T. Sensitivity analysis of discrete systems[J]. Progress in Astronautics and Aeronautics,1993,150:291-291.
[18] HAFTKA R T,ADELMAN H M. Recent developments in structural sensitivity analysis[J]. Structural Optimization,1989,1(3):137-151. doi: 10.1007/BF01637334
[19] 万志强,杨超. 设计敏度在气动弹性遗传优化中的应用[J]. 北京航空航天大学学报,2006,32(5):508-512. DOI: 10.3969/j.issn.1001-5965.2006.05.003 WAN Z Q,YANG C. Application of design sensitivity in aeroelastic genetic optimization[J]. Journal of Beijing University of Aeronautics and Astronautics,2006,32(5):508-512. doi: 10.3969/j.issn.1001-5965.2006.05.003
-
期刊类型引用(1)
1. 李强，操小龙. 超声速进气道压力估算方法及验证. 航空工程进展. 2020(06): 894-899 . 
百度学术
其他类型引用(0)
下载:
计量
- 文章访问数: 328
- HTML全文浏览量: 120
- PDF下载量: 35
- 被引次数: 1
