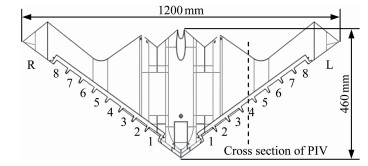
The wind tunnel test of the active flow control on the flying wing model based on the plasma synthetic jet
-
摘要: 为探究等离子体合成射流对三维模型的流动控制效果和机理,在中等展弦比飞翼布局模型前缘布置等离子体合成射流激励器开展低速风洞实验研究。通过六分量天平测力,考察沿弦向、展向不同分布位置的等离子体合成射流对飞翼模型气动力和气动力矩的作用;采用PIV(Particle Image Velocimetry,粒子图像测速)测量模型表面流场分布,研究等离子体合成射流流动控制机理。结果表明:在飞翼模型单侧布置等离子体合成射流,能够有效改善其气动特性,并能产生附加的滚转力矩,滚转力矩系数变化量最高达到0.009;在飞翼模型左右弦布置等离子体合成射流,能显著增强飞翼模型横向稳定性,滚转力矩系数波动范围减小66.7%。沿弦向,等离子体合成射流位置离前缘越近,控制效果越好,距前缘0mm的激励器控制效果最好;沿展向,布置的等离子体合成射流越多,对模型的升力特性改善作用越明显,布置方式以均布为优。在失速迎角前后,等离子体合成射流的流动控制机理不同:在小迎角下,等离子体合成射流在前缘起到了使转捩提前的作用;在失速迎角附近,则加速了分离区的流动、减小了分离区厚度。Abstract: To explore the effects and mechanisms of plasma synthetic jet flow control of the 3D model, a wing layout model with medium aspect ratio decorated with plasma synthetic jets on the leading edge is studied by means of low speed wind tunnel tests. The effects of the aerodynamic force and the aerodynamic moment on the airfoil model are investigated by measuring the force of the six component balance and the different distribution positions of the synthetic jet of the plasma. The flow field distribution on the surface of the model measured by PIV(Particle Image Velocimetry) is used to study the mechanism of the plasma jet flow control. Test results show that the unilateral arrangement of the plasma synthetic jet actuator can effectively improve the aerodynamic characteristics of the flying wing model, and can produce an additional roll moment with the variation of the roll moment coefficient reaching 0.009; The lateral stability of the flying wing model can be significantly enhanced by using the plasma synthetic efflux on the left and right side of the flying wing model, and the range of the rolling torque coefficient fluctuation decreases by 66.7%. Along the string, the closer the position of the plasma jet to the leading edg is, the better the control effect is, and the control effect of the exciter at the leading edge is the best. The more the plasma synthesized jet flows along the exhibition are arranged, the more obvious the improvement of the lift characteristics of the model is, and the uniform arrangement is the best. The flow control mechanism of the plasma synthetic jet actuator is different before and after the stall angle of attack. Under the small angle of attack, the synthesis of the plasma jet advances the transition, and near the stall angle of attack, the plasma synthetic jet accelerates the separation of the flow and reduces the separation-zone thick-ness.
-
Keywords:
- active flow control /
- flying wing model /
- plasma synthetic jet /
- wind tunnel test /
- PIV
-
0 引 言
湍流边界层是工程中常见的流动现象,同时也是湍流领域研究的热点问题之一。在实际流动中通常会遇到在曲面上发展的湍流边界层现象[1],而曲面上的流动往往也会受到由曲率引起的压力梯度影响[2-3]。一般来说,带有凹曲率和凸曲率的壁面会分别增加和减少湍流活动[4],同时由曲率引起的压力梯度也会影响湍流活动[5]。针对曲率和压力梯度影响的研究也一直受到船舶、航天等领域的重视。
迄今为止,研究者们主要研究了曲率和压力梯度分别对湍流边界层的影响,其中针对压力梯度的研究一般采用在光滑平板上施加压力梯度的方法。Spalart[6]通过数值模拟发现顺压梯度在达到一定的强度后会使湍流边界层发生层流化。Aubertine等[7]对逆压梯度的影响进行了激光多普勒测速(LDV)实验,发现逆压梯度会扩大尾迹区域,使得对数律区向下收缩,雷诺应力剖面与平板类似,但外层的应力比平板更强。Joshi等[8]对顺压梯度的流场进行了粒子图像测速(PIV)实验,发现近壁区的涡结构受到了限制,而加速流动也使得涡结构的倾角减小。最近,Volino[9]对不同压力梯度下的湍流边界层进行了激光多普勒测速实验,认为顺压梯度抑制湍流,且使相干结构的流向尺度更大,而在逆压梯度中则会产生相反的现象。
曲率对湍流边界层单独影响的相关研究大多使用带有曲率的管道来尽可能地抑制由于过流截面变化产生的压力梯度。目前针对曲壁面的实验研究方式一般为单点速度测量,如热线等。Meroney等[10]使用毕托管对流向曲壁面进行了测量,发现凹曲面上的流速比平板更高,而凸曲率对湍流边界层的影响则完全相反。So等[11]在针对凹壁面的热线实验中发现凹曲率会增强湍流强度。Arolla等[12]通过数值模拟研究了凹曲率和由凹曲率引起的压力梯度对湍流边界层的影响,发现在曲率起始处会出现逆压梯度,使壁面摩擦减小,而凹曲率对流场中的法向分量影响最大。Matsubara等[13]对弯曲槽道进行了模拟研究,发现曲壁面会显著增加大尺度结构的强度。
曲壁面上的湍流边界层会不可避免地受到由曲率引起的压力梯度作用[12],因此曲壁面湍流边界层相比平板湍流边界层是一个更加复杂的流动。目前针对曲率和压力梯度综合影响下湍流边界层的研究仍局限于最基本的统计量,而对于内部流动及其结构的实验研究较少。本文利用高时间分辨率粒子图像测速技术(Time-Resolved Particle Image Velocimetry,TRPIV),获取凹壁面湍流边界层上不同流向位置的二维速度矢量场,利用大小视场获取法向高度上完整的平均速度剖面以及雷诺应力剖面,选取不同的法向高度并应用可以体现涡旋转方向的
$ {\varLambda _{ci}} $ 准则进行条件相位平均,提取流场中的顺向涡(即沿顺时针旋转的展向涡),然后利用空间两点相关方法研究不同法向高度的相干结构形态,分析凹壁面上湍流边界层内部流动的变化。1 实验装置
实验在天津大学流体力学实验室重力溢流式低湍流度循环水洞中进行。水洞实验段尺寸为
${{4}}{{.1 \;{\rm{m}}}} \times {{0}}{{.6 \;{\rm{m}}}} \times {{0}}{{.7 \;{\rm{m}}}}$ (长×宽×高),流速最高可达${{0}}{{.5 \;{\rm{m}}/{\rm{s}}}}$ 。实验模型为带有流向凹曲率的曲面模型,总长度为$ {\text{2}}{\text{.75 m}} $ ,其前半部分为平板,尺寸为${{1}}{{.20\;{\rm{m}}}} \times {{0}}{{.59\;{\rm{m}}}} \times {{0}}{{.01\;{\rm{m}}}}$ (长×宽×高),后半部分为曲板,尺寸为${{1}}{{.55\;{\rm{m}}}} \times {{0}}{{.59\;{\rm{m}}}} \times {{(0}}{{.01~}} {{0.18)\;{\rm{m}}}}$ (长×宽×高)。在实际工程中,湍流边界层流动常存在不同程度的曲率作用情况,而发生小曲率作用的情况较为普遍,加之实验段尺寸也存在一定限制,最终选定曲面的型线为函数$y = 0.01{e^x}$ 。由于该模型的曲率半径较大,相机视野中拍摄区域的壁面接近水平,因此在以互相关算法进行计算时可以选择矩形计算域。为获得充分发展的湍流边界层,在平板前缘下游$ {\text{50 mm}} $ 处增加了直径$d = {{2\;{\rm{ mm}}}}$ 的绊线。实验装置如图1所示,图中x、y和z分别代表流向、法向和展向。为了获得较为完整的流场速度分布以及近壁面处的精细流动,采用大视场和小视场相结合的方式进行实验:共使用3台高速相机进行拍摄,其中2台相机分别布置在实验段的两侧,用于大小视场的拍摄,第3台高速相机用于拍摄实验段前端的自由来流速度。实验中,在两个不同位置使用不同激光进行照射。
由于实验模型带有沿流向的凹曲率,使得湍流边界层在不同流向位置受到的影响程度各不相同,因此在模型曲面部分的上游和下游各选择一个位置进行测量(图2),两个位置与模型前端的距离定义为L。为便于后期计算,调整高速相机视场与来流呈一定夹角,使得测量时观察到的壁面尽可能平行于相机视场。图中
$ \theta $ 为相机视场与来流方向的夹角,在上游和下游测量位置分别为$ {\theta _1}{\text{ = }}5.5^\circ $ 和$ {\theta _2}{\text{ = }}9.0^\circ $ 。由于模型的拍摄表面为曲面,且在拍摄范围内其曲率变化不明显,在分析曲面流场时选取矩形计算域进行计算。为便于分析,定义x*为在不同位置选取的流场计算区域内的流向,y*为法向,U *和V *、u*和v*分别为流向和法向的平均速度和脉动速度。
实验使用的示踪粒子为直径20 µm的空心玻璃微珠,密度为
$ 1.04{\text{ kg/}}{{\text{m}}^{\text{3}}} $ 。3台高速相机为丹麦Dantec公司的SpeedSense 9072 CMOS相机,分辨率为$ {{1\;280 \;{\rm{像素}}}} \times {{800\;{\rm{像素}}}} $ 。大视场相机对应的物理空间尺寸为$ {\text{80}}{\text{.39 mm}} \times {\text{50}}{\text{.25 mm}} $ (流向×法向),小视场相机对应的物理空间尺寸为$ {\text{28}}{\text{.26 mm}} \times {\text{17}}{\text{.66 mm}} $ (流向×法向),小视场包含于大视场中。采样频率$ f = 1\;000\;{\text{Hz}} $ ,激光片光的厚度约为1 mm。两个位置的测量分两次进行,因此入口处的自由来流速度存在一定波动,在测量上游和下游时分别为$ {\text{0}}{\text{.316 m/s}} $ 和$ {\text{0}}{\text{.328 m/s}} $ 。实验水温$ T = 20^\circ $ ,水的密度$\;{\rho _{\rm{w}}} = {\text{998.2 kg/}}{{\text{m}}^{\text{3}}}$ ,水的运动黏度$\nu = {{1}}{{.01}} \times {{1}}{{{0}}^{{{ - 6}}}}\;{{{{\rm{m}}}}^{{2}}}{{/{\rm{s}}}} $ 。实验共采集了3组流场数据,每组实验获取了两个不同位置大小视场各8216张流场照片。大视场使用${\text{32 像素}} \times {\text{32 像素}}$ 的查询窗口,小视场由于粒子浓度较低,使用${\text{48 像素}} \times {\text{48 像素}}$ 的查询窗口;大小视场查询窗口的重叠率均为$ {\text{75\% }} $ 。以互相关算法进行计算,小视场相邻矢量的间距为$ {\text{0}}{\text{.26 mm}} $ ,大视场相邻矢量的间距为$ {\text{0}}{\text{.5 mm}} $ 。目前,尚无法在实际实验中将流动中压力梯度和流向曲率的影响进行单独分析。此前相关研究常采用零压力梯度的光滑平板流动作为基准进行对比研究。本文亦开展了光滑平板实验。实验中同样使用2台高速相机进行大小视场的拍摄。来流速度为
$ {\text{0}}{\text{.267 m/s}} $ ;采样频率$f' = 800\;{{{\rm{Hz}}}}$ ;大视场相机对应的物理空间尺寸为$ {\text{126 mm}} \times {\text{77 mm}} $ (流向×法向),小视场相机对应的物理空间尺寸为$ {\text{27 mm}} \times {\text{17 mm}} $ (流向×法向),小视场位于大视场中;其余参数与曲面流场相同。计算矢量场时同样选取矩形计算域,因此使用与前文相同的坐标系$ {x^*} $ 和$ {y^*} $ 定义。2 实验结果与分析
流向凹曲率壁面的湍流边界层流动不仅会受到凹曲率的作用,还会受到由凹曲率引起的流向顺压梯度的影响,使得湍流边界层存在沿流向逐渐增大的加速度。由于模型型线曲率半径较大,在初期测试中发现该模型壁面上的湍流边界层受到的凹曲率作用较弱,而受到的顺压梯度作用相对较大。对于带有流向顺压梯度的流动,需要了解流向顺压梯度引起的加速度强弱,研究者普遍使用加速度参数K[14-17] 来表征这一强弱程度:
$$ K = \frac{\nu }{{U_0^2}}\frac{{{\rm{d}}{U_0}}}{{{\rm{d}}x}} $$ (1) 式中,
$ {U_0} $ 表示当前测量位置的自由来流速度。当K$ > 3.0 \times {10^{ - 6}} $ 时,湍流边界层会发生层流化现象[6]。此外,曲面会使流体在不同流向位置流过的截面大小非线性变化,从而使得流向加速度在流向上非均匀;但本实验测量区域尺寸不足以使K产生明显变化,因此选取平均加速度参数作为测量位置的加速度参数。通过对K的计算发现,在上游和下游测量位置均满足K$ < 2.0 \times {10^{ - 6}} $ ,流向顺压梯度的作用较弱,因此可以认为在该曲面上的湍流边界层未发生层流化现象。为比较其与平板的湍流边界层流动情况,引入光滑平板模型的实验数据进行对比,平板数据同样被分为大视场和小视场数据。本实验顺压梯度和流向曲率对湍流边界层的作用较弱,传统的对数律方程仍然具有较强的鲁棒性[6, 18-19],因此本文利用平均速度剖面的对数律区与对数律公式$ {U^ + } = (1/\kappa ){\rm{ln}}\;{y^ + } + B $ 进行拟合来获取壁面摩擦速度$ {u_{\tau} } $ ,其中${y^ + } = y{u_{\tau} }/\nu$ 、${U^ + } = U/{u_{\tau} }$ 分别为内尺度无量纲化的法向高度和平均速度,$ \kappa $ 为卡门常数,B为积分常数。由于研究对象为曲面湍流边界层,其对数律方程可能产生变化,因此将卡门常数$ \kappa $ 与积分常数B均设为变量进行拟合,此外,还应用Spalding曲线[20]进行了拟合验证。结果发现:$ \kappa $ 和B均未发生明显变化,Spalding曲线拟合结果也与对数律方程拟合结果相似,可以认为拟合得到的壁面摩擦速度未发生较明显变化。表1列出了实验基本湍流参数,其中,U∞为入口处来流速度,${u_{\tau,{\rm{large}}}}、{u_{\tau,{\rm{small}}}}$ 分别为大小视场的壁面摩擦速度(本实验将小视场的${u_{\tau,{\rm{small}}}} $ 用于后续数据处理),边界层厚度$ {\delta _{99}} $ 按照0.99倍当前测量位置的平均来流速度确定,剪切雷诺数$ R{e_{\tau} } = {u_{\tau} }\delta /\nu $ 表示内尺度雷诺数($ {u_{\tau} } $ 随着边界层向下游的发展逐渐增大,且下游增长幅度大于上游)。表 1 边界层参数Table 1 Boundary layer parameters上游(L=2.0 m) 下游(L=2.3 m) 平板实验 U∞/(m·s−1) 0.316 0.328 0.267 uτ,large/(m·s−1) 0.0175~0.0180 0.0196~0.0203 0.0116 uτ,small/(m·s−1) 0.0179 0.0202 0.0116 δ99/mm 36.85 37.29 60.16 Reτ 659.6 753.3 697.9 K 9.03×10−7 1.68×10−6 — 2.1 基本统计量
图3为在曲面模型上两个不同流向位置得到的内尺度无量纲平均速度剖面,横轴为两个测量位置与壁面垂直的内尺度无量纲法向高度,定义
$ {U}^{*+}= {U}^{*}/{u}_{\tau ,\text{small}} $ ,${y^{* + }} = {y^*}{u_{\tau,{\rm{small}}}}/\nu$ 。为获取高法向空间分辨率及近壁处平均速度剖面,对小视场利用单行互相关算法(Single-Row Cross Correlation,SRCC)思想进行流场高法向空间分辨率速度矢量计算[21-23]。SRCC算法的思想是通过牺牲流向分辨率来提升法向分辨率,以获得更高法向空间分辨率的速度矢量。因此,基于该算法的思想将查询窗口大小调整为$ {\text{256 像素}} \times {\text{8 像素}} $ (流向×法向),重叠率为$ 50\% $ 。经实际计算,速度矢量的法向间距可达$ {\text{0}}{\text{.09 mm}} $ ,同时可测量到的流场矢量最高可以达到黏性底层。由于实验模型为曲面模型,大视场不同流向位置的平均速度剖面存在较为明显的变化,为了统一无量纲化后的结果,大小视场均使用小视场的壁面摩擦速度${u_{\tau,{\rm{small}}}}$ 进行无量纲化,同时选取大视场与小视场拍摄位置重合的流向位置进行绘制。从图3可以看出,凹壁面上游速度剖面的对数律区变化不明显,但下游速度剖面的对数律区发生了明显偏离,速度剖面在对数律区向上隆起且对数律的斜率小于传统对数律方程。在缓冲层及以下区域,凹壁面与光滑平板情况下的速度分布无明显差异,这可能是由于凹曲率和顺压梯度对边界层内流向速度的影响相互抵消所导致[10,24]。在对数律区以上,两个测量位置的流动均受到抑制[9],说明顺压梯度在对数律区以上造成的影响更强。
图4为不同位置的内尺度无量纲化雷诺应力随
$ {y^{* + }} $ 变化的曲线,雷诺应力各分量均使用壁面摩擦速度实现内尺度无量纲化。$$ \left\{ \begin{gathered} u_{{\rm{rms}}}^{* + } = u_{{\rm{rms}}}^*/{u_{\tau,{\rm{small}}}} \\ v_{{\rm{rms}}}^{* + } = v_{{\rm{rms}}}^*/{u_{\tau,{\rm{small}}}} \\ \left\langle {u^*}{v^*} \right\rangle ^+= \left\langle {u^*}{v^*} \right\rangle/u_{\tau,{\rm{small}}}^2 \\ \end{gathered} \right. $$ (2) 从图中可以看到:凹壁面湍流边界层的湍流强度显著减小,且随着边界层向下游发展,流向雷诺正应力在近壁处的峰值逐渐沿法向向上移动,达到
$ {y^{* + }} = 20 $ 左右;在对数律区以上时,与光滑平板情况之间差距增大;法向湍流强度和雷诺应力在近壁附近无明显变化,而在对数律区及以上区域明显下降。这说明流向顺压梯度对湍流有显著的削弱作用,且随着法向高度增大,削弱作用先增大后减小。2.2 涡结构识别
从2.1节对凹壁面流场基本统计量的分析中可以发现,湍流边界层在受到凹曲率和流向顺压梯度的组合影响后,湍流强度整体呈现下降趋势,这一影响势必也会对边界层内的流动结构产生影响。为了研究凹壁面流场内流动结构的变化,本文利用
$ {\lambda _{ci}} $ 准则进行流场内涡的识别[25-27]。$ {\lambda _{ci}} $ 为速度梯度张量的共轭复特征值,该值可以表示流场中某一矢量点处的旋涡强度。应用该准则可以有效避免将剪切运动识别为涡旋运动。若将旋涡强度与展向涡涡量符号$ {\rm{sgn}}({\omega _z}) $ 结合,即可识别出流场内涡结构的旋转方向:$$ {\varLambda _{ci}} ={\rm{ sgn}}({{\omega} _{\textit{z}}}) \times {\lambda _{{{ci}}}} $$ (3) 式中,
${\varLambda _{ci}}$ 表示获得涡量符号后的$ {\lambda _{ci}} $ 值。图5给出了凹壁面湍流边界层不同流向位置的
${\varLambda _{{{ci}}}}$ 识别结果,$ {x^*} $ 与$ {y^*} $ 均使用内尺度进行无量纲化。当${\varLambda _{{{ci}}}}$ 为负时,检测到顺向涡,为正时,则检测到逆向涡。为减少环境噪声对识别结果的影响,使用阈值条件$|{\varLambda _{ci}}| \geqslant T \times \varLambda _{ci,\rm{rms}}(y)$ (T为检测涡结构边界的阈值,本文取0.5)来确定涡结构的边界,同时考虑到流场的空间分辨率影响,将仅有单个网格节点大小的涡结构过滤,以减弱背景噪声影响[28]。从图中可以看出,流场中${\varLambda _{{{ci}}}}$ 较大的区域与速度矢量中直观显示出的涡结构吻合程度较高,流场内存在顺向涡和逆向涡的涡对,以及由发卡涡组成的发卡涡包结构。为进一步了解凹壁面流场中涡结构的强度沿法向分布情况,对大视场中的
$ {\lambda _{ci}} $ 进行了时间和沿流向的平均,并绘制了大视场$ {\lambda _{ci}} $ 沿内尺度无量纲化法向高度$ {y^{* + }} $ 的变化曲线,如图6所示。从图中可以发现,凹壁面和光滑平板上的$ {\lambda _{ci}} $ 均显示出随着法向高度的变化先增大后减小的趋势,而凹壁面上不同流向位置的旋涡强度在各法向位置上均大于平板情况,且在对数律区附近相差更大。这说明虽然凹壁面边界层内的湍流强度被削弱,但由于凹壁面对湍流边界层的影响,流场内不同位置的速度梯度增强,进而使得旋涡强度增大,同时也使涡的分布更加集中于对数律区附近。2.3 条件相位平均
顺时针旋转的展向涡通常被认为与发卡涡的涡头密切相关,而发卡涡在向下游迁移的过程中会对周围流场施加诱导作用,产生猝发事件[29],对湍流内部的能量产生和输运起到了重要作用,发卡涡的形成与分布也与湍流脉动密切相关[30]。
条件相位平均是研究流场中涡结构的典型方法。为研究凹壁面上展向发卡涡头的变化,2.3小节使用该方法提取了小视场内顺向涡(即顺时针旋转的展向涡)的统计特征。展向涡的识别条件使用2.2小节所述的
${\varLambda _{{\text{ci}}}}$ 准则[31],可表示为:$$ {\varLambda _{ci}}({x^*},{y^*}) < { - } \varLambda _{ci,{\rm{rms}}}( {{y^{{*}}}} ) $$ (4) 当检测位置达到检测条件,提取该时刻检测位置附近的流场。本文在小视场内选取了2个法向参考高度进行条件采样。
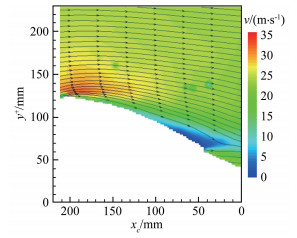
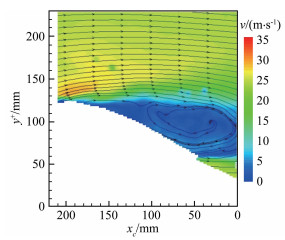
图7为参考法向高度
$y_{{\text{ref}}}^{{\text{*+ }}} = 30$ 附近流向脉动速度的条件相位平均结果,流向脉动速度在参考位置的上方主要为正脉动,下方为负脉动。从图中可以看出:在凹壁面上游,顺向涡上方正脉动的峰值比平板情况下更强,以${{{u}}^{\text{*}}} =0.004$ m/s的等值线为基准(红色虚线),其空间尺度小于平板情况,顺向涡下方的负脉动也强于平板情况;而在凹壁面下游,正脉动峰值被削弱,空间尺度明显增大,但小于平板情况,下方负脉动的强度和空间尺度则仍在继续增大。在
$y_{{\text{ref}}}^{{\text{*+ }}} = 80$ 附近也对顺向涡进行了提取,图8为提取出的顺向涡结果。图中表明,在凹壁面湍流边界层中,顺向涡上方正脉动的空间尺度随着边界层向下游的发展逐渐缩小,但峰值的范围逐渐增大,同时二者均强于平板情况。此外,随着湍流边界层向下游发展,顺向涡下方的负脉动明显增强且均强于平板情况。2.4 两点相关分析
从之前分析可知,流场内的顺向涡在凹曲率和流向顺压梯度的组合影响下,产生了较大变化。众所周知,顺向涡与发卡涡头有着密切联系,而发卡涡是壁湍流中普遍存在的相干结构[32],因此,在凹曲率和流向顺压梯度的影响下,湍流边界层内相干结构的运动和发展也会产生一定变化。
针对相干结构在不同法向高度的流向分布特征,本文使用两点流向脉动速度相关法来体现凹壁面上湍流边界层内部相干结构在受到凹曲率和流向顺压梯度组合影响时产生的变化[13, 33-34]。两点流向脉动速度相关计算公式如下:
$$ {R_{{{uu}}}}( {\Delta x,y,{y_{{\rm{ref}}}}} ) = \frac{{\left\langle {u( {x,{y_{_{{\rm{ref}}}}}} )u( {x + \Delta x,y} )} \right\rangle }}{{{\sigma _u}( {{y_{{\rm{ref}}}}} ){\sigma _u}( y )}} $$ (5) 式中,
${y_{{\rm{ref}}}}$ 表示计算选取的参考法向高度,$ \Delta x $ 表示两点之间的流向空间延迟,$ {\sigma _u} $ 表示流向脉动速度的均方根。为研究近壁面附近相干结构的空间形态,图9绘制了小视场两点相关结果,所选取的参考高度与近壁处条件平均所选取的高度一致,
$ {x^*} $ 与$ {y^*} $ 均使用内尺度进行无量纲化。从图中可以看到,相较于光滑平板情况,凹壁面近壁面处相干结构的空间尺度呈现先缩小后增大的趋势。在两点相关结果中,相干结构呈现出椭圆外形。筛选出某一等值线上的所有点,并对这些点进行椭圆拟合,即可获得椭圆方程,基于此方程可以获取相干结构与壁面之间的夹角。本文选取${R_{{{u^*u^*}}}}=0.4$ 等值线(红色虚线)上的点作为参考点,计算出的相干结构与壁面夹角已在图9中指出。可以发现:位于缓冲层附近的相干结构与壁面的夹角明显小于光滑平板情况;随着边界层向下游发展,相干结构逐渐向壁面倾斜,其沿流向的尺度也被逐渐拉长,这与仅有流向顺压梯度影响时的趋势类似[10]。但由于流向凹曲率的影响,相干结构的空间尺度在上下游增长不均匀,下游的空间尺度增长幅度更大。小视场可以呈现出流场近壁处细致的空间形态,而大视场则可以较为完整地表征相干结构的空间尺度大小。图10为不同工况下大视场两点相关系数的结果,选取的参考法向高度在
$y_{{\text{ref}}}^{{\text{*+ }}} = 80$ 附近,$ {x^*} $ 与$ {y^*} $ 均使用内尺度进行无量纲化。在该高度附近,湍流边界层受到凹曲率和流向顺压梯度的影响,对数律区相干结构的尺度明显增大,且随着湍流边界层向下游的发展,相干结构的空间尺度逐渐增大,在下游位置超过了1倍边界层厚度(内尺度无量纲化后的边界层厚度$ {\delta ^{{ + }}}{{ = }}\delta {{{u}}_{\tau} }/\nu {{ = }} 753.26 $ )。3 结 论
通过双相机大小视场的TRPIV实验,对带有纵向凹曲率的壁面进行了测量并获取了瞬时速度场,经过数据处理和分析得出以下结论:
1)在流向凹曲率壁面上得到的平均速度剖面随着向下游发展逐渐偏离传统对数律,同时尾迹区被抑制。在相同法向高度的湍流强度均弱于平板情况。这说明流向凹曲率壁面上的湍流活动被明显抑制,且尾迹区的抑制作用相对更强。
2)相比于平板情况,凹壁面湍流边界层中涡的强度在不同法向高度均明显增强,且随着向下游的发展而逐渐增大。对数律区及其下方区域与尾迹区旋涡强度的差值增大,这表明凹壁面上湍流边界层内的涡强度显著增强,且更集中于近壁附近。
3)对凹壁面湍流边界层对数律区内的顺向涡进行条件相位平均,发现凹壁面会增强顺向涡下方负的流向脉动速度。缓冲层附近顺向涡上方正脉动峰值被削弱,但空间尺度有所增大,而对数律区上侧正脉动更加集中于顺向涡上方较小的区域内,且脉动强度明显增大。随着向下游的发展,缓冲层附近顺向涡上方正脉动的峰值和空间尺度均弱于平板情况,而在对数律区上侧则均强于平板情况。
4)两点相关结果表明,凹壁面上相干结构向外层迁移的趋势减弱,其空间尺度随着向下游的发展呈现出不断增大的趋势,其中上游的空间尺度增长被抑制,而在下游则相反。
-
表 1 FL-5风洞主要参数
Table 1 FL-5 wind tunnel parameters
Parameter Value Cross-section diameter/m 1.5 Test-section length/m 1.95 Cross-sectional area/m2 1.76625 Design speed/(m·s-1) 53 Mean turbulence 0.19% Static pressure gradient 0.0055 Drop coefficient 1.0 表 2 单侧布置激励器参数
Table 2 Actuator parameters on one side
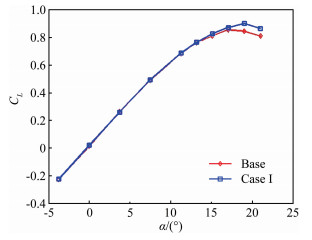
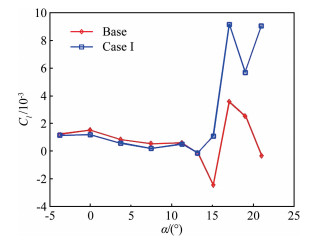
Case Voltage/kV Frequency/Hz Duty cycle Left wing actuator position Base — — — 1~8 Case Ⅰ 27.5 250 20 1~8 表 3 激励器位置及电源参数
Table 3 The position of actuator and electrical parameters
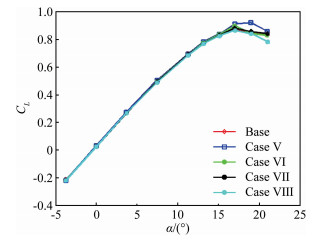
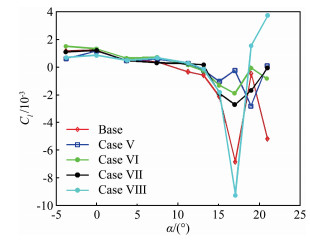
Case Voltage/kV Frequency/Hz Duty cycle Left wing actuator position Right wing actuator position Base OFF — — — — Case Ⅴ 27.5 250 20 2, 4, 6, 8 2, 4, 6, 8 Case Ⅵ 27.5 250 20 6, 7, 8 6, 7, 8 Case Ⅶ 27.5 250 20 3, 6 3, 6 Case Ⅷ 27.5 250 20 2 2 -
[1] Grossman K R, Cybyk B Z, VanWie D M, et al. SparkJet actuators for flow control[R]. AIAA-2003-0057, 2003.
[2] Grossman K R, Cybyk B Z, Rigline M C, et al. Characteri-zation of SparkJet actuators for flow control[R]. AIAA-2004-0089, 2004.
[3] Cybyk B Z, Simon D H, Land H B Ⅲ. Experimental characterization of a supersonic flow control actuator[R]. AIAA-2006-0478, 2006.
[4] Haack S J, Land H B, Cybyk B, et al. Characterization of a high-speed flow control actuator using digital speckle tomogra-phy and PIV[R]. AIAA-2008-3759, 2008.
[5] Popkin S H, Cybyk B Z, Land H B Ⅲ, et al. Recent performance-based advances in SparkJet actuator design for supersonic flow applications[R]. AIAA-2013-0322, 2013.
[6] Popkin S H, Cybyk B Z, Foster C H, et al. Experimental estimation of SparkJet efficiency[J]. AIAA Journal, 2016, 54(6):1831-1845. DOI: 10.2514/1.J052694
[7] Emerick T, Ali M Y, Foster C, et al. SparkJet characteri-zations in quiescent and supersonic flowfields[J]. Experiments in Fluids, 2014, 55(12):1858. DOI: 10.1007/s00348-014-1858-6
[8] Narayanaswamy V, Shin J, Clemens N T, et al. Investigation of plasma-generated jets for supersonic flow control[R]. AIAA-2008-0285, 2008.
[9] Greene B R, Clemens N T, Micka D. Control of shock boundary layer interaction using pulsed plasma jets[R]. AIAA-2013-0405, 2013.
[10] Anderson K, Knight D D. Characterization of single pulse of plasma jet[R]. AIAA-2012-0188, 2012.
[11] Golbabaei-Asl M, Knight D, Wilkinson S. Noveltechnique to determine SparkJet efficiency[J]. AIAA Journal, 2015, 53(2):501-504. DOI: 10.2514/1.J053034
[12] Reedy T M, Kale N V, Dutton J C, et al. Experimental characterization of a pulsed plasma jet[J]. AIAA Journal, 2013, 51(8):2027-2031. DOI: 10.2514/1.J052022
[13] Ostman R J, Herges T G, Craig D J, et al. Effect on high-speed boundary-layer characteristics from plasma actuators[R]. AIAA-2013-0527, 2013.
[14] Belinger A, Naudé N, Cambronne J P, et al. Plasma synthetic jet actuator:electrical and optical analysis of the discharge[J]. Journal of Physics D:Applied Physics, 2014, 47(34):345202. DOI: 10.1088/0022-3727/47/34/345202
[15] Sary G, Dufour G, Rogire F, et al. Modeling and parametric study of a plasma synthetic jet for flow control[J]. AIAA Journal, 2014, 52(8):1591-1603. DOI: 10.2514/1.J052521
[16] Chedevergne F, Léon O, Bodoc V, et al. Experimental and numerical response of a high-Reynolds-number M=0.6 jet to a plasma synthetic jet actuator[J]. International Journal of Heat and Fluid Flow, 2015, 56: 1-15.
[17] Shin J. Characteristics of high speed electro-thermal jet activated by pulsed DC discharge[J]. Chinese Journal of Aeronautics, 2010, 23(5):518-522. DOI: 10.1016/S1000-9361(09)60249-1
[18] Chiatto M, de Luca L. Numerical and experimental frequency response of plasma synthetic jet actuators[R]. AIAA-2017-1884, 2017.
[19] Zong H H, Kotsonis M. Effect of slotted exit orifice on performance of plasma synthetic jet actuator[J]. Experiments in Fluids, 2017, 58:17. DOI: 10.1007/s00348-016-2299-1
[20] 张攀峰, 王晋军, 施威毅, 等.等离子体激励低速分离流动控制实验研究[J].实验流体力学, 2007, 21(2):35-39. DOI: 10.3969/j.issn.1672-9897.2007.02.008 Zhang P F, Wang J J, Shi W Y, et al. Experimental study on the separation control by plasma actuator in subsonic flow[J]. Journal of Experiments in Fluid Mechanics, 2007, 21(2):35-39. DOI: 10.3969/j.issn.1672-9897.2007.02.008
[21] Wang J, Choi K S, Feng L H, et al. Recent developments in DBD plasma flow control[J]. Progress in Aerospace Sciences, 2013, 62:52-78. DOI: 10.1016/j.paerosci.2013.05.003
[22] 王健磊, 孟宣市, 李华星, 等.等离子体控制下前体分离涡的研究[J].空气动力学学报, 2015, 33(6):740-746. http://d.old.wanfangdata.com.cn/Periodical/kqdlxxb201506005 Wang J L, Meng X S, Li H X, et al. Study on forebody separation vortices using plasma actuations[J]. Acta Aerodyna-mica Sinica, 2015, 33(6):740-746. http://d.old.wanfangdata.com.cn/Periodical/kqdlxxb201506005
[23] 单勇, 张靖周, 谭晓茗.火花型合成射流激励器流动特性及其激励参数数值研究[J].航空动力学报, 2011, 26(3):551-557. http://d.old.wanfangdata.com.cn/Periodical/hkdlxb201103011 Shan Y, Zhang J Z, Tan X M. Numerical study of the flow characteristics and excitation parameters for the SparkJet actuator[J]. Journal of Aerospace Power, 2011, 26(3):551-557. http://d.old.wanfangdata.com.cn/Periodical/hkdlxb201103011
[24] 朱晨彧.高性能零质量射流激励器试验研究与参数优选[D].南京: 南京航空航天大学, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D280754 Zhu C Y. Experimental research and parameters optimization on high-performance zero-mass-jet actuator[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D280754
[25] 程林, 孙姝, 谭慧俊, 等.直缝式等离子体合成射流激励器特性的实验研究[J].推进技术, 2017, 38(9):1937-1942. http://d.old.wanfangdata.com.cn/Periodical/tjjs201709003 Cheng L, Sun S, Tan H J, et al. Experimental study on characteristics of plasma synthetic actuator with normal slot[J]. Journal of Propulsion Technology, 2017, 38(9):1937-1942. http://d.old.wanfangdata.com.cn/Periodical/tjjs201709003
[26] 吕元伟, 单勇, 张靖周, 等.火花型激励合成射流瞬时流场测试[J].航空动力学报, 2017, 32(10):2371-2377. http://d.old.wanfangdata.com.cn/Periodical/hkdlxb201710009 Lyu Y W, Shan Y, Zhang J Z, et al. Measurement on instantaneous flow fields of a spark-excited synthetic jet[J]. Journal of Aerospace Power, 2017, 32(10):2371-2377. http://d.old.wanfangdata.com.cn/Periodical/hkdlxb201710009
[27] 刘朋冲, 李军, 贾敏, 等.等离子体合成射流激励器的流场特性分析[J].空军工程大学学报:自然科学版, 2011, 12(6):22-25. http://d.old.wanfangdata.com.cn/Periodical/kjgcdxxb201106005 Liu P C, Li J, Jia M, et al. Investigation on flow filed of the plasma synthetic jet device[J]. Journal of Air Force Engineering University:Natural Science Edition, 2011, 12(6):22-25. http://d.old.wanfangdata.com.cn/Periodical/kjgcdxxb201106005
[28] Jin D, Cui W, Li Y H, et al. Characteristics of pulsed plasma synthetic jet and its control effect on supersonic flow[J]. Chinese Journal of Aeronautics, 2015, 28(1):66-76. DOI: 10.1016/j.cja.2014.12.012
[29] 宗豪华, 吴云, 宋慧敏, 等.等离子体合成射流的理论模型与重频激励特性[J].航空学报, 2015, 36(6):1762-1774. http://d.old.wanfangdata.com.cn/Periodical/hkxb201506004 Zong H H, Wu Y, Song H M, et al. Analytical model and repetitive working characteristic of plasma synthetic jet[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6):1762-1774. http://d.old.wanfangdata.com.cn/Periodical/hkxb201506004
[30] Zhang Z B, Wu Y, Jia M, et al. The multichannel discharge plasma synthetic jet actuator[J]. Sensors and Actuators A:Physical, 2017, 253:112-117. DOI: 10.1016/j.sna.2016.11.011
[31] Wang L, Luo Z B, Xia Z X, et al. Review of actuators for high speed active flow control[J]. Science China Technological Sciences, 2012, 55(8):2225-2240. DOI: 10.1007/s11431-012-4861-2
[32] 王林, 罗振兵, 夏智勋, 等.等离子体合成射流能量效率及工作特性研究[J].物理学报, 2013, 62(12):125207. DOI: 10.7498/aps.62.125207 Wang L, Luo Z B, Xia Z X, et al. Energy efficiency and performance characteristics of plasma synthetic jet[J]. Acta Physica Sinica, 2013, 62(12):125207. DOI: 10.7498/aps.62.125207
[33] Wang L, Xia Z X, Luo Z B, et al. Three-electrode plasma synthetic jet actuator for high-speed flow control[J]. AIAA Journal, 2014, 52(4):879-882. DOI: 10.2514/1.J052686
[34] 杨瑞, 罗振兵, 夏智勋, 等.高超声速导弹等离子体合成射流控制数值研究[J].航空学报, 2016, 37(6):1722-1732. http://d.old.wanfangdata.com.cn/Periodical/hkxb201606002 Yang R, Luo Z B, Xia Z X, et al. Numerical study of plasma synthetic jet control on hypersonic missile[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6):1722-1732. http://d.old.wanfangdata.com.cn/Periodical/hkxb201606002
[35] Zhou Y, Xia Z X, Luo Z B, et al. Effect of three-electrode plasma synthetic jet actuator on shock wave control[J]. Science China Technological Sciences, 2017, 60(1):146-152. DOI: 10.1007/s11431-016-0248-4
[36] 李亮, 李修乾, 车学科, 等.等离子体增强射流掺混的激励参数影响研究[J].实验流体力学, 2018, 32(5):41-47. http://www.syltlx.com/CN/abstract/abstract11142.shtml Li L, Li X Q, Che X K, et al. Study on the influence of incentive parameters on plasma-enhanced jet mixing[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(5):41-47. http://www.syltlx.com/CN/abstract/abstract11142.shtml
[37] Liu R B, Niu Z G, Wang M M, et al. Aerodynamic control of NACA 0021 airfoil model with spark discharge plasma synthetic jets[J]. Science China Technological Sciences, 2015, 58(11):1949-1955. DOI: 10.1007/s11431-015-5881-5
[38] 刘汝兵, 王萌萌, 郝明, 等.补气式等离子体射流发生器实验研究[J].航空学报, 2016, 37(6):1713-1721. http://d.old.wanfangdata.com.cn/Periodical/hkxb201606001 Liu R B, Wang M M, Hao M, et al. Experimental research on air supplementing type plasma synthetic jet generator[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6):1713-1721. http://d.old.wanfangdata.com.cn/Periodical/hkxb201606001
[39] 刘汝兵, 牛中国, 王萌萌, 等.等离子体射流控制机翼气动力矩的实验研究[J].工程力学, 2016, 33(3):232-238. http://d.old.wanfangdata.com.cn/Conference/8358353 Liu R B, Niu Z G, Wang M M, et al. Aerodynamic moments control of wing model using plasma jet[J]. Engineering Mechanics, 2016, 33(3):232-238. http://d.old.wanfangdata.com.cn/Conference/8358353
[40] Caruana D, Barricau P, Gleyzes C. Separation control with plasma synthetic jet actuators[J]. International Journal of Aerodynamics, 2013, 3(1-3):71-83. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=d80179bda165b41e95a63f895ad7d758
[41] 李洋, 梁华, 贾敏, 等.等离子体合成射流改善翼型气动性能实验研究[J].推进技术, 2017, 38(9):1943-1949. http://d.old.wanfangdata.com.cn/Periodical/tjjs201709004 Li Y, Liang H, Jia M, et al. Experimental investigation of enhancing wing aerodynamic performance by plasma synthetic jet[J]. Journal of Propulsion Technology, 2017, 38(9):1943-1949. http://d.old.wanfangdata.com.cn/Periodical/tjjs201709004
-
期刊类型引用(4)
1. 卢子寅,张晓源,李进平,马虎. 爆轰驱动惰性气体磁流体发电试验研究. 力学学报. 2023(04): 1019-1027 .  百度学术
百度学术
2. 唐路,刘保林,夏琦,黄铭冶,彭爱武. 喉部面积对盘式磁流体发电机性能影响分析. 科学技术与工程. 2022(06): 2298-2304 .  百度学术
百度学术
3. 化为卓,高岭,陈戈,李益文,巩耕,王延涛,魏彪. 基于等离子体炬的磁流体动力学实验系统. 航空学报. 2022(S2): 4-10 .  百度学术
百度学术
4. 罗凯,汪球,李逸翔,李进平,赵伟. 基于高温气体效应的磁流体流动控制研究进展. 力学学报. 2021(06): 1515-1531 .  百度学术
百度学术
其他类型引用(2)
















 下载:
下载: