0   引　言

生理流体往往是复杂流体，即介于理想固体和理想流体之间具有复杂本构关系的物质^[1]，如细胞质、胞外基质、黏液、淋巴液等。生理流体中的粒子运动基本方式为扩散和对流。粒子尺寸降低至纳米尺度，扩散逐渐占据主导地位。生理流体中的纳米粒子扩散在生命演化^[2]、信息传递^[3]、药物输运^[4-5]等过程中均具有重要的意义。

在细胞内部，扩散是细胞质中分子输运的基本方式。细胞质和细胞间质均为复杂介质^[6-7]，其复杂性不仅在于大分子拥挤导致的多孔结构，还在于生命活动导致的小雷诺数流动（${{Re}} \ll 1$），如微管运动诱导的涡流^[8-9]、组织液流动^[10-11]等。蛋白质、核酸、囊泡等生物颗粒的实际输运过程为流动介导的扩散运动，其微观表征是解读细胞功能潜在分子机制的基本途径^[12]。在纳米医学领域，纳米药物在人体中的输运必须克服诸多生理障碍，如黏液^[13]、肿瘤间质等。相关研究^{[5, 13]}指出，扩散是黏液、肿瘤间质等生理介质中的纳米药物输运的主要途径，纳米药物的输运过程往往还受到微观生理流动的影响，如肿瘤间质流动等。当前，如何提高纳米药物在生理介质中的输运效率仍是亟待解决的问题，了解纳米粒子在生理介质中的运动机制是解决该问题的重要前提。

颗粒输运的流动与扩散效应之比可由佩克莱特数Pe（Péclet number）表示，Pe = ud/D，其中，u为平均流速，d为颗粒粒径，D为颗粒扩散系数。宏观上，流动环境中的纳米粒子输运可由经典的对流–扩散方程描述；微观上，受扩散与流动的相互影响，纳米粒子输运变得异常复杂，尤其是在生理流体的微尺度流动环境（Pe～O(1)）中，且相关微观机理目前仍不清楚^[14]。

理论上，临床或动物实验是探索此类问题的最佳方法，但其难度极大且存在伦理问题，因此实际研究往往基于模型化介质开展。高分子溶液是具有缠结网络结构特征的黏弹性复杂流体，与细胞质、黏液的多孔结构和物理性质相似，其流体特质赋予了其模拟生理流动环境的可能性。

目前，对于高分子溶液中的纳米粒子输运，研究者主要关注静态条件下的纳米粒子扩散特性^[15]。早期关于粒子输运的研究大多关注的是流动占主导（Pe > 1）的微米粒子运动，多孔介质模型也较多采用胶体悬浮液或颗粒流^[16-17]。近年来，陆续有研究者开始关注受限流动环境中的纳米粒子扩散特性。其中部分研究提出了滤膜^[18]或纳米柱阵列^[19]等较好的微观流动体系，但其流体介质往往使用纯水等简单流体，相应结论并不适用于复杂流体的微流动环境；还有一些研究采用高分子溶液作为复杂流体，但一般基于早期的泰勒弥散（Taylor dispersion）效应，考察粒子浓度的整体分布，较少关注粒子的微观运动机制^[20-21]。需要指出，在流动环境中，受流动剪切力的影响，高分子溶液中的分子链会发生构象和特征尺度改变，粒子运动的限制及相关微观运动机制也可能随之改变。

本文利用微流控芯片技术和高分子溶液构建复杂流体微尺度流动环境，采用粒子追踪技术测量该环境中的纳米粒子运动。在流动信息有效去除的基础上，基于均方位移（Mean Squre Displacement, MSD）、位移概率分布（Displacement Probability Density, DPD）、非高斯特性系数等统计特征量表征纳米粒子扩散运动特性，分析微尺度流动对高分子溶液中纳米粒子扩散运动的影响规律。

1   材料和方法

1.1   溶液配置与流变表征

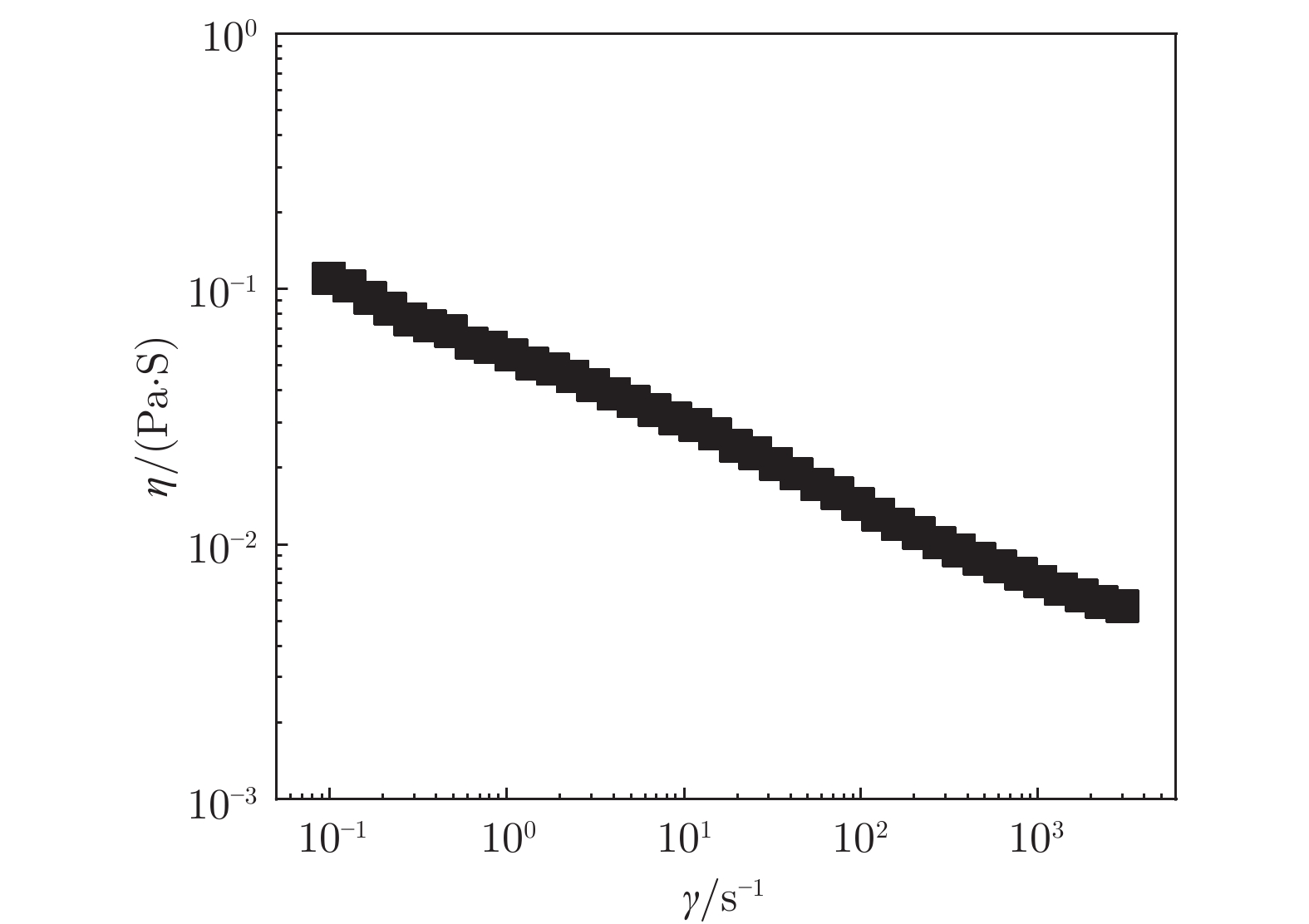
选用摩尔质量M_w = 8 × 10⁶ g/mol、浓度c = 2000 mg/kg的聚环氧乙烷（Polyethylene Oxide, PEO, Sigma-Aldrich）溶液作为模型化复杂流体。选用粒径d = 200 nm的聚苯乙烯荧光颗粒（poly-styrene, ThermoFisher）作为示踪粒子，其体积分数为1 × 10⁻⁶%～1 × 10⁻⁴%。极低的体积分数能够最大限度避免运动粒子之间的相互作用。实验前，将PEO粉末和荧光示踪粒子加入去离子水中，放置在摇床（转速设置为60 r/min）上进行混合，经1～2 d后可得到均匀的PEO溶液。

PEO溶液是具有网络结构特征的复杂流体，其网络结构与浓度c密切相关。当c > c*时，PEO分子会相互交叠进入缠结状态，形成具有一定网格尺寸的网络结构（c* = 3M_w/4πR_g³N_A为PEO溶液的重叠浓度阈值，N_A为阿伏伽德罗常数，R_g = 0.02M_w^0.58为回转半径）。溶液中PEO网络结构的平均网格特征尺寸ξ = R_g(c/c*)^−0.76。PEO溶液的流变特性采用锥板旋转流变仪（Physica MCR302, Anton Paar GmbH）测量。所用锥板直径为50 mm，锥角为0.3 rad。测量温度利用珀尔帖平台（Peltier stage）保持为25 ℃。图1给出了剪切率γ在10⁻¹～10³ s⁻¹范围内的 PEO 溶液黏度η的测量结果，可以发现体积分数极低（1 × 10⁻⁶%～1 × 10⁻⁴%）的纳米粒子对溶液流变性质几乎不产生影响。

图  1  PEO溶液的黏度测量结果

Fig.  1  Viscosity measurement results of PEO solution

下载: 全尺寸图片 幻灯片

1.2   微流控芯片设计与加工

所设计微流控芯片的直通道高度H = 50 μm、宽度W = 100 μm、长度L = 2 cm。鉴于现有商用微泵在极低流量下稳定性差，且难以实现${{Re}} \ll 1$和Pe～O(1)的流动条件，采用重力驱动的方式进行流动驱动。调节入口与出口溶液高度差∆h可产生静压力p（p = ρg∆h，其中ρ为流体密度，g为重力加速度），实现微通道中的极低流速流动^[22]。该流动驱动设计不需要添加泵或振荡元件等，易于实现。需要指出的是，在极低流量条件下，出入口溶液高度差变化极小，单工况实验（测量时间约90 min）的流速近似恒定。

以Auto CAD软件设计直通道结构，基于SU–8模具，采用软刻法制作聚二甲基硅氧烷（Polydi-methylsiloxane, PDMS）微流控芯片。利用配胶、匀胶、倒胶、干燥、切胶、打孔、清洗等标准化微加工技术将PDMS微流控芯片和洁净玻璃片进行氧气等离子处理（采用Plasma Cleaner, PC–6S）后永久键合，置于恒温加热箱中烘焙以加固键合，形成具有良好光学透性的PDMS微流控芯片。PDMS微流控芯片实物如图2所示。微加工完成后，以硅橡胶将20和100 μL量程的移液管和PDMS微流控芯片打孔处固定在一起，作为入口装置。微流控芯片出口为半径2 mm的圆孔。

图  2  微流控芯片的实物图

Fig.  2  Physical diagram of microfluidic chip

下载: 全尺寸图片 幻灯片

1.3   粒子追踪实验与图像处理

采用基于荧光显微成像的粒子追踪技术测量聚苯乙烯荧光粒子的运动。粒子追踪实验平台如图3所示。以460～550 nm波长的绿光（X–Cite® 200DC）激发纳米粒子荧光，采用奥林巴斯倒置荧光显微镜（Olympus IX73）观察纳米粒子运动全过程，采用电子倍增的电荷耦合器件（EMCCD, IXON–L–897）记录纳米粒子运动图像。显微镜使用100倍油浸物镜，数值孔径为1.4。CCD相机成像区域为512像素 × 512像素，单像素尺寸约为158 nm，曝光时间设置为0.01 s，连续拍摄帧数为600帧，单次采集时长为6 s，每次实验在90 min内完成。所有实验均在室温下进行。

图  3  实验平台装置图

Fig.  3  Diagram of the experimental platform

下载: 全尺寸图片 幻灯片

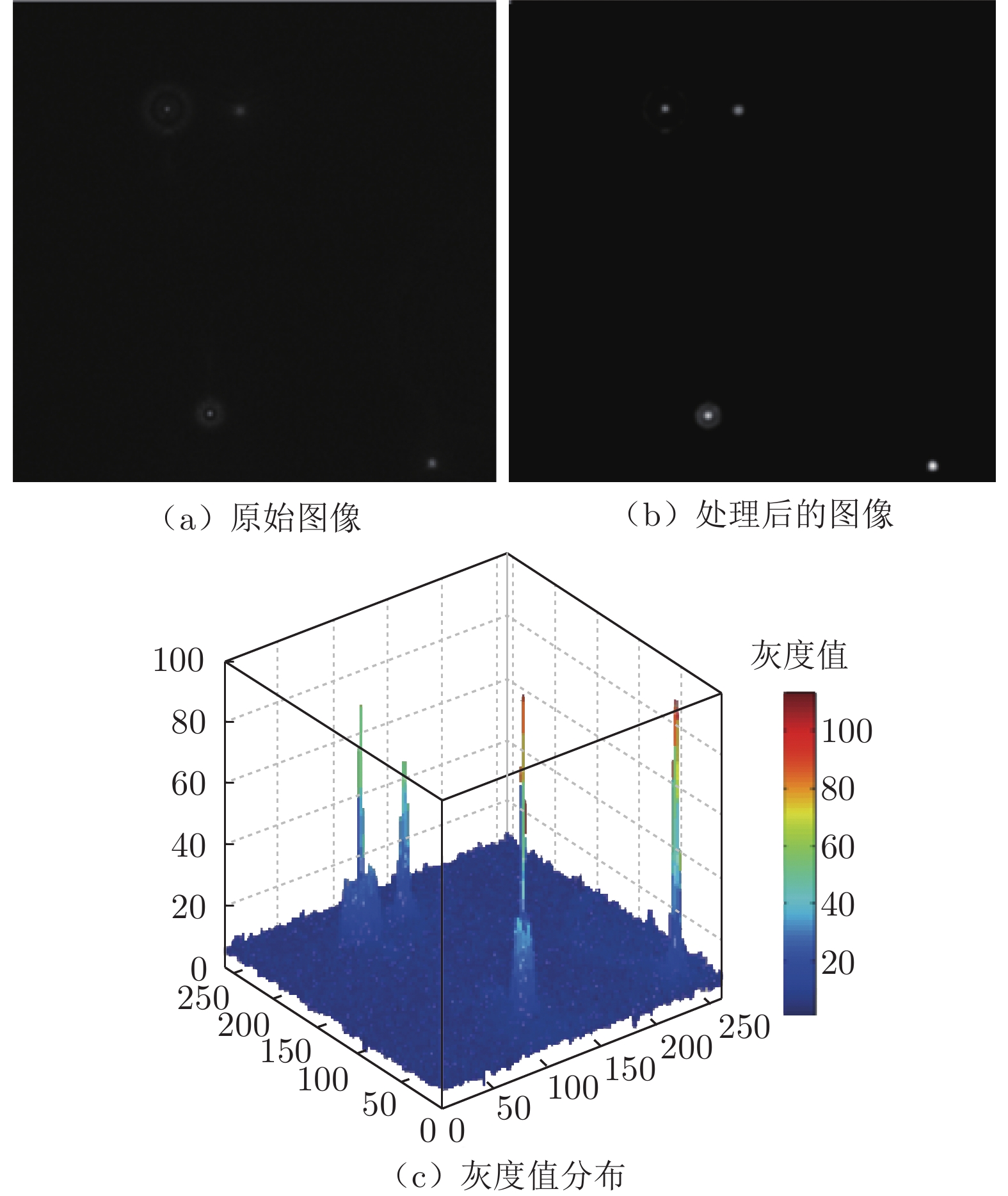
在获取足够多的运动图像后，进行图像处理以得到纳米粒子运动信息，如图4所示。采用Image J（NIH）图像处理软件对原始图像依次进行“锐化（Sharpen）”、“高斯模糊（Gaussian blur）”以及“色彩平衡调节（Color balance）”处理，得到更清晰的粒子图像。基于灰度图分布可以清楚识别纳米粒子位置。利用自编程算法（Matlab 2019a）识别粒子质心位置，并在每个质心周围（10像素 × 10像素的区域）搜索，以获取示踪粒子下一个位置，最终得到纳米粒子的运动轨迹。

图  4  纳米粒子的图像处理

Fig.  4  Image processing of nanoparticles

下载: 全尺寸图片 幻灯片

1.4   流动信息去除方法

PEO溶液沿直通道单向流动，将流动方向定义为x方向，垂直于流动的方向定义为y方向。筛选x方向上连续运动步长大于100帧的粒子进行分析，连续运动帧数之间的粒子位移∆x可表示为：

式中： λ为提取的粒子连续运动帧数， x_k为粒子在第 k（k为整数）帧x方向上的坐标， x_{k +λ} 表示粒子在第k + λ帧x方向上的坐标。利用单像素尺寸（158 nm），将∆x换算为实际运动位移（单位为m）。

采用数据统计分析方法，对n个粒子（n > 100）x方向上的位移求平均，减小随机误差。粒子在x方向上的平均位移$\overline {\Delta x} $可表示为：

PEO溶液的流速$ v $可表示为：

式中：τ_s为曝光时间，单位为s；λ−1为间隔帧数。

粒子在时间间隔∆t内沿x方向流动发生的位移∆x(t)为：

去除流动分量后，t时刻粒子在x方向上的位置坐标x′(t)为：

式中：x(t)为t时刻粒子在x方向上的原始位置坐标。

1.5   主要特征量

表征纳米粒子运动特性的统计特征量包括：系综均方位移（ensemble-averaged MSD, e–MSD）$\langle $r²(t)$\rangle $（式（6））、时间平均均方位移（time-averaged MSD, t–MSD）$ \overline {r^2{{(t)}}} $（式（7））、x方向的时间平均均方位移$ \overline {x^2{{\left( t \right)}}} $（式（8））、y方向的时间平均均方位移$ \overline {y^2{{\left( t \right)}}} $（形式同式（8），x替换为y）、x方向的均方位移$\langle $x²(t)$\rangle $（式（9））、y方向的均方位移$\langle $y²(t)$\rangle $、x方向去除流动分量后的均方位移$\langle $$x{'^2}\left(t \right)$$\rangle $（式（10））、位移概率分布G_r（式（11））、x方向去除流动分量后的位移概率分布G_x'（式（12））、y方向的位移概率分布G_y（形式同式（12），$x'$替换为y）、非高斯系数α（式（13））、x方向去除流动分量后的遍历性破坏参数（ergodicity breaking parameter, E_x'）（式（14））和y轴方向的遍历性破坏参数E_y（形式同式（14），$x'$替换为y）。

式中：$\langle $ $\rangle $表示系综平均，T为总测量时间，σ为位移的标准方差。

2   结果和讨论

2.1   纳米粒子运动轨迹

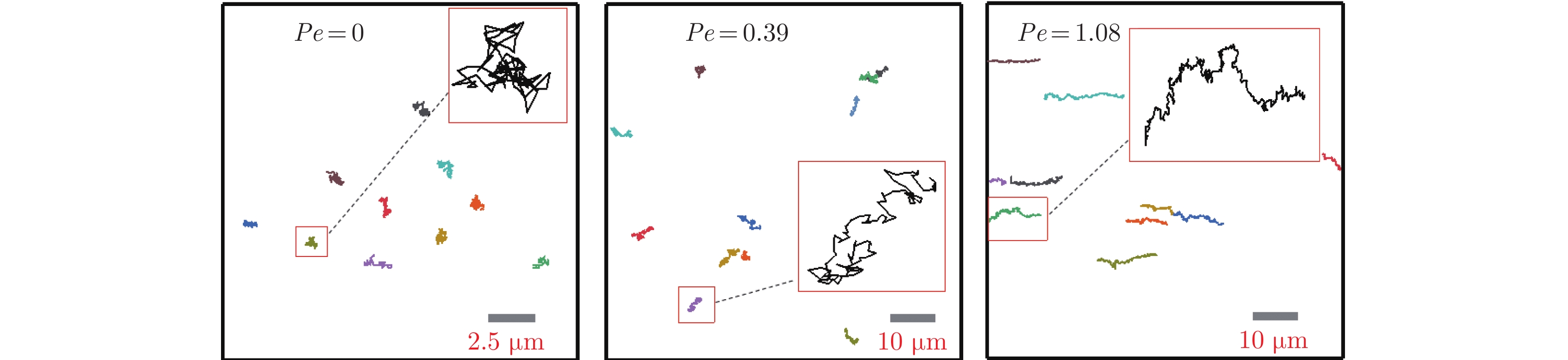
图5展示了纳米粒子在3种Pe下的代表性运动轨迹。本文聚焦探索Pe～O(1)条件下流动对扩散的影响，实验中的平均流速v及对应的Pe见表1。可以看出，无流动状态（Pe = 0）下，纳米粒子进行布朗扩散，运动轨迹呈现无规则随机特性^[23-24]。有流动状态下，纳米粒子在跟随流体流动的同时亦发生自由扩散：当流动速度极低（Pe = 0.39）时，纳米粒子自由扩散仍占主导地位，可观察到微弱的粒子定向运动；当流体流动速度增大，Pe = 1.08时，纳米粒子运动轨迹已展现出显著的流动跟随现象。以上现象表明，即使在Pe～O(1)范围内，随着直通道中PEO溶液流速增大，纳米粒子的流动跟随现象愈加明显。

图  5  3种Pe下的纳米粒子运动典型轨迹

Fig.  5  Typical trajectories of individual nanoparticles at three Pe

下载: 全尺寸图片 幻灯片

表  1  实验中的平均流速与Pe的对应关系

Table  1  Corresponding relationship between average flow velocity and Pe in experiment

流速v/(μm·s−1)	Pe
1.9 ± 0.12	0.39
4.9 ± 0.17	1.08
1.8 ± 0.07	3.69

下载: 导出CSV 

| 显示表格

2.2   均方位移

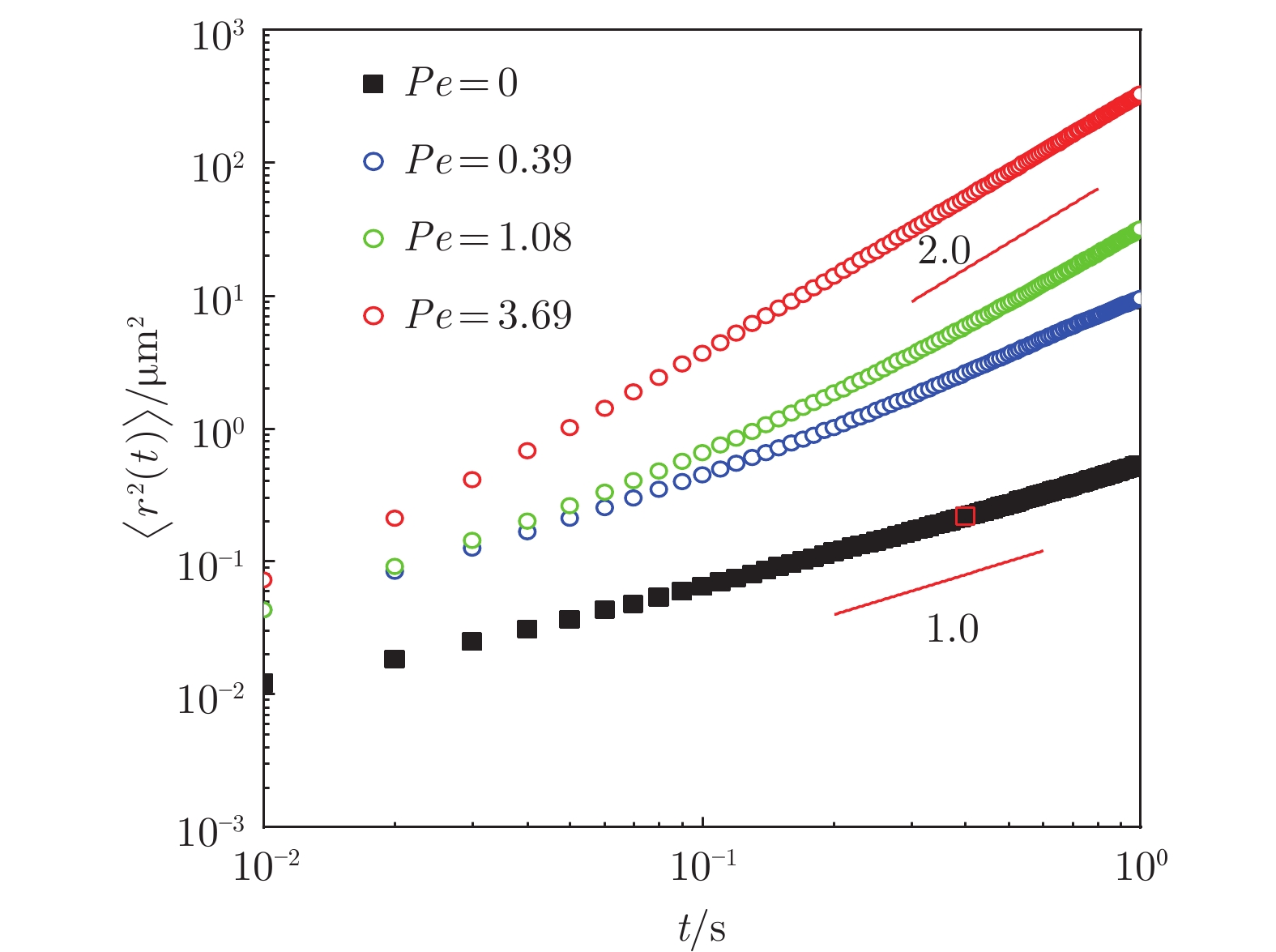
首先对纳米粒子运动的系综均方位移$\langle$r²(t)$\rangle $进行定量分析。图6展示了对数坐标系中不同Pe条件下$\langle$r²(t)$\rangle $随时间变化曲线。可以看出，无流动状态（Pe = 0）下，$\langle $r²(t)$\rangle $～t^β，斜率β = 1.0，表明纳米粒子进行正常（布朗）扩散。在有流动状态下：当Pe = 0.39时，可观察到$\langle $r²(t)$\rangle $的值明显增大，斜率β微弱增大；当流动速度增大，Pe = 1.08时，$\langle $r²(t)$\rangle $斜率明显增大；当Pe = 3.69时，$\langle $r²(t)$\rangle $的值和斜率均有显著增大，且斜率β > 1。上述结果表明，微尺度流动下复杂介质中纳米粒子的运动有所增强，纳米粒子运动的$\langle$r²(t)$\rangle $随着Pe增大而增大，并呈现“超扩散”现象（β > 1）。这些结果与已有实验报道一致^[25-26]。

图  6  不同Pe下纳米粒子运动的e–MSD曲线

Fig.  6  e–MSD curves of nanoparticle motion at different Pe

下载: 全尺寸图片 幻灯片

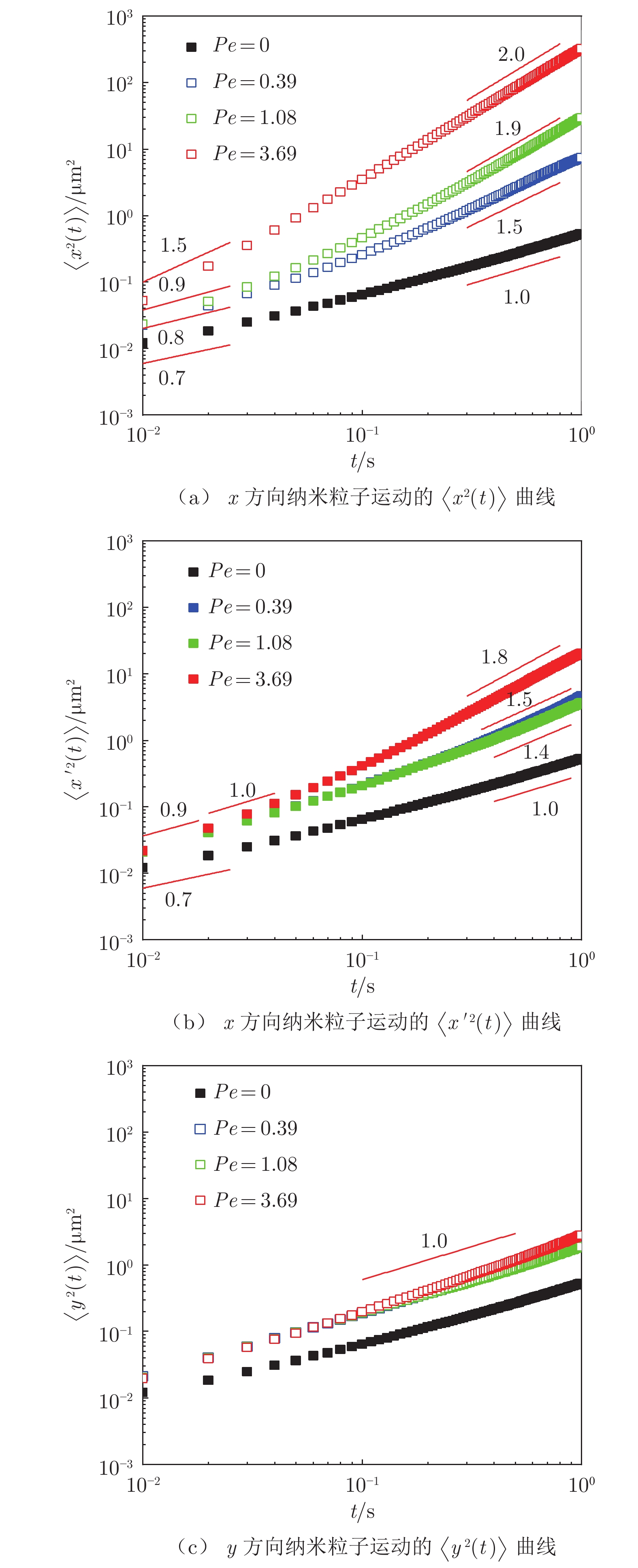
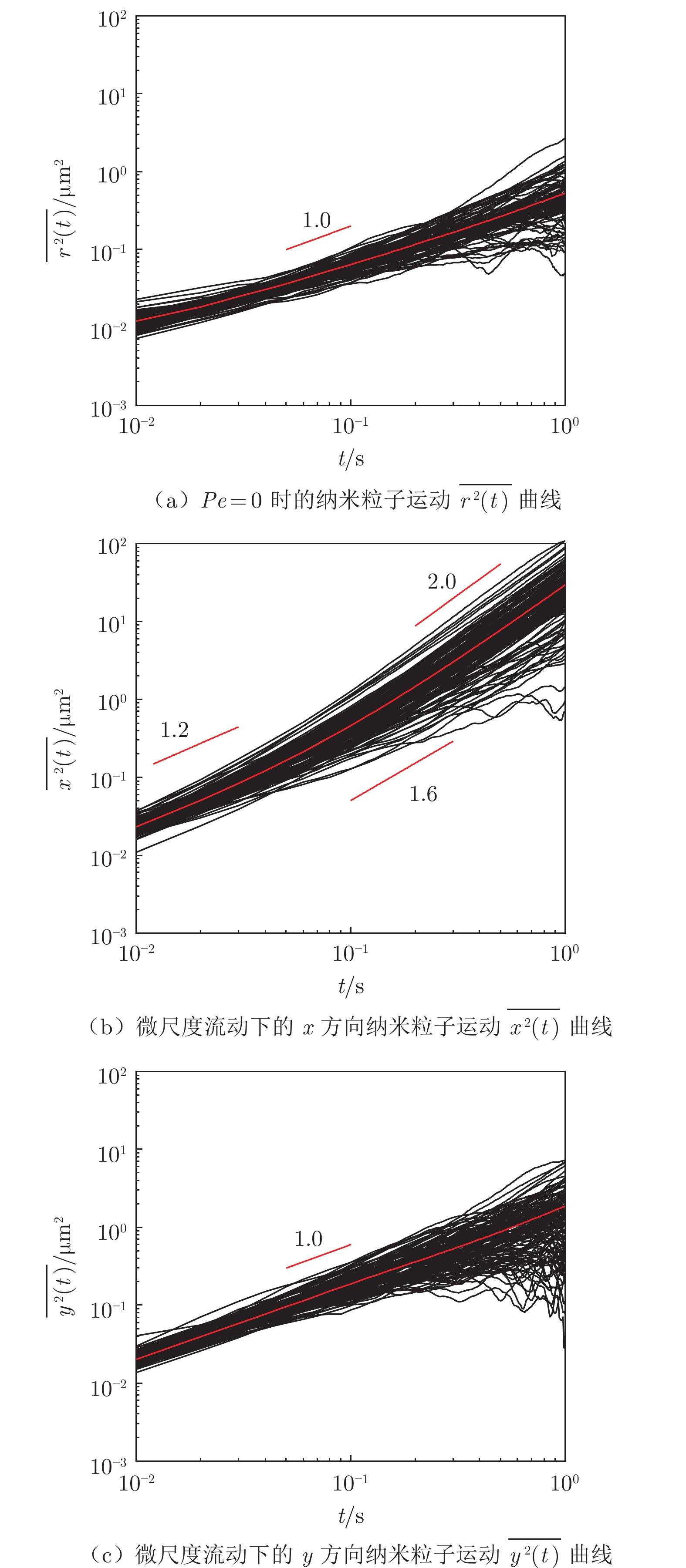
进一步研究粒子运动的系综均方位移，分析微尺度流动对纳米粒子扩散的影响。图7（a）展示了x方向粒子运动的e–MSD（$\langle $x²(t)$\rangle $）曲线。不同于静态条件下e–MSD曲线的“次线性（β = 0.7）—线性（β = 1.0）”两阶段转变，流动条件下的e–MSD曲线呈多样性变化，且与Pe有关。当Pe = 0.39、Pe = 1.08时，e–MSD曲线呈现“次线性（β < 1）—线性（β = 1）—超线性（β > 1）”三阶段变化；当Pe = 3.69时，e–MSD曲线在所考察时间内均呈现出超线性现象（β = 1.5～2.0）。

图  7  不同Pe下的纳米粒子运动e–MSD曲线

Fig.  7  e–MSD curves of nanoparticle motion at different Pe

下载: 全尺寸图片 幻灯片

将x方向的流动信息去除后，可以得到相应的$\langle $$x{'^2}(t)$$\rangle $曲线，如图7（b）所示。对比图7（a）和（b）可以看出，3种Pe条件下$\langle $$x{'^2}(t)$$\rangle $均呈现“次线性—线性—超线性”三阶段变化，但斜率β相较$\langle $x²(t)$\rangle $均有明显减小。这种减小反映了流动信息去除的效果。

相关研究表明，在短时间尺度上，次线性现象与PEO溶液中非均匀结构的限制有关^[27-28]。在静态条件下，PEO溶液浓度较大时（c > c*），PEO分子链缠结成网络结构，纳米粒子的短时间运动会受到网络结构的限制，呈现受限次扩散现象^[29]。均方位移转变为正常扩散的时间与高分子溶液的弛豫时间相关。

在本文研究中，均方位移转变为正常扩散的时间约0.4 s（在图6中用红点标出）。高分子溶液弛豫时间τ_rep可根据理论公式${\tau _{{\rm{rep}}}} = {\tau _0}[{N^3}/ {Ne}(1)]{c^{3(1 - f)/(3f - 1)}}$计算，其中：常温下 PEO 单体的松弛时间τ₀ ≈ 0.2 ns；Ne(1)为高分子溶液中一个缠结链段在熔体中的 Kuhn 单体个数，对于 PEO，Ne(1) ≈ 14；Flory系数f ≈ 0.6；整条高分子链上的 Kuhn 单体个数N = M_w/M₀，PEO 的 Kuhn 单体的摩尔质量M₀ = 140 g/mol。经计算，高分子溶液弛豫时间约为0.24 s。这种局部限制效应会随着时间增长逐渐消失，纳米粒子运动在长时间尺度上呈现为正常扩散，其扩散系数可由斯托克斯–爱因斯坦公式预测^[30-31]。

在流动条件下，流动剪切会使流动方向上高分子网络特征尺寸发生变化，对纳米粒子运动的限制减弱，导致短时间尺度上次线性现象减弱（图7（b），β = 0.9 > 0.7）。需要指出的是，长时间尺度上的“超扩散”现象是由流动信息去除不完全所导致。在有限宽高比的微通道流动中，通道宽度方向的流速呈抛物线分布。本研究在去除流动信息时采用平均流速，故单个粒子运动的实际流动分量并未完全去除。图7（c）展示了y方向上粒子运动e–MSD曲线。可以看出，3种Pe条件下的e–MSD曲线均与时间呈线性相关（β = 1.0），但其β值较静态条件下有一定增大，表明流动垂直方向上的运动有所增强，这也与流动引起的PEO网络限制减弱相关，流动分量一定程度上削弱了高分子网络对纳米粒子的限制。由流体流动的连续性方程可知，微通道流动并非一维流动，y方向也必然存在流动分量，导致y方向纳米粒子输运增强。此外，当前研究结果显示这种增强与Pe的相关性极弱，这可能是由实验系统及测量误差所致，有待进一步开展系统研究。

2.3   位移概率分布与非高斯系数

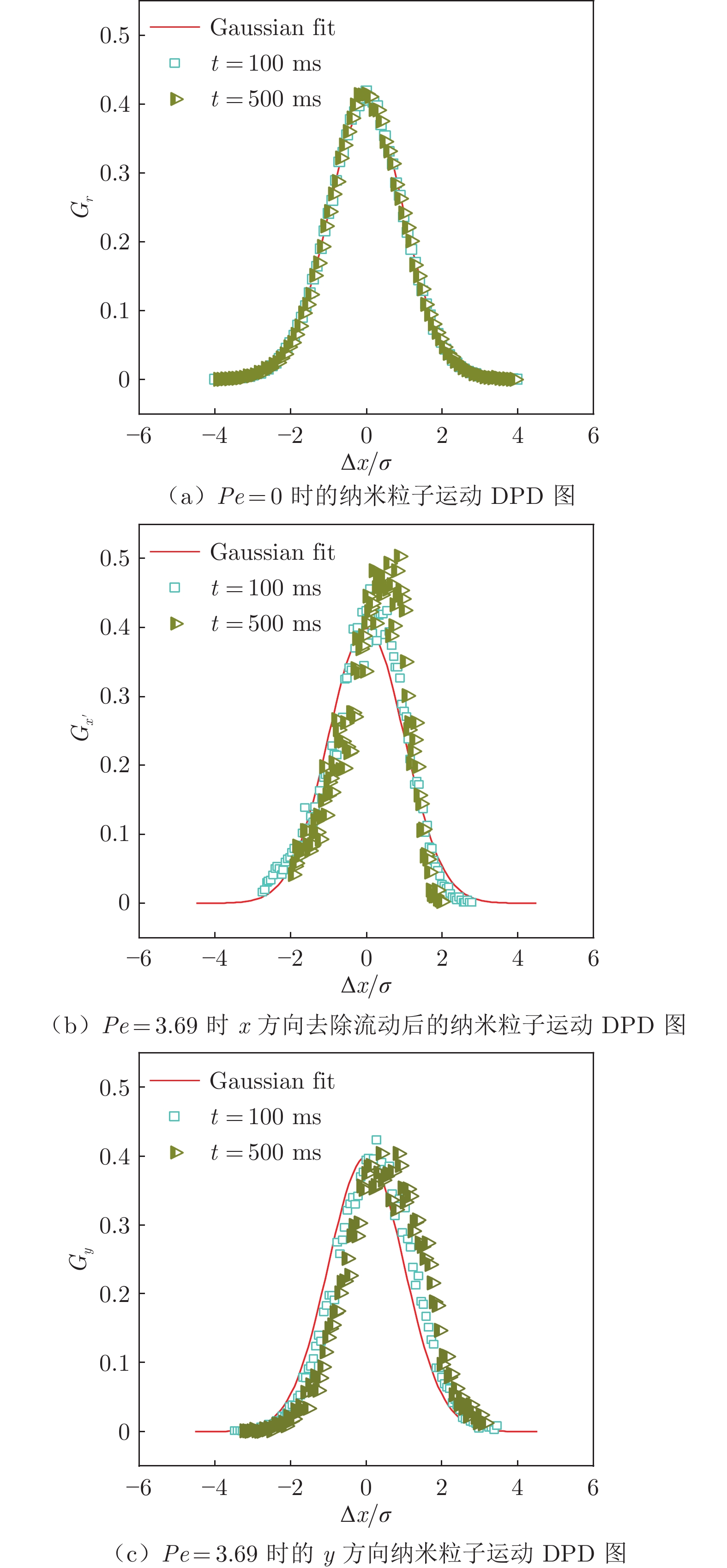
考察纳米粒子运动的位移概率分布（DPD）及非高斯特性，从微观尺度进一步分析微尺度流动对扩散运动的影响。在静态条件下，纳米粒子运动的DPD基本符合标准高斯分布，如图8（a）所示，该结果与已有文献研究结果一致^[32-33]。图8（b）和（c）分别给出了Pe = 3.69时去除流动信息后x方向和y方向运动分量的DPD。结果表明，2个方向上运动分量的DPD均不符合高斯分布，且具体特征也有所不同：x方向DPD的非高斯特征主要表现为小位移概率增大，大位移概率减小；y方向DPD的非高斯特征主要表现为概率分布整体向右平移，且时间越长越明显。

图  8  流动条件下的典型纳米粒子运动DPD图

Fig.  8  Typical DPD diagram of nanoparticle motion under flow conditions

下载: 全尺寸图片 幻灯片

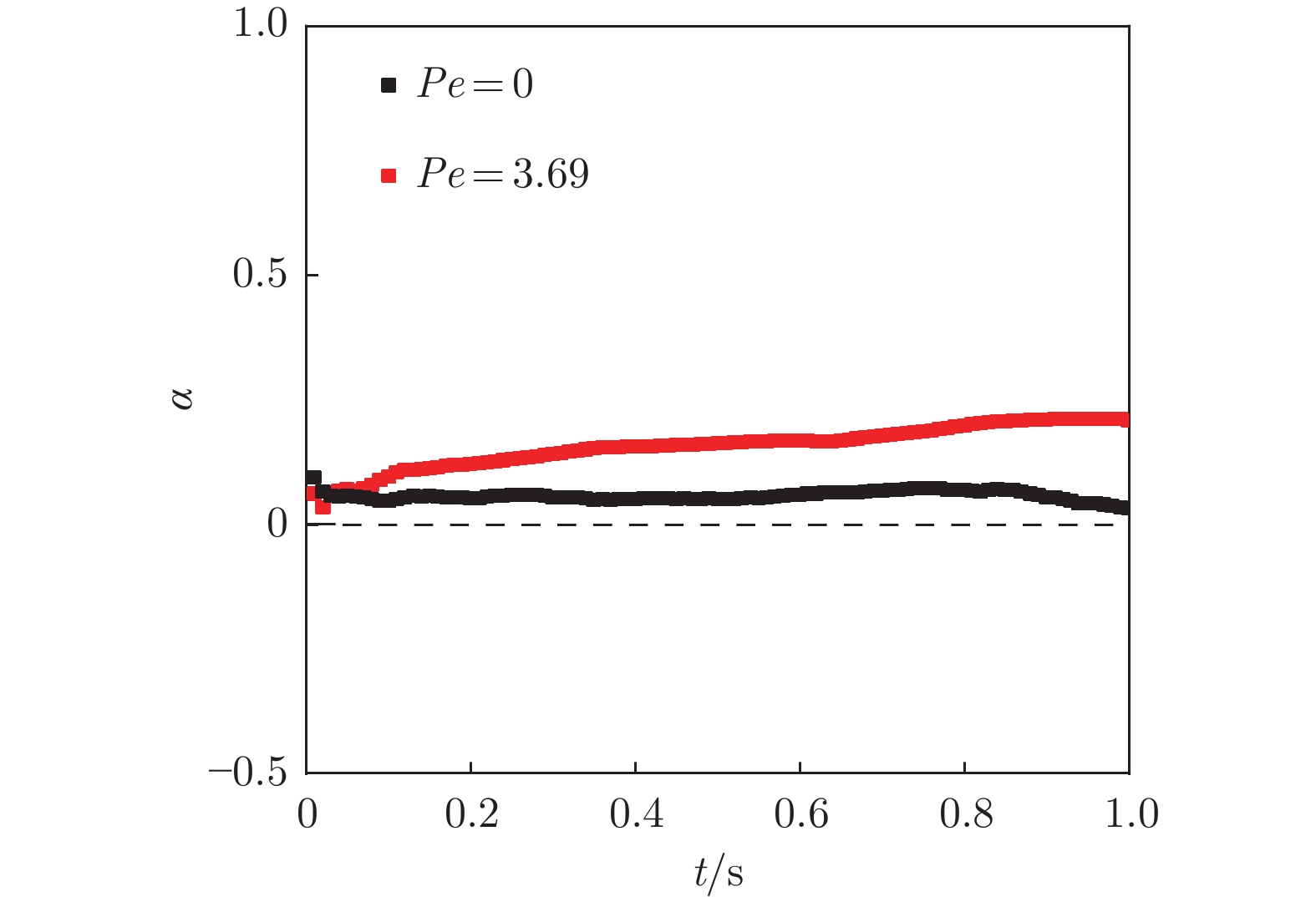
流动方向上的位移概率分布变化表明，流动在影响PEO网络特征尺寸的同时减缓了高分子链的松弛过程，增强了对纳米粒子运动的限制，小位移运动概率增大；而垂直于流动方向的位移概率分布明显偏离高斯分布，反映了前文所述y方向实际存在的流动对PEO网络结构的影响。图9进一步对比了流动和静态条件下纳米粒子运动在流动方向上的非高斯系数α。非高斯系数α是定量衡量一个分布偏离标准高斯分布程度的表征参数，α = 0时，纳米粒子呈高斯运动。结果显示，Pe = 3.69时的非高斯系数比静态条件下显著提高，表明在该条件下存在更为强烈的局部非均匀限制，从侧面验证了流动剪切减缓了PEO高分子网络松弛的推论。

图  9  纳米粒子运动的非高斯系数随时间的变化典型曲线

Fig.  9  Typical curves of non-Gaussian coefficients of nanoparticle motion with time

下载: 全尺寸图片 幻灯片

2.4   非遍历特性

对纳米粒子的时间平均均方位移$ \overline {r^2{{(t)}}} $进行分析。图10中弥散分布的黑色曲线为t–MSD曲线，单条红色曲线为相应的e–MSD曲线。对比图10（a）和（b）可以看出，在流动方向（即x方向）上，纳米粒子的$ \overline {r^2{{(t)}}} $及其斜率均比静态条件下明显增大，且弥散分布增强。对比图10（a）和（c）则可看出，在与流动垂直的方向（y方向）上，$ \overline {r^2{{(t)}}} $近似于静态扩散运动的均方位移，但长时间尺度上的弥散分布有一定增强。这些结果进一步表明，微尺度流动条件下，PEO分子网络会受到流动剪切的影响^[34]，继而影响纳米粒子的运动特性。

图  10  流动条件下的典型纳米粒子运动t–MSD曲线

Fig.  10  Typical t–MSD curve of nanoparticle motion under flow conditions

下载: 全尺寸图片 幻灯片

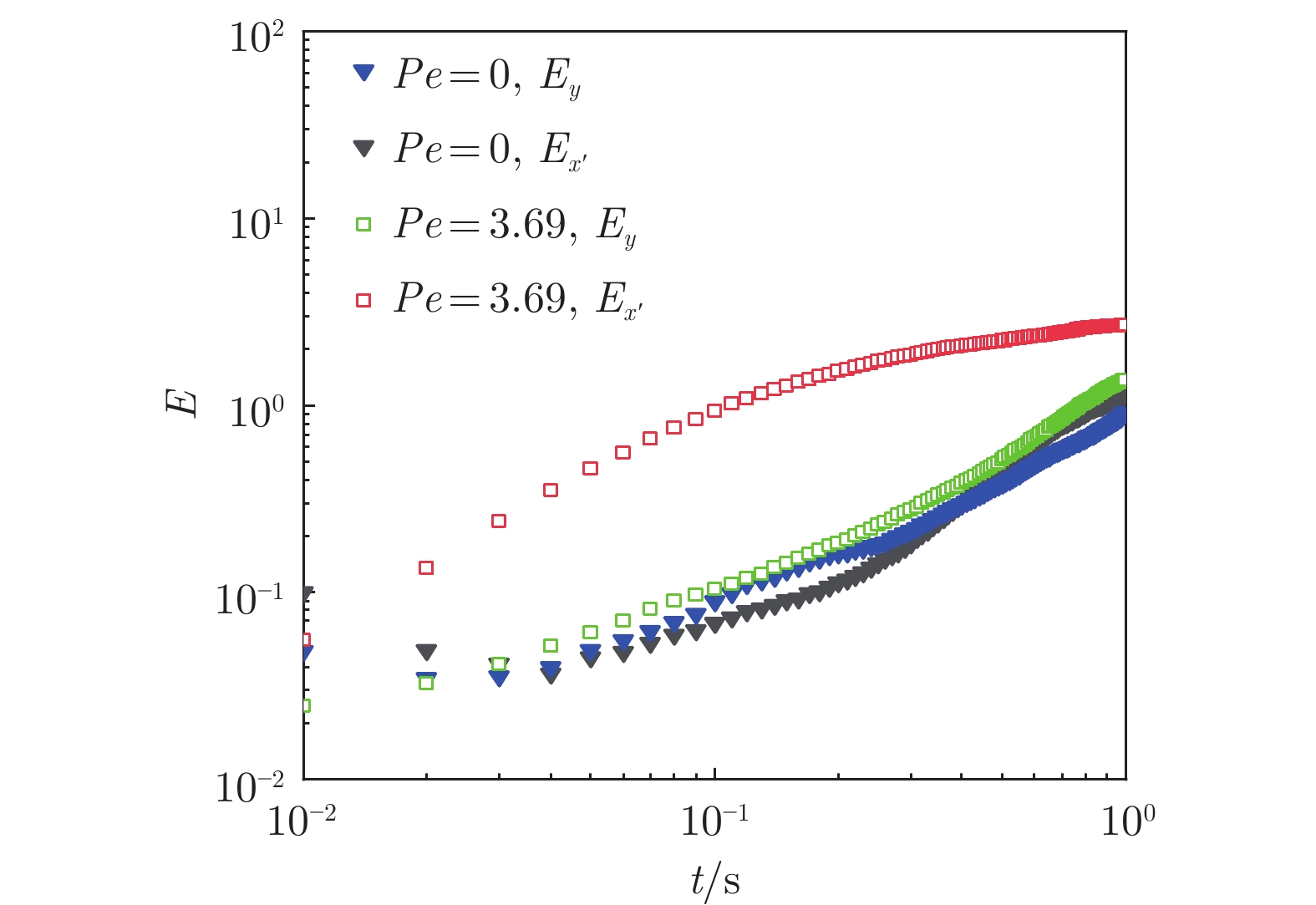
t–MSD曲线与e–MSD曲线的不一致性反映了PEO溶液的非遍历特性。非遍历特性可用遍历性破坏参数E来表征^[35]：E = 0意味着遍历，即时间平均与系综平均特性完全一致，均匀介质（如水）满足这一特点；E越大则意味着非遍历性越强。图11展示了流动信息去除后x和y方向上的E随时间的变化。与静态条件下的遍历性破坏参数相比，流动垂直方向的E_y略增大，流动方向上的E_x'显著增大。这些结果进一步揭示了微尺度流动对PEO溶液结构特性的影响。对纳米粒子而言，流动方向上PEO溶液的无序、非均匀性显著增大，而垂直于流动方向上的溶液性质与静态条件下近乎相当。此外，E随时间的变化与非高斯系数随时间变化趋势一致，说明在流动影响下，纳米粒子扩散的非遍历性与非高斯性高度相关^[36]。

图  11  去除流动分量后x和y方向上纳米粒子运动遍历性破坏参数随时间变化的典型曲线

Fig.  11  Typical time-varied curves of ergodicity breaking parameters of nanoparticle motion at x and y axes under the condition of removing flow information

下载: 全尺寸图片 幻灯片

3   结论与展望

采用微流控技术构建了直通道中PEO溶液微尺度流动环境，利用粒子追踪技术测量了纳米粒子的运动，基于统计特征量表征纳米粒子的运动特性，发现复杂流体的微尺度流动对流动方向和垂直于流动方向上的纳米粒子扩散运动均产生显著影响，主要结论如下：

1）流动方向上的纳米粒子运动为布朗运动与微尺度流动效应的叠加，呈现次扩散、正常扩散和超扩散等3种特征；垂直于流动方向上的纳米粒子运动呈现正常扩散特征，但其扩散系数相较于静态条件下有显著提高。

2）在流动方向上，纳米粒子扩散的非高斯特征主要表现为小位移概率增大，大位移概率减小；在垂直于流动方向上，则主要表现为概率分布整体向右平移。

3）高分子溶液中的微尺度流动对纳米粒子扩散的影响来源于高分子网络结构及其动力学特性的改变。在流动方向上，剪切流动减缓高分子网络结构的松弛，增强高分子溶液的非遍历特性，导致非高斯特性增强；在垂直于流动的方向上，流动分量削弱了高分子网络对纳米粒子的限制，导致扩散系数有所提高。

本文工作可为解读生理介质中的纳米粒子输运机制及纳米药物设计与输运增强应用提供参考。未来可进一步优化设计，采用微流控阻力通道和压力泵精准控制流动，量化考察微尺度流动对高分子网络结构的影响。