0   引　言

激波/边界层干扰广泛存在于超声速、高超声速飞行器内外流场中，影响着飞行器的流量捕获、总压恢复、气动力热载荷等关键指标^[1]。对进气道而言，激波/边界层干扰问题若处理不当，将在进气道内引发显著的流动分离，偏离设计工况，甚至发生进气道喘振^[2]。在侧压式或内转式进气道中，由进气道内侧面诱导的斜激波在进气道内相交形成交叉激波，进而与进气道底部边界层发生复杂三维干扰，形成大尺度涡结构。这种干扰会增加进气道总压损失，加剧流场畸变，还会引起局部高热流区域的出现。因此，需要针对此类三维激波/边界层干扰问题开展深入的流动机理及控制方法研究。

2块安装于平板上的垂直楔构型是研究上述三维激波/边界层干扰问题的一个典型构型。国内外学者针对该构型的激波/湍流边界层干扰问题开展了深入实验和计算研究^[3-9]。Zheltovodov等^[6-8]分别在俄罗斯科学院西伯利亚分院理论与应用力学研究所T–333超声速风洞和德国宇航院（DLR）Ludwig管内对6种对称/非对称垂直楔构型开展了详细试验，给出了壁面压强、油流图谱、热传导系数和摩阻系数的分布。基于大量试验数据，Zheltovodov等^[8-9]结合油流显示技术和数值模拟方法，给出了双垂直楔交叉激波/湍流边界层干扰随着楔角增大由弱到强的干扰模式及各种干扰模式下的流场结构。

在真实飞行条件下，当飞行高度和马赫数较高时，边界层在与交叉激波干扰前仍可能保持为层流状态。在激波的逆压梯度作用下，边界层很有可能发生转捩，形成激波/转捩边界层干扰。在这种情况下，一方面，激波扮演着扰动触发者的角色，能够提前触发转捩；另一方面，当转捩发生于干扰区时，不稳定性的发展使得层流间的动量交换增加，对干扰流场结构产生极大影响^[10]。

Knight等^[11]系统回顾了1993年后的高超声速激波/转捩边界层干扰研究：针对激波/转捩边界层干扰的研究主要采用风洞试验和直接数值模拟（DNS）方法开展，研究对象包括压缩拐角、带扩张角的轴对称构型、安装于平板上的圆柱构型以及入射激波/平板边界层干扰问题。在超声速领域，相关研究也以入射激波/平板边界层干扰^[12-13]、机翼激波/边界层干扰^[14]和压缩拐角^[15]等问题为主。高超声速条件下的多个试验结果均表明，转捩干扰会导致比层流干扰或湍流干扰更高的热流峰值^[11]，这就使实际热载荷可能超出采用层流或湍流模型得到的评估值，给飞行器带来安全隐患。

国内的激波/转捩边界层干扰研究主要针对压缩拐角构型。武宇等^[16-17]采用NPLS和PIV技术获得了马赫数3时不同拐角角度下来流边界层为层流、转捩和湍流状态的干扰区近壁流场结构。童福林等^[18-21]采用直接数值模拟方法对马赫数2.9来流条件下压缩拐角中的激波/转捩边界层干扰进行了研究，结果表明拐角内的干扰加速了转捩过程，转捩干扰在干扰区内的强湍动能和高雷诺剪切应力使其局部峰值摩阻系数高于湍流干扰。解少飞等^[22]针对马赫数8来流条件下的压缩拐角开展了试验测量，研究结果表明，当转捩发生于分离区时，转捩脉动与分离泡脉动的相互作用会诱导出更高的脉动能量。

综上所述，激波/转捩边界层干扰研究主要还是针对压缩拐角、安装于平板上的圆柱构型和入射激波/平板边界层干扰，而对于更为复杂的双垂直楔交叉激波与转捩边界层的三维干扰，目前尚无相关研究。本文结合风洞试验和数值模拟，对马赫数3.0来流条件下交叉激波与转捩边界层的干扰开展研究，测量干扰区的壁面热流和压力，获取流场中的纹影照片；基于湍流边界层抗逆压梯度能力明显强于层流的特点，采用在干扰区上游添加涡流发生器、粗糙带等控制措施，将边界层强制转捩为湍流，获得控制措施对激波/边界层干扰在壁面热流、压力分布及流场结构上的影响，进而验证控制效果。

1   试验模型、来流条件及测量方法

1.1   试验模型

试验模型几何构型如图1所示。一对斜劈角度为9°的垂直楔安装于尖前缘底板上，其前缘距底板前缘250 mm；两垂直楔尖的间距为100 mm，经过斜劈角压缩后，两楔相距65 mm。垂直楔高度为167 mm，沿流向长度为230 mm。底板尺寸为500 mm × 196 mm。图1还给出了Oxyz坐标系统，原点O位于垂直楔尖前缘连线的中点，x轴对应流动方向，y轴对应垂直于底板的方向，z轴垂直于xOy平面，由右手系确定。

图  1  垂直楔几何构型示意图

Fig.  1  Sketch of the geography of vertical wedges

下载: 全尺寸图片 幻灯片

1.2   来流条件

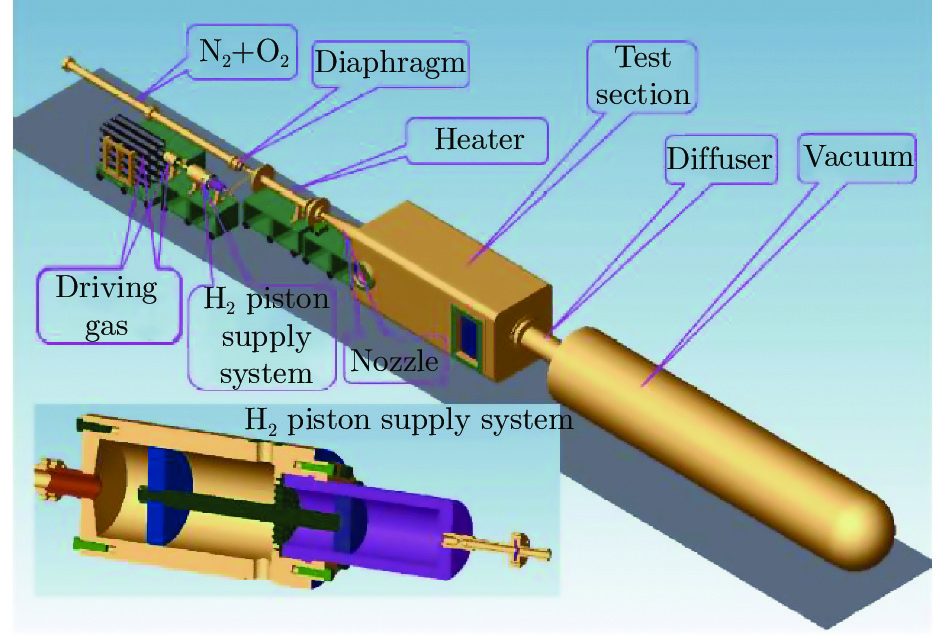
试验在中国空气动力研究与发展中心（CARDC）的Φ600 mm脉冲燃烧风洞中开展。该风洞^[23-24]主要由富氧空气管、稳压供氢装置、大口径快速阀系统、燃烧加热器、型面喷管（出口直径600 mm）、试验段、扩压器、真空箱等组成，如图2所示。试验采用马赫数3的喷管，有效试验时间约200～300 ms。具体来流条件见表1。

图  2  脉冲燃烧风洞示意图^[24]

Fig.  2  Sketch of pulse combustion wind tunnel^[24]

下载: 全尺寸图片 幻灯片

表  1  试验来流条件

Table  1  Freestream condition of the test

马赫数	总温 Tt/K	总压 pt/MPa	单位雷诺数 Re/(106 m−1)	来流组分摩尔比 O2∶N2∶H2O	比热比
3.0	1350	0.335	2.1	0.21∶0.56∶0.23	1.34

下载: 导出CSV 

| 显示表格

1.3   测量方法

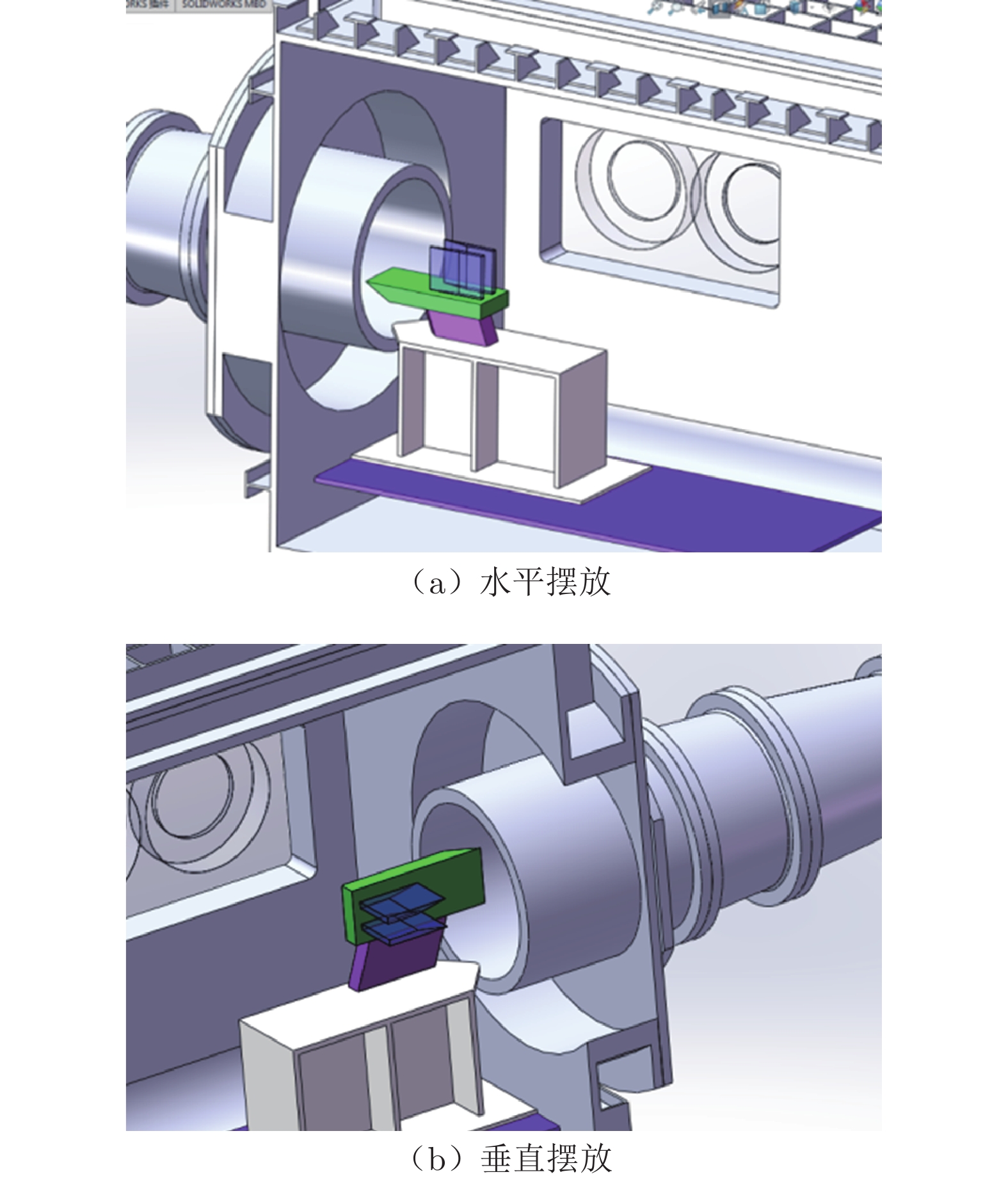
为在试验中获取尽可能多的测量数据，加工了2套相同的模型，分别对应2种摆放方式（如图3所示）：水平摆放时，底板为碳钢材料，通过壁面测量孔测量底板的热流和压力，垂直楔为玻璃材料，通过纹影测量其平行于中心对称面的流场；垂直摆放时，底板为玻璃材料，垂直楔为碳钢材料，通过纹影测量获取交叉激波位置。

图  3  试验中的2种模型摆放方式

Fig.  3  Two ways of placing the model during the test

下载: 全尺寸图片 幻灯片

热流测量采用E型同轴热电偶，热电偶直径为1.8 mm，材料为镍铬和康铜，对应的热扩散系数a分别为6.71和5.52 mm²/s。试验耗时t从有气流进入试验段至有效试验结束约400 ms，若采用半无限大假设，所需传感器长度$ l \geqslant 4\sqrt {at} =\, 6.55\;{\rm{mm}} $^[25]。本文采用的同轴热电偶长度为20 mm，可以采用半无限大假设进行数据处理。热流值采用下式求解^[25]：

式中：Q为热流值；t_n为第n个采样点对应的时刻；ρ、c、k_Q分别为热电偶材料的密度、比热容和导热系数；T_i为第i个采样点对应的温度值。

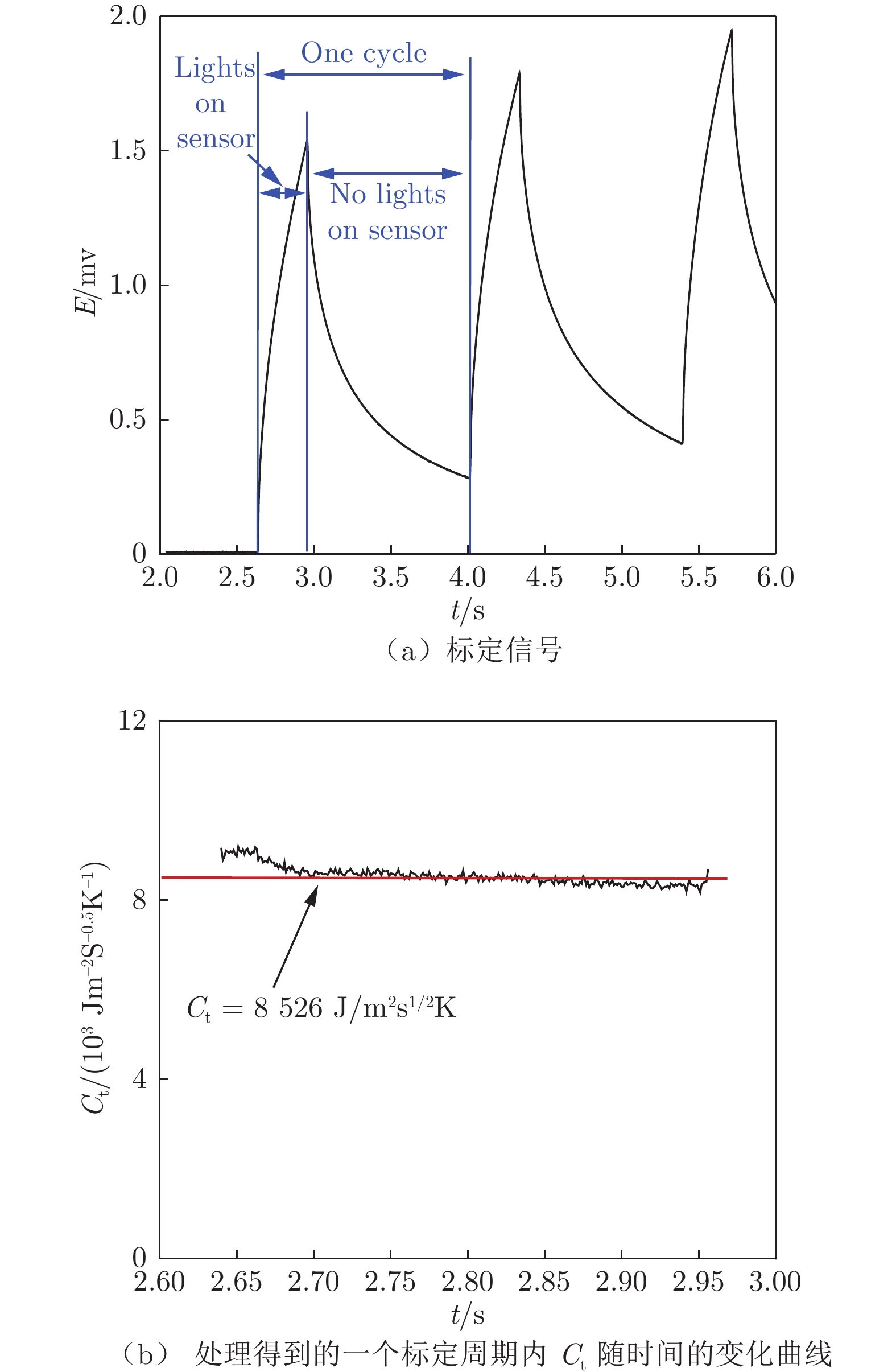
实际处理时，假设热电偶的系数C_t = $ \sqrt {\rho c{k_Q}} $为常数。试验前，采用激光标定系统对C_t进行标定。标定时，将稳定功率的激光对准热流传感器一段时间t（t与风洞有效试验时长相近，约300 ms）；以功率计获得激光功率，采集热电偶的电压信号，结合标准热电偶分度表，可得到热电偶表面温度随时间变化的数据；代入式（1），即可获得C_t的取值。

标定时的典型输出信号如图4（a）所示（纵轴为电压E）。基于该信号，处理得到不同t_n下的C_t的分布，如图4（b）所示。对不同t_n下的C_t取平均值，得到该热电偶的标定C_t。进行热流测量时，将标定得到的C_t和测得的热电偶表面温度随时间变化的数据代入式（1），即可得到Q(t_n)的分布。

图  4  E型同轴热电偶典型标定信号和标定结果

Fig.  4  Calibration signal and results of type E coaxial thermocouple

下载: 全尺寸图片 幻灯片

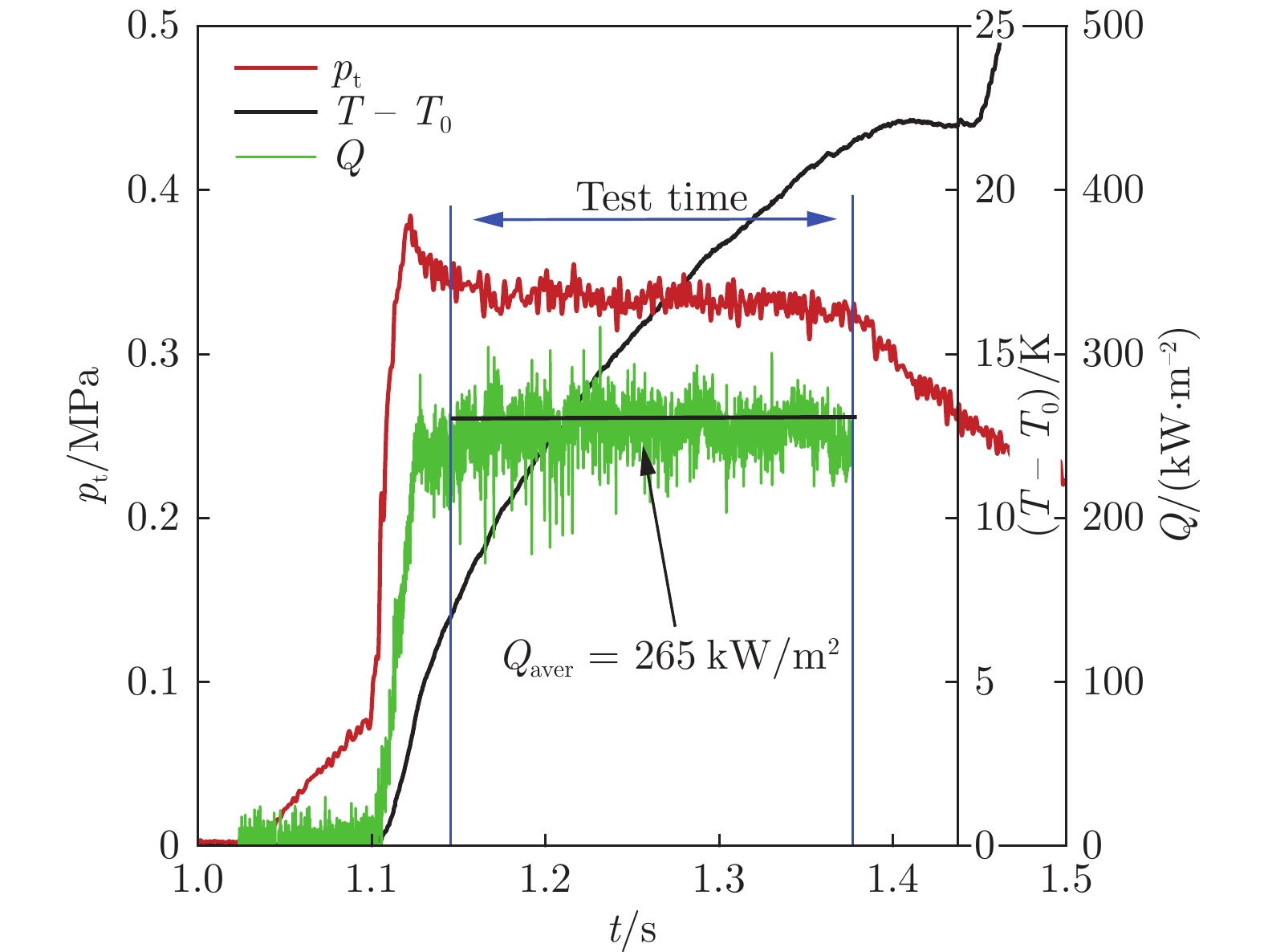
图5为试验期间的典型测量信号及处理后的热流值，T₀表示试验开始前的热电偶表面温度值。对有效试验时间内的热流值取平均，得到最终热流值Q_aver。标定和测量时的采样频率均为10 kHz。

图  5  试验期间的典型热流值

Fig.  5  Typical heat fluxes during test

下载: 全尺寸图片 幻灯片

2   计算方法及控制装置设计

2.1   数值计算方法

为与试验进行对比，获取更多流场信息，本文采用数值计算方法对试验工况进行了模拟。本文计算均采用CARDC开发的三维大规模并行CFD软件平台AHL3D^[26]开展。AHL3D采用基于网格平均的有限体积法离散求解可压缩Navier–Stokes方程组，支持完全气体、热完全气体及多组分化学反应的定常/非定常计算，支持两相流计算。定常时间推进采用LU–SGS方法，非定常计算则包括显式龙格–库塔法和隐式双时间步法。无黏通量采用重构–推进方法：重构采用三阶MUSCL重构或五阶WENO重构，推进可以采用Steger–Warming通量分裂、AUSM+、AUSMPW+和LDFSS等4种计算格式。黏性通量计算采用改进的Gauss定理。湍流模型包括k–ε、k–ω、TNT、BLS、SST等双方程湍流模型。近期发展了γ–Re_θt转捩模型^[27]、DES类方法^[28]和基于IDDES的转捩模式方法^[29]。此前，AHL3D已经应用于双垂直楔交叉激波/湍流边界层干扰的数值模拟研究，取得了与试验结果吻合较好的壁面压力结果^[30]，但干扰区壁面热流与试验结果存在一定差别，这是目前采用RANS方法计算该类复杂干扰存在的共性问题。本文的讨论有助于进一步加深对该问题的理解。

本文采用定常计算，研究了自然转捩和全湍流这2种状态：自然转捩状态计算时，采用γ–Re_θt转捩模型，设置来流湍流度为1.0%，来流黏性比μ_T/μ = 10；全湍流状态计算时，采用SST双方程湍流模型。无黏通量采用三阶MUSCL重构、AUSMPW+格式，气体热力学性质采用多组分热完全气体模型，气体组分及体积比参考表1设置，壁面设置为300 K无滑移等温壁。

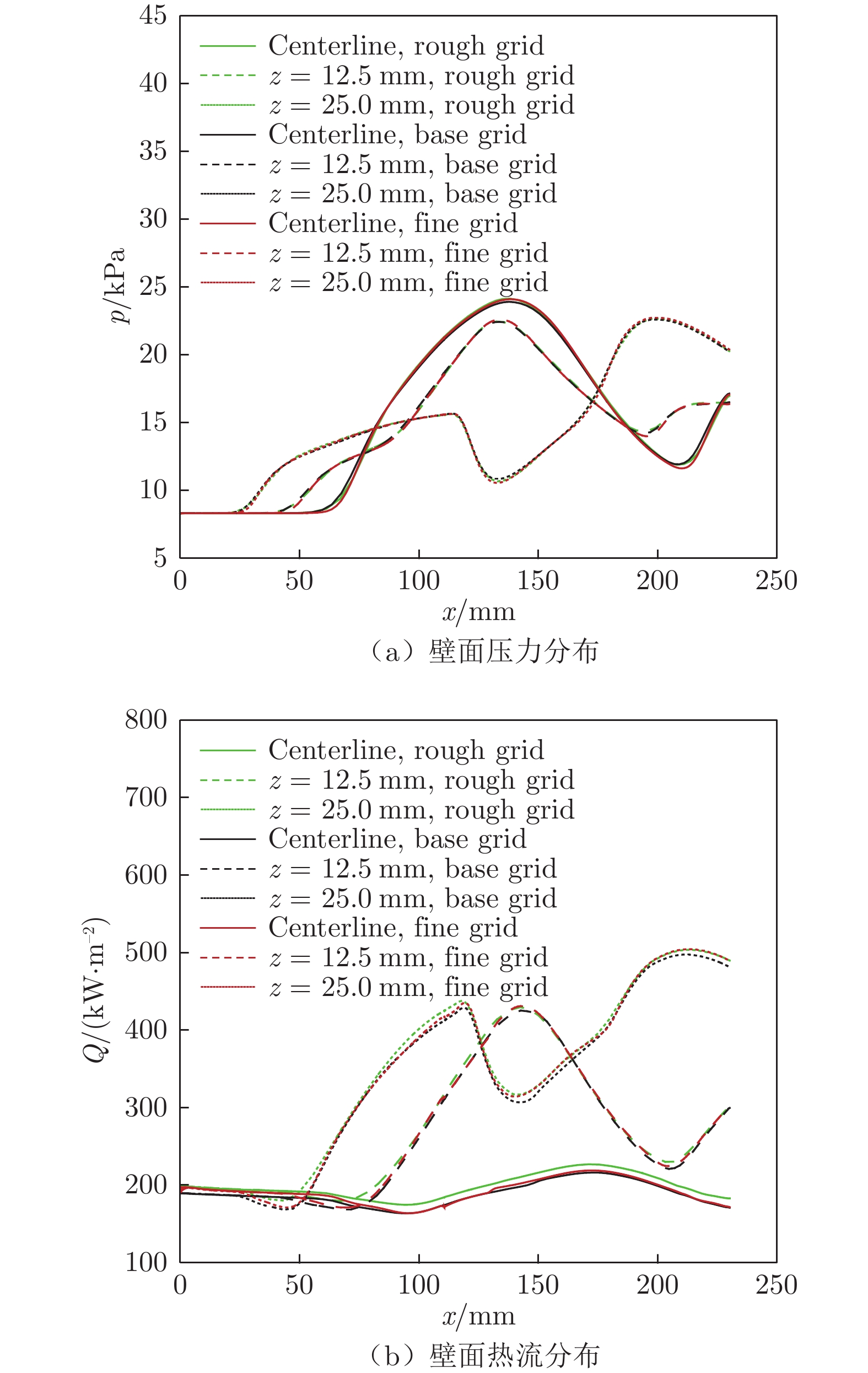
采用半模开展计算，中心对称面上采用对称边界条件，保持垂直壁面第一层网格距离小于0.002 mm，对应的y⁺小于1.0。计算前，对网格进行收敛性分析，采用SST湍流模型在3套结构网格上对试验工况开展了模拟。表2给出了x = 0 mm下游（垂直楔激波干扰区）流场的x、y和z方向网格数n_x、n_y和n_z。基准网格（base）在x = 0 mm下游流场的网格数为250万；粗网格（rough）在3个方向上分别将网格数降为基准网格的70%～75%，对应网格数为80万；细网格（fine）则是在基准网格的基础上在3个方向上进行了1.5～2.0倍加密，网格数增加至1090万。

表  2  x > 0区域x、y、z方向上网格数

Table  2  Grid numbers in x, y, z directions in the x > 0 area

网格	nx	ny	nz
粗网格（rough）	141	81	71
基准网格（base）	201	121	101
细网格（fine）	401	181	151

下载: 导出CSV 

| 显示表格

通过计算，得到了3个等z截面上的壁面压力和热流，如图6所示。从图中可以看到，3套网格得到的壁面压力曲线几乎完全重合，壁面热流最大差别小于8%，表明网格基本满足计算需求。后文均采用基准网格开展计算。

图  6  采用不同网格计算得到的壁面压力和热流分布

Fig.  6  Heat fluxes and pressure distribution calculated using different grids

下载: 全尺寸图片 幻灯片

2.2   控制装置设计

为将干扰区上游的边界层强制转捩为湍流，当模型水平摆放时，在干扰区上游设计加装了2种强制转捩装置，分别为粗糙带和斜坡型涡流发生器。粗糙带为20 mm × 100 mm的80目砂纸，粘贴于干扰区上游的底板表面，其前缘距底板前缘10 mm。

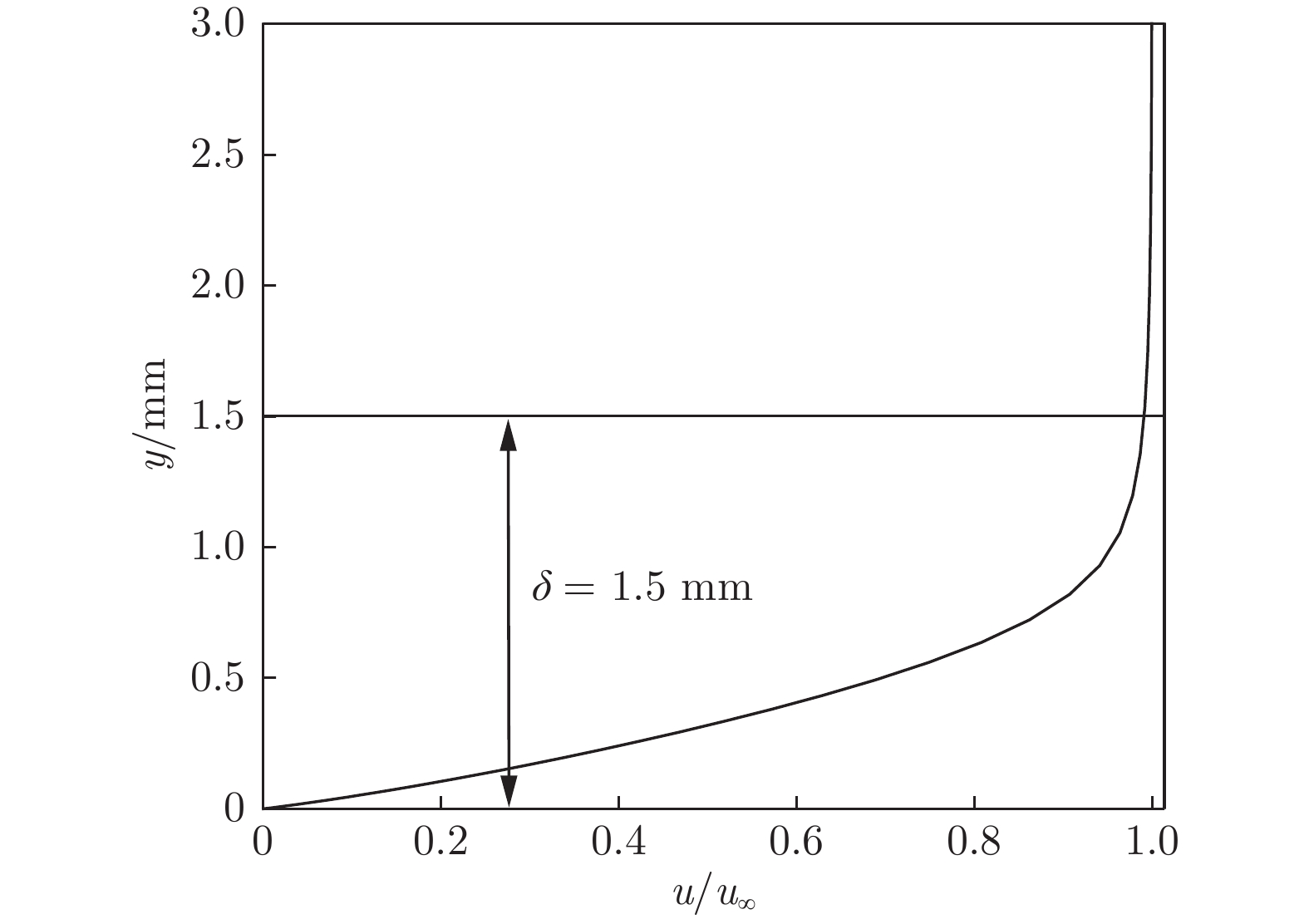
粗糙带具有较好的强制转捩效果，但实际使用中易损坏，因此还设计了斜坡型涡流发生器。从引入最小扰动达到最强控制效果的角度而言，涡流发生器安装位置不宜过于靠前（根据线性稳定性理论，雷诺数较小时，属于稳定流场，施加的扰动会不断衰减），也不宜过于靠后（被粗糙颗粒诱导出的流向涡对结构，需发展一定流向距离才能转捩为湍流），最终选定涡流发生器安装于x = –120 mm处（距底板前缘130 mm），如图1中的粉色线段所示。在风洞来流条件（表1）下，根据全层流条件下的数值评估，x = –120 mm处的层流边界层厚度δ约为1.5 mm，如图7所示。

图  7  计算得到的x = –120 mm处边界层内速度分布

Fig.  7  Velocity distribution of the x = –120 mm boundary layer by calculation

下载: 全尺寸图片 幻灯片

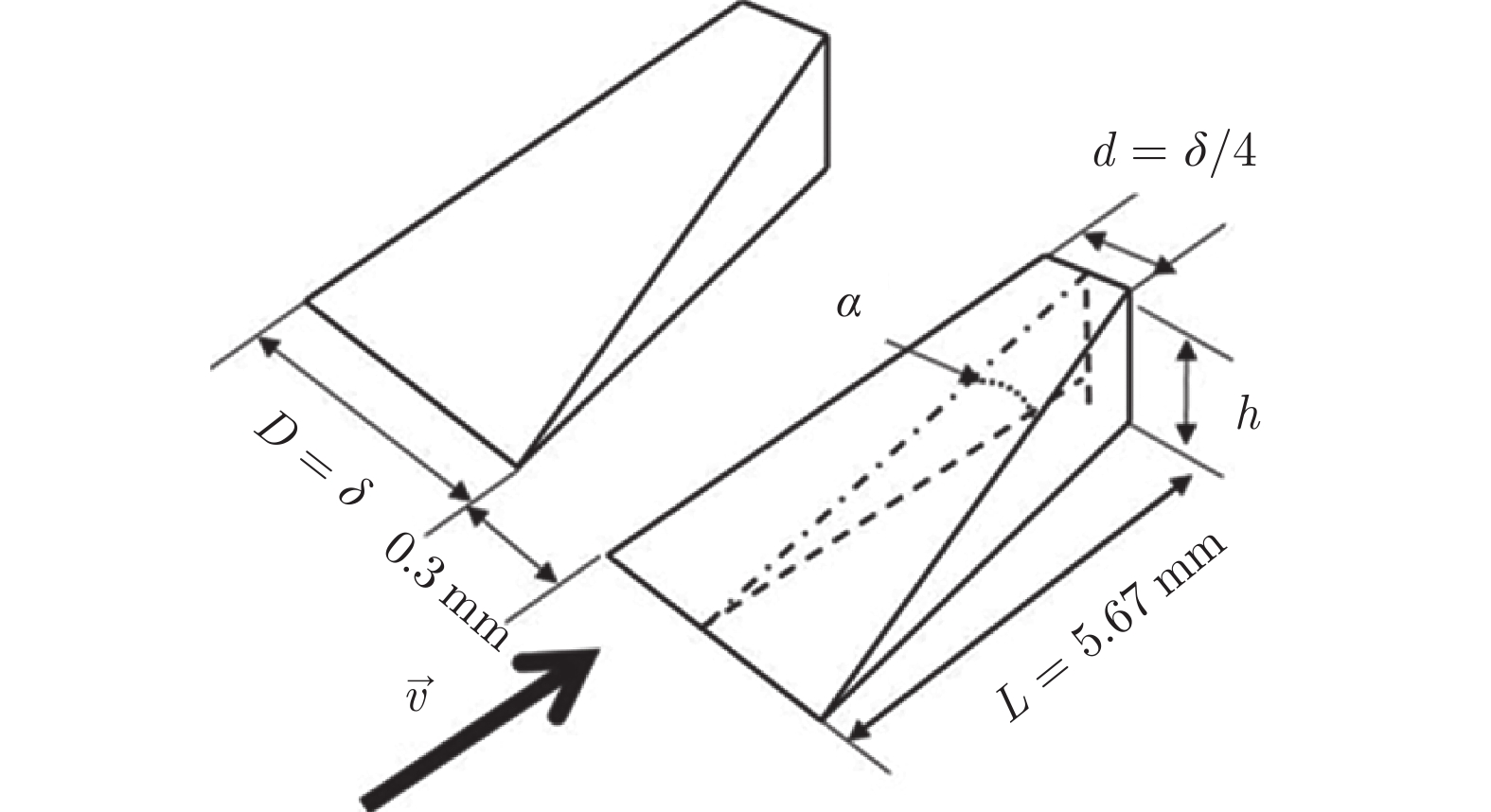
为使涡流发生器作用于所有进入干扰区的流体，其宽度设为约100 mm，由沿z方向展布的55个斜坡型粗糙颗粒组成（颗粒间距为0.3 mm）。斜坡型粗糙颗粒构型如图8所示，其高度h为最重要的几何参数，本文选取了2种高度：1.0 mm和1.5 mm，对应的h/δ分别为70%和100%（δ为边界层厚度）、斜坡角度α分别为10°和15°；长度L均为5.67 mm，宽度D均设置为D = δ = 1.5 mm。

图  8  斜坡型粗糙颗粒尺寸

Fig.  8  The geography of ramp vortex generators

下载: 全尺寸图片 幻灯片

3   结果分析

3.1   流场结构

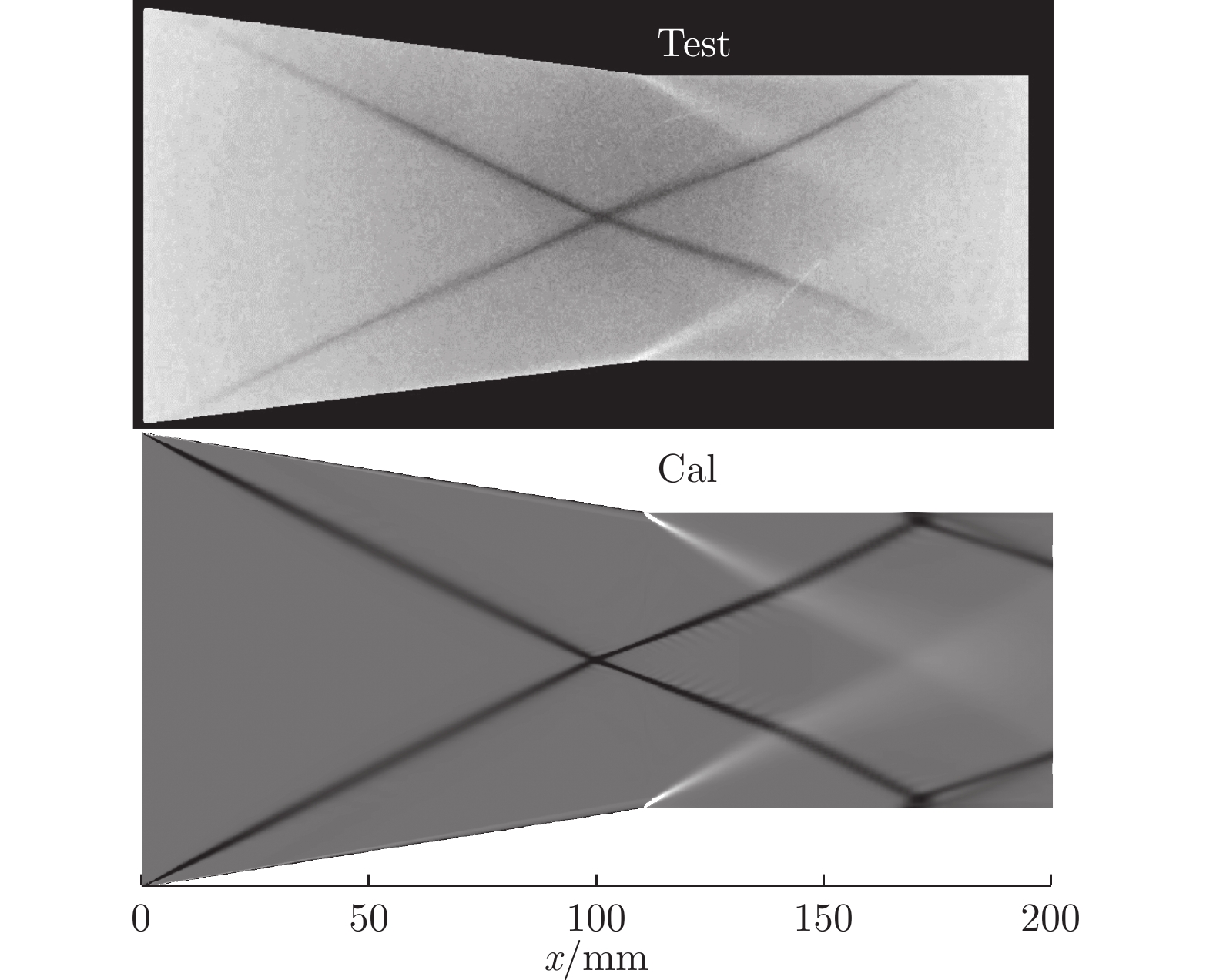
图9为试验得到的平行于底板的纹影图像与计算得到的数值纹影结果。数值纹影结果取自边界层外的无黏区。从图中可以看到：垂直楔诱导的2道斜激波在下游汇聚形成第一类激波干扰，垂直楔的拐角诱导出2道膨胀波结构；试验得到的激波结构基本对称，数值模拟和风洞试验得到的激波交汇点比较一致，均位于x ≈ 98 mm处；下游的激波膨胀波结构也基本一致。

图  9  计算和试验得到的激波结构

Fig.  9  Shock waves structures obtained by tests and simulation

下载: 全尺寸图片 幻灯片

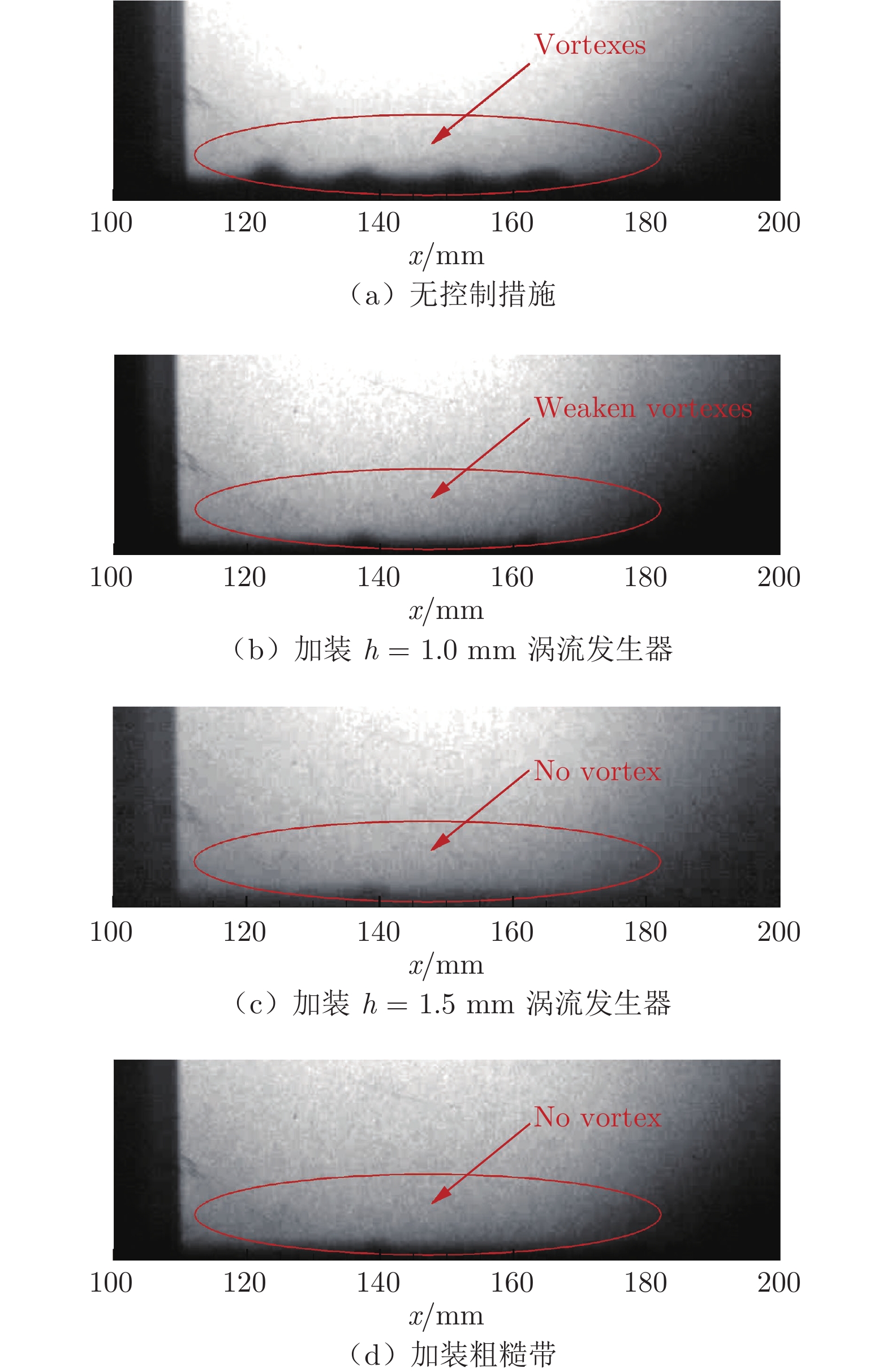
图10为试验测量得到的平行于中心对称面的纹影图像，纹影窗口最左侧对应垂直楔的拐角位置，即x = 110.4 mm位置。从图10可知：未施加控制时，边界层附近有较明显的涡结构；加装h = 1.0 mm的斜坡型涡流发生器后，边界层内的涡结构得到明显抑制；h增大至1.5 mm或在底板前缘加装粗糙带后，边界层内涡结构基本消失。图10表明：控制措施有效抑制了激波/边界层干扰诱导的涡结构。

图  10  试验测量纹影图像

Fig.  10  Schlieren maps during test

下载: 全尺寸图片 幻灯片

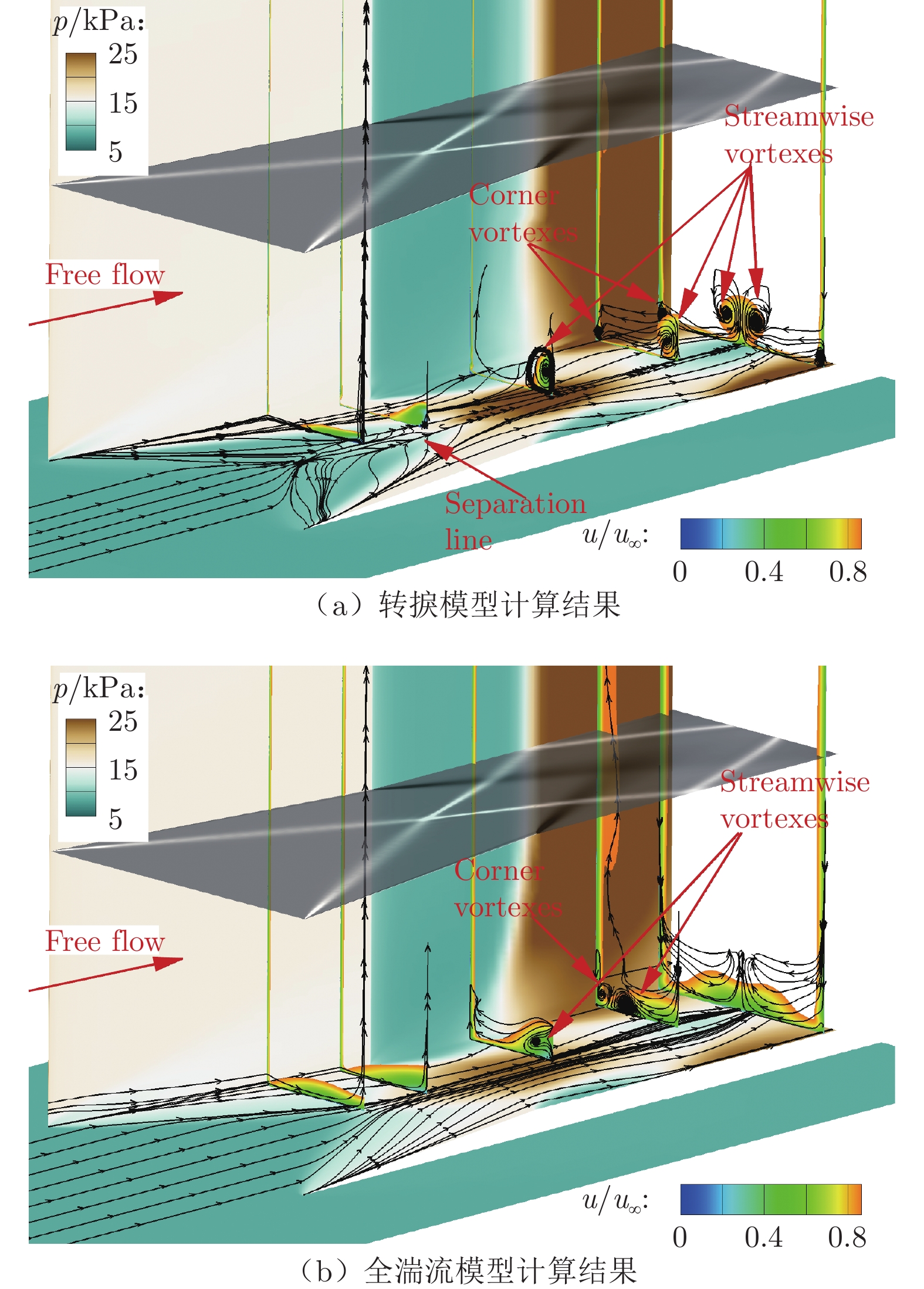
图11为采用转捩模型和全湍流模型计算得到的流场结构。图中给出了壁面压力及底板的极限流线、多个流向截面的速度云图及二维流线，灰度图为边界层外的激波结构。从图中可以看到：流体流过垂直楔尖后，向中心线汇聚，在交叉激波的干扰作用下，穿过激波后的边界层明显增厚（呈中心偏厚、两侧偏薄形态）。对于转捩边界层，与交叉激波干扰产生了复杂的三维分离与再附结构（图11（a）中的壁面极限流线）；经过垂直楔拐角后，中心线附近的边界层内形成了反向旋转的流向涡对；在向下游发展过程中，流向涡对不断增强，在更下游区域，底板与垂直楔侧壁相接的角区出现了明显的角涡。对于湍流边界层，虽然流体也在交叉激波作用下向中心线汇聚，但并未产生三维分离（图11（b）中的壁面极限流线）；垂直楔尖下游的流向涡对明显偏弱，且在向下游发展过程中逐渐偏离中心线区域，并在出口处基本衰减耗散。底板与垂直楔侧壁相接的角区的涡结构也在出口处基本消失。

图  11  计算得到的流场结构

Fig.  11  Flow field structures obtained by calculation

下载: 全尺寸图片 幻灯片

综上所述，无控制措施时，测量得到的流场结构与转捩模型计算结果更为吻合，在干扰区内产生了明显的分离涡结构；采取控制措施后，分离涡结构基本消失，与湍流模型计算结果基本吻合。

3.2   壁面热流

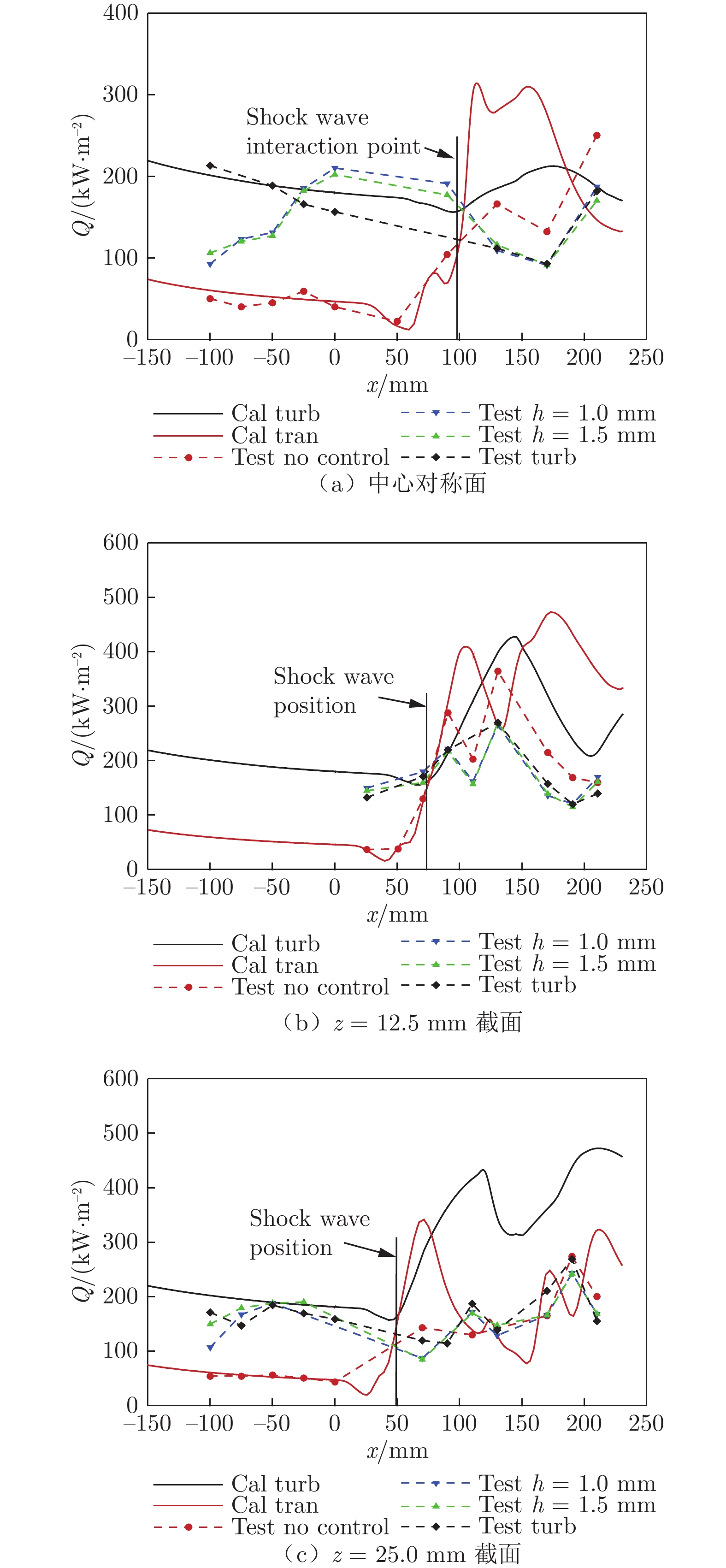
图12给出了对称中心线、z = 12.5 mm和z = 25.0 mm这3个截面的壁面热流分布。图中“tran”表示采用转捩模型得到的计算结果，“turb”表示在底板前缘加装粗糙带的试验结果或采用全湍流模型得到的计算结果。从图中可知：无控制措施时（“Test no control”），壁面热流在遇到激波干扰前一直保持为层流值；加装h = 1.0 mm或1.5 mm的斜坡型涡流发生器后，壁面热流从x = –100 mm处偏离层流状态并逐渐增大，直至达到x = 0 mm处的极大值，此时中心线上热流超过全湍流值，表明x = 0 mm处边界层已完全转捩为湍流；加装粗糙带（20 mm × 100 mm砂纸）后，边界层在x = –100 mm处即达到了全湍流值，表明加装粗糙带后，边界层完成转捩发生于x = –100 mm上游。在干扰区内，上述控制措施下获得的壁面热流分布基本保持一致，且上游的热流分布表明各控制措施均诱导边界层在干扰区上游达到了全湍流状态。因此，只要在干扰前将边界层诱导为充分发展的湍流状态，则无论采取何种强制转捩措施，对干扰区的热流影响均不大。在采取了控制措施的3个车次中，激波/湍流边界层干扰热流基本一致，表明风洞试验重复性良好。无控制措施时，热流在遇到交叉激波后急剧增大，甚至超过全湍流状态时的热流，表明在激波的逆压梯度作用下，边界层在干扰区迅速转捩为湍流。

图  12  试验与计算壁面热流分布对比

Fig.  12  Heat flux distributions obtained from test and calculation

下载: 全尺寸图片 幻灯片

图13给出了采用转捩模型得到的不同x–y截面的间歇因子γ分布。由于γ–Re_θt转捩模型本身的特点，在边界层外的无黏区γ均为1.0^[30]，因此必须通过边界层内的γ分布判断转捩位置。结合图13的间歇因子分布和图12的热流分布可以得到边界层转捩情况。在中心对称面和z = 12.5 mm截面上，采用转捩模型得到的壁面热流均在干扰区迅速增大并达到或超过全湍流值，这2个截面上边界层内的间歇因子也在x = 50 mm下游开始迅速由0增大至1，表明这两个截面的边界层转捩发生于干扰区内。对于z = 25.0 mm截面，壁面热流虽在第一道激波附近急剧增大，但在更下游区域却迅速下降且明显低于全湍流值；边界层内间歇因子也在第一道激波附近迅速由0增大至1，但在100 mm < x < 200 mm区域内，却又保持为明显小于1的值，表明该区域既非全湍流状态，也非全层流状态。这是由于受到侧壁拐角的扩张作用，在顺压梯度作用下，边界层在此处（100 mm < x < 200 mm）出现了再层流化的趋势，之后又在x > 200 mm区域再次转捩为全湍流。作为对比，图13还给出了z = 60 mm截面（非激波边界层干扰区）的间歇因子分布。从图中可知，由于未受到逆压梯度作用，边界层在x < 250 mm区域内一直保持为层流状态，表明干扰区内的转捩确实是由激波干扰导致的。

图  13  转捩模型计算得到的不同z截面γ分布

Fig.  13  Contours of γ in different z constant planes obtained by transition model

下载: 全尺寸图片 幻灯片

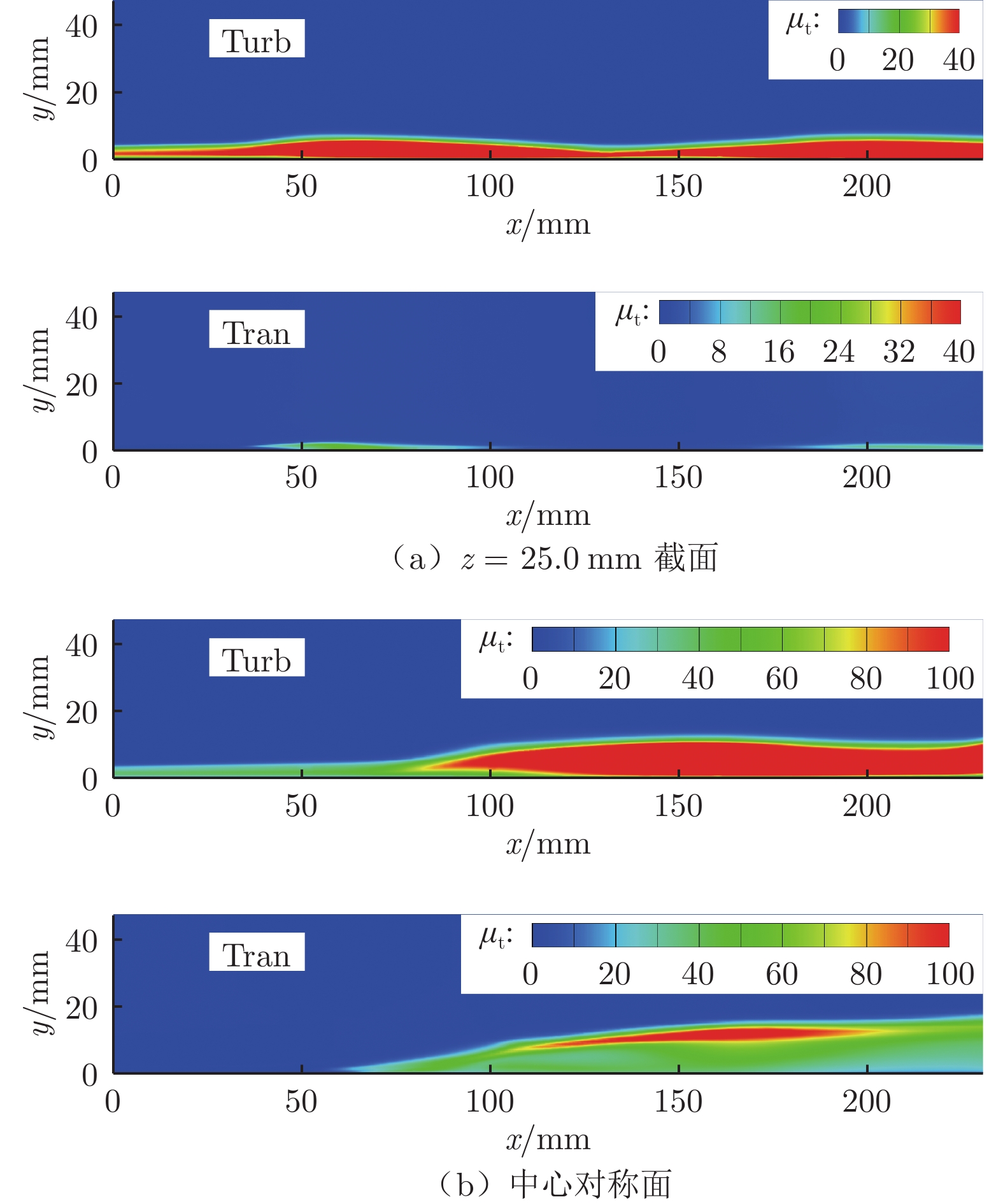
计算和试验得到的激波干扰前的壁面热流吻合良好，在干扰区则差别较大，这是目前采用RANS类方法模拟激波边界层干扰时的共性问题。在文献[30, 31]中均出现了热流计算值远大于试验值的问题。Thivet等^[31]认为，湍动能k经过激波后被目前的两方程湍流模型过度放大，k被输运进边界层底部后，导致湍流黏性系数过大，最终导致摩阻、热流偏大。对k进行限制后，得到的壁面热流有所降低，但与试验值仍有较大偏差。图12中z = 25.0 mm截面的壁面热流数据表明，采用转捩模型得到的壁面热流与试验测得的有/无控制措施下的热流吻合相对较好。根据图14（a），仔细分析该截面上采用来流空气黏性无量纲化的湍流黏性系数μ_t，结合图13（c）中的间歇因子分布可知，在转捩条件下，该截面上的间歇因子出现了“增大→减小→增大”的现象，得到的湍流黏性系数因此远小于湍流模型，得到的壁面热流也远小于湍流模型。这与Thivet等^[31]的说法吻合，在该截面上（不存在分离情况）热流计算值远大于风洞试验值，主要是RANS方法给出的湍流黏性系数过大所导致的。采用转捩模型在该截面上给出了更小的湍流黏性系数，获得了与试验吻合更好的计算结果。如图14（b）所示，对于中心对称面，采用转捩模型得到的μ_t也低于全湍流模型，但得到的壁面热流仍明显偏高，显然Thivet等^[31]的猜测在该截面上并不适用。结合纹影图像（图10）可知，未加装任何控制装置时，干扰区内存在三维分离和再附，此时壁面热流不仅受到湍流黏性系数影响，更受到流动分离和再附影响。对三维分离模拟不准，也可能导致对z = 0 mm截面热流模拟不准。

图  14  计算得到的不同z截面μ_t分布

Fig.  14  Contours of μ_t in different z planes

下载: 全尺寸图片 幻灯片

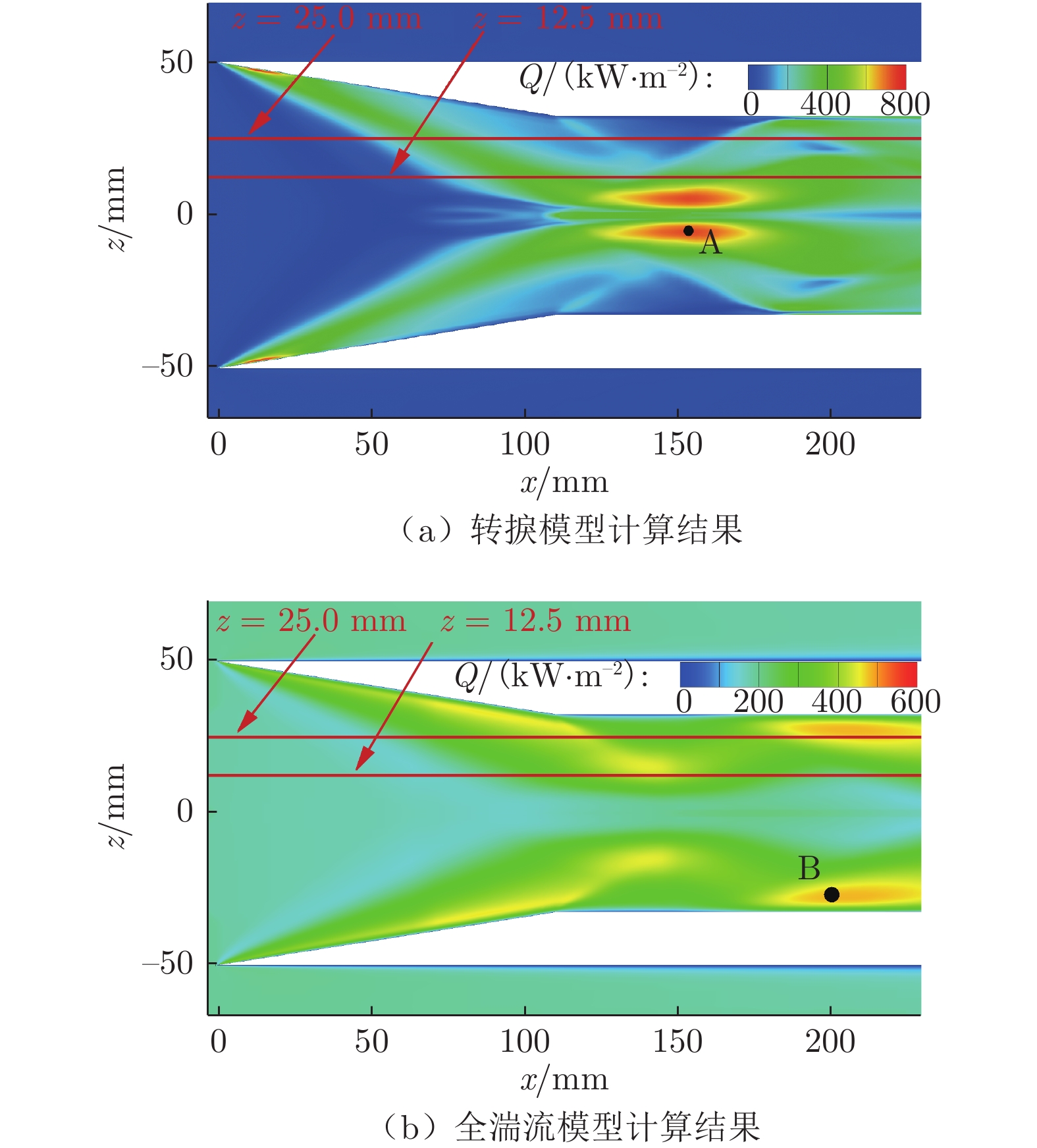
虽然热流计算值与试验值存在一定偏差，但在有/无控制措施对壁面热流的影响上，计算和试验得到的规律是一致的。对比不同边界层状态下的干扰区热流可知，在大部分干扰区域内，激波/转捩边界层干扰导致的热流明显高于激波/湍流边界层干扰。试验测得的激波/转捩边界层干扰热流峰值在x = 130 mm、z = 12.5 mm处，约为360 kW/m²，而边界层在干扰区上游转捩为湍流后，该处热流得到明显抑制，降低为约260 kW/m²，降幅超过25%。从数值模拟结果（图15壁面热流云图）可知，干扰导致的热流峰值由转捩状态的A点约730 kW/m²降为湍流状态的B点约480 kW/m²，降幅约34%。对比图11中的流场可知，激波/转捩边界层干扰时，干扰区内存在明显的三维分离与再附；在再附区，热流会因壁面受到流体的冲击而急剧增大，故干扰区的热流明显偏大。而对于激波/湍流边界层干扰，由于没有三维分离与再附，干扰区热流相对更小。

图  15  计算得到的底板壁面热流云图

Fig.  15  Calculated contours of heat fluxes in the base flat plate

下载: 全尺寸图片 幻灯片

3.3   壁面压力

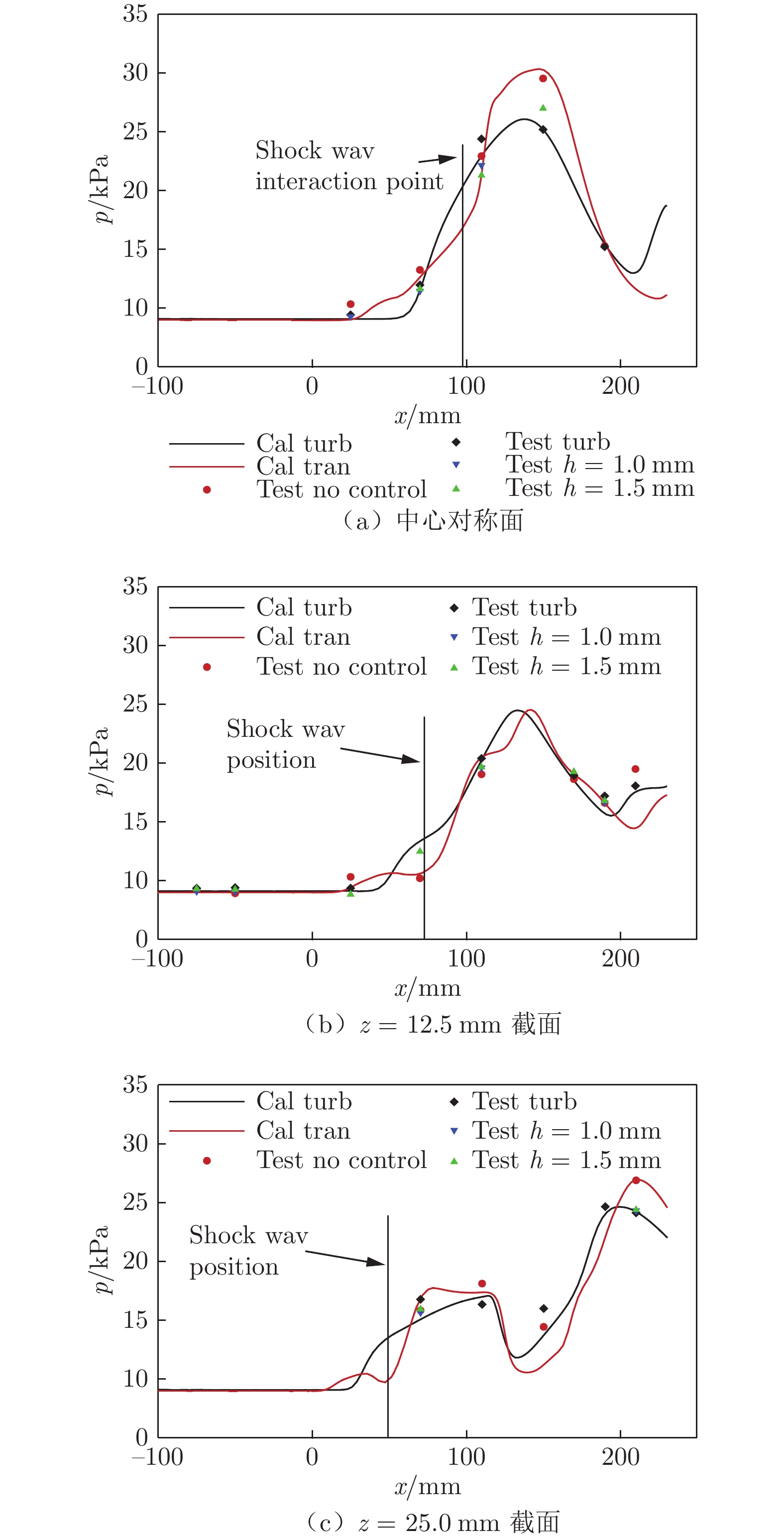
图16给出了中心对称面、z = 12.5 mm和z = 25.0 mm截面的壁面压力分布。从试验结果看，加装涡流发生器的结果与加装粗糙带的结果吻合较好，与无控制措施时的结果在部分干扰区存在较明显差别。与加装粗糙带或涡流发生器的情况相比，无控制措施时的干扰区压力峰值更高，第一次压升位置明显更为靠前，中心对称面和z = 12.5 mm截面的壁面压力均在x = 25.0 mm处就已出现较为明显的抬升。

图  16  试验与计算壁面压力对比

Fig.  16  Pressure distributions obtained from test and calculation

下载: 全尺寸图片 幻灯片

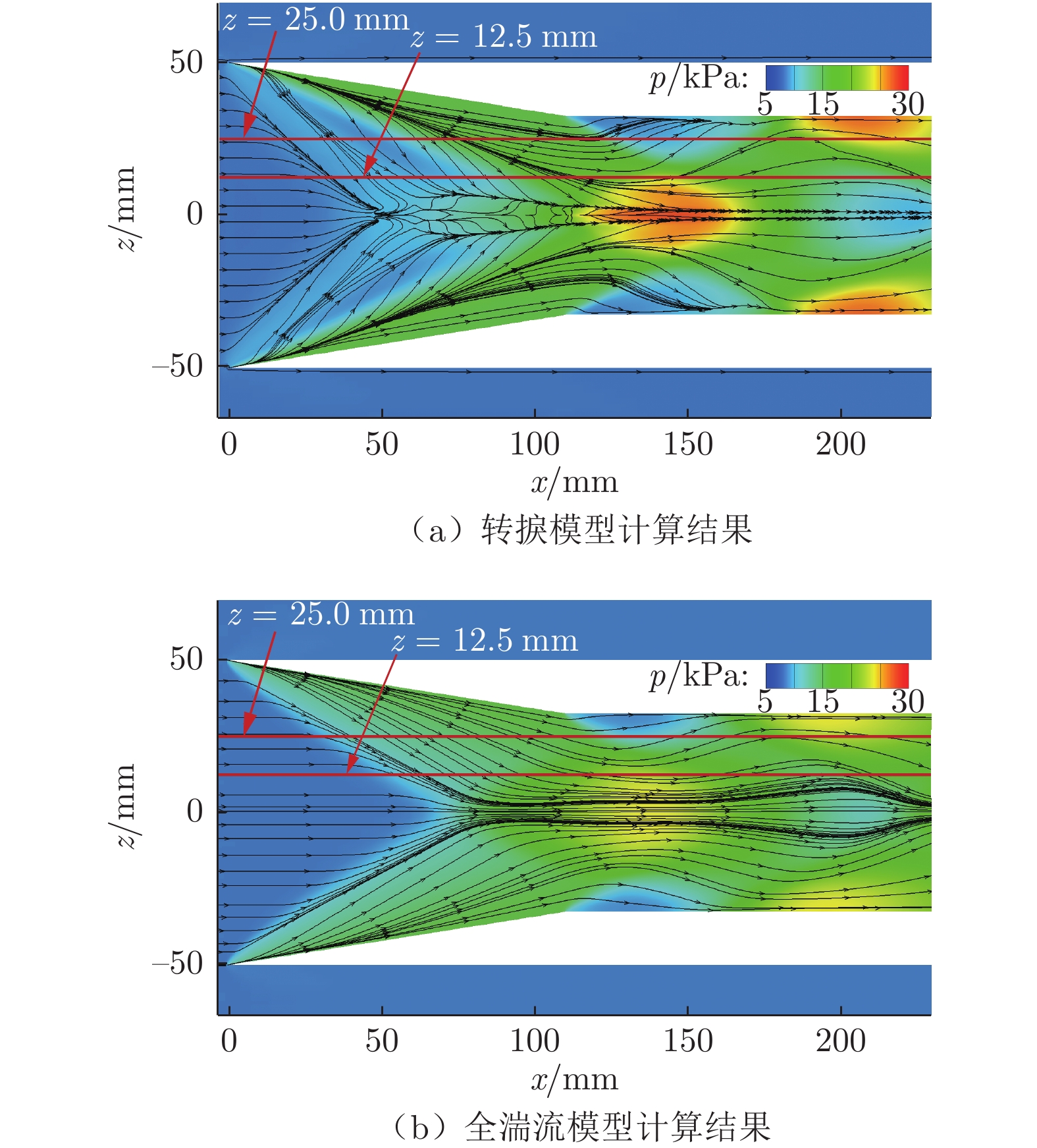
从数值模拟结果可以看到，压力抬升后，出现一压力平台段。结合图17的壁面压力云图及壁面摩擦力线可知，压力平台段出现了明显的三维分离涡结构，因此，试验测得的压力首次明显抬升是由边界层内的分离所导致。而加装斜坡型涡流发生器或粗糙带后，x = 25.0 mm处的压力与上游完全一致，压力平台段对应的空间位置并未发生分离。全湍流计算结果也表明，即使在激波交汇区也未发生明显分离。在中心线x = 150 mm处，无控制措施时的壁面压力也明显偏高。结合图17可知，该处存在分离后的再附，壁面受流体冲击，压力明显升高。采取控制措施后，分离和再附均不存在，压力明显更低。无控制措施时，在激波干扰位置上游出现的压力抬升现象与纹影测得的干扰区分离涡现象吻合，也与计算结果显示的干扰区内存在复杂三维分离情况吻合。

图  17  计算得到的底板壁面压力云图及摩擦力线分布

Fig.  17  Calculated contours of pressure in the base flat plate

下载: 全尺寸图片 幻灯片

综上所述，壁面压力分布的数值模拟与试验结果吻合良好，但干扰区内热流分布存在较大差别。对于无分离区域（如图12（c）的z = 25.0 mm截面），如前文所述，模拟热流偏大主要是由湍流模型在干扰区给出了过大的湍流黏性系数所导致；对于有分离区域（如图12（a）无控制措施下的z = 0 mm截面），数值模拟的压力分布结果与试验吻合良好，表明本文数值模拟可以较好地模拟干扰导致分离这一现象，且分离区大小和位置与试验结果差别不大。

由于分离区内部为亚声速区，压力变化并不明显，因此分离区内的流场结构模拟准确与否并不会明显影响压力分布的准确性。但对于热流而言，分离区内部的二次流场结构会直接影响边界层底部的速度和温度分布，进而对热流产生巨大影响。根据Zheltovodov等^[8]针对同类构型激波/湍流边界层干扰底部流动的拓扑计算和试验对比，采用RANS方法得到的干扰区二次分离结构确实与试验存在差异。因此，本文计算方法可以给出整体流场结构，也可以给出干扰所导致的分离区的大致大小和区域，但无法精确描述分离区内部的流场结构，也就无法给出准确的分离区热流分布。

4   结　论

采用风洞试验与数值模拟相结合的方法，针对马赫数3、单位来流雷诺数Re = 2.1 × 10⁶ m⁻¹、高焓来流条件下的双垂直楔交叉激波/转捩边界层干扰问题进行了研究。在风洞试验中获得了流场纹影图像、壁面压力和壁面热流，结合数值模拟结果，得到以下结论：

1）在无控制措施时，边界层在与交叉激波干扰前保持为层流状态；受交叉激波影响，边界层在激波交汇处产生分离，并在干扰区迅速发生转捩。

2）通过加装高度为1.0 或1.5 mm的斜坡型涡流发生器，或在底板前缘粘贴粗糙带，均能有效促进边界层在干扰区上游转捩为湍流。入口边界层转捩为湍流后，由激波/转捩边界层干扰所导致的分离区消失，干扰区下游流向涡结构明显减弱，干扰区热流大面积降低。风洞试验结果显示热流峰值降低超过25%，数值模拟结果则显示热流峰值降幅达34%。

3）通过数值模拟得到的激波结构、壁面压力分布与风洞试验结果吻合良好，但干扰区的壁面热流计算值与试验值存在较大偏差。热流模拟存在偏差的原因可能主要包括2部分：在无分离区域，通过RANS模拟得到了明显过高的湍流黏性系数，在z = 25.0 mm截面（无分离），与湍流模型相比，转捩模型给出了更小的湍流黏性系数，获得了与试验更为接近的热流值；在有分离区域，目前的计算方法虽可以较好地描述干扰所导致的分离区大小和位置，但无法精确给出二次分离结构，进而导致对分离区内边界层底部的温度模拟不准，最终难以给出较为准确的热流分布。