Experimental study on flow structure of transition boundary layer of the underwater vehicles
-
摘要:
采用激光诱导荧光(Laser Induced Fluorescence, LIF)和粒子图像测速(Particle Image Velocimetry, PIV)技术,对自由湍流条件下SUBOFF模型转捩边界层中的流动结构进行精细测量。实验在北京航空航天大学大型低速回流水洞中进行,SUBOFF模型长度为1.436 m,基于模型长度和来流速度的实验雷诺数为3.35 × 105。采用流动显示灰度场和有限时间李雅普诺夫指数(Finite-Time Lyapunov Exponents, FTLEs)对转捩边界层中的涡结构进行识别,并对转捩过程中发卡涡、二次涡等典型拟序结构的生成演化过程进行分析。采用两点相关方法提取转捩区拟序结构,同时采用椭圆拟合方法计算相干结构倾角,计算结果表明,结构倾角沿法向先增大后减小,在边界层附近达到最大值。为深入研究转捩流动结构特性,发展了基于流动显示的湍流/非湍流界面(T/NT)识别方法,并对界面几何特性进行了研究。研究结果表明,在转捩过程中,界面的法向高度和分形维数沿程增长。
-
关键词:
- 边界层转捩 /
- 流动显示 /
- 有限时间李雅普诺夫指数 /
- 湍流/非湍流界面
Abstract:Laser induced fluorescence (LIF) and particle image velocimetry (PIV) are used to measure the flow field of the transition boundary layer of the SUBOFF model subject to the free-stream turbulence (FST). The experiment is conducted in the water tunnel at Beihang University. The length of the SUBOFF model is L = 1.436 m, and the Reynolds number is ReL = 3.35 × 105 based on the length of the model and the free-stream velocity. The vortex structures during the transition process are identified using the grayscale field of laser-induced fluorescence and Finite-Time Lyapunov Exponents methods, which illustrate the generation and evolution process of typical structures, such as hairpin vortices and the induced secondary vortices. The coherent structures of the transition boundary layer are extracted using two-point correlation. Simultaneously, the elliptical fitting method is used to calculate the inclination angle of coherent structures. The inclination angle increases initially, and then decreases along the normal direction, reaching its maximum near the boundary layer. The visualization-based method is proposed for identifying turbulent/non-turbulent interfaces, with a focus on studying the geometric characteris-tics of the interface during the transition process. It is shown that the height and the fractal dimension of the interface increase along the transition.
-
0 引 言
曲面边界层转捩一直是流体力学研究的热点[1-2]。边界层转捩的显著特征是流场中出现了随时空演变的复杂涡结构[3],这些涡结构的生成演化及其相互作用对转捩特性和下游流场发展会产生很大影响。
潜艇模型由凹凸表面的首部、尾部及平行中体构成。潜艇在水下高速行进时,首部边界层转捩及大尺度涡脱落等复杂流场现象对其操纵、机动、噪声和续航等性能具有决定性影响。针对俯仰和偏航条件下潜艇模型的流场结构,研究者开展了大量实验和数值模拟研究。Sreenivas等[4]通过数值模拟指出,在潜艇大俯仰角或大偏航角下,马蹄形涡和横流涡等大尺度结构从壁面分离,影响其航行稳定性和操纵性。研究者还采用油流、染色液、烟线等[5-9]流动显示方法对回转体模型脱落涡和分离线开展了大量研究。Saeidinezhad等[10-11]采用烟线流动显示方法研究了大迎角下脱落的三维涡结构。Lee[12]采用china clay流动显示技术研究了不同迎角下3种回转体模型表面分离线的拓扑结构。Ashok等[13-14]采用体视粒子图像测速(Stereoscopic Particle Image Velocimetry, SPIV)技术拍摄了SUBOFF模型尾迹区不同截面的流场,研究了不同雷诺数、迎角、侧滑角条件下的尾涡不对称特性及发展演化特性。针对潜艇俯仰、偏航条件下大尺度脱落涡结构及尾迹区流场结构的研究相对较多,而针对潜艇巡航条件下近壁边界层流场结构的研究则较少。
Kumar等[15]采用大涡模拟方法分析了无附体SUBOFF模型边界层及尾迹区统计量,并与平板边界层的数据进行对比,发现轴对称湍流边界层中湍动能和雷诺应力沿法向的衰减比平面湍流边界层快得多,其原因可能是曲率抑制了边界层对数区域的大尺度结构。Morse等[16]首次在流线–法线和对称平面正交坐标系下导出了轴对称雷诺平均Navier–Stokes方程,从新的视角详细研究了流线型体湍流边界层。Manovski等[17]基于高空间分辨率PIV技术对无附体Joubert模型的湍流边界层进行了精细化测量,同时使用热线和皮托管进行了单点测量,并选取典型站位与平板边界层DNS数据进行对比,发现回转体边界层内的雷诺应力大于对应平板边界层的雷诺应力。
针对流线型回转体近壁边界层的数值模拟和实验研究十分有限。Morse[16]和Manovski[17]等对回转体曲面湍流边界层进行了初步讨论,但关于边界层如何由层流转捩为湍流的研究较少。本文采用激光诱导荧光(Laser Induce Fluorescence, LIF)流动显示技术和粒子图像测速技术,对高湍流度来流条件下SUBOFF模型边界层的转捩过程进行捕获。基于流动显示灰度场和有限时间李雅普诺夫指数场提取流场转捩过程中的典型涡结构,并采用两点相关方法研究不同法向高度的相干结构形态。发展基于流动显示的湍流/非湍流界面识别方法,对转捩过程中的界面几何特性进行分析。
1 实验装置与测试方法
1.1 实验模型
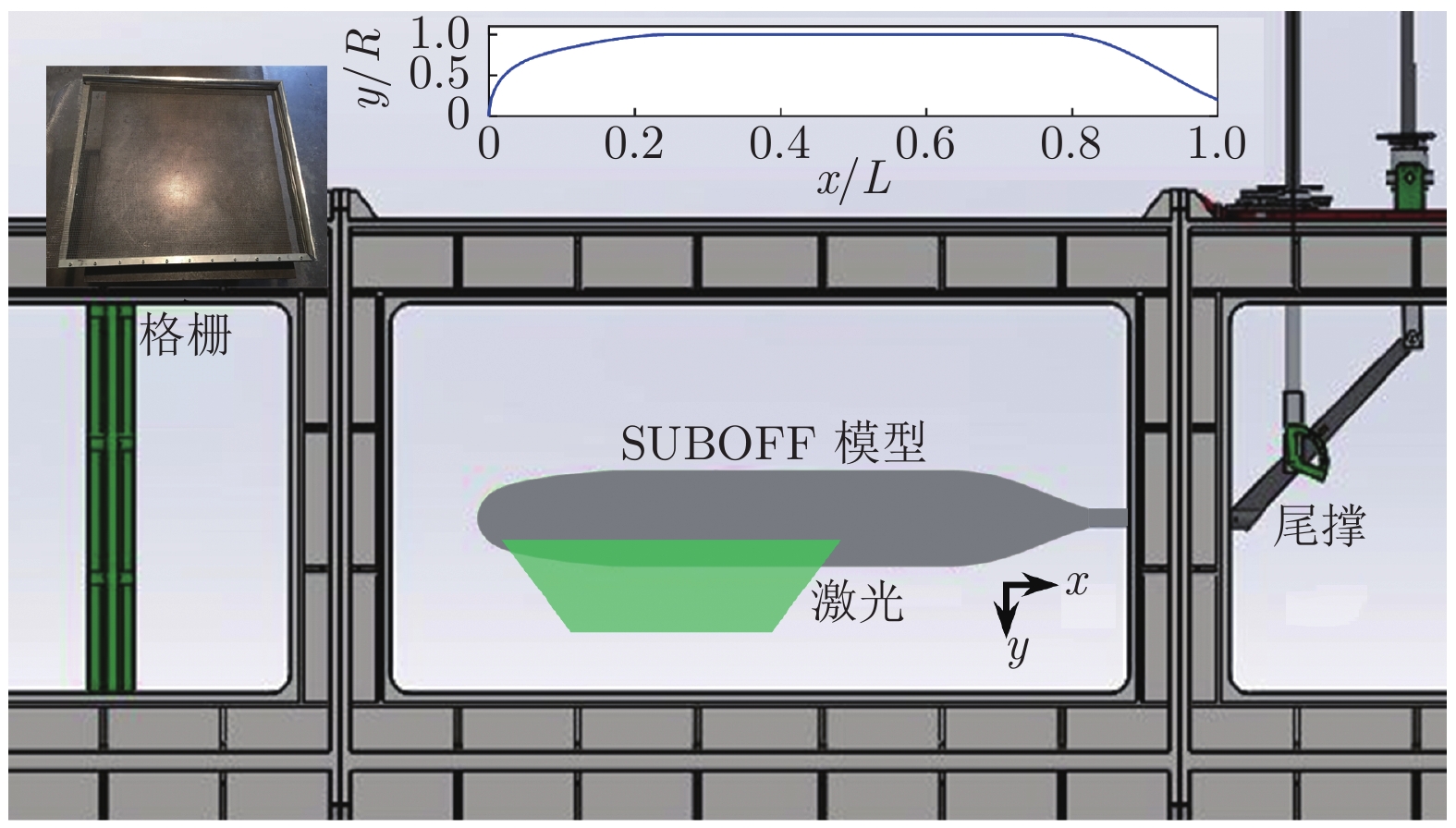
实验在北京航空航天大学大型低速回流水洞中进行。该水洞实验段尺寸为16 m × 1.2 m × 1 m(长 × 高 × 宽)。实验模型为无附体SUBOFF模型,根据水洞截面尺寸进行模型缩比,长度L = 1.436 m,回转体最大半径R = 0.1 m,模型堵塞比为2.6%。实验来流速度u∞ = 0.25 m/s,基于模型长度和来流速度的实验雷诺数ReL = u∞L/ν = 3.35 × 105。实验模型以有机玻璃加工而成,满足水动力光滑条件。
实验装置如图1所示。模型以尾部支撑方式固定于水洞中央,实验时无迎角和侧滑角。坐标原点固定于模型首部前端点,流向定义为x轴,重力方向定义为y轴。实验时,使用湍流格栅提高来流湍流度,促使边界层转捩。湍流格栅安装于模型上游,湍流格栅细柱直径d = 6 mm,格栅间隙比为6。
1.2 实验方法
1.2.1 激光诱导荧光流动显示
采用激光诱导荧光流动显示方法对近壁区流场结构进行可视化。实验所用荧光粒子为罗丹明B(Rhodamine B),在连续激光器激发下发出550 nm波长的荧光。在模型首部下游30 mm处沿周向加工宽1 mm、周长50 mm的狭缝,用于释放罗丹明染料。用注射泵将罗丹明染料经内置导管注射至狭缝内。经测试,罗丹明染料引入流场的扰动可忽略不计。激光从水洞下方照亮拍摄平面,以3台CMOS高速相机(Photron FASTCAM SA2)拍摄x/L = 0.10~0.60范围内的近壁流动结构。采样频率f = 50 Hz,采集超过30000个瞬时速度场,以保证统计特性收敛。在相机镜头前方配置滤光片(截止波长为565~1100 nm),以降低背景噪声或其他粒子对拍摄效果的影响。
1.2.2 粒子图像测速
使用二维PIV对边界层内流动进行高时空分辨率测量。激光光源为Vlite–Hi–30k型高频双脉冲固体激光器,每脉冲输出能量为30 mJ,从水洞下方照射拍摄流场。以直径20 μm、密度1.05 g/cm3的空心玻璃微珠作为示踪粒子。采用2台配备Nikon AF Nikkor 180 mm定焦镜头的CMOS高速相机(型号为Photron FASTCAM SA2)拍摄x–y平面的粒子图像。CMOS相机采集频率为500 Hz,分辨率为2048像素 × 2048像素,由于边界层较薄,每台相机拍摄范围为65 mm × 40 mm,对应速度场空间分辨率为0.032 mm/像素。速度场计算采用Pan等[18]发展的多重迭代Lucas–Kanade(Multiple Iterations Lucas–Kanade, MILK)光流算法。MILK算法的等效查询窗口尺寸为32像素 × 32像素,重叠率为75%,速度场分辨率每个矢量约为0.25 mm。通过多次向下游移动相机拍摄位置,得到一个较大的拍摄范围(x/L = 0.10~0.55)。每个相机拍摄位置捕获超过50000个瞬时速度场,以保证统计收敛。
1.3 格栅湍流
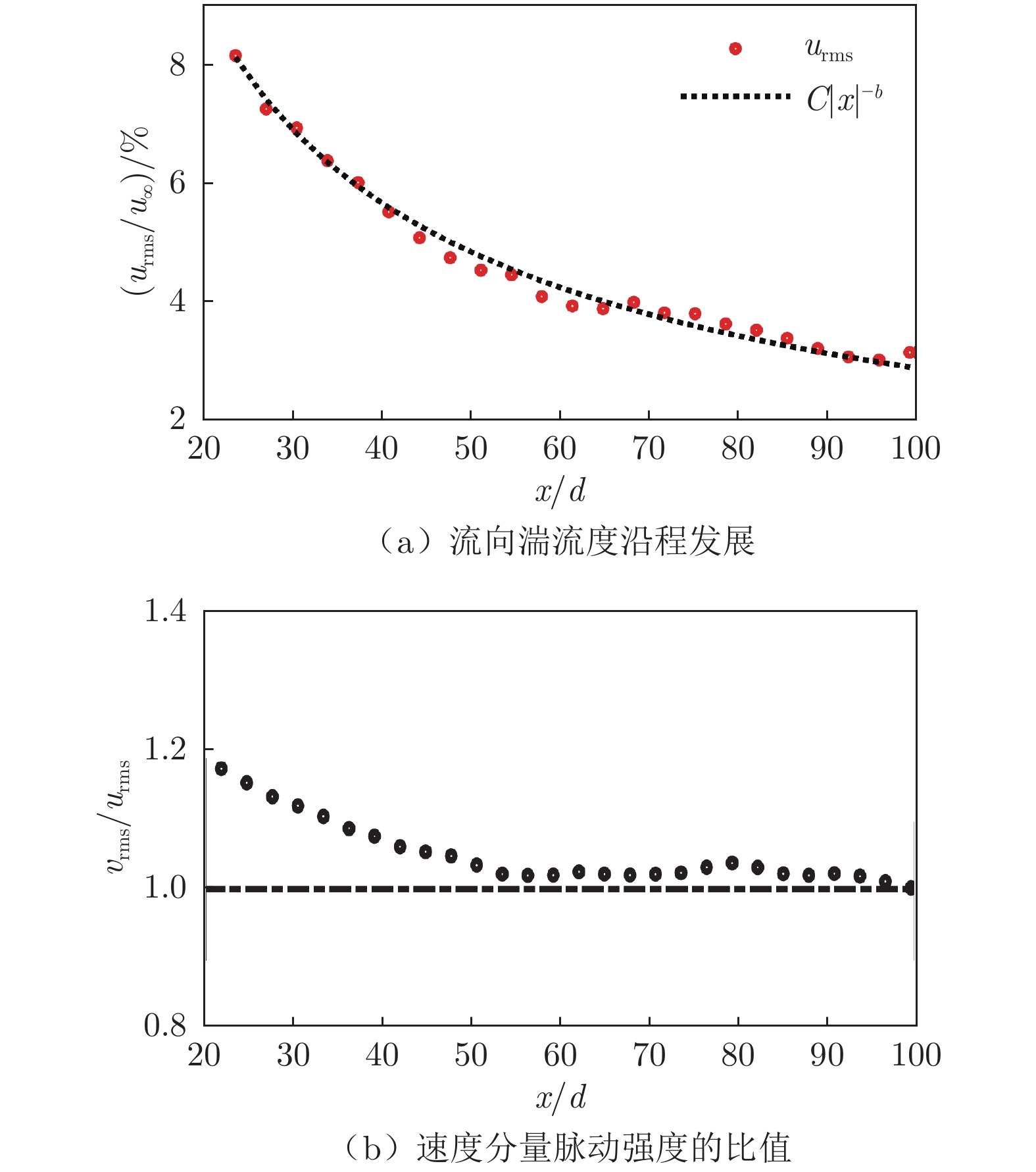
在研究来流湍流度对无附体SUBOFF模型流场的影响之前,需标定湍流格栅尾迹区的湍流特性,以确定放置格栅的流向位置。采用PIV测量格栅后方20d~100d范围内的流场。以双脉冲Nd:YAG激光器(镭宝光电Vlite 380,波长532 nm,每脉冲输出能量380 mJ)作为光源。使用2台配备180 mm腾龙微距镜头的CCD相机(IMPERX–B6640)采集粒子图像,采样频率为1 Hz。相机传感器尺寸为6600像素 × 4400像素,图像空间分辨率为14.7 μm/像素。如图2(a)所示,流向湍流度沿程变化遵循典型的幂律衰减分布规律(图中C、b为格栅湍流常用的幂律拟合系数)。图2(b)为2个速度分量脉动强度的比值vrms/urms。x/d > 50后,2个速度分量脉动强度的比值逐渐趋近于1,可近似为各向同性湍流,故将格栅置于x/d = 50处。来流速度u∞ = 0.25 m/s时,流向湍流度urms/u∞ = 4.8%。
2 转捩区典型流动结构
2.1 激光诱导荧光流动显示
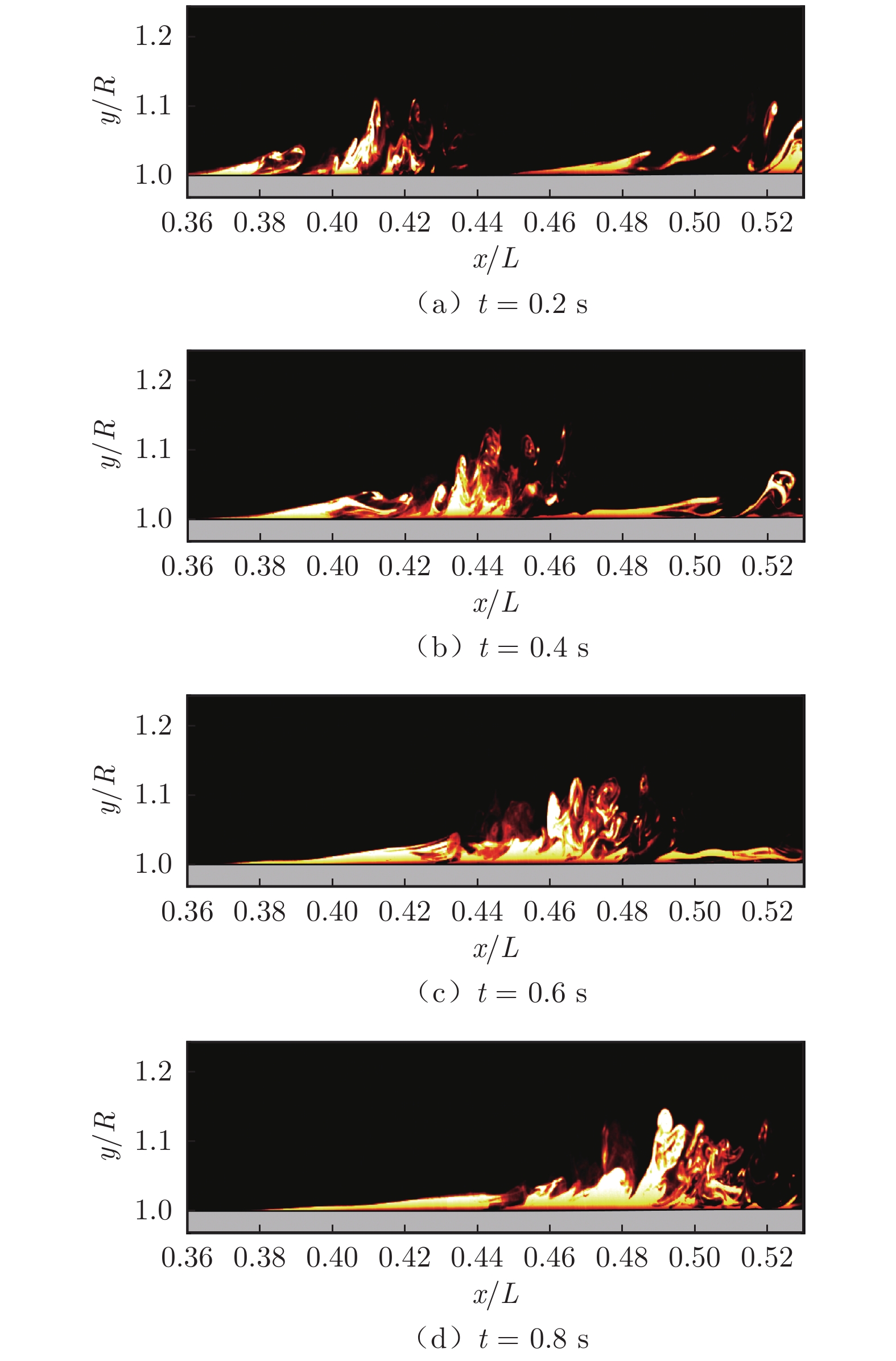
对于SUBOFF模型流场转捩过程中的近壁流场大尺度结构,采用激光诱导荧光流动显示技术测量。图3为0.36 < x/L < 0.53流向范围内4个瞬时的LIF流动显示结果,展示了流场由条带失稳发展为发卡涡的过程。如图3(a)所示,近壁条带结构从壁面抬升,近壁流体携带染色液被“喷射”至远壁区发展为发卡涡。之后,多个发卡涡结构形成大尺度涡包结构,在向下游(0.46 < x/L < 0.52)对流的过程中逐渐湍流化,如图3(b)和(c)所示。同时,上游0.36 < x/L < 0.45范围的流动趋于平稳,如图3(d)所示,表明本次湍流猝发结束。这种间歇性猝发事件是转捩进入非线性演化的典型标志。
2.2 李雅普诺夫指数场
上述流动显示结果清晰展示了边界层内大尺度结构的演化过程,但染料的扩散性使得小尺度结构无法较好地呈现。基于有限时间李雅普诺夫指数(Finite-Time Lyapunov Exponents, FTLEs)的涡判别准则可以清晰显示涡结构边界,近年来被广泛应用于涡结构识别[19-20]。以FTLEs表征流体质点组在一定积分时间内相对位移的应变量,其出现极值处即对应旋涡边界。因其描述了流场的拉格朗日运动特性,故在一定程度上具有流动显示效果。使用Cauchy–Green张量平方的最大特征值λmax表征相邻流体质点组在t0~t1时刻运动过程中的位移变动率σ:
$$ {\sigma _{t{\text{1}}}}\left( {{x_{\text{0}}}{\text{,}}{t_{\text{0}}}} \right){\text{ = }}{\lambda _{{\text{max}}}}\left\{ {{{{\text{[}}\nabla F_{{t_{\text{0}}}}^{{t_{\text{1}}}}{\text{(}}{x_{\text{0}}}{\text{)]}}}^{\text{T}}}{\text{[}}\nabla F_{{t_{\text{0}}}}^{{t_{\text{1}}}}{\text{(}}{x_{\text{0}}}{\text{)]}}} \right\} $$ (1) 式中,$ F_{{t_{\text{0}}}}^{{t_{\text{1}}}}{\text{(}}{x_{\text{0}}}{\text{)}} $表示x0处的质点从初始t0时刻至t1时刻的积分距离。
李雅普诺夫指数场FTLEt1(x0, t0)定义为:
$$ {\mathrm{FTLE}}_{t1}\left( {{x_0},{t_0}} \right) = \frac{1}{{2{t_1}}}\ln {\sigma _{t1}}({x_0},{t_0}) $$ (2) 图4为2个典型转捩结构的FTLEs演化过程。李雅普诺夫指数场(FTLEs场)由PIV速度场积分得到,积分步长为500步,每步时间间隔0.02 s,积分总时长为−1 s(后向积分)。FTLEs场中的脊线(图中较亮区域)很好地展示了初级发夹涡、发卡涡自维持及其诱导的二次涡的演变过程。图4(a1)展示了2个孤立发夹涡结构(A1、B1),发夹涡B1涡头的抬升角度接近90°,该结构与Green等[21]的研究结果一致。随着发夹涡演化,B1涡腿向上诱导抬升形成的剪切层清晰可见,而剪切层的不稳定性也已开始显现,在下游诱导出新的发卡涡结构C1。此外,在靠近壁面处还诱导出了二次涡结构D1,该结构向壁面撞击是典型的扫掠事件。
图4(a2)、(b2)和(c2)展示了转捩边界层中发卡涡包的演化过程。从图中可以看到,该结构似由5个发卡涡构成,最大的初级发夹涡A2位于下游,新生成的发夹涡E2位于上游。该涡包流向尺度大于5倍当地边界层厚度,结构倾角约为12°(图中白色虚线所示)。尽管该站位(0.48 < x/L < 0.52)处于转捩过程中,但其间歇性发卡涡包结构与湍流边界层中发卡涡包的几何结构相似。
2.3 两点相关方法
根据前文针对瞬时流动结构的分析可知,转捩区流场由条带和发卡涡等结构所主导。采用两点相关方法进一步研究转捩区拟序结构的空间形态,相关系数为:
$$ R({x_0},{{\textit{y}}_0},{\text{Δ}} x,{\text{Δ}} {\textit{y}}) = \frac{{\overline {{f_A}({x_0},{{\textit{y}}_0}){f_B}({x_0} + {\text{Δ}} x,{{\textit{y}}_0} + {\text{Δ}} {\textit{y}})} }}{{{\phi _A}{\phi _B}}} $$ (3) 式中:x0和y0为参考点A的位置,${\text{Δ}} x $和${\text{Δ}} \textit{y} $为动点B距离参考点A的相对位置;f(·)为进行空间相关的物理量,如流向脉动速度等,这里分别基于流动显示和FTLEs场进行计算;${\phi _A}$、${\phi _B} $分别为参考点A和动点B时序脉动信号的标准差。选取流向站位x/L = 0.5,yn/δ = 0.10、0.25、0.50、1.00和1.25等5个法向参考点进行空间相关计算(yn定义为距离当地壁面的法向高度,δ为边界层厚度)。
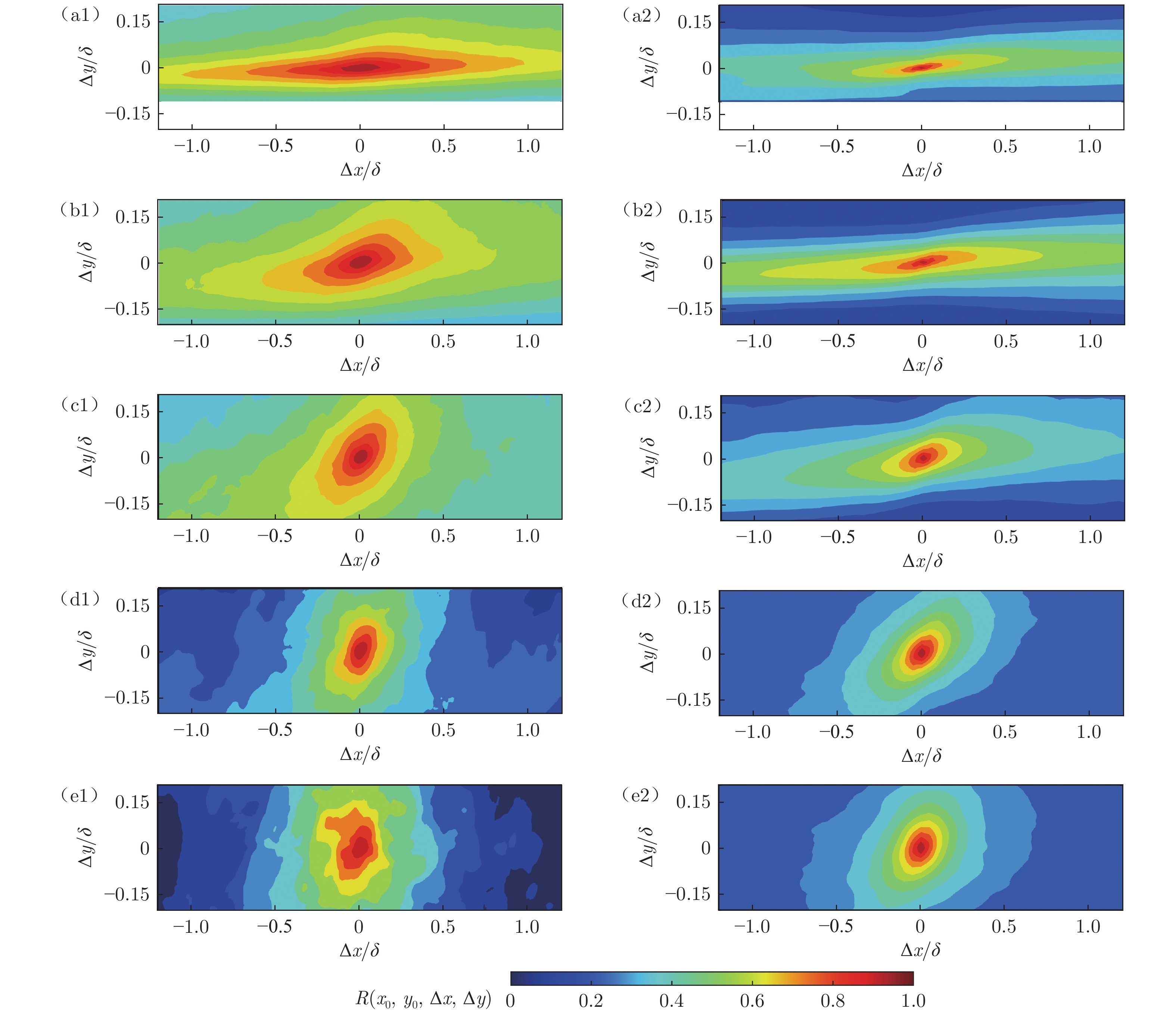
图5(a1~e1)、图5(a2~e2)分别为基于LIF流动显示和基于FTLEs场的两点相关系数分布。由于边界层内高层流体运动速度快、低层流体运动速度慢,两点分布表征的结构为正的几何倾角。从图中可以看到:在靠近壁面处(yn/δ = 0.10),两者的两点相关系数分布都呈现为明显的狭长条带;yn/δ增大至0.25和0.50时,相关结构逐渐抬升至更高流层,相关流向范围逐渐缩短,结构倾角明显变大;在yn/δ = 1.00和1.50的流层中,已经没有明显的狭长条带结构,而是呈现近似圆形的分布,这种分布可归因于高湍流度自由来流中均匀各向同性湍流成分的贡献。对比基于LIF流动显示和基于FTLEs场的两点相关系数分布,可以在近壁附近看到后者的相关结构更为狭长,这可能是由FTLEs场中的近壁剪切层导致的。采用椭圆拟合方法,选取相关区域性高于0.9的区域,对相干结构进行拟合[22-23],进而评估拟序结构倾角。
![]() 图 5 不同法向高度的两点相关系数分布,从上至下对应法向高度为yn/δ = 0.10、0.25、0.50、1.00、1.25,(a1~e1)基于LIF流动显示的两点相关系数分布,(a2~e2)基于FTLEs的两点相关系数分布Fig. 5 The contour of two points correlation coefficient at different normal positions. Five rows from the top to the bottom are the results at yn/δ = 0.10, 0.25, 0.50, 1.00 and 1.25, respectively. (a1–e1) two-point correlation distribution based on LIF flow visualization, (a2–e2) two-point correlation distribution based on FTLEs
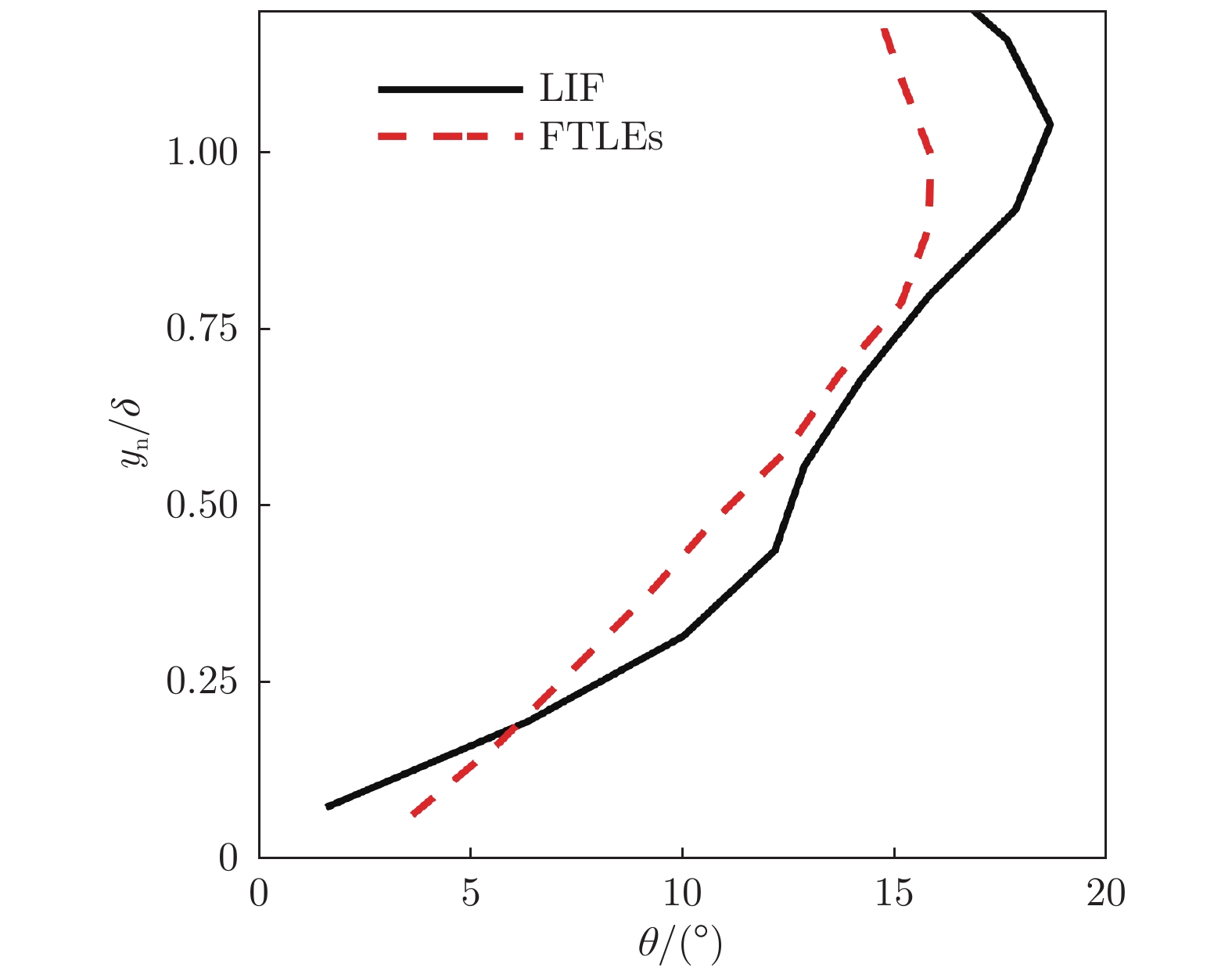
图 5 不同法向高度的两点相关系数分布,从上至下对应法向高度为yn/δ = 0.10、0.25、0.50、1.00、1.25,(a1~e1)基于LIF流动显示的两点相关系数分布,(a2~e2)基于FTLEs的两点相关系数分布Fig. 5 The contour of two points correlation coefficient at different normal positions. Five rows from the top to the bottom are the results at yn/δ = 0.10, 0.25, 0.50, 1.00 and 1.25, respectively. (a1–e1) two-point correlation distribution based on LIF flow visualization, (a2–e2) two-point correlation distribution based on FTLEs从图6中拟序结构倾角沿法向高度的变化可以看到:近壁附近拟序结构倾角最小;随着流层升高,马蹄涡及涡包等使结构倾角增大,边界层附近结构倾角增大到最大值。从瞬时流动结构(图4)可以看到边界层附近主要为马蹄涡涡头,这与湍流边界层中结构倾角沿法向高度的变化趋势一致[24]。
3 转捩区湍流/非湍流界面特性
为进一步研究转捩过程中流动结构的几何特性,发展了基于流动显示的湍流/非湍流界面(即T/NT界面,指流场中湍流区域和包围湍流的无旋流动区域之间的薄层)识别方法。转捩过程中存在间歇性湍流事件,但前人主要针对射流、尾流、湍流边界层等开展研究[25-28],针对转捩边界层湍流/非湍流界面特性的研究工作则相对较少。
3.1 界面识别
通常,研究者针对流场中某一物理量,通过设置合适阈值提取其等值面作为湍流界面。基于涡量或拟涡能的识别方法是目前应用最为广泛的一种T/NT界面识别方法。另外,还可以将标量场应用于界面识别。Gampert等[29]基于标量场判据和涡量判据对界面进行了识别,发现当前者阈值选取合适时,识别出的界面位置与后者几乎一致。Holzner[30]和Westerweel[31]等采用LIF流动显示技术测量了射流的荧光强度标量场分布,通过计算荧光强度大于阈值区域的灰度平均值,对湍流非湍流界面进行识别。图7展示了本文基于灰度场的界面识别方法:首先,对原始灰度图像进行平均值去背景处理;由于不同空间位置的荧光强度分布不均,采用局部增强方法使灰度场在空间上分布均匀;最后,采用二值化方法提取湍流边界。图7中的红色虚线即为识别出的界面位置。因此,采用上述方法可以有效识别流动结构的边界[22]。
3.2 界面几何特性
图8给出了界面高度概率分布的沿程变化。从图中可以看到:在上游x/L = 0.45处,界面法向高度主要分布于近壁区内(yn/δ < 0.25),这是因为转捩前期相干结构主要集中于近壁附近;随着流动向下游发展,界面位置向高流层移动,且概率分布更为分散,表明相干结构更加丰富,但转捩过程中的界面高度概率分布峰值低于充分发展的湍流边界层[25]。
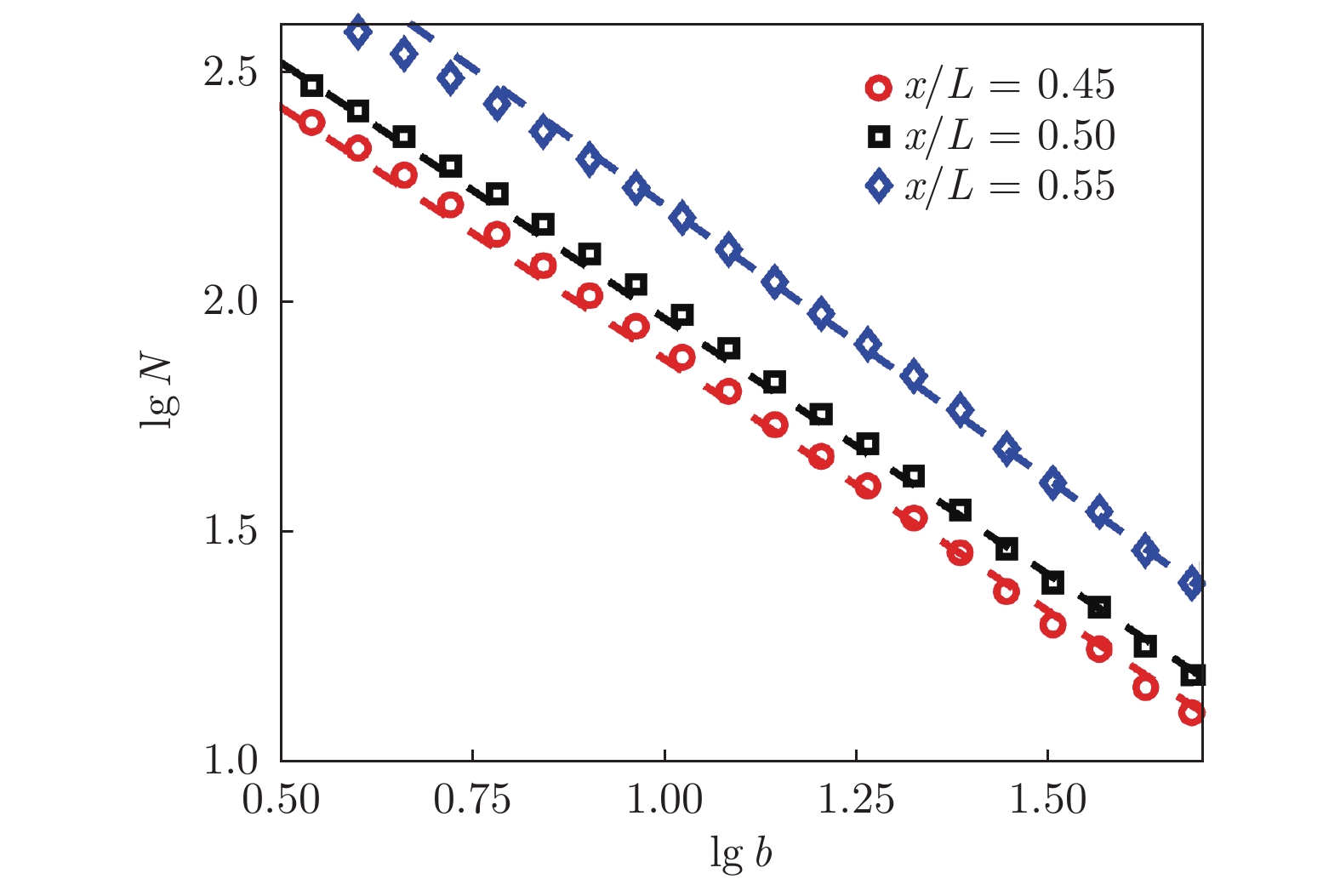
除界面高度概率分布外,界面的另一个重要多尺度特征是界面存在分形特性。本文采用盒维法计算了界面的分形维数:以尺寸为b × b的方格划分每个时刻的界面,为完全包含界面,至少需要N个方格;对于不同的方格大小b,在每一帧图像中均重复上述步骤,即可得到所有时刻平均后的方格大小与所需方格数的关系:在合适的方格大小范围内,两者满足N∝b−D,其中D为分形维数,在双对数坐标系下,b与N满足线性关系,且斜率为−D。
图9给出了界面分形维数的沿程变化:在沿程发展过程中,分形维数逐渐增大至1.08、1.11和1.19。根据Mandelbrot等[32]提出的余维度理论,对应于三维坐标系下的分形维数Df为2.08、2.11和2.19。由于流动处于转捩过程,不同尺度之间没有完全分离,导致所得到的分形维数低于完全发展湍流界面的分形维数理论值7/3。
4 结 论
采用激光诱导荧光流动显示技术和粒子图像测速技术,对高来流湍流度条件下无附体SUBOFF模型转捩边界层流动结构进行了精细测量,得到以下结论:
1)基于流动显示灰度场和有限时间李雅普诺夫指数场对转捩结构进行了识别。在流向–法向平面内,条带失稳形成发夹涡,这些涡结构在向下游对流过程中组成发夹涡包,最后湍流化,这是典型的旁路转捩过程。
2)相干结构在近壁附近主要为狭长条带结构,随着相关结构逐渐抬升至更高流层,相关流向范围逐渐缩短。结构倾角沿法向先增大后减小,在边界层附近达到最大值。
3)发展了基于流动显示的湍流/非湍流界面识别方法,研究发现转捩过程中界面高度和分形维数沿程增长,但低于完全发展湍流界面的分形维数。
-
图 5 不同法向高度的两点相关系数分布,从上至下对应法向高度为yn/δ = 0.10、0.25、0.50、1.00、1.25,(a1~e1)基于LIF流动显示的两点相关系数分布,(a2~e2)基于FTLEs的两点相关系数分布
Fig. 5 The contour of two points correlation coefficient at different normal positions. Five rows from the top to the bottom are the results at yn/δ = 0.10, 0.25, 0.50, 1.00 and 1.25, respectively. (a1–e1) two-point correlation distribution based on LIF flow visualization, (a2–e2) two-point correlation distribution based on FTLEs
-
[1] 陈久芬, 徐洋, 蒋万秋, 等. 升力体外形高超声速边界层转捩红外测量实验[J]. 实验流体力学. doi: 10.11729/syltlx20220030. CHEN J F, XU Y, JIANG W Q, et al. Infrared thermogram measurement experiment of hypersonic boundary-layer transition of a lifting body[J]. Journal of Experiments in Fluid Mechanics. doi: 10.11729/syltlx20220030.
[2] 张石玉, 赵俊波, 付增良, 等. 钝锥动态转捩风洞试验[J]. 实验流体力学, 2022, 36(6): 61–66. DOI: 10.11729/syltlx20210120 ZHANG S Y, ZHAO J B, FU Z L, et al. Dynamic boundary layer transition wind tunnel test of blunt cone[J]. Journal of Experiments in Fluid Mechanics, 2022, 36(6): 61–66. doi: 10.11729/syltlx20210120
[3] 李存标, 吴介之. 壁流动中的转捩[J]. 力学进展, 2009, 39(4): 480–507. DOI: 10.6052/1000-0992-2009-4-J2009-008 LEE C B, WU J Z. Transition in wall-bounded flows[J]. Advances in Mechanics, 2009, 39(4): 480–507. doi: 10.6052/1000-0992-2009-4-J2009-008
[4] SREENIVAS K, HYAMS D, MITCHELL B, et al. Physics based simulation of Reynolds number effects in vortex intensive incompressible flows[C]//Proc of the RTO AVT Symposium on “Advanced Flow Management: Part A – Vortex Flows and High Angle of Attack for Military Vehicles”, RTO-mp-069(I). 2001.
[5] PANTELATOS D K, MATHIOULAKIS D S. Experimental flow study over a blunt-nosed axisymmetric body at incidence[J]. Journal of Fluids and Structures, 2004, 19(8): 1103–1115. doi: 10.1016/j.jfluidstructs.2004.07.004
[6] GROSS A, KREMHELLER A, FASEL H. Simulation of flow over suboff bare hull model[C]//Proc of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. 2011. doi: 10.2514/6.2011-290
[7] QUICK H, WIDJAJA R, ANDERSON B, et al. Phase I experimental testing of a generic submarine model in the DSTO low speed wind tunnel[R]. DSTO-TN-1101, 2012.
[8] ASHOK A, SMITS A. The turbulent wake of a submarine model at varying pitch and yaw angle[C]//Proc of the 18th Australasian Fluid Mechanics Conference. 2012.
[9] 潘家鑫, 耿子海, 李国强, 等. 基于水洞激光诱导荧光技术的不同气动构型流动特性研究[J]. 气动研究与实验, 2022, 34(2): 100–107. DOI: 10.12050/are20220212 PAN J X, GENG Z H, LI G Q, et al. Research on the flow characteristics of different aerodynamic configurations based on water tunnel laser-induced fluorescence technology[J]. Aerodynamic Research & Experiment, 2022, 34(2): 100–107. doi: 10.12050/are20220212
[10] SAEIDINEZHAD A, DEHGHAN A A, DEHGHAN MANSHADI M. Nose shape effect on the visualized flow field around an axisymmetric body of revolution at incidence[J]. Journal of Visualization, 2015, 18(1): 83–93. doi: 10.1007/s12650-014-0226-1
[11] SAEIDINEZHAD A, DEHGHAN A A, DEHGHAN MANSHADI M. Experimental investigation of hydrodyna-mic characteristics of a submersible vehicle model with a non-axisymmetric nose in pitch maneuver[J]. Ocean Engineering, 2015, 100: 26–34. doi: 10.1016/j.oceaneng.2015.03.010
[12] LEE S K. Longitudinal development of flow-separation lines on slender bodies in translation[J]. Journal of Fluid Mechanics, 2018, 837: 627–639. doi: 10.1017/jfm.2017.886
[13] ASHOK A, VAN BUREN T, SMITS A J. The structure of the wake generated by a submarine model in yaw[J]. Experiments in Fluids, 2015, 56(6): 123. doi: 10.1007/s00348-015-1997-4
[14] ASHOK A, VAN BUREN T, SMITS A. Asymmetries in the wake of a submarine modelinpitch[J]. Journal of Fluid Mechanics, 2015, 774: 416–442. doi: 10.1017/jfm.2015.277
[15] KUMAR P, MAHESH K. Large-eddy simulation of flow over an axisymmetric body of revolution[J]. Journal of Fluid Mechanics, 2018, 853: 537–563. doi: 10.1017/jfm.2018.585
[16] MORSE N, MAHESH K. Large-eddy simulation and streamline coordinate analysis of flow over an axisymmetric hull[J]. Journal of Fluid Mechanics, 2021, 926: A18. doi: 10.1017/jfm.2021.714
[17] MANOVSKI P, JONES M B, HENBEST S M, et al. Boundary layer measurements over a body of revolution using long-distance particle image velocimetry[J]. Inter-national Journal of Heat and Fluid Flow, 2020, 83: 108591. doi: 10.1016/j.ijheatfluidflow.2020.108591
[18] PAN C, XUE D, XU Y, et al. Evaluating the accuracy performance of Lucas-Kanade algorithm in the circumstance of PIV application[J]. Science China Physics, Mechanics & Astronomy, 2015, 58(10): 104704. doi: 10.1007/s11433-015-5719-y
[19] HE G S, PAN C, FENG L H, et al. Evolution of Lagrangian coherent structures in a cylinder-wake disturbed flat plate boundary layer[J]. Journal of Fluid Mechanics, 2016, 792: 274–306. doi: 10.1017/jfm.2016.81
[20] HALLER G. Lagrangian coherent structures[J]. Annual Review of Fluid Mechanics, 2015, 47: 137–162. doi: 10.1146/annurev-fluid-010313-141322
[21] GREEN M A, ROWLEY C W, HALLER G. Detection of Lagrangian coherent structures in three-dimensional turbulence[J]. Journal of Fluid Mechanics, 2007, 572: 111–120. doi: 10.1017/s0022112006003648
[22] 杨强, 袁先旭, 陈坚强, 等. 不可压壁湍流中基本相干结构[J]. 空气动力学学报, 2020, 38(1): 82–99. DOI: 10.7638/kqdlxxb-2019.0117 YANG Q, YUAN X X, CHEN J Q, et al. On elementary coherent structures in incompressible wall-bounded turbulence[J]. Acta Aerodynamica Sinica, 2020, 38(1): 82–99. doi: 10.7638/kqdlxxb-2019.0117
[23] 王轩, 范子椰, 陈乐天, 等. 流向凹曲率壁面湍流边界层的TRPIV实验研究[J]. 实验流体力学, 2022, 36(6): 1–9. DOI: 10.11729/syltlx20210084 WANG X, FAN Z Y, CHEN L T, et al. Experimental study of TRPIV for turbulent boundary layer of longitudinal concave curvature wall[J]. Journal of Experiments in Fluid Mechanics, 2022, 36(6): 1–9. doi: 10.11729/syltlx20210084
[24] PAN C, WANG J J, ZHANG C. Identification of Lagrangian coherent structures in the turbulent boundary layer[J]. Science in China Series G: Physics, Mechanics and Astronomy, 2009, 52(2): 248-257. doi: 10.1007/s11433-009-0033-1
[25] 李思成, 吴迪, 崔光耀, 等. 低雷诺数沟槽表面湍流/非湍流界面特性的实验研究[J]. 力学学报, 2020, 52(6): 1632–1644. DOI: 10.6052/0459-1879-20-211 LI S C, WU D, CUI G Y, et al. Experimental study on properties of turbulent/non-turbulent interface over riblets surfaces at low Reynolds numbers[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(6): 1632–1644. doi: 10.6052/0459-1879-20-211
[26] LONG Y G, WU D, WANG J J. A novel and robust method for the turbulent/non-turbulent interface detection[J]. Experiments in Fluids, 2021, 62(7): 138. doi: 10.1007/s00348-021-03231-6
[27] EISMA J, WESTERWEEL J, VAN DE WATER W. Do coherent structures organize scalar mixing in a turbulent boundary layer?[J]. Journal of Fluid Mechanics, 2021, 929: A14. doi: 10.1017/jfm.2021.821
[28] XU C Y, LONG Y G, WANG J J. Entrainment mechanism of turbulent synthetic jet flow[J]. Journal of Fluid Mechanics, 2023, 958: A31. doi: 10.1017/jfm.2023.102
[29] GAMPERT M, KLEINHEINZ K, PETERS N, et al. Experimental and numerical study of the scalar turbulent/non-turbulent interface layer in a jet flow[J]. Flow, Turbulence and Combustion, 2014, 92(1): 429–449. doi: 10.1007/s10494-013-9471-y
[30] HOLZNER M, LIBERZON A, NIKITIN N, et al. Small-scale aspects of flows in proximity of the turbulent/nonturbulent interface[J]. Physics of Fluids, 2007, 19(7): 071702. doi: 10.1063/1.2746037
[31] WESTERWEEL J, HOFMANN T, FUKUSHIMA C, et al. The turbulent/non-turbulent interface at the outer boundary of a self-similar turbulent jet[J]. Experiments in Fluids, 2002, 33(6): 873–878. doi: 10.1007/s00348-002-0489-5
[32] MANDELBROT B B. The fractal geometry of nature[M]. San Francisco: W. H. Freeman, 1982.






 下载:
下载: