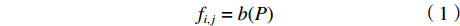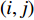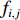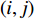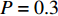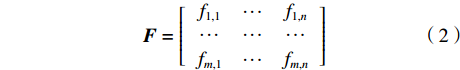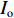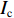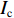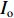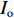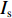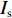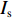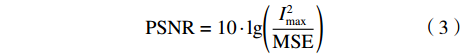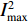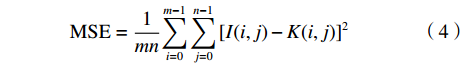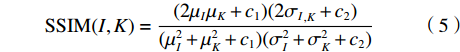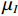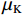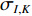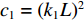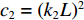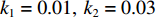0   引　言

高速摄影技术是爆炸力学、流体力学、弹道观测等科研试验中重要的测试手段，用于观测、记录快速变化的物理现象^[1-5]。高速摄影系统包括胶片式高速摄影系统和电子式高速摄影系统。与胶片式高速摄影系统相比，电子式高速摄影系统^[6]成本低、使用灵活，具有极大的应用前景。但是，受电子系统带宽限制，它难以长时间拍摄高速视频。达争尚等^[7]通过理论分析与实际应用测试指出，电子系统带宽限制是制约电子式高速摄像系统应用于导弹观测的主要因素，使之还不能完全取代传统的胶片式高速摄影系统。

近十年来电子技术的快速发展使电子系统带宽得到极大提高，但仍无法满足高达20 GB/s的海量视频数据实时传输需求。为拍摄高速视频，现有电子式高速摄影系统通常将拍摄的图像数据存储于内存中；但有限的内存容量难以存储海量视频，无法持续拍摄高分辨率图像序列（如弹道观测拍摄）。为延长拍摄时间，现有电子式高速摄像机通常采用TOM（Thin Out Mode）模式^[6]降低成像分辨率，以增加帧率或延长拍摄时间；但降低图像分辨率会影响图像清晰度，无法满足定性分析和定量测量需求。

图像数据在空域、频域都存在极大冗余，通过图像压缩方法，可在保证在图像内容不明显失真的情况下，降低图像传输与存储容量。近年来，学者们针对图像/视频压缩问题，研究了大量压缩算法，比如JPEG、MPEG、H.264、H.265等，特别是H.265等视频压缩算法，极大地降低了视频数据量。但是，现有图像/视频压缩算法涉及图像频域变换、帧间预测等复杂操作，计算量大，以目前硬件水平还不能在电子式高速摄像机中实现海量视频数据实时压缩。

学者们受压缩传感理论^[8]的启发，提出了压缩成像技术：在光学成像过程中，通过光学物理方法获取比传统成像方法更少的数据，达到降低成像数据量的目的，再通过压缩感知重建算法，计算期望图像。如图1所示，压缩成像^[9-10]采用只有1 像素的摄像机对观测对象进行多次成像，每次成像获取被观察对象的1次测量值（1 像素）。对于一幅256 像素×256 像素的图像（图1（b）），经过1300次单像素成像，获取1300个像素值，再通过压缩感知重建算法估计原图像内容（图1（c））。单像素相机具有成本极低的优势，以1个像素即可完成任意分辨率图像获取。实现压缩成像的核心在于找到合适的光学物理方法模拟压缩感知中测量矩阵的观测过程。学者们将编码光圈^[11]、编码曝光^[12]等计算摄影技术用于压缩成像，并取得了一定成果。Raskar等^[11]采用编码光圈实现了周期性运动对象的压缩成像；Gu等^[12]采用编码曝光实现了高速成像；Agrawal等^[13]采用低速摄像机阵列合成了高速视频；Liu等^[14]采用偏振光选通技术实现了10倍超帧率成像。压缩成像为实现低成本高速成像开辟了一条新的道路，但其采用的物理方法还难以落地应用。

对于电子式高速摄像系统而言，现有CCD特别是ICCD的感光灵敏度已能满足高速成像需求，制约其应用的是电子系统带宽不足的问题。因此，对拍摄图像进行压缩以降低图像数据量，在现有带宽条件下实现高速视频同步传输与存储，具有极大实用价值。为此，本文提出一种简单、易于硬件实现的图像压缩方法——伯努利采样图像压缩。在CCD或CMOS图像采集过程中，通过伯努利采样，随机保存部分像素，实现图像快速压缩；在计算机端，通过对未采样像素进行估计实现图像解压缩（重建）。

图  1  单像素相机及成像结果^[9]

Fig.  1  Single pixel camera and its imaging result^[9]

下载: 全尺寸图片 幻灯片

1   伯努利采样图像压缩

为了降低计算复杂度、减小计算量、实现简单高效的图像压缩，本文在图像空域进行伯努利采样，达到像素流同步压缩目的。伯努利采样定义为服从伯努利分布的随机抽样过程，伯努利分布函数为：

其中：$(i,j)$表示像素坐标；P为分布概率；$ {f_{i,j}} $为分布输出结果，取值为1或0，1表示$(i,j)$位置处像素被采样，0表示不被采样。定义图像压缩率 r =1–P，P越大，采样像素越多，图像压缩率 r 越小。

图2（a）为源图像（Lena的人脸图像），图2（b）为对图2（a）进行伯努利采样的图像，未采样像素分布输出结果设置为0，$P = 0.3$，图2（c）为根据已经采样的像素采用开关中值滤波（Switch Median Filter, SMF）^[15]算法恢复出邻域内未采样像素的结果。从图2可以看出重建图像与原始图像之间不存在明显视觉差异。因此，在高速摄像机成像采集过程中，对CCD或CMOS采集的图像像素执行伯努利采样操作，抽取部分像素，可达到图像压缩目的。

图  2  图像伯努利采样与重建效果示例

Fig.  2  Image Bernoulli sampling and reconstruction effect example

下载: 全尺寸图片 幻灯片

在具体实现时，可根据式（1）设置一个采样标记矩阵，根据标记矩阵中标志位执行抽样操作。具体方法为：根据设定的压缩率 r，设定伯努利分布参数 P = 1– r ，根据压缩图像尺寸（m×n）生成一个$ m \times n $维的标记矩阵：

标记矩阵F中元素取值为1或0，1表示当前位置像素进行采样，0表示当前位置像素不采样，m、n分别为图像高度和宽度。

伯努利采样图像压缩过程如图3（a）所示，在摄像机端，通过标记矩阵F判定原始图像${I_{\rm{o}}}$中像素是否被采样，重新排序后得到压缩图像${I_{\rm{c}}}$。

图  3  伯努利采样图像压缩及图像重构算法流程

Fig.  3  The framework of image compression with Bernoulli sampling and image reconstruction

下载: 全尺寸图片 幻灯片

2   压缩图像重建

伯努利采样图像压缩本质上是对原始数据在空域进行随机抽样，因此，图像解压就是利用采样的已知像素去估计未采样的未知像素的过程。计算机端的具体流程如图3（b）所示：首先，根据标记矩阵F计算压缩图像${I_{\rm{c}}}$中像素在原始图像${I_{\rm{o}}}$中的坐标，并保存为查找表（Look Up Table, LUT）；其次，根据查找表对压缩图像进行重排列，得到与${I_{\rm{o}}}$同分辨率的重排列图像${I_{\rm{s}}}$；最后，根据图像局部邻域相关先验知识，选择合适的方法，根据采样像素估计出未采样像素，完成图像解压缩（重建）。

当把重排序图像${I_{\rm{s}}}$中的未采样像素取值为0时，${I_{\rm{s}}}$中未采样像素估计问题可视为图像冲击噪声去除问题。中值滤波是最早应用的冲击噪声去除方法。因中值滤波并未检测、识别冲击噪声，导致找到的中值仍可能包含噪声，使图像修复效果欠佳。针对该问题，Chen等^[15]提出了开关中值滤波算法，在进行中值滤波前，先对图像邻域内像素执行冲击噪声检测，仅利用非噪声图像像素估计中值。与中值滤波方法相比，开关中值滤波算法在估计中值时，利用的是真实的非噪声像素，从而大幅提升了重建效果。本文选择开关中值滤波算法用于未采样像素估计。

当图像压缩率增大时，相同局部邻域内采样像素数量减小。比如：当压缩率为50%时，3×3邻域内约有4 像素被采样；当压缩率为90%时，3×3邻域内可能没有像素被采样，此时将无法进行未采样像素估计。在开关中值滤波算法^[15]中，可以采用增大邻域尺寸的方式解决，但增大邻域尺寸会导致图像重建时间大幅增加。针对该问题，本文对开关中值滤波算法^[15]进行了改进，提出了小尺寸邻域迭代开关中值滤波算法。基本思想是：设定局部邻域窗口尺寸后，进行循环迭代，每一轮循环在对未采样像素进行估计时，只在设定尺寸邻域内进行未知像素估计，直至所有未采样像素都完成重建；在循环迭代过程中，重建的像素在下一轮循环迭代中视为已采样像素。小尺寸邻域迭代重建方法可以适应任意压缩率图像，当压缩率低时，迭代次数较少；当压缩率高时，迭代次数增加。在高压缩率情况下，与采用更大邻域尺寸的开关中值滤波算法^[15]相比，图像重建速度更快。

3   实验与分析

3.1   实验方法

选用图2中的Lena图像（Image 1）和原子弹爆炸图像（Image 2）对本文方法进行验证，图像压缩率分别设定为90%、95%、99%。TOM是高速摄像机通过降低图像分辨率提升帧率的方法，为此，本文模拟高速摄像机TOM成像方式，并采用插值方法对低分辨率图像进行放大。定量分析采用常用图像质量评价标准：峰值信噪比PSNR、图像结构相似性SSIM。PSNR定义为：

其中，${I_{\rm{max}}^2}$表示图像像素最大值，本文取255；MSE为均方误差，定义为：

其中，I（i，j）表示大小为m×n的原始图像像素，K（i，j）表示测试图像像素。

SSIM的定义如下：

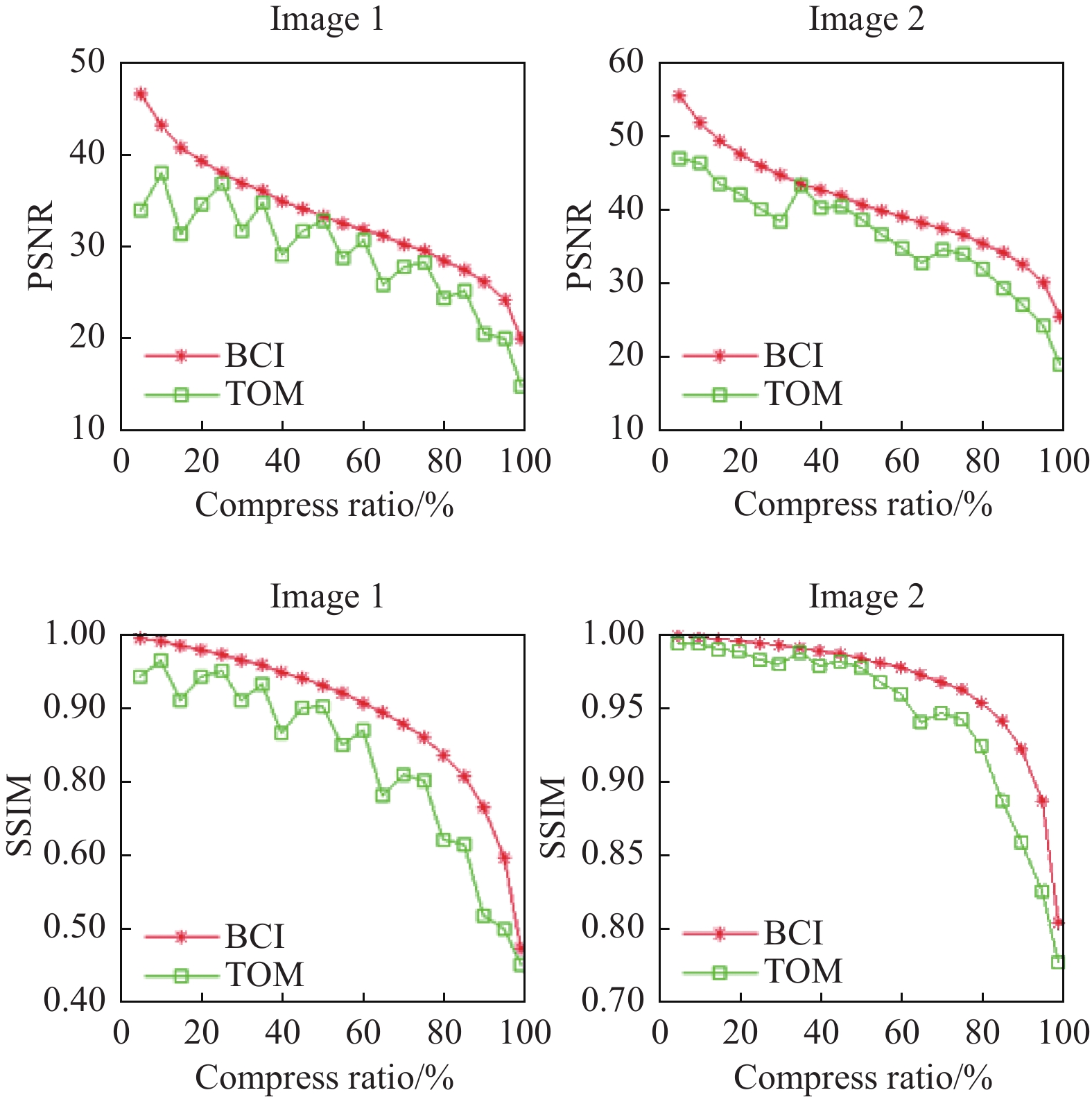
其中，$\;{\mu _{{I}}}$、$\; {\mu _{{{\rm{K}}}}}$为原始图像、测试图像像素的均值；${\sigma _{{I}}}{\text{、}} {\sigma _{{K}}}$为原始图像、测试图像像素的方差；${\sigma _{{I,K}}}$为原始图像、测试图像像素的协方差；${{{c}}_1} = {({k_1}L)^2}$、$ {c_2} = {({k_2}L)^2} $为用于维持稳定的常数，L为像素值的动态范围，$ {k}_{1}=0.01,\;{k}_{2}=0.03 $。

图4为Image 2分别在99%、95%、90%压缩率下的图像压缩、重建结果，图5为Image 1、Image 2在不同压缩率条件下的PSNR、SSIM定量测量结果。其中，TOM为高速摄像机低分辨率成像 + 插值放大方法，BCI为本文方法。

图  4  Image 2试验结果

Fig.  4  Experimental results of image 2

下载: 全尺寸图片 幻灯片

图  5  PSNR、SSIM定量分析结果

Fig.  5  The quantity comparison results of PSNR and SSIM

下载: 全尺寸图片 幻灯片

采用小尺寸邻域迭代开关中值滤波算法进行压缩图像重建时，在压缩率为99%时，邻域尺寸设置为11×11，经5次迭代，完成图像重建；在压缩率为95%时，邻域尺寸设置为7×7，经4次迭代，完成图像重建；在压缩率为90%时，邻域尺寸设置为5×5，经2次迭代，完成图像重建。

与图1（b）中单像素相机^[9]获取的R字母图像进行对比，单像素相机进行了1300次测量，重建图像分辨率为256像素×256像素，本文等效压缩率为98%，对比结果如图6所示。

图  6  与单像素相机压缩成像结果对比

Fig.  6  Comparison results with single pixel camera

下载: 全尺寸图片 幻灯片

3.2   实验结果与分析

在图4中，第一行图像为Image 2的原始图像；第二行为TOM采集图像，从左至右，分别为按原图像分辨率的0.01、0.05、0.10大小进行降分辨率成像（TOM采集图像实际尺寸较小，为了方便展示，对采集图像进行了一定放大）；第三行为TOM采集图像进行插值放大的结果；第四行为伯努利采样图像，未采样像素赋值为0，从左至右，压缩率r分别为99%、95%、90%；第五行为采用小尺寸邻域迭代开关中值滤波算法对第四行采样图像重建的结果。

在图4中，压缩率达到极限（99%）时，TOM采集图像信息损失严重，在插值放大图像中，已无法看出与原子弹爆炸相关的任何影像；而本文方法（第五行）保留了原子弹爆炸场景粗略信息，可以辨别。随着压缩率的降低，重建图像细节不断丰富。当压缩率降到90%时，本文算法可以清晰地展现原子弹爆炸影像，但TOM + 插值方法结果仍较模糊。

从图4可以看出，随着压缩率增大，图像压缩后空间尺度分辨率降低。比如：当压缩率为90%时，从概率上看，在3×3邻域内会采样1 像素，从而部分保留3×3邻域空间尺度信息；当压缩率增大到99%时，从概率上看，在10×10邻域内会采样1 像素，此时，仅能部分保留10×10邻域空间尺度信息，与90%压缩率相比，损害了图像空间尺度信息。不过，从图4中的重建图像细节可以看出，本文算法的空间尺度损失明显小于TOM + 插值方法。对于高速成像时间尺度，存在同样的规律。

图5是两种方法进行PSNR、SSIM定量对比结果。其中，PSNR越大效果越好，SSIM越接近1效果越好。在两个定量对比中，本文算法都优于TOM + 插值方法。采用本文方法，Image 1、Image 2的PSNR在压缩率为99%时达到了20.20、25.60，在压缩率为90%时达到了26.00、32.47。由此可见，本文算法可在一定信噪比条件下实现高速摄像机图像高效压缩。

图6（a）为单像素相机^[9]成像目标，图6（b）和（c）分别为单像素相机和本文方法结果。可以看出，与单像素相机重建图像相比，本文算法得到的图像细节更丰富，且图像尺寸与真实图像更接近。由于单像素相机需要特殊光学单元用于模拟压缩感知过程，因此，它无法直接与现有高速摄像机进行结合；同时，单像素相机1次只能获取1个测量值，获取目标图像需多次测量，这使单像素相机难以应用于高速成像场景。本文算法仅在高速成像采集过程中对图像传感器获取的图像执行伯努利采样操作，无需额外光学机构，只需在图像采集软件上进行适当调整即可应用于现有高速摄像机中。当采用FPGA实现上述操作时，还可实现与像素时钟同步的像素流实时压缩。

本文方法可适用于以下高速摄像机：科学级高速相机，如FASTCAM，其成像分辨率为1024 像素×1024 像素，满画幅帧率为20000 帧/s，图像位深为8 bits时，数据带宽为20 GB/s；工业级高速相机，比如NXA5，其分辨率为2560 像素×1920 像素，满画幅帧率为700 帧/s，位深为8 bits时，传输容量为3.5 GB/s。上述两类相机的数据传输带宽需求，都超过了现有最快摄像机数据接口CLHS-F的极限（1.2 GB/s）。针对该问题，现有高速摄像机采用具有更高数据带宽的DDR内存进行海量高速图像序列存储。DDR成本较高，容量有限。比如FASTCAM 8GB型高速相机，在分辨率为1024 像素×1024 像素，帧率为20000 帧/s时，只能拍摄0.399 s。此外，DDR内存是断电数据丢失的存储介质，在使用过程中必须持续供电，并在拍摄结束后需及时将数据转移到固态非失电存储介质中（如SSD硬盘）。若采用本文方法对其进行软件改造，在相同成像参数条件下，当压缩率设置为90%时，拍摄时长可达到3.99 s。同样地，对于工业级高速相机，当压缩率设置为85%时，即可采用现有标准数据接口进行实时数据传输，压缩后数据带宽需求为0.52 GB/s，采用CLHS-F接口即可。因此，本文方法与磁盘矩阵结合，即可实现长时高速成像。

4   结论及展望

在高速成像过程中，采用伯努利采样方法对图像进行随机采样存储，可以达到高速图像实时压缩目的，显著降低高速摄像机数据传输带宽和存储容量需求，延长高速摄像机拍摄时长。与压缩感知技术相比，伯努利采样图像压缩无需额外的光学单元，仅需对现有高速摄像机软件进行改造即可实现。特别地，当采用FPGA时，可以极小的硬件成本实现与像素时钟同步的像素流实时压缩。

在高速序列成像中，时空域也存在较大冗余，本文仅展示了空域伯努利采样压缩，未来将开展时空域采样压缩以及感兴趣对象的非均匀采样压缩，以进一步提升高速成像序列压缩率，并更多地保留感兴趣对象的细节。虽然本文提出的小尺寸邻域迭代开关中值滤波算法实现了未采样图像重建，但重建图像细节还需提升，未来将采用稀疏表示^[16-17]、张量表示^[18]、自动编码器^[19]等方法进一步提升压缩图像重建质量。