Measurement and numerical simulation of flow field parameters of free flight spheres with flight velocity from 5 to 7 km/s in CO2
-
摘要: 为研究火星进入条件下的非平衡流动特性,在中国空气动力研究与发展中心超高速空气动力研究所弹道靶上测量了CO2中针对火星探测器进入速度范围5~7 km/s条件下的自由飞圆球的激波脱体距离。实验数据基于阴影法测量,并将其与数值计算结果进行对比,进一步计算了实验流场温度和组分分布等流场参数。一般认为激波脱体距离随来流速度升高而呈单调减小趋势,但研究结果表明:实验状态下,圆球飞行速度约5.5~7.0 km/s的范围内,圆球激波脱体距离随飞行速度升高而增大;采用Park的双温度非平衡模型和5组分6反应的CO2化学反应动力模型可基本再现本文自由飞圆球激波脱体距离的实验测量数据;根据计算结果推测,本实验状态下自由飞圆球波后靠近激波一侧区域的流场主要处于热化学非平衡状态;当来流速度在约5.5~7.0 km/s的范围内时,流场组分CO开始发生显著离解,是引起圆球激波脱体距离在该速度范围内随速度升高反而增大的可能原因。Abstract: To investigate the nonequilibrium flow characteristics under Mars entry condition, shock standoff distances over free flight spheres with flight velocities from 5 to 7 km/s in CO2 are measured in the ballistic range at Hypervelocity Aerodynamics Institute of China Aerodynamics Research and Development Center (HAI, CARDC). Test data are measured by the shadowgraph and compared with calculated results, based on which the temperature and species profiles of the test flow field are further calculated. Shock standoff distance is generally supposed to decrease monotonously as the free steam velocity increases. However, it is found through the present test results that, the shock standoff distances over spheres actually increase with the increase of the flight velocity from 5.5 to 7.0 km/s. Using Park's two-temperature model and a 5-species 6-reactions chemical reaction model can basically reproduce the measured shock standoff distances of the present test. It is shown from the test results that the flow field shortly after the shock over the spheres is mainly in theromchemical nonequilibrium. The specie CO starts to dissociate at the free stream velocity from 5.5 to 7.0 km/s, which is the possible cause of the increase of the shock standoff distances over spheres within this range of velocity.
-
0 引 言
附着在交通工具表面的边界层流态大部分为湍流,其所产生的摩阻较层流边界层高出约一个量级。通过控制湍流边界层内多尺度流动结构可有效减小边界层的摩阻并实现总阻力的降低,对节能减排具有重要意义。
随着雷诺数的升高,湍流边界层内小尺度流动结构对湍动能和摩阻的贡献逐渐降低,以近壁面小尺度结构为主要控制对象的传统主/被动控制技术的减阻效果随之降低。近期对湍流边界层内跨流层跨尺度湍流结构相互作用的研究表明,外区大尺度流动结构影响着湍流边界层内跨流层能量传递和近壁雷诺切应力的生成[1-2]。因此,通过控制较高流层中的大尺度流动结构,既可直接降低其在壁面留下的大尺度摩阻成分,亦可抑制其对近壁小尺度结构的调制作用,降低小尺度结构对壁面摩阻的贡献,进而有望在高雷诺数条件下降低壁面摩阻[3-5]。
目前针对湍流边界层的减阻流动控制技术包括沟槽壁面[6-9]、超疏水壁面[10]、局部吹吸气[11]、近壁面行波[12]和涡流发生器(Vortex Generator, VG)[13-15]等。其中,VG具有结构简单、附加重量低、易于维护等优点,工程应用潜力较大。VG的特征高度h与边界层厚度δ相当(h/δ~1),存在附加压差阻力大的缺点。与之相比,微型涡流发生器(Micro Vortex Generator, MVG)几何尺寸更小(h/δ < 0.5)、附加阻力更低[16-17],具有比常规VG更好的减阻控制能力[13, 17-18]。因其特征高度h的差异,MVG也被称为低形阻VG(Low-Profile VGs, LPVG)[18-20]、亚边界层VG(Sub-Boundary-Layer VGs, SBVG)[21]、浸没式VG(Submerged VGs)[16]等。MVG有叶片形、楔形、车辙形及叉骨形等多种形状。当来流绕过MVG时,在其下游会形成较为稳定的时均流向涡对,从而对近壁流动施加控制。
目前,对MVG流动控制技术的研究主要集中于3个方向:1)分析不同形式MVG在零压梯度或逆压梯度边界层中诱导产生的流动结构及其沿程演化规律[19, 21-22];2)应用MVG进行边界层分离流动控制[18, 20-21];3)将MVG应用于二维翼型、三维机翼、机身等处进行流动减阻试验[20-21, 23-26]。为解决MVG在湍流边界层减阻控制中的工程应用问题,需明确MVG对流场产生有效控制的流向范围。文献[20]中提到,当基于边界层动量厚度θ的特征雷诺数Reθ ≈ 3.5 × 105时,MVG产生的时均流向涡对沿程抬升并在其下游约50h处耗散殆尽。Zaman等[22]的研究表明,当Reθ ≈ 1.1 × 104时,MVG所产生的流向高、低速流动区域沿主流方向逐渐融合,并在其下游约24h处形成较厚的均匀低速流层。
本文针对上述第一个研究方向开展实验测量,旨在研究MVG对经典零压梯度湍流边界层不同下游位置流动特性和摩阻的影响,为掌握MVG控制效果的沿程演化规律提供新的认识,为MVG在中高雷诺数湍流边界层中的减阻流动控制应用提供机理支撑。为此,本文使用体视粒子图像测速(Stereo-scopic Particle Image Velocimetry, SPIV)技术和免标定双层热膜摩阻传感器,在低速风洞中测量中等雷诺数条件下平板湍流边界层内单排楔形MVG阵列下游不同流向站位的法向–展向平面内的三分量速度场和当地壁面摩阻,使用统计分析、能谱分析和本征正交分解(Proper Orthogonal Decomposition, POD)等方法研究MVG对湍流边界层内流场统计特性和流动结构的影响,并讨论MVG下游摩阻的沿程变化及MVG几何参数对减摩阻能力的影响。
1 实验设备与研究方法
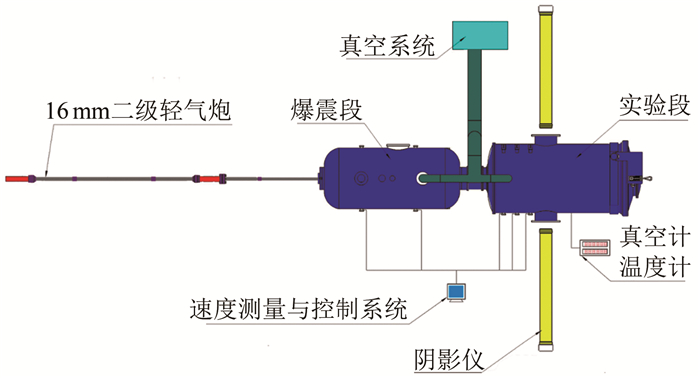
1.1 实验模型布置
风洞实验在北京航空航天大学D6低速风洞中进行。该风洞为直流吸气式,风速可调范围为0~50 m/s。实验段总长度为5 m,收缩比约为9∶1,采用变截面设计以减小洞壁体发展边界层对主流区流场均匀性的影响,其入口、出口横截面尺寸分别为0.4 m × 0.5 m、0.48 m × 0.5 m。
实验模型布置如图1所示。在风洞实验段内放置长4.5 m、厚0.015 m、宽0.40~0.48 m的有机玻璃平板,用于产生零压力梯度平板湍流边界层。平板距风洞底壁0.085 m,平板前缘距风洞实验段入口约0.1 m,前缘具有9.5°切角以防止流动在前缘产生局部分离。在距平板前缘0.300 m的下游位置,沿展向布置一根直径1 mm的圆柱形碳棒作为绊线,以触发边界层转捩。本文所使用的笛卡尔坐标系原点位于平板展向中心处MVG后缘与壁面的接触点,x、y、z分别代表流向、法向和展向,各方向的速度、时均速度和脉动速度分别记为(U、V、W)、($\overline{U}$、$\overline{V}$、$\overline{W}$)和(u、v、w)。U∞为自由来流速度。如无特殊说明,在下文光滑壁面湍流和MVG壁面湍流各工况结果中,具有上标“+”的速度和长度单位均已使用光滑壁面湍流边界层的内尺度(摩擦速度uτ及涡黏尺度l*)作无量纲化。
在距绊线3.1 m的下游位置,沿展向布置一排3D打印加工的MVG阵列。边界层在此流向位置已经完全转捩为湍流边界层。表1为自由来流速度U∞ = 14 m/s时该处湍流边界层的主要特征参数,其中Reτ为摩擦雷诺数(Reτ = uτδ/ν,ν为运动黏性系数),Reθ为动量厚度雷诺数,H为形状因子,Δy+、Δz+为空间分辨率,uτT/δ为以边界层外尺度无量纲的采样总时长(T为各工况实验的拍摄时间,用于衡量计算结果是否收敛)。上述特征参数系利用Chauhan等[27]提出的复合速度型公式对SPIV所测流向时均速度型函数${\overline{U}}^{ + }$(y+)进行拟合得到,综合考虑了内区及尾迹区内的流向时均速度的分布特点。
表 1 光滑壁面湍流边界层主要特征参数Table 1 Main characteristic parameters of the studied smooth-wall TBLU∞/(m·s−1) δ/cm uτ/(m·s−1) Reτ Reθ H Δy+ Δz+ uτT/δ 14 9.98 0.55 3453 6353 1.3 4.5 4.5 11000 1.2 MVG尺寸参数
MVG阵列特征尺寸如图2所示,其中l为流向长度,a为展向宽度,s为展向间距。本文以Ashill等[21]提出的前向三角楔形MVG(Forwards Wedge MVG)作为基准模型。该构型的MVG在已有研究中表现出最小的附加阻力及较优的控制性能[21, 28]。本文中,基准楔形MVG记作MVG0,其特征高度h0 = 5 mm、展向间距s0 = 0 mm(即相邻MVG无间隙)、展向宽度a0 = 10 mm、流向长度l0 = 20 mm。下文中的部分空间坐标将使用MVG0的特征高度h0进行无量纲化。此外,本文还对比研究了具有更大展向间距的MVG阵列(记作MVGs)及更高特征高度的MVG阵列(MVGh)。3种MVG阵列的主要几何参数如表2所示。
表 2 3种MVG阵列的主要几何参数Table 2 Main size of the three MVG array模型名称 s/mm h/mm l/mm a/mm MVG0 0 5 20 10 MVGs 5 5 20 10 MVGh 0 10 20 10 1.3 SPIV测量
当U∞ = 14 m/s时,对3种MVG阵列下游x/h0 = 10(近尾迹区)和x/h0 = 30(远尾迹区)这2个流向站位开展SPIV测量,获得该x站位y–z平面内的三分量速度场,并与无MVG条件下的光滑壁面流场测量结果进行对比。SPIV实验所使用的示踪粒子为平均粒径约2 μm的癸二酸二异辛酯(DEHS)液滴,通过网格状的分布式粒子布撒装置注入直流式风洞的进气口,被吸入风洞后流经收缩段、稳定段与主流充分掺混。双曝光脉冲激光器(Beamtech Vlite–380)激发能量为380 mJ/pulse的激光束,经透镜组整形后形成片光,从风洞侧壁垂直入射照亮测量平面。片光厚度为3 mm,以降低流向速度的测量不确定度。2台超高分辨率跨帧CCD相机(Imperx CLB–B6620M,分辨率为6600像素 × 4400像素)搭配180 mm微距镜头(TAMRON SP AF 180 mm F/3.5 MACRO1∶1)记录测量平面内的示踪粒子信息,其物理分辨率是0.016 mm/像素。2台相机分别布置于测量平面的上、下游两侧,以异侧布局的形式拍摄,相机透视角约为65°。使用经GPU加速的光流法速度场求解器(Multi–iterative Lucas–Kanade, MILK)[29]分别计算2台相机像平面内的粒子图像,获得二维二分量速度场,计算时对粒子图像进行了4次降采样,最终查询窗口尺寸为16像素 × 16像素,重叠率为75%,最大跨帧位移不超过12像素。之后,将2台相机像平面上的二维二分量速度场通过空间标定映射至测量平面,获得二维三分量速度场[30-32]。SPIV测量的有效视野范围为80 mm(法向)× 60 mm(展向)。示踪粒子以14 m/s的速度在跨帧时间20 μs内沿流向最多前进2.8 mm(小于片光厚度3 mm),可保证在跨帧粒子图像对上计算出互相关峰。各工况均采样1000对瞬时速度场,相机的采样频率为0.5 Hz。经检验,SPIV测量得到的湍流二阶统计量在此样本量下达到收敛。
应用MILK算法得到粒子位移的不确定度约为0.1像素[29],根据陈启刚和钟强[30]给出的估算方法,面内速度分量(V、W)的测量精度约为0.4%,面外速度分量(U)的测量精度约为1.0%。图3为SPIV测量得到的光滑壁面湍流边界层的流向时均速度型函数$ {\overline{U}}^{ +} $(y+)、雷诺正应力曲线($ {\overline{uu}}^{ + } $(y+)、$ {\overline{vv}}^{ + } $(y+)、$ {\overline{ww}}^{ + } $(y+))和雷诺切应力曲线($ {\overline{uv}}^{ + } $(y+)),同时给出Watanabe等[33]在Reτ = 3058条件下开展时间发展湍流边界层直接数值模拟(Direct Numerical Simulation, DNS)得到的结果作为对比,图中κ为卡门常数,${\overline{{{u}_{i}{u}_{j}}}}^{ + }$(i = j = 1, 2, 3)中u1、u2、u3分别表示脉动速度u、v、w。可以看到,SPIV实验测量得到的$ {\overline{U}}^{ + } $在近壁区y + = 10处仍然能够和DNS的结果相吻合;在雷诺应力方面,实验测量的$ {\overline{vv}}^{ + } $、$ {\overline{ww}}^{ + } $及$ {\overline{uv}}^{ + } $沿法向的变化趋势和DNS的结果吻合,两者的数值在y + = 30以上的流层基本一致;但$ {\overline{uu}}^{ + } $在y + = 10~20以内(内区)总体低于DNS的结果,究其原因,一方面是本文研究的体发展湍流边界层和DNS模拟的时间发展边界层[33]在流动特性上存在差异,另一方面则是本文采用的SPIV实验布置方式导致测量面外的U分量不确定度更大,且较高的片光厚度使得沿片光厚度方向的体平均效应较强,进一步降低了对U分量小尺度脉动的解析能力,从而使$ {\overline{uu}}^{ + } $内区测量结果相较于DNS结果偏低。
1.4 壁面摩阻测量
湍流边界层的壁面摩阻由高南和刘玄鹤[34]发展的一种新型免标定双层热膜摩阻传感器测量得到。该传感器装置如图4(a)所示,其工作原理为:在外接恒温开尔文电桥的控制下,双层热膜(镍箔)同温协同工作,此时下膜的存在将上膜向壁面的传热损失限制在总产热量的5%以内,使上膜热量几乎只传给流体,解决了传统单层热膜摩阻测量技术因壁面热损失而导致的测量偏差问题。Liu等在此基础上发展了根据上层热膜发热量计算壁面摩阻的免标定测量技术,其计算原理详见文献[35-37]。本文使用的矩形镍箔流向长度为1.75 mm、展向宽度为30 mm、厚度约为40 μm,可测量矩形镍箔表面的平均摩阻。传感器电桥所测得的瞬时电压数据由数据采集卡(NI USB–6259)实时采集,采样频率为1024 Hz。
壁面时均摩阻τw理论值[38]的半经验关系式为:
$$ {\tau _{\rm{w}}} = \frac{1}{2}\rho U_\infty ^2 \cdot 0.059\;2\;Re_x^{- 0.2} $$ (1) 式中:Rex表示以距边界层起点长度(绊线位置)为特征尺寸的雷诺数。
对各工况均开展7次摩阻重复测量实验,多次测量所得不确定度用误差条表示。摩阻单次测量持续时间为40 s(满足Ashill等[21]建议的收敛性准则)。如图4(b)所示,在不同自由来流速度下利用摩阻传感器测得的光滑壁面湍流边界层的时均摩阻τw(红色曲线)与式(1)估计的理论值(黑色曲线)相比较,二者最大误差约为4.7%。图4(b)中也给出了U∞ = 14 m/s时经SPIV所测$ {\overline{U}}^{ + } $(y+)估算所得的τw(蓝色点),比摩阻传感器的测量结果高14%。此外,本文还利用摩阻传感器测量了U∞ = 14 m/s时光滑壁面及3组MVG阵列下游x/h0 = 10~80范围内的壁面摩阻,研究发现:即便是大间距的MVGs阵列,摩阻传感器的展向测量尺寸仍然包含了2个MVG的展向周期尺寸,这意味着摩阻传感器获得的是具有展向平均意义的当地摩阻。
2 MVG下游速度场统计量
图5给出了3种MVG阵列下游近、远尾迹区2个x站位(x/h0 = 10和30)的y–z平面内的时均速度场。彩色云图表示垂直平面的流向速度分量$ {\overline{U}}^{ + } $,黑色箭头表示法向速度分量$ {\overline{V}}^{ + } $和展向速度分量$ {\overline{W}}^{ + } $合成的面内速度矢量。蓝色虚线为MVG阵列下游时均速度场$ {\overline{U}}^{ + } $ = 17等值线,红色点划线为光滑壁面工况下$ {\overline{U}}^{ + } $ = 17等值线。可以看到,在3种MVG阵列的下游近尾迹区,边界层近壁区均出现时均流向涡对和时均流向速度亏损区,时均流场的展向不均匀性显著,与前人研究相符[21-22];时均流向涡对结构强度及时均流向速度亏损区沿程逐渐衰减,在下游远尾迹区仅表现为近壁处的低动量层,展向不均匀性明显减弱。相较于基准MVG0工况(图5(b)),大间距MVGs工况(图5(a))在远尾迹区形成的近壁低动量层更薄、更接近光滑壁面水平;而更高的MVGh(图5(c))则显著增厚了远尾迹区的近壁低动量层。
考虑到MVG引入的展向不均匀性,对流场统计量沿展向进行了平均。图6给出了3种MVG阵列的近、远尾迹区(x/h0 = 10和 30)时均流向速度型和雷诺应力型的展向平均结果。图中,“$\langle \rangle $”表示沿时间和展向的系综平均,蓝色和红色的点划线分别为MVG阵列h = 5、10 mm所对应的法向位置。从图6(a)可以看到,MVG阵列对近尾迹区(x/h0 = 10)流场统计量的影响主要体现在3个方面:1)在MVG高度的流层(y = h)附近,产生低平均动量及高湍流脉动区,主要由MVG诱导产生的时均流向涡对和时均流向速度亏损区所致;2)在MVG高度以下的近壁区(y < h),雷诺正应力(即湍流脉动强度)及雷诺切应力均有所降低,可归因于时均流向涡对近壁湍流结构的规则化作用,在一定程度上反映了MVG的减摩阻潜力;3)MVG的h越高、s越小,对边界层的扰动作用越强,诱导产生的时均流向涡对越强。从图6(b)可以看到,在远尾迹区(x/h0 = 30),MVG对平均流场的诱导作用随时均流向涡对的耗散而减弱,但仍然在湍流脉动强度场上留下峰值“印记”,且峰值出现的流层相比近尾迹区更高,反映了时均流向涡对从壁面逐渐抬升的bottom-up过程[21, 39]。值得注意的是,在x/h0 = 30处,3种MVG阵列工况下近壁区(y + < 15)的流向雷诺正应力和雷诺切应力均低于光滑壁面湍流边界层的水平,降低的幅度仍和MVG高度及间距相关,预示MVG在远尾迹区具有减摩阻潜力。
3 展向能谱特性
为从尺度空间上厘清MVG对湍流脉动特性的影响,对SPIV测量得到的速度场进行展向能谱分析。图7给出了MVG0阵列近、远尾迹区(x/h0 = 10和30)u、v、w分量的展向预乘能谱及u和v的互相关展向预乘能谱,即$ {k}_{z}{\widehat{\phi }}_{{u}_{i}{u}_{j}} $(i = j = 1, 2, 3或i = 1, j = 2),同时给出光滑壁面的情况作为对比。各预乘能谱均使用所对应的光滑壁面工况的能谱峰值进行无量纲化,即${k}_{z}{\widehat{\phi }}_{{u}_{i}{u}_{j}}={k}_{z}{\phi }_{{u}_{i}{u}_{j}}/ {k}_{z}{\phi }_{{u}_{i}{u}_{j},\mathrm{光}\mathrm{滑}}^{{\rm{max}}}$。其余工况(MVGh和MVGs)的能谱特性与MVG0工况类似,受限于篇幅不再给出。如图7(a)所示,SPIV测量能够解析到光滑壁面能谱${k}_{z}{\widehat{\phi }}_{uu}$的内区峰P1和外区峰P2,峰值的法向高度和峰值波长均与前人的DNS结果[40]一致。此外,${k}_{z}{\widehat{\phi }}_{vv}$、${k}_{z}{\widehat{\phi }}_{ww}$的内区峰P1和${k}_{z}{\widehat{\phi }}_{uv}$的外区峰P2也和DNS结果[40]吻合,但现有的SPIV测量难以解析到${k}_{z}{\widehat{\phi }}_{uv}$在y+ ≈ 20处的内区峰。图7(b)表明,在MVG作用下,近尾迹区$ {k}_{z}{\widehat{\phi }}_{uu} $、$ {k}_{z}{\widehat{\phi }}_{vv} $、$ {k}_{z}{\widehat{\phi }}_{ww} $和$ {k}_{z}{\widehat{\phi }}_{uv} $的能谱中均出现一个独立的能谱峰PMVG(即第二外区峰),其所诱导的流动结构展向波长$ {\lambda }_{z}^{ + } $与MVG的展向周期(相邻MVG的中心距离,${\lambda }_{{\rm{MVG}}}^{+}$ ≈ 350,如图7(b)中竖直虚线所示)基本一致,其法向高度对应于图6显示的${{\langle uu \rangle }}^{+}$、${{ \langle vv \rangle }}^{ + }$、${{ \langle ww \rangle }}^{ + }$和${{ \langle uv \rangle }}^{ + }$在对数区的峰值位置。此外,近尾迹区$ {k}_{z}{\widehat{\phi }}_{uu} $和$ {k}_{z}{\widehat{\phi }}_{uv} $分量的外区峰P2有所增强,并能够持续到远尾迹区。从图7(c)可以看到,由MVG所导致的能谱峰PMVG在远尾迹区各分量能谱中基本消失,且$ {k}_{z}{\widehat{\phi }}_{uu} $、$ {k}_{z}{\widehat{\phi }}_{vv} $和$ {k}_{z}{\widehat{\phi }}_{ww} $的内区峰相较于光滑壁面工况均有降低、$ {k}_{z}{\widehat{\phi }}_{uv} $能谱内区峰值区域有所收缩,表明MVG对近壁小尺度结构的抑制及对内外区不同尺度结构间的传能与调制作用降低,导致图6中近壁处雷诺应力低于光滑壁面水平。
4 POD模态分解
对SPIV测得的光滑壁面及MVG阵列下游速度场用POD进行模态分解,以厘清MVG所引入的流动结构在湍动能层面的表征。使用Snapshot POD算法对各工况的1000帧三分量平面速度场进行POD分解[41-42]。图8给出了光滑壁面及MVG0阵列工况下各阶模态的能量占比及能量积累曲线,其中i为模态阶数。图9给出了光滑壁面及MVG0工况下近尾迹区(x/h0 = 10)和远尾迹区(x/h0 = 30)的部分典型POD模态的空间基$ {\varPsi }_{i} $(y, z),云图为流向分量$ {\varPsi }_{i}^{u} $,黑色箭头表示法向分量$ {\varPsi }_{i}^{v} $、与展向分量$ {\varPsi }_{i}^{w} $的合成矢量。
从图9可以看到,光滑壁面工况下,第1阶POD模态${\varPsi }_{i\;=\;1}$以贯通内外区的超大尺度结构为典型特性,高阶POD模态${\varPsi }_{i\;=\;5,\;10,\;20}$则表现出内外区分离的双层结构特征。MVG0阵列工况下,近尾迹区第1阶POD模态中出现了类似图5近壁处半圆形时均流向速度亏损区的“印记”结构,从壁面延伸到对数区中部。值得注意的是,该“印记”一直持续至第20阶模态,说明MVG所诱导的流动结构(时均流向涡对)贡献了整个SPIV测量视野范围内的大部分湍动能(即该流动结构与湍流边界层内的大、超大尺度结构对湍动能的贡献相当),并由此造成图8中MVG0阵列工况下低阶POD能量贡献率明显高于光滑壁面工况。这与Bai等[43]在湍流边界层内利用斜置沟槽产生大尺度流向环流时所观察到的各阶POD模态能量分布情况类似。在MVG0阵列下游的远尾迹区,其所诱导的流动结构不再明显呈现于低阶POD模态中,结合${{\langle uu \rangle }}^{+}$、${{ \langle vv \rangle }}^{ + }$及${{ \langle ww \rangle }}^{ + }$仍然在对数区存在峰值的观察,可以推测,MVG所诱导的时均流向涡对结构在远尾迹区难以维持规则的完整外形,而是衰减为沿展向蜿蜒的涡量层并继续影响速度统计量的分布。对比图9中的第20阶模态可以发现,MVG0诱导的流动结构影响了近壁处含能结构分布,间接表征了MVG对下游结构的控制作用。MVGs和MVGh阵列工况下的低阶POD模态在近、远尾迹区的空间分布特性与MVG0阵列工况下类似,不再另行给出。
5 MVG阵列的减摩阻特性
本节讨论MVG阵列下游的摩阻沿程变化,主要评估各型MVG阵列的减摩阻效果,并分析间距、高度对MVG减摩阻特性的影响。减摩阻率RD(Drag Reduction)根据下式计算:
$$ R_{\rm{D}}=\left(\frac{{\tau }_{光滑}-{\tau }_{{\rm{MVG}}}}{{\tau }_{光滑}}\right)\times 100\% $$ (2) 式中:$ {\tau }_{\mathrm{光}\mathrm{滑}} $与$ {\tau }_{{\rm{MVG}}} $分别为免标定双层热膜摩阻传感器所测的光滑壁面和MVG工况下同一流向位置的当地时均摩阻。
当U∞ = 14 m/s时,3种MVG阵列下游x/h0 = 10~80范围内减摩阻率RD的沿程变化如图10所示,其中误差条表示多次重复实验的不确定度。可以看到,在x/h0 = 10处,3种MVG工况下的当地时均摩阻相较于光滑壁面工况均略有增大(RD < 0),增阻量在5%以内。增阻的主要原因是MVG产生的时均流向涡对在该处距壁面较近,其诱导产生的上洗、下洗运动增强了近壁区各流层的动量掺混。当x/h0 ≥ 20后,3种MVG均呈现出明显的减摩阻效果,增大MVG阵列高度能显著提升减摩阻率。已有研究表明[21],高度越高的MVG阵列能够诱导时均流向涡对产生更大的环量,因而对近壁处湍流结构的抑制和规则化作用也更强,最终表现为减摩阻率的提升,这与Cheng等[4]以等离子体涡流发生器产生时均流向涡对减摩阻的研究结果相符(Cheng等通过增大电极电压提升时均流向涡对的强度,实现了减摩阻率的提升)。大间距MVG阵列所诱导的时均流向涡对展向排列稀疏(图5(a)),对边界层内流动结构的不规则运动影响作用有限,在摩阻测量中则体现为大间距MVGs的减摩阻率低于MVG0阵列。但更高更密的MVG具有更大的型阻,在实际应用时需考虑MVG所引起的附加阻力。高度更高、展向间距更小的MVG阵列的最优减阻位置更靠近上游,在峰值减阻率后,各型MVG阵列的减摩阻率均沿程逐渐衰减,但在x/h0 = 80处MVGh及MVG0仍然具有超过5%的减摩阻率,说明MVG阵列的减摩阻效果能够至少持续至下游80倍自身特征高度处。
6 结 论
在U∞ = 14 m/s、Reτ = 3453的湍流边界层中,利用SPIV及免标定双层热膜摩阻传感器对3种MVG阵列下游速度场统计特性及减摩阻的效果开展实验测量,结论如下:
1)MVG在近尾迹区诱导产生时均流向涡对和时均流向速度亏损区,并在MVG特征高度附近流层产生低平均动量及高湍流脉动区。随着时均流向涡对的沿程抬升,MVG对湍流统计量的峰值扰动也在下游抬升至更高的流层。此外,MVG引起近壁区雷诺切应力的降低,说明了MVG的减摩阻能力。
2)展向预乘能谱表明,MVG导致近尾迹区出现了第二外区峰值,其所诱导流动结构的展向波长与相邻MVG的中心距离一致,并显著影响了近尾迹区湍流边界层外区峰的强度与形貌。POD模态分析表明,MVG所诱导的流动结构与湍流边界层内的大、超大尺度结构对湍动能的贡献相当,并影响了近尾迹区近壁含能结构的分布。
3)实验证实MVG阵列具有减摩阻效果,减摩阻有效范围至少可持续至下游80倍自身特征高度处。
后续应在MVG减摩阻机理与参数影响规律等方面开展进一步研究,并在减阻应用中综合考虑MVG的减摩阻效果及其额外型阻。
致谢:北京航空航天大学龙彦光博士、朱熠辰博士生在2D–PIV的基础上开发并完善了本实验所用的SPIV基础程序。加拿大新不伦瑞克大学高南教授、大连航华科技有限公司刘玄鹤博士研发了本实验所用的免标定双层热膜摩阻测量设备,天津大学王昊博士生指导了热膜传感器的制备。北京航空航天大学张清福、于悦、李拓、徐颢文等多名研究生协助开展了实验测量工作。在此,对上述个人与机构提供的帮助表示感谢。
-
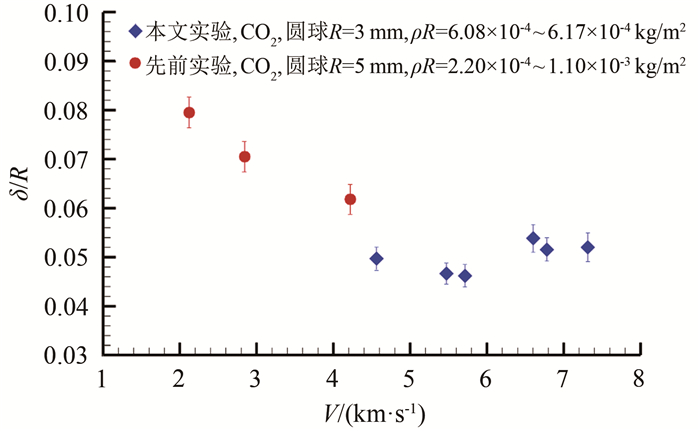
表 1 激波脱体距离实验测量数据和对应实验状态
Table 1 Measured shock standoff distances and corresponding test conditions of present test
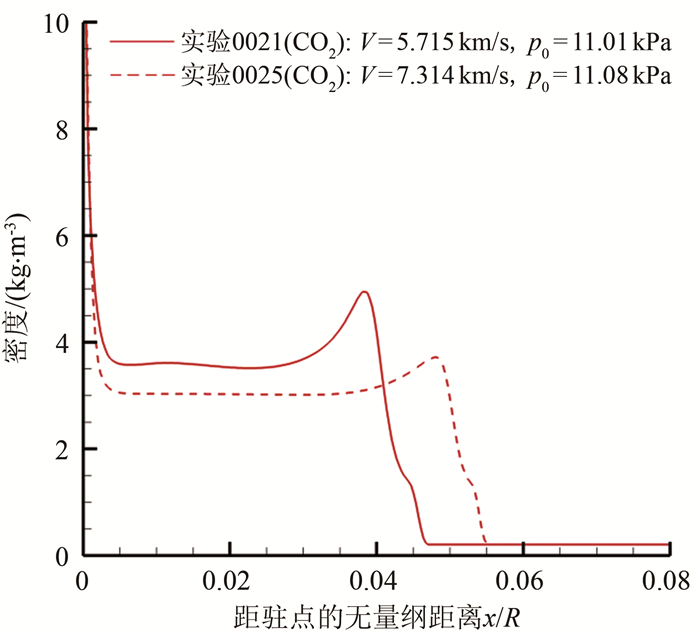
编号 模型直径D/mm 靶室温度T0/K 靶室压力p0/kPa 双尺度参数ρR/(kg·m-2) 模型速度V/(km·s-1) 马赫数Ma δ/R测量值 测量误差 0018 6 282.25 10.81 6.08×10-4 5.473 20.8 0.0467 ±4.53% 0021 6 283.15 11.01 6.17×10-4 5.715 21.7 0.0462 ±4.98% 0022 6 282.55 10.99 6.17×10-4 6.603 25.1 0.0538 ±5.20% 0023 6 282.55 10.99 6.17×10-4 6.781 25.7 0.0515 ±5.56% 0024 6 284.65 11.07 6.17×10-4 4.562 17.3 0.0497 ±4.62% 0025 6 285.15 11.08 6.17×10-4 7.314 27.6 0.0520 ±6.21% 表 2 双温度模型和5组分6反应模型计算的激波脱体距离与实验数据的偏差
Table 2 Comparison between the measured and calculated shock standoff distances using the two temperature model and 5 species and 6 reactions model
编号 δ/R测量值 测量误差 δ/R计算值 计算值相对测量值偏差 0018 0.0467 ±4.53% 0.0470 0.64% 0021 0.0462 ±4.98% 0.0474 2.60% 0022 0.0538 ±5.20% 0.0547 1.67% 0023 0.0515 ±5.56% 0.0547 6.21% 0024 0.0497 ±4.62% 0.0500 0.60% 0025 0.0520 ±6.21% 0.0557 7.12% -
[1] KUTTY P, KARLGAARD C D. Mars science laboratory aerodatabase trajectory reconstruction and uncertainty assess-ment[C]//Proc of the AIAA Atmospheric Flight Mechanics Conference. 2014.
[2] MAGIN T, CHAZOT O. Review of the VKI research on nonequilibrium phenomena in hypersonics[R]. AIAA 2012-0725, 2012.
[3] PARK C. Assessment of a two-temperature kinetic model for dissociating and weakly ionizing nitrogen[J]. Journal of Thermo-physics and Heat Transfer, 1988, 2(1):8-16. DOI: 10.2514/3.55
[4] PARK C, HOWE J T, JAFFE R L, et al. Review of chemical-kinetic problems of future NASA missions, Ⅱ:Mars entries[J]. Journal of Thermophysics and Heat Transfer, 1994, 8(1):9-23. http://www.onacademic.com/detail/journal_1000035806006310_8873.html
[5] KAY R D, NETTERFIELD M P. Thermochemical non-equilibrium computations for a Mars entry vehicle[R]. AIAA 93-2841, 1993.[C]//Proc of the 28th Thermophysics Conference. 1993.
[6] SUZUKI K, ABE T. Thermochemical nonequilibrium viscous shock-layer analysis for a Mars aerocapture vehicle[J]. Journal of Thermophysics and Heat Transfer, 1994, 8(4):773-780. DOI: 10.2514/3.611
[7] NOEDING H P, SCHRAMM J M. Numerical rebuilding of shock tube experiments in CO2 flow under conditions relevant for Mars entry probes[C]//Proc of the 11th AIAA/ASME Joint Thermophysics and Heat Transfer Conference. 2014.
[8] HORNUNG H, WEN C Y. Nonequilibrium dissociating flow over spheres[C]//Proc of the 33rd Aerospace Sciences Meeting and Exhibit. 1995.
[9] SHARMA M, AUSTIN J M, GLUMAC N G, et al. Expansion tube investigation of shock stand-off distances in high-enthalpy CO2 flow over blunt bodies[R]. AIAA 2010-1566, 2010.
[10] MACLEAN M, HOLDEN M. Catalytic effects on heat transfer measurements for aerothermal studies with CO2[R]. AIAA 2006-182, 2006.
[11] MACLEAN M, DUFRENE A, HOLDEN M. Spherical capsule heating in high enthalpy carbon dioxide in LENS-XX expansion tunnel[R]. AIAA 2013-0906, 2013.
[12] SHARMA M, SWANTEK A B, FLAHERTY W, et al. Experi-mental and numerical investigations of hypervelocity carbon dioxide flow over blunt bodies[J]. Journal of Thermophysics and Heat Transfer, 2010, 24(4):673-683. DOI: 10.2514/1.49386
[13] MACLEAN M, HOLDEN M. Numerical assessment of data in catalytic and transitional flows for Martian entry[R]. AIAA 2006-2946, 2006.
[14] MATTHEW G L, AUSTIN J M. Assessment of reflected shock tunnels for Mars entry vehicle ground testing[C]//Proc of the 2018 AIAA Aerospace Sciences Meeting. 2018.
[15] 柳森, 王宗浩, 谢爱民, 等.高超声速锥柱裙模型边界层转捩的弹道靶实验[J].实验流体力学, 2013, 27(6):26-31. http://www.syltlx.com/CN/abstract/abstract10409.shtml LIU S, WANG Z H, XIE A M, et al. Ballistic range experiments of hypersonic boundary layer transition on a cone-cylinder-flare configuration[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(6):26-31. http://www.syltlx.com/CN/abstract/abstract10409.shtml
[16] KIRK D B, INTRIERI P F, SEIFF A. Aerodynamic behavior of the viking entry vehicle: ground test and flight results[C]//Proc of the Guidance and Control Conference. 1977.
[17] BROWN J, YATES L, BOGDANOFF D, et al. Free flight testing in support of the Mars smart lander aerodynamics database[R]. AIAA 2002-4410, 2002.
[18] LIAO D J, LIU S, JIAN H X, et al. Measurement and calculation of shock stand-off distances over hypersonic spheres in CO2[C]//Proc of the 21st AIAA International Space Planes and Hypersonics Technologies Conference. 2017.
[19] 廖东骏, 柳森, 黄洁, 等. CO2中激波脱体距离的弹道靶实验测量和数值计算[J].实验流体力学, 2018, 32(3):69-74, 93. http://www.syltlx.com/CN/abstract/abstract11108.shtml LIAO D J, LIU S, HUANG J, et al. Ballistic range measure-ment and numerical calculation of shock standoff distances in CO2[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(3):69-74, 93. http://www.syltlx.com/CN/abstract/abstract11108.shtml
[20] Park C. The limits of two-temperature model[C]//Proc of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. 2010.
[21] WANG Z H, LIU S, XIE A M, et al. Shadowgraph imaging and post-processing for hypersonic boundary layer transition in ballistic range[J]. Journal of Flow Visualization and Image Processing, 2015, 22(4):229-238. DOI: 10.1615/JFlowVisImageProc.2016016555
[22] LOBB R K. Experimental measurement of shock detachment distance on spheres fired in air at hypervelocities[J]. The High Temperature Aspects of Hypersonic Flow, 1964, 68:519-527. http://www.sciencedirect.com/science/article/pii/B978148319828650031X







 下载:
下载: