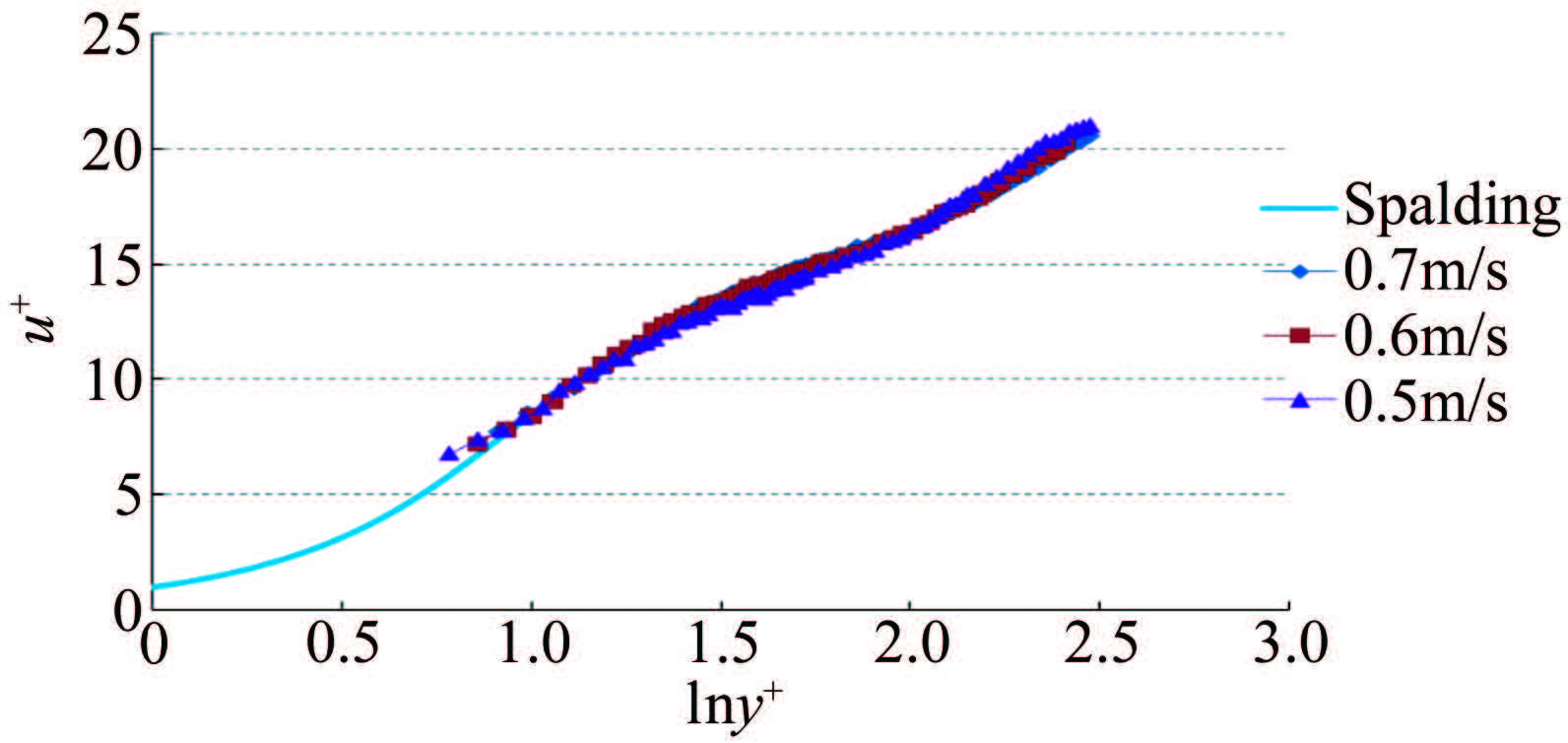
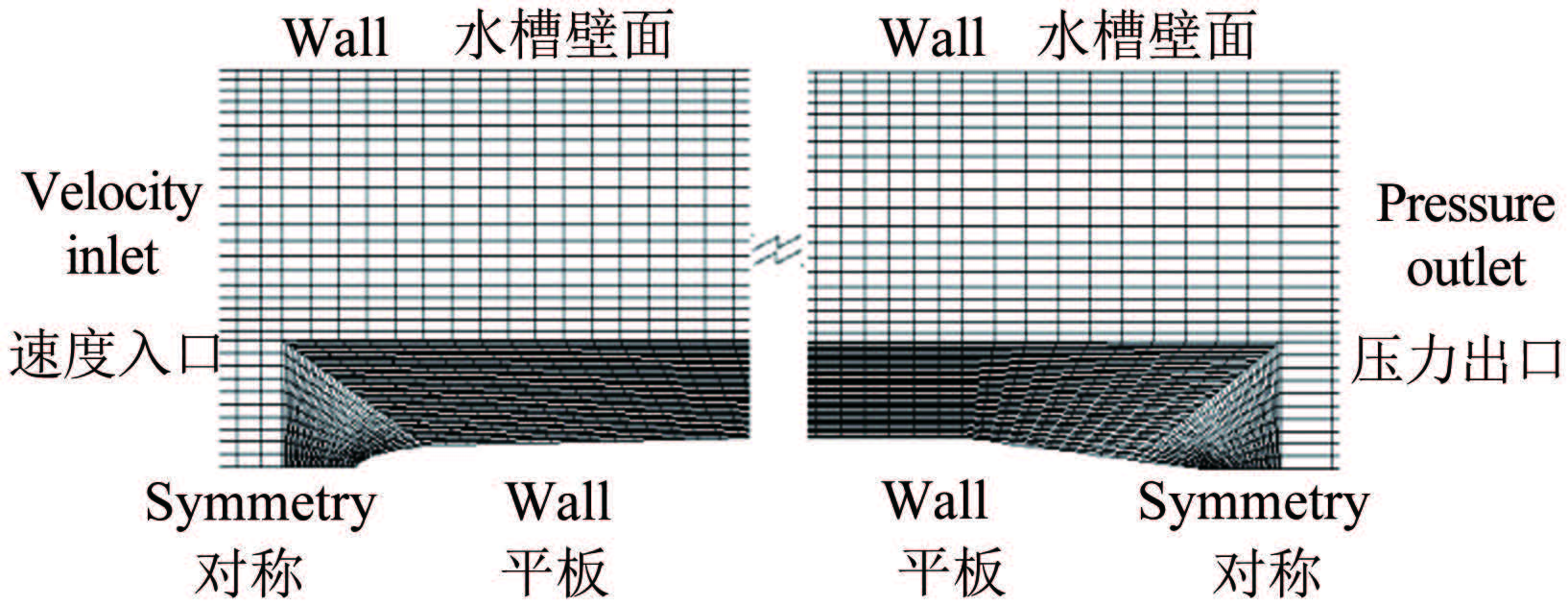
Experimental and numerical investigations of the boundary layer parameters of an underwater flat plate model
-
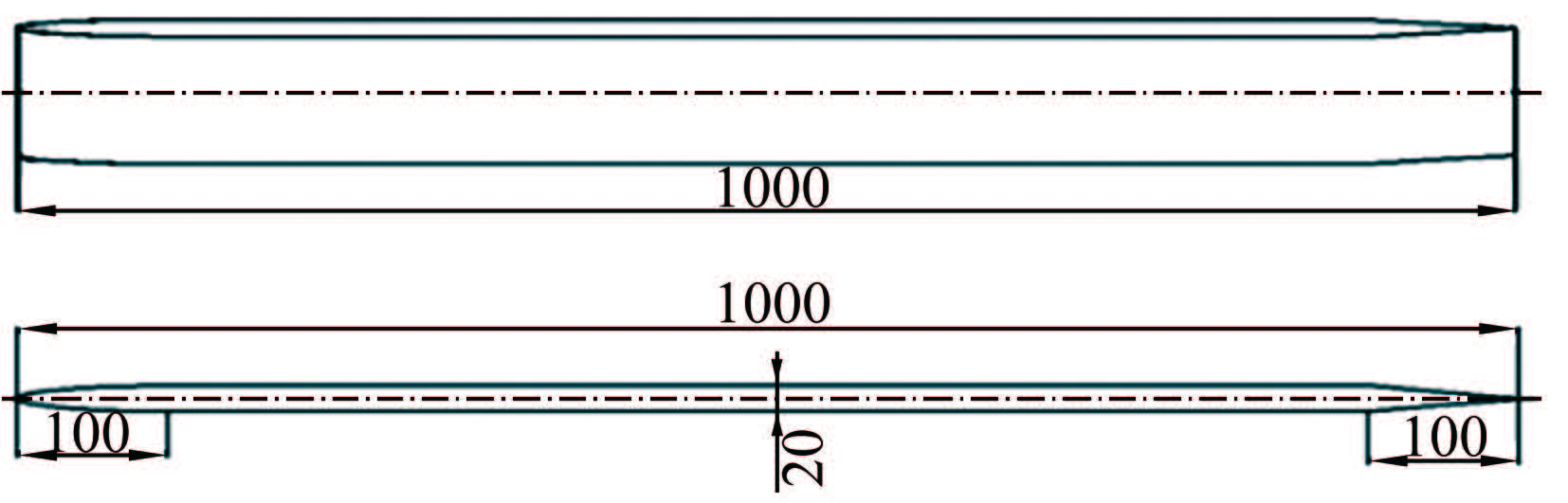
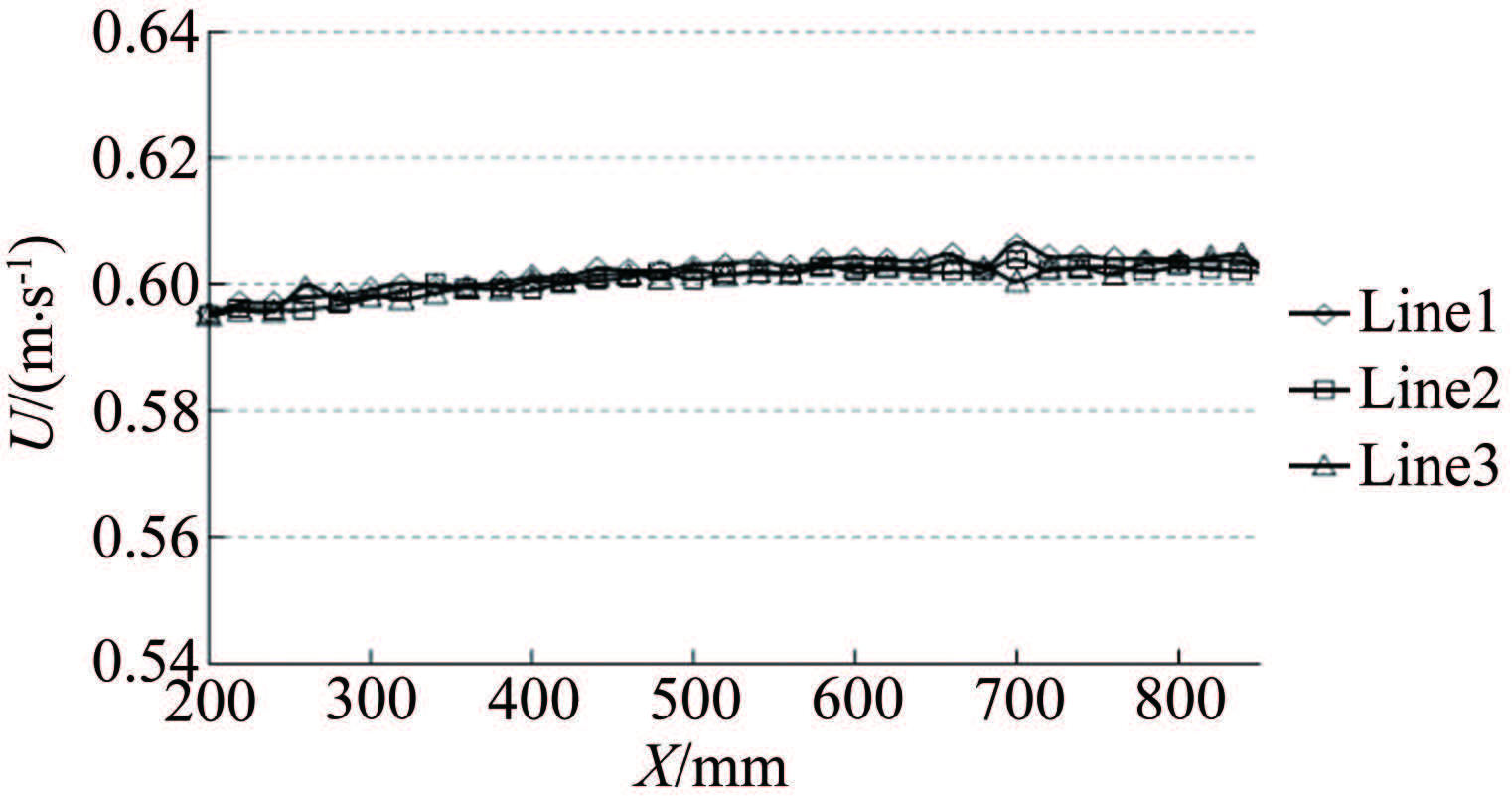
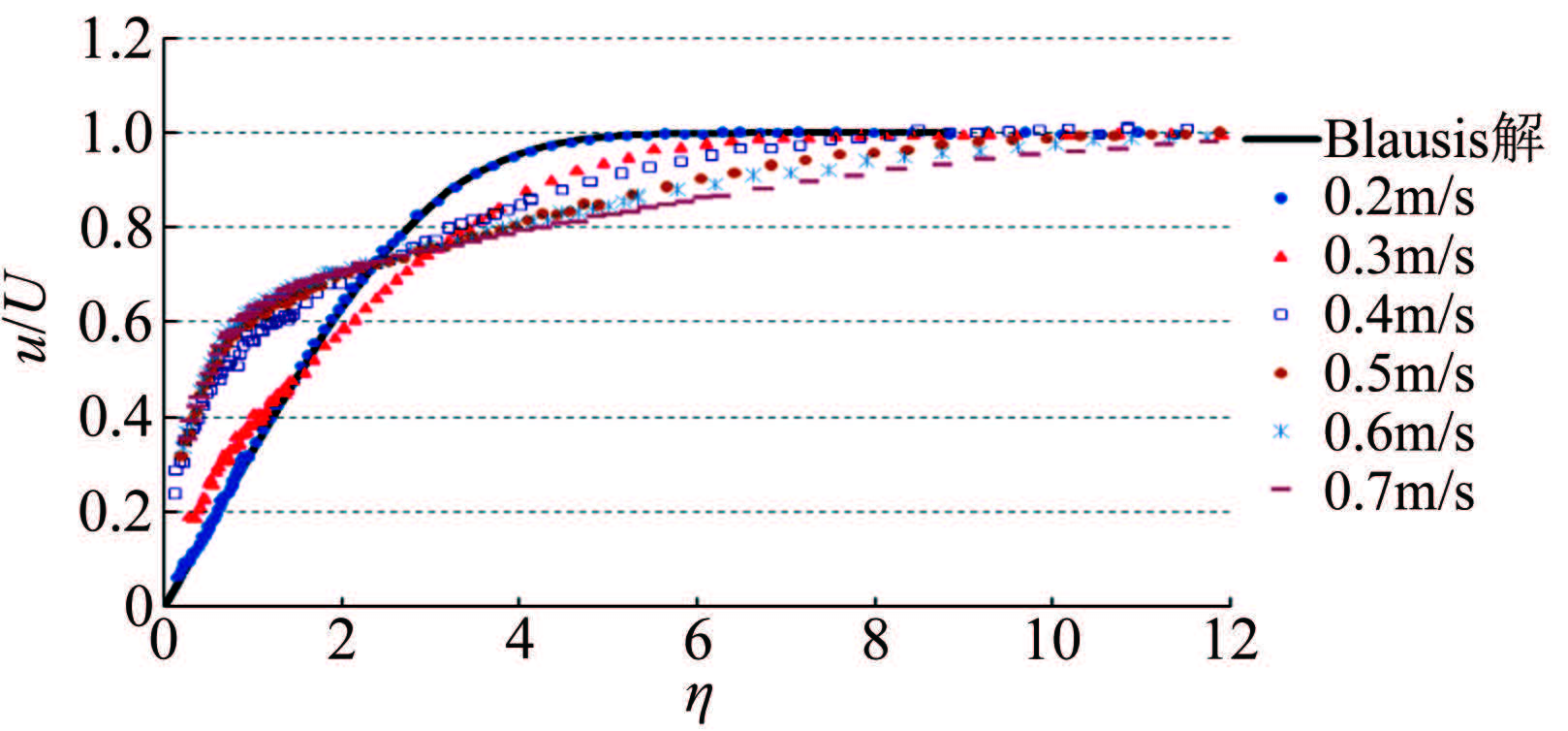
摘要: 利用LDV测试技术,在小型水槽中对零压力梯度的光滑平板边界层进行了平均速度剖面测量。利用测得的速度数据进行从壁面到对数律层尾区全壁面律的拟合求解获得壁面摩擦速度和其他边界层流动参数。在实验测量之外还开展了平板绕流CFD仿真分析,并将实验结果、仿真计算结果和平板经验公式计算结果进行比较。结果表明,基于LDV的全壁面律拟合求解平板表面边界层流动参数具有较高精度,结合仿真分析,可为利用平板开展水中MEMS壁面剪应力传感器标定提供理想的输入。Abstract: On the basis of the turbulent boundary layer mean velocity profile over a zero pressure gradient flat plate measured in a water flume using Laser Doppler Velocimetry (LDV), this paper obtains the friction velocity and other boundary layer parameters by using the fit of velocity data to the full boundary layer profile from the wall to the top of the log region. Complementary to the measurements, numerical investigations of the flow field around the flat plate have also been performed. The wall shear stress extrapolated from the profile curve is compared with empirical formula results and CFD results. The data agreement shows that the fit of the LDV measured velocity data to the full boundary layer profile is of high precision for measuring the boundary parameters. Combined with simulation analysis, it can provide the ideal wall shear stress input for the calibration of MEMS wall shear stress sensors.
-
Keywords:
- LDV /
- boundary layer parameters /
- CFD /
- underwater flat plate
-
0 引 言
气波制冷技术是20世纪70年代由法国NAT公司发展起来的一种新型的气体膨胀制冷技术[1]。气波制冷机又称“热分离机”[2],是通过压缩波与膨胀波的交互作用实现冷热能量交换,从而达到制冷目的的装置。波转子作为气波制冷机的核心部件,由多根压力振荡管环向排列组成。Hanson等[3]将固定长度的激波管沿时间叠加,构画出激波管波图,直观地展示了管内的波系运动。若将周向分布的压力振荡管沿轴线展开,即可得到如图1所示的波转子波图。图中,LT为低温端口,HP为高压端口,MP为中压端口,HT为高温端口,S1为压缩波,E1~E3为膨胀波。高压气体由HP入射振荡管,与管内低压形成压差并产生压缩波,随后压缩波发展为激波并向振荡管尾部传播。激波到达振荡管尾部时,HT打开,形成与激波运动方向相反的膨胀波。管道在激波作用下增压升温,在膨胀波作用下降压降温,激波和膨胀波之间由接触面分隔。在周期性喷射进气和排气下,激波和膨胀波在管内不断运动,低温气体从LT排出,实现制冷[4]。为方便分析波图,一般将波图划分为①~④区,如图1所示。①区为管内初始状态,②区为激波波后区域,③区为膨胀波波前区域,④区为膨胀波波后区域,0区为高压入射气体。
在整机实验方面,研究者们探究了喷嘴角、中压喷嘴安装角等结构参数对气波制冷机制冷效率的影响[5-7]。同时,为更加直观地得到波转子内部的波系运动特征,部分研究者在波转子可视化实现方面做了很多工作。Okamoto等[8-9]运用纹影测量技术和激光多普勒测速技术,对长度为186 mm微型振荡管内的波系运动进行了研究,捕捉到了微型管道内的波系运动行为和波速,首次实现了对振荡管内激波和膨胀波的可视化观测。Kurec等[10]搭建了长度为500 mm、截面积为20 mm × 40 mm的单管固定、两端接口周期性转动的可视化压力振荡管,以油气溶胶作为示踪粒子对管内气体流动进行了PIV测量,观测到了接触面的流动和形态变化。Ozawa[11]搭建了长度为7 m的激波管可视化实验装置,利用高温温敏涂料对管内激波、反射激波的非定常流动现象实现了可视化观测。
在上述振荡管和激波管的可视化实验中,受纹影凹面镜直径的限制[12],可视化通道长度大多小于200 mm,更短的通道意味着波转子需要更高的转速。因此,为形成有效的激波,需将转速提升至
8000 ~10000 r/min[13],远远偏离了工程应用的转速范围。同时,短的通道结构会使波系运动识别愈加困难,难以完整全面地呈现管内波系运动形态,导致管内波系运动定量观测结果较为缺乏,无法建立起压力脉动与纹影图像之间的同步响应关系。为深入研究压力振荡管内的波系运动特征,提高气波制冷机制冷效率,本文设计了一套独特的双开口压力振荡管可视化实验装置,可视段长度为450 mm。在利用传感器、高速相机同步测量压力、纹影的基础上,提出了一种新的纹影视场拼接算法来获取管道内的波系运动。通过对纹影图像的标定和后处理,可得到管内密度梯度场的定量表达。此外,采用求解二维欧拉方程的解析方法,用NND格式 (Non-oscillatory and Non-free-parameters Dissi-pative scheme)[14]对管道内的波系运动进行了模拟。结合实验与数值计算结果,对压力振荡管内复杂的动力学行为进行直观的实验和理论研究。
1 实验系统
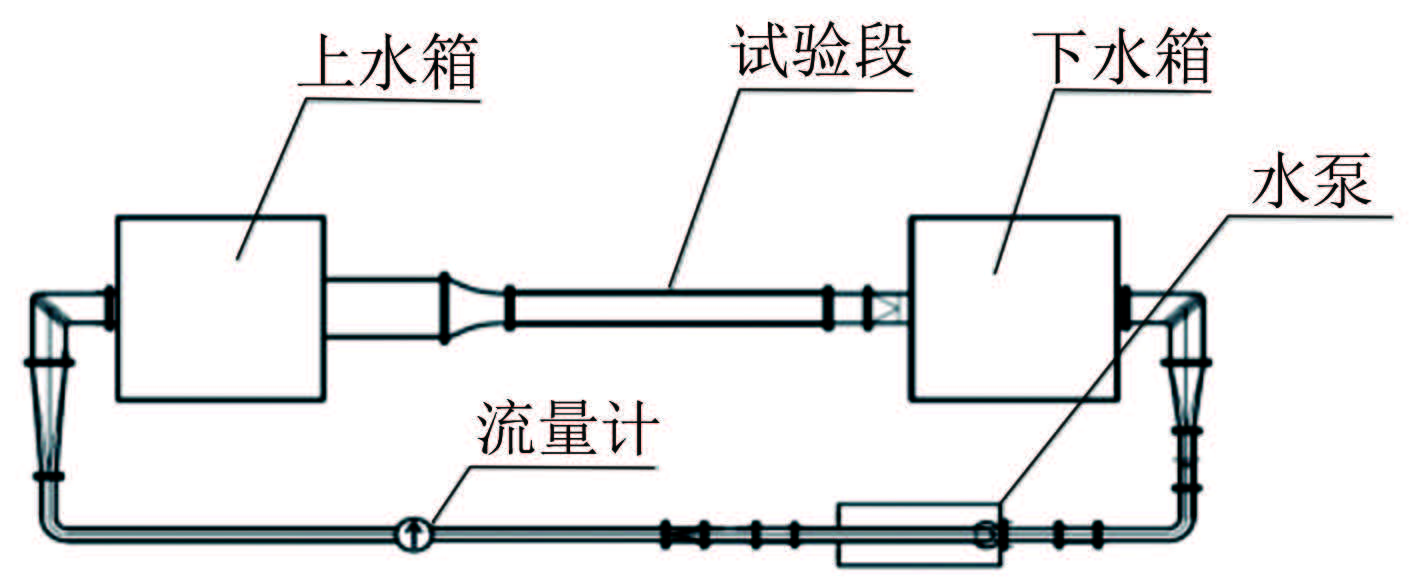
1.1 实验平台
如图2所示,实验设备主要由固定压力振荡管、2个带旋转喷嘴的腔体组成,用于模拟入射和流出过程。测量系统由高速纹影成像系统和压力传感器(P1~P6为6个压力监测点)组成,用于测量流场信息。喷嘴在旋转过程中周期性地向压力振荡管喷射气流,诱发管内产生激波、膨胀波等复杂波系运动。利用高速纹影成像系统捕捉管内因压力波动导致的密度梯度变化,可绘制出波系随时空发展的路径。
本实验中高速纹影成像系统采用Z形布置。为实现图像拼接,实验时凹面镜分别布置在图2中的Ⅰ、Ⅱ和Ⅲ处,拍摄区域有一定重叠,方便进行坐标定位和数据处理,确保全管道拍摄无遗漏。
图3为实验平台实物图。2个旋转式喷嘴由同一台电机驱动,转矩由同步齿轮带传递,确保了压力振荡管两侧喷嘴的相位差稳定。转子转速采用变频器调节,在变频器前后设置电路滤波器,消除电磁工频干扰对测量的影响。
设备设计参数及运行参数如表1所示,表中喷嘴压力与电机转速均可调。压比α为高压喷嘴进口压力(绝对压力)与振荡管内低压(绝对压力)之比,可调范围为1.5~3.0。电机转速n可调范围为800~
2400 r/min。压力振荡管总长为600 mm,可视段长度为450 mm。表 1 设备设计参数及运行参数Table 1 Equipment design parameters and operating parameters参数名称 参数值 参数名称 参数值 管道长度 600 mm 可视段长度 450 mm 管道截面 12 mm × 12 mm 喷嘴截面 32 mm × 15 mm 喷嘴压力 150~300 kPa (绝对压力) 最大压力 110 kPa (绝对压力) 电机转速 800~ 2400 r/min最大流量 0.4 kg/s 1.2 数据采集系统
1.2.1 纹影与密度梯度定量测量
纹影是一种常用的波系运动可视化观测手段。为全面完整地描述管内波系运动,本文提出了一种纹影视场拼接算法,利用长焦透镜[15]标定方法,获得了基于纹影图像的密度梯度场定量表达。算法和处理步骤如图4所示。
首先分别获得3个位置(Ⅰ、Ⅱ和Ⅲ,图4(a))的原始纹影图像(图4(b)),并对其进行去除背景噪声处理,将彩色纹影图像转变为灰度图(图4(c))。然后按照坐标锚定空间位置,将3个位置的灰度图拼接为一幅整体灰度图(图4(e))。根据灰度强度的标定数据(图4(d)),就可以将灰度图转变为密度梯度场的定量表达图像(图4(f))。
需要指出的是,拼接算法仅适用于准定常周期性运动。在单周期内,压力振荡管内的波系运动是非定常行为,但从多周期宏观角度可近似为准定常周期性行为,满足拼接算法的适用条件。拼接单元能够实现空间精准锚定定位,定位精度取决于高速相机的空间分辨率。实验中使用的长焦透镜直径为25.4 mm,在标定数字图像中对应174个像素,因此测试的空间分辨率约为0.146 mm/像素。本文采用了信号同步触发方式,压力传感器和纹影图像同步高速采集,两者协同进行波系运动的表达。
高速相机型号为Photron SA4,全画幅像素为
1024 像素×1024 像素,采集频率为75000 帧/s。高速相机被置于纹影光刀之后,承接光像并记录纹影图像。1.2.2 压力数据测量
管道内压力采集使用高频动态压力传感器,量程为0~500 kPa,频率为20 kHz。搭配高频同步数据采集卡使用,采样频率为100 kHz。如图2所示,在可视化管道顶部等间距布置6个压力监测点,记录管道内压力。传感器端面与管道内壁保持齐平,确保测量值准确[16]。
2 实验结果与讨论
2.1 压力振荡管内波系运动
2.1.1 压力振荡管可视化波图
将高速相机记录的不同位置的原始纹影图像按图4流程进行处理,得到纹影和密度梯度全周期运动图像。
图5(a)和(b)分别为压比α = 2、转速n =
1400 r/min时的振荡管内波系运动纹影灰度波图和密度梯度波图。为便于分析,后文等时间间隔选取管道进行图像处理。图中,x为到左侧高压入射端口(HP)的距离,t为时间,$\partial \rho {\text{/}}\partial x $为密度梯度。橘红色阶表示密度梯度为正值($\partial \rho {\text{/}}\partial x > 0$),即该处密度小于右侧点密度,为膨胀波;反之,蓝色阶表示密度梯度为负值($\partial \rho {\text{/}}\partial x < 0$),即该处密度大于右侧点密度,为压缩波;黄绿色阶表示密度梯度值接近零值,即该处基本无密度变化。波图左下角位置可以明显看到蓝色梯度线有汇合的现象,这是由于压缩波在管道中“追赶”前波造成的。2.1.2 管内纹影图
图6展示了压比为1.5、转速为800 r/min时的纹影灰度波图。可以看到,高压气体由喷嘴入射,管道左端首先出现压缩现象,压缩波逐渐向右传递,强度逐渐增强。这是因为喷嘴在旋转过程中逐渐接通管道,产生一系列压缩波S1,在向右传递的过程中,后一道波会“追上”前一道波,使得压缩波逐渐增强。S1向右运动1.3 ms后,到达管道右侧,并在管尾自由边界条件下反射性质相反的膨胀波E1[17],并向左传递。膨胀波E2在0.67 ms时出现并向右侧传递,在传递过程中逐渐减弱,这是由膨胀波“追赶”不上前一道波所导致的。如图6所示,膨胀波E2中掺杂有弱压缩波S2,说明入射端口在“切出”振荡管的过程中,仍有少量高压气体入射,与高压入射端口逐渐关闭过程中形成的弱膨胀波掺杂呈现。
2.1.3 管内密度梯度波图
图7是图6对应的密度梯度波图。图7更加直观地展示了压缩波S1、膨胀波E1与E2的运动行为,与理论波图(图1)基本一致。实验中,膨胀波E2在向右传递的过程中,掺杂了一系列压缩波S2。这是由于在高压喷嘴完全关闭产生膨胀波E2的同时,近管口区间形成了低于大气压的低压环境,致使左侧转盘腔内气体通过喷嘴固壁段与管道的间隙涌入振荡管,腔内高压气体压缩近管口区间的低压气体,产生了一系列压缩波S2。
2.2 压力振荡管内压力分布
图8给出了压比为2.0时,不同转速(800、
1400 、2000 、2400 r/min)条件下6个压力监测点记录的压力变化,其中p1~p6分别对应压力监测点P1~P6的压力。可以看出,当高压喷嘴接通管道时,高压气体涌入管道形成压缩波,在0~1 ms内,P1~P6的压力在压缩波作用下明显依次逐渐升高。由图8(a)可以注意到,不同监测点处的压力峰值有所变化,位置靠后的监测点压力峰值更高,这是因为压缩波S1不断向前“追赶”,当后一道波追上前一道波时就会加强波的强度,压力也会升高。喷嘴与管道完全接通后,压力维持一定时间,图中显示为一段压力“平台期”,其长度与喷嘴接通管道的时间有关,即与转速有关,转速越小则接通时间越长,高压维持时间就越长。渡过“平台期”后,高压喷嘴完全关闭,这时近管口区间产生膨胀波E2。当E2扫过各监测点时,压力值开始下降。在实验中,由于压缩波S2的产生,压力下降速率有所减缓,甚至在距离管口较近的P1、P2处,压力还有小幅度上升,随后在E2的作用下开始下降。当压缩波S1到达管尾后,在曲线上可以观察到反射的膨胀波E1从P6点逐渐向P1传播,对近管口区间气体进一步膨胀冷却。
2.3 实验可靠性验证
为验证实验数据特别是视场拼接结果的准确性,对实验进行了模拟验证。在实验工况下,使用NND差分格式对二维欧拉方程进行求解,获得了密度梯度云图,如图9所示。从图中可以看到,在压比为2.0、转速为
1400 r/min的工况下,实验结果与数值计算获得的云图有着相同的形态结构。在计算云图中,实验数据中的压缩波S1、S2和膨胀波E1、E2均有对应的波形。图10给出了x = 500 mm处的中心轴线密度梯度对照曲线。可以看到,实验结果对管内波动形态的展示比模拟结果更为精细,实验和模拟的密度梯度曲线趋势吻合,捕捉到的压缩波与膨胀波位置一致,压缩波强度仅相差3.2%。图11还进行了压力数据对比,可以看到,实验和模拟的压力变化规律一致。因此,可以认为实验数据真实可靠。
2.4 压力振荡管波系运动的影响因素
在图1的波图中,④区为膨胀波E2的波后区域。④区的温度T4直接影响气波制冷机的温降[18],因此T4的大小反映了制冷效果的好坏。
2.4.1 压比对管内波系运动的影响
激波马赫数Mas是表征激波强度的重要参量,是激波相对于波前气流运动的马赫数,可由下式计算:
$$ {Ma_{\text{s}}} = \frac{{{v_{\text{s}}} - {v_1}}}{{{c_1}}} $$ (1) 式中:激波波速vs为激波运动的绝对速度;v1为激波波前区域(①区)的气流速度,喷嘴打开前管内气流视为静止,因此v1为0;c1为①区的当地声速。
管内气体压力和温度在激波的作用下发生变化,激波波后区域(②区)压力、马赫数、温度均可通过公式计算得出[17]。其中,②区温度T2的计算方法如下:
$$ \frac{{{T_2}}}{{{T_1}}} = \dfrac{{\dfrac{{{p_2}}}{{{p_1}}} + \dfrac{{\gamma + 1}}{{\gamma - 1}}}}{{\dfrac{{\gamma + 1}}{{\gamma - 1}} + \dfrac{{{p_1}}}{{{p_2}}}}} $$ (2) 式中:T1为①区温度;p1和p2分别为①区和②区的压力;γ为气体绝热指数,取值1.4。③区温度T3的计算方法如下:
$$ \frac{{{p_0}}}{{{p_3}}} = {\left( {\frac{{{T_0}}}{{{T_3}}}} \right)^{\frac{\gamma }{{\gamma - 1}}}} $$ (3) 式中:p0和p3分别表示0区和③区的压力;T0为0区温度。
由于膨胀波可视为等熵过程,因此③区与④区满足右行波黎曼不变量关系,联立式(4)和(5)可计算得到④区温度T4,即:
$$ {v_4} - \frac{2}{{\gamma - 1}}{c_4} = {v_3} - \frac{2}{{\gamma - 1}}{c_3} $$ (4) $$ \frac{{{p_4}}}{{{p_3}}} = {\left( {\frac{{{T_4}}}{{{T_3}}}} \right)^{\frac{\gamma }{{\gamma - 1}}}} $$ (5) 式中:v3和v4分别为③区和④区的气流速度;c3和c4分别为③区和④区的当地声速;p4为④区压力。
图12给出了不同转速条件下各参量(激波波速、激波马赫数及④区温降)与压比的关系图。从图中可以看出,膨胀波的制冷效果随压比的增大而增强。但压比增大也会增强激波对管内气体的制热效果,这在一定程度上抑制了膨胀波制冷。压比每提高0.5,各转速下温降平均提升22.53、16.86、13.01 K,在图中显示为斜率减小。
除马赫数和温度外,密度梯度也是波的重要参量之一。图13为转速800 r/min、不同压比下的波图。可以看出,压比从1.5提升至3.0的过程中,压缩波S1密度梯度随压比的增大而增大,激波强度在增压的影响下有所提升。同时,膨胀波E1、E2的密度梯度随压比的增大稳步提升,膨胀波膨胀效应增强,提高了制冷效果。
2.4.2 转速对管内波系运动的影响
当波转子几何结构固定时,压比、转速都会对气波制冷机的制冷效率产生影响。在固定压比下,进行了转速分别为800、
1400 、2000 、2400 r/min的实验研究。采用式(1)~(5)计算不同转速下的激波波速、激波马赫数和④区温降。图14给出了不同压比下激波波速、激波马赫数和④区温降随转速的变化情况。可以看到,激波波速、激波马赫数随转速提高而增大。激波强度与转速有关,转速越大,管内激波越强。④区温降随转速提高略有增大,即提高转速有利于增强制冷效果。
图15为压比α = 2.5时不同转速下的密度梯度波图。对比4个工况下的密度梯度波图可以看出,转速对密度梯度峰值有一定影响但不明显,密度梯度随转速提高小幅增大。但膨胀波E2的运动形态(引导线a~d依次对应转速由低到高4个工况下膨胀波E2的运动形态)随转速的改变发生了较大的变化,由800 r/min时的直线逐渐向凹曲线变化。b线在波头处向上弯曲,表明波头处波速逐渐减小。c线与d线则在近管口区间就发生了弯曲,说明在转速的作用下,膨胀波E2波速下降,加强了对近管口区间气体的膨胀过程。
2.4.3 压比和转速对结构设计的影响
由图13~15可知,压比增大、转速提高都加快了压缩波S1后波追赶前波的过程,表现为波图中S1密度梯度最大值位置随着转速提高而前移。这是由于转速影响了激波形成的位置和时间。将高压喷嘴入射过程近似为激波管触发激波时的“活塞运动”,即在喷嘴与管道的接通时间内,活塞速度由0迅速增大至喷嘴出口气流速度,可以得到活塞加速度的值。激波形成位置可由下式计算[17]:
$$ {x_*} = \frac{{2c_0^2}}{{(\gamma + 1)A}} $$ (6) 式中:$ {x_*} $为激波形成位置,mm;c0为0区的当地声速,m/s;加速度A为气流速度与接通时间的比值,m/s2。
图16为实验工况中激波密度梯度最大值位置与压比和转速的关系曲线。可以看到,随着压比的增大或者转速的提高,出现最大值的位置距离管口越来越近。这是由于喷嘴入射时长与转速成反比,喷嘴气流速度与压比成正比,即加速度A随转速提高与压比增大而增大。可以有以下结论:激波形成位置受压比和转速的影响,压比越大,转速越高,激波形成位置越靠近管口。因此,在设计压力振荡管尺寸时,管长应与压比和转速匹配,可以采用增大压比或提高转速的方法缩短管长,从而轻量化气波制冷机,降低成本。
3 结 论
本文以600 mm长的压力振荡管为主体搭建了一套双开口压力振荡管可视化流场测量平台。采用高速纹影成像系统和纹影视场拼接算法获得了管内的密度梯度场定量表达,与二维欧拉方程计算结果进行了验证对比,并对不同压比和转速条件下的压力振荡管内波系运动行为进行了可视化实验研究。得到以下主要结论:
1)压力振荡管内波系运动主要由压缩波S1、S2和膨胀波E1、E2构成,其中E1为左行波,其余均为右行波。波系运动的压缩与膨胀特性符合理论预期。
2)激波马赫数与压比和转速均有关,增大压比或提高转速均可增大激波马赫数。压比由1.5增至3.0时,激波强度和膨胀波强度显著提升,强化了对近管口区间气体的膨胀作用。转速由800 r/min提高至
2400 r/min时,膨胀波波系运动路径逐渐向管口方向弯曲,膨胀波在近管口区间运动的速度降低,增加了膨胀波对近管口区间气体的作用时间。3)激波形成位置受压比和转速影响,压比越大,转速越高,激波形成位置越靠近管口。在工业制造中,可通过增大压比或提高转速缩减整机规模。
-
表 1 平板边界层流动参数
Table 1 Flat plate boundary layer parameters

0.2 0.3 0.4 0.5 0.6 0.7 δ/mm 10.35 11.50 12.17 22.76 21.86 21.25 δ*/mm 3.43 2.32 1.95 3.06 2.87 2.79 θ/mm 1.33 1.24 1.06 2.11 2.01 1.96 H 2.58 1.98 1.84 1.45 1.43 1.42 表 2 不同外流速度下的壁面剪切应力值
Table 2 Wall shear stress of different freestream velocities

0.5 0.6 0.7 u* 0.0233 0.0276 0.0321 y0/mm 0.26 0.26 0.25 τw/Pa (LDV速度剖面) 0.5419 0.7632 1.0313 τw/Pa(经验公式) 0.5463 0.7610 1.0058 表 3 不同外流速度下数值计算与速度剖面计算结果比较
Table 3 Shear stress obtained from CFD simulation and mean profiles of different freestream velocities
外流速度
/(m·s-1)CFD
τw/Pa经验公式
τw/PaLDV速度剖面
τw/Pa0.5 0.5546 0.5463 0.5419 0.6 0.7745 0.7610 0.7632 0.7 1.0224 1.0058 1.0313 -
[1] 樊星, 姜楠. 用平均速度剖面法测量壁面湍流摩擦阻力[J]. 力学与实践, 2005, 27 (1): 28-30. http://www.cnki.com.cn/Article/CJFDTOTAL-LXYS200501007.htm Fan X, Jiang N. Skin friction measurement in turbulent boundary layer by mean velocity profile method[J]. Mechanics in Engineering, 2005, 27 (1): 28-30. http://www.cnki.com.cn/Article/CJFDTOTAL-LXYS200501007.htm
[2] Patel V C. Calibration of Preston tube and limitations on its use in pressure gradients[J]. Fluid Mechanics, 1965, 23: 185-208. DOI: 10.1017/S0022112065001301
[3] 沈熊. 激光多普勒测速技术及应用[M]. 北京: 清华大学出版社, 2004. Shen X. Laser Doppler velocimetry and application[M]. Beijing: Tsinghua University Press, 2004.
[4] Meinhart C D, Adrian R J. Measurement of the zero-pressure gradient turbulent boundary layer using particle image velocimetry[R]. AIAA-95-0789, 1995.
[5] 王洪平, 高琪, 魏润杰, 等. 基于层析PIV的湍流边界层展向涡研究[J]. 实验流体力学, 2016, 30 (2): 59-66. http://www.syltlx.com/CN/abstract/abstract10918.shtml Wang H P, Gao Q, Wei R J, et al. Study of spanwise vortices in turbulent boundary layer flow based on tomographic PIV[J]. Journal of Experiments in Fluid Mechanics, 2016, 30 (2): 59-66. http://www.syltlx.com/CN/abstract/abstract10918.shtml
[6] 王光华, 刘宝杰, 刘涛, 等. 利用PIV技术对平板湍流边界层的实验研究[J]. 自然科学进展, 1999, 9 (12): 1198-1203. http://www.cnki.com.cn/Article/CJFDTOTAL-ZKJZ1999S1007.htm Wang G H, Liu B J, Liu T, et al. Experimental study of the turbulent boundary layer using PIV[J]. Progress in Natural Science, 1999, 9 (12): 1198-1203. http://www.cnki.com.cn/Article/CJFDTOTAL-ZKJZ1999S1007.htm
[7] 王晋军, 兰世隆, 苗福友. 沟槽面湍流边界层减阻特性研究[J]. 中国造船, 2001, 42 (4): 1-5. http://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC200104000.htm Wang J J, Lan S L, Miao F Y. Drag-reduction characteristics of turbulent boundary layer flow over riblets surface[J]. Shipbuilding of China, 2001, 42 (4): 1-5. http://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC200104000.htm
[8] Niederschulte M A, Adrian R J, Hanratty T J. Measurements of turbulent flow in a channel at low Reynolds numbers[J]. Experiments in Fluids, 1990, 9: 222-230. DOI: 10.1007%2FBF00190423
[9] 李存标, 吴介之. 壁流动中的转捩[J]. 力学进展, 2009, 39 (4): 480-507. Lee C B, Wu J Z. Transition in wall bounded flows[J]. Advance in Mechanics, 2009, 39 (4): 480-507.
[10] 何霖. 超声速边界层及激波与边界层相互作用的实验研究[D]. 长沙: 国防科技大学, 2011. He L. Experimental investigation of supersonic boundary layer and shock wave/boundary layer interaction[D]. Changsha: National University of Defense Technology, 2011.
[11] Clauser F H. The turbulent boundary layer[J]. Advances in Applied Mechanics, 1956, 4: 1-51. DOI: 10.1016/S0065-2156(08)70370-3
[12] Eggels J G M, Unger F, Weiss M H, et al. Fully developed turbulent pipe flow: A comparison between direct numerical simulation and experiment[J]. Fluid Mechanics, 1994, 268: 175-209. DOI: 10.1017/S002211209400131X
[13] Palikaras A, Yakinthos K, Goulas A. Transition on a flat plate with a semi-circular leading edge under uniform and positive shear free-stream flow[J]. International Journal of Heat and Fluid Flow, 2002, 23: 455-470. DOI: 10.1016/S0142-727X(02)00146-7
[14] 崔杰. 湍流边界层速度分布的显式表示[J]. 空气动力学学报, 1994, 12 (2): 208-211. http://www.cnki.com.cn/Article/CJFDTOTAL-KQDX402.013.htm Cui J. Explicit expression for the velocity distribution in a turbulent boundary layer[J]. Acta Aerodynamic Sinica, 1994, 12 (2): 208-211. http://www.cnki.com.cn/Article/CJFDTOTAL-KQDX402.013.htm
[15] 潘光, 黄桥高, 胡海豹, 等. 基于热线技术的脊状表面湍流边界层流动参数测试方法研究[J]. 测控技术, 2009, 28 (4): 18-24. http://www.cnki.com.cn/Article/CJFDTOTAL-IKJS200904005.htm Pan G, Huang Q G, Hu H B, et al. Research about the testing method of flow parameters of turbulent boundary layer over riblet surface based on hot wire technology[J]. Measurement&Control Technology, 2009, 28 (4): 18-24. http://www.cnki.com.cn/Article/CJFDTOTAL-IKJS200904005.htm
[16] Meloy J, Griffiny J, Sells J, et al. Experimental verification of a MEMS based skin friction sensor for quantitative wall shear stress measurement[C]. 41st AIAA Fluid Dynamics Conference and Exhibit, Honolulu, Hawaii, 2011.
[17] 王福军. 计算流体动力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. Wang F J. Computational fluid dynamics analysis -CFD software principles and applications[M]. Beijing: Tsinghua University Press, 2004.
[18] 黄欢, 孙海浪, 田于逵, 等. 水下MEMS壁面剪应力传感器标定方案仿真分析与实验验证[J]. 实验流体力学, 2016, 30 (2): 79-83, 102. http://www.syltlx.com/CN/abstract/abstract10921.shtml Huang H, Sun H M, Tian Y K, et al. CFD analysis and experimental validation on the scheme of calibration for MEMS wall shear stress sensors array for underwater applications[J]. Journal of Experiments in Fluid Mechanics, 2016, 30 (2): 79-83, 102. http://www.syltlx.com/CN/abstract/abstract10921.shtml
-
期刊类型引用(2)
1. 倪章松,张军,符澄,王邦毅,李宇. 磁浮飞行风洞试验技术及应用需求分析. 空气动力学学报. 2021(05): 95-110 .  百度学术
百度学术
2. 赵亚玲,陈斐. 水下航行器电子设备环境应力测试方法研究. 舰船科学技术. 2019(20): 43-45 .  百度学术
百度学术
其他类型引用(2)







 下载:
下载: