Effects of the spatial resolution of planar PIV on measured turbulence multi-point statistics
-
摘要:
粒子图像测速（Particle Image Velocimetry, PIV），尤其是平面PIV，因其技术成熟且能提供瞬时流场，被广泛应用于湍流统计特性实验研究。PIV测量的空间分辨率（实验测量中所能解析的最小流场尺度，由图像处理时问询域窗口大小决定）不能准确分辨湍流中的小尺度运动，导致PIV测量获得的湍流多点统计量的定量信息（如速度结构函数、湍流耗散率等）包含一定误差。为定量分析这一误差，本文采用空间滤波模型模拟PIV测量对单点速度矢量的作用，进而推导出PIV测得的速度结构函数及湍流耗散率随滤波尺度的变化规律。为检验该模型，通过模拟示踪粒子在基于均匀各向同性湍流直接数值模拟（DNS）得到的湍流速度场中的运动及PIV系统对其的成像，获得了计算合成的PIV粒子图像，采用标准PIV算法对该图像进行处理，获得了速度场并计算得到了相关的湍流统计量，将其与基于真实DNS数据计算得到的统计量对比，获得了定量的误差信息，并与模型的预测结果进行了对比。研究结果表明：本文建立的模型反映了PIV测量中空间分辨率对湍流统计量的影响。在冯·卡门旋流系统产生的近似均匀各向同性流场中进行了平面PIV测量，针对测量得到的速度结构函数与K41理论结果的误差，采用基于本文模型得到的结论进行了分析与校正。本文工作为PIV测量得到的湍流统计量（尤其是小尺度多点统计量）给出了一个基于理论指导的修正方案。
Abstract:Particle Image Velocimetry (PIV), in particular planar PIV, has been widely implemented in the experimental study of statistical characteristics of turbulence because of its maturity in technology and capability to provide instantaneous flow fields. The spatial resolution of PIV measurement, i.e., the smallest scale of the flow field resolvable by PIV, is determined by the size of the Interrogation Window (IW) during image processing. Hence, small-scale turbulence fluctuations might not be accurately resolved, which leads to deviations in measured turbulence multi-point statistics, such as velocity structure functions, turbulent dissipation rate and so on. To quantify this deviation, we model the effect of PIV measurement on the instantaneous single-point velocity vectors as spatial filtering, which allows the change of the velocity structure functions and the turbulent dissipation rate measured by PIV with filter size to be derived. To check these predictions, synthetic PIV image pairs were generated based on simulated tracer particle motions following the velocity fields from direct numerical simulation (DNS) of isotropic turbulence, which were then processed by a standard PIV algorithm. Turbulence statistics obtained from such measured velocity fields were then compared with those from the exact DNS data to evaluate quantitative deviations. The results show that our model captures the effect of spatial resolutions on turbulence statistics in PIV measurement. Experimentally, planar PIV measurements were carried out in the center of a von Kármán swirling flow device, where the turbulence is nearly homogeneous and isotropic. The deviation between measured velocity structure functions and the K41 theory was also analyzed and corrected using the aforementioned model prediction. This work provides a theoretical guidance for examing turbulence statistics measured by PIV, especially multi-point statistics at small scales.
-
0 引言
FL-12风洞作为主力风洞承担着大量重要试验任务，其中包括进气道、吹气流动控制、引射短舱和TPS等多项试验，这些试验任务都需要供气控制系统输送稳定、可控的气流到试验模型，并要达到优于±3g/s的绝对控制精度，同时要求流量调节范围大、稳定时间短，因此实现流量宽范围快速精确控制是供气试验最为基础和关键的环节[1-3]。
目前模拟调节阀的高精度阀门定位器死区0.1%，综合误差0.5%[4]，达不到试验要求的流量控制精度，而且在实际工况中其工作流量特性随着试验模型的变化而变化，同时存在死区、调节滞后严重、调节范围不宽、密封件易磨损等问题，因此无法满足当前供气试验要求。
与模拟调节阀相比，数字阀具有可调范围宽、控制精度高、响应速度快、结构简单、鲁棒性强、可靠性高等特点[5-7]，目前数字阀主要分为PWM(脉冲宽度调制)数字阀和PCM(脉冲编码调制)数字阀[8-9]。PWM数字阀也称高速开关式数字阀，通过调节PWM信号的占空比来控制阀的平均流量，但是数字阀的流量和得失电时间存在一定的矛盾。PCM数字阀是将开关阀按照一定规律的排列组合(二进制、斐波那契数列等)实现对流量的控制，但是离散化的形式会导致流量输出的不连续性，同时小口径喷嘴的加工难度较高，进退阶时波动较大，频繁切换阀会造成冲击和噪声，缩短低位开关阀的寿命。
为解决PWM数字阀流量和得失电时间的矛盾和PCM数字阀的流量不连续性和低位开关阀的寿命问题，本文设计了PCM+PWM数字阀。该数字阀通过PCM数字阀提供基准流量，PWM数字阀在基准流量的基础上再进行调节，其中PCM数字阀采用多路文丘里喷嘴与开关阀按照二进制规律排列组合而成，PWM数字阀由单路小口径文丘里喷嘴与高频开关阀组成。
1 数字阀的设计指标和设计方案
1.1 设计指标
依据试验任务需求，FL-12风洞供气控制系统中数字阀设计的主要技术指标：(1) 阀前压力范围：6.0~8.0MPa；(2) 阀后压力范围：0.1~6.0MPa；(3) 流量控制范围：0.1~6.0kg/s；(4) 绝对控制精度：≤±3g/s；(5) 稳定控制时间：≤30s。
1.2 设计方案
本文中设计的数字阀由13位半PCM数字阀+ PWM数字阀，共计16路喷嘴和16路开关阀组成。图 1为数字阀支路示意图，气流依次通过喷嘴、高压金属软管、电磁阀后流出，系统先通过开关不同位的电磁阀来控制每路管道的通断以达到组合出不同流量的目的，当流量输出值与给定值的差值进入预先设定的误差带内，则停止动作PCM数字阀，由PWM数字阀通过脉宽调制控制。在实际流量控制中，PCM数字阀起到量程调节作用，PWM数字阀起到精细调节作用。
2 数字阀设计的关键技术
2.1 喷嘴的选择与设计
为使喷嘴流量特性不受后端试验模型状态变化及背压影响，采用了临界流喷嘴。临界流喷嘴主要包括临界流标准喷嘴和临界流文丘里喷嘴，其中临界流标准喷嘴结构如图 2所示。如果保持喷嘴入口压力p1和温度T1不变，使其出口压力p2逐渐减小，则通过喷嘴的气体流量qm将逐渐增加。当出口压力下降至pc时，通过喷嘴的流量将达到最大值，气体流速为当地声速，再继续降低出口压力，通过喷嘴的流量将不再增加，流速也保持声速不变。将喷嘴出口的流速达到声速的压力pc称为临界压力，pc/p1称为临界压力比，通过喷嘴的流量(qm)max称为临界流量[10]。
![]()
图 2 临界流标准喷嘴的结构和流量特性Fig. 2 Structure and flow characteristic of the critical flow standard nozzle对于空气(γ=1.4)，可以通过公式1计算得到临界压力比为0.528。由于数字阀前压力一般稳定在8MPa，因此要保证“恒流”特性不变，出口压力p2必须低于临界压力4.224MPa，显然无法满足最大出口压力为6MPa的设计要求，而且压力损耗太大。
(1) 为使出口压力得到恢复，采用喉道后面带扩压管的临界流文丘里喷嘴，其出口压力高低与其扩散段尺寸有关[11]。根据JJG620-2008《临界流文丘里喷嘴》，可以计算出最大背压比p2/p1与扩散段面积比A2/A*的对应参数表(见表 1)，其中p1为入口压力，p2为出口压力，A*为喉道面积，A2为扩散段出口面积。
表 1 临界流文丘里喷嘴的最大允许背压比表(γ=1.4)Table 1 Maximum allowable back pressure ratio of the critical flow Venturi-type nozzleA2/A* p2/p1 A2/A* p2/p1 1.1 0.6863 1.9 0.8495 1.2 0.7376 2.0 0.8554 1.3 0.7701 2.5 0.8743 1.4 0.7930 3.0 0.8842 1.5 0.8101 3.5 0.8900 1.6 0.8233 4.0 0.8937 1.7 0.8339 5.0 0.8981 1.8 0.8424 10.0 0.9038 依据表 1，选择喷嘴扩散段面积比为4.0，在理想条件下，当出口压力低于0.8937倍入口压力，即可达到临界状态，喷嘴喉道流速为声速，流量由入口压力、入口温度与喉道面积唯一确定。依据圆环形喉道临界流文丘里喷嘴设计准则[12]，喷嘴的结构设计如图 3所示。
2.2 喉道面积的分配
PCM数字阀的喷嘴喉道面积按照二进制规律排列，通过这些不同的喉道可以组合不同喉道面积，组合喉道面积范围在所有喉道面积之和与最小喉道面积之间，最小分辨率是最小喉道面积，因此设计足够小的喉道面积就可以解决定位精度的问题，设计足够多的位数就可以解决流量调节范围的问题。
PCM数字阀的设计工况是入口压力为8.0MPa，入口温度为20℃，流量为6.0kg/s，在最大允许背压比范围内，根据公式(2) 可得PCM数字阀需要的喉道总面积为3.176cm2。
(2) 式中：p1为喷嘴入口压力(Pa)；T1为喷嘴入口温度(K)；A*为喉道面积(m2)。
经计算，将喉道总面积按照13位半二进制分配，各喷嘴喉道面积分配值及工作流量分配值如表 2所示。
表 2 PCM数字阀各喷嘴喉道面积及对应流量计算表Table 2 Nozzle throat area and calculated flow value of the PCM digital valveBit位 临界流量/(kg·s-1) 喷嘴喉道面积/cm2 喉道通径/mm 1 0.00059332 0.00031416 0.2000 2 0.0011866 0.00062832 0.2828 3 0.0023733 0.0012566 0.4000 4 0.0047466 0.0025133 0.5657 5 0.0094932 0.0050265 0.8000 6 0.018986 0.010053 1.1314 7 0.037973 0.020106 1.6000 8 0.075945 0.040212 2.2627 9 0.15189 0.080425 3.2000 10 0.30378 0.16085 4.5255 11 0.60756 0.3217 6.4000 12 1.2151 0.6434 9.0510 13 2.4303 1.2868 12.8000 13半 1.2151 0.6434 9.0510 合计 6.075 3.2170 实际设计PCM数字阀总喉道面积为3.217cm2，在不考虑喷嘴加工误差的情况下，其喉道面积分辨率(定位精度)为1/10239，在设计工况下对应的最小流量为0.6g/s。
PWM喷嘴喉道面积的选取需依据试验流量精度要求(±3g/s)，并充分考虑裕量，预设误差带为±6g/s，可在表 2中选取喉道口径0.8mm的喷嘴作为PWM数字阀的喷嘴。
2.3 电磁阀参数计算与型号选择
流量系数CV是电磁阀主要的计算参数，表征为阀门流通能力大小，根据设计工况，并按照公式(3) 进行计算，结果如表 3所示。
(3) 表 3 电磁阀流量系数计算与型号选择Table 3 Magnetic valve flow coefficient calculation and model selectionBit位 计算流量系数/(m3·h-1) 电磁阀流量系数/(m3·h-1) 电磁阀阀座口径/mm 电磁阀型号 PWM 0.02892 0.05 8.0 2/943 1 0.00195 0.13 2.0 A5232 2 0.00390 0.13 2.0 A5232 3 0.00781 0.13 2.0 A5232 4 0.01563 0.13 2.0 A5232 5 0.03125 2.0 8.0 B4623 6 0.0625 2.0 8.0 B4623 7 0.12501 2.0 8.0 B4623 8 0.25003 2.0 8.0 B4623 9 0.50005 2.0 8.0 B4623 10 1.00010 2.0 8.0 B4623 11 2.00021 8.0 25.0 A4625 12 4.00042 8.0 25.0 A4625 13 7.99895 20.0 32.0 A4827 13半 4.00042 8.0 25.0 A4625 式中：Q为标准状态下最大流量，Nm3/h；G为空气比重，为1.1kg/Nm3; T为气体温度, ℃; p1为入口压力, kg/cm2; p2为出口压力, kg/cm2; Δp=p1-p2, kg/cm2。
PCM数字阀的开关阀采用德国GSR二位二通系列的电磁阀, PWM数字阀的高频开关阀采用德国GSR 2/943，该阀动作频率可达1kHz，具有脉宽调制功能，线性流量控制。为使各喷嘴入口压力、温度等条件一致，入口压力稳定，出口压力满足喷嘴喉道气流为声速流要求，电磁阀的流量系数尽量选大，以减小工作压力降，同时需要一定容积的阀体/管道作为稳定段，增加喷嘴入口压力的稳定性[13]。
由于电磁阀不同口径的开关时间存在一定差异，其口径不大于25mm时阀门开关时间约为0.1s，而口径为32mm时阀门开关时间长达0.44s。为了减少各阀门在时间上的差异，增加阀门切换过程中的稳定性，电磁阀的口径都选用25mm以内的。口径32mm的电磁阀则由2个口径25mm的电磁阀组合替代，因此13位半的PCM数字阀具有15个支路，再加上PWM数字阀，共计16个支路。
3 流量控制策略
3.1 供气控制系统
供气控制系统的高压气源来自12~22MPa的高压储气罐，经减压阀降低至稳定的8MPa，再通过数字阀输出试验需要的流量值。在数字阀后端有高精度的文丘里流量计实时监测和反馈输出的流量值，从而组成闭环控制系统，如图 4所示。
3.2 流量调节运算方法
供气控制系统采用了微分前置非线性PID流量调节运算方法，其控制量通过数字阀完成，实现主管路流量的控制。该运算方法首先根据主管路流量给定与流量反馈完成PID运算，然后通过PID运算结果和数字阀气流入口总压总温，计算数字阀阀位偏差，将此偏差作为数字阀阀位补偿值重新调整阀位，从而调整主管路流量输出值，当流量输出值与给定值的差值进入预先设定的误差带内(±6g/s)，则停止动作PCM数字阀，由PWM数字阀通过脉宽调制控制。该运算的微分前置环节可对供气管道及管道设备(数字阀后的供气管道、空气换热器、空气过滤器等)容积造成的流量滞后进行补偿，缩短调节过渡过程时间，增加系统稳定性；比例和积分环节的运算律按照大误差小比例、小积分增益，以及小误差大比例、大积分增益的控制策略构建。
4 调试与应用
4.1 调试
FL-12风洞供气控制系统的数字阀安装示意图如图 5所示。
在调试中，需要在不同流量、不同试验模型状态的情况下，多次调整PID运算的比例增益、积分增益和调节微分增益等参数，使流量控制达到最佳状态。表 4给出了流量闭环控制的测试结果，当给定流量1.2、2.4、3.55和4.67kg/s时，系统流量控制的最大绝对误差分别为1.9、2.2、2.5和2.6g/s，最大相对误差分别为0.15%、0.09%、0.07%、和0.06%。调试数据表明，该套数字阀的流量控制精度能够满足设计指标±3g/s，同时能够实现宽范围的流量调节，且效果平稳，重复性好，可靠性高。
表 4 流量闭环控制的测试结果(单位:kg/s)Table 4 Test results of the flow closed loop control给定流量 1.2 2.4 3.55 4.67 均值流量 1.2012 2.3984 3.5518 4.6688 最大流量 1.2019 2.4022 3.5525 4.6720 最小流量 1.1996 2.3979 3.5480 4.6674 极差 0.0023 0.0043 0.0045 0.0046 最大绝对误差 0.0019 0.0022 0.0025 0.0026 最大相对误差 0.15% 0.09% 0.07% 0.05% 4.2 应用
数字阀在供气控制系统中调试完成后，开展了数十项供气试验。其中以某型飞机进气道试验为例，本次试验的供气流量为1.0和3.2kg/s，流量控制调节过程曲线和稳态过程曲线分别如图 6和7所示。
当供气流量为1.0kg/s时，流量稳定时间为15s，最大绝对误差为1.8g/s，最大相对误差为0.15%；当供气流量为3.2kg/s时，流量稳定时间为16s，最大绝对误差为2.7g/s，最大相对误差为0.08%。
5 结论
大量的供气试验结果表明，采用13位半PCM数字阀和PWM数字阀组合的数字阀在FL-12风洞供气控制系统中的应用是成功的，全面达到了设计指标。其控制精度高、响应时间短、调节范围宽和可靠稳定等特点，为风洞供气试验提供了强有力的支撑。
-
![]()
图 6 模拟PIV得到的湍流耗散率DNS数据及二阶和四阶拟合结果
Fig. 6 The variations of DNS turbulent dissipation rate obtained from the PIV calculations and the second- and fourth-order fitting curves
![]()
图 1 空间任意两点速度差对问询域中心点速度差的贡献
Fig. 1 The effects of velocity differences of two arbitrary points on the measurement of velocity differences of two interrogation windows
![]()
图 2 基于DNS数据模拟得到的PIV合成图像及速度矢量
Fig. 2 A pair of PIV synthetic images using DNS data and diagram of velocity vectors
![]()
图 3 利用DNS数据模拟PIV测量所得二阶纵向速度结构函数及其绝对误差
Fig. 3 The longitudinal structure function and its absolute errors obtained from the DNS data used to simulate PIV measure-ments
![]()
图 4 绝对误差δDLL(r)在惯性区的平均值随分辨率的变化及拟合结果
Fig. 4 The trend of the mean values of absolute errors δDLL(r) of second-order structure function in the inertial region with the resolution of PIV and its fitting
![]()
图 5 二阶纵向速度结构函数及其绝对误差
Fig. 5 The trend of the longitudinal second-order structure function and its absolute errors
![]()
图 7 冯·卡门旋流系统流场示意图及实验布置图
Fig. 7 Schematic diagram of flow field and experimental arrangement of von Kármán swirling system
![]()
图 8 实验中随机误差修正前后对结构函数的影响
Fig. 8 The influence of random errors on longitudinal second-order structure function before and after correction in the experiments
![]()
图 9 实验测量的二阶速度结构函数修正前后对比
Fig. 9 Comparison of the second-order structure function measured by experiment before and after correction
![]()
图 10 冯·卡门旋流实验中湍流耗散率测量值及拟合结果
Fig. 10 The variations of measured turbulent dissipation rate with respect to PIV resolution in von Kármán swirling system and its fittings
表 1 高斯滤波函数对多点统计量的显式误差影响
Table 1 Explicit filtering errors of Gaussian filter function on measured turbulence multi-point statistics
多点
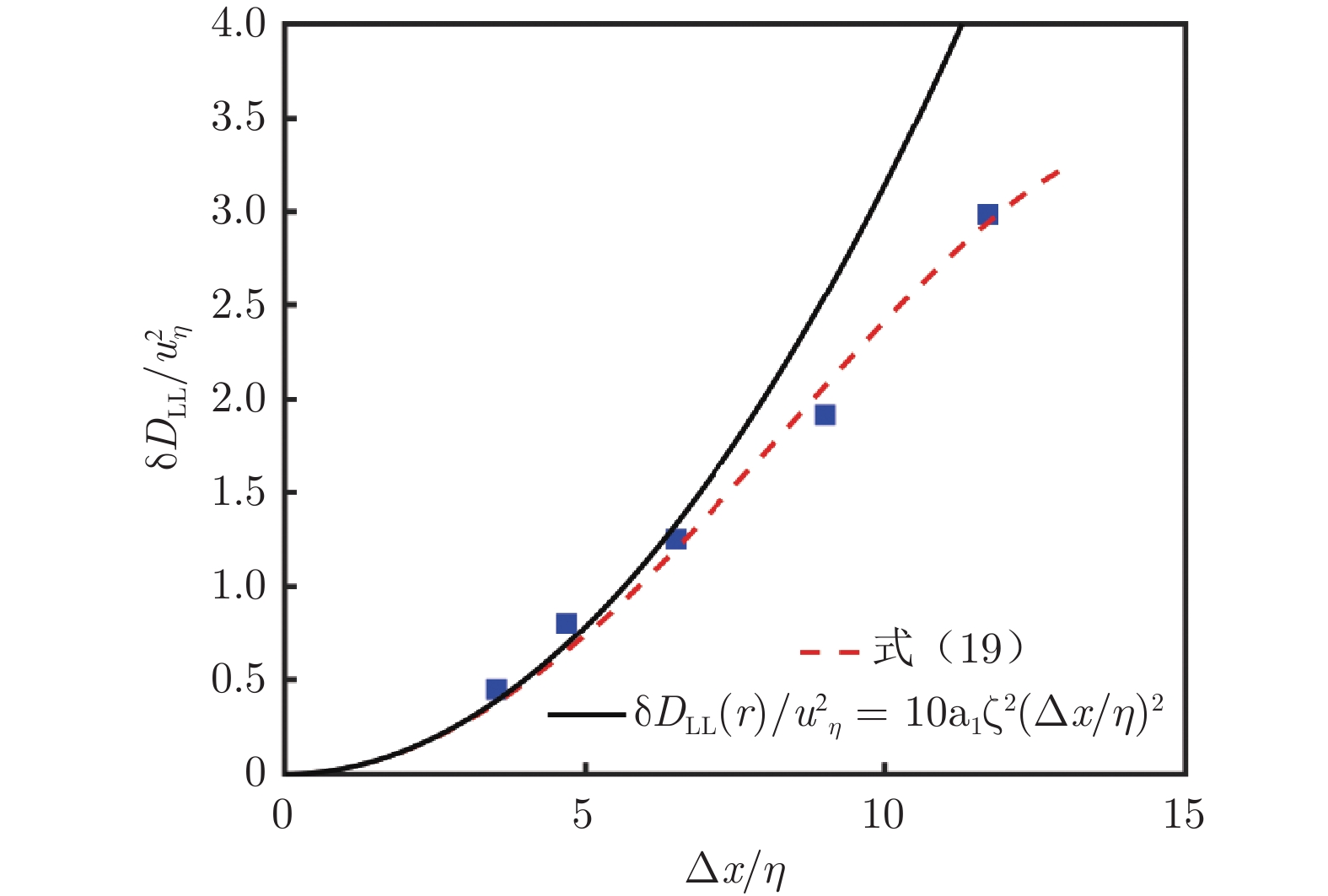
统计量误差形式 二阶纵向结构函数绝对误差 耗散区 $ \dfrac{{{\text{δ}} {D_{{\mathrm{LL}}}}}}{{u_\eta ^2}} = \left[ { - 28{a_2}{\zeta ^2}{{\left( {\dfrac{{{\text{Δ}} x}}{\eta }} \right)}^2} - 756{a_3}{\zeta ^4}{{\left( {\dfrac{{{\text{Δ}} x}}{\eta }} \right)}^4}} \right]{\left( {\dfrac{r}{\eta }} \right)^2} $ 惯性区 $ \dfrac{{{\text{δ}} {D_{{\mathrm{LL}}}}}}{{u_\eta ^2}} = 10{a_1}{\zeta ^2}{\left( {\dfrac{{{\text{Δ}} x}}{\eta }} \right)^2} + 140{a_2}{\zeta ^4}{\left( {\dfrac{{{\text{Δ}} x}}{\eta }} \right)^4} $ 二阶横向结构函数绝对误差 耗散区 $ \dfrac{{{\text{δ}} {D_{{\mathrm{NN}}}}}}{{u_\eta ^2}} = \left[ { - 56{a_2}{\zeta ^2}{{\left( {\dfrac{{{\text{Δ}} x}}{\eta }} \right)}^2} - 1512{a_3}{\zeta ^4}{{\left( {\dfrac{{{\text{Δ}} x}}{\eta }} \right)}^4}} \right]{\left( {\dfrac{r}{\eta }} \right)^2} $ 惯性区 $ \dfrac{{{\text{δ}} {D_{{\mathrm{NN}}}}}}{{u_\eta ^2}} = 8{a_1}{\zeta ^2}{\left( {\dfrac{{{\text{Δ}} x}}{\eta }} \right)^2} + 100{a_2}{\zeta ^4}{\left( {\dfrac{{{\text{Δ}} x}}{\eta }} \right)^4} $ 湍流耗散率比值 $ \dfrac{{\bar \varepsilon }}{\varepsilon } = 1 + 420{a_2}{\zeta ^2}{\left( {\dfrac{{{\text{Δ}} x}}{\eta }} \right)^2} + 11340{a_3}{\zeta ^4}{\left( {\dfrac{{{\text{Δ}} x}}{\eta }} \right)^4} $ 
下载: 导出CSV
表 2 DNS数据库流场数据（DNS单位）
Table 2 Parameters of the DNS database (DNS unit)
泰勒
雷诺数Reλ运动黏性
系数νKolmogorov
特征长度ηKolmogorov
特征速度uη湍流
耗散率ε418 1.85 × 10−4 2.8 × 10−3 6.60 × 10−2 1.03 × 10−1
下载: 导出CSV
表 3 基于DNS数据模拟PIV图像的参数设置
Table 3 Parameter settings for DNS data to simulate PIV images
模拟激光片
相对厚度Δh/η问询域窗口
相对大小Δx/η问询域
窗口大小Δx问询域窗口
之间的重合度2 3.5 48像素 × 48像素 50% 4 4.7 32像素 × 32像素 50% 6 6.6 32像素 × 32像素 50% 8 9.1 32像素 × 32像素 50% 10 11.8 32像素 × 32像素 50%
下载: 导出CSV
表 4 高斯滤波作用下的二阶速度结构函数绝对误差函数形式
Table 4 The specific forms of absolute errors of second-order structure function under the role of Gaussian filtering
多点统计量 绝对误差函数形式（忽略包含系数a3的高阶项） 二阶纵向
速度结构函数d1 $ - 28{a_2}{\zeta ^2}{\left( {\frac{{{\text{Δ}} x}}{\eta }} \right)^2} $ d2 $ {{{d_1}} \mathord{\left/ {\vphantom {{{d_1}} {\left[ {10{a_1}{\zeta ^2}{{\left( {\frac{{{\text{Δ}} x}}{\eta }} \right)}^2} + 140{a_2}{\zeta ^4}{{\left( {\frac{{{\text{Δ}} x}}{\eta }} \right)}^4}} \right]}}} \right. } {\left[ {10{a_1}{\zeta ^2}{{\left( {\frac{{{\text{Δ}} x}}{\eta }} \right)}^2} + 140{a_2}{\zeta ^4}{{\left( {\frac{{{\text{Δ}} x}}{\eta }} \right)}^4}} \right]}} $ 二阶横向
速度结构函数D1 $ - 56{a_2}{\zeta ^2}{\left( {\frac{{{\text{Δ}} x}}{\eta }} \right)^2} $ D2 $ {{{D_1}} \mathord{\left/ {\vphantom {{{D_1}} {\left[ {8{a_1}{\zeta ^2}{{\left( {\frac{{{\text{Δ}} x}}{\eta }} \right)}^2} + 100{a_2}{\zeta ^4}{{\left( {\frac{{{\text{Δ}} x}}{\eta }} \right)}^4}} \right]}}} \right. } {\left[ {8{a_1}{\zeta ^2}{{\left( {\frac{{{\text{Δ}} x}}{\eta }} \right)}^2} + 100{a_2}{\zeta ^4}{{\left( {\frac{{{\text{Δ}} x}}{\eta }} \right)}^4}} \right]}} $
下载: 导出CSV
表 5 模拟PIV得到的湍流耗散率计算值与真实值之间的相对误差
Table 5 The relative errors between the calculated values and the true value of the turbulent dissipation rate obtained by simulating PIV
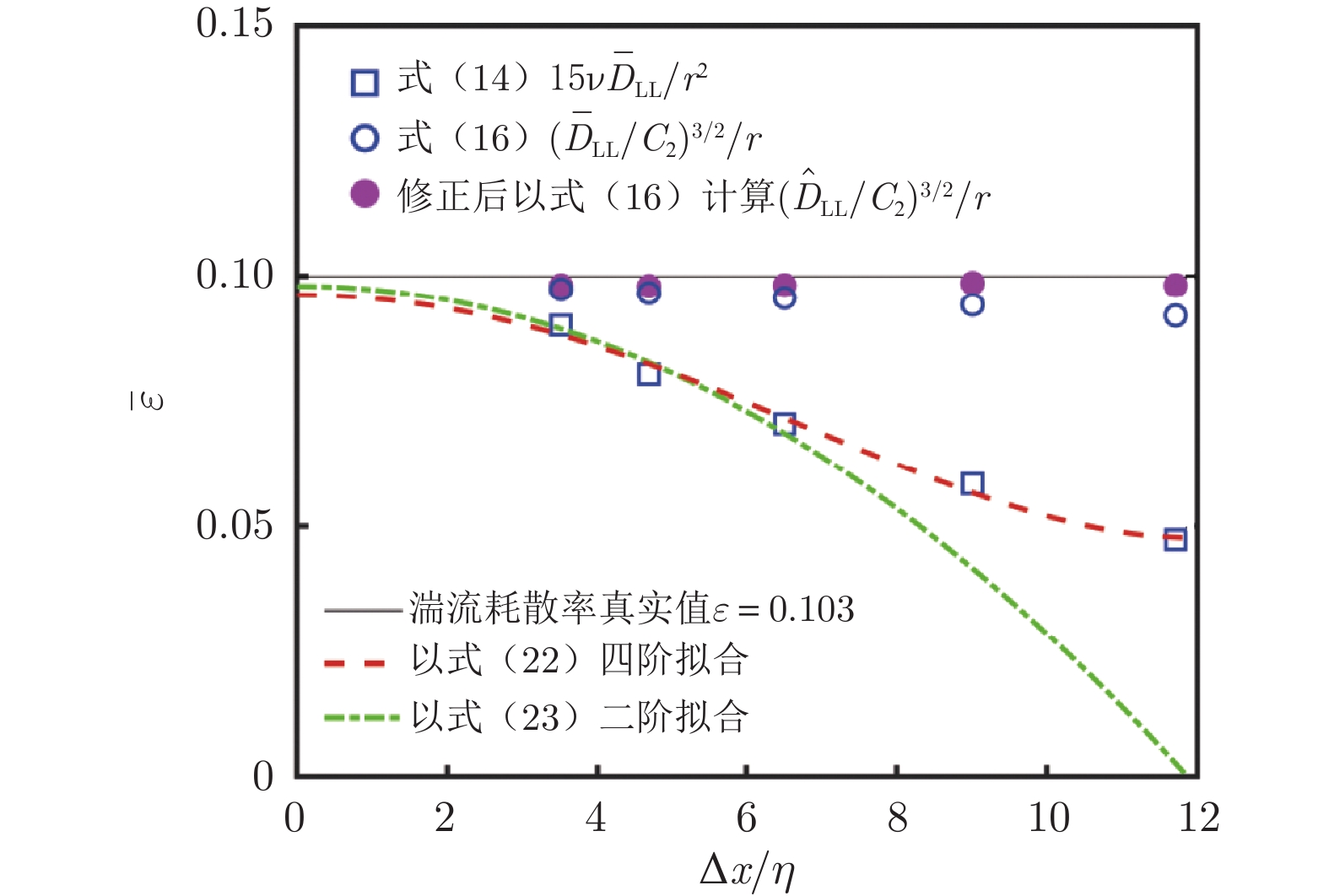
Δx/η 相对误差 耗散区 惯性区 式（14） 式（22） 式（23） 式（16） 修正后再以
式（16）计算3.5 9.8% 3.7% 2.0% 2.6% 1.8% 4.7 19.6% 3.7% 2.0% 3.4% 2.0% 6.6 29.4% 3.7% 2.0% 4.3% 1.8% 9.1 41.5% 3.7% 2.0% 5.7% 1.3% 11.8 52.7% 3.7% 2.0% 7.9% 1.8%
下载: 导出CSV
表 6 冯·卡门旋流PIV实验参数设置
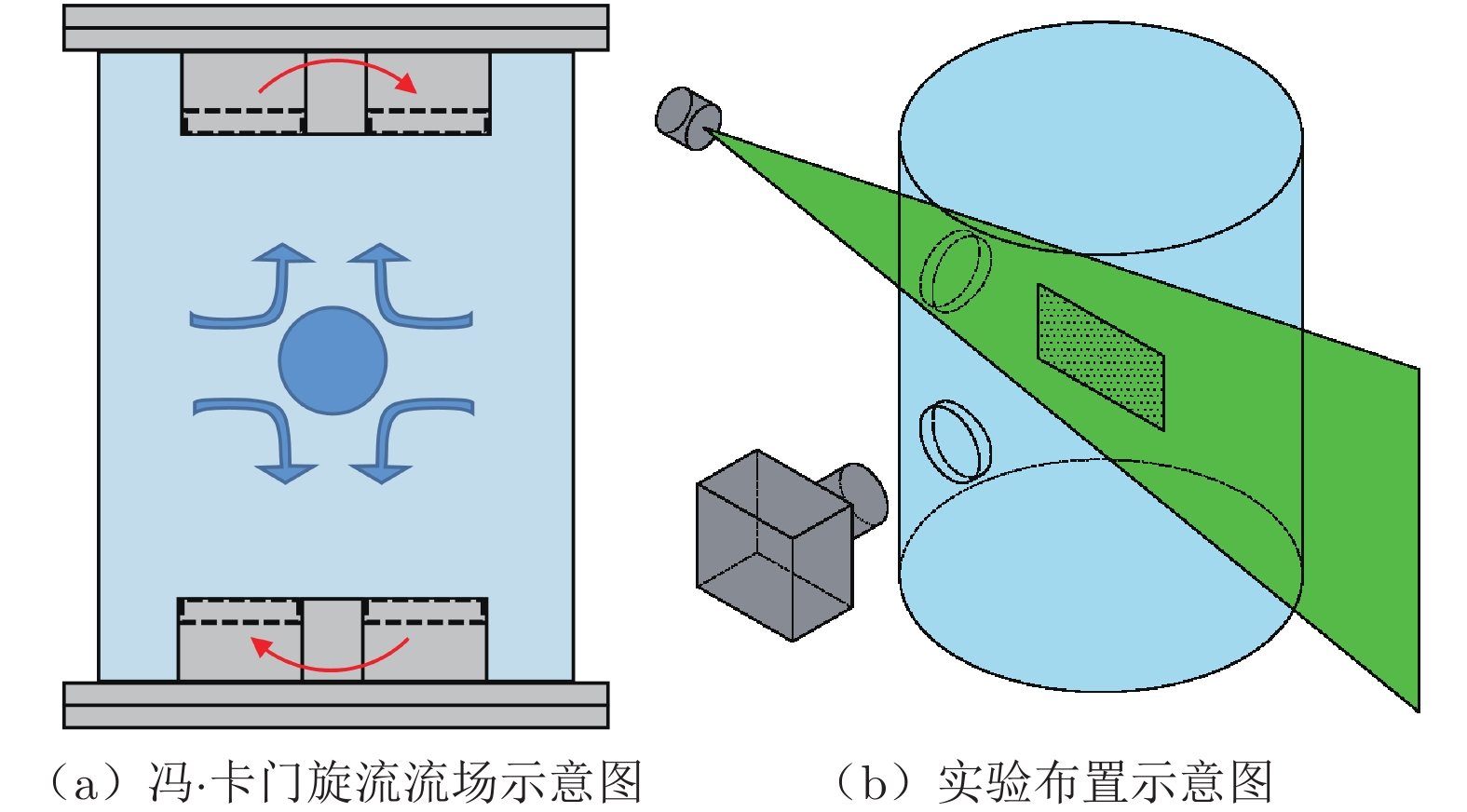
Table 6 Parameter settings of von Kármán swirling PIV experiment
实验装置 描述 PIV系统
运行平台DynamicStudio 光源设备 Nd:Yag双脉冲固体激光器 Vlite‒200，波长532 nm，脉冲能量2 × 200 mJ。示踪粒子为聚酰胺颗粒，平均直径5 μm 数据采集
设备IMPERX B3440相机， 3388 像素 ×2712 像素，像素尺寸3.69 μm，有效像素物理尺寸12.2 μm/像素
下载: 导出CSV
-
[1] WESTERWEEL J, ELSINGA G E, ADRIAN R J. Particle image velocimetry for complex and turbulent flows[J]. Annual Review of Fluid Mechanics, 2013, 45: 409–436. doi: 10.1146/annurev-fluid-120710-101204
[2] SCHROEDER A, WILLERT C E. Particle Image Velocimetry: New Developments and Recent Applications[M]. Berlin: Springer, 2008.
[3] 王福君, 王洪平, 高琪, 等. 鱼游动涡结构PIV实验研究[J]. 实验流体力学, 2020, 34(5): 20–28. DOI: 10.11729/syltlx20200039 WANG F J, WANG H P, GAO Q, et al. PIV experimental study on fish swimming vortex structure[J]. Journal of Experiments in Fluid Mechanics, 2020, 34(5): 20–28. doi: 10.11729/syltlx20200039
[4] 赵航, 佘文轩, 高琪, 等. 基于层析PIV的椭圆水翼近尾迹梢涡实验研究[J]. 实验流体力学, 2022, 36(2): 82–91. DOI: 10.11729/syltlx20210108 ZHAO H, SHE W X, GAO Q, et al. TPIV study for near-field tip vortex from an elliptical hydrofoil[J]. Journal of Experiments in Fluid Mechanics, 2022, 36(2): 82–91. doi: 10.11729/syltlx20210108
[5] WORTH N A, NICKELS T B. Acceleration of Tomo-PIV by estimating the initial volume intensity distribution[J]. Experiments in Fluids, 2008, 45(5): 847–856. doi: 10.1007/s00348-008-0504-6
[6] 刘朝阳, 王鑫蔚, 王轩, 等. 微结构超疏水壁面湍流边界层减阻机理的TRPIV实验研究[J]. 实验流体力学. doi: 10.11729/syltlx20220016. LIU Z Y, WANG X W, WANG X, et al. Experimental study of the mechanism of drag reduction in turbulent boundary layers on the superhydrophobic structured wall with microstructure[J]. Journal of Experiments in Fluid Mechanics. doi: 10.11729/syltlx20220016.
[7] WILLERT C E, GHARIB M. Digital particle image velocimetry[J]. Experiments in Fluids, 1991, 10(4): 181–193. doi: 10.1007/BF00190388
[8] SAIKRISHNAN N, MARUSIC I, LONGMIRE E K. Assessment of dual plane PIV measurements in wall turbulence using DNS data[J]. Experiments in Fluids, 2006, 41(2): 265–278. doi: 10.1007/s00348-006-0168-z
[9] ATKINSON C, BUCHMANN N A, AMILI O, et al. On the appropriate filtering of PIV measurements of turbulent shear flows[J]. Experiments in Fluids, 2013, 55(1): 1654. doi: 10.1007/s00348-013-1654-8
[10] LI Q Y, PENG Z B, LIU L, et al. A comparison of different methods for estimating turbulent dissipation rate in under-resolved flow fields from synthetic PIV images[J]. Chemical Engineering Research and Design, 2021, 175: 161–170. doi: 10.1016/j.cherd.2021.09.004
[11] VASSILICOS J C. Dissipation in turbulent flows[J]. Annual Review of Fluid Mechanics, 2015, 47: 95–114. doi: 10.1146/annurev-fluid-010814-014637
[12] HASSID S, POREH M. A turbulent energy dissipation model for flows with drag reduction[J]. Journal of Fluids Engineering, 1978, 100(1): 107–112. doi: 10.1115/1.3448580
[13] WANG G C, YANG F, WU K, et al. Estimation of the dissipation rate of turbulent kinetic energy: a review[J]. Chemical Engineering Science, 2021, 229: 116133. doi: 10.1016/j.ces.2020.116133
[14] LAVOIE P, AVALLONE G, DE GREGORIO F, et al. Spatial resolution of PIV for the measurement of turbulence[J]. Experiments in Fluids, 2007, 43(1): 39–51. doi: 10.1007/s00348-007-0319-x
[15] DE JONG J, CAO L, WOODWARD S H, et al. Dissipation rate estimation from PIV in zero-mean isotropic turbu-lence[J]. Experiments in Fluids, 2009, 46(3): 499–515. doi: 10.1007/s00348-008-0576-3
[16] XU D, CHEN J. Accurate estimate of turbulent dissipation rate using PIV data[J]. Experimental Thermal and Fluid Science, 2013, 44: 662–672. doi: 10.1016/j.expthermflusci.2012.09.006
[17] BUXTON O R H, LAIZET S, GANAPATHISUBRAMANI B. The effects of resolution and noise on kinematic features of fine-scale turbulence[J]. Experiments in Fluids, 2011, 51(5): 1417–1437. doi: 10.1007/s00348-011-1159-2
[18] GANAPATHISUBRAMANI B, LAKSHMINARASIMHAN K, CLEMENS N T. Investigation of three-dimensional structure of fine scales in a turbulent jet by using cinematographic stereoscopic particle image velocimetry[J]. Journal of Fluid Mechanics, 2008, 598: 141–175. doi: 10.1017/s0022112007009706
[19] STOLZ S, ADAMS N A. An approximate deconvolution procedure for large-eddy simulation[J]. Physics of Fluids, 1999, 11(7): 1699–1701. doi: 10.1063/1.869867
[20] SCARANO F. Iterative image deformation methods in PIV[J]. Measurement Science and Technology, 2002, 13(1): R1–R19. doi: 10.1088/0957-0233/13/1/201
[21] GAO Q, LIN H T, TU H, et al. A robust single-pixel particle image velocimetry based on fully convolutional networks with cross-correlation embedded[J]. Physics of Fluids, 2021, 33(12): 127125. doi: 10.1063/5.0077146
[22] SCHARNOWSKI S, HAIN R, KÄHLER C J. Reynolds stress estimation up to single-pixel resolution using PIV-measurements[J]. Experiments in Fluids, 2012, 52(4): 985–1002. doi: 10.1007/s00348-011-1184-1
[23] TANAKA T, EATON J K. A correction method for measuring turbulence kinetic energy dissipation rate by PIV: Validated by random Oseen vortices synthetic image test[J]. Experiments in Fluids, 2007, 42(6): 893–902. doi: 10.1007/s00348-007-0298-y
[24] BUARIA D, BODENSCHATZ E, PUMIR A. Vortex stretching and enstrophy production in high Reynolds number turbulence[J]. Physical Review Fluids, 2020, 5(10): 104602. doi: 10.1103/physrevfluids.5.104602
[25] BUARIA D, PUMIR A, BODENSCHATZ E, et al. Extreme velocity gradients in turbulent flows[J]. New Journal of Physics, 2019, 21(4): 043004. doi: 10.1088/1367-2630/ab0756
[26] TANAKA T, EATON J K. Sub-Kolmogorov resolution particle image velocimetry measurements of particle-laden forced turbulence[J]. Journal of Fluid Mechanics, 2010, 643: 177–206. doi: 10.1017/s0022112009992023
[27] ZHANG Y B, BODENSCHATZ E, XU H T, et al. Experimental observation of the elastic range scaling in turbulent flow with polymer additives[J]. Science Advances, 2021, 7(14): eabd3525. doi: 10.1126/sciadv.abd3525
[28] SHENG J, MENG H, FOX R O. A large eddy PIV method for turbulence dissipation rate estimation[J]. Chemical Engineering Science, 2000, 55(20): 4423–4434. doi: 10.1016/s0009-2509(00)00039-7
[29] WESTERWEEL J. On velocity gradients in PIV interrogation[J]. Experiments in Fluids, 2008, 44(5): 831–842. doi: 10.1007/s00348-007-0439-3
[30] BATCHELOR G K. Pressure fluctuations in isotropic turbulence[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1951, 47(2): 359–374. doi: 10.1017/s0305004100026712
[31] KOLMOGOROV A N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers[J]. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, 1991, 434(1890): 9-13. doi: 10.1098/rspa.1991.0075
[32] POPE S B. Turbulent flows[M]. Cambridge: Cambridge University Press, 2000. doi: 10.1017/CBO9780511840531
[33] BUARIA D, SREENIVASAN K R. Lagrangian acceleration and its Eulerian decompositions in fully developed turbulence[J]. Physical Review Fluids, 2023, 8(3): L032601. doi: 10.1103/physrevfluids.8.l032601
[34] NI R, XIA K Q. Kolmogorov constants for the second-order structure function and the energy spectrum[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2013, 87(2): 023002. doi: 10.1103/PhysRevE.87.023002
[35] LI Y, PERLMAN E, WAN M P, et al. A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence[J]. Journal of Turbulence, 2008, 9: 1–29. doi: 10.1080/14685240701767332
[36] RAFFEL M, WILLERT C E, SCARANO F, et al. Particle Image Velocimetry: a practical guide[M]. Cham: Springer International Publishing, 2018. doi: 10.1007/978-3-319-68852-7
[37] THIELICKE W, SONNTAG R. Particle Image Velocimetry for MATLAB: Accuracy and enhanced algorithms in PIVlab[J]. Journal of Open Research Software, 2021, 9(1): 12. doi: 10.5334/jors.334
[38] 张亿宝. 高聚物添加剂对湍流能量级串过程的影响[D]. 西安: 西北工业大学, 2021: 19-29. [39] DOUADY S, COUDER Y, BRACHET M E. Direct observation of the intermittency of intense vorticity filaments in turbulence[J]. Physical Review Letters, 1991, 67(8): 983–986. doi: 10.1103/PhysRevLett.67.983
[40] MAURER J, TABELING P, ZOCCHI G. Statistics of turbulence between two counterrotating disks in low-temperature helium gas[J]. EPL (Europhysics Letters), 1994, 26(1): 31–36. doi: 10.1209/0295-5075/26/1/006
[41] VOTH G A, SATYANARAYAN K, BODENSCHATZ E. Lagrangian acceleration measurements at large Reynolds numbers[J]. Physics of Fluids, 1998, 10(9): 2268–2280. doi: 10.1063/1.869748
[42] BOURGOIN M, OUELLETTE N T, XU H T, et al. The role of pair dispersion in turbulent flow[J]. Science, 2006, 311(5762): 835–838. doi: 10.1126/science.1121726
计量
- 文章访问数: 770
- HTML全文浏览量: 50
- PDF下载量: 91
