Numerical study on turbulent combustion in high Mach number scramjet engine considering thermal non-equilibrium effect
-
摘要:
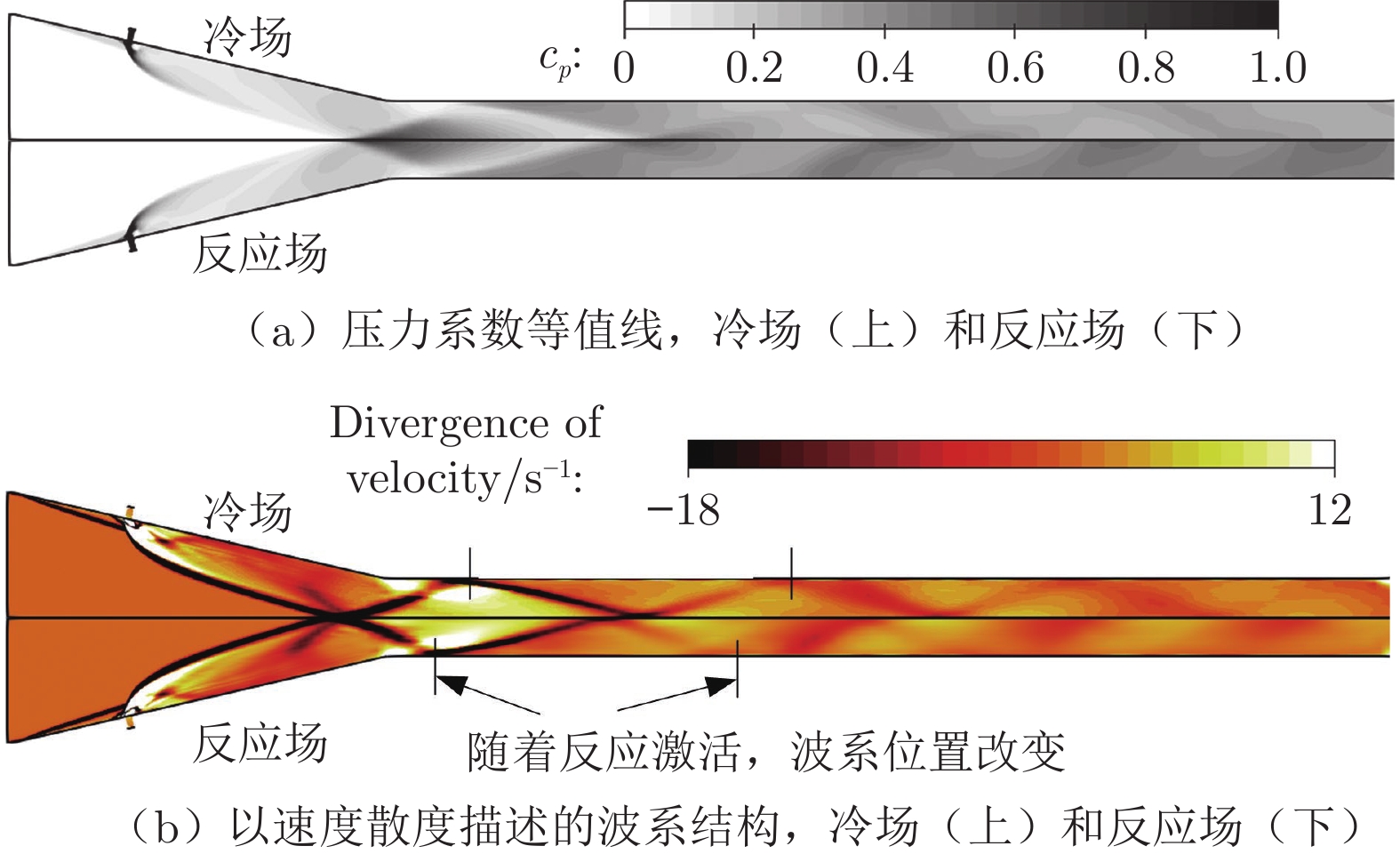
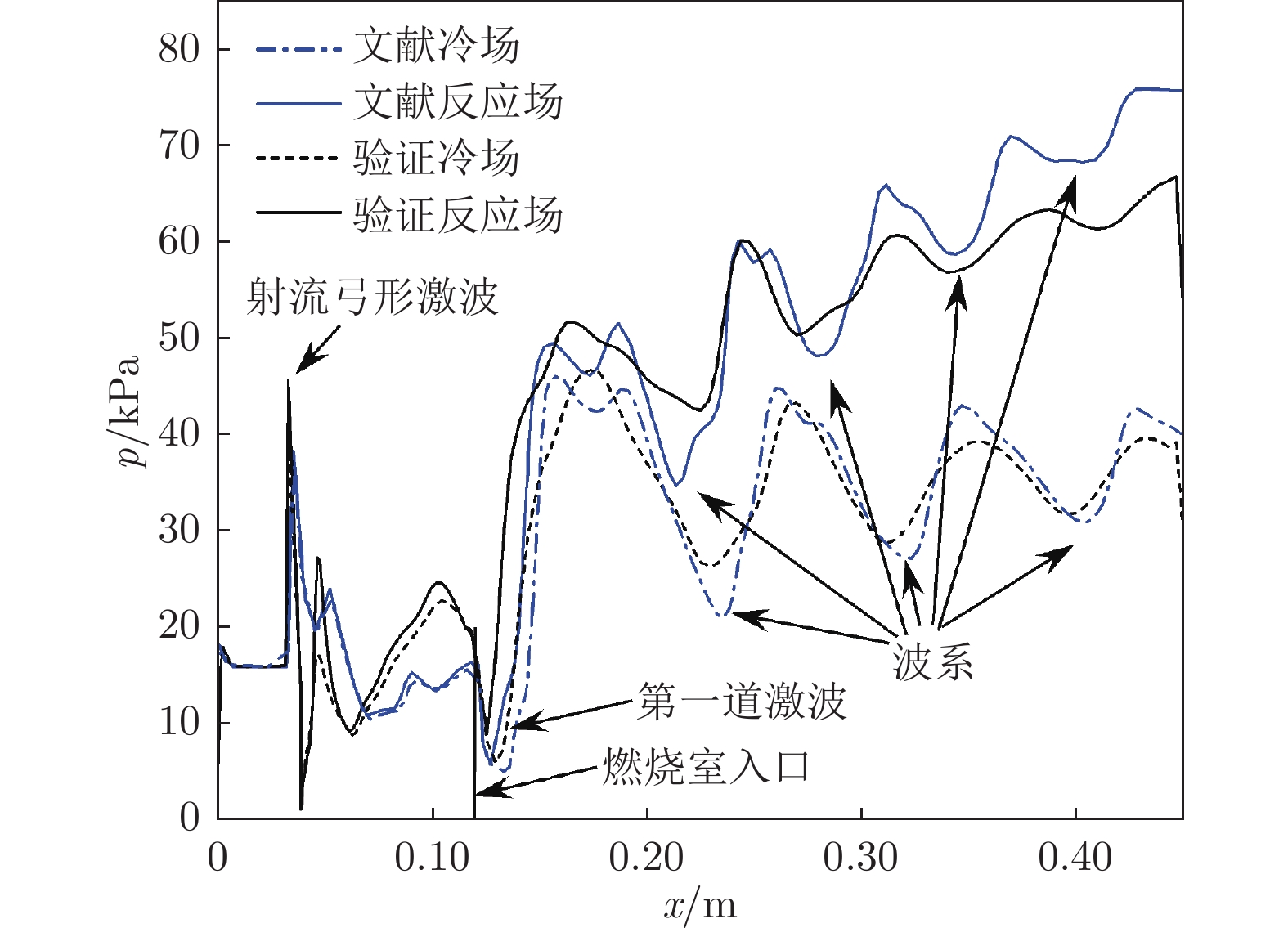
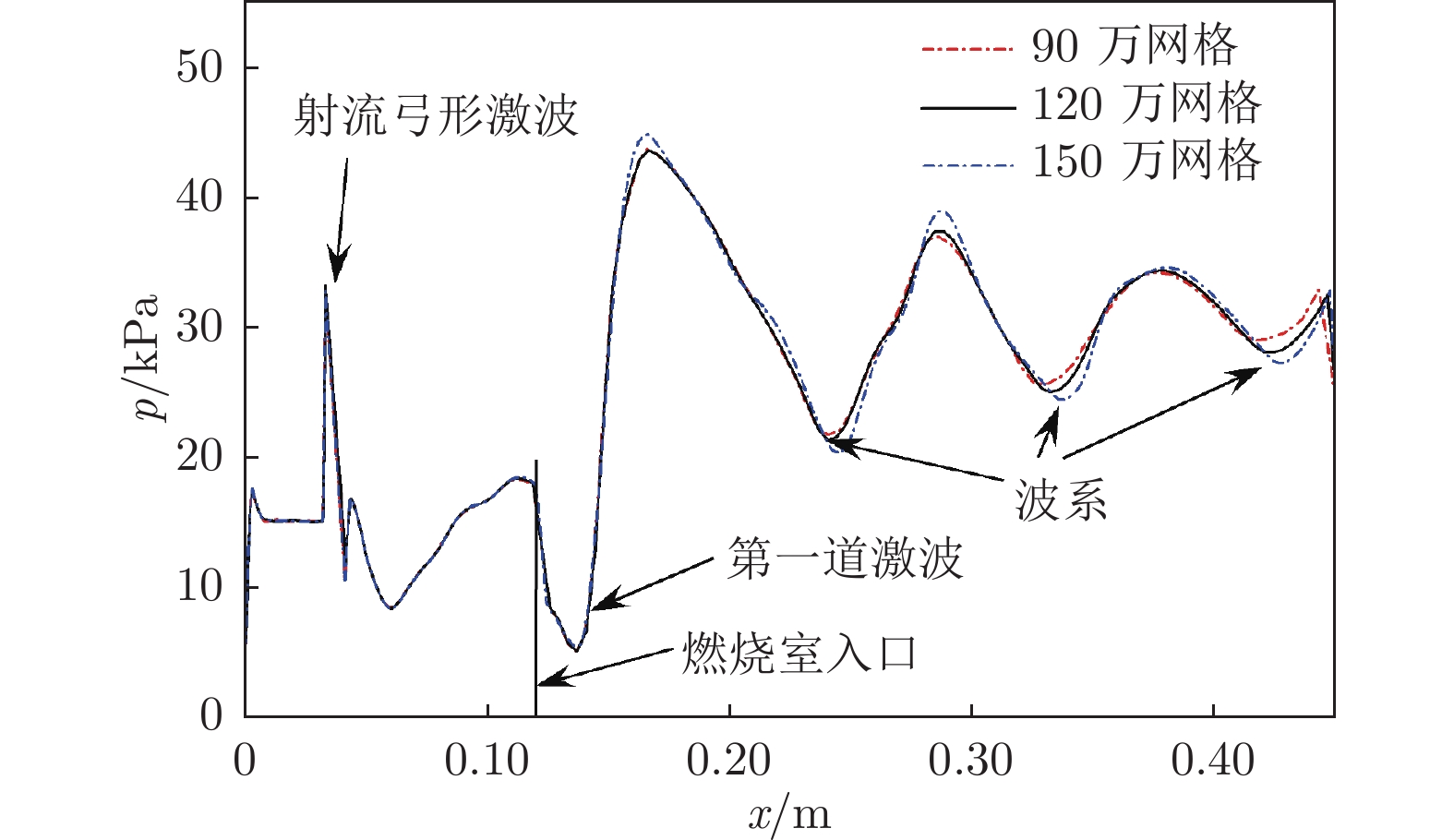
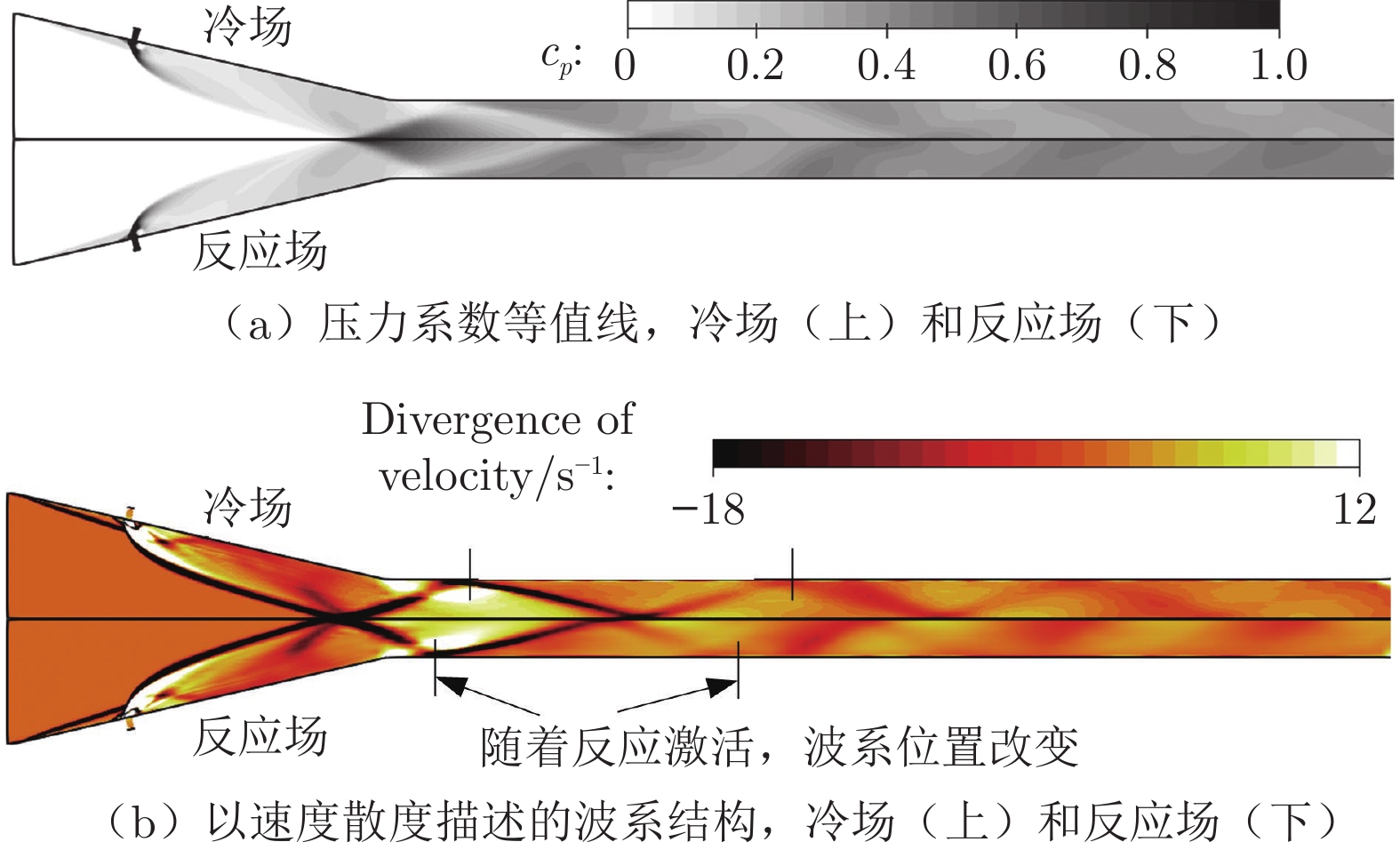
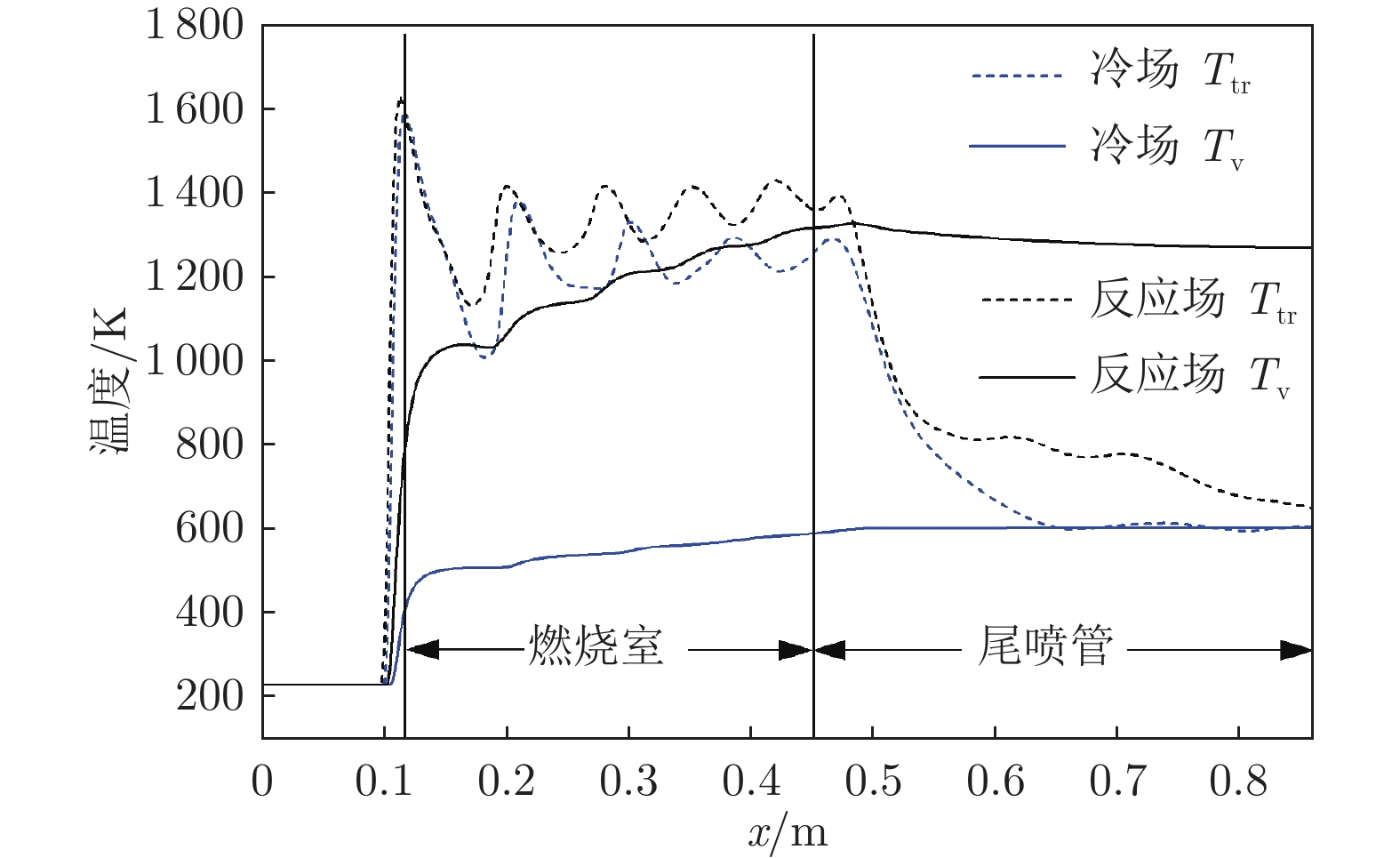
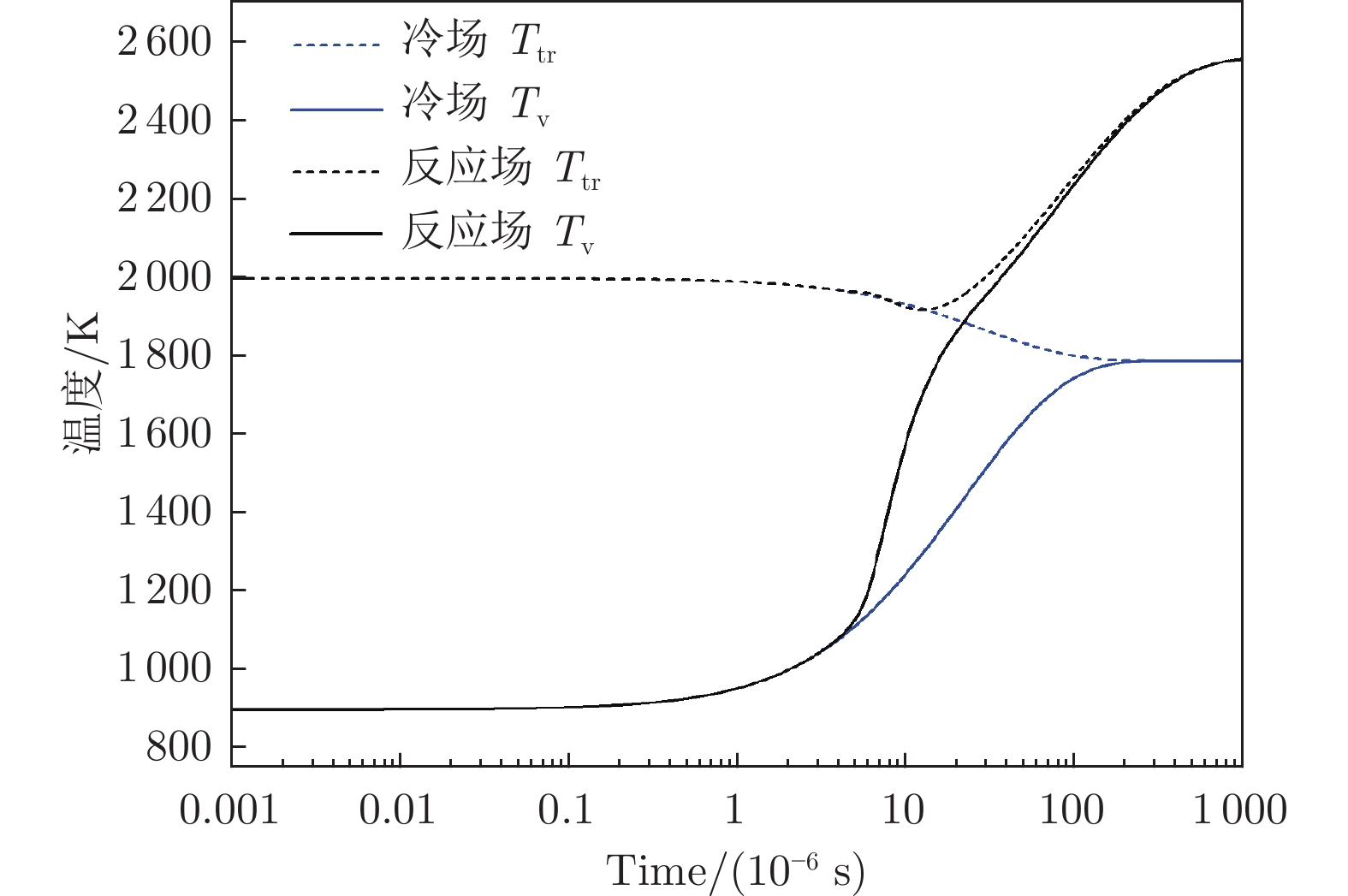
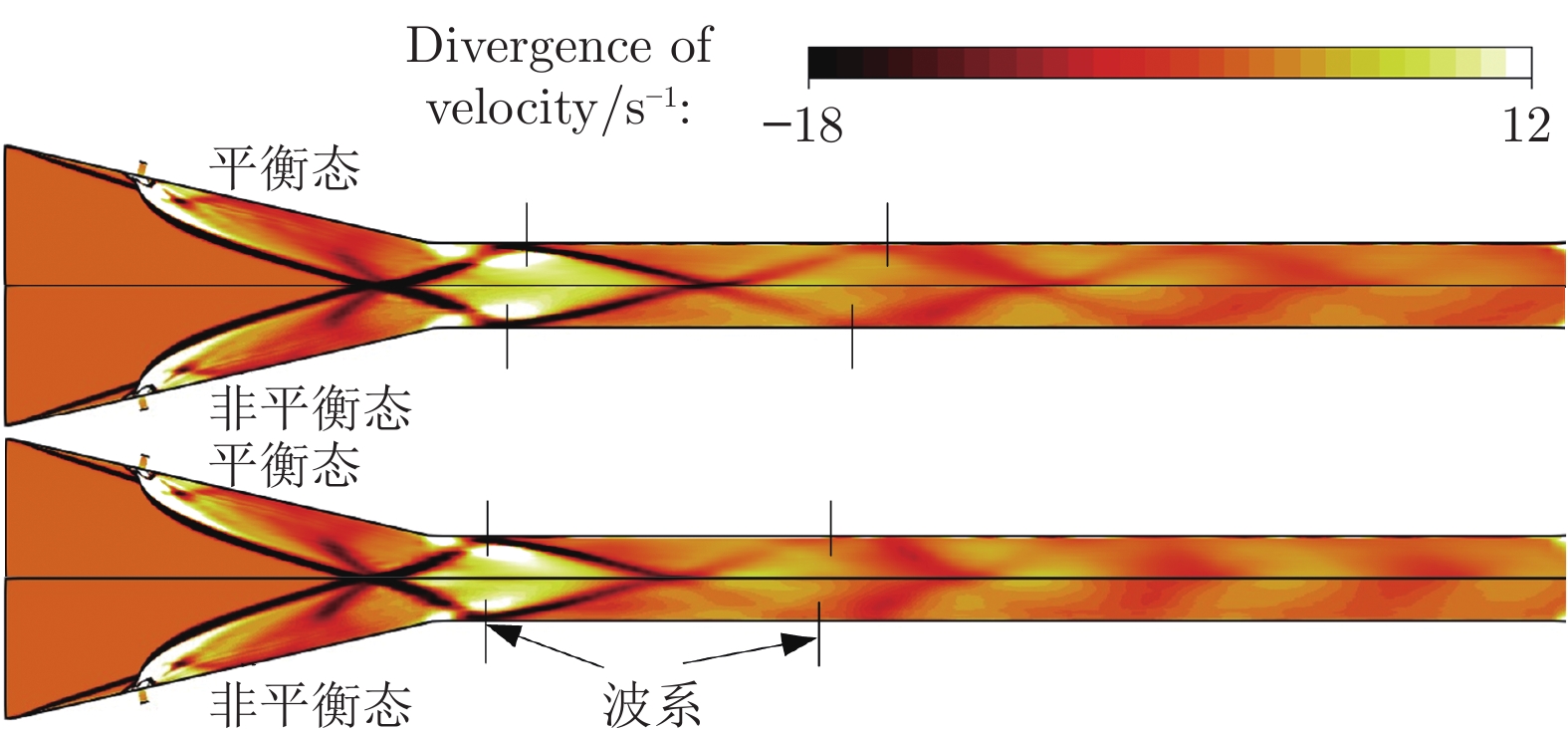
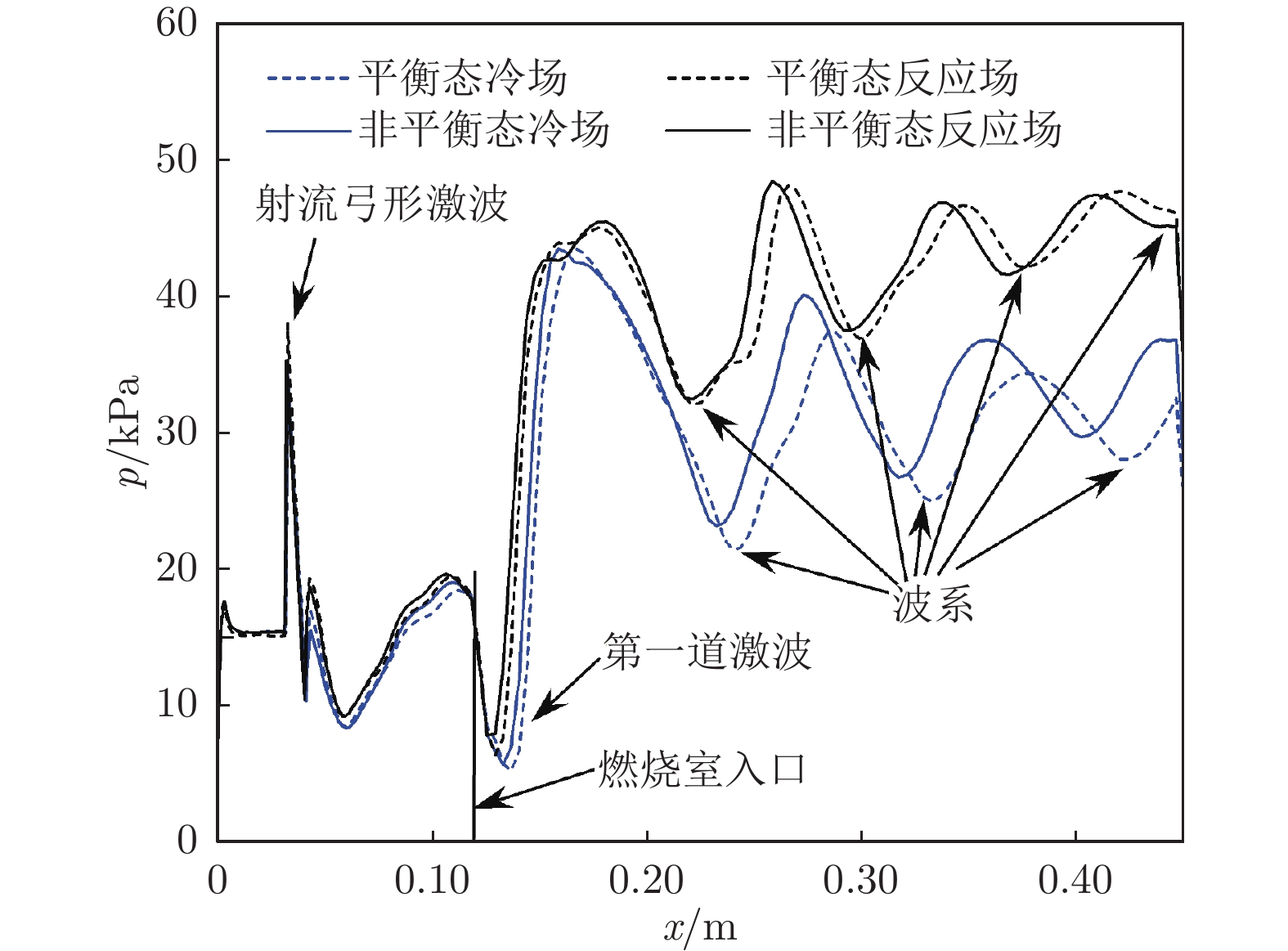
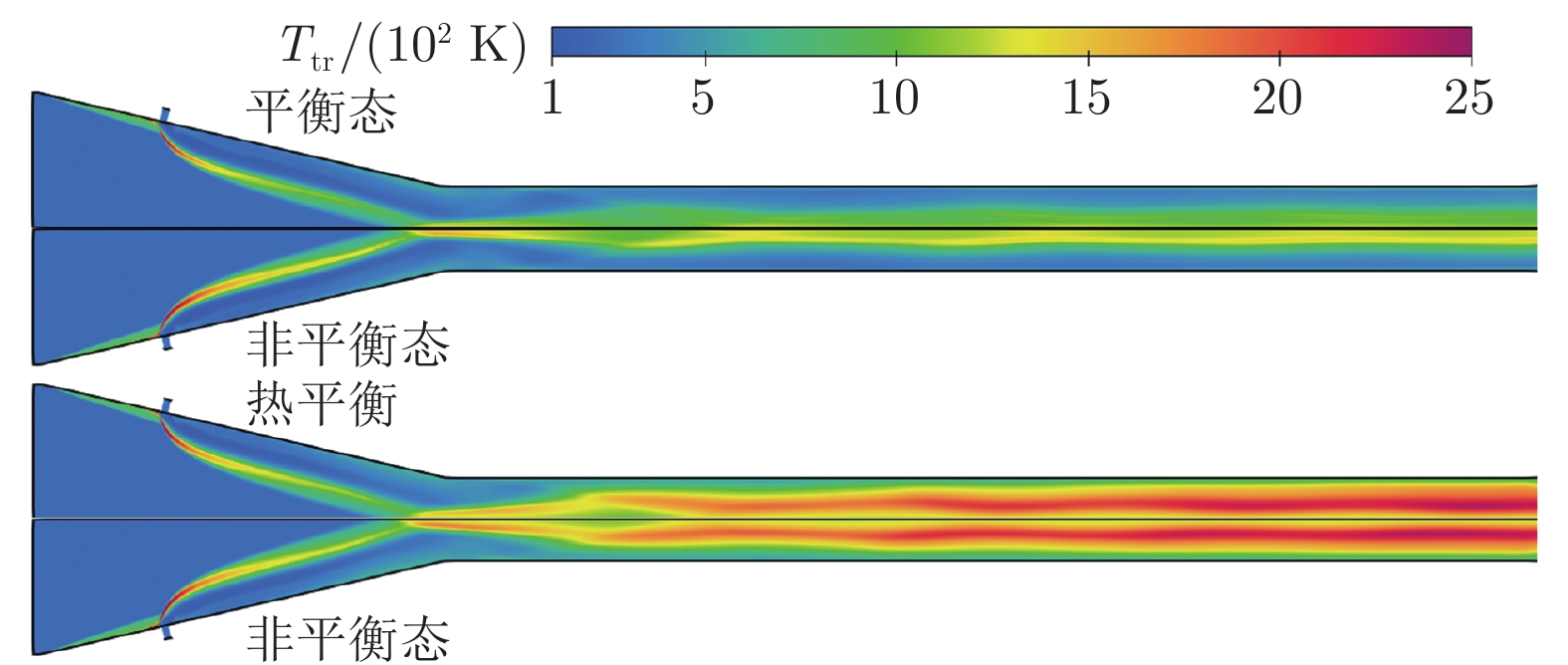
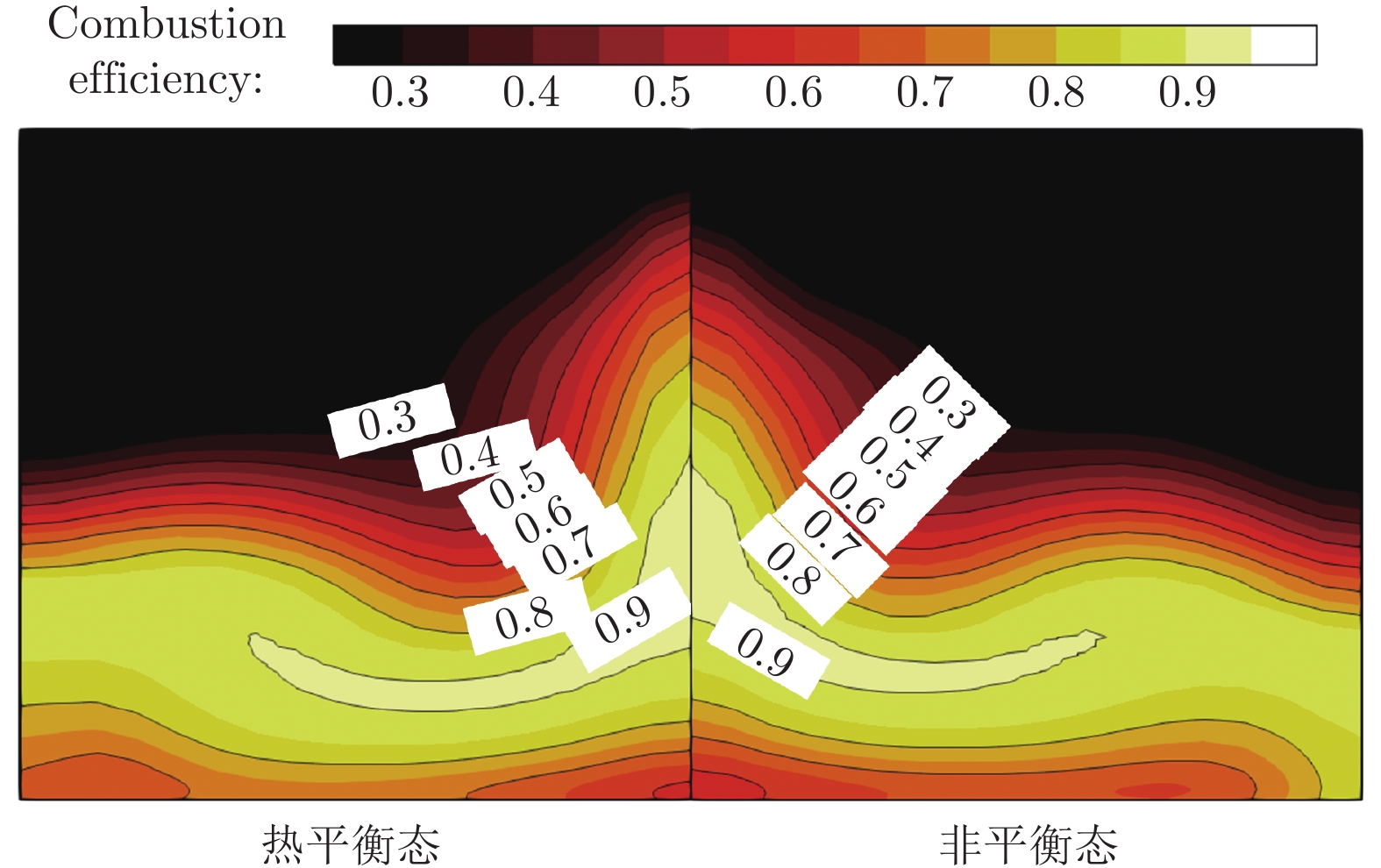
高超声速飞行过程中,随着马赫数升高,边界层内温度快速上升,分子振动能、电子能被激发,气体分子发生离解甚至电离,使得量热完全气体假设失效。针对高温热化学非平衡气体,采用热力学平衡模型及Park的双温度非平衡模型对飞行马赫数Ma = 12条件下的超燃冲压发动机进行了数值模拟。研究结果表明:与平衡态计算结果相比,非平衡效应使得波系位置前移,激波间峰值压力升高,对冷场的影响更加明显;非平衡态平动温度场与平衡态差别不大,热力学非平衡效应使平动温度Ttr略微升高;非平衡态燃烧室出口截面燃烧效率更低,热力学非平衡效应会降低反应程度。
Abstract:During hypersonic flight, the temperature inside the boundary layer rapidly increases with the increase of Mach number, leading to the excitation of molecular vibration and electron energy. Gaseous molecules undergo dissociation or even ionization, making the assumption of complete gas calorimetry invalid, and thereby affecting the characteristics of the scramjet engine. The turbulent combustion in the scramjet engine under the Ma = 12 flight condition is numerically studied via a thermodynamic equilibrium model and the Park's dual temperature non-equilibrium model where the high-temperature thermal non-equilibrium effects are considered. The results indicate that compared to the equilibrium case, the non-equilibrium effect causes the position of the shock wave trains to shift forward, and the increase of the peak pressure between shock waves. This is more significant for the frozen flow field. The temperature field Ttr in the non-equilibrium case is not significantly different from that of the equilibrium case, and the thermodynamic non-equilibrium effect slightly increases Ttr. The combustion efficiency at the outlet section is lower in the non-equilibrium case, and the thermodynamic non-equilibrium effect slightly weakens the intensity of the reactions.
-
0 引 言
近年来,无人机不再局限于军事应用,在消防、测绘、植保等民用方面也应用广泛[1-2],对航程远、航时长且更为自主化、智能化的无人机的需求也日益迫切[3]。目前,能源系统是限制无人机飞行能力的主要因素,由于无人机的负载和动力系统会消耗大量能量,且所能携带的能源容量有限,导致其难以获得理想的续航能力[3-4]。
为提高无人机的续航能力,可以对气动外形进行优化[5-6],减小空中飞行的阻力,也可以增大翼展以提升无人机的滑翔能力,还可以在飞行器表面安装太阳能板,通过光伏技术为无人机提供能量[7-8]。这2种措施能够有效提升无人机续航能力,但对于小型无人机而言,优化气动外形难以显著增大其续航能力。光伏技术须安装太阳能板,这会给机翼材料增加负担,且太阳能的获取受天气影响较大,对小型无人机续航能力的提升有限。
众所周知,自然界的鸟类可以利用风能提升飞行时间和距离,如军舰鸟、秃鹰等鸟类会借助环境中的热上升气流进行静态滑翔飞行[9]。国内外研究者尝试将其原理应用到无人机上,并取得了一定的成果。在热上升气流建模方面:Bencatel等[10]总结了Chimney和Bubble[11]2种热上升气流的模型;Allen[12]对沙漠地区的热上升气流进行了数据统计,基于Chimney模型建立了热上升气流数学模型。在无人机滑翔控制策略方面:Allen等[13]利用飞行器的总能量状态估计热上升气流的强度和位置,并基于此设计了定位气流中心的控制方法;Wharington[14]应用强化学习设计了滑翔控制方法;Kahveci等[15]利用LQR(Linear Quadratic Regulator)控制方法定位与跟踪热上升气流中心。在设计用于控制无人机进入和脱离热上升气流的模式切换逻辑方面:Allen[13]和Edwards[16]等设计了能量估计器,并利用能量估计器的输出(能量的一阶和二阶导数)设计模式切换逻辑。
模式切换问题是无人机利用热上升气流进行自主滑翔的关键问题之一。 本文针对这一问题设计了一套基于七孔探针和嵌入式技术的气流感知系统,并将其应用于自主滑翔的模式切换逻辑,相比于Allen等[13]基于无人机能量设计的模式切换逻辑,本文所设计的模式切换逻辑无需对不同无人机进行动力装置辨识建模。为验证所设计的模式切换逻辑,在风洞中搭建了一套热上升气流模拟装置,利用风洞虚拟飞行试验平台,分析所设计的模式切换逻辑的可行性。
1 气流感知系统
1.1 七孔探针的结构
七孔探针的结构外形如图1所示。探针长度为125 mm,直径为4.6 mm,头部锥度为30°。从七孔探针头部看,7号孔位于中心,其余6孔围绕7号孔均匀分布,探针体表面红点对应1号孔。各孔连接的导管伸出探针体的长度不同,导管由长到短依次连接1~7号孔。
1.2 七孔探针的校准
1.2.1 流动分区
当气流方向与探针轴线夹角很大时,会出现流动分离现象[17],如图2所示。按照7个孔的压力值,将探针头部划分为7个区,7区为内区,其余6个区为外区。
1.2.2 气流角定义
如图3所示,建立直角坐标系Oxyz,u、v、w分别为流动速度在x、y、z方向上的分量。在小流动角情况下,来流方向用迎角α和侧滑角β表示;在大流动角情况下,来流方向用俯仰角θ和滚转角ϕ表示。
1.2.3 压力系数定义
在内区,对7个孔测得的压力进行数据处理,定义无量纲压力系数C1、C2、C3[18]如下:
$$ {C_{1}} = \frac{{{p_4} - {p_1}}}{{{p_7} - {{\overline p }_{1\sim6}}}} $$ (1) $$ {C_{2}} = \frac{{{p_6} - {p_3}}}{{{p_7} - {{\overline p }_{1\sim6}}}} $$ (2) $$ {C_{3}} = \frac{{{p_5} - {p_2}}}{{{p_7} - {{\overline p }_{1\sim6}}}} $$ (3) 式中:p1~p7分别为七孔探针7个孔的压力,${{\overline p }_{1\sim6}}$为外圈6个孔压力的平均值。
对C1、C2、C3进行加权平均,得到迎角系数Cα和侧滑角系数Cβ:
$$ {C_\alpha } = \frac{1}{3}(2{C_{1}} - {C_{2}} + {C_{3}}) $$ (4) $$ {C_\beta } = \frac{1}{{\sqrt 3 }}({C_{2}} + {C_{3}}) $$ (5) 为得到来流总压和静压,定义总压系数C0和动压系数Cq如下:
$$ {C_{\rm{0}}} = \frac{{{p_7} - {p_0}}}{{{p_7} - {{\overline p }_{1\sim6}}}} $$ (6) $$ {C_{{q}}} = \frac{{{p_7} - {{\overline p }_{1\sim6}}}}{{{p_0} - {p_\infty }}} $$ (7) 式中:p0为局部总压,p∞为局部静压,校准时通过皮托管测量得到。
在外区,通过对压力值最高的孔及其相邻2个孔的压力数据进行处理,获得俯仰角系数${C_{\theta i}} $、滚转角系数$ {C_{\phi i}} $、总压系数C0i和动压系数Cqi如下:
$$ {C_{\theta i}} = \frac{{{p_i} - {p_7}}}{{{p_i} - 0.5({p_{i - }} + {p_{i + }})}} $$ (8) $$ {C_{\phi i}} = \frac{{{p_{i - }} - {p_{i + }}}}{{{p_i} - 0.5({p_{i - }} + {p_{i + }})}} $$ (9) $$ {C_{0i}} = \frac{{{p_i} - {p_0}}}{{{p_i} - 0.5({p_{i - }} + {p_{i + }})}} $$ (10) $$ {C_{{{q}}i}} = \frac{{{p_i} - 0.5({p_{i - }} + {p_{i + }})}}{{{p_0} - {p_\infty }}} $$ (11) 式中:下标i、i+、i−分别代表外区压力孔编号及其相邻2个孔的编号。
1.2.4 多项式拟合
用四次多项式表示流动参数A(即来流的方向角、总压和动压等)[19]。内区用Cα和Cβ作为变量,外区用Cθi和Cϕi作为变量。以内区为例,多项式拟合矩阵如下:
$$ \left[ \begin{array}{*{20}{c}} {A_1} \\ {A_2} \\ \vdots \\ {A_n} \\ \end{array} \right] = \left[ {\begin{array}{*{20}{c}} 1&{{C_{\alpha 1}}}&{{C_{\beta 1}}}& \cdots &{C_{\beta 1}^4} \\ 1&{{C_{\alpha 2}}}&{{C_{\beta 2}}}& \cdots &{C_{\beta 2}^4} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1&{{C_{\alpha n}}}&{{C_{\beta n}}}& \cdots &{C_{\beta n}^4} \end{array}} \right]\left[ \begin{array}{*{20}{c}} K_1^A \\ K_2^A \\ \vdots \\ K_{15}^A \\ \end{array} \right] $$ (12) 式中:KA是流动参数A的校准系数。
1.3 压力数据采集处理模块
为实现探针压力的精确实时测量,选用体积小、重量轻的MS4515DO–DS3BK004DP数字式压力传感器(图4)。传感器测量压差,工作电压3.3 V,测量频率最快为1 kHz,量程为−996.328~996.328 Pa,输出接口为两线I2C接口。
本文基于嵌入式技术开发了数据采集处理模块,如图5所示。主控芯片为STM32F407,通过I2C连接MS4515压力传感器以读取探针的压力数据,然后利用探针校准拟合多项式解算得到流动速度、迎角和侧滑角,同时将采得的压力数据和解算出的气流参数通过UART串口发送。
气流感知系统主要由七孔探针和数据采集处理模块组成,两者之间通过软管连接。所设计的气流感知系统的压力数据采集频率最大可达50 Hz,压力测量时延(经过探针和软管传递给传感器,软管越长,时延越长)不超过0.025 s。
2 试验模型及方法
2.1 试验模型
试验模型是仿滑翔状态的军舰鸟设计的。模型全长543.2 mm,展长1000 mm。表1为试验模型的几何参数,图6为试验模型设计图和实物图。试验模型采用3D打印技术加工制作,内部装有舵机以控制舵面,头部装有七孔探针,内嵌数据采集处理模块和Pixhawk飞行控制器[20],可实现姿态解算、控制律执行和数据记录等功能。
表 1 试验模型几何参数Table 1 Geometric parameters of the test model几何参数 值 参考面积S/m2 0.095 参考展长L/m 1 平均气动弦长c/m 0.16 质心位置 内翼根弦长35%处 2.2 热上升气流模拟装置
图7(a)为热上升气流模拟装置设计图。该装置由5个部分组成:金属底座,动力段,稳定段1、2、3。金属底座起支撑的作用,为了制作方便,将其拆分为若干零部件进行加工。动力段放置有3个呈等边三角形分布的金属涵道,用以提供气流。稳定段1内有蜂窝器,由方形小格子构成,稳定段1与2、稳定段2与3之间布置有阻尼网。稳定段的功能在于稳定涵道产生的不均匀气流,使旋涡衰减、速度大小和方向的分布更为均匀[21]。动力段、稳定段(包括蜂窝器)都采用3D打印技术制作,如图7(b)所示。热上升气流模拟装置虽然装有1层蜂窝器和2层阻尼网,但其出口气流的均匀性低于常规风洞。
热上升气流模拟装置采用PWM(脉冲宽度调制)控制,PWM信号通过单片机产生[22]。通过调节PWM信号的占空比,控制动力段金属涵道转速,从而控制热上升气流速度。以直流电源为热上升气流模拟装置动力段供电,工作电压25 V。在距出口330 mm处架设皮托管,标定该装置产生的热上升气流速度,标定结果如表2所示。
表 2 热上升气流速度标定Table 2 Calibration of updraft velocity占空比/% 电压/V 电流/A 上升气流速度/(m·s−1) 7.500 25 0 0 7.750 25 4.4 2.7 8.000 25 9.2 4.9 8.250 25 17.2 6.6 8.500 25 26.2 8.0 8.875 25 34.2 9.0 9.000 25 44.1 9.8 2.3 模式切换逻辑
模式切换逻辑对于无人机自主滑翔非常重要:当飞行器飞经热上升气流区域时,须通过模式切换逻辑使飞行器进入滑翔模式,利用热上升气流获取能量;当热上升气流不足以提供额外能量时,则须通过模式切换逻辑使飞行器脱离滑翔模式[23]。对于保持定直平飞的无人机,其飞行速度和高度变化不大,热上升气流影响的主要是飞行迎角及其变化率,因此,选择飞行迎角及其变化率来设计模式切换逻辑。
典型的热上升气流由空气吸收太阳辐射能引起,如图8所示,其在水平方向呈高斯分布,中心气流速度最大,离中心越远,气流速度越小。据文献[24]的研究,当飞行器以姿态增稳模式定直平飞经过图8所示的热上升气流区域时,迎角从α0逐渐增大,达到一定值后逐渐减小,最后再恢复到α0,如图9所示(图中横轴t为时间,纵轴标值α0表示定直平飞时的配平迎角)。在此过程中,迎角变化率由正变负再由负变正。根据这些特征,设计如图10所示的模式切换逻辑。
图10中,$\dot \alpha $为迎角变化率,Soarmode为用以判别飞行器是否进入滑翔模式的变量,Soarmode = 1表示进入滑翔模式,Soarmode = 0表示脱离滑翔模式。当飞行器进入热上升气流区域,α逐渐增大,$\dot \alpha $由正变负,以α大于某个阈值且$\dot \alpha $小于0作为进入滑翔模式的判别条件;当热上升气流消失或强度太小时,α减小,以α小于某个阈值并持续2 s作为脱离滑翔模式的判别条件。切换逻辑中使用的阈值可以根据飞行器类型及期望飞行器进入和离开热上升气流的时间进行修改。
2.4 虚拟飞行试验方法
虚拟飞行试验在南京航空航天大学回流式低湍流度开口风洞中进行。该风洞开口试验段长度为1.7 m,截面尺寸为1.5 m × 1.0 m,最大稳定风速为30 m/s。虚拟飞行试验模型及安装如图11所示。模型与模型支撑件以一个多轴承式三自由度机构(图12)连接,该机构可使模型绕俯仰轴和滚转轴转动 ± 30°、绕偏航轴转动任意角度。模型内部留有配重位置,以保证模型重心与转动中心基本重合[25]。
飞行器在飞经热上升气流区域的过程中,遇到的热上升气流的速度会先增大后减小。为模拟此现象,将热上升气流模拟装置安装于风洞试验段下部以免影响风洞来流,装置出口尽可能向上对准模型下表面,试验中控制装置产生的气流速度先增大,再减小到某个值后持续一段时间,最后减小到0。
将模式切换逻辑写入飞行控制器,控制热上升气流模拟装置。在试验中,观察模式切换逻辑能否判别热上升气流并自主控制飞行器进入和脱离滑翔模式。据MacGready的研究[26],飞行器遇到热上升气流时,可以通过盘旋长时间地停留在热上升气流区域。在试验中,当模式切换逻辑判别飞行器应进入滑翔模式时,发送滚转角指令,飞行控制器控制飞行器向一侧滚转;当模式切换逻辑判别飞行器应脱离滑翔模式时,控制飞行器滚转角为0°,以此判别模式切换逻辑的可行性。试验过程中,实时采集记录迎角、姿态角、Soarmode值等的变化情况。
3 结果与分析
3.1 七孔探针的校准结果
图13给出了小流动角下(7区)竖直平面内 Cα随α的变化曲线,图14给出了小流动角下(7区)水平面内Cβ随β的变化曲线。从图中可以看出:2条曲线的线性都非常好,且都接近经过原点,斜率也基本相同。
图15给出了大流动角下不同滚转角所对应的1区Cθ1随θ的变化情况。从图中可以看出:当24° ≤ θ ≤ 72°时,Cθ1随θ单调增大;当θ >72°时,Cθ1随θ的增大而减小,这是由吸力开始减小、压力回升导致的。结果表明所设计的探针可测量72°以内的俯仰角。此外,在θ < 72°的情况下,ϕ为155°与205°、165°与195°、175°与185°的曲线基本重合,这表明该区Cθ1~θ曲线对称性很好。图16给出了1区θ = 60°时Cϕ1随ϕ的变化情况。图中Cϕ1~ϕ曲线线性度较好,且该区中心处(ϕ = 180°)Cϕ1 ≈ 0。其他外区的滚转角系数曲线与1区基本相似,这有利于多项式的拟合。
受探针加工和压力传感器温漂、零漂等因素影响,校准结果难免存在误差。根据误差理论,采用试验数据Ae与拟合值Ap之间的标准偏差σ(A)来衡量拟合精度,即:
$$ \sigma (A) = \sqrt {\frac{1}{{n - 15}}\sum\limits_{j = 1}^n {{{({A_{\rm{e}}} - {A_{\rm{p}}})}^2}} } $$ (13) 各区流动参数的偏差分析结果如表3所示,表中外区流动参数的偏差分析结果是1~6区的平均值。可以看到:外区流动参数的拟合精度比内区略低,且标准偏差都在较小的范围内。
表 3 七孔探针校准曲线拟合的标准偏差Table 3 Standard deviation of calibration curve fitting of seven hole probe内区 外区 标准偏差 值 标准偏差 值 σ(α) 0.15° σ(θ) 0.46° σ(β) 0.11° σ(ϕ) 0.50° $\dfrac{\sigma (p_0)}{(p_0-p_\infty )} $ 0.46% $\dfrac{\sigma (p_0)}{(p_0-p_\infty )} $ 0.77% $\dfrac{\sigma (p_0-p_\infty)}{(p_0-p_\infty )} $ 1.29% $\dfrac{\sigma (p_0-p_\infty)}{(p_0-p_\infty )} $ 2.25% 3.2 风洞虚拟飞行试验
为观察模式切换逻辑在不同速度的热上升气流下的可行性,开展了风洞虚拟飞行试验。试验中,风洞来流速度为10 m/s,热上升气流模拟装置产生的气流与风洞来流夹角为90°,设置进入滑翔模式的滚转角指令ϕcmd = 11.5°(0.2 rad)。试验中,热上升气流装置模拟3种不同速度的热上升气流:
气流Ⅰ:气流速度从0 m/s增大到4.9 m/s,再减小到2.7 m/s,维持一段时间后,减小到0 m/s;
气流Ⅱ:气流速度从0 m/s增大到8.0 m/s,再减小到4.9 m/s,维持一段时间后,减小到0 m/s;
气流Ⅲ:气流速度从0 m/s增大到9.8 m/s,再减小到6.6 m/s,维持一段时间后,减小到0 m/s。
图17~19分别是热上升气流Ⅰ、Ⅱ和Ⅲ的风洞虚拟飞行试验结果,各图的子图(a)是控制热上升气流装置的PWM信号占空比的变化情况,子图(b)是Soarmode值的变化情况,子图(c)是迎角和迎角变化率的变化情况,子图(d)是滚转角指令和滚转角的变化情况。
从图17(a)可以看出:在约5.8、44.6 s处,热上升气流装置启动;在约7.8、46.6 s处,热上升气流装置产生的气流速度达到最大值;在约26.5、64.5 s处,热上升气流装置关闭。从图17(b)可以看出:在约7.8、46.6 s处,模式切换逻辑的Soarmode值从0变为1,触发进入滑翔模式的判别条件;在约29.0、66.8 s处,Soarmode值从1变为0,触发脱离滑翔模式的判别条件。从图17(c)可以看出:在触发进入滑翔模式的这2个时间点,飞行器迎角α > 4°,当α从最大值开始减小时,迎角变化率$\dot \alpha $变为负值,触发进入滑翔模式的判别条件;结合图17(a),在热上升气流装置关闭后的27.0~29.0 s、64.8~66.8 s这2个2 s的时间段内,飞行器迎角α始终小于2.5°,触发脱离条件。从图17(d)可以看出:在进入滑翔模式的这2个时间点,模式切换逻辑判别飞行器进入滑翔模式,飞行器接收到滚转角指令ϕcmd = 11.5°,向右滚转到11°附近;在脱离滑翔模式的这2个时间点,飞行器脱离滑翔模式,滚转角回到0°附近。
图18和19中也有与图17相似的现象,这说明在不同速度的热上升气流下,所设计的模式切换逻辑都能够自主控制飞行器进入和脱离滑翔模式。
为观察所设计的模式切换逻辑在不同滚转角指令下能否控制飞行器自主脱离滑翔模式,开展了风洞虚拟飞行试验。试验中,设置风洞来流速度为10 m/s,热上升气流模拟装置模拟热上升气流Ⅱ(与风洞来流夹角为90°),进入滑翔模式的滚转角指令分别为ϕcmd = 11.5°(0.2 rad)、ϕcmd = 22.9°(0.4 rad)、ϕcmd = 34.4°(0.6 rad)和ϕcmd = 45.8°(0.8 rad)。
图20为滚转角指令和滚转角随时间的变化情况。可以看到:不同的滚转角指令下,模式切换逻辑都能够成功地控制飞行器自主脱离滑翔模式。
比较图17(d)、18(d)和19(d)可以看出:热上升气流的速度越大,进入滑翔模式时的滚转角与滚转角指令的稳态误差越大。从图20中可以看出:随着滚转角指令的增大,滚转角与滚转角指令的稳态误差越来越大。出现稳态误差的原因是:试验模型的滚转运动通过尾舵的左右偏转控制,但尾舵的左右偏转又会使模型出现偏航运动。
4 结 论
本文针对无人机自主滑翔中的模式切换问题,设计了气流感知系统、热上升气流模拟装置和模式切换逻辑,搭建了风洞虚拟飞行试验平台,得到结论如下:
1)基于七孔探针和嵌入式技术设计的气流感知系统可测量流动角高达72°的气流方向和速度,该系统测得的流动角的标准偏差小于0.5°。
2)所设计的热上升气流模拟装置可模拟10 m/s以下的热上升气流,通过PWM信号控制装置模拟随时间变化的热上升气流。
3)风洞虚拟飞行试验结果表明:在不同速度的热上升气流作用下,模式切换逻辑都能够控制无人机自主进入和脱离滑翔模式;在不同的滚转角指令下,模式切换逻辑都能控制无人机脱离滑翔模式。因此基于气流感知系统测得的迎角及其变化率所设计的模式切换逻辑能够使无人机在遇到热上升气流时自主进入滑翔模式,在热上升气流消失时自主脱离滑翔模式。
本文所设计的气流感知系统和模式切换逻辑可应用于通信中继、监视和侦察等小型固定翼无人机,使其能够在进行巡航任务时利用环境中出现的热上升气流节省能量,提高续航能力。
-
表 1 组分特征振动温度
Table 1 The characteristic vibrational temperature of the species
组分 θv,s/K N2 3371 O2 2256 H2 6215 H2O 2294 、5180 、5400 OH 5375 HO2 1577 、2059 H2O2 1250 、1970、2030、2070 、4130 、4910 表 2 空气和燃料边界条件
Table 2 Boundary conditions for air and fuel stream
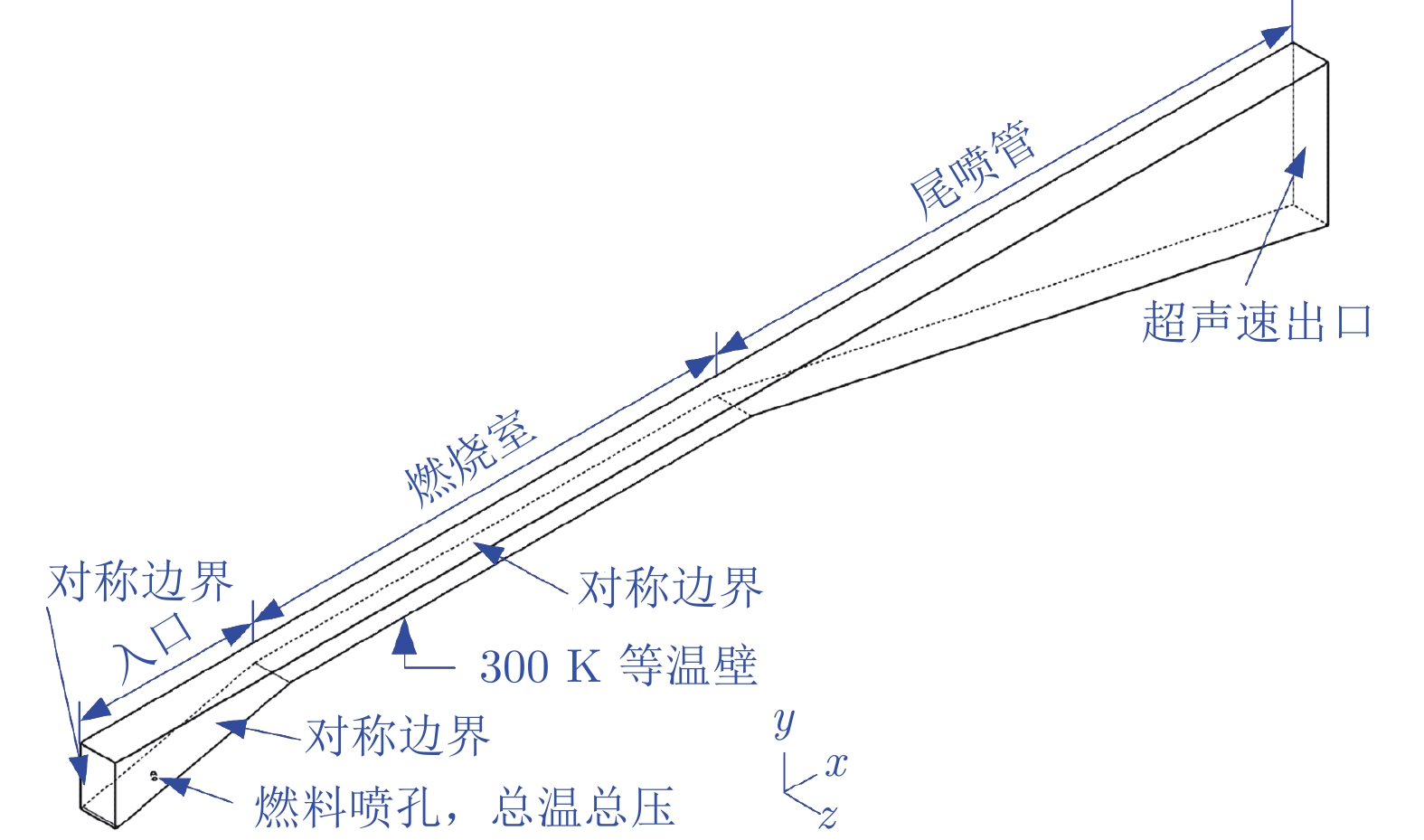
马赫数Ma 流速u∞/(m·s−1) 静压p∞/Pa 平动温度Ttr/K 空气入口 10 3000 1450 227 燃料入口 1 1208 541778 249 表 3 初始条件
Table 3 Initial conditions
Ttr/K Tv/K p∞/Pa XN2 XO2 XH2 2000 900 70000 0.69 0.21 0.10 -
[1] 陈贤亮, 符松. 热化学非平衡高超声速平板边界层线性稳定性分析[J]. 空气动力学学报, 2020, 38(2): 316–325. DOI: 10.7638/koqdIlxxl-2019.0156 CHEN X L, FU S. Linear stability analysis of hypersonic boundary layer on a flat-plate with thermal-chemical non-equilibrium effects[J]. Acta Aerodynamica Sinica, 2020, 38(2): 316–325. doi: 10.7638/koqdIlxxl-2019.0156
[2] 袁军娅, 任翔, 蔡国飙, 等. 双锥/双楔流动中的高温气体效应仿真模拟[J]. 气体物理, 2022, 7(4): 10–18. DOI: 10.19527/j.cnki.2096-1642.0927 YUAN J Y, REN X, CAI G B, et al. Simulation of high temperature gas effects in high enthalpy double cone/wedge flows[J]. Physics of Gases, 2022, 7(4): 10–18. doi: 10.19527/j.cnki.2096-1642.0927
[3] 傅杨奥骁, 董维中, 丁明松, 等. 高焓电弧风洞试验热化学非平衡流场数值模拟[J]. 实验流体力学, 2019, 33(3): 1–12. DOI: 10.11729/syltlx20180138 FU-Y A X, DONG W Z, DING M S, et al. Numerical simulation of thermochemical non-equilibrium flow field in arc-jet tunnel[J]. Journal of Experiments in Fluid Mechanics, 2019, 33(3): 1–12. doi: 10.11729/syltlx20180138
[4] 岳连捷, 张旭, 张启帆, 等. 高马赫数超燃冲压发动机技术研究进展[J]. 力学学报, 2022, 54(2): 263–288. DOI: 10.6052/0459-1879-21-547 YUE L J, ZHANG X, ZHANG Q F, et al. Research progress on high-mach-number scramjet engine technologies[J]. Chinese Journal of Theoretical and Applied Mechanics, 2022, 54(2): 263–288. doi: 10.6052/0459-1879-21-547
[5] LONGO J M A, HANNEMANN K, HANNEMANN V. The challenge of modeling high speed flows[C]//Proceedings of the 6th EUROSIM Congress on Modelling and Simulation. 2007.
[6] ANNA A. Numerical modeling of surface chemistry processes for hypersonic entry environments[D]. Ann Arbor, MI, US: The University of Michigan, 2013.
[7] 熊文韬. 高温非平衡效应下双楔绕流中激波干扰研究[D]. 合肥: 中国科学技术大学, 2017. XIONG W T. On shock-shock interaction in double-wedge flow with high temperature non-equilibrium effects[D]. Hefei: University of Science and Technology of China, 2017.
[8] BRICALLI M G, BROWN L, BOYCE R R, et al. Scramjet performance with nonuniform flow and swept nozzles[J]. AIAA Journal, 2018, 56(10): 3988–4003. doi: 10.2514/1.j056963
[9] CASSEAU V, ESPINOZA D E R, SCANLON T J, et al. A two-temperature open-source CFD model for hypersonic reacting flows, part two: multi-dimensional analysis[J]. Aerospace, 2016, 3(4): 45. doi: 10.3390/aerospace3040045
[10] CASSEAU V. An open-source CFD solver for planetary entry[D]. Glasgow, United Kingdom: University of Strathclyde, 2017. doi: 10.48730/fc4y-6m27
[11] LANDAU L D, TELLER E. On the theory of sound dispersion[J]. Physikalische Zeitschrift der Sowjetunion, 1936, 10(34): 1. doi: 10.1016/B978-0-08-010586-4.50027-4
[12] JOHNSON R D Ⅲ. NIST Computational chemistry comparison and benchmark database[R]. NIST Standard Reference Database Number 101, 2016.
[13] MENTER F R, KUNTZ M, LANGTRY R. Ten years of industrial experience with the SST turbulence model[J]. Turbulence, heat and mass transfer, 2003, 4(1): 625–632.
[14] CONAIRE M Ó, CURRAN H J, SIMMIE J M, et al. A comprehensive modeling study of hydrogen oxidation[J]. International Journal of Chemical Kinetics, 2004, 36(11): 603–622. doi: 10.1002/kin.20036
[15] AO Y, WU K, LU H B, et al. Combustion dynamics of high Mach number scramjet under different inflow thermal nonequilibrium conditions[J]. Acta Astronautica, 2023, 208: 281–295. doi: 10.1016/j.actaastro.2023.04.020
[16] BRICALLI M G, BROWN L M, BOYCE R R. Numerical investigation into the combustion behavior of an inlet-fueled thermal-compression-like scramjet[J]. AIAA Journal, 2015, 53(7): 1740–1760. doi: 10.2514/1.j053513
[17] 白贺之, 陈兵, 徐旭. 基于PNS方程的高超声速热化学非平衡喷管流动数值模拟[J]. 战术导弹技术, 2018(4): 25–31. DOI: 10.16358/j.issn.1009-1300.2018.7.197 BAI H Z, CHEN B, XU X. Numerical simulation of hypersonic nozzle flow in thermochemical nonequilibrium based on parabolized Navier–Stokes equation[J]. Tactical Missile Technology, 2018(4): 25–31. doi: 10.16358/j.issn.1009-1300.2018.7.197
[18] VATANSEVER D, ÇELİK B. An open-source hypersonic solver for non-equilibrium flows[J]. Journal of Aeronautics and Space Technologies (Havacilik ve Uzay Teknolojileri Dergisi), 2021, 14(1): 35–52.
-
期刊类型引用(15)
1. 赵照,熊建军,冉林,易贤. 大型结冰风洞热气供气防除冰试验技术. 航空动力学报. 2024(05): 16-22 .  百度学术
百度学术
2. 赵照,王梓旭,熊建军,冉林,易贤. 大型结冰风洞双供水供气喷雾控制系统研制. 测控技术. 2024(07): 48-54 .  百度学术
百度学术
3. 张晏鑫,张鸿健,熊建军,赵照,冉林,易贤. 基于超声导波的积冰量辨识及定位方法. 航空学报. 2024(16): 53-67 .  百度学术
百度学术
4. 王小辉,马庆林,孔维梁,韩王超,常红亮. 面向过冷大水滴适航验证的结冰探测技术研究. 南京航空航天大学学报. 2023(02): 265-273 .  百度学术
百度学术
5. 余柏杨,王明振,王婷婷,虞建,刘学军,吕宏强. 基于机器学习的机翼气动载荷重构及传感器优化布置. 南京航空航天大学学报. 2023(05): 798-807 .  百度学术
百度学术
6. 苏鑫,管润程,王桥,苑伟政,吕湘连,何洋. 基于深度学习的结冰区域和厚度检测方法. 航空学报. 2023(S2): 205-213 .  百度学术
百度学术
7. 赵照,熊建军,冉林,郭向东,李自雨. 基于ZigBee技术的结冰风洞温度无线测量系统设计. 电子设计工程. 2022(05): 51-55+60 .  百度学术
百度学术
8. 李彬. 某型耗量传感器改进设计. 科技与创新. 2022(13): 107-109 .  百度学术
百度学术
9. 甘茂锐,丁力,张进. 某型航空发动机结冰检测技术仿真和验证研究. 传感器世界. 2022(05): 7-11 .  百度学术
百度学术
10. 马玉敏,廉佳,孔满昭,谢露. 机头结冰对大气数据系统测量影响研究. 测控技术. 2022(09): 96-100+132 .  百度学术
百度学术
11. 张洁珊,朱剑鋆,闵现花,苏杰. 一种航空发动机防冰传感器测温特性试验研究. 南京航空航天大学学报. 2022(06): 1092-1099 .  百度学术
百度学术
12. 熊建军,刘锡,冉林,赵照. 基于控制律的电加热防除冰系统设计与验证. 测控技术. 2021(02): 130-134+139 .  百度学术
百度学术
13. 赵照,熊建军,张平涛,冉林,李自雨. 基于分布式光纤测温的结冰风洞喷雾耙温度场测量. 计算机测量与控制. 2021(03): 14-17+22 .  百度学术
百度学术
14. 赵照,熊建军,冉林,何苗. 基于动态神经网络的喷雾耙供气温度数据重构. 仪表技术与传感器. 2021(04): 116-121 .  百度学术
百度学术
15. 熊建军,梁鉴,郭龙,赵照,冉林. 结冰风洞试验段上壁面自动顶盖装置设计与应用. 计算机测量与控制. 2020(12): 135-138 .  百度学术
百度学术
其他类型引用(10)







 下载:
下载: