0   引　言

水下航行体首部边界层转捩引起局部脉动压力激增，压力作用在声纳导流罩外表面，引起壁面振动，产生噪声辐射，并透过声纳导流罩几乎无损耗地传播到首部声纳，成为中高航速下首部声纳自噪声的主要来源^[1-3]。因此，为了最大程度地延迟首部边界层转捩，降低首部声纳自噪声，开展水下航行体首部边界层流动控制的研究尤为重要。

水下航行体首部边界层转捩控制，主要通过对流体施加某些物理作用（力、动量、电磁等）使流体的运动状态发生改变，进而对壁面摩擦阻力、噪声和流动分离等进行有效控制。流动控制方法主要分为被动式和主动式两大类。被动式控制不需要额外输入能量，仅需在流动环境上进行一定程度的改变，与主动式相比，其控制元件通常安装简单、使用方便、性能可靠。其中，柔性壁面是常用的被动式流动控制技术之一，最早在1957年由Kramer^[4]提出，其减阻原理通常被解释为黏弹性材料的柔性壁面可提高层流边界层的稳定性，从而推迟边界层转捩，这一思想来源于海豚皮肤表面大面积流动为层流。因此，柔性表皮具有延迟边界层转捩的流动控制能力。

在上述工作的启发下，Choi等^[5]开展了弹性橡胶表面湍流边界层减阻实验，取得了明显的湍流减阻效果；Endo等^[6]对柔性壁面湍流边界层的直接数值模拟研究结果表明：柔性壁面产生的被动形变可以减小流体阻力。Kulik等^[7]采用直接数值模拟方法对柔性壁面减阻效果进行了研究，结果表明：柔性壁面不仅实现了17%的减阻效果，还减弱了流动噪声。Shu等^[8]利用激光多普勒测速仪分别对刚性和柔性壁面的平板边界层速度场进行了实验测试，结果表明：与刚性表面相比，柔性表面使湍流边界层对数律区范围向外延伸、近壁区湍流度最大值减小，且使湍流猝发频率显著降低。孙卫红等^[9]采用种子乳液聚合法和物理共混交联法制备了以水为溶剂的聚氨酯‒聚丙烯酸乙酯（PU/PEA）乳液柔性壁和聚氨酯‒聚丙烯酸丁酯（PU/PBA）乳液柔性壁，小型水洞平板阻力测试结果表明，PU/PEA复合乳液具有一定的减阻作用，在来流速度为3 m/s时，减阻率最高为8.8%。

在工程应用领域中，在壳体表面敷设柔性蒙皮是解决水下航行体减阻降噪问题的一种新思路，蒙皮的柔性表面可在一定程度上抑制和吸收流场的脉动压力，从而在水下航行体的减阻和降噪方面取得效益^[10-11]。敷设蒙皮对水下航行体本身结构的变动极小，易于实现，具有良好的应用前景。近年来，兼顾减阻和降噪特性的新型水下航行体蒙皮研究已成为各国湍流研究的热点^[12-15]。

为保证水下航行体首部声纳正常工作，选取的蒙皮材料须为透声材料。随着超材料的发展，水下航行体首部蒙皮的材料也变得更加丰富，其中，水凝胶（图1^[16]）作为一种物理与力学特性类水的固体柔性超材料，普遍存在于海洋生物机体（海参、水母等）以及人和陆生动物体内，比如，人体的肌腱、关节处的韧带和软骨等与机械运动相关的组织均由水凝胶构成。水凝胶具备海洋环境适应性良好、声学阻抗与水完全匹配等优点，且能够承受一定的作用力，满足作为声纳导流罩材料属性的基本要求。

图  1  水凝胶超材料^[16]

Fig.  1  Hydrogel metamaterial^[16]

下载: 全尺寸图片 幻灯片

本文在高速水洞中探索水凝胶超材料在水下回转体边界层转捩控制方面的应用前景，形成高速水洞中的大视场PIV^[17]速度场测试技术，基于速度场的时域信号，采用多路径积分法^[18]对水下回转体绕流空间脉动压力场进行估算；基于转捩区瞬时速度场连续子波变换与脉动压力频谱分析，对水下回转体边界层自然转捩特性、水凝胶超材料与水下回转体边界层流动耦合机制，以及水凝胶延迟水下回转体边界层自然转捩机理进行深入分析。

1   实验设施与初步测试结果

1.1   小型多功能高速水洞与实验模型

实验测试主要在中国船舶科学研究中心小型多功能高速水洞中完成。该水洞于2012建成并投入使用，是目前国内唯一一座可控制水中溶解气体含量和气核的高速水洞，水洞为立式循环水洞，可根据实验需要更换方形、圆形2种试验段。其方形试验段尺寸为1600 mm（长） × 225 mm（宽） × 225 mm（高），最高水速可达25 m/s；圆形试验段内径350 mm，长1.6 m，最高水速可达15 m/s。水洞试验段背景湍流度小于0.5%，中心压力调节范围为5～500 kPa。水洞主体结构为不锈钢材料，试验段采用不锈钢框架和光学有机玻璃，既保证了水洞整体的结构强度，又兼顾了实验观测的便利性。水洞整体结构如图2（a）所示。

图  2  小型多功能高速水洞示意图

Fig.  2  Schematic sketch of small multi-functional high-speed water tunnel

下载: 全尺寸图片 幻灯片

实验模型为最大直径D = 60 mm的SUBOFF模型（缩尺比为1∶8.5，下同），阻塞比为7.1%，模型长度L = 514.5 mm，长径比L/D = 8.57。SUBOFF模型以尾部（直径27 mm不锈钢圆柱）支撑的方式，通过测力天平安装在水洞试验段上壁面（不锈钢），激光片光源从水洞下壁面（有机玻璃）照亮实验模型周围流场。试验段及模型与测试系统布置如图2（b）所示。PIV相机布置在试验段侧面，拍摄方向垂直指向纸面内。实验来流速度U_∞ = 3～7 m/s，基于SUBOFF模型长度的雷诺数Re_L = U_∞L/ν = 1.5 × 10⁶～3.5 × 10⁶，ν为水介质运动黏性系数，取0.802 × 10⁻⁶ m²/s。

SUBOFF模型有刚性和柔性表面模型2类，如图3所示。图3（a）中的刚性SUBOFF模型由不锈钢制成（后文简称“刚性模型”），缩尺比1∶8.5的SUBOFF模型与尾部支撑一体加工，保证了实验模型的结构强度。图3（b）中的柔性表面SUBOFF模型（后文简称“柔性模型”）外形与刚性模型一致，且均为水力光滑。二者主要区别在于外层材料：柔性模型表面是5 mm厚的水凝胶，水凝胶交联在不锈钢内芯外表面，内芯最大直径为50 mm，与尾部支撑一体加工。水凝胶材料的弹性模量为24 kPa，断裂应力为108 kPa，断裂应变高达770%，其力学性能测试结果如图3（c）所示。

图  3  实验模型实物照片与水凝胶力学性能测试

Fig.  3  Photos of test model and mechanics performance test of the hydrogel

下载: 全尺寸图片 幻灯片

1.2   实验测试方法与初步结果

在中国船舶科学研究中心的小型多功能高速水洞中，完成了刚性和柔性模型总阻力和周围速度场的大视场PIV实验，测试仪器及主要参数见表1。

表  1  测试仪器及主要参数

Table  1  Test facilities and major parameters

仪器	型号参数
测力天平	型号：L6H5‒4kg
	量程：4 kg
	精度：0.03%
应变放大器	型号：DH3840
	输出电压：10V
	增益：300
高频激光器	型号：Beamtech Vlite‒Hi‒35型
	量程：200 Hz～10 kHz
	精度：能量不稳定性$\leqslant1\% $
高速相机	型号：Phantom LAB310
	像素：1280 像素 × 800 像素
	帧速：满幅帧率3260 Hz

下载: 导出CSV 

| 显示表格

1.2.1   模型总阻力测试

SUBOFF模型总阻力测试系统固定于试验段上壁面不锈钢窗体上（替换了试验段原有机玻璃窗体），其中，测力天平固定在不锈钢窗体上，并与SUBOFF模型尾支撑相连。如图2（b）和图3（a）所示，测力天平外壳为流线型导流罩，以减小对上游SUBOFF模型绕流场的干扰。

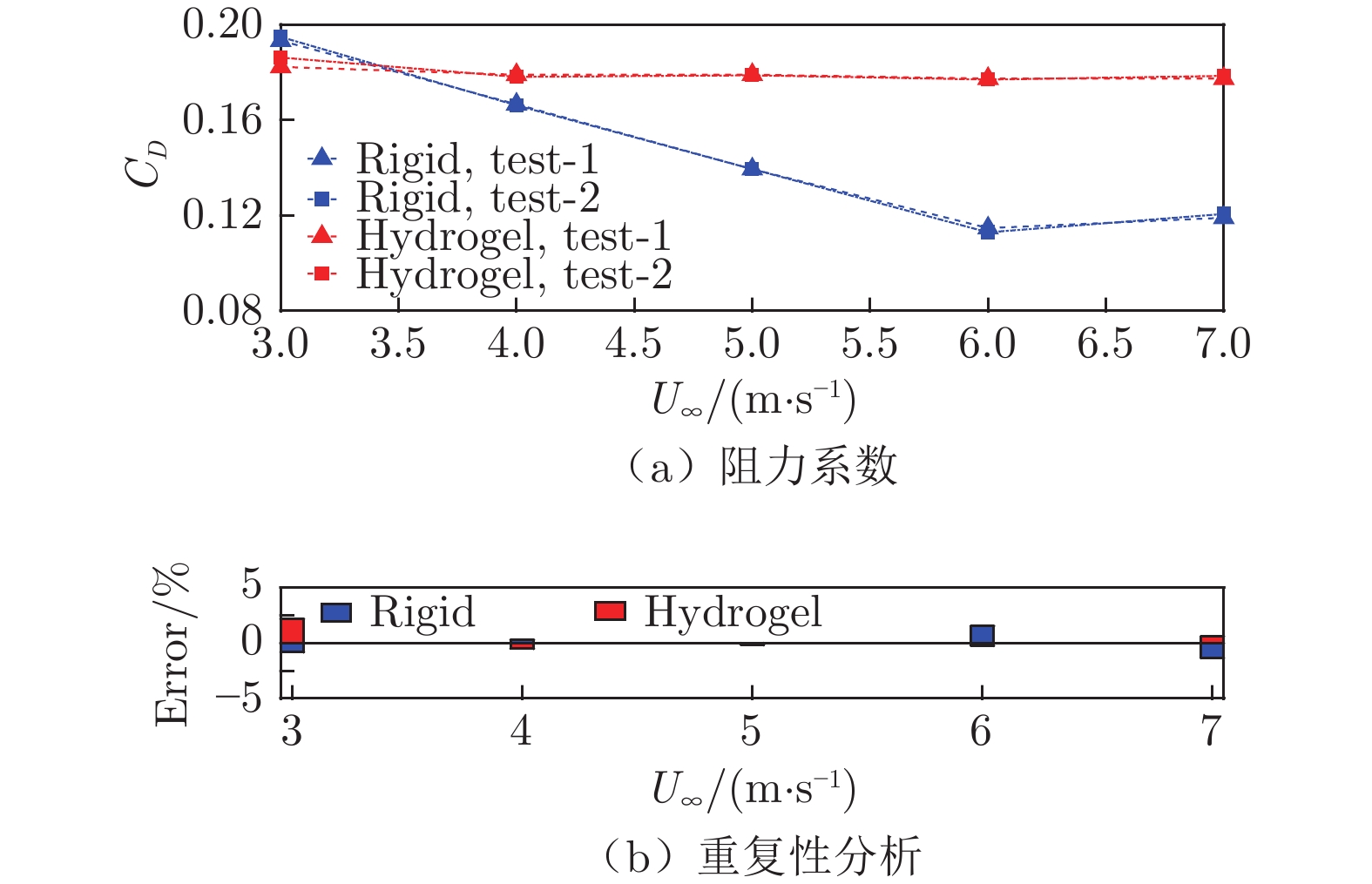
实验前对测力天平进行标定，建立加载力F_D与总阻力测试系统输出电压值E的关系，得到标定系数k = 5.8496 N/V。SUBOFF模型阻力测试时，首先采集零水速下的系统零点电压E₁₀，然后采集实验工况下各天平电压值E₁。SUBOFF模型阻力系数C_D = k(E₁−E₁₀)/0.5$\rho \mathop {{U}}\nolimits_{ {\infty}} ^2 s$，其中s为SUBOFF模型表面积，ρ为水介质密度，取996 kg/m³。分别对刚性模型和柔性模型的总阻力进行实验测试，采样频率200 Hz、采样时长10 s，所得SUBOFF模型阻力系数C_D及误差如图4所示。实验结果表明，在实验流速U_∞ = 3～7 m/s范围内，随着流速增大，刚性模型阻力系数由0.19开始显著减小，U_∞达到6 m/s后，阻力系数开始趋于稳定，而柔性模型阻力系数基本保持不变，约0.18，如图4（a）所示。测试的重复性分析结果如图4（b）所示，重复性误差在 ± 2.5%以内。

图  4  SUBOFF模型总阻力系数及重复性分析

Fig.  4  Drag coefficient of the SUBOFF test model

下载: 全尺寸图片 幻灯片

根据文献[19]，对于长径比为8的椭圆体，边界层为层流和湍流时的阻力系数分别为0.20、0.08。由于外形、表面材料的差异，柔性模型的阻力系数与椭圆体层流阻力系数量值接近但略有差别。这表明在实验流速范围内，柔性模型边界层流动未完成从层流到湍流的转变。刚性模型在3 m/s来流速度下的阻力系数与文献[19]中椭圆体层流边界层阻力系数相当；但随着流速增大，刚性模型阻力系数明显降低，当流速达到6 m/s时，阻力系数趋于稳定，数值与椭圆体湍流边界层阻力系数^[19]相当。这表明在实验流速范围内，刚性模型边界层流动实现了从层流向湍流的转变，转捩位置在6 m/s来流速度下趋于稳定。因此，本文在来流速度U_∞ = 7 m/s条件下开展刚性和柔性模型绕流速度场实验研究。

1.2.2   大视场PIV测试

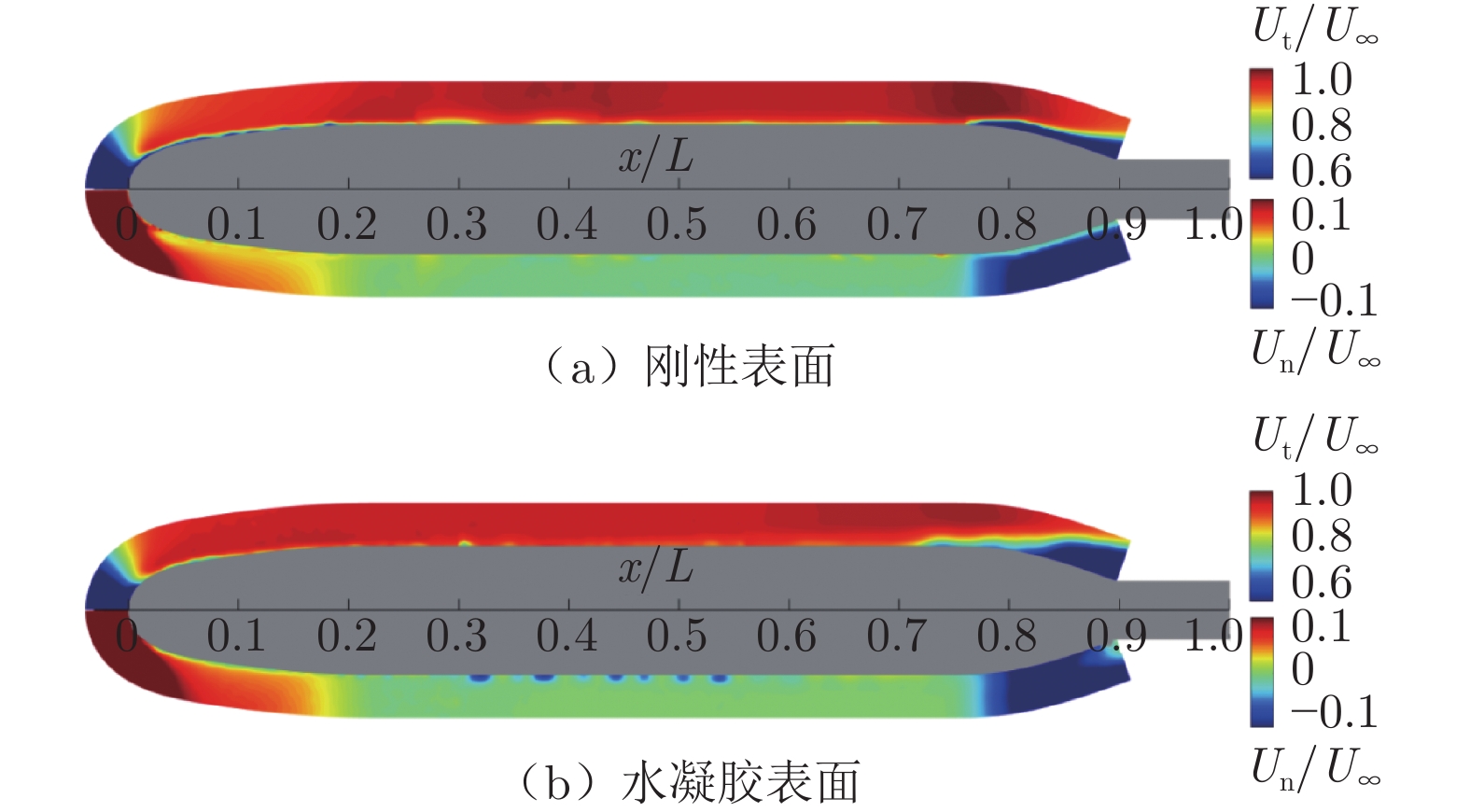
在来流速度7 m/s的条件下，使用二维PIV对SUBOFF模型绕流速度场进行测试。激光光源采用Beamtech Vlite‒Hi‒35型高频双脉冲固体激光器，每脉冲输出能量为30 mJ，激光发射频率为200 Hz～10 kHz。激光片光源从水洞下方照亮待测流场，以直径10 μm、密度1.05 × 10³ g/cm的空心玻璃微珠作为示踪粒子；采用搭配Nikkor 180 mm定焦镜头的分辨率为1280像素 × 800 像素的CMOS高速相机（Phantom LAB310）对测试平面内的示踪粒子图像以双帧模式进行采集，帧速为2000帧/s，相邻2帧图像曝光时间间隔60 μs，在每个工况下连续采集10424对粒子图像（图5（a）），采样时长约为5.2 s，以保证速度场统计收敛。采用专业后处理软件Dantec DynamicStudio 7.5中的Adaptive PIV算法对PIV粒子图像进行互相关计算，从128 像素 × 128 像素至16 像素 × 16 像素，采用4步互相关计算，最终得到二维速度矢量空间分辨率约为1.5 mm（相当于SUBOFF模型最大直径的1/40）。将SUBOFF模型绕流场分4个站位进行PIV测试，所得初始法向瞬时速度场如图5（b）所示。其中，流向分量U以顺流向为正，法向分量V以垂直向上为正。相邻站位的速度场沿点划线所示位置由上游向下游依次进行拼接，并以贴体曲面坐标对速度场在测试区域内部进行插值，进而得到模型周围整体绕流速度场。因SUBOFF模型首部存在曲率，故将二维速度场进行当地坐标分解，分别得到模型表面切向分量U_t、法向分量U_n，如图6所示。其中，切向分量U_t以顺流向为正，U_n以垂直于模型表面向外为正，即在SUBOFF模型平行中体段下表面，−U_n与V同方向。

图  5  粒子图像与法向瞬时速度云图

Fig.  5  Particle images and primary velocity field

下载: 全尺寸图片 幻灯片

图  6  SUBOFF模型周围二维速度云图

Fig.  6  Contour of 2D velocity field around SUBOFF

下载: 全尺寸图片 幻灯片

1.2.3   线性稳定性分析方法

采用基于线性稳定性分析的e^N方法开展水介质中曲面边界层自然转捩稳定性分析，基本原理^[20]简介如下：

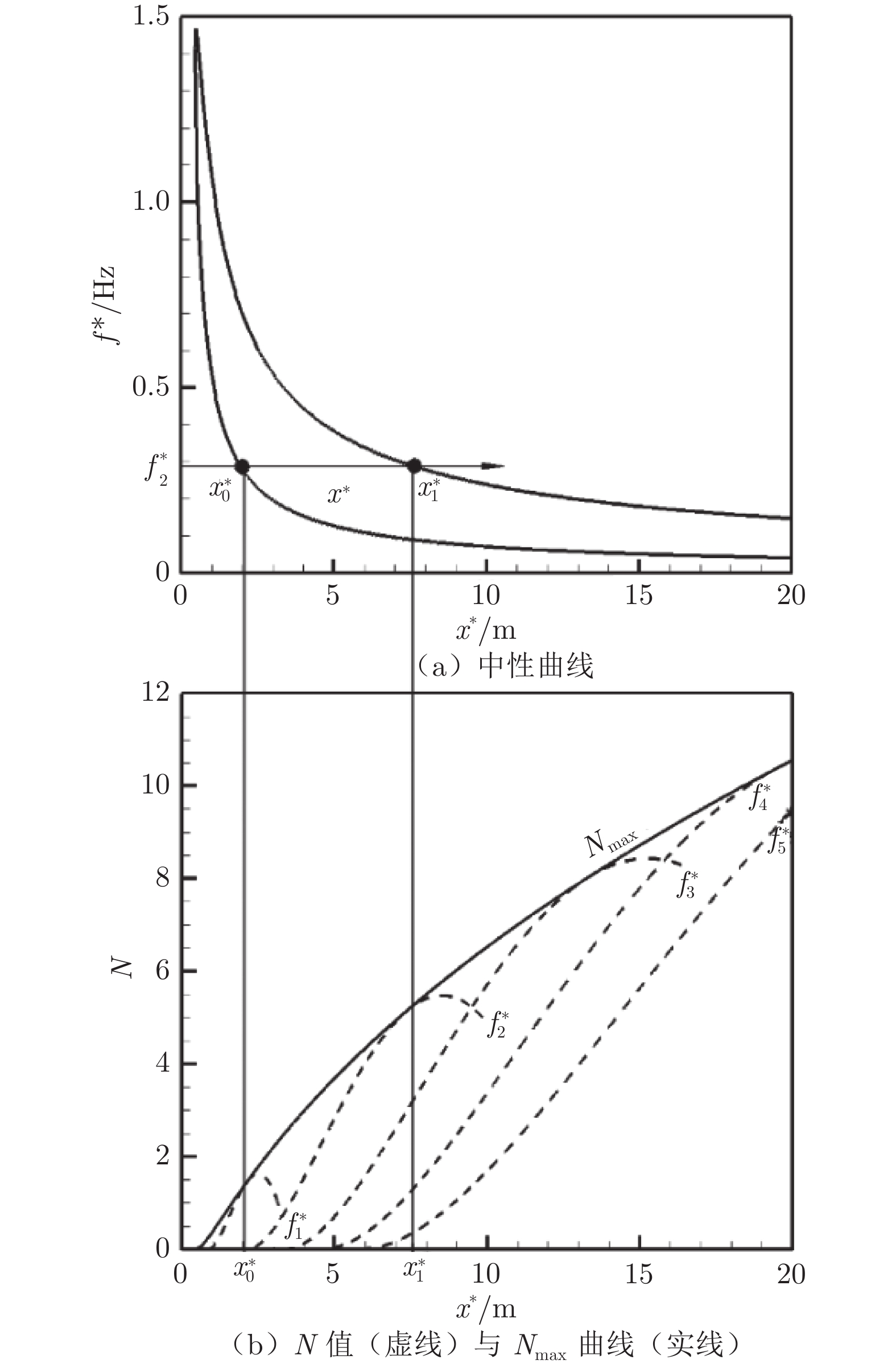
通过线性稳定性分析得到中性曲线，如图7（a）所示，其内部为不稳定区域，满足条件增长率$ {\sigma ^*} > 0 $（空间模式增长率$ {\sigma ^*} = - \alpha _i^* $）。先考虑一个以固定频率$ f_2^* $沿流向往下游传播的二维扰动，该扰动首先经过稳定区域，在$ x_0^* $处进入不稳定区域后开始增长，一直增长到$ x_1^* $处，最后在$ x_1^* $处穿出不稳定区并开始衰减。在$ x_0^* $下游给定的$ {x^*} $处，扰动幅值的放大因子定义为：

图  7  e^N方法示意图^[20]

Fig.  7  Sketch of e^N method^[20]

下载: 全尺寸图片 幻灯片

式中，$ {\text{d}}{s^*} $为沿壁面切向向下游的弧长微元。基于式（1）计算所得N值对应的$ {{\text{e}}^N} $值为扰动从$ x_0^* $处增长至当地幅值的放大倍数。求得$ f_1^* $、$ f_2^* $、$ f_3^* $、$ f_4^* $和$ f_5^* $等不同频率下的$ N $值曲线，从而得到不同频率下$ N $值的包络，即$ {N_{\max }} $曲线，如图7（b）所示，其表达式为：

当$ {N_{\max }} $达到某个门限值$ {N_{{\text{tr}}}} $时（$ {N_{{\text{tr}}}} $一般由实验测试的转捩位置得到），即$ {N_{\max }} $曲线满足条件$ {N_{\max }}({x^*}) = {N_{{\text{tr}}}} $，则此处即为转捩开始位置。这表示某一频率扰动通过线性增长，其幅值至此已经增长了$ {{\text{e}}^{{N_{{\text{tr}}}}}} $倍，足够引起强非线性作用并导致转捩。

采用Lauchle等 ^[21]实验所用的首部线型和测试雷诺数范围，对基于线性稳定性分析的e^N方法进行验证，结果表明：选取N_tr = 7，自然转捩位置预报结果与实验结果基本相符^[22]。因此，N_tr取5～9时，e^N方法适用于较宽雷诺数和背景湍流度范围的水介质中曲面边界层自然转捩稳定性分析和转捩预报。

1.2.4   连续子波分解方法

连续子波分解变换（Continuous Wavelet Transform, CWT）是一种冗余变换，其系数取决于所用子波函数。子波变换适用于检测信号的不连续性和奇异点：一方面，信号突变处具有较大的绝对值系数；另一方面，平稳信号在子波与信号特征最相关的尺度上会产生相对较大的子波系数。因此，子波变换适用于SUBOFF模型绕流速度场中强间歇性、强相关性的流动分析。Ren ^[23]和Khujadze^[24]等将子波分析应用于三维瞬时速度场的间歇性和相关性分析。

1.2.5   空间脉动压力估算

在风洞^[3]和水洞^[2,21]中开展的壁面脉动压力实验测试结果表明：壁面脉动压力信号可体现边界层的流态变化，以及包括层流边界层中Tollmien‒Schlichting波在内的扰动结构形成的流动激励特性，且转捩区壁面脉动压力比湍流区高约10 dB^[25]。因此，本文以壁面脉动压力信号为体现水下航行体边界层转捩激励特性和水凝胶延迟转捩的关键物理量。在水凝胶柔性表面脉动压力测试中，为避免压力传感器（承压面一般为刚性金属表面）局部表面特性的影响，采用基于速度场的间接脉动压力估算测试方法。基于PIV脉动速度矢量$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} ({t_i}) $，对不可压N‒S方程压力梯度项（式（3））以多路径积分算法^[18]进行直接积分，得到$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {s_1} }\left( {{x_1},{y_1}} \right) $、$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {s_2} }\left( {{x_2},{y_2}} \right) $两点间压力差（式（4）），即得到PIV测试平面内任意点$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {s_2} }\left( {{x_2},{y_2}} \right) $相对于参考点$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {s_1} }\left( {{x_1},{y_1}} \right) $的脉动压力p(t_i)。

式中：$\nabla p $为压力梯度；u为流向瞬时速度；t为时间，t_i为第i个时刻；p₁、p₂分别为参考点$ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {s_1} }\left( {{x_1},{y_1}} \right) $和${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {s_2} }\left( {{x_2},{y_2}} \right) $的压力。

基于PIV测试平面内任意点(x, y)脉动压力p(t_i)，得到脉动压力均方根$ p_{\text{rms}}=\sqrt{\left[\sum\nolimits_{i=1}^np^2(t_i)\right]/n} $，其中n为PIV测试平面内任意点处脉动压力时域上的数据点数。以来流动压无量纲化，得到脉动压力均方根系数$ C_{p\text{,rms}}=p_{\text{rms}}\mathord{\left/\vphantom{p_{\text{rms}}0.5\rho u_{\infty}^2}\right.}0.5\rho U_{\infty}^2 $，以表征边界层转捩区流动激励统计特性和频谱特征。因SUBOFF模型首部存在曲率，故将脉动压力均方根在与二维速度场相同的贴体网格上进行重采样（近壁第一层网格在模型壁面上）。

2   水介质中曲面边界层自然转捩特性

2.1   自然转捩流动激励特性

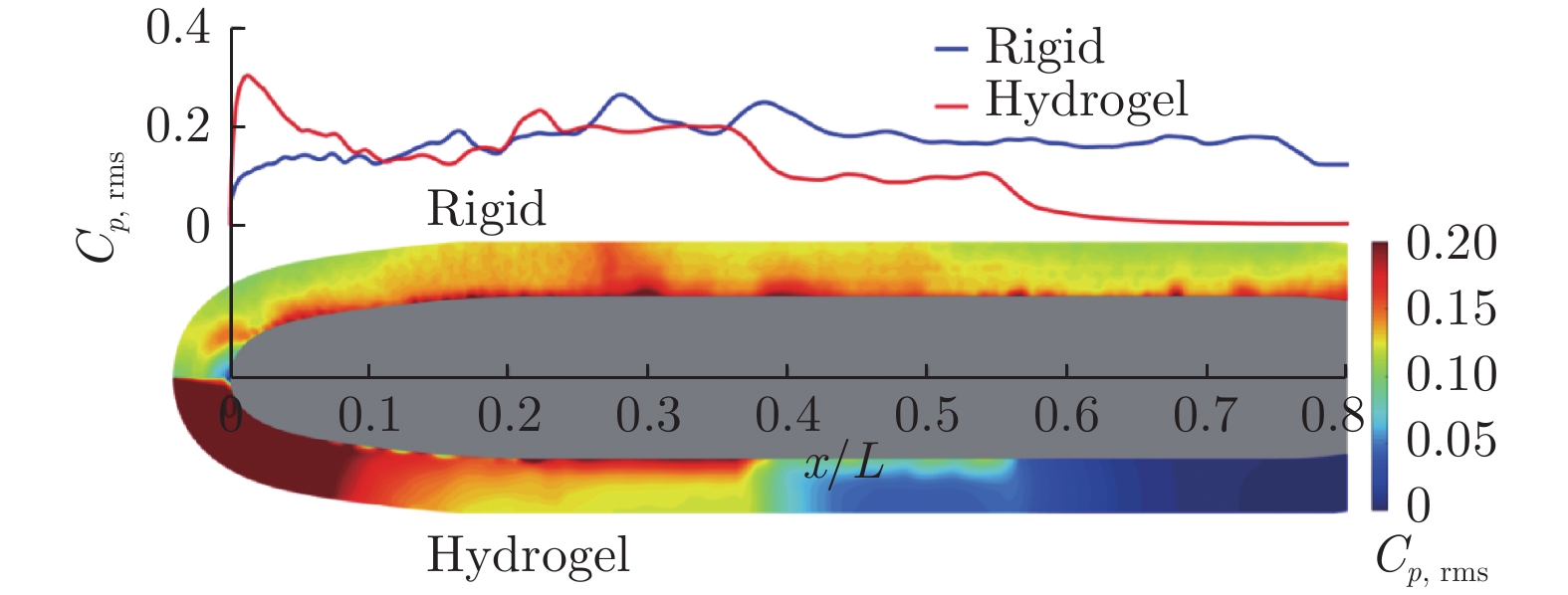
刚性模型周围流向、法向平均速度云图如图6（a）所示，其中，灰色部分为SUBOFF模型，上半部为流向平均速度云图，下半部为法向平均速度云图。由图可知，刚性模型首部前缘驻点区为低速区，随着边界层向下游发展，流向、法向平均速度逐渐恢复，形成曲面边界层流动。在刚性模型平行中体段（0.3L～0.4L），边界层变厚，在尾部型线收缩段则存在边界层分离，分离始于0.76L，并在下游形成低速区。基于瞬时速度场估算的刚性模型周围及近壁脉动压力均方根沿艇长分布如图8上部分云图和蓝色曲线所示（为便于对比，柔性模型结果也于图8中绘制，后文详述）。由图8可知：脉动压力均方根在驻点区下游开始快速增长，且在0.3L附近（峰值对应流向位置x_tr = 143.9 mm）达到峰值，之后逐渐减小且伴随着较大幅度的波动，最后在尾部达到最小值，但仍然明显大于刚性首部前缘脉动压力均方根值。因此，刚性模型绕流边界层产生的脉动压力均方根在首部前缘驻点区最小，在尾部分离区次小，在边界层转捩区最大，在湍流区则基本介于转捩区和尾部分离区之间。

图  8  SUBOFF模型周围脉动压力均方根沿艇长分布（刚性表面为上方云图与蓝色实线，水凝胶表面为下方云图与红色实线）

Fig.  8  Contour of 2D velocity field around the SUBOFF test model (contour above and the blue solid line represent rigid surface, contour below and the red solid line represent soft surface)

下载: 全尺寸图片 幻灯片

2.2   自然转捩流动稳定性分析

采用基于线性稳定性分析的e^N方法对本文实验测试工况下的刚性模型绕流边界层进行稳定性分析和转捩预测，得到中性曲线和N_max曲线，如图9所示。基于实验测试得到的脉动压力均方根最大值对应的流向位置x_tr = 143.9 mm，得到转捩对应的N_tr = 8.1，处于水介质中曲面边界层自然转捩对应的N值范围内。由此可知，在本文实验工况下，刚性模型绕流边界层转捩模式为Tollmien‒Schlichting波主导的自然转捩。

图  9  刚性SUBOFF模型首部边界层稳定性分析

Fig.  9  Instability analysis of boundary layer flow around the bow of the rigid SUBOFF test model

下载: 全尺寸图片 幻灯片

平板Blasius边界层自然转捩的中性曲线只存在1个不稳定区，扰动进入不稳定区并穿出之后，其幅值一直衰减，如图7（a）所示。而刚性模型绕流边界层自然转捩的中性曲线则明显不同，其存在2个不稳定区，如图9（a）中“①”“②”所示。这表明频率为500～1400 Hz的扰动两次进入不稳定区（700 Hz附近很窄的频段除外），即不稳定波经历了“失稳‒稳定‒再次失稳”的过程，因此，与平板Blasius边界层相比，刚性模型首部边界层扰动失稳频带更宽、扰动增长率更大^[20]。基于脉动压力均方根最大值确定的转捩位置x_tr = 143.9 mm，对应中性曲线的第二不稳定区“②”，这表明在本文高速水洞实验雷诺数和背景湍流度下，刚性模型首部边界层内的不稳定波经历了2次失稳，最终在第二不稳定区发生转捩。

2.3   SUBOFF模型曲面边界层自然转捩机理

上述实验测试和线性稳定性分析结果表明，刚性模型首部边界层为Tollmien‒Schlichting波主导的自然转捩，存在2个不稳定区，其转捩过程比平板Blasius边界层复杂得多。

分析边界层流动在刚性模型表面形成壁面脉动压力的频谱特征，以呈现边界层内不稳定波的生成与演化过程。图10给出了近壁脉动压力频谱L_p沿流向的分布云图。由图10（a）可见，刚性模型首部即存在显著的低频扰动，高速水洞试验段中心区的来流扰动通过驻点直接进入刚性模型首部边界层，而平板Blasius边界层的初始扰动幅值很小（刚性模型边界层与平板Blasius边界层的第一个显著差别）。在顺压梯度作用下，进入边界层的驻点扰动得到抑制，使扰动幅值显著衰减；随着向下游发展，边界层内的扰动幅值得以增长，在0.2L附近实现第一次幅值增长，之后再次衰减，随后在0.3L附近实现第二次增长且幅值较大（与平板Blasius边界层的第二个显著差别），扰动频率范围急剧扩大^[26]，幅值增长最高频段从第一次的40 Hz急剧扩大到250 Hz，判断0.3L附近为流动激励最强的区域，即基于脉动压力均方根最大值所确定的转捩位置，而转捩区持续了约0.1L。之后，刚性模型绕流为湍流，并最终在尾部发生分离，流动激励幅值大幅衰减，但仍存在几个孤立频段的扰动，对应于湍流分离区（图6（a））涡系运动产生的壁面压力脉动。

图  10  SUBOFF模型近壁脉动压力频谱云图

Fig.  10  Contour of spectrum of pressure fluctuations in the near wall region around the SUBOFF test model

下载: 全尺寸图片 幻灯片

综上所述，刚性模型绕流边界层自然转捩机理可归纳为以下3个方面：1）前缘驻点扰动直接进入边界层，但在首部顺压梯度的作用下，扰动幅值快速衰减；2）中性曲线存在2个不稳定区，特定频段的不稳定波经历了“失稳‒稳定‒再次失稳”，最终在第二不稳定区发生转捩；3）边界层流动壁面脉动压力频谱云图体现了边界层不稳定波经历二次失稳才发生转捩的过程，占主导的壁面脉动压力频段位于中性曲线第二不稳定区内。

3   水凝胶延迟边界层自然转捩机理

3.1   水凝胶柔性表面流动激励特性

柔性模型绕流平均速度场如图6（b）所示，与刚性模型相比，存在以下3个方面的显著差别：1）对于SUBOFF模型首部（< 0.25L）曲面边界层，刚性模型边界层较厚，且流向低速区、法向高速区均更加显著；2）进入平行中体（0.25L～0.60L），刚性模型边界层依然保持首部边界层流向、法向平均速度的分布特征，但柔性模型边界层厚度明显增大，尤其是在流向上，法向平均速度存在明显正、负交替现象；3）柔性模型尾部型线收缩段（> 0.6L）的边界层分离更为显著，流向平均速度低速区显著增大，在进入分离区之前，法向平均速度先显著增大，再减小。

进一步分析柔性模型周围脉动压力均方根及近壁脉动压力频谱沿流向分布情况，分别如图8（b）和10（b）所示。与刚性模型相比，水凝胶SUBOFF模型前缘驻点扰动产生的空间和近壁脉动压力均方根均显著增大，具体表现为驻点扰动频带更宽（高频至500 Hz）、扰动存续空间更长（流向至0.2L附近）。进入平行中体后，柔性模型边界层扰动实现了幅值一次增长，其扰动频段与刚性模型边界层转捩频段相当，但低频扰动强度远不如刚性模型，甚至远低于刚性模型边界层扰动幅值一次增长区的低频扰动强度。在柔性模型0.4L处，近壁脉动压力扰动幅值和频段均“断崖式”衰减，并在0.6L附近出现第二次“断崖式”衰减，呈现出比刚性模型更宽的尾部分离区。

3.2   水凝胶表面流‒固耦合作用机制

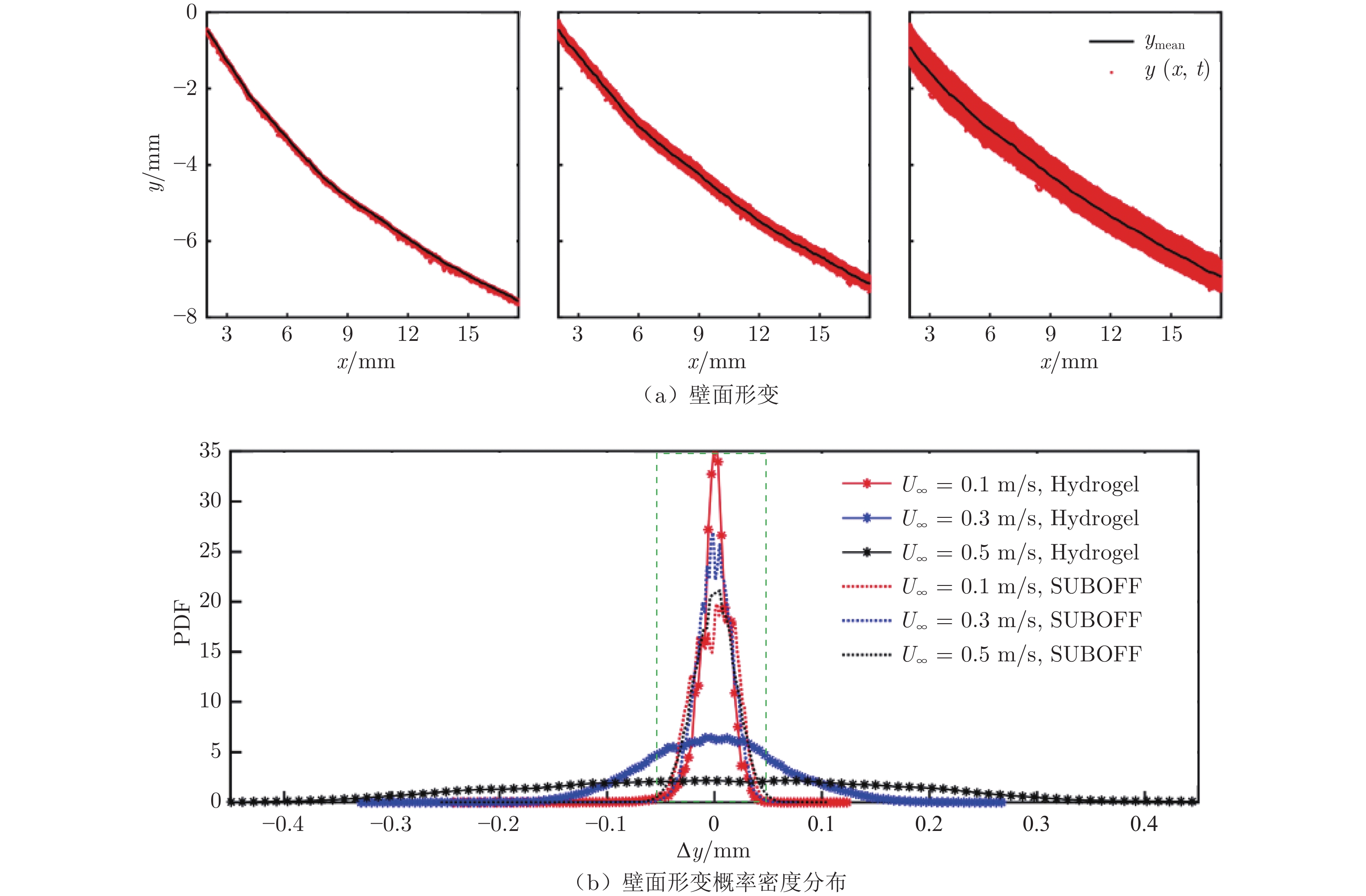
在上述柔性模型绕流边界层流动激励下，在高速水洞中观测到水凝胶壁面产生了明显形变。在北京航空航天大学的低速水槽^[27]中，分别在0.1、0.3和0.5 m/s来流速度下，进行了柔性模型（模型长度356 mm）壁面动态形变高速摄影（拍摄区域35 mm × 35 mm，对应像素点为2048 像素 × 2048 像素），并采用“比光强”^[28]算法对图像进行处理，记录了x/L = 0.016处水凝胶壁面的法向位移及概率密度函数（Probability Density Function, PDF）分布，如图11所示（图中红点为瞬时壁面位置，黑色实线为时间平均的壁面位置，绿色虚线框为壁面形变测试的置信区间）。从图11可以看出：当来流速度增大，壁面局部形变量显著增大，在0.3和0.5 m/s来流速度下，最大形变量分别达到± 0.15和± 0.3 mm；在0.1 m/s来流速度下，柔性模型壁面形变量与刚性模型相当，均在 ± 50 μm以内。由于刚性模型在理论上不应存在局部壁面形变，所以壁面形变测试的置信区间为 ± 50 μm。因此，大于置信区间的壁面形变测试结果是可靠的。

图  11  柔性模型壁面形变及其概率密度分布

Fig.  11  Surface deformation and probability density distribution of the hydrogel SUBOFF model

下载: 全尺寸图片 幻灯片

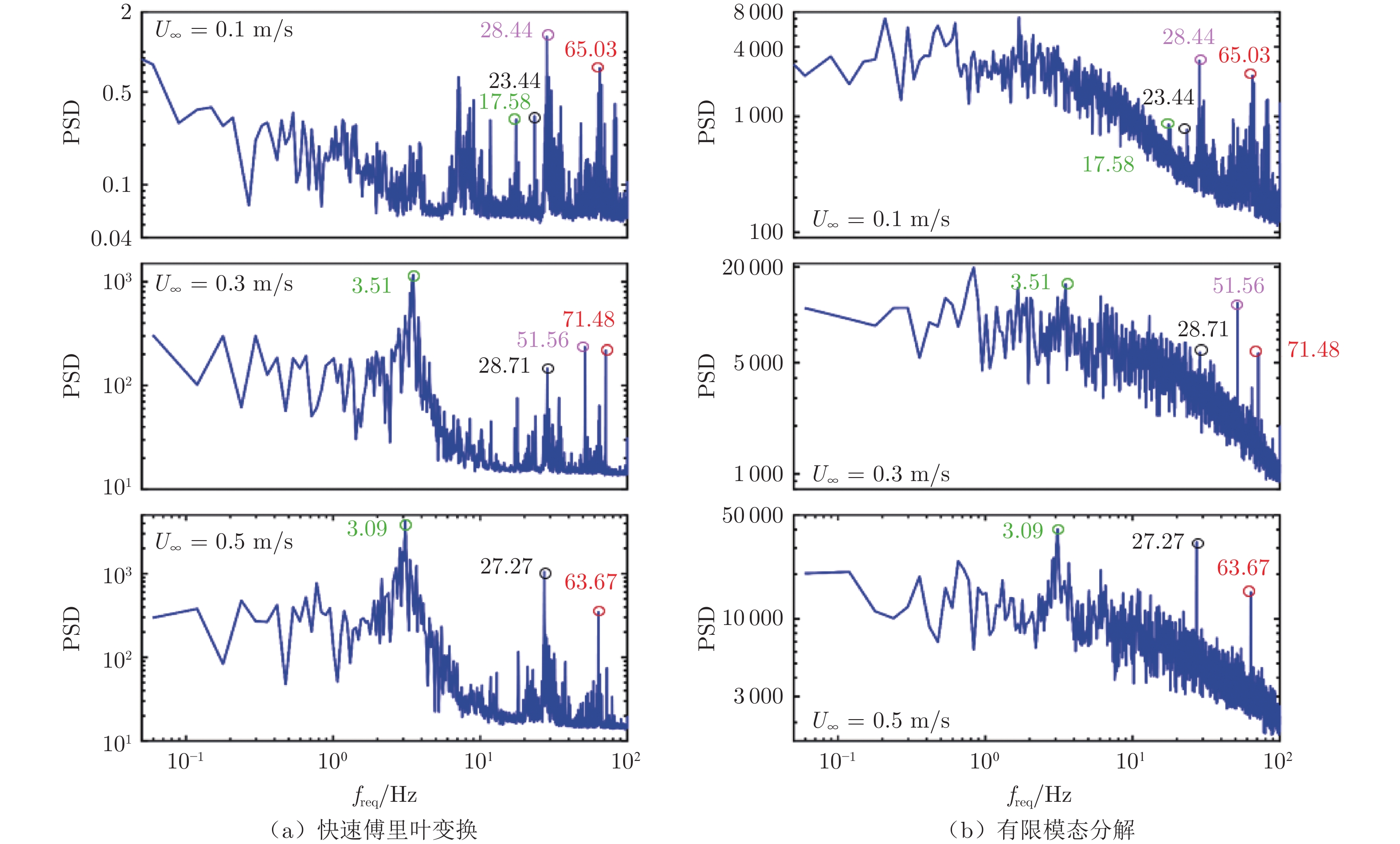
进一步地，对水凝胶壁面形变进行快速傅里叶变换，同时对相应流场（x/L = 0.016、y/δ < 0.15）的流向速度进行有限模态分解（FMD），如图12所示（图中PSD为功率谱密度，f为频率）。由图12可知：柔性模型边界层流向速度的主要峰值频率与水凝胶壁面形变的主要峰值频率吻合较好，且壁面形变中未标出的能量较高的峰值与标注的主频信息大多存在倍频关系。这一结果表明，在边界层流动激励下，低速水洞中的柔性模型壁面与边界层流场存在流‒固耦合作用机制；随着来流速度增大，水凝胶壁面形变量增大（如图11所示），因此，在高速水洞3～7 m/s来流速度下，边界层流动更容易激起水凝胶壁面形变。

图  12  低速水洞中柔性模型壁面形变快速傅里叶变换和有限模态分解

Fig.  12  Fast Fourier Transform (FFT) and Finite Mode Decomposition (FMD) of longitudinal velocity in the near wall region of a hydrogel surface of a SUBOFF test model in a low-speed water tunnel

下载: 全尺寸图片 幻灯片

3.3   水凝胶延迟边界层自然转捩机理

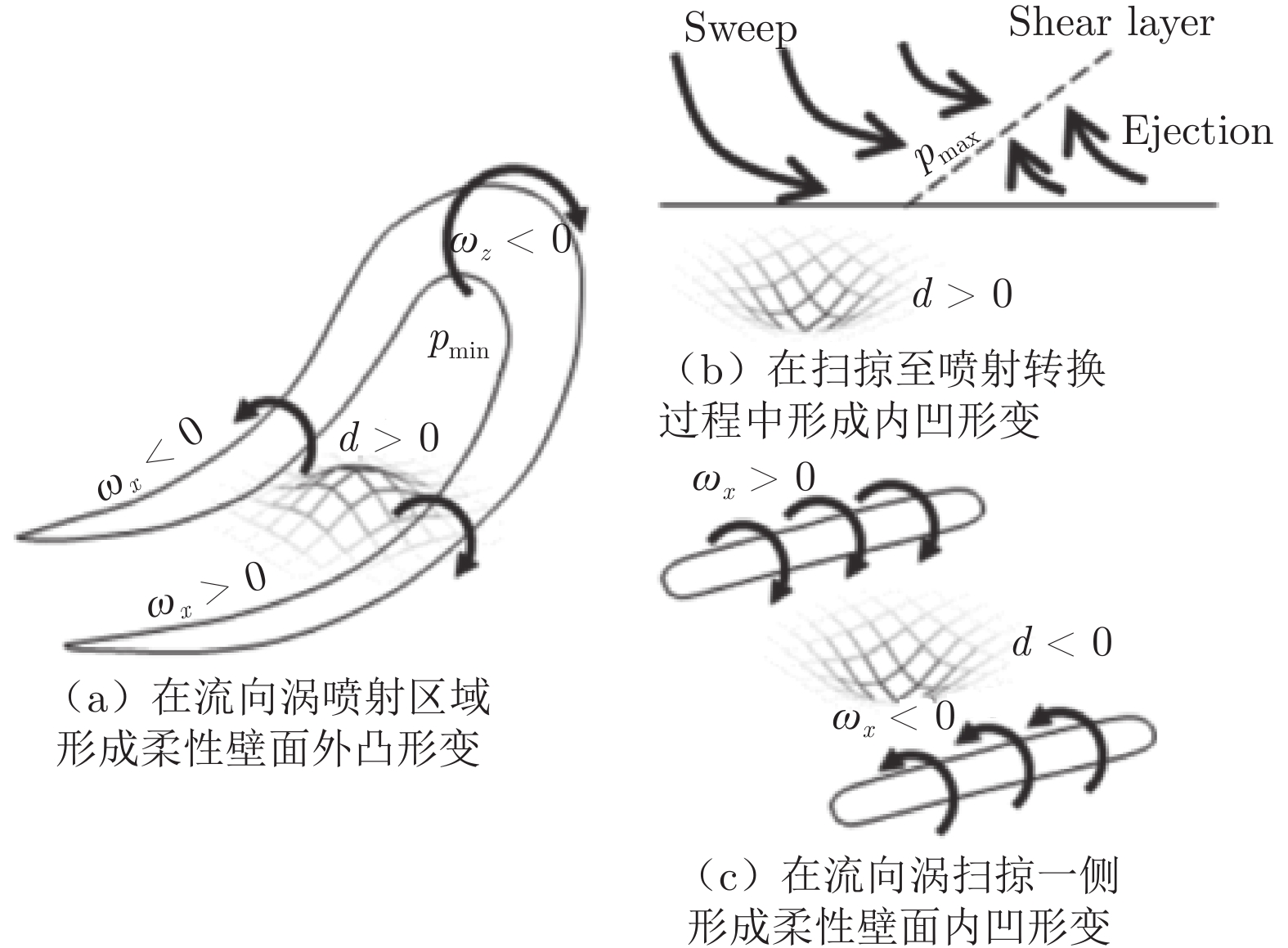
基于上述柔性模型壁面流‒固耦合机制作用，对高速水洞中柔性模型近壁流场进行深入分析。由图10（b）可知，柔性模型近壁脉动压力频谱在0.4L附近急剧削弱。分别提取0.35L～0.55L流向范围内的刚性和柔性模型近壁区二维瞬时速度场，如图13（a）和（b）所示。图中纵坐标正向表示SUBOFF模型表面法向向外，B₀为平行中体半径，即B₀ = D/2，“■”表示“A”点相对位置。近壁点“A”处的来流速度无量纲流向、法向瞬时速度时域信号u/U_∞与v/U_∞，以及基于瞬时速度估算得到的瞬时脉动压力系数$C_p' $如图13（c）所示。图13（c）的虚线表示图13（a）和（b）中二维瞬时速度场所对应的时刻，依次为150、160、170 ms，横坐标为0时表示PIV测试开始时刻，蓝、红小圆圈“○”分别表示虚线对应时刻的无量纲速度和脉动压力。由图13可知：与刚性模型相比，柔性模型周围流场中存在大尺度结构，而无量纲法向速度时域信号呈现了由大尺度结构引起的准周期性（时长约40 ms）法向速度脉动，且脉动幅值高达0.5U_∞，显著高于刚性模型近壁法向速度脉动幅值。根据图14^[29]所示的流动结构与壁面形变对应关系可知，正法向速度脉动是由反向运动流向涡对之间的喷射事件引起的。因此，在柔性模型平行中体段的边界层中，可能存在流向涡对或“Λ”涡等失稳边界层流动中的典型流动结构^[30-31]。

图  13  SUBOFF模型周围瞬时流场

Fig.  13  Instantaneous flow field over the SUBOFF test models

下载: 全尺寸图片 幻灯片

图  14  流动结构与壁面形变对应关系示意图^[29]

Fig.  14  Conceptual models for the relationships between coherent flow structure and wall deformation^[29]

下载: 全尺寸图片 幻灯片

由于瞬时法向速度很好地体现了柔性模型近壁区大尺度结构的典型特征，因此对SUBOFF模型平行中体段近壁区“A”点处的瞬时法向速度进行连续子波变换（CWT），结果如图15所示。在16～32 Hz频段，水凝胶壁面存在稳定的流动结构，且在时间轴上持续存在，不同时刻对应的频率略有差别。刚性、柔性模型壁面在128～512 Hz频段均存在流动强间歇性，二者主要差别在于：刚性模型表面流动间歇性存在于多时间尺度上，而柔性模型表面流动间歇性在时间尺度上比较固定，以多个孤立事件的形式出现，而在过渡频段（30～128 Hz）则呈现了多时间尺度的流动结构。

图  15  SUBOFF模型近壁法向瞬时速度连续子波变换

Fig.  15  Contour of 2D velocity field around SUBOFF

下载: 全尺寸图片 幻灯片

上述结果表明，在流‒固耦合机制和模型绕流边界层流动激励的作用下，水凝胶壁面出现了准周期性局部形变，而流场中瞬时法向速度对水凝胶表面局部形变较为敏感，法向瞬时速度的CWT结果呈现了法向速度的频域和时域特性，通过水凝胶壁面局部形变向边界层引入了准周期性（16～32 Hz）大尺度结构，并通过过渡频段（32～128 Hz）影响边界层内固有流动结构（128～512 Hz），使柔性模型表面流动间歇性在时间尺度上比较固定，以多个孤立事件（时长约40 ms）的形式出现，这明显区别于刚性模型多时间尺度上的间歇性。换言之，一方面，柔性模型在边界层流动激励下出现了局部形变，引入了大尺度结构，并通过过渡频段使边界层内固有频段的强间歇性流动结构变得规则，抑制了边界层内流动结构的间歇性，限制了边界层内扰动幅值的增长，延迟了边界层转捩；另一方面，边界层流动变得规则，使柔性模型近壁脉动压力减弱，这揭示了近壁脉动压力频谱出现“断崖式”衰减（图10（b））的原因。

4   主要结论与展望

4.1   主要结论

在高速水洞中开展了刚性模型、柔性模型阻力与速度场实验测试，采用多路径积分算法^[18]对模型周围脉动压力场进行估算，结合刚性模型边界层流动线性稳定性分析，获得了刚性模型边界层自然转捩特性。采用“比光强”算法^[28]，对低速水洞中柔性模型局部形变与近壁区速度场进行频谱分析，揭示了水凝胶壁面流−固耦合作用机制。采用连续子波变换，对边界层瞬时流场间歇性进行了分析，揭示了水凝胶延迟SUBOFF模型边界层自然转捩机理。主要结论如下：

1）在3～7 m/s（1.5 × 10⁶ < Re_L < 3.5 × 10⁶）流速下：刚性模型阻力系数从3 m/s开始随流速增大显著降低，至流速6 m/s时趋于稳定且与类似模型湍流绕流的阻力系数相当，这表明在实验雷诺数范围内，刚性模型边界层流动发生了从层流向湍流的流态转变；柔性模型阻力系数随流速增大基本不变，且与类似模型层流绕流的阻力系数相当，这表明在实验雷诺数范围内，柔性模型边界层未完成从层流至湍流的流态转变。在平均速度场中，水凝胶SUBOFF模型尾部较大的分离区也证明了层流分离，即柔性模型绕流边界层至尾部仍为层流。

2）在7 m/s（Re_L = 3.5 × 10⁶）流速下，刚性模型绕流边界层自然转捩机理主要体现在以下3个方面：①前缘驻点扰动直接进入边界层，但在首部强顺压梯度作用下，扰动快速衰减；②中性曲线存在2个不稳定区，特定频段的不稳定波经历“失稳‒稳定‒再次失稳”，最终在第二不稳定区发生转捩；③边界层激励力的频谱云图体现了边界层不稳定波经历2次失稳才发生转捩的过程，占主导的激励力频段包含于中性曲线第二不稳定区频段范围内。

3）基于低速水洞柔性模型呈现的流‒固耦合作用机制，在7 m/s（Re_L = 3.5 × 10⁶）流速下，柔性模型在边界层流动激励下出现了局部形变，引入了大尺度结构，并通过过渡频段使边界层内固有频段的强间歇性流动结构变得规则，抑制了边界层内流动结构的间歇性，限制了边界层内扰动幅值的增长，延迟了边界层转捩；并且，边界层流动变得规则，使柔性模型近壁脉动压力强度得以减弱，这揭示了近壁脉动压力频谱出现“断崖式”衰减的原因。

4.2   展　望

在流−固耦合作用机制下，水凝胶兼具被动控制与主动（闭环）控制的优势，无需额外能量消耗即可自适应于边界层内非定常流动，以绕流边界层内出现的规则大尺度流动结构抑制边界层内不稳定波的增长，进而起到延迟水下航行体首部曲面边界层转捩的作用，显著降低由边界层转捩引起的局部脉动压力。针对水凝胶延迟边界层转捩的研究，未来可着重开展以下两方面工作：一是发展强大的稳定性理论分析工具，用于开展流−固耦合作用下水凝胶等非定常形变材料表面的边界层流动稳定性分析，为柔性材料应用于延迟转捩提供理论支撑；二是水凝胶作为一种物理与力学特性类水的固体柔性材料，海洋环境适应性良好，声学阻抗与水完全匹配，且能够承受一定的作用力，若在大尺度低成本制备、与耐压金属壳体交联强度提升等方面取得关键突破，则有望应用于水下航行体边界层转捩控制。