Mechanism of natural transition delay by hydrogel metamaterial over a body of revolution
-
摘要:
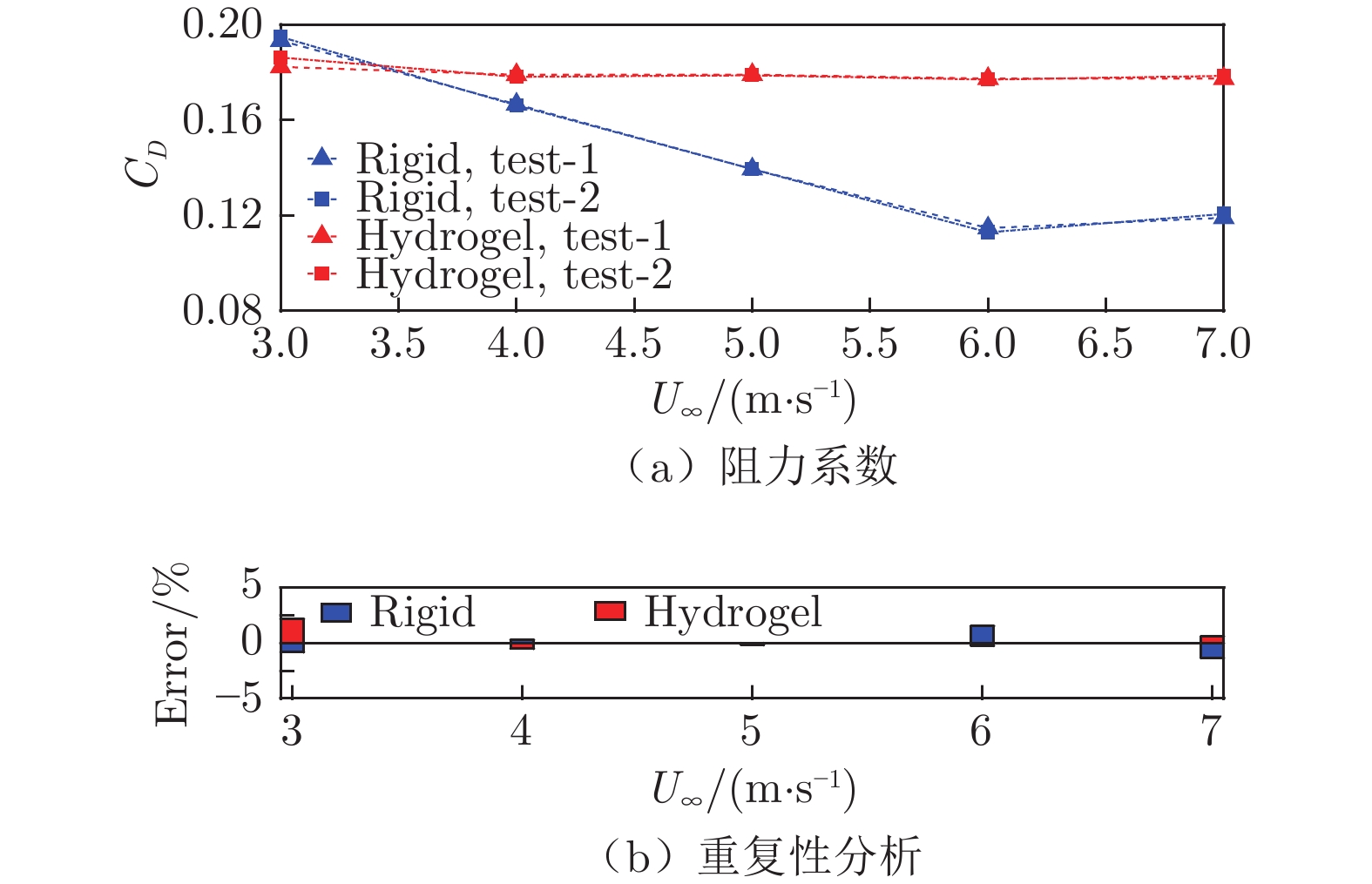
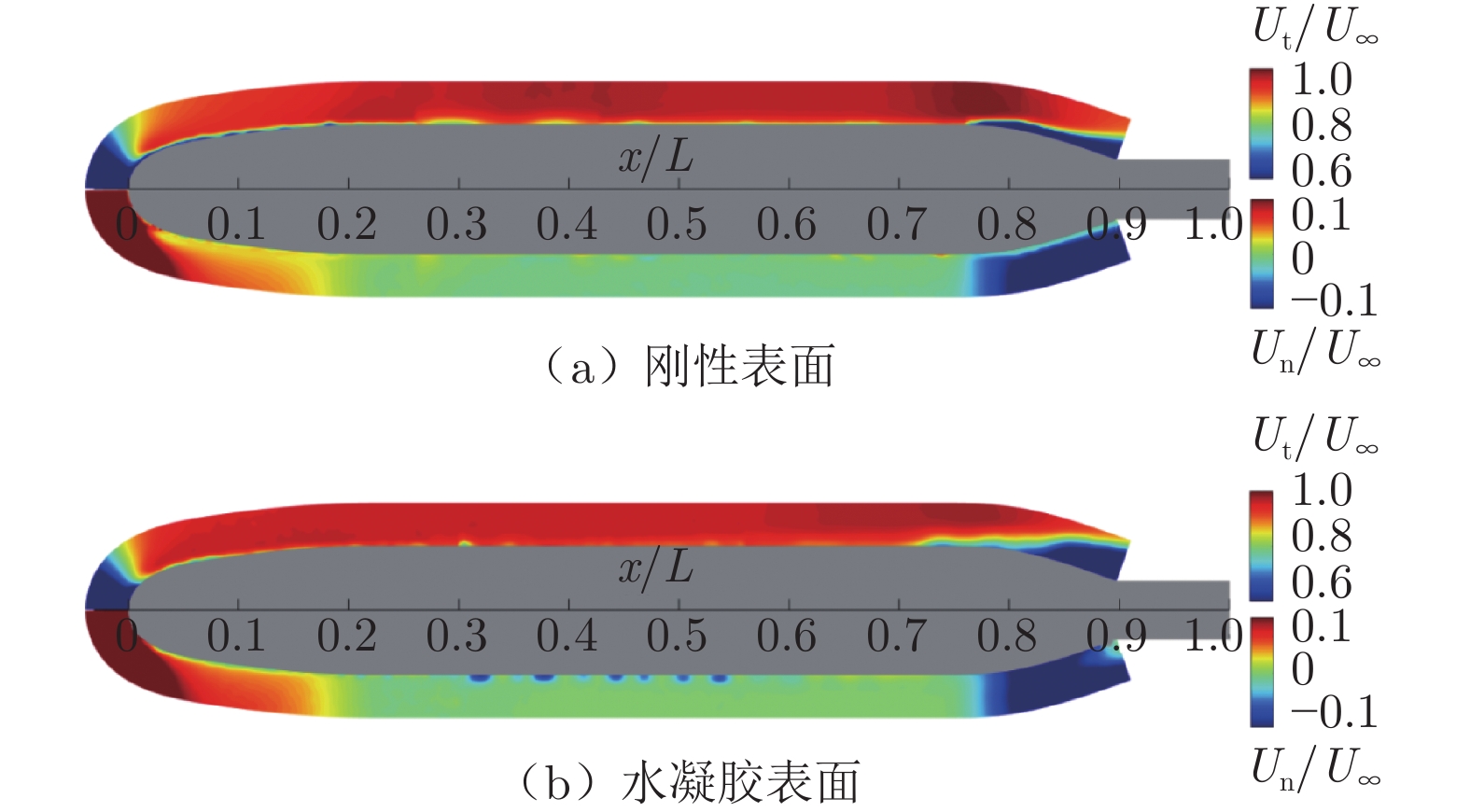
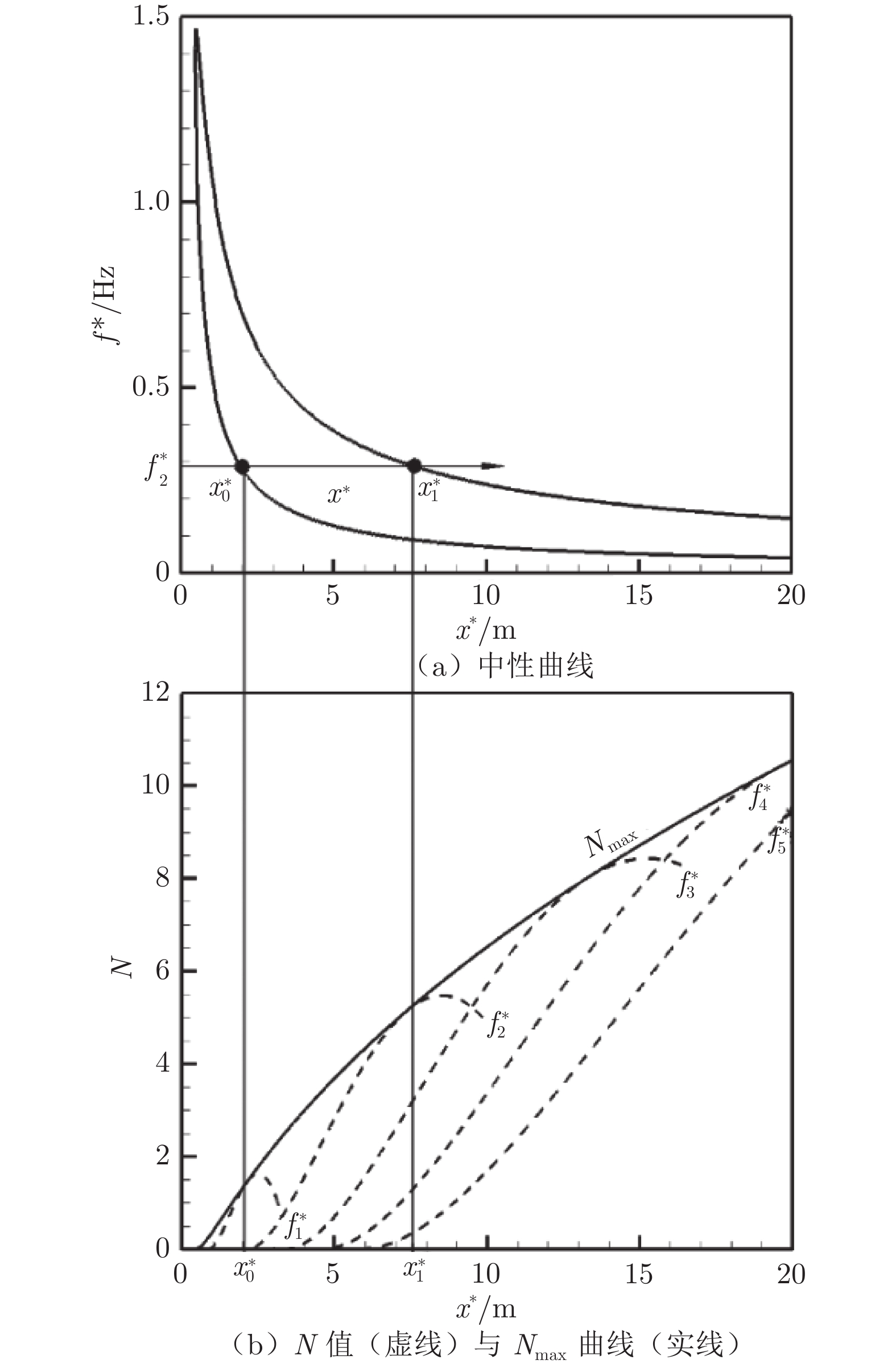
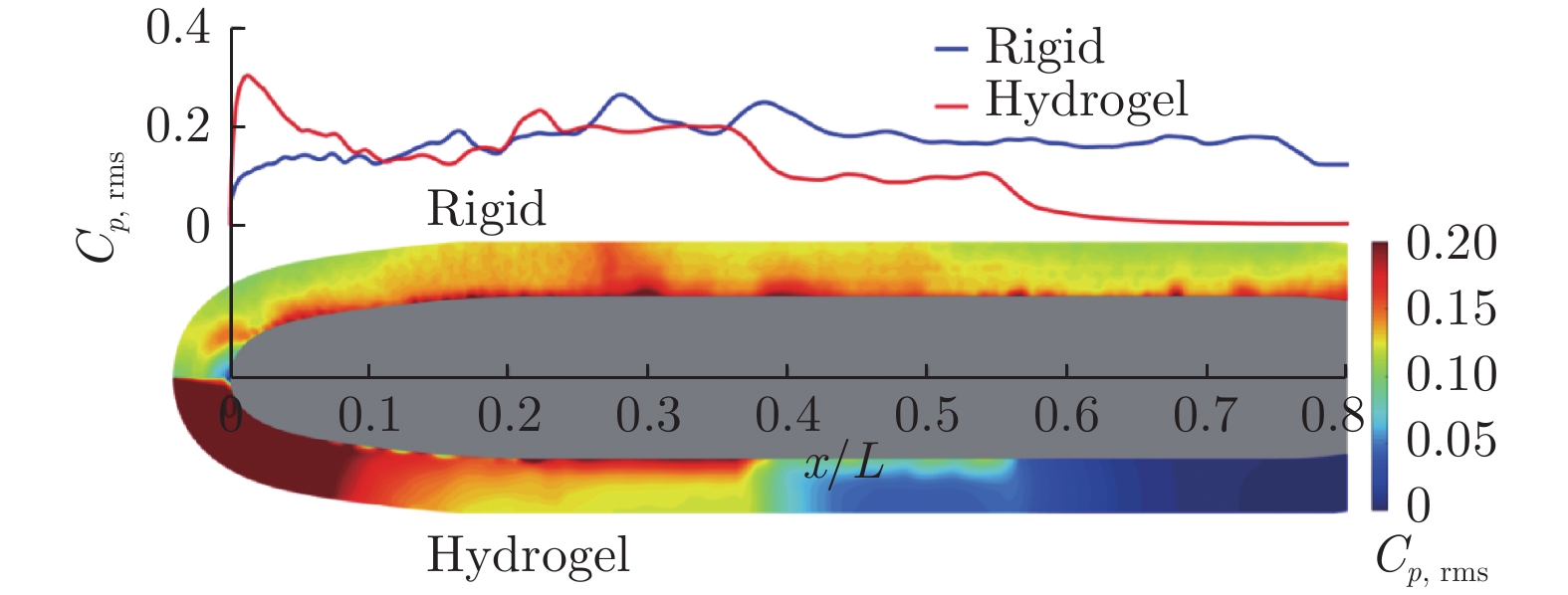
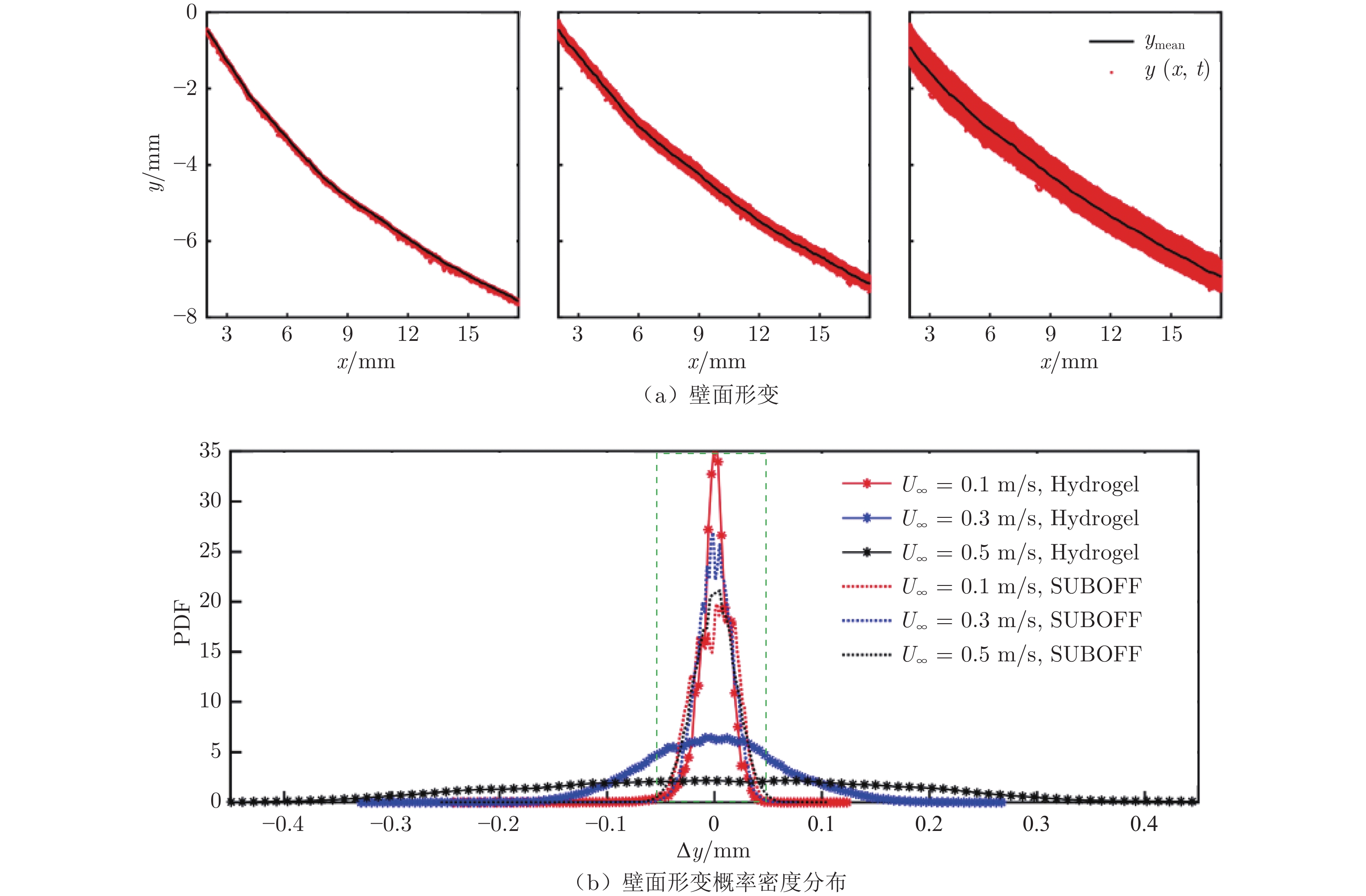
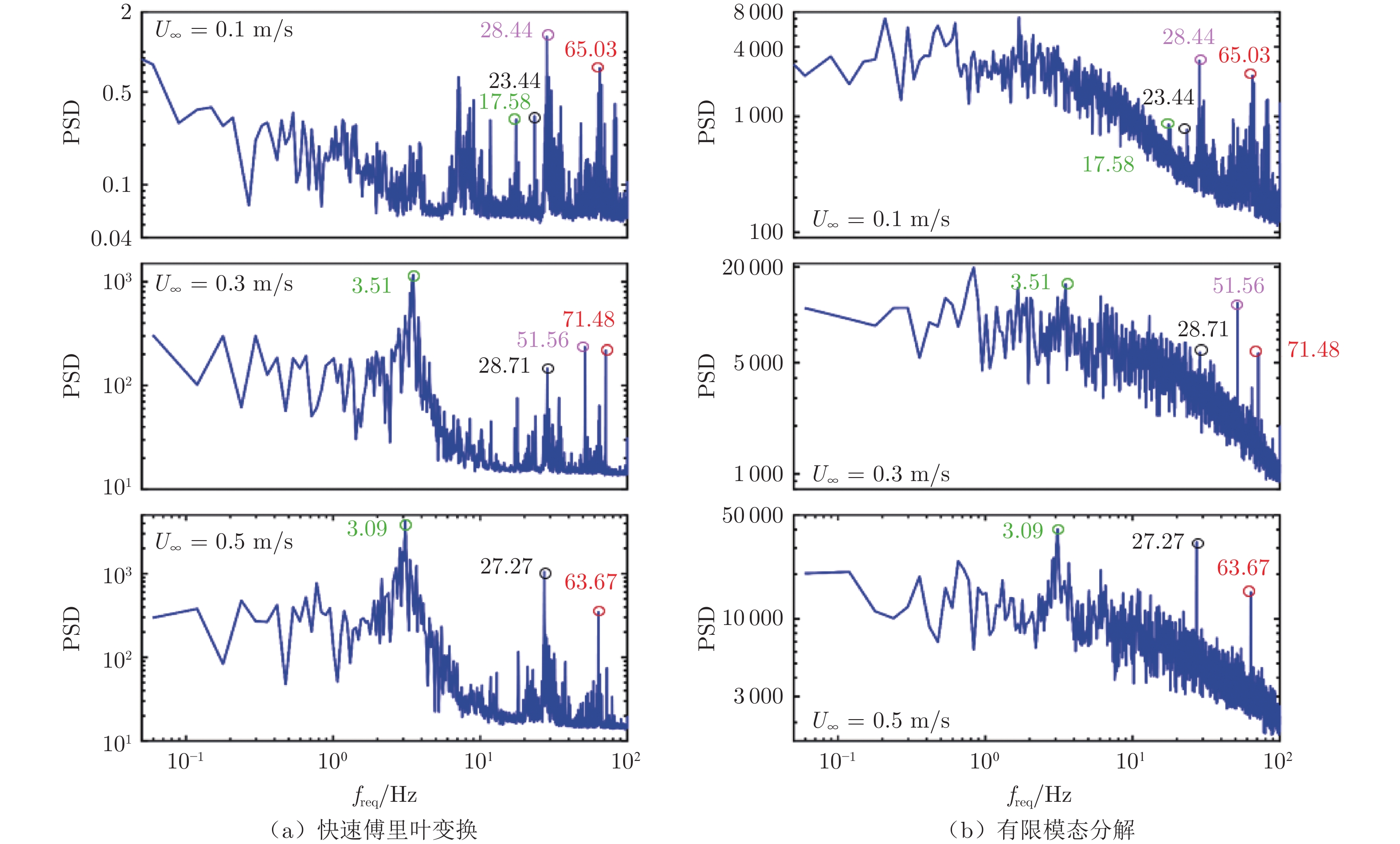
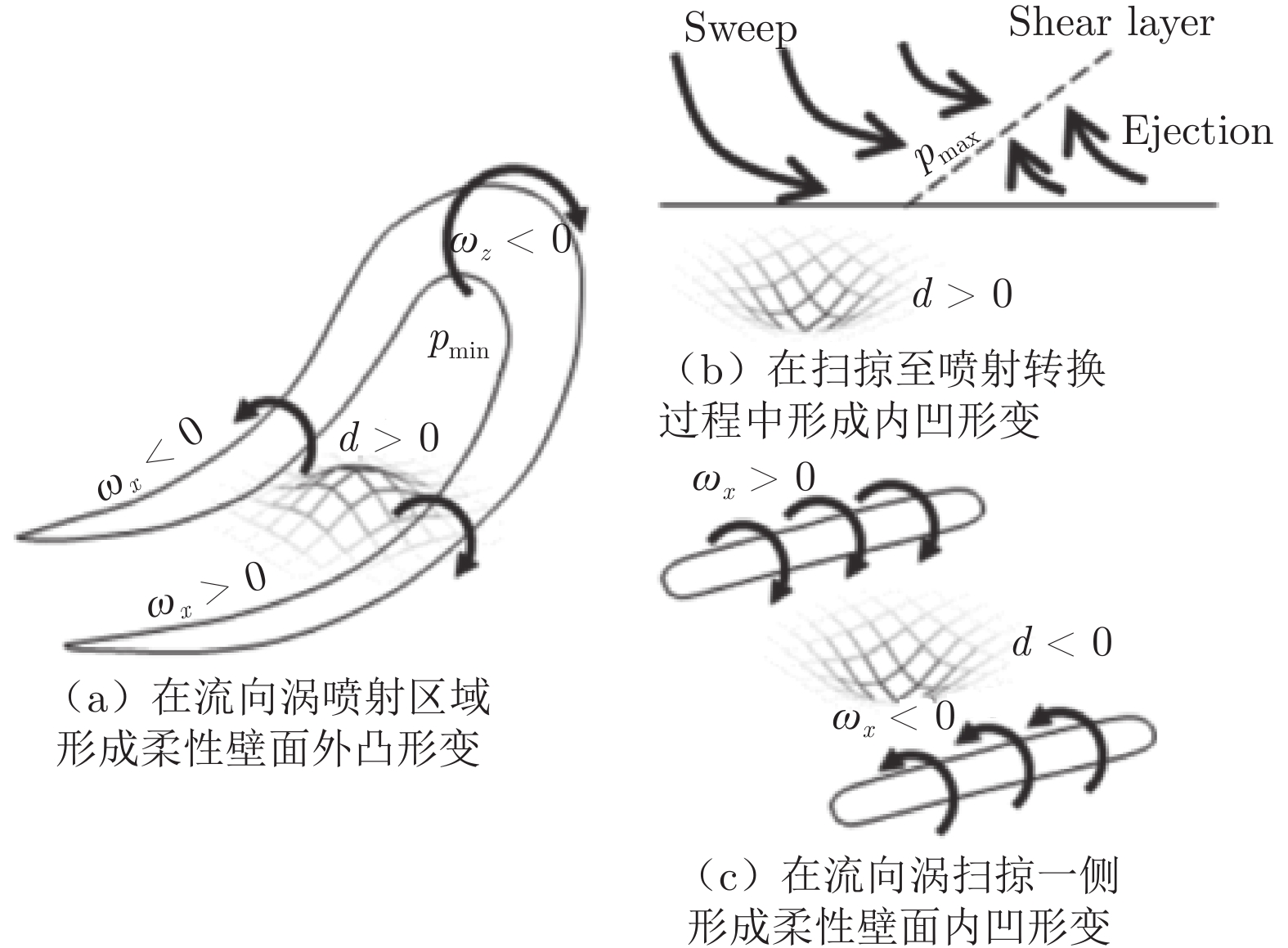
水下航行体首部声纳探测能力与边界层转捩密切相关。本文开展了水凝胶超材料在延迟水下航行体边界层自然转捩方面的应用基础研究，并探究了其内在机理。在高速水洞中分别开展了刚性和水凝胶表面的SUBOFF模型总阻力系数与二维瞬时速度场大视场PIV实验测试，采用多路径积分算法对SUBOFF模型周围脉动压力场进行估算；结合刚性SUBOFF模型边界层流动线性稳定性分析与PIV流场测试结果，获得刚性SUBOFF模型边界层自然转捩特性；采用“比光强”算法，对低速水洞中水凝胶表面SUBOFF模型局部形变与近壁区速度场进行频谱分析，揭示水凝胶表面流−固耦合作用机制；基于法向瞬时速度分量的连续子波变换，对边界层瞬时流场间歇性进行分析，揭示水凝胶在流−固耦合作用下延迟SUBOFF模型边界层自然转捩的机理。
Abstract:Laminar-turbulence transition in a bow boundary layer is crucial for the performance of the bow sonar of an underwater vehicle. An investigation on the application of the hydrogel metamaterial on natural transition delay is conducted and the underlying mechanism is analyzed. The two-dimensional velocity fields around both rigid and hydrogel SUBOFF models are acquired by a long-distance PIV in a high-speed water tunnel, and drag coefficients are measured as well. Based on the velocity fields, the pressure fluctuations around the SUBOFF models are calculated through the multi-path integration algorithm. Combining the linear instability analysis and PIV measurement, the characteristics of natural transition of the boundary layer over the rigid SUBOFF model are analyzed. The flow-hydrogel coupling is figured out, according to the spectral analysis of local deformation of the hydrogel surface and the velocity above the hydrogel SUBOFF model in a low-speed water tunnel. The intermittency of the instantaneous boundary layer flows are denoted by continuous wavelet transform of the wall-normal velocity components. Eventually, compared with the flow intermittency of the rigid SUBOFF model, the mechanisms of natural transition delay by the hydrogel metamaterial are discussed, under the influence of the flow-hydrogel coupling.
-
-
![]()
图 2 小型多功能高速水洞示意图
Fig. 2 Schematic sketch of small multi-functional high-speed water tunnel
![]()
图 3 实验模型实物照片与水凝胶力学性能测试
Fig. 3 Photos of test model and mechanics performance test of the hydrogel
![]()
图 8 SUBOFF模型周围脉动压力均方根沿艇长分布（刚性表面为上方云图与蓝色实线，水凝胶表面为下方云图与红色实线）
Fig. 8 Contour of 2D velocity field around the SUBOFF test model (contour above and the blue solid line represent rigid surface, contour below and the red solid line represent soft surface)
![]()
图 9 刚性SUBOFF模型首部边界层稳定性分析
Fig. 9 Instability analysis of boundary layer flow around the bow of the rigid SUBOFF test model
![]()
图 10 SUBOFF模型近壁脉动压力频谱云图
Fig. 10 Contour of spectrum of pressure fluctuations in the near wall region around the SUBOFF test model
![]()
图 11 柔性模型壁面形变及其概率密度分布
Fig. 11 Surface deformation and probability density distribution of the hydrogel SUBOFF model
![]()
图 12 低速水洞中柔性模型壁面形变快速傅里叶变换和有限模态分解
Fig. 12 Fast Fourier Transform (FFT) and Finite Mode Decomposition (FMD) of longitudinal velocity in the near wall region of a hydrogel surface of a SUBOFF test model in a low-speed water tunnel
![]()
表 1 测试仪器及主要参数
Table 1 Test facilities and major parameters
仪器 型号参数 测力天平 型号：L6H5‒4kg 量程：4 kg 精度：0.03% 应变放大器 型号：DH3840 输出电压：10V 增益：300 高频激光器 型号：Beamtech Vlite‒Hi‒35型 量程：200 Hz～10 kHz 精度：能量不稳定性$\leqslant1\% $ 高速相机 型号：Phantom LAB310 像素：1280 像素 × 800 像素 帧速：满幅帧率3260 Hz 
下载: 导出CSV
-
[1] ARAKERI V H. A note on the transition observations on an axisymmetric body and some related fluctuating wall pressure measurements[J]. Journal of Fluids Engineering, 1975, 97(1): 82–86. doi: 10.1115/1.3447222
[2] LAUCHLE G C. Noise generated by axisymmetric turbulent boundary-layer flow[J]. The Journal of the Acoustical Society of America, 1977, 61(3): 694–703. doi: 10.1121/1.2003213
[3] HONG C, SHIN K K, JEON J J, et al. Transitional wall pressure fluctuations on axisymmetric bodies[J]. The Journal of the Acoustical Society of America, 2008, 124(5): 2767–2773. doi: 10.1121/1.2988291
[4] KRAMER M O. Boundary-layer stabilization by distributed damping[J]. Naval Engineers Journal, 1960, 27(1): 69. doi: 10.2514/8.8380
[5] CHOI K S, YANG X, CLAYTON B R, et al. Turbulent drag reduction using compliant surfaces [C]// Proc of the Royal Society A: Mathematical, Physical and Engineering Sciences. 1997. doi: 10.1098/rspa.1997.0119
[6] ENDO T, HIMEO R. Direct numerical simulation of turbulent flow over a compliant surface [J]. Journal of Turbulence, 2002, 3(7): 1-10. doi: 10.1088/1468-5248/3/1/007.
[7] KULIK V M, SEMENOV B N, BOIKO A V, et al. Measurement of dynamic properties of viscoelastic materials[J]. Experimental Mechanics, 2009, 49(3): 417–425. doi: 10.1007/s11340-008-9165-x
[8] SHU W, LIU W M. The effect of compliant coatings on coherent structure in turbulent boundary layers[J]. Acta Mechanica Sinica, 1990, 6(2): 97–101. doi: 10.1007/BF02488439
[9] 孙卫红, 刘波, 晏欣. 聚氨酯-丙烯酸酯柔性壁的减阻性能[J]. 高分子材料科学与工程, 2017, 33(9): 59–64. DOI: 10.16865/j.cnki.1000-7555.2017.09.011 SUN W H, LIU B, YAN X. Drag reduction properties of polyurethane-poly (acrylate) hybrid emulsions[J]. Polymer Materials Science & Engineering, 2017, 33(9): 59–64. doi: 10.16865/j.cnki.1000-7555.2017.09.011
[10] 郝英泽, 林凡彩, 刘百顺. 浅析潜艇水下航行阻力及减阻措施[C]// 2009特大型船舶操纵和船舶安全与管理论文集. 2009: 148-151. [11] ZHANG S S, OUYANG X, LI J, et al. Underwater drag-reducing effect of superhydrophobic submarine model[J]. Langmuir, 2015, 31(1): 587–593. doi: 10.1021/la504451k
[12] YAO H L, ZHANG H X, LIU H T, et al. Numerical study of flow-excited noise of a submarine with full appendages considering fluid structure interaction using the boundary element method[J]. Engineering Analysis with Boundary Elements, 2017(77): 1–9. doi: 10.1016/j.enganabound.2016.12.012
[13] 王磊, 常书刚. 潜艇噪声与综合降噪技术的应用[J]. 航海技术, 2007(2): 44–48. WANG L, CHANG S G. Submarine noise and application of comprehensive noise reduction technology[J]. Marine Technology, 2007(2): 44–48.
[14] 魏以迈. 我国船舶水下噪声研究进展综述[J]. 上海造船, 2000, 16(1): 27–32, 2. WEI Y M. The progress or the researches on the marine underwater noise in China[J]. Shanghai Shipbuilding, 2000, 16(1): 27–32, 2.
[15] 汪伟, 李本昌, 罗笛. 潜艇水声对抗及水声对抗器材的应用[J]. 指挥控制与仿真, 2008, 30(5): 102–105. WANG W, LI B C, LUO D. Acoustic warfare of submarine and application of acoustic countermeasure equipment[J]. Command Control & Simulation, 2008, 30(5): 102–105.
[16] YUK H, ZHANG T, PARADA G A, et al. Skin-inspired hydrogel–elastomer hybrids with robust interfaces and functional microstructures[J]. Nature Communications, 2016, 7: 12028. doi: 10.1038/ncomms12028
[17] MANOVSKI P, JONES M B, HENBEST S M, et al. Boundary layer measurements over a body of revolution using long-distance particle image velocimetry[J]. International Journal of Heat and Fluid Flow, 2020, 83: 108591. doi: 10.1016/j.ijheatfluidflow.2020.108591
[18] DABIRI J O, BOSE S, GEMMELL B J, et al. An algorithm to estimate unsteady and quasi-steady pressure fields from velocity field measurements[J]. The Journal of Experimental Biology, 2014, 217: 331–336. doi: 10.1242/jeb.092767
[19] WHITE F H. Fluid Mechanics[M]. 6th edition. New York: The McGraw-Hill, 2006: 483.
[20] 刘竟成. 水下回转体首部边界层自然转捩的数值研究[D]. 天津: 天津大学, 2023. LIU J C. Numerical investigation of natural transitions of bow boundary layers over underwater axisymmetric bodies [D]. Tianjin: Tianjin University, 2023.
[21] LAUCHLE G C, EISENHUTH J J, GURNEY G B. Boundary-layer transition on a body of revolution[J]. Journal of Hydronautics, 1980, 14(4): 117–121. doi: 10.2514/3.48181
[22] LIU J C, LIU J H, ZHANG Y M. Influence of Reynolds number on the natural transition of boundary layers over underwater axisymmetric bodies[J]. Physics of Fluids, 2023, 35(4): 1–16. doi: 10.1063/5.0143497
[23] REN J, MAO X R, FU S. Image-based Flow Decomposition using Empirical Wavelet Transform[J]. Journal of Fluid Mechanics, 2021(906): A22. doi: 10.1017/jfm.2020.817
[24] KHUJADZE G, DRIKAKIS D, RITOS K, et al. Wavelet analysis of high-speed transition and turbulence over a flat surface[J]. Physics of Fluids, 2022, 34(4): 046107. doi: 10.1063/5.0088479
[25] HONG C. Wall pressure fluctuations in naturally developing boundary layer flows on axisymmetric bodies[J]. International Journal of Mechanical, Industrial and Aerospace Sciences, 2016, 10(1): 10–15.
[26] 周恒, 赵耕夫. 流动稳定性[M]. 北京: 国防工业出版社, 2004. ZHOU H, ZHAO G F. Hydrodynamic stability[M]. Beijing: National Defense Industry Press, 2004.
[27] HE G S, PAN C, FENG L H, et al. Evolution of Lagrangian coherent structures in a cylinder-wake disturbed flat plate boundary layer[J]. Journal of Fluid Mechanics, 2016, 792: 274–306. doi: 10.1017/jfm.2016.81
[28] WANG L W, PAN C, LIU J H, et al. Ratio-cut background removal method and its application in near-wall PTV measurement of a turbulent boundary layer[J]. Measurement Science and Technology, 2021, 32(2): 025302. doi: 10.1088/1361-6501/abb483
[29] ZHANG C, WANG J, BLAKE W, et al. Deformation of a compliant wall in a turbulent channel flow[J]. Journal of Fluid Mechanics, 2017, 823: 345–390. doi: 10.1017/jfm.2017.299
[30] WU X H, MOIN P, WALLACE J M, et al. Transitional-turbulent spots and turbulent-turbulent spots in boundary layers[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(27): E5292–E5299. doi: 10.1073/pnas.1704671114
[31] HAMED A M, SADOWSKI M, ZHANG Z, et al. Transition to turbulence over 2D and 3D periodic large-scale rough-nesses[J]. Journal of Fluid Mechanics, 2016, 804: R6. doi: 10.1017/jfm.2016.575
计量
- 文章访问数: 705
- HTML全文浏览量: 34
- PDF下载量: 57
