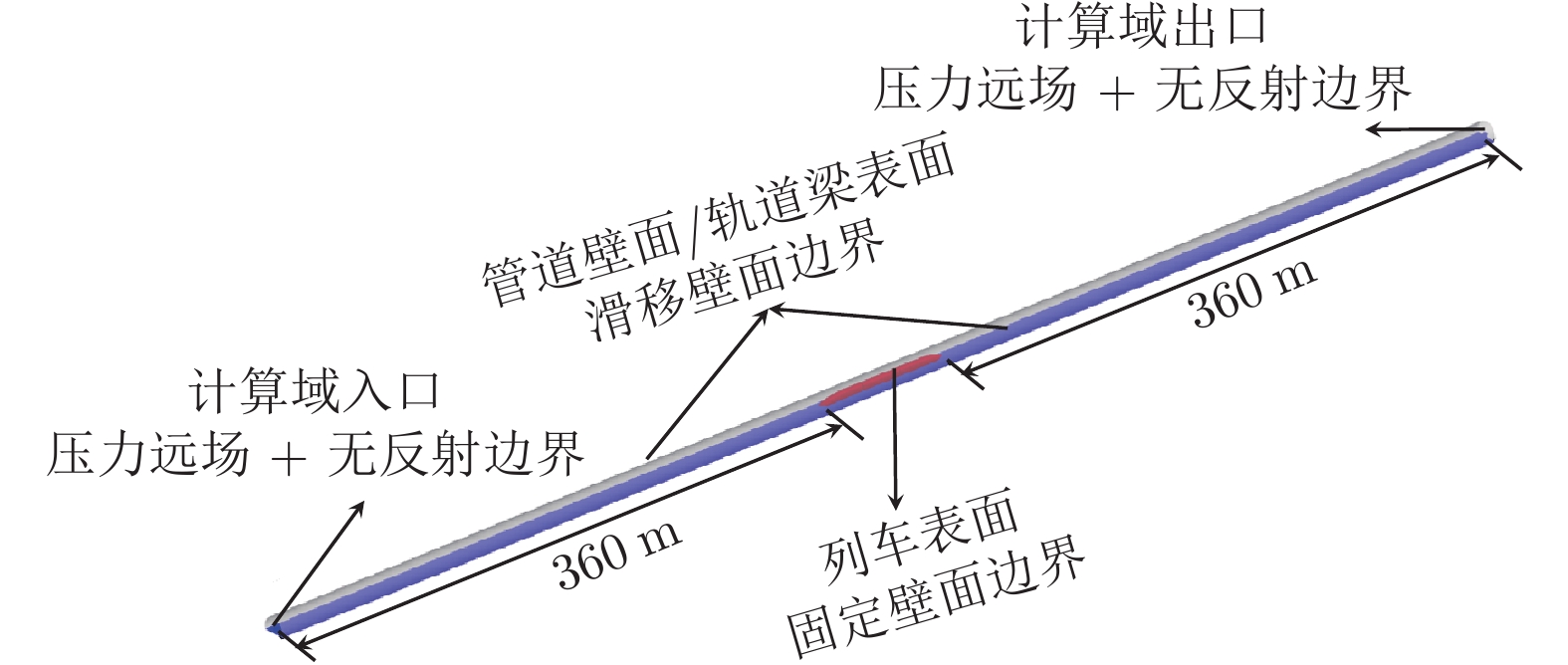
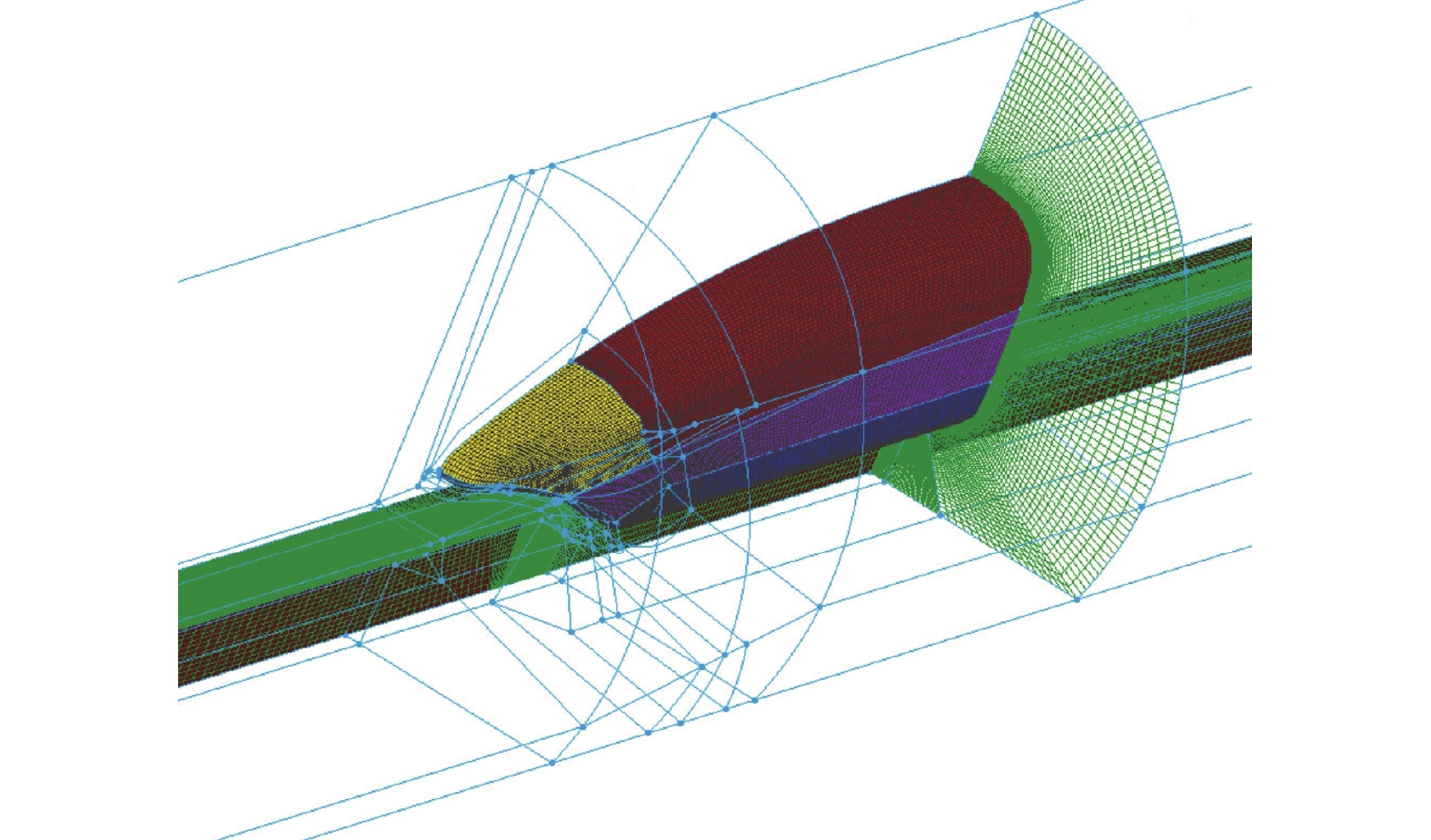
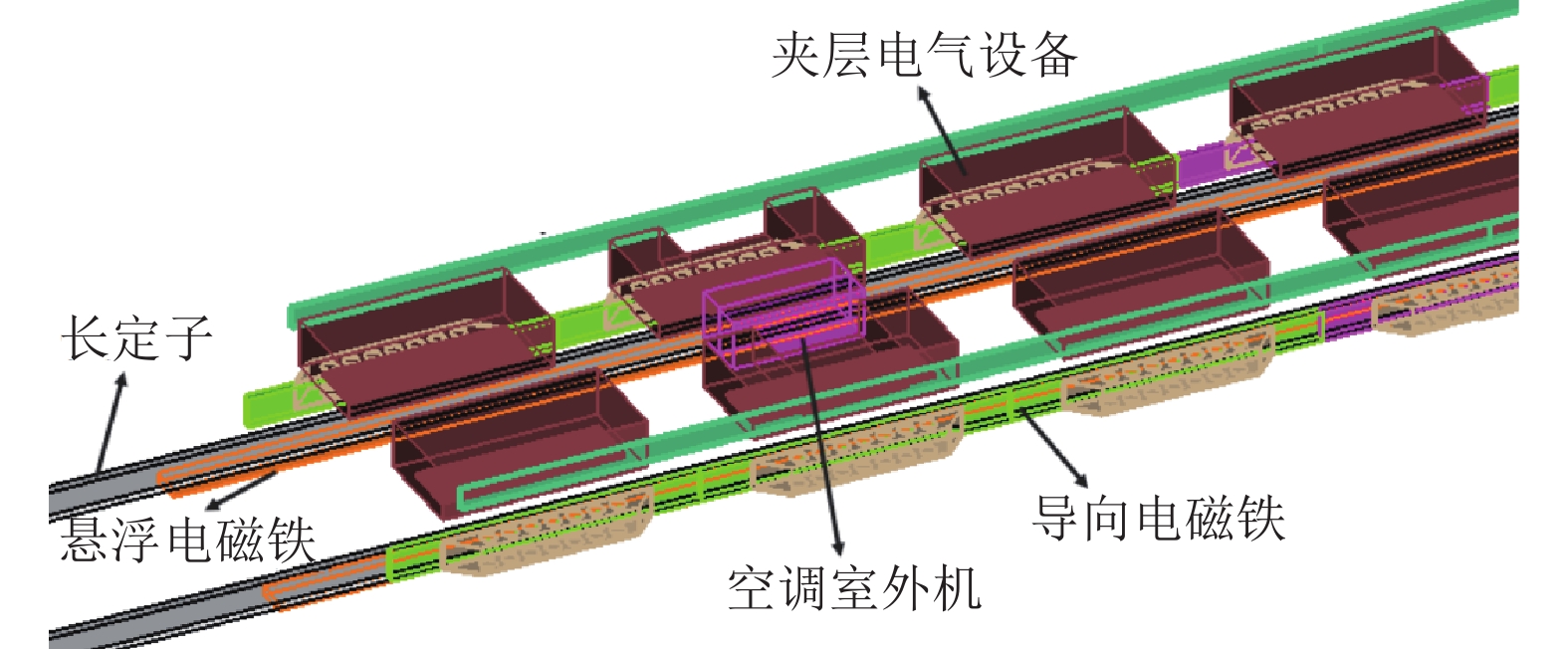
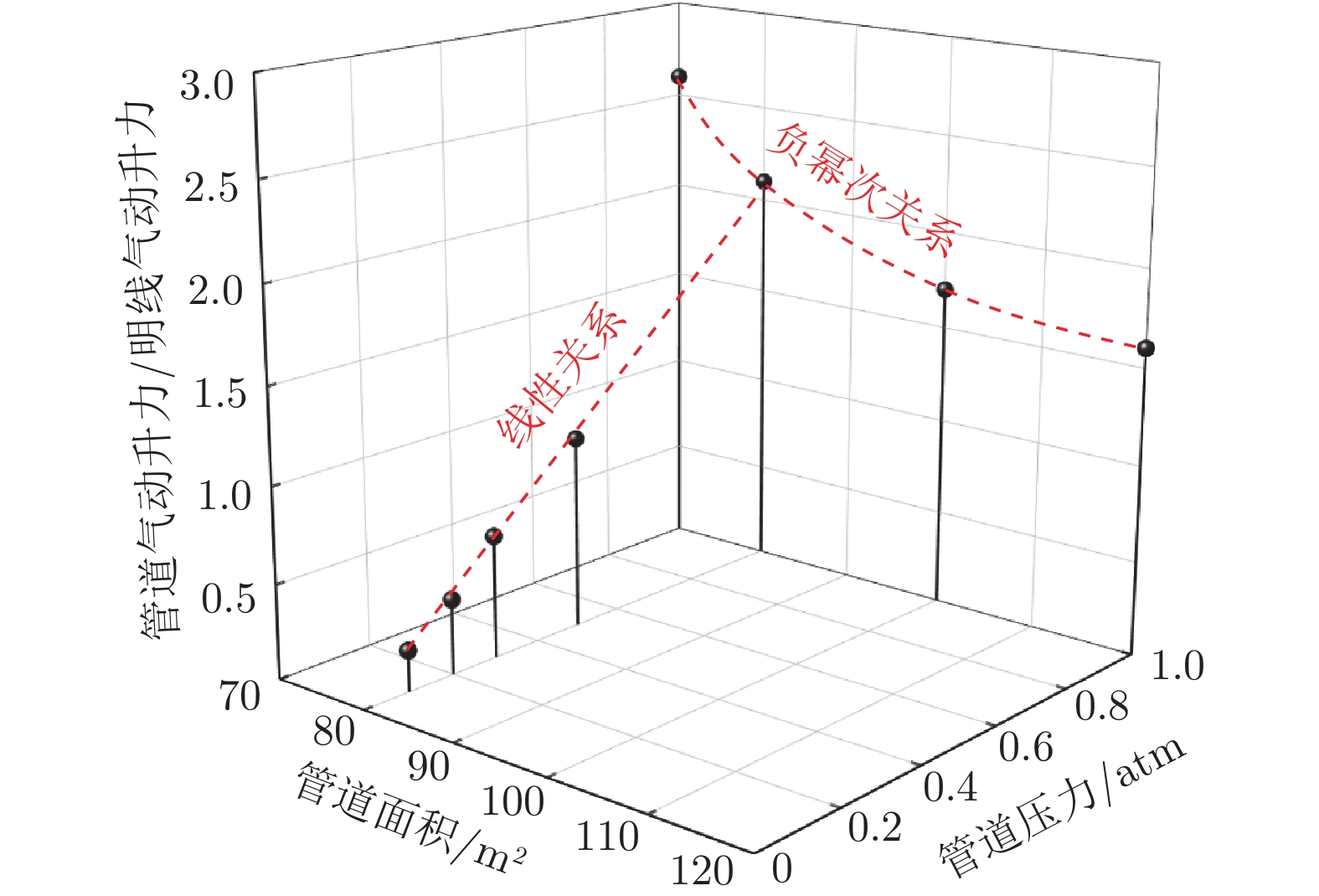
Preliminary study on system configuration of ultra high-speed maglev train aerodynamic problem in the low vacuum tube
-
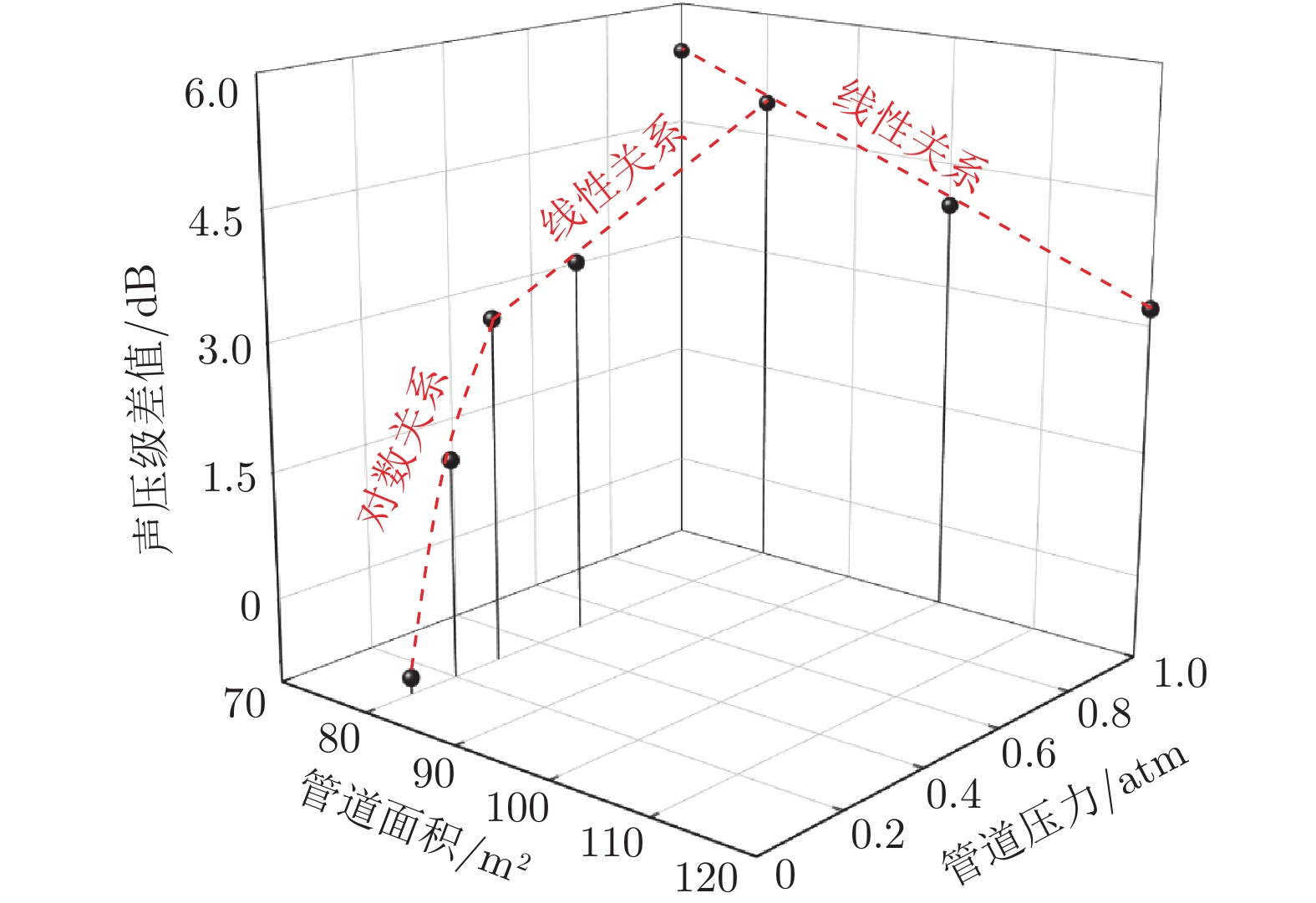
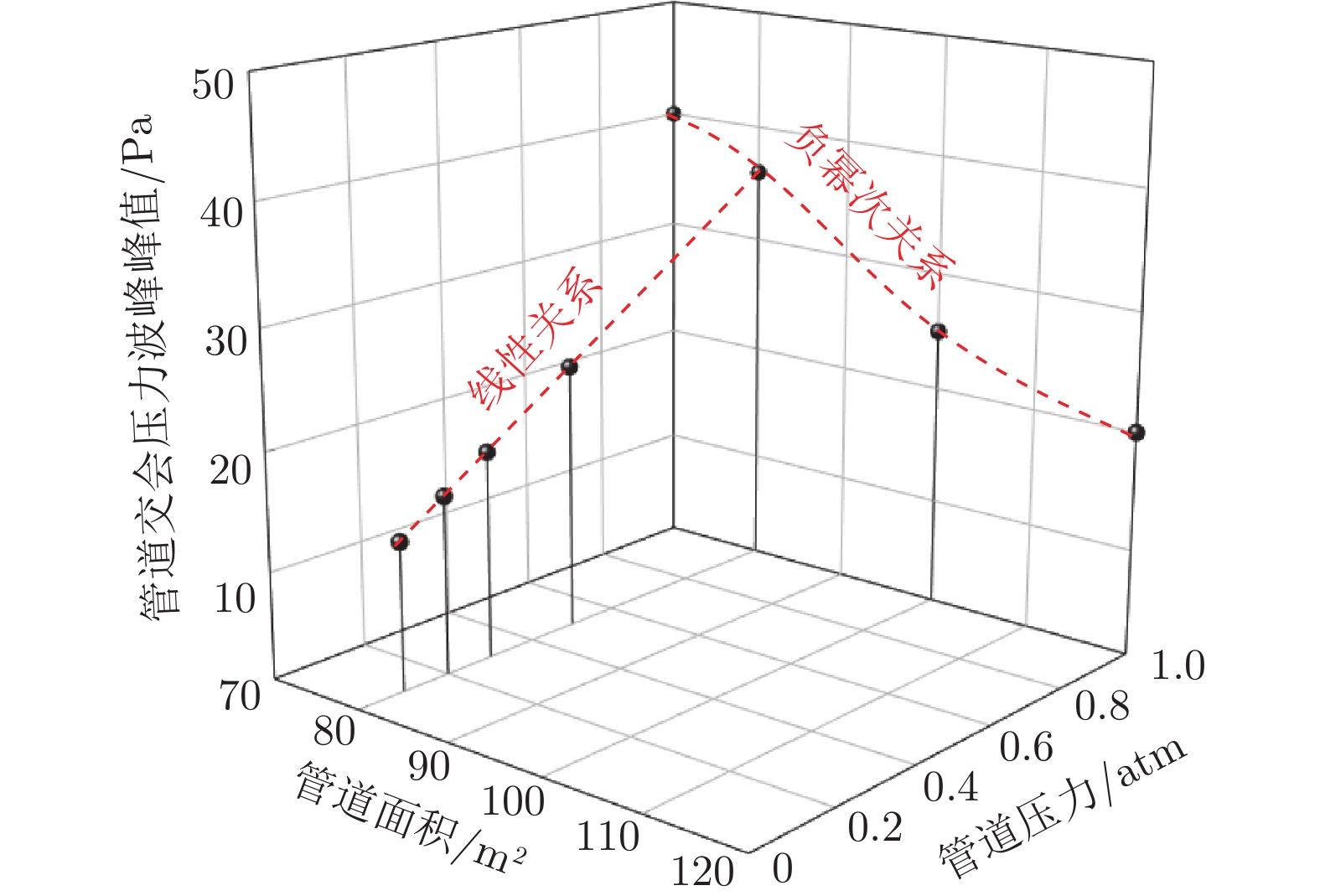
摘要: 低真空管道超高速磁浮系统是将低真空管道和高速磁浮技术结合的新型超高速地面交通系统，可有效降低列车超高速运行时的气动阻力及气动噪声，实现800～1000 km/h甚至1000 km/h以上的运行速度。本文探讨了低真空管道超高速磁浮列车空气动力学数值模拟方法，研究了管道压力、管道面积、列车速度对低真空管道超高速磁浮列车气动阻力、气动升力、气动噪声源、管道交会压力波、发热设备温度等空气动力学性能的影响规律，并针对低真空管道超高速磁浮系统典型场景进行了初步工程化探讨。研究表明：当列车速度为600 km/h时，管道常压–管道面积100 m2和管道压力0.3 atm–管道面积40 m2的配置具备工程可行性；而管道压力0.3 atm–管道面积100 m2下的设备散热存在问题，工程可行性存在一定挑战；当列车速度为1000 km/h时，管道压力0.3 atm–管道面积100 m2下的设备散热问题显著，工程可行性挑战较大；若进一步降低管道压力，设备散热与气密强度设计难度将进一步加大。Abstract: The low vacuum tube ultra high-speed maglev system is the next generation of the ultra high-speed ground transportation system, which combines the low vacuum tube and high-speed maglev technologies, and thus can effectively reduce the aerodynamic resistance and aerodynamic noise of the train running at ultra high-speed, to achieve a running speed of 800～1000 km/h, or even more than 1000 km/h. In the present paper, the aerodynamic numerical simulation method of the ultra high-speed maglev train in the low vacuum tube was discussed. The influence of the tube pressure, tube area, and train speed on the aerodynamic performance of the ultra high-speed maglev train in the low vacuum tube, such as the aerodynamic drag, aerodynamic lift, aerodynamic noise source, tube intersection pressure wave, and heating equipment temperature, was studied. And the typical scenarios of the low vacuum tube ultra high-speed maglev system were preliminarily discussed in engineering. The research shows that, when the train speed is 600 km/h, the tube pressure of 1.0 atm–tube area of 100 m2, and the tube pressure of 0.3 atm–tube area of 40 m2, have engineering feasibility; the tube pressure of 0.3 atm–tube area of 100 m2 has the problem of equipment heat dissipation, and the engineering feasibility has certain challenges. When the train speed is 1000 km/h, the equipment head dissipation under the tube pressure of 0.3 atm–tube pressure of 100 m2 is significant, and the engineering feasibility is challenged. If the tube pressure is further reduced, the design difficulty of equipment heat dissipation and airtight strength would be further increased.
-
Keywords:
- low vacuum tube /
- ultra high-speed maglev train /
- tube pressure /
- tube area /
- train speed
-
0 引 言
低真空管道超高速磁浮系统是面向未来的新型超高速地面交通系统，其将低真空管道技术和超高速磁浮技术结合起来，可有效降低列车超高速运行时的气动阻力及气动噪声等问题[1-2]。低真空管道超高速磁浮列车可以实现800～1000 km/h甚至1000 km/h以上的运行速度。目前，低真空管道超高速磁浮技术已经在国内外引起广泛重视。在国外，1999年，Daryl取得了“真空管道运输系统”的发明专利。2013年，Elon Musk提出了超级高铁（Hyperloop）的计划方案，引起了广泛关注。在国内，2004年，沈志云、钟山在西南交通大学举办 “真空管道高速交通”院士学术报告会，会议对真空管道高速交通系统进行讨论。2014年，西南交通大学建成了真空管道高温超导磁悬浮车实验平台“Super-Maglev”[3]。2017年，中国航天科工集团宣布开展“高速飞行列车”项目研究论证，拟将飞行技术与轨道交通技术相结合，利用超导磁浮技术和真空管道实现“近地飞行”。
目前，低真空管道超高速磁浮系统的空气动力学研究尚处于起步阶段。周晓等[4-5]采用二维不可压缩模型研究了低真空管道列车的气动特性，分析了列车气动阻力的影响因素及影响规律。该研究采用的是二维模型，且流动为不可压缩，与实际情况差异较大。Kim等[6]采用二维可压缩模型研究了真空管道高速列车气动特性，获得了列车气动阻力与车速、阻塞比、管道压力的关系。刘加利等[7-9]采用三维可压缩模型研究了低真空管道高速列车气动特性，分析了列车气动阻力、偶极子声源、四极子声源等气动性能随车速、阻塞比、管道压力的变化规律，提出了管道压力、阻塞比和列车速度的组合关系。陈大伟等[10]采用三维可压缩模型研究了低真空管道超高速磁浮列车的气动特性，分析了列车气动阻力、气动升力随着管道面积、管道压力的变化规律，发现列车与管道之间的环状空间类似于拉瓦尔喷管，当列车达到临界速度时，列车尾部会出现激波。黄尊地等[11]建立了有限密闭空间的真空空气动力学三维静态和动态数值模拟模型，分析了真空管道列车外流场仿真方法的合理性，并指出列车和管道间气体的三维效应、压缩效应和非定常效应对列车外流场的影响显著。Oh等[12]研究了阻塞比、列车速度、管道长度、管道压力、管道温度等对Hyperloop列车气动阻力的影响规律，发现随着列车速度增大，列车尾部会出现强激波。Braun等[13]针对Hyperloop列车开展了列车气动外形设计及优化研究，在一定的气动升力条件下，降低了列车的气动阻力。以上研究主要针对低真空管道列车的特定气动性能开展，本文针对复杂低真空管道超高速磁浮系统，综合研究管道压力、管道面积、列车速度对其气动性能的影响规律，并初步探索低真空管道超高速磁浮气动问题系统配置方案。
1 计算模型
1.1 流体模型
由于涉及低真空下的数值模拟，须采用适当的流体模型。当管道内压力降低时，管道内的空气密度随之降低，空气变得越来越稀薄。采用克努森数（Kn）表示空气的稀薄程度，定义为分子平均自由程$ \lambda $与流动特征长度L的比值：
$$ Kn = \frac{\lambda }{L} $$ (1) 根据空气的稀薄程度，可以将空气流动分为3个领域：当$ 0.01 \leqslant Kn < 0.1 $时，空气流动处于滑移领域；当$ 0.1 \leqslant Kn < 10 $时，空气流动处于过渡领域；当$ Kn \geqslant 10 $时，空气流动处于自由分子流领域；而当$ Kn < 0.01 $时，可以认为空气流动处于连续领域，在连续领域内可采用连续介质模型描述空气流动。
温度298 K、标准大气压下，$ \lambda = 6.11 \times {10^{ - 8}}\;{\text{m}} $。本文中，低真空管道内最低压力为0.1 atm（1 atm = $1.01 \times 10^5 $ Pa），相应的分子平均自由程为$6.11 \times 10^{-7} $。流动特征长度L取为超高速磁浮列车的高度（4198 mm）。因此，对于低真空管道超高速磁浮列车（下文简称“超高速磁浮列车”）：
$$ Kn = 1.46 \times {10^{ - 8}} \ll 0.01 $$ (2) 可见，本文超高速磁浮列车周围的空气流动处于连续领域内，可以连续介质模型进行描述。
1.2 数学模型
本文中，超高速磁浮列车运行速度为600～1000 km/h，相应的马赫数为0.49～0.82，明显大于0.3，须考虑空气压缩性的影响；同时，低真空管道是封闭结构，也须考虑空气压缩性的影响。因此，可以采用三维瞬态可压缩Navier‒Stokes方程描述超高速磁浮列车流场。假设空气为理想气体，其控制方程为[14]：
$$ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}} \right)}}{{\partial {x_j}}} = 0 $$ (3) $$ \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{{\partial {\tau _{ij}}}}{{\partial {x_j}}} $$ (4) $$ \frac{{\partial (\rho e)}}{{\partial t}} + \frac{{\partial (\rho {u_j}h)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left( {K\frac{{\partial T}}{{\partial {x_j}}} + {u_i}{\tau _{ij}}} \right) $$ (5) $$ p = p\left( {\rho ,T} \right) $$ (6) 式中：ρ为密度，t为时间，xi 、xj （i = 1, 2, 3）为直角坐标分量，ui、uj分别为xi、xj方向上的速度分量，p为压力，h为焓，e为内能，K为热传导系数，T为温度，τij为黏性应力张量。
超高速磁浮列车流场是复杂的湍流流场，在进行数值模拟时考虑湍流流动。湍流模型采用SST k‒ω模型，其控制方程为[14]：
$$ \frac{\partial\left( {\rho k} \right) }{{\partial t}} + \frac{\partial\left( {\rho k{u_i}} \right) }{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k} $$ (7) $$ \begin{split}& \frac{\partial \left( {\rho \omega } \right)}{{\partial t}} + \frac{\partial \left( {\rho \omega {u_i}} \right)}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) \\ &\qquad + {G_\omega } - {Y_\omega } + {D_\omega } + {S_\omega } \end{split} $$ (8) 式中：$ k $和$ \omega $分别为湍流动能和湍流频率；湍流生成项$ {G_k} $和$ {G_\omega } $、湍流耗散项$ {Y_k} $和$ {Y_\omega } $、交叉扩散项$ {D_\omega } $均为$ k $和$ \omega $的函数；Sk 、$S_\omega $为自定义源项；$\varGamma_k、\varGamma_\omega$分别为k、$ \omega $的有效扩散率。
利用Lilly宽频带噪声源模型近似模拟超高速磁浮列车表面的偶极子声源声功率。
1.3 数值模型
图1为超高速磁浮列车几何模型，采用3车编组：头/尾车长度均为28211 mm，中车长度为24768 mm；车辆宽度为3700 mm；车辆高度为4198 mm[15]。
图2给出了超高速磁浮列车空气动力学数值计算区域，低真空管道横截面为扇形、面积为40～100 m2。为降低计算区域对超高速磁浮列车气动性能的影响，同时考虑到计算网格量及计算效率，在纵向上，列车最前端到计算区域入口的距离取360 m，列车最后端到计算区域出口的距离也取360 m；在横向上，列车位于计算区域的中部。
计算区域出入口都设置为压力远场边界与无反射边界条件。低真空管道壁面和轨道梁表面设置为滑移壁面边界条件，滑移速度与来流速度一致。超高速磁浮列车表面设置为固定壁面边界条件。
计算区域采用结构化网格进行划分。图3为部分计算区域的网格图，壁面的第一层网格高度为10−5 m，增长比为1.2，保证无量纲壁面距离y + <1，计算网格数量约为4500万。
对于管道交会工况，计算网格采用多块划分方式，每列列车周围建立一个长方形空间块。利用滑移网格来实现不同块之间的相对运动，同时利用层状网格方法维持计算网格区域的不变性。
超高速磁浮列车的发热设备主要包括悬浮电磁铁、夹层电气设备、空调室外机和长定子等，各设备分布如图4所示，各设备发热功率如表1所示。
表 1 发热设备功率Table 1 Power of heating equipment发热设备 功率 悬浮电磁铁 330 kW 导向电磁铁 120 kW 夹层电气设备 54 kW 空调室外机 120 kW 长定子 1.05/3.32/8.10 kW/m (600/800/1000 km/h) 数值计算时，流动控制方程离散采用有限体积法，湍流模型为SST k‒ω模型，空间离散格式采用Roe格式，黏性项采用二阶中心差分格式，时间离散采用LU‒SGS隐式离散方法。
2 车隧耦合气动性能分析
2.1 流场特性
在低真空管道内，气流流经超高速磁浮列车时，超高速磁浮列车与低真空管道之间形成的环状空间与拉瓦尔喷管相似。忽略超高速磁浮列车局部结构，此环状空间即可近似为一维变截面管道，管道内的空气流动符合一维定常等熵流动的特征，即具有膨胀加速或压缩减速的流动特性：收敛管道内的亚声速流动和扩张管道中的超声速流动是膨胀加速的，而扩张管道内的亚声速流动和收敛管道内的超声速流动是压缩减速的。
超高速磁浮列车在低真空管道内运行，气流流经头车流线型区域时，列车与管道之间的有效面积减小，气流不断加速，到直线段时，列车与管道之间的有效面积最小，气流速度不再增大。若此时流速小于临界速度，则尾车流线型处由于有效管道面积增大，流速减小，流场变化规律与常规工况相似；若此时流速达到临界速度（即在直线段达到声速），气流将在尾车流线型处膨胀形成激波，导致局部压力急降，尾车阻力、升力、气动噪声等迅速增大。
图5为列车速度600 km/h、管道压力0.3 atm、管道面积80 m2时，低真空管道纵向对称面上的气流流动马赫数。由图5可以看出，在超高速磁浮列车周围的管道空间内，气流全部都是亚声速气流，此时在低真空管道内，没有超声速气流和激波产生。
![]()
图 5 纵向对称面上的气流马赫数（列车速度600 km/h，管道压力0.3 atm，管道面积80 m2）Fig. 5 Mach number of airflow on the longitudinal symmetry plane (train speed: 600 km/h, tube pressure: 0.3 atm, tube area: 80 m2)继续增大超高速磁浮列车的运行速度，当达到某一临界值时，尾车附近的管道内将出现超声速气流，类似于拉瓦尔喷管喉部的气流达到临界声速，当前后压力比在某一范围内时，喷管扩张段内会产生一道正激波。如图6所示，当列车速度增大到800 km/h时，尾车处局部的气流达到了超声速，在尾车附近的管道空间内出现了一道激波，类似于拉瓦尔喷管产生管内正激波的工况。
![]()
图 6 纵向对称面上的气流马赫数（列车速度800 km/h，管道压力0.3 atm，管道面积80 m2）Fig. 6 Mach number of airflow on the longitudinal symmetry plane (train speed: 800 km/h, tube pressure: 0.3 atm, tube area: 80 m2)列车运行速度继续增大，尾车气流的超声速区域随之增大，激波位置不断后移，当列车运行速度达到某一临界值时，尾车处的气流全部达到超声速，类似于拉瓦尔喷管管口产生正激波的工况；列车速度继续增大，则类似于拉瓦尔喷管管外产生斜激波的工况。图7为列车速度增至1000 km/h时，管道纵向对称面上气流的马赫数，可以看出，此时尾车附近的气流已经全部达到了超声速。
![]()
图 7 纵向对称面上的气流马赫数（列车速度1000 km/h，管道压力0.3 atm，管道面积80 m2）Fig. 7 Mach number of airflow on the longitudinal symmetry plane (train speed: 1000 km/h, tube pressure: 0.3 atm, tube area: 80 m2)低真空管道内激波的产生主要与列车速度和管道面积有关。随着列车速度提高，管道面积减小，气流在流线型区域的加速明显，在直线段时速度达到当地声速，由于尾车流线型处有效管道面积增大，气流膨胀加速至超过声速，产生激波。管道面积减小，产生激波的临界速度减小。要提高临界速度，须增大管道面积：管道面积40 m2时，出现激波的临界速度约为600 km/h；管道面积80 m2时，临界速度约为800 km/h；管道面积≥100 m2时，临界速度则提高至1000 km/h。
图8给出了列车速度为600 km/h，管道面积为80 m2，管道压力分别为1.0和0.3 atm时，超高速磁浮列车头车的横截面温度分布。从图8可以看出：由于悬浮电磁铁和导向电磁铁是主要的发热设备，其温度升高。随着管道压力的降低，低真空管道内的空气对流换热能力下降，发热设备周围的温度梯度增大，从而导致悬浮电磁铁及导向电磁铁的温升进一步增大。
2.2 气动载荷特性
通过计算分析超高速磁浮列车的气动阻力、气动升力、气动噪声源、管道交会压力波、发热设备温度等与管道压力、管道面积及列车速度的关系，聚焦牵引能力−噪声−能耗问题，初步探索低真空管道超高速磁浮系统“管道压力−管道面积−列车速度”匹配特性。
2.2.1 气动阻力
图9为列车速度600 km/h时，低真空管道内整车气动阻力与明线气动阻力的比值随管道压力及管道面积的变化规律。从图9可以看出：超高速磁浮列车的气动阻力与管道压力近似成线性关系，与管道面积近似成负幂次关系。在低真空管道内，管道压力每降低0.1 atm，整车气动阻力降低约10%。
![]()
图 9 整车气动阻力随管道压力及管道面积的变化规律Fig. 9 Variation of aerodynamic drag with tube pressure and tube area无激波时，超高速磁浮列车气动阻力与列车速度近似成平方关系；出现激波时，气动阻力迅速增大。
2.2.2 气动升力
在低真空管道内，超高速磁浮列车尾车气动升力最大，而头车和中间车气动升力较小。当尾车流线型区域产生激波时，其表面压力急剧降低，气动升力迅速增大。
图10为列车速度600 km/h时，低真空管道内超高速磁浮列车尾车气动升力与明线尾车气动升力的比值随管道压力及管道面积的变化规律。从图10可以看出：超高速磁浮列车的气动升力与管道压力近似成线性关系，与管道面积近似成负幂次关系。低真空管道内，管道压力每降低0.1 atm，尾车气动升力降低约10%。
![]()
图 10 尾车气动升力随管道压力及管道面积的变化规律Fig. 10 Variation of aerodynamic lift with tube pressure and tube area无激波时，超高速磁浮列车尾车气动升力与列车速度近似成平方关系；出现激波时，尾车气动升力迅速增大。
2.2.3 气动噪声源
图11为列车速度600 km/h时，低真空管道内偶极子声源与明线偶极子声源声压级的差值随管道压力及管道面积的变化规律。从图11可以看出：超高速磁浮列车偶极子声源声压级与不超过0.3 atm的管道压力近似成对数关系，与0.3 atm以上的管道压力近似成线性关系；与管道面积近似成线性关系。
![]()
图 11 偶极子声源声压级差值随管道压力及管道面积的变化规律Fig. 11 Variation of sound pressure level difference of dipole sound source with tube pressure and tube area无激波时，超高速磁浮列车气动噪声的主要声源为偶极子声源；出现激波时，车尾四极子声源声压级迅速增大，超过偶极子声源，成为主要声源。
2.2.4 管道交会压力波
管道内交会压力变化规律与明线交会相似，由于列车始终在管道内高速运行，没有明显的隧道压缩波与膨胀波，压力波峰峰值仅存在于交会期间。
图12为列车速度600 km/h时，超高速磁浮列车在低真空管道内交会的压力波峰峰值随着管道压力及管道面积的变化规律。从图12可以看出：超高速磁浮列车管道交会压力波峰峰值与管道压力近似成线性关系，与管道面积近似成负幂次关系。低真空管道内，真空度每降低0.1 atm，管道交会压力波峰值降低约2655 Pa。
![]()
图 12 管道交会压力波随管道压力及管道面积的变化规律Fig. 12 Variation of tube crossing pressure wave with tube pressure and tube area无激波时，超高速磁浮列车管道交会压力波峰峰值与列车速度近似成平方关系；出现激波时，管道交会压力波峰峰值迅速增大。
2.2.5 发热设备温度
在低真空管道内，随着管道压力降低，低真空下空气对流传热能力下降，发热设备周围温度梯度变大，温升变得显著。
图13为列车速度600 km/h时，低真空管道内超高速磁浮列车悬浮电磁铁平均温度与明线悬浮电磁铁平均温度的差值随管道压力及管道面积的变化规律。由图13可以看出：超高速磁浮列车的电磁铁平均温度与管道压力近似成负幂次关系，与管道面积近似成线性关系。随着管道压力降低，电磁铁平均温度快速升高，而管道面积对电磁铁平均温度的影响相对较小。
![]()
图 13 悬浮电磁铁平均温度差值随管道压力及管道面积的变化规律Fig. 13 Variation of electromagnet average temperature with tube pressure and tube area在0.3 atm的管道压力下，当列车速度为600 km/h时，悬浮电磁铁平均温度已超过许用值约12 ℃。随着列车速度提升，空气对流换热能力提升，但长定子的发热功率呈幂次增大，导致电磁铁温度进一步升高。当列车速度为1000 km/h时，悬浮电磁铁平均温度超过许用值约46 ℃。
3 典型场景工程化初探
管道压力、管道面积、列车速度是影响低真空管道超高速磁浮列车气动性能的关键参数。为此，针对典型的管道压力（1.0、0.3 atm）、管道面积（单线40 m2、双线100 m2）和列车速度（600、1000 km/h）场景，根据气动性能计算结果初步探讨低真空管道超高速磁浮列车的工程可行性。
1）管道常压‒列车速度600 km/h
采用100 m2双线管道，与常压明线600 km/h运行工况相比，气动阻力与升力约为明线的1.6与1.7倍，现有的超高速磁浮列车牵引能力可满足要求。气动噪声源声压级增大2 dB，压力波峰峰值25 kPa。通过开展超高速磁浮列车气动升力控制优化，并采取降噪措施，可以满足运行要求。
2）管道压力0.3 atm‒列车速度600 km/h
采用40 m2单线管道，与常压明线600 km/h运行工况相比，气动阻力与升力约为明线的2.6与2.9倍，须提升现有的超高速磁浮列车牵引能力。气动噪声源声压级增大2.8 dB；车辆气密强度为±（50～70） kPa。悬浮电磁铁平均温度超过许用值约6 ℃，设备散热虽存在一定挑战，但具备工程可行性。
采用100 m2双线管道，与常压明线600 km/h运行工况相比，气动阻力与升力约为明线的0.5与0.4倍，现有的超高速磁浮列车牵引能力充裕。气动噪声源声压级相当，气密强度为±（50～70） kPa。悬浮电磁铁平均温度超过许用值约15 ℃，设备散热存在问题，工程可行性存在一定挑战。
3）管道压力0.3 atm‒列车速度1000 km/h
采用100 m2双线隧道，与常压明线600 km/h运行工况相比，气动阻力与升力约为明线的3.9与1.5倍，须大幅提升现有超高速磁浮列车牵引能力。气动噪声源声压级增大10.4 dB，气密强度为±（50～70） kPa。悬浮电磁铁平均温度超过许用值约46 ℃，工程可行性挑战较大，须重点解决设备散热问题。如继续降低管道压力，气密强度与设备散热设计难度将进一步加大。
4 结 论
本文建立了低真空管道超高速磁浮交通系统空气动力学数值模拟方法，研究了管道压力、管道面积和列车速度对低真空管道超高速磁浮列车空气动力学性能的影响规律，并针对典型场景进行了初步工程化探讨，主要结论如下：
1）低真空管道内的超高速磁浮列车绕流流动符合一维定常等熵流动的特征，即具有膨胀加速/压缩减速的流动特性。
2）低真空管道内激波的产生主要与列车速度和管道面积有关。激波出现在尾车流线型处，会导致局部压力急降，尾车阻力、升力、气动噪声等迅速增大。
3）随着管道压力的降低，超高速磁浮列车的气动阻力、气动升力、气动噪声源等性能得到较大改善，但由于空气对流换热能力降低，设备散热问题变得显著，须特别关注低真空下的设备散热问题，初步考虑从管道通风散热、液冷等方面开展低真空散热问题研究。
4）当列车速度为600 km/h时，管道常压‒管道面积100 m2、管道压力0.3 atm‒管道面积40 m2具备工程可行性，而管道压力0.3 atm‒管道面积100 m2的工程可行性存在一定挑战。当列车速度为1000 km/h时，管道压力0.3 atm‒管道面积100 m2的工程可行性挑战较大。若进一步降低管道压力，设备散热与气密强度设计难度将进一步加大。
低真空管道是一种有吸引力的技术，可有效解决列车超高速运行时的气动阻力、气动升力、气动噪声等问题。然而，随着列车速度提升，管道内激波效应增强，还有大量问题须深入研究，如低真空管道内超高速磁浮列车多尺度局部激波效应、车隧耦合气动性能、车隧系统热平衡、激波噪声等。除气动相关问题外，列车追踪与管隧控制匹配、管隧内低压绝缘、管隧‒车辆气密指数、管隧升降压与人体耐受、客室生命保持、救援逃生技术等也须进行深入探讨。
-
![]()
图 5 纵向对称面上的气流马赫数（列车速度600 km/h，管道压力0.3 atm，管道面积80 m2）
Fig. 5 Mach number of airflow on the longitudinal symmetry plane (train speed: 600 km/h, tube pressure: 0.3 atm, tube area: 80 m2)
![]()
图 6 纵向对称面上的气流马赫数（列车速度800 km/h，管道压力0.3 atm，管道面积80 m2）
Fig. 6 Mach number of airflow on the longitudinal symmetry plane (train speed: 800 km/h, tube pressure: 0.3 atm, tube area: 80 m2)
![]()
图 7 纵向对称面上的气流马赫数（列车速度1000 km/h，管道压力0.3 atm，管道面积80 m2）
Fig. 7 Mach number of airflow on the longitudinal symmetry plane (train speed: 1000 km/h, tube pressure: 0.3 atm, tube area: 80 m2)
![]()
图 9 整车气动阻力随管道压力及管道面积的变化规律
Fig. 9 Variation of aerodynamic drag with tube pressure and tube area
![]()
图 10 尾车气动升力随管道压力及管道面积的变化规律
Fig. 10 Variation of aerodynamic lift with tube pressure and tube area
![]()
图 11 偶极子声源声压级差值随管道压力及管道面积的变化规律
Fig. 11 Variation of sound pressure level difference of dipole sound source with tube pressure and tube area
![]()
图 12 管道交会压力波随管道压力及管道面积的变化规律
Fig. 12 Variation of tube crossing pressure wave with tube pressure and tube area
![]()
图 13 悬浮电磁铁平均温度差值随管道压力及管道面积的变化规律
Fig. 13 Variation of electromagnet average temperature with tube pressure and tube area
表 1 发热设备功率
Table 1 Power of heating equipment
发热设备 功率 悬浮电磁铁 330 kW 导向电磁铁 120 kW 夹层电气设备 54 kW 空调室外机 120 kW 长定子 1.05/3.32/8.10 kW/m (600/800/1000 km/h) 
下载: 导出CSV
-
[1] 邓自刚, 张勇, 王博, 等. 真空管道运输系统发展现状及展望[J]. 西南交通大学学报, 2019, 54(5): 1063–1072. DOI: 10.3969/j.issn.0258-2724.20180204 DENG Z G, ZHANG Y, WANG B, et al. Present situation and prospect of evacuated tube transportation system[J]. Journal of Southwest Jiaotong University, 2019, 54(5): 1063–1072. doi: 10.3969/j.issn.0258-2724.20180204
[2] 沈志云. 关于我国发展真空管道高速交通的思考[J]. 西南交通大学学报, 2005, 40(2): 133–137. DOI: 10.3969/j.issn.0258-2724.2005.02.001 SHEN Z Y. On developing high-speed evacuated tube transportation in China[J]. Journal of Southwest Jiaotong University, 2005, 40(2): 133–137. doi: 10.3969/j.issn.0258-2724.2005.02.001
[3] DENG Z G, ZHANG W H, ZHENG J, et al. A high-temperature superconducting maglev-evacuated tube transport (HTS maglev-ETT) test system[J]. IEEE Transactions on Applied Superconductivity, 2017, 27(6): 1–8. doi: 10.1109/TASC.2017.2716842
[4] 周晓, 张殿业, 张耀平. 真空管道中阻塞比对列车空气阻力影响的数值研究[J]. 真空科学与技术学报, 2008, 28(6): 535–538. DOI: 10.3969/j.issn.1672-7126.2007.01.015 ZHOU X, ZHANG D Y, ZHANG Y P. Numerical simulation of blockage rate and aerodynamic drag of high-speed train in evacuated tube transportation[J]. Chinese Journal of Vacuum Science and Technology, 2008, 28(6): 535–538. doi: 10.3969/j.issn.1672-7126.2007.01.015
[5] 周晓. 真空管道运输高速列车空气阻力数值仿真[D]. 成都: 西南交通大学, 2008. ZHOU X. Numerical simulation on the aerodynamic drag of high-speed train of evacuated tube transportation system [D]. Chengdu: Southwest Jiaotong University, 2008.
[6] KIM T K, KIM K H, KWON H B. Aerodynamic characteristics of a tube train[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011, 99(12): 1187–1196. doi: 10.1016/j.jweia.2011.09.001
[7] 刘加利, 张继业, 张卫华. 真空管道高速列车气动特性分析[J]. 机械工程学报, 2013, 49(22): 137–143. DOI: 10.3901/JME.2013.22.137 LIU J L, ZHANG J Y, ZHANG W H. Analysis of aerodynamic characteristics of high-speed trains in the evacuated tube[J]. Journal of Mechanical Engineering, 2013, 49(22): 137–143. doi: 10.3901/JME.2013.22.137
[8] 刘加利, 张继业, 张卫华. 真空管道高速列车气动阻力及系统参数设计[J]. 真空科学与技术学报, 2014, 34(1): 10–15. DOI: 10.3969/j.issn.1672-7126.2014.01.03 LIU J L, ZHANG J Y, ZHANG W. Impacts of pressure, blockage-ratio and speed on aerodynamic drag-force of high-speed trains[J]. Chinese Journal of Vacuum Science and Technology, 2014, 34(1): 10–15. doi: 10.3969/j.issn.1672-7126.2014.01.03
[9] 刘加利, 张继业, 张卫华. 真空管道高速列车气动噪声源特性分析[J]. 真空科学与技术学报, 2013, 33(10): 1026–1031. DOI: 10.3969/j.issn.1672-7126.2013.10.14 LIU J L, ZHANG J Y, ZHANG W. Simulation of noise source for high speed train in evacuated tube[J]. Chinese Journal of Vacuum Science and Technology, 2013, 33(10): 1026–1031. doi: 10.3969/j.issn.1672-7126.2013.10.14
[10] 陈大伟, 郭迪龙. 低真空管道磁浮列车气动特性[J]. 力学研究, 2019(2): 109–117. DOI: 10.12677/ijm.2019.82013 CHEN D W, GUO D. Aerodynamic characteristics of maglev train on low evacuated tube[J]. International Journal of Mechanics Research, 2019(2): 109–117. doi: 10.12677/ijm.2019.82013
[11] 黄尊地, 梁习锋, 常宁. 真空管道交通列车外流场仿真算法分析[J]. 工程热物理学报, 2018, 39(6): 1244–1250. HUANG Z D, LIANG X F, CHANG N. Analysis on simulation algorithm for train outflow field of vacuum pipeline traffic[J]. Journal of Engineering Thermophysics, 2018, 39(6): 1244–1250.
[12] OH J S, KANG T, HAM S, et al. Numerical analysis of aerodynamic characteristics of hyperloop system[J]. Energies, 2019, 12(3): 518. doi: 10.3390/en12030518
[13] BRAUN J, SOUSA J, PEKARDAN C. Aerodynamic design and analysis of the hyperloop[J]. AIAA Journal, 2017, 55(12): 4053–4060. doi: 10.2514/1.J055634
[14] VERSTEEG H K, MALALASEKERA W. An introduction to computational fluid dynamics: the finite volume method[M]. 2nd ed. Harlow, England: Pearson Education Ltd. , 2007.
[15] 丁叁叁. 时速600 公里高速磁浮交通系统[M]. 上海: 上海科学技术出版社, 2022. -
期刊类型引用(1)
1. 王肖寒，张霆风，吴啸宇，卞立双. 基于改进CRITIC-QTM的高速磁浮列车安全性评估模型. 交通科技与经济. 2024(04): 67-74 . 
百度学术
其他类型引用(3)
计量
- 文章访问数: 279
- HTML全文浏览量: 79
- PDF下载量: 32
- 被引次数: 4
