Experimental research on the influence of turbulence intensity on boundary layer transition in Mach 3 supersonic flow
-
摘要:
针对超声速来流湍流度对转捩影响的风洞试验数据缺乏的现状，开展了马赫数3条件下不同来流湍流度对平板模型边界层转捩影响的试验研究。在中国空气动力研究与发展中心0.3 m × 0.3 m跨超声速风洞（FL–24y）内，通过改变风洞稳定段内的稳流参数，实现了来流湍流度在0.82%～1.63%范围内变化。利用干涉瑞利散射技术测量来流湍流度，利用红外热图技术测量平板模型表面温度分布，得到了来流湍流度对转捩起始和结束位置影响的试验数据。根据试验来流条件，采用γ–Reθ转捩模型对平板模型边界层转捩进行数值计算，并将计算结果与风洞试验数据进行对比。结果表明：平板模型转捩试验测量结果和数值计算结果符合较好，2种方法得到的转捩起始位置相对误差小于2%，转捩结束位置相对误差小于5%。本文试验结果可以为研究超声速来流湍流度对边界层转捩的影响规律提供数据支撑。
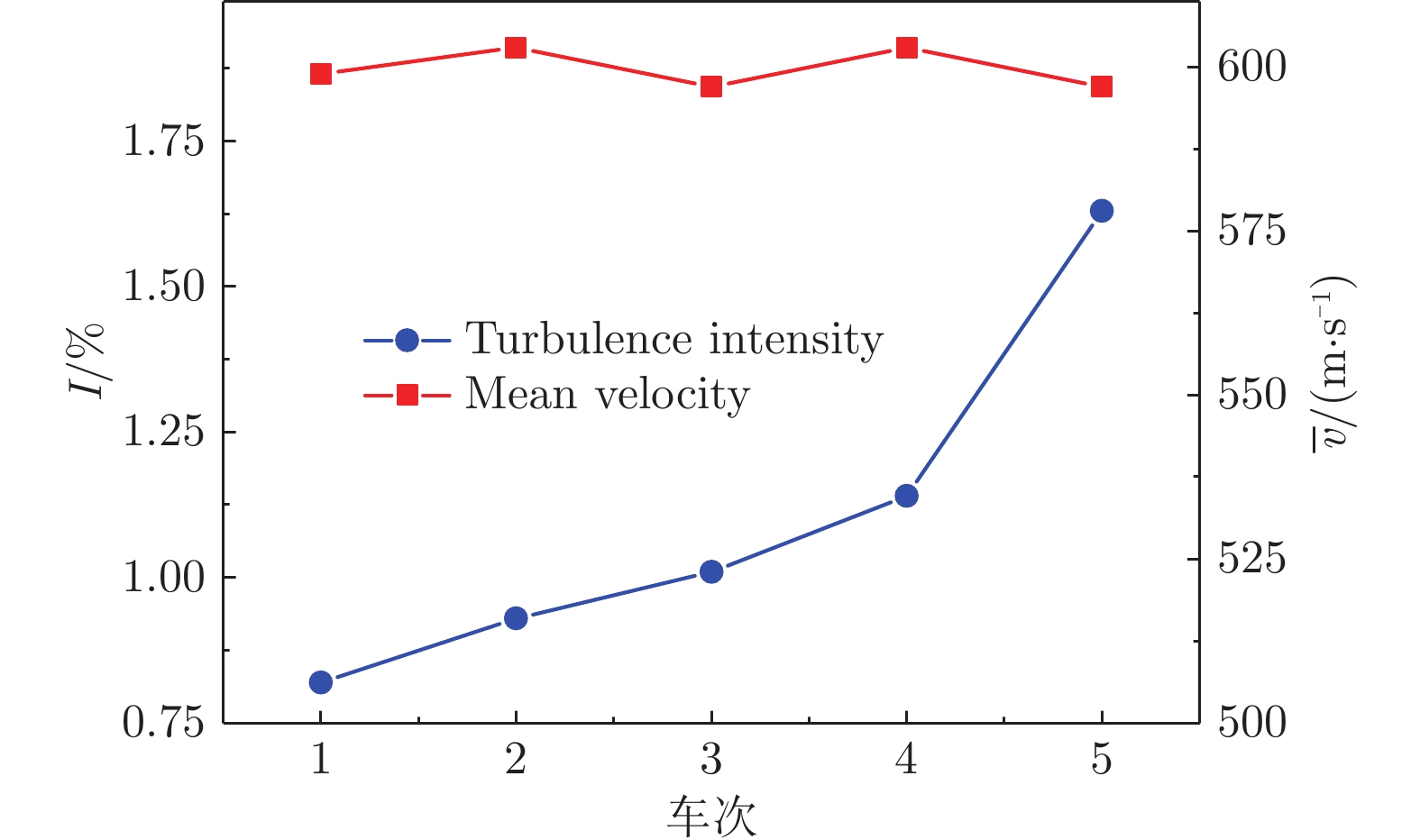
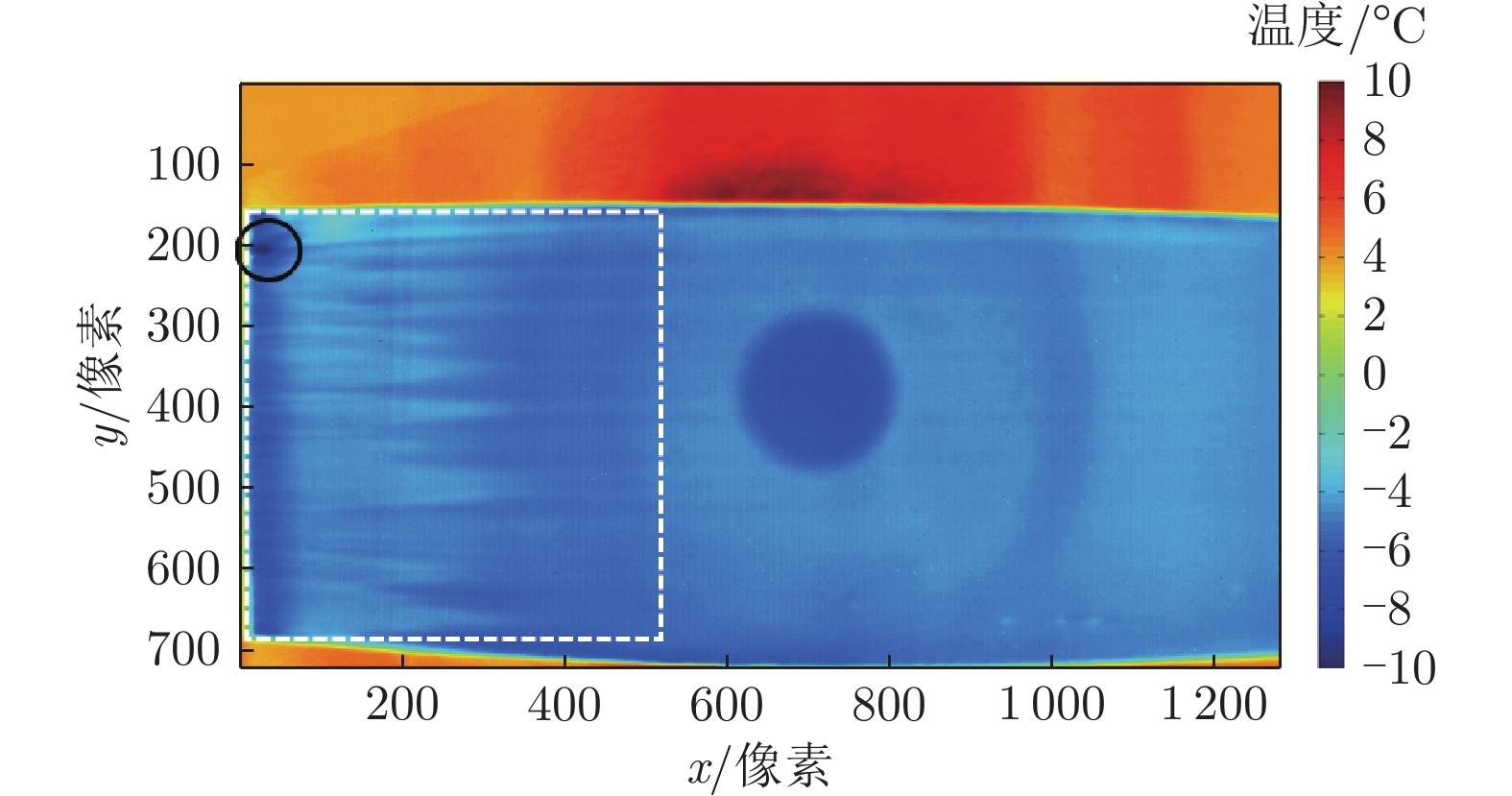
Abstract:There is still a shortage of the experimental research of boundary layer transition in compressible flows nowadays due to the difficulty in measuring the turbulence intensity. Aiming at studying the influence of the turbulence intensity on supersonic boundary layer transition, a plate model is tested in a blow-down facility (FL–24y of China Aerodynamics Research and Development Center) at Mach 3. The turbulence intensity of the flow is changed by adjusting the arrangements in the stabilization section of the wind tunnel, which covers a range from 0.82% to 1.63%. The turbulence intensity is measured by interferometric Rayleigh scattering, while the boundary layer transition is derived by infrared thermography. The CFD simulation of the plate model transition is conducted based on the γ–Reθ transition model. The results show that the transition onset position and transition end position obtained by the experiment and the simulation agree well, with the maximum relative error coefficient of 2% in the transition onset position and of 5% in the transition end position, which provides support to gain a deeper insight into the boundary layer transition mechanism in supersonic flows.
-
0 引言
研究声场与火焰的作用有着重要的工程价值和理论意义。一方面，声与火焰的耦合，将有效地组织燃烧过程，不仅强化了燃烧和传热，而且有效降低污染物的排放量，脉动燃烧技术是其典型代表；另一方面，燃烧过程中放热波动与压力脉动满足一定相位关系(瑞利准则)，将诱发热声振荡，也称为燃烧不稳定，是航空发动机、燃气轮机等重要动力装置设计与运行中所遇到的技术难题，目前为止，一直没有得到有效的解决。此外，基于流动与燃烧的关系，火焰在声场速度脉动作用下的响应行为，如放热、火焰动力学等，对于认识湍流火焰燃烧特性具有重要意义。
学术界当前主要关注声场作用下贫燃预混火焰的响应行为，代表性的思想是构建描述速度脉动与放热量变化之间关系的火焰传递函数。Durox等[1]测量了不同几何形状的火焰在声场下的火焰传递函数，根据传递函数增益和相位差2方面的数据，比较了形状不同带来的非线性响应差别，分析了几何形状对火焰动力学的影响。Balachandran等[2]实验研究了速度脉动作用下湍流预混火焰的非线性响应行为，重点关注贫燃预混火焰在大振幅声场作用下的饱和机理。Lieuwen [3]以本生型锥焰为建模对象，通过求解恒定火焰传播速度的锋面动力学方程(G-方程)，研究了火焰结构特征参量对声场作用下火焰动力学特性的影响，分析了火焰传递函数从线性响应发展为非线性响应的条件。
这些工作存在1个共同的特点：研究对象是化学当量比为1左右的预混火焰，其原因可能有2点，一是工程中燃气轮机燃烧室热声振荡的条件是贫燃预混燃烧，二是理论上描述火焰锋面动力学特性的G-方程是基于一维火焰的假设。值得注意的是，作为燃烧方式中同样重要的部分预混火焰(Partially premixed flame)，其在声场下的响应行为则很少被人关注。最近，Kim等[4]以燃气轮机燃烧室内的部分预混旋流燃烧器火焰为对象，研究了火焰在受到声场机理下的响应行为，作者认为声场作用下部分预混火焰的响应行为目前还没有被很好地认识，原因是其间的作用关系更为复杂，涉及化学、火焰动力学等方面的难点更为突出。
本文以Rijke型驻波声场为声环境，以本生型层流部分预混火焰为关注对象，借助多种测试手段，通过分析声波振荡周期内火焰的时间序列红外图像和纹影图像，揭示火焰锋面的运动过程及由此带来的热量演化行为。
1 实验系统与方法
1.1 声场发生系统
激励火焰的声环境由Rijke管实现，管内要实现激励的声场需满足以下条件：(1) Rijke管两端开口，保证管内存在一定的平均流速；(2)距管下端1/4管长处存在热源，且热源需形成一定的温度梯度；(3)保证Rijke管为良好的声保持系统，即管侧壁需完全密封，不发生声泄漏；(4) Rijke管长径比大于10。
综合考虑上述条件，设计Rijke管为两端开口的直管，管径为150mm，管长为1.6m。如图 1所示，在管内距离下端口400mm (管长的1/4)处设置一通透性较好的近似平面热源，在热源加热过程中，热对流产生的管内气体流动与热源放热过程互相作用，使声压与放热满足一定的相位关系，最终激发管内的热声振荡。这种声环境是典型的一维驻波声场[5]，图 1右侧给出了压力脉动量和速度脉动量的管内分布特征，管内中点位置压力振幅最大，速度振幅最小，管口两端则与此相反，在距管下端1/4管长位置，该点的压力振幅和速度振幅的乘积最大，最易于激发热声振荡。实验中的Rijke管采用内径150mm、壁厚4mm的碳钢管，热源由螺旋状电炉丝盘绕而成。为确保管内的流动通畅，热源支架由5根宽度为10mm的硅条按72°等角度均布排列。火焰受激励位置选择压力振幅和速度振幅相对较大的上1/4位置。声压特征通过在Rijke管侧壁上设置压力传感器提取，位置与火焰基部(燃烧器出口)对应。
理论上n阶的声压和速度波动表示为：
式中：An为压力振幅；kn=ωn/c为波数；ωn=nπc/L为n阶声场的频率；ρ0为气体密度；c是声速；L是管长。由上述公式可知，管内声场频率由本地声速和管长决定，振幅由热源的输出功率决定。实际测得的声场参数为：火焰位置的声压级(SPL)为144dB，管内声频率为111Hz，对应周期为9ms。
1.2 燃烧系统
燃烧系统的实验装置如图 2所示，甲烷和空气分别由各自供气系统送入混合腔4，流量用热式流量计测量，预混后的气体经混气管2进入烧嘴3，烧嘴由内径13mm、厚度2.5mm的不锈钢管加工而成，在没有声场作用的情况下火焰为本生型。Rijke管上方管段设置了一对平行放置的石英视窗，尺寸为90mm×400mm，供纹影法和红外摄像观测火焰。火焰的特征参量为甲烷流量1000mL/min，一次空气当量比为1.57，燃烧器内气流Re数为790，这种火焰在没有声场作用的条件下表现为双火焰(Double flame)结构。
1.3 纹影和红外拍摄系统
纹影系统的布置如图 3所示，光源处发出的光线，经过多组光学元件后，以平行光穿过Rijke管内的火焰区域，而后经一组球面反射镜汇聚于主反射镜(二)焦点位置的光刀处，纹影图像由光刀后方的相机记录, 刀口布置的方向与狭缝方向设置相同。
![]()
图 3 纹影摄像系统示意图1 光源;2 狭缝;3 小反射镜(一);4 主反射镜(一);5 石英玻璃观测 窗;6 Rijke管;7 主反射镜(二);8 小反射镜(二);9 光刀;10 照相机Fig. 3 Schlieren system拍摄火焰红外图像的CCD光谱如图 4所示，红外CCD的平均响应主要集中在近红外波段。拍摄中对整体火焰结构进行拍摄，相机至于视窗前方一定位置(物距约22cm)，另一视窗的内侧加设黑色云母板，目的是为拍摄过程提供慢反射背景，避免由于石英玻璃表面光线发生镜面反射对图像记录构成影响。
1.4 相位锁定同步拍摄系统
通过压力相位锁定的记录方式，对压力信号和红外图像进行同步触发，其系统如图 5所示。
![]()
图 5 压力信号与红外图像同步触发试验系统1 信号发生器;2 信号开关;3 红外相机;4 数据采集器;5 信号放大器;6 压力传感器;7 计算机;8 火焰观察视窗Fig. 5 Synchronous system for pressure signal and infrared image信号发生器1发出连续的TTL电平触发信号，经过信号开关2后被分为2路，一路与红外相机3的触发接口连接，另一路与数据采集器4的触发通道连接，压力传感器6与数据采集器4的其它采集通道连接。相机和数据采集器设置为单次触发模式，对应的作业方式为：由TTL电平信号触发后，仪器以自身的采样频率连续采集信号。具体的试验过程为：断开触发信号开关，分别激活红外相机和数据采集器的采集状态，当二者均为等待触发信号的状态时，闭合信号开关，TTL信号分别触发红外相机和数据采集器，实现了红外时序图像和声场压力信号的同步连续采集。为确保触发时刻足够短，红外相机和数据采集器均设置为上升沿(Rising)触发，信号发生器TTL电平信号的脉冲频率为8kHz，对应的信号周期远小于声周期。此外，红外相机的曝光时间和快门等待时间分别为0.1和10ms，数据采集器的采样频率与相机的快门时间相匹配，设置为10 kHz。
2 结果与讨论
2.1 红外和纹影技术的优势
火焰的红外图像用于描述声周期下火焰锋面的运动特性和热量演化，具有以下优势：
(1)在红外成像的物理过程上，火焰自发光红外光谱波段的光辐射具有较高的能量。火焰红外图像是由燃烧区域能够辐射红外光线的物质在CCD上成像而得到的，对于甲烷-空气的燃烧反应而言，二氧化碳和水是主要的燃烧产物，二者主要集中在红外波段[6-7]，即便是缺氧条件下形成碳烟，其辐射强度最大值也处于红外区[8]，因此，形成甲烷火焰红外图像的光线具有较大的辐射强度，图像中的平均灰度值更高，火焰区域与背景区域的对比度更大。
(2)甲烷火焰的红外图像，在物理意义上，描述了燃烧反应后产生高温产物的分布及运动。这些高温产物包围在燃烧反应区域附近，近似地表征了反应区域的运动过程。顾璠等[9]利用湍流火焰的红外图像表征大涡逆序结构的做法可说明这一点。
图 6对可见图像和红外图像进行了对比，对火焰整体分别采用单反和红外相机进行拍摄。其中，可见图像通过单反相机获得，快门时间为0.25ms，红外图像的快门时间为0.1ms。外轮廓上，二者都具有对称的尖头(Cusp)结构，数量和空间分布几乎相同，但红外图像比单反图像中的尖头结构尺寸更大，对应总体的火焰幅面更宽。因此，对于描述锋面运动过程中尖头结构的发展与变化而言，红外图像更能够突显特征结构的发展。
火焰的纹影图像则可用于描述径向的热量传递，根据Dunn-Rankin等[10]的观点，纹影信息描述了燃烧区域温度梯度较大的位置，那么火焰纹影轮廓将反映火焰前锋附近的温度梯度，由此可推导对应的热量传递。最终，火焰红外和纹影2类图像的综合信息将有效揭示甲烷火焰的热量演化过程及特征。
2.2 部分预混火焰的锋面结构
图 7给出了采用相位锁定方法拍摄的不同时刻的红外火焰图像，以此描述声场作用下部分预混火焰的锋面运动过程，其中红外相机的曝光时间为0.1ms。靠近燃烧器出口附近的火焰区域为火焰的上游，远离燃烧器出口的火焰顶部区域处为火焰的下游，对不同高度的尖头结构进行编号，在45°相位图像中由上游至下游的4层尖头依次编号为1~4号，1号和2号定义为上游，3号和4号定义为下游，以此描述锋面运动过程和结构特征。
由图 7可知，对于部分预混火焰锋面而言，各个相位下的火焰具有相似的空间结构特征，尖头结构仍是其在声激励下的典型动力学特征。火焰结构呈现层状分布，锋面上尖头的数量相对固定，连续的火焰区域存在约4对；火焰下游的幅面更宽，上游的幅面相对较窄，同时距离下游火焰顶部一定距离处均存在弧线状孤立区域。
对预混火焰的研究表明[3]，预混锋面在声场作用下存在2种运动行为，包括沿锋面法向的传播运动和沿锋面切向的对流运动。对流波是2种运动形式产生的主要锋面几何特征，对应着预混锋面上轴对称的褶皱和尖头结构。对流波的波长决定锋面切向相邻2个尖头结构之间的距离，由锋面对流运动形成；对流波的幅值决定尖头结构的明显程度，由锋面传播运动形成。
而根据扩散锋面的研究结果，声激励的作用下，锋面运动由单方向对流转为往复式的变速运动。Hardalupas Y等[11]提出的唯象模型(Phenomenological model)描述，这种往复式的变速运动将在扩散锋面的外围区域形成一系列的涡街，相邻2个涡团的卷吸作用产生了锋面上的尖头结构。因此，尖头结构的明显程度应主要与涡团的运动行为有关。
综上所述，对于部分预混火焰而言，其在声作用下的结构应为对流波和涡团2种行为的综合结果。根据对流波的运动特征，声周期的不同时刻，锋面形成脉动位移最大值的位置不同，在火焰的下游和上游区域分别形成火焰基部和顶部的变形。因此，将火焰锋面上有尖头出现的区域进行划分，4个区域的出现描述了沿锋面法向的传播运动。
2.3 火焰锋面的运动行为
如图 7所示，上半周期：前1/4周期内(0°~90°相位)，上游的1号尖头包围燃烧器外壁的面积逐渐增大，红外轮廓的幅面增加，最低点略有下降；2号尖头的尖角上翘，在空间高度略有降低；3号尖头和4号尖头之间连接部分不断减小，4号尖头在空间上绝对高度保持不变，3号尖头处于下降过程，二者之间呈现了明显的分离特征，从整体上看，火焰在该时间段内呈现下降的运动形式。随后(90°~180°相位)，90°相位下的4号尖头从火焰本体上脱离，形成了空间上孤立的红外区域，如180°相位的图像所示，这一过程描述了高温产物随火焰锋面运动最终脱离火焰本体的过程；同时，火焰基部红外轮廓的幅面逐渐减小，最低点不断上升，包围燃烧器外壁的特征消失，基部轮廓的宽度在135°后几乎接近燃烧器内径，尖头结构的尖角收缩，整个火焰呈拉伸状，运动形式表现为上升。
下半周期：锋面由向上运动转为向下运动，向上拉伸过程中逐渐减小的尖头尖角在下降过程中不断扩大，在火焰下游区域，顶部逐渐展开，幅面变宽，表现为压缩的锋面变形特征。此后(270°~360°相位)，火焰锋面再次上升，呈现出90°~180°相位时间段内的锋面运动行为。
2.4 火焰的热量演化
整个周期内火焰区域的高温产物经历了2次下降和上升的过程，同时扩散锋面上尖头结构周期性地发展。结合锋面的运动行为和尖头结构的发展过程，认为声波作用下部分预混火焰沿轴向的热量演化路径为：火焰基部处的反应热，以高温产物为载体，由上游至下游运动，沿程汇聚不同位置(各层各处的尖头结构)产生的反应热，最终从火焰顶部脱离反应区域，以较大的表面积向下游的气体传递。
图 8为拍摄的火焰时间序列纹影图像，使用的纹影系统光刀沿水平方向移动，因此图中亮暗区域及其对比度反映的是火焰区域沿水平方向的温度梯度，目的是说明径向的热量演化。总体结构上，包括内锥和外轮廓2部分，外轮廓的空间分布方式与红外图像相似，以一层一层的形式存在，但红外图像的尖头结构在纹影图像上表现为“手指状”结构。周期运动过程中，纹影图像的各层结构也存在下降和上升2个阶段，下面就上述存在的异同及反映的实际物理现象进行讨论。
由于红外图像表征的是高温产物的空间分布，而纹影图像描述的是水平方向温度梯度的分布，从热量与温度梯度的关系考虑，尖头结构作为“热源”，所形成的径向温度梯度轮廓线表现“手指状”的弧线是合理的，而“热源”一层一层分布也决定了温度梯度的分布形式。为验证上述分析的正确性，拍摄了纹影和红外信息一体化的图像。具体的做法是，以红外相机作为纹影系统的记录装置，将图 3中的狭缝2尽量关小，使穿过火焰区域平行光的亮度与火焰自身发出的红外光线亮度接近，同时设置红外相机的增益程度，提高CCD的感光度(ISO)，获得如图 9所示的图像。图 9中，明亮的区域与红外信息对应，依然表现为尖头状的特征，亮暗相间的区域为纹影信息，外轮廓线为“手指状”。“手指状”的纹影轮廓与“尖状体”位于同一高度，二者在“分层”和“配合”2个方面都比较吻合。
由此可知，声波作用下的部分预混火焰区域中，由于高温产物与周围二次空气之间存在温度差和流速差，在火焰锋面的运动过程中存在径向的热量传递，结构上分层的尖头结构形成分层的“手指状”温度梯度轮廓，升降式的运动方式使不同时刻的径向热量传递过程差别较大。
3 结论
(1)声波作用下的部分预混火焰，在结构上表现为多层对称的尖头结构，尖头结构与对流波和涡团运动有关；锋面在声波振荡的周期内经历2次上升和下降的过程，热量演化由这些结构发展过程和锋面运动方式决定。
(2)轴向热量传递：火焰基部处的反应热，以高温产物为载体，由上游至下游运动，沿程汇聚不同位置(各层尖头结构)产生的反应热，最终从火焰顶部脱离反应区域，以较大的表面积向下游的气体传递。
(3)径向热量传递：形成分层的“手指状”温度梯度轮廓，发生径向传热过程的轴向位置随相位的改变周期性变化。
-
![]()
图 3 湍流度与边界层转捩测量光路布局
Fig. 3 Optical arrangement of turbulence intensity and boundary layer transition measurement
![]()
图 5 来流湍流度和平均速度测量结果
Fig. 5 Measurement results of turbulence intensity and mean velocity
![]()
图 7 工况4边界层转捩3个车次的重复性测量结果
Fig. 7 Repeatability measurement results of three times of the boundary layer transition in condition 4
![]()
图 9 来流湍流度对壁面摩擦系数影响的计算结果
Fig. 9 The calculation results of the influence of turbulence intensity on skin fraction coefficient
表 1 试验参数
Table 1 Flow conditions
工况 烧结丝网层数 阻尼网层数 pt/kPa Tt/K 1 2 5 470 293 2 2 3 471 293 3 1 5 470 293 4 1 3 470 293 5 0 5 471 293 
下载: 导出CSV
表 2 试验结果与数值计算结果对比
Table 2 Comparison between experimental result and CFD simulation
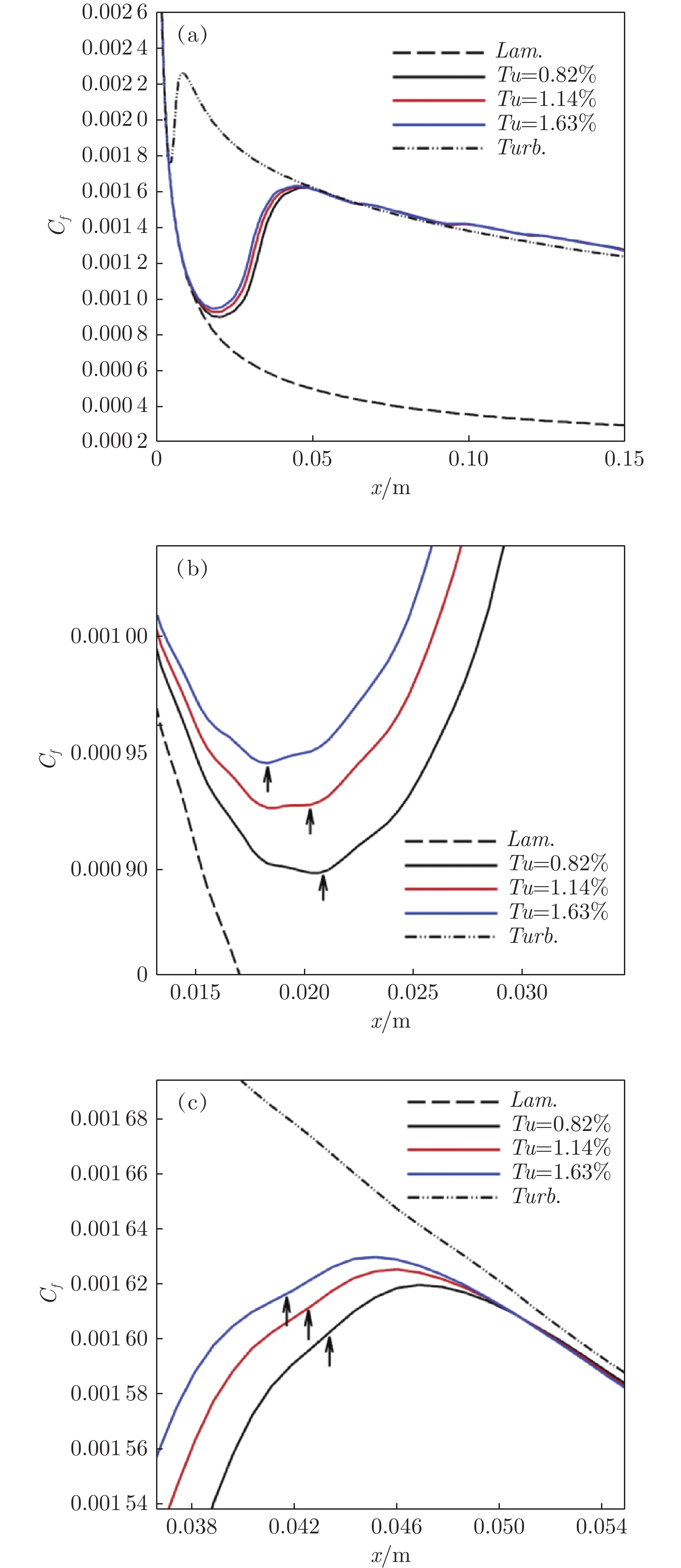
I Fonset Fend 试验值/mm 计算值/mm e 试验值/mm 计算值/mm e 0.82% 21.29 20.87 −1.97% 43.88 43.34 −1.23% 1.14% 20.54 20.26 −1.36% 41.93 42.52 1.41% 1.63% 17.92 18.27 1.95% 39.83 41.67 4.62% 注：相对误差e = （计算值 − 试验值） / 试验值 × 100%
下载: 导出CSV
-
[1] 张扣立, 常雨, 孔荣宗, 等. 温敏漆技术及其在边界层转捩测量中的应用[J]. 宇航学报, 2013, 34(6): 860–865. ZHANG K L, CHANG Y, KONG R Z, et al. Temperature sensitive paint technique and its application in measurement of boundary layer transition[J]. Journal of Astronautics, 2013, 34(6): 860–865.
[2] 刘向宏, 赖光伟, 吴杰. 高超声速边界层转捩实验综述[J]. 空气动力学学报, 2018, 36(2): 196–212. DOI: 10.7638/kqdlxxb-2018.0017 LIU X H, LAI G W, WU J. Boundary-layer transition experiments in hypersonic flow[J]. Acta Aerodynamica Sinica, 2018, 36(2): 196–212. doi: 10.7638/kqdlxxb-2018.0017
[3] 陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311–337. DOI: 10.7638/kqdlxxb-2017.0030 CHEN J Q, TU G H, ZHANG Y F, et al. Hypersnonic boundary layer transition: what we know, where shall we go[J]. Acta Aerodynamica Sinica, 2017, 35(3): 311–337. doi: 10.7638/kqdlxxb-2017.0030
[4] LANGTRY R B, MENTER F R. Correlation-based transition modeling for unstructured parallelized computa-tional fluid dynamics codes[J]. AIAA Journal, 2009, 47(12): 2894–2906. doi: 10.2514/1.42362
[5] LANGTRY R B, SENUPTA K, YEH D T, et al. Extending the γ–Reθt local correlation based transition model for crossflow effects[R]. AIAA-2015-2474, 2015. doi: 10.2514/6.2015-2474
[6] ABU-GHANNAM B J, SHAW R. Natural transition of boundary layers—the effects of turbulence, pressure gradient, and flow history[J]. Journal of Mechanical Engineering Science, 1980, 22(5): 213–228. doi: 10.1243/jmes_jour_1980_022_043_02
[7] 袁湘江, 沙心国, 时晓天, 等. 高超声速流动中噪声与湍流度的关系[J]. 航空学报, 2020, 41(11): 123791. YUAN X J, SHA X G, SHI X T, et al. Noise-turbulence relationship in hypersonic flow[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(11): 123791.
[8] SCHNEIDER S P. Flight data for boundary-layer transition at hypersonic and supersonic speeds[J]. Journal of Spacecraft and Rockets, 1999, 36(1): 8–20. doi: 10.2514/2.3428
[9] 盛森芝, 徐月亭, 袁辉靖. 热线热膜流速计[M]. 北京: 中国科学技术出版社, 2003. SHENG S Z, XU Y T, YUAN H J. Hot-wire hot-film anemometer[M]. Beijing: China Science and Technology Press, 2003.
[10] 王彦植, 陈方, 刘洪, 等. 高速流动PIV示踪粒子跟随响应特性实验研究[J]. 实验流体力学, 2018, 32(3): 94–99. DOI: 10.11729/syltlx20170160 WANG Y Z, CHEN F, LIU H, et al. Experimental investigation on response characteristics of PIV tracer particles in high speed flow[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(3): 94–99. doi: 10.11729/syltlx20170160
[11] SEASHOLTZ R G, BUGGELE A E, REEDER M F. Flow measurements based on Rayleigh scattering and Fabry-Perot interferometer[J]. Optics and Lasers in Engineering, 1997, 27(6): 543–570. doi: 10.1016/S0143-8166(96)00063-2
[12] FAGAN A F, ZAMAN K Q, ELAM K. Two-point dynamic Rayleigh scattering measurements in a free jet[C]//Proc of the 32nd AIAA Aerodynamic Measurement Technology and Ground Testing Conference. 2016. doi: 10.2514/6.2016-3109
[13] CHEN L, YANG F R, SU T, et al. High sampling-rate measurement of turbulence velocity fluctuations in Mach 1.8 Laval jet using interferometric Rayleigh scattering[J]. Chinese Physics B, 2017, 26(2): 345–348.
[14] 杨富荣, 陈力, 闫博, 等. 干涉瑞利散射测速技术在跨超声速风洞的湍流度测试应用研究[J]. 实验流体力学, 2018, 32(3): 82–86. DOI: 10.11729/syltlx20170103 YANG F R, CHEN L, YAN B, et al. Measurement of turbulence velocity fluctuations in transonic wind tunnel using Interferometric Rayleigh Scattering diagnostic technique[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(3): 82–86. doi: 10.11729/syltlx20170103
[15] 陈爱国, 陈力, 李志辉, 等. 瑞利散射测速技术在高超声速流场中应用研究[J]. 实验流体力学, 2017, 31(6): 51–55. DOI: 10.11729/syltlx20170020 CHEN A G, CHEN L, LI Z H, et al. Research on application of Rayleigh scattering velocity measurement in hypersonic low density wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2017, 31(6): 51–55. doi: 10.11729/syltlx20170020
[16] ZUCCHER S, SARIC W S. Infrared thermography investigations in transitional supersonic boundary layers[J]. Experiments in Fluids, 2008, 44(1): 145–157. doi: 10.1007/s00348-007-0384-1
[17] MERTENS C, WOLF C C, GARDNER A D, et al. Advanced infrared thermography data analysis for unsteady boundary layer transition detection[J]. Measurement Science and Technology, 2020, 31(1): 015301. doi: 10.1088/1361-6501/ab3ae2
[18] 耿子海, 何显中, 王勋年, 等. 红外成像非接触转捩测量低速风洞试验技术研究[J]. 实验流体力学, 2010, 24(6): 77–82. DOI: 10.3969/j.issn.1672-9897.2010.06.017 GENG Z H, HE X Z, WANG X N, et al. Non-intrusive test technique investigation of transition measurement with infrared image in low speed wind tunnel[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(6): 77–82. doi: 10.3969/j.issn.1672-9897.2010.06.017
[19] YOON S, JAMESON A. Lower-upper Symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations[J]. AIAA Journal, 1988, 26(9): 1025–1026. doi: 10.2514/3.10007
[20] KIM K H, KIM C, RHO O H. Methods for the accurate computations of hypersonic flows[J]. Journal of Computa-tional Physics, 2001, 174(1): 38–80. doi: 10.1006/jcph.2001.6873
[21] ANDERSON W K, THOMAS J L, VAN LEER B. Comparison of finite volume flux vector splittings for the Euler equations[J]. AIAA Journal, 1986, 24(9): 1453–1460. doi: 10.2514/3.9465
[22] 沙心国, 郭跃, 纪锋, 等. 高超声速圆锥边界层失稳条纹结构实验研究[J]. 空气动力学学报, 2020, 38(1): 143–147. DOI: 10.7638/kqdlxxb-2019.0141 SHA X G, GUO Y, JI F, et al. Experimental study on instability streak structure over a hypersonic cone[J]. Acta Aerodynamica Sinica, 2020, 38(1): 143–147. doi: 10.7638/kqdlxxb-2019.0141
-
期刊类型引用(2)
1. 李慧鑫，徐多. 被动标量湍流混合的实验研究方法与进展. 实验流体力学. 2024(04): 90-103 . 
本站查看
2. 张宇，唐湛棋，崔晓通，姜楠. 壁面局部动态扰动作用下湍流边界层多尺度相互作用. 气体物理. 2024(05): 19-29 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 331
- HTML全文浏览量: 139
- PDF下载量: 57
- 被引次数: 2
