0   引　言

在超声速/高超声速飞行过程中，飞行器轴对称前体通常存在着高度非定常的流动现象^[1-2]。为了降低高速来流对飞行器局部的气动热烧蚀，并为机组人员和机载设备提供更大空间，高超声速飞行器前体通常会进行钝化处理。但该方法存在一些缺点：钝体前方的强弓形激波会导致飞行器头部承受更大的波后总压和总温，同时过大的波阻也会降低飞行器的升阻比。因此，解决高超声速飞行器前体减阻与热防护的矛盾尤为重要。目前，针对高超声速飞行器前体减阻与热防护的主要措施有结构优化、流体注入、能量沉积等。在结构优化领域，最具代表性的措施便是在飞行器前体来流滞止点加装细长的圆柱支杆，形成“支杆–钝体”构型^[3]。加装支杆可以使流场的主要流动结构发生改变，将钝体前方的强弓形激波转化为强度较弱的斜激波，同时还可以诱导出剪切层和回流区，进一步降低钝体迎风面压力和温度。此外，在支杆前部进一步加装气动圆顶所形成的“气动支杆”构型^[4]可以在更宽的工作范围内应用。

1947年，Alexander^[5]在Langley研究中心通过风洞试验证明了支杆–钝体构型的减阻作用。1954年，Stalder和Nielsen^[6]针对支杆–钝体构型的热防护效果开展了相关研究，得到了气动加热效果与来流湍流度成正比的结论。1959年，Crawford^[7]在马赫数Ma = 6.8来流条件下对支杆开展了大量研究，建立了支杆长度对流场影响的庞大数据库，这是支杆–钝体研究的第一个里程碑。1962年，Wood^[8]探索了钝体形状对流场结构的影响，这是支杆–钝体研究的第二个里程碑。随后，Holden^[9]通过对多种支杆–钝体的组合体开展试验，将Wood^[8]的研究成果推广到了更宽的马赫数和雷诺数范围。

近年来，Ahmed^[10-11]和Huang^[12-17]等对前体激波控制方法进行了深入研究。研究结果表明，在钝体前方加装支杆可以将分离的弓形激波变成弱锥形激波，为飞行器前体减阻和热防护提供了有效解决方案。Xue等^[18]通过使用延迟脱落涡，在类似钝体前方加装支杆构型上观察到“振荡（oscillation）”与“脉动（pulsation）”2种不同的流场振荡模式，前者表现为锥形前体激波波面形状的周期性变化，后者表现为锥形前体激波与钝体前弓形激波在支杆轴向范围内的周期性移动。Kenworthy^[19]在Ma = 2.21和6.00的来流条件下对支杆–锥柱体开展了大量试验研究，并通过剪切层能量假设证明了振荡模式是通过不断变化的剪切层肩部再附准则来建立反馈的，而脉动模式则是由激波间的相互作用导致的。基于Kenworthy^[19]的试验结果，Feszty等^[20-21]采用雷诺平均（Reynolds Average Navier–Stokes, RANS）方法，证实了Kenworthy^[19]关于振荡模式的剪切层能量假设的正确性，并对压力变化沿剪切层的传播进行了修正。Qin等^[22]将振荡模式和脉动模式分别命名为第一类和第二类流场振荡模式，并对第二类流场振荡模式开展了试验研究。Sahoo等^[23-24]对支杆–钝体构型的激波不稳定性开展了试验研究，观察到钝体外形与支杆–钝体流场的激波不稳定性密切相关，流线型钝体可以有效降低激波不稳定性。

本文通过风洞试验对支杆–钝体构型的流场结构及流场振荡现象开展研究，根据瞬态结果解释流场典型结构和演化历程，基于残差收敛历程评估统计结果的可靠性，从时均流场和脉动流场两方面分析流场的振荡特性。

1   试验装置与方法

1.1   直连式风洞试验台

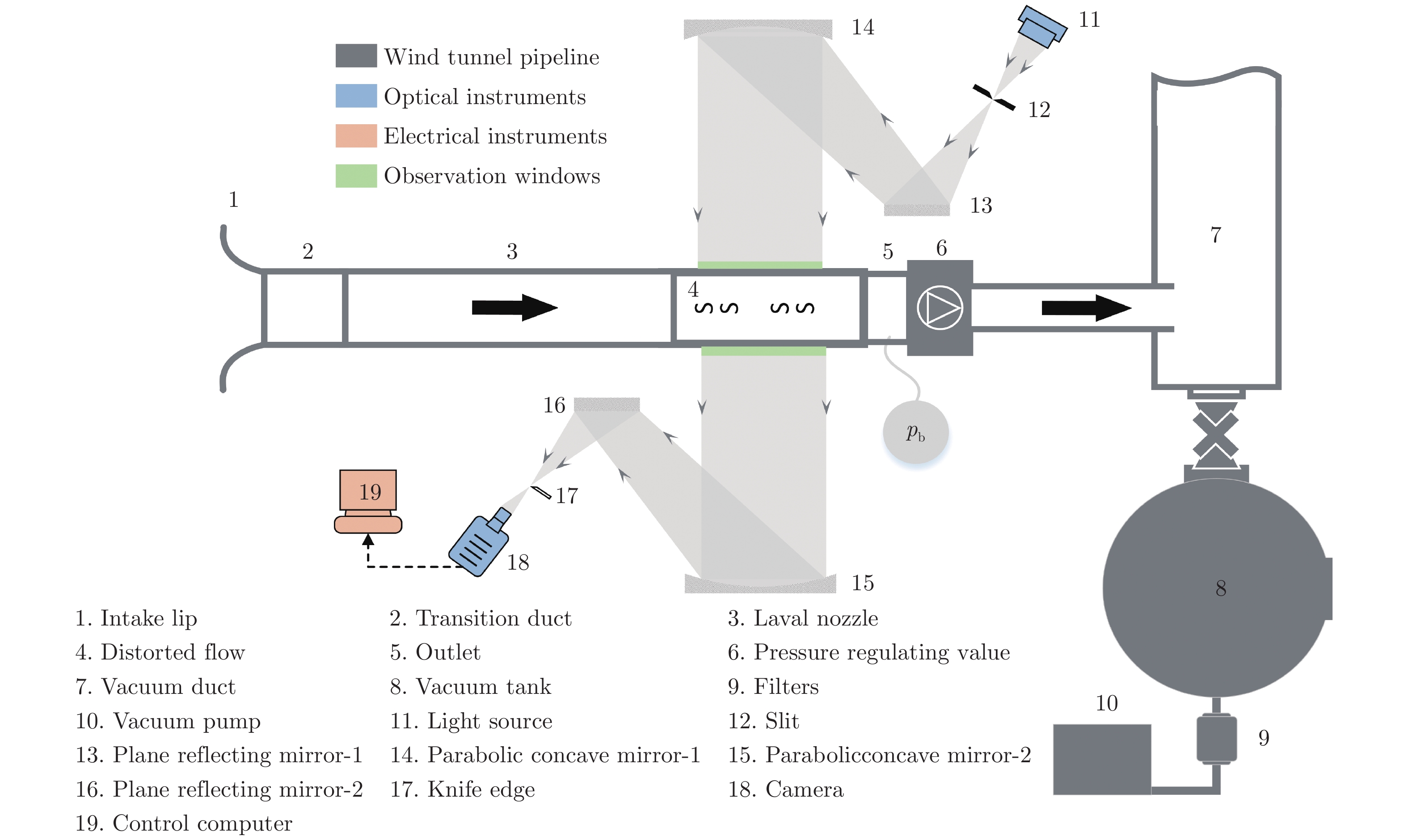
试验在南京航空航天大学航空航天结构力学及控制全国重点实验室的直连式风洞中进行，该风洞主要结构如图1所示。由于试验马赫数较低，故采用了大气进气结合真空抽吸的方式进行试验。来流气体经设备喷管加速至超声速，随后进入试验段，最后经下游管道排入容积为400 m³的真空球罐内。试验段的尺寸为400 mm × 120 mm × 160 mm，四周侧壁均为有机玻璃，以便开展高速纹影测量试验。试验条件如表1所示。

图  1  直连式风洞及“Z”字形纹影光路示意图

Fig.  1  Direct-connected wind tunnel and Z-type schlieren light path

下载: 全尺寸图片 幻灯片

表  1  试验条件

Table  1  Experimental conditions

马赫数Ma	总温Tt/K	总压pt/kPa	背压pb/kPa	雷诺数Re
2.2	305	101	8.5	2.6 × 105

下载: 导出CSV 

| 显示表格

1.2   支杆–钝体构型

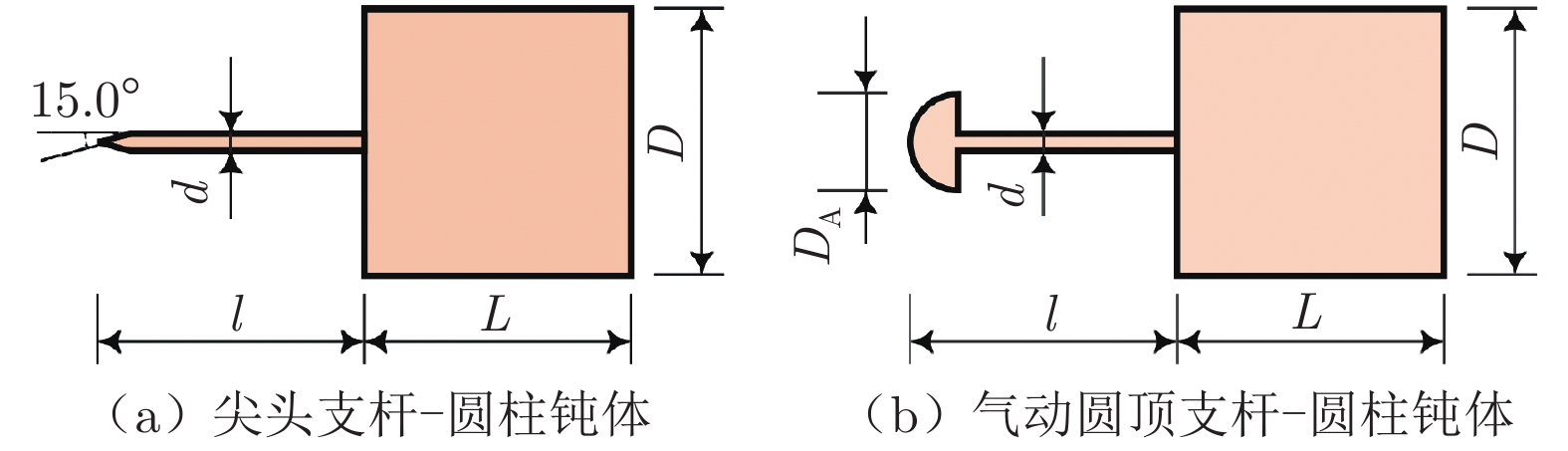
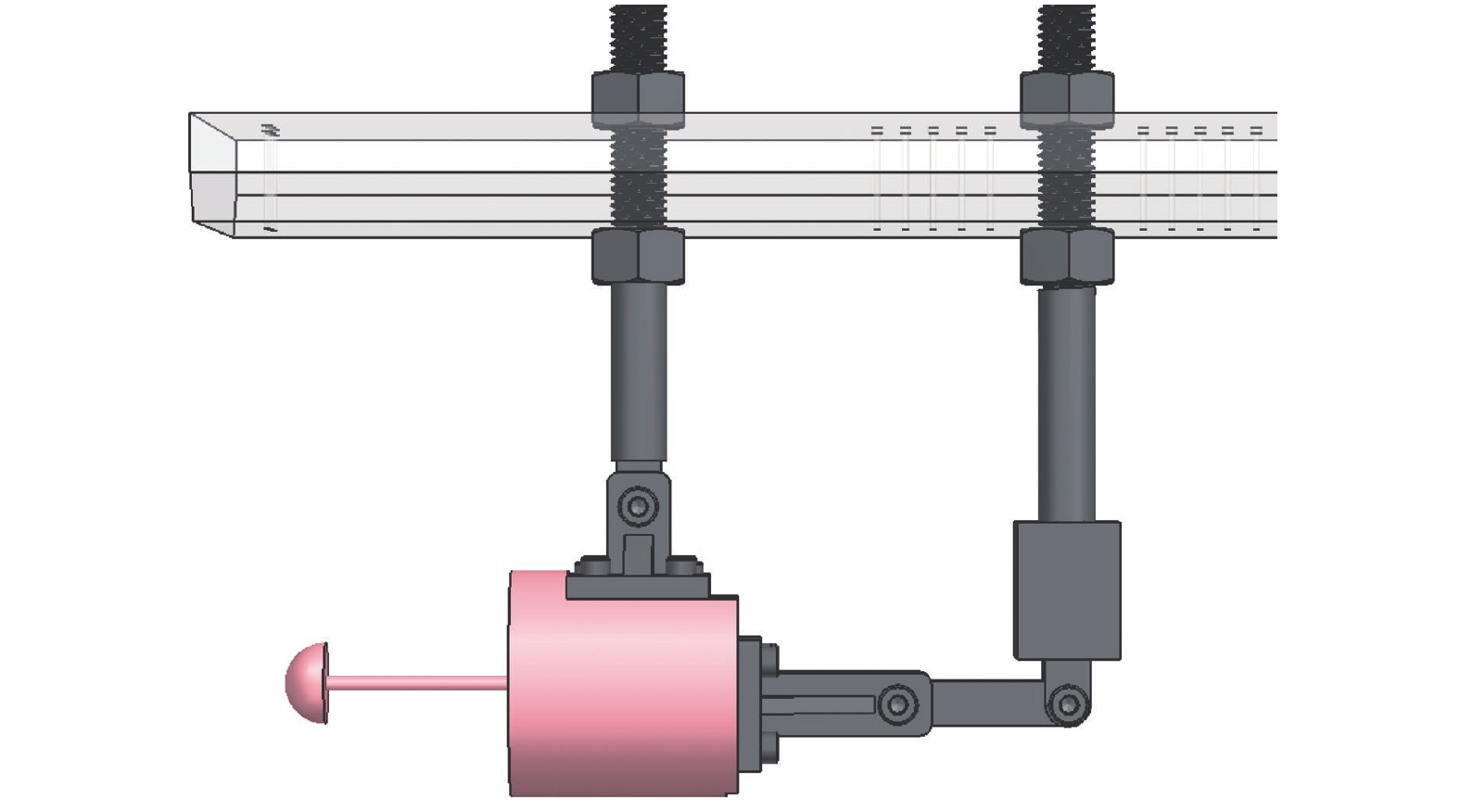
试验中使用的模型包含圆柱钝体与2组不同支杆（分别为尖头支杆与气动圆顶支杆，构型如图2所示）的组合。为避免风洞内流场出现不起动现象，将圆柱钝体直径D设置为40 mm，圆柱钝体轴向长度L = D。设置支杆长度l = D，支杆根部直径d = 0.065D，气动圆顶直径D_A = 0.36D，尖头支杆尖端倾斜角度为15°，详细尺寸见表2。支杆与钝体之间用螺纹连接，并通过支杆根部的台阶面实现定位。2组支杆–钝体构型均采用顶支撑方式，通过两根螺纹杆固定于风洞上壁面。图3给出了0°迎角下气动圆顶支杆–钝体构型的装配示意图，尖头支杆–钝体构型同理。此外，通过调节模型后方连杆的位置可以实现模型迎角的调节，有助于进一步开展变迎角对流场振荡的影响试验研究。

图  2  支杆–钝体构型

Fig.  2  Spiked cylinder configurations

下载: 全尺寸图片 幻灯片

表  2  试验构型几何参数

Table  2  Geometric parameters of experimental models

参数	参数符号	参数数值/mm
圆柱钝体直径	D	40
圆柱钝体轴向长度	L	40
支杆长度	l	40
支杆根部直径	d	2.6
气动圆顶直径	DA	14.4

下载: 导出CSV 

| 显示表格

图  3  气动圆顶支杆–钝体构型的装配示意图

Fig.  3  Assembly diagram of spiked cylinder with aerodome

下载: 全尺寸图片 幻灯片

1.3   高速纹影测量技术

本次试验采用“Z”字形纹影光路（如图1所示）。平行光垂直穿过等直试验段，并以Phantom VEO 710L科学级高速相机（图4）搭配0～100 W连续可调LED光源对非定常流场进行采集，曝光时间为1.74 μs。试验中，将刀口方向与狭缝长度方向均设置为竖直方向，调整刀口以便在焦点位置进行切割，所得纹影图像反映了被测流场在水平方向上的密度梯度变化^[25]。

图  4  Phantom VEO 710L科学级高速相机

Fig.  4  Phantom VEO 710L scientific high-speed camera

下载: 全尺寸图片 幻灯片

1.4   统计分析方法

运用数学手段对流场结构进行统计分析，可获得原始图像无法直接看出的流动特征。Combs等^[26]利用纹影图像的灰度均方根（Root Mean Square, RMS）值研究了垂直圆柱体前激波边界层干扰（Shock Wave/Boundary Layer Interaction, SWBLI）的波动。Sun等^[27-28]研究了高速相机所采集的图像集合中纹影强度统计结果的收敛性，揭示了CR–SWBLI区域的非定常特性。本文对试验中连续采集的40000张纹影图像进行时均处理和RMS处理，以获得振荡流场的时均特征和脉动特征。定义纹影时均强度I_mean和纹影脉动强度I_RMS为：

式中：I为纹影图像的强度，(i, j)为纹影图像中流向和法向的像素坐标；N为图像集合中的图像总数（N = 40000）；上标n表示图像集合中按拍摄时间顺序所选取的第n张图像。

2   结果与分析

2.1   瞬时流场结构

图5展示了采用高速纹影测量技术得到的2组支杆–钝体构型在Ma = 2.2来流条件下的典型流场结构。在尖头支杆与圆柱钝体的组合中，尖头支杆头部产生了弱锥形激波，并迅速向下游发展，圆柱钝体迎风面则产生了强烈的再附激波；弱锥形激波与再附激波在流动的下游区域存在相互干扰，影响流场的演化过程。在气动圆顶支杆与圆柱钝体的组合中，由于气动圆顶相比于尖头支杆具有更大的直径，使前体激波在法向与展向得到延展，且前体激波产生的位置向上游移动，脱离了支杆本体，在圆顶的前方形成弓形脱体激波。因此，前体激波与圆柱钝体前方产生的再附激波已无明显相交现象，二者之间的相互干扰现象有所减弱。相比于尖头支杆–钝体构型，在气动圆顶支杆–钝体构型下，圆柱钝体迎风面的复杂小尺度流场结构有所减少，再附激波呈现出较为稳定的弓形。

图  5  支杆–钝体构型的典型流场结构图

1. 前体激波 2. 再附激波

Fig.  5  Typical flow field structure of spiked cylinder configurations

下载: 全尺寸图片 幻灯片

超声速来流经过支杆与圆柱钝体的组合时会产生强烈的流场振荡现象。图6展示了2组支杆–钝体构型的振荡流场在同一时间间隔（8Δt，Δt = 45.44 μs，为相邻2帧图像的拍摄间隔；时间间隔8Δt的选取依据是尖头支杆–钝体构型的一个完整振荡周期大致为8Δt）内流场典型结构的演化历程。其中，t₁、t₂分别为2组构型的流场振荡起始阶段。在t₁～(t₁ + 4Δt)过程中，尖头支杆前部的锥形激波逐渐向下游移动，且其法向宽度逐渐向支杆轴线收缩、轮廓逐渐向内凹陷；与此同时，圆柱钝体前方的再附激波呈现出向上游移动以及向四周膨胀的趋势。在(t₁ + 4Δt)～(t₁ + 8Δt)过程中，前体激波反过来向上游移动、轮廓逐渐向外膨胀至凸形；而圆柱钝体前方的再附激波的运动趋势同样与t₁～(t₁ + 4Δt)过程相反，逐渐向下游移动，轮廓逐渐向内收缩，并紧附在钝体前部及肩部。可以看到，尖头支杆–钝体构型的振荡流场在t₁～(t₁ + 8Δt)内完成了一个完整周期的振荡，尖头支杆前部的锥形激波与圆柱钝体前方的再附激波以相反的方向沿流向前后往复移动、交替膨胀和收缩，进而造成流场的周期性振荡。与尖头支杆–钝体构型作对照分析，从气动圆顶支杆–钝体构型的流场振荡历程图可以看到，由于产生前体弓形激波的位置已经向上游移动，且激波强度也明显减弱，气动圆顶前方的弓形激波在视场中已不再清晰可辨，只能看到模糊的轮廓。由于高速来流受到气动圆顶的阻挡作用，在圆顶后方可以观察到纹影图像灰度值的升高，而此处灰度值的分界线（图中以白色虚线标出）便是分离剪切层，分离剪切层“包裹”的流动区域为回流区。尽管在气动圆顶支杆–钝体构型中前体激波和再附激波的强度均有所下降，但仍可以从激波随时间的变化中观察到流场振荡现象，只是流场振荡的一个完整周期已不再是尖头支杆–钝体构型的8Δt，振荡范围相比于尖头支杆–钝体构型也明显变小，流场的稳定性有所提高。

图  6  支杆–钝体构型在同一时间间隔内的流场振荡历程图

1. 前体激波 2. 再附激波 3. 剪切层 4. 回流区

Fig.  6  Flow field pulsating evolution in the same time interval for spiked cylinder configurations

下载: 全尺寸图片 幻灯片

2.2   统计结果的收敛性

通过考察残差值的收敛历程来评估统计结果的可靠性。I_mean、I_RMS的残差值$ \varepsilon _{{\rm{mean}}}^{} $、$ \varepsilon _{{\rm{RMS}}}^{} $由式（3）和（4）计算：

图7为2组不同的支杆–钝体构型的原始纹影图像经时均处理或RMS处理后，残差值随数据份数增加的收敛历程，其中横坐标为数据份数，纵坐标为残差值，红色曲线为时均处理结果，绿色曲线为RMS处理结果。通过残差收敛历程，可以看出2种统计方法得到的残差值均随数据份数增加而逐渐减小，这是由于随着数据份数增加，统计结果的波动会逐渐减弱，并最终趋于收敛。另外，可以观察到RMS处理结果的残差水平基本保持在时均处理结果的残差水平之上，这是由于灰度均方根值是二阶量，而均值仅为一阶量，因此RMS处理结果需要更多的样本数才能收敛到均值处理结果的残差程度。特别地，当样本数量达到10000时，2种统计结果的残差值由最初10⁰量级迅速下降至10⁻²量级，当样本数量达到40000时，2种统计结果的残差值均降至10⁻²～10⁻³之间并基本保持稳定。由此可见，当样本数目足够多时，对2组支杆–钝体构型的流场采用时均处理或RMS处理后的结果均具有良好的收敛性。

图  7  统计结果的残差收敛历程

Fig.  7  Residual convergence process of statistical results

下载: 全尺寸图片 幻灯片

2.3   时均流场结构

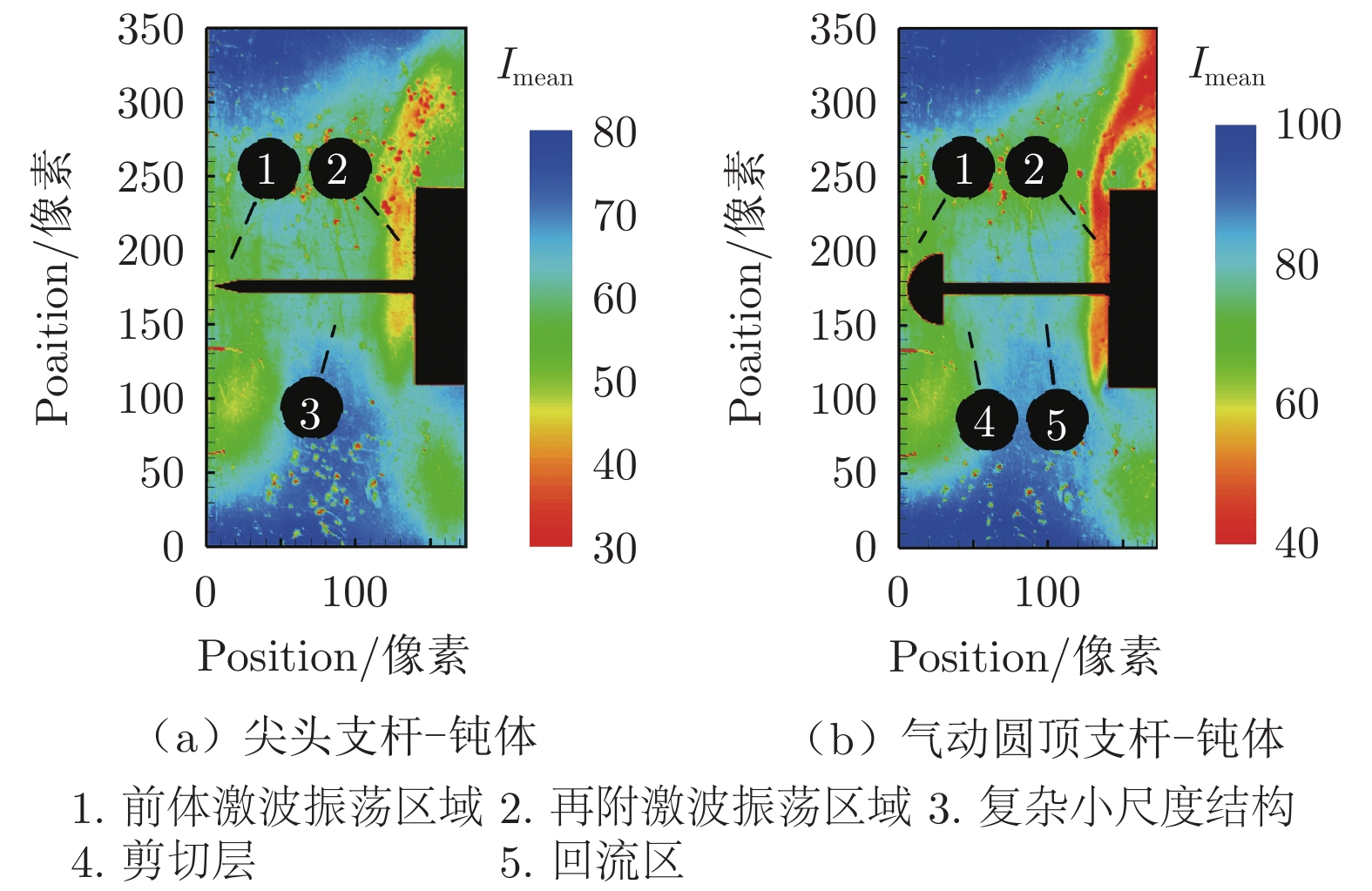
对2组支杆–钝体构型分别连续采集40000张图片并进行时均处理，结果如图8所示。值得注意的是，由于试验构型采用顶支撑的安装方式（图3），自由来流经过圆柱钝体上方的螺纹杆时会对流场本身造成一定影响，故在时均流场图中，流场结构表现出了不对称性。从尖头支杆–钝体构型的时均流场可以看出，超声速来流经过尖头支杆时，在尖头体头部位置产生强度较弱的前体激波，且该前体激波沿流向前后振荡，并不断膨胀、收缩，故在时均处理下表现出强度较低、但振荡范围较宽的特征。尽管时均处理可以消除外在轻微扰动对流场造成的影响，但是由于伴随流场振荡现象而产生的复杂小尺度结构的存在，以及前体激波与圆柱钝体前方的再附激波之间相互作用的影响，使得该构型的时均流场在支杆附近仍表现出非定常的流动特征，具体表现为时均流场云图中支杆附近流场的蓝色区域内散布有绿色不规则结构。与此同时，在流向下游110像素处，可以观察到圆柱钝体前部和肩部的再附激波，且该再附激波在流向110～120像素内表现出较低的强度，在流向下游120像素处表现出较高的强度，这表明钝体再附激波的主要运动区域集中于流向下游120像素处，只是在向上游振荡的过程中到达流向110像素附近，因此上下游时均强度有一定差别。而气动圆顶支杆–钝体构型的时均流场则表现出截然不同的流动特征：圆顶前方出现相对稳定的弓形激波，下游的再附激波紧贴圆柱钝体的前部和肩部。尖头支杆–钝体构型时均流场云图中的绿色不规则结构在气动圆顶支杆–钝体构型中已大幅减少，流动结构基本稳定，这表明随着流场振荡现象的减弱，复杂小尺度结构减少，激波间相互干扰也受到削弱。特别地，在圆顶后方流动区域出现了分离剪切层及其内部的回流区，该区域内流体在前后体压差的作用下沿流向前后振荡。另外，圆柱钝体前方再附激波的位置出现在流向下游125像素处，这表明此时钝体再附激波在向上游振荡的过程中最多只运动到流向125像素附近，之后便以一定频率沿流向前后振荡，且与尖头支杆–钝体构型相比，流场振荡范围更小，这证明了采用气动圆顶支杆比尖头支杆更能有效抑制流场中的周期性振荡现象。

图  8  支杆–钝体构型的时均流场云图

Fig.  8  Time-averaged flow field contours for spiked cylinder configurations

下载: 全尺寸图片 幻灯片

2.4   脉动流场结构

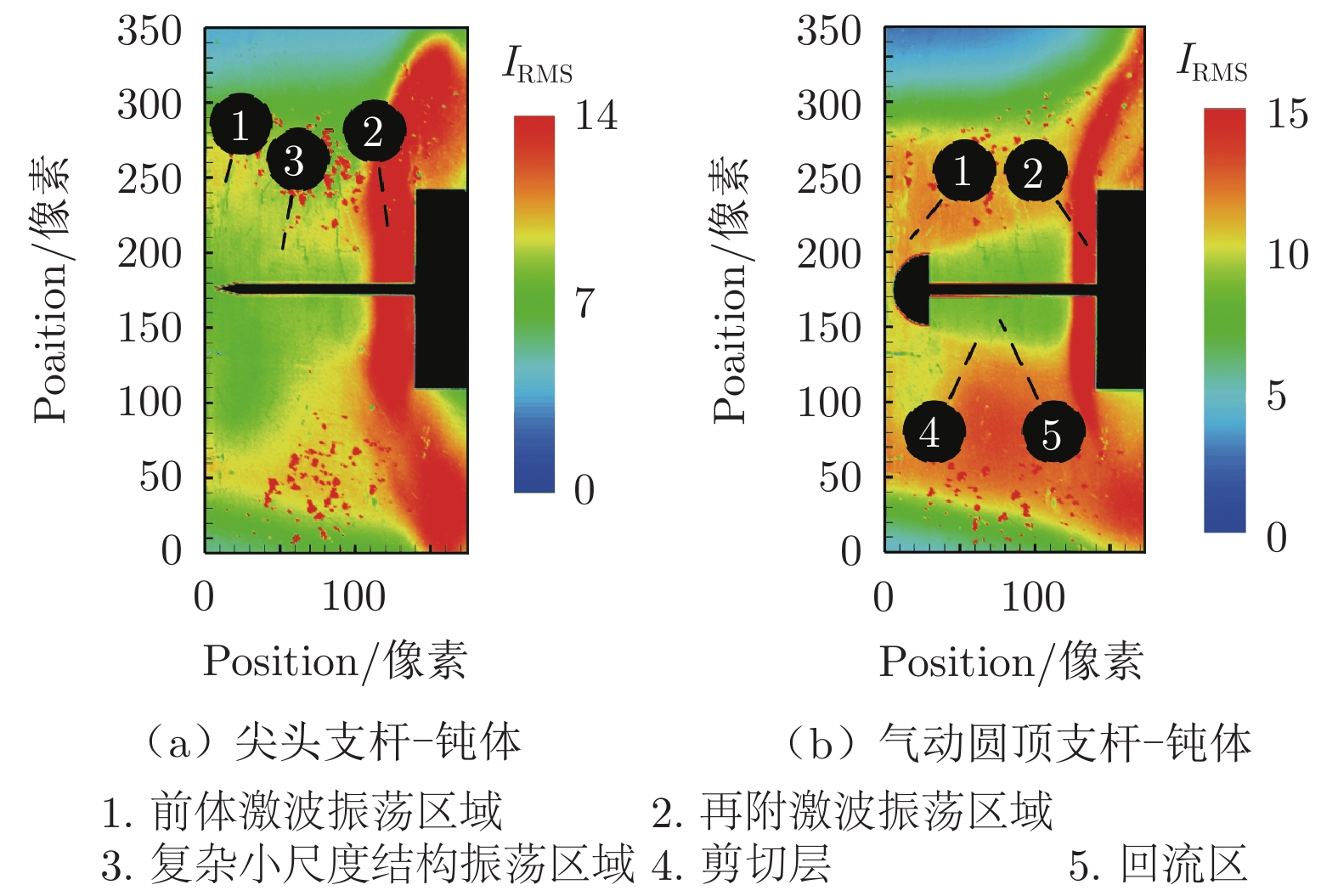
对2组不同支杆–钝体构型分别连续采集40000张图片并进行RMS处理，结果如图9所示。从尖头支杆–钝体构型的脉动流场中可以看出，尖头支杆前方的超声速来流相对稳定，而在流经支杆中部时，支杆周围区域出现流场脉动现象，这种脉动是由前体激波沿流向前后振荡造成的。同时，在流向110像素附近出现了纹影脉动强度峰值，且该峰值区域的位置与2.3节尖头支杆–钝体构型时均流场中圆柱钝体再附激波均值突变的位置吻合。在气动圆顶支杆–钝体构型的脉动流场中，可以看到沿圆顶肩部分离的剪切层及圆顶后方的回流区，其位置与时均流场中二者的位置基本一致，回流区流场的灰度均方根值较小，表明高速来流受到气动圆顶的阻挡，在圆顶后方形成了相对稳定的流动结构。同时，圆柱钝体再附激波峰值的位置仅出现在流向120像素附近，与2.3节此构型时均流场中再附激波时均值突变的位置基本一致，表明钝体前方的再附激波在沿流向周期性前后振荡时，由于采用了气动圆顶支杆，再附激波振荡的范围缩小，流场振荡现象减弱。结合脉动流场结构与2.3节的时均流场结构可以看到，2组支杆–钝体构型的时均流场与脉动流场之间均表现出相似的流动特征且存在一定相关性，二者相互印证，进一步证明了气动圆顶支杆可以对流场振荡现象进行有效的抑制。

图  9  支杆–钝体构型的流场脉动特性

Fig.  9  Flow field fluctuating characteristics of spiked cylinder configurations

下载: 全尺寸图片 幻灯片

3   结　论

本文基于南京航空航天大学航空航天结构力学及控制全国重点实验室的直连式风洞试验台，利用高速纹影测量技术对Ma = 2.2来流条件下的2组支杆–钝体构型的非定常流场进行测量。对采集的高速纹影图像采取直接观测和统计分析的方法，从瞬时流场、时均流场、脉动流场3个方面进行了分析，主要结论如下：

1）通过典型流场结构图和同一时间间隔内的流场振荡历程，对2组支杆–钝体构型的瞬时流场进行研究，发现相比于尖头支杆，采用气动圆顶支杆时的流场更稳定。

2）通过统计结果的残差收敛历程检验了2种统计方法的收敛性，计算结果表明，残差值随着样本数的增加显著下降，当样本数为40000时，残差值达到10⁻²以下，证明了2种统计方法的收敛性良好。

3）通过对原始图像进行时均处理，可以排除不稳定外在因素带来的影响。时均流场云图反映出，气动圆顶支杆–钝体构型中的前体激波比于尖头支杆–钝体构型具有更加稳定的弓形，且圆柱钝体前方再附激波的振荡范围更小，证明了采用气动圆顶支杆对流场振荡现象具有抑制作用。

4）通过对原始图像做RMS处理，可以得到流动过程中的流场脉动特性。脉动流场云图反映出2组构型的脉动强度峰值均出现在均值流场云图的均值急剧变化处，即前体激波与再附激波沿流向周期性前后振荡区域。时均流场与脉动流场相互印证，进一步证明了Ma = 2.2来流条件下的支杆–钝体流场均存在非定常流场振荡现象，且采用气动圆顶支杆对该现象具有良好的抑制作用。