The aerodynamic heating consistency study between CFD and experiment for air-breathing integrated vehicle
-
摘要:
以内外流一体化设计的飞行器为研究对象，对比分析了内外流场气动热仿真和风洞试验的一致性，定量分析了气动热仿真与风洞试验之间的差异，并研究了产生差异的原因。气动热仿真采用有限体积法求解Navier−Stokes方程，湍流模型为SA，空间格式为Roe的FDS，时间格式为LU−SGS。在FD−20a激波风洞中开展风洞试验，来流马赫数Ma∞ = 6，单位雷诺数ReL = 1.14 × 107～2.98 × 107 m−1，迎角α = 0°～8°。仿真与试验的对比结果表明：沿流向流动干扰复杂程度增大，热流模拟一致性降低；压缩面流动以附着流和小分离为主，仿真与试验一致性较好，平均差异约22.3%；在分离与激波边界层干扰等作用下，与压缩面相比，内流的仿真与试验差异增大，其中喉道平均差异约43.5%，隔离段平均差异约31.8%。受Edney型激波干扰的作用，唇口的仿真与试验在三维空间分布上的最大差异达到100%。从网格、数值方法、非定常特性和不确定度评估等方面，归纳总结了沿流向气动热仿真与试验差异增大的原因。
Abstract:In order to improve the accuracy of simulation and obtain the aerodynamic heating consistency of the prediction method for the typical integrated design of the aircraft forebody model, experiments were carried out at FD−20a shock tunnel under the condition of Ma∞ = 6, ReL = 1.14 × 107～2.98 × 107 m−1, α = 0°～8°. Numerical simulations were applied through the compressible Navier−Stokes equation implemented with the finite volume method, Roe’s flux difference splitting scheme, LU−SGS spatial method and Spalart–Allmaras (SA) turbulence model. Simulation results were compared with the experimental data to validate the prediction methods. Results show that with the increase of the complexity and disturbance intensity, the heat flux consistency decreases. The compression surface flow was dominated by the attached flow and small separation, where relative good consistency was found between the simulation and experimental data with the average difference being about 22.3%. The throat boundary layer was interfered by shock waves, and 43.5% difference was found between the heat flux simulation and experimental data. The heat flux difference in the isolation section increased to 31.8%. When the oblique shock impinged on the subsonic part of the bow shock and three dimensional flow patterns were obvious, the difference of heat flux reached the maximum of around 100% in three dimensional areas. Mesh, simulation methods and unsteady characteristics are concluded as the reasons for heat flux consistency decreasing along the airflow.
-
0 引 言
内外流一体化飞行器是机体与动力系统一体化设计的飞行器，其主要设计思路在于飞行器前体既是进气道预压缩面，又是飞行器的基本构型[1]。根据压缩形式的不同，前体可分为二元压缩、三维曲面压缩等构型。在各种压缩形式下，前体激波压缩气流，并与进气道前缘激波相互耦合，以确保足够的流量捕获能力。内外流一体化飞行器具有高马赫数下激波相交、分离、再附等复杂流动特征，激波后温度迅速升高，同时高压射流撞击唇口前缘，出现温度极高的气动热环境，对飞行安全造成负面影响[2-3]。
近年来的高速飞行器内外流场研究多基于分区模拟、局部精细化处理的思路，通过压缩拐角[4-5]、后掠圆柱[6-8]、钝化V形前缘[9-10]等模型取得了丰富的试验数据，总结形成了适用于各类条件的改进数值方法、湍流模型和网格雷诺数[11-13]，使得干扰严重的局部区域气动热预示精度达到20%～30%，其他无干扰区域气动热预示精度达到15%，为进一步认识内外流场流动机理和热环境设计提供了重要支撑。
目前，宽马赫数飞行与低马赫数起动等设计需求逐渐凸显，内外流一体化耦合程度提升。来流经过前体多道激波后，干扰区近壁面流场参数分布及边界层特征均发生了变化，干扰区之间的气动热影响不能忽略[14-17]。因此，有必要深入分析研究内外流一体化气动热仿真与试验的一致性，以量化仿真方法对飞行器真实气动热的预示精度。
本文在气动热数值模拟方法及热流测量的基础上，开展内外流一体化气动热数值模拟，开展多个状态下的激波风洞试验，获得热流分布和压力分布试验数据以及激波干扰纹影图像。通过量化仿真和试验数据的差异，初步评估内外流场气动热预示精度，为飞行器精细化热设计提供支撑。
1 试验设计
为研究气动热仿真与试验的一致性，本文自主设计了一种内外流一体化飞行器模型。参考X–51A飞行器前体外形，压缩面为“初始楔 + 等熵压缩”二元曲面构型，曲面沿展向呈凹形。构造沿展向的压力梯度，以此减弱前体横向溢流，确保三维效应下的压缩效率。试验模型总长约1 m，包含飞行器前体、喉道与隔离段等内外流一体化部件，其中隔离段为长矩形，喉道与压缩面以圆弧平滑过渡方式连接。如图1所示，压缩面相对于水平面的物面角分别为δ1、δ2、δ3。在模型上的关键位置布置热流测点24个（图中红点）、压力测点14个。试验模型坐标原点位于头部前缘，x轴正方向与来流方向相同，y轴沿高度方向，z轴沿展向，H为模型总高度，L为模型总长度。
![]()
图 1 内外流一体化气动热试验模型中心截面及热流测点位置示意图Fig. 1 Illustration of symmetry surface for integrated forebody experimental model and heat flux sensor positions测热试验在中国空气动力技术研究院FD‒20a激波风洞（喷管出口直径1 m，有效运行时间5～15 ms）中进行。为解决小尺寸前缘（唇口前缘半径1 mm）热流测量不准确的问题，唇口部位采用一体化型面热流传感器，将薄膜电阻温度计与模型作一体化设计，热流测点沿展向分布，共计7个。薄膜电阻温度计经传感器热物性参数标定，大面积区域热流测量允许的重复性误差为10%，复杂干扰区域为20%。对热流作无量纲化处理，将相同流场条件下同一尺寸头部前缘驻点的热流作为参考值qref，无量纲热流记为q/qref。
选取名义马赫数6（实际Ma∞ = 5.95）的2个典型流场作为试验流场，单位雷诺数ReL为1.14 × 107 m−1、2.98 × 107 m−1，试验迎角α为0°～8°。具体如表1所示。
表 1 风洞模拟流场参数表Table 1 Experimental flow field parameter试验编号 前室
总温/K前室
总压/MPaMa∞ ReL α/(°) 1 773 2.77 5.95 1.14 × 107 0 2 773 2.77 5.95 1.14 × 107 4 3 773 2.77 5.95 1.14 × 107 6 4 773 2.77 5.95 1.14 × 107 8 5 582 4.51 5.95 2.98 × 107 0 6 582 4.51 5.95 2.98 × 107 4 7 582 4.51 5.95 2.98 × 107 6 8 582 4.51 5.95 2.98 × 107 8 2 数值模拟
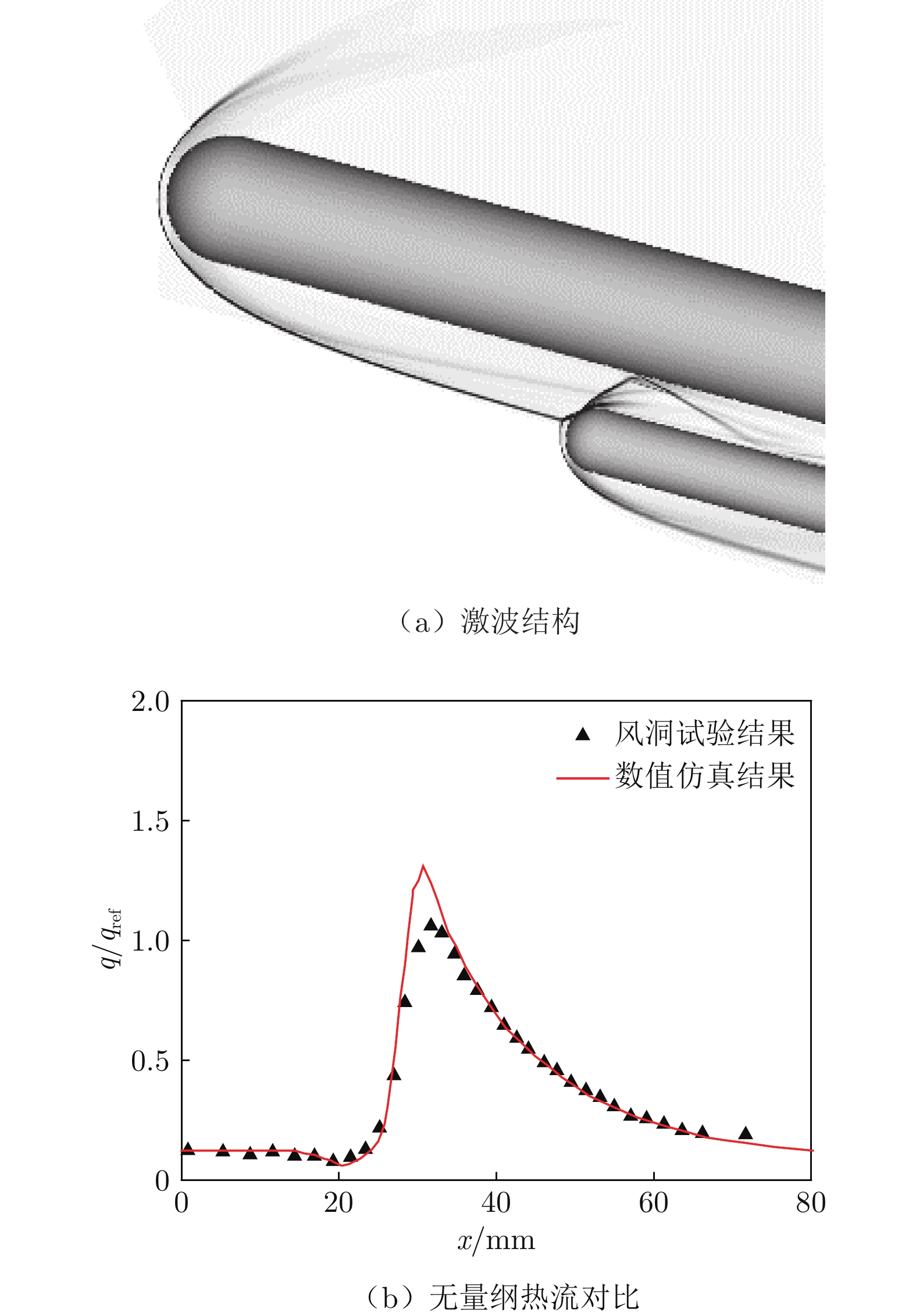
采用有限体积法求解Navier‒Stokes方程，黏性通量通过中心差分进行离散，无黏通量的空间离散格式为Roe的FDS格式，时间格式为LU–SGS格式，湍流模型为SA模型。本文基于上述数值方法和湍流模型，对日本国家航空航天实验室（National Aerospace Laboratory of Japan, NAL）高超声速风洞测热试验模型[18]进行了数值模拟，并与试验数据进行了对比。对比结果表明，在来流马赫数Ma∞ = 9.58、单位雷诺数ReL = 2 × 106 m−1、总压pt = 2.5 MPa条件下，本文的数值方法清晰捕捉到了图2（a）下方球头部类似Edney第三类干扰的热流峰值，如图2所示。
![]()
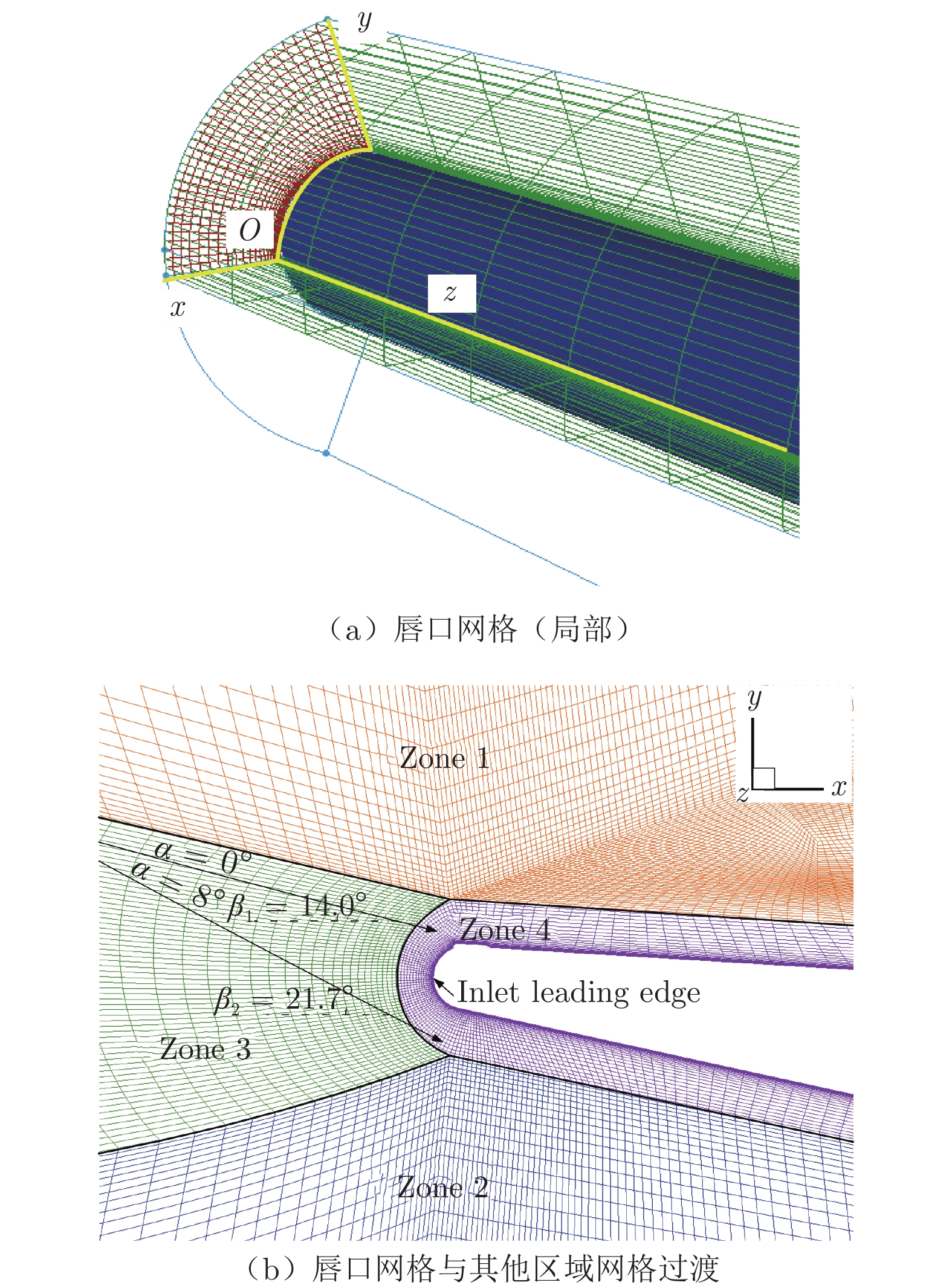
图 2 气动热仿真数据与NAL HWT模型试验数据对比Fig. 2 Comparison of non-dimensional heat flux with NAL HWT experiment interaction area在网格处理方面，针对半径为1 mm的前缘驻点，考察了第一层法向网格高度降低时的热流相对增量，研究了法向网格变化对壁面热流的影响。计算条件选择表1中典型试验条件（Ma∞ = 5.95，α = 0°，静温T = 95.6 K，静压p =
1846.9 Pa）。第一层法向网格高度由0.010 mm降至0.005 mm，保持网格延伸率1.05不变，对圆柱形前缘热流的大小及分布规律不会产生影响[19]。在保证热流模拟精度的前提下，减小网格量可以提高计算效率，因此唇口壁面第一层法向网格高度设置为0.010 mm。唇口网格（局部）、唇口网格及其他各区域的网格拓扑结构如图3所示（β1和β2分别为迎角0°和8°下的激波角）。来流斜激波主要位于Zone 3，整体的网格拓扑布局一定程度上能够保证干扰区流场网格的密度，也兼顾了其他区域与唇口网格的过渡。3 仿真与试验一致性指标
将仿真与试验的一致性指标定义为同一来流条件下仿真数据、试验数据的差值与试验数据的比值：
$$ e =|q_{{\rm{sim}}}− q_{\exp}|/q_{\exp} $$ (1) 式中：e表示衡量仿真与试验差异的参数，qsim为热流的仿真计算值，qexp为3次测热试验数据的算术平均值[20]。在仿真前处理过程中，固化壁面法向网格高度，确保局部热流计算数据重复度较高，使获得的热流计算数据能够代表不同网格条件下的平均值。
4 结果分析
4.1 唇口
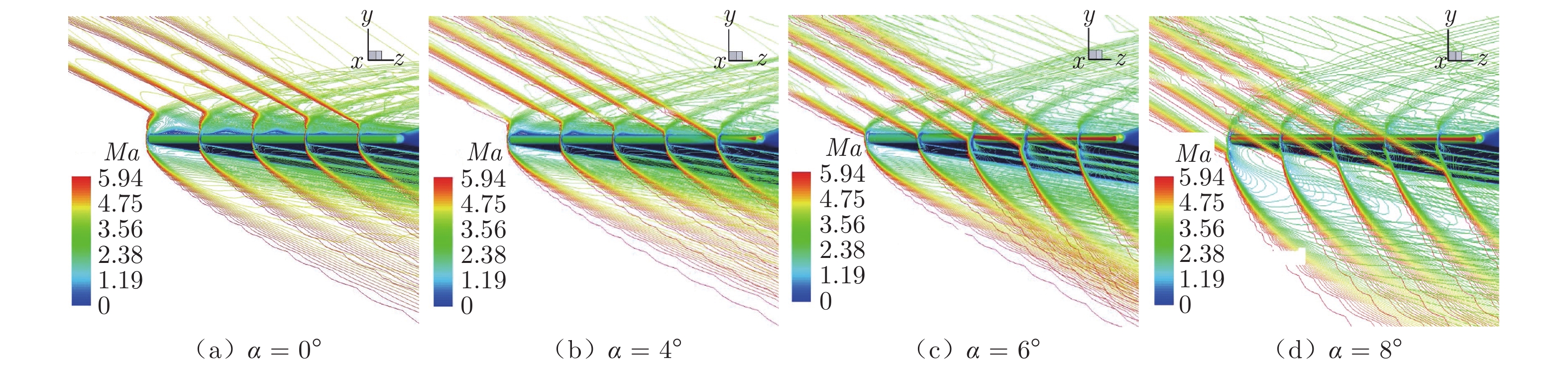
图4为α = 0°～8°时唇口干扰区试验纹影照片（ReL = 2.98 × 107 m−1）。由波系结构可以看出，迎角增大，斜激波入射位置自唇口上方向下方移动，唇口逐渐暴露于斜激波影响范围中。同时，压缩面的三维效应导致同一流场条件下斜激波沿展向的角度分布不同，形成一个斜激波面，与唇口激波出现了不同的干扰作用，增大了仿真难度。例如，迎角较小时（α = 0°），唇口附近出现了2道明显的斜激波，一道交于唇口弓形激波上方，一道与内流边界层相交；迎角较大时（α = 6°），斜激波分别与唇口弓形激波上方、中部和下方相交，对唇口激波影响较大。
相同条件下的数值仿真结果（图5，Ma为流场马赫数）也验证了斜激波与弓形激波干扰的位置沿展向变化这一规律。从唇口干扰波系的分析可知，在内外流场联合作用下，唇口干扰具有三维流动特征。因此，对该位置的气动热仿真和试验的一致性研究，应分为针对典型截面和三维整体这2个层次的量化评估。
表2为唇口中心截面xOy上的无量纲峰值热流。热流试验和仿真结果表明：迎角为8°时，无量纲峰值热流较大，试验和仿真一致性较差，最大相差42.9%；迎角为0°和4°时，无量纲峰值热流较小，试验和仿真一致性较好，两者最大相差25.0%。
表 2 唇口中心截面上无量纲峰值热流对比Table 2 Comparison of simulation and experiment results of dimensionless heat flux for inlet lip at symmetry surface试验编号 ReL α/(°) 无量纲峰值
热流（仿真）无量纲峰值
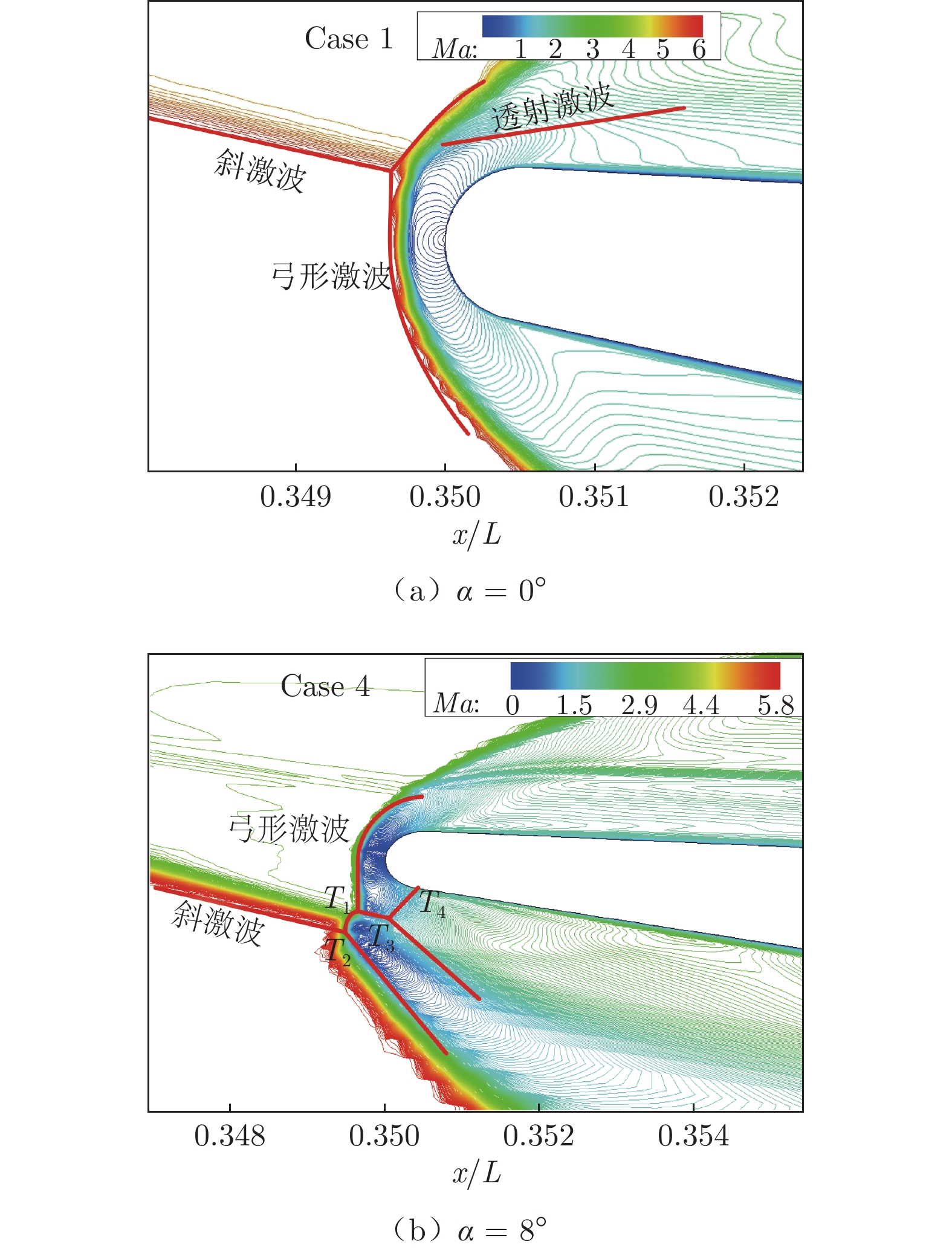
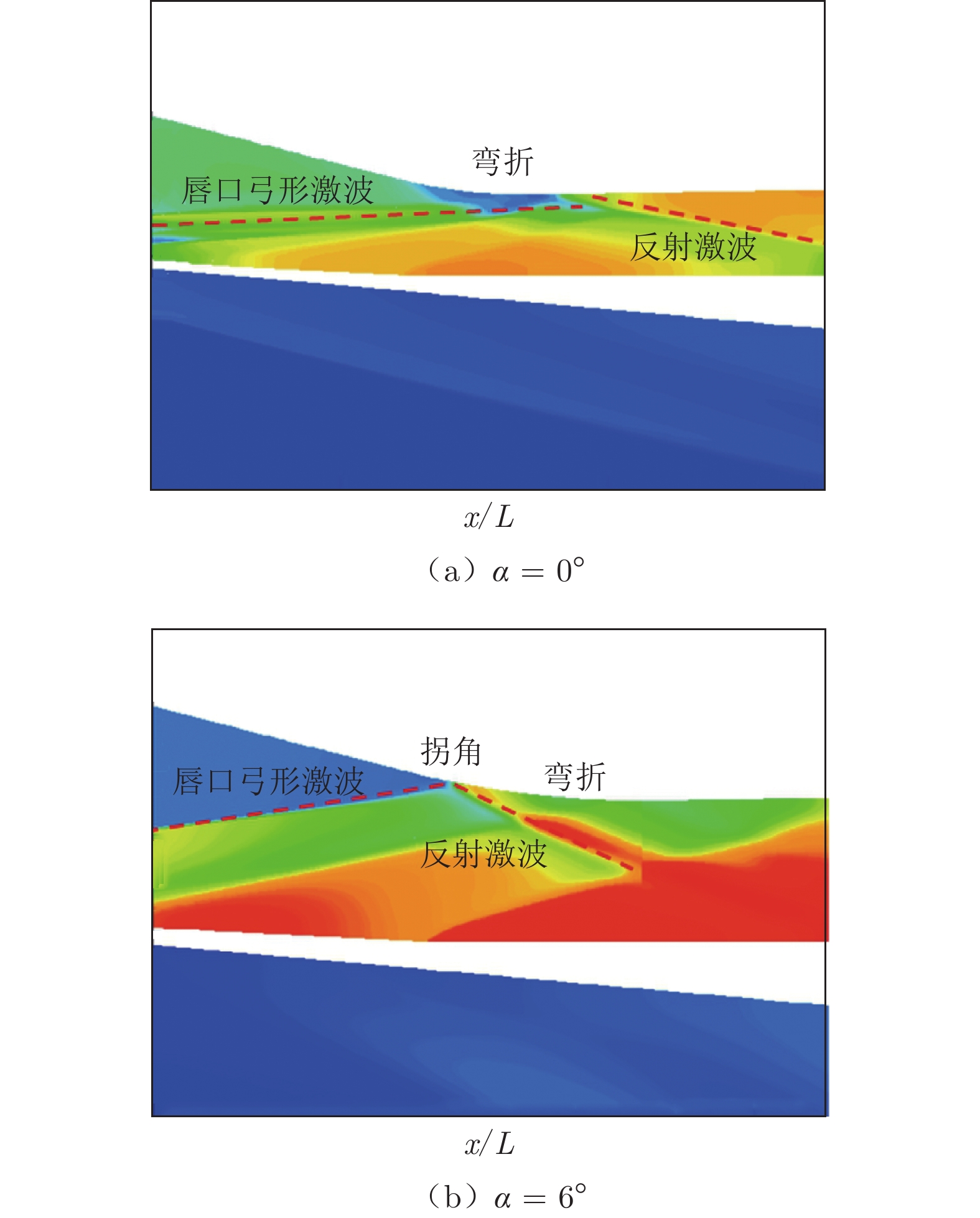
热流（试验）e 1 1.14 × 107 0 1.1 0.9 22.2% 2 1.14 × 107 4 1.1 0.9 22.2% 3 1.14 × 107 6 1.0 1.5 33.3% 4 1.14 × 107 8 1.9 1.7 11.7% 5 2.98 × 107 0 1.0 0.9 11.1% 6 2.98 × 107 4 1.0 0.8 25.0% 7 2.98 × 107 6 0.8 0.8 0 8 2.98 × 107 8 2.0 1.4 42.9% 结合不同迎角下的流场数值仿真结果分析差异产生的原因。如图6所示：α = 0°时，唇口中心截面上的入射激波分为2道斜激波，其中仅有1道斜激波与弓形激波异侧相交；入射激波受干扰后形成透射激波，透射激波未与唇口前缘边界层发生干扰，弓形激波形状也基本未发生变化，判断激波干扰类型可能为Edney第一类激波干扰[21]。α = 8°时，入射激波与弓形激波发生异侧干扰，产生2个三波点T1和T2，其间由马赫杆连接；马赫杆后产生了2道透射激波，其中透射激波T3在下游发展出透射激波T4，以适应新的流动条件；透射激波T4传向壁面，引起壁面热流升高，判断激波干扰类型可能为Edney第二类激波干扰[22]。可以看出，迎角增大后，入射激波强度增大，其与唇口弓形激波之间的干扰流动更加复杂，数值方法对复杂流动结构的模拟精度降低。
![]()
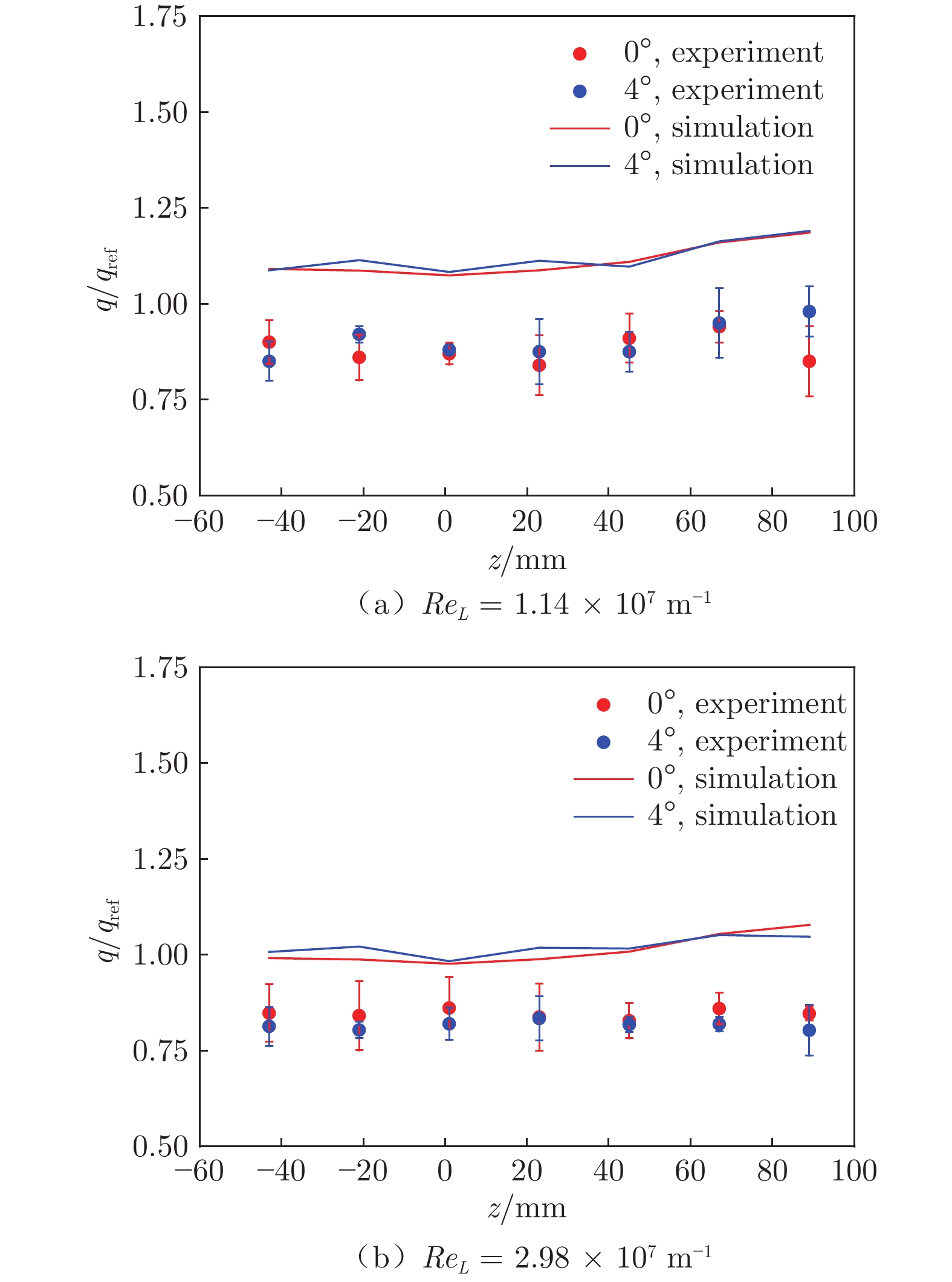
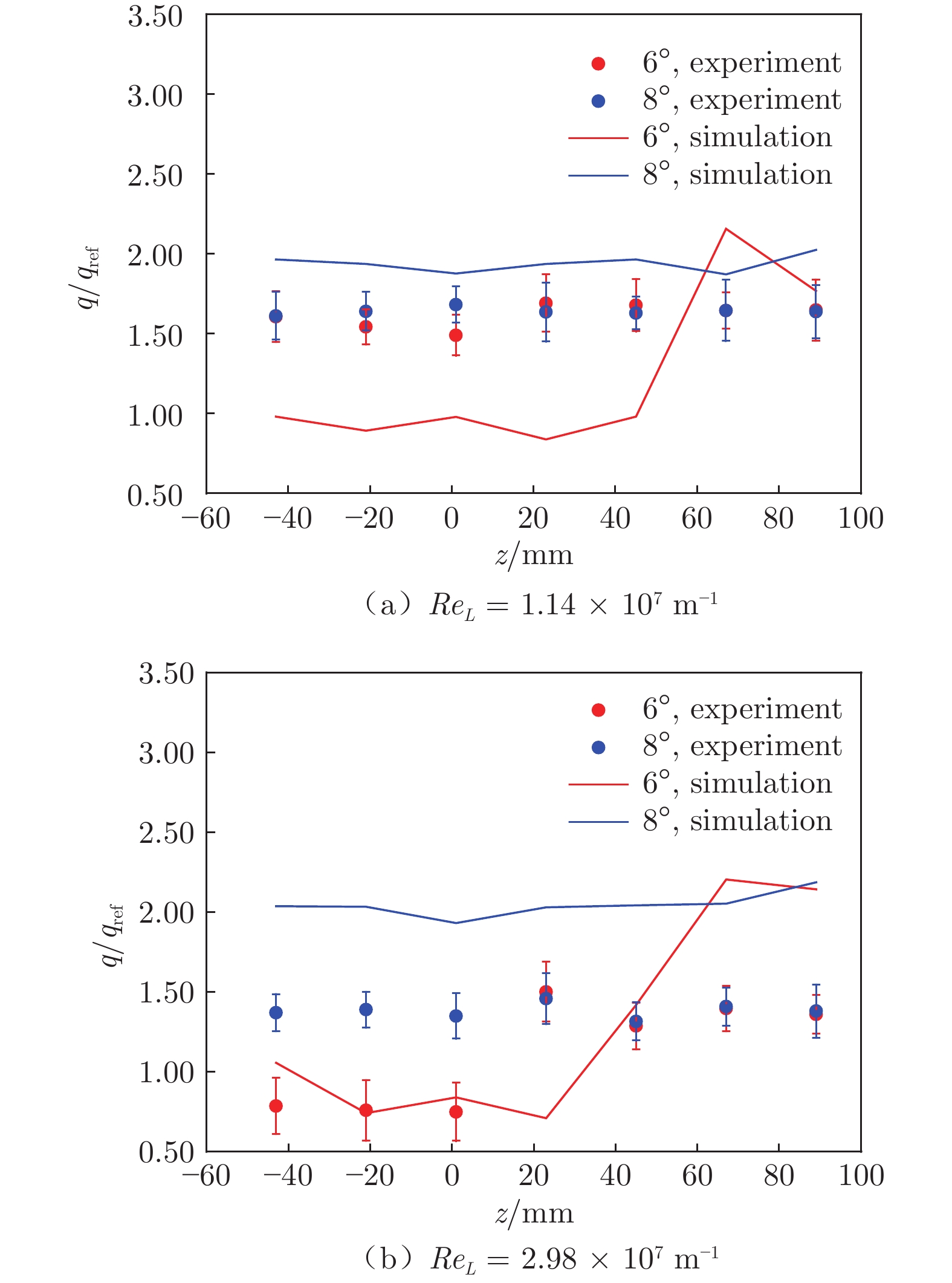
图 6 不同迎角下唇口中心截面的干扰流场云图Fig. 6 Flow fields for inlet leading edge under typical attack angles基于唇口三维热流分布进一步分析仿真和试验的一致性。唇口沿展向（z方向）的无量纲热流分布如图7和8所示，试验数据给出了热流的平均值、最大值和最小值。在ReL = 1.14 × 107 m−1条件下，α = 0°时，热流仿真与试验的最大差异为34.8%；α = 4°时，两者最大差异为21.2%，如图7（a）所示。在ReL = 2.98 × 107 m−1条件下，两者最大差异为33.7%，如图7（b）所示。当ReL = 1.14 × 107 m−1、α = 6°时，仿真与试验最大差异约为100%，出现于z = 20、40 mm处，如图8（a）所示。当ReL = 2.98 × 107 m−1、α = 8°时，两者最大差异为60%，出现于z = 89 mm处，如图8（b）所示。
![]()
图 7 唇口热流仿真与试验对比（α = 0°、4°）Fig. 7 Comparison of simulation and experimental results of dimensionless heat flux for inlet lip (α = 0°、4°)![]()
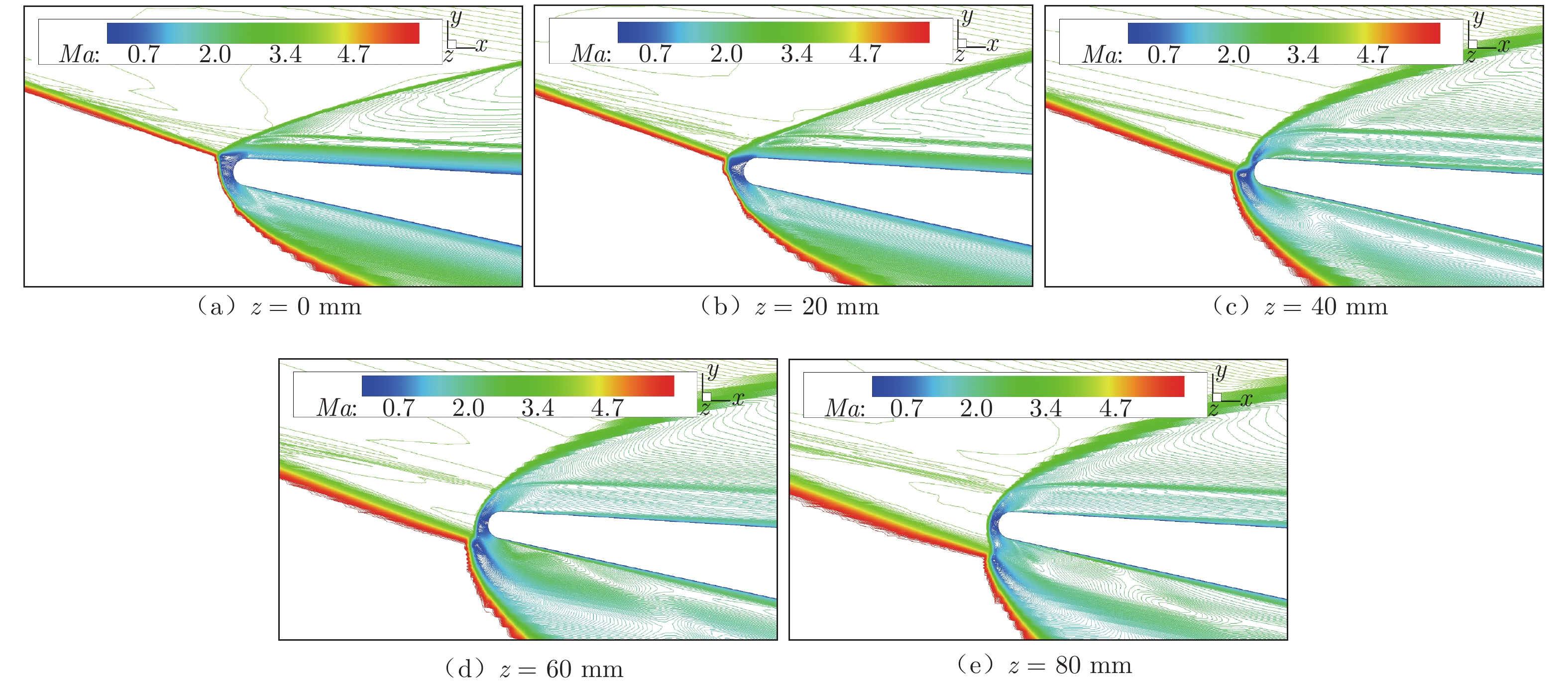
图 8 唇口热流仿真与试验对比（α = 6°、8°）Fig. 8 Comparison of simulation and experimental results of dimensionless heat flux for inlet lip (α = 6°、8°)从图7和8可以看出，在较大迎角下，唇口热流沿展向变化较大。为分析该现象，图9给出了Re = 1.14 × 107 m−1、α = 6°时唇口展向（z = 0～80 mm）截面的流场云图。在z = 0、20 mm截面中，唇口弓形激波内部流场差异不大，与驻点无干扰的流动结构相当，呈现出较为光滑的亚声速流场分布，仿真获得的热流与驻点热流相当，无量纲热流约为1.0。在z = 60、80 mm截面中，弓形激波内部流场出现了马赫杆，类似Edney第二类激波干扰结构，无量纲热流迅速增大至约2.0。因此，唇口热流沿展向变化更大，主要是由于弓形激波内部流动结构更为复杂。沿唇口展向远离对称面，斜激波入射角和强度增大，这是产生复杂流动结构的外部原因。为提升强干扰下的唇口气动热仿真精度，一方面，需采用更接近真实条件的动量输运方程、高阶格式和LES方法等[23]；另一方面，可能需对唇口网格作精细化处理，提升沿展向分布的网格密度和壁面法向网格密度，改善唇口网格和其他区域网格的正交性分布。
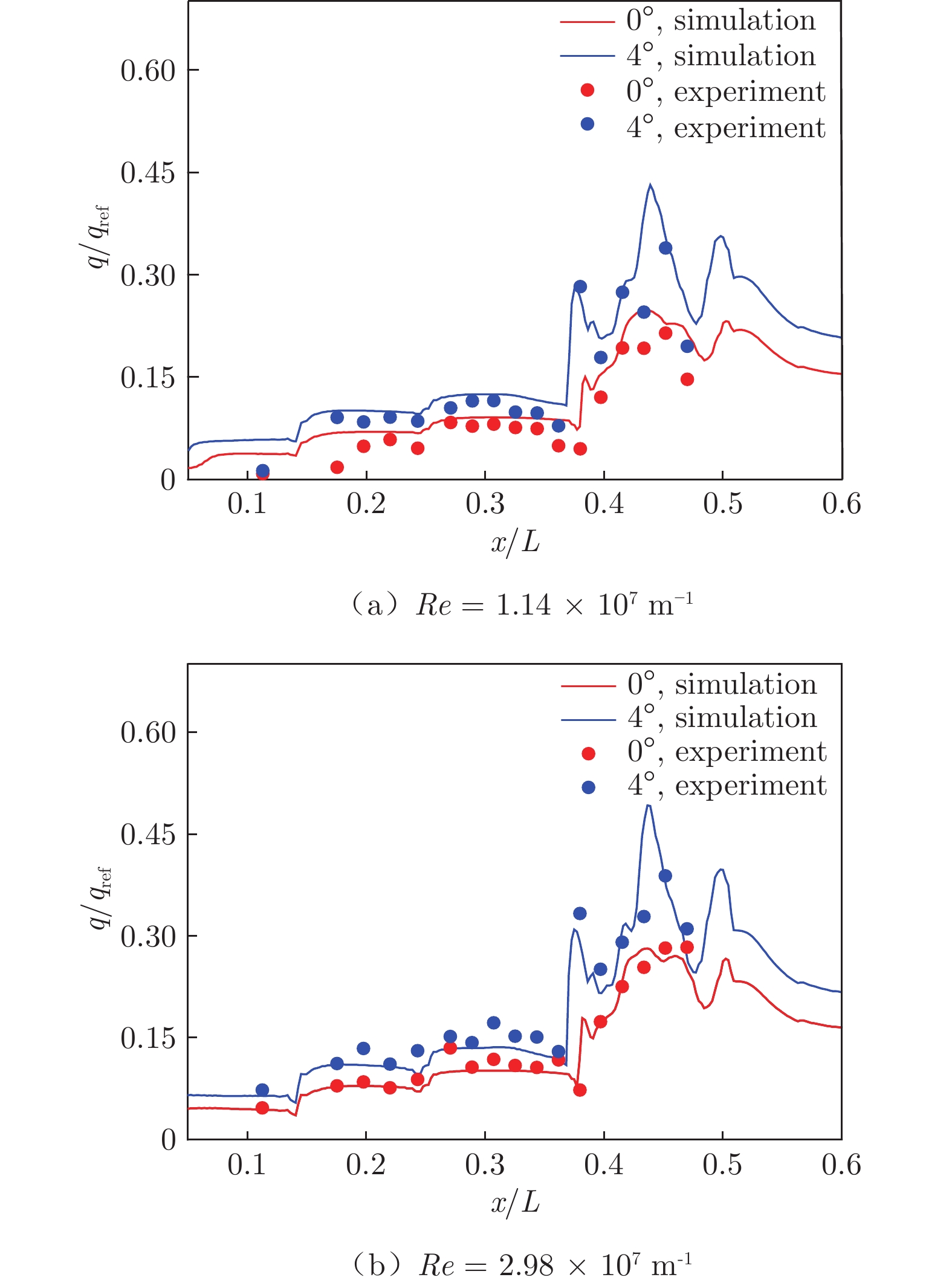
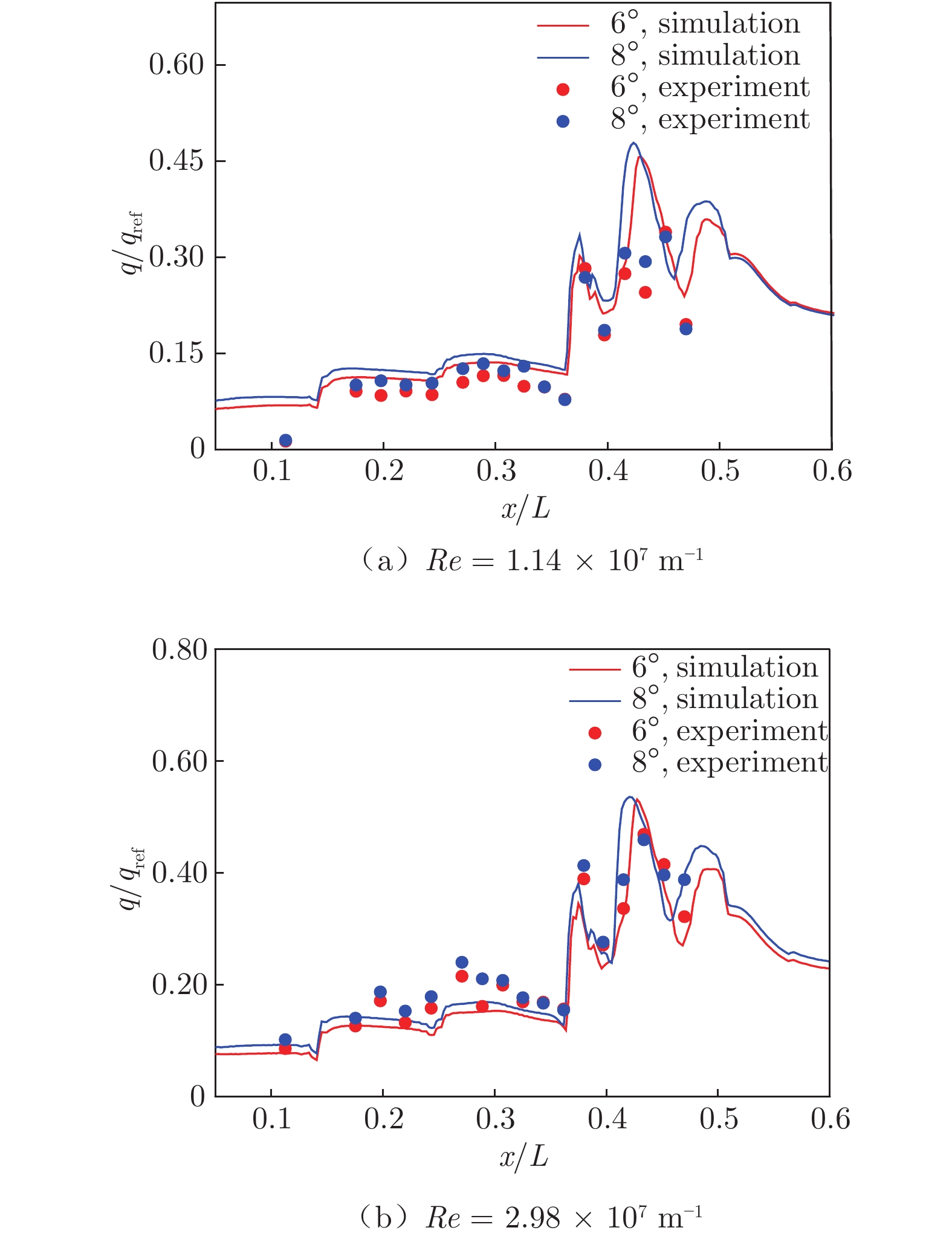
4.2 内外流场大面积区域
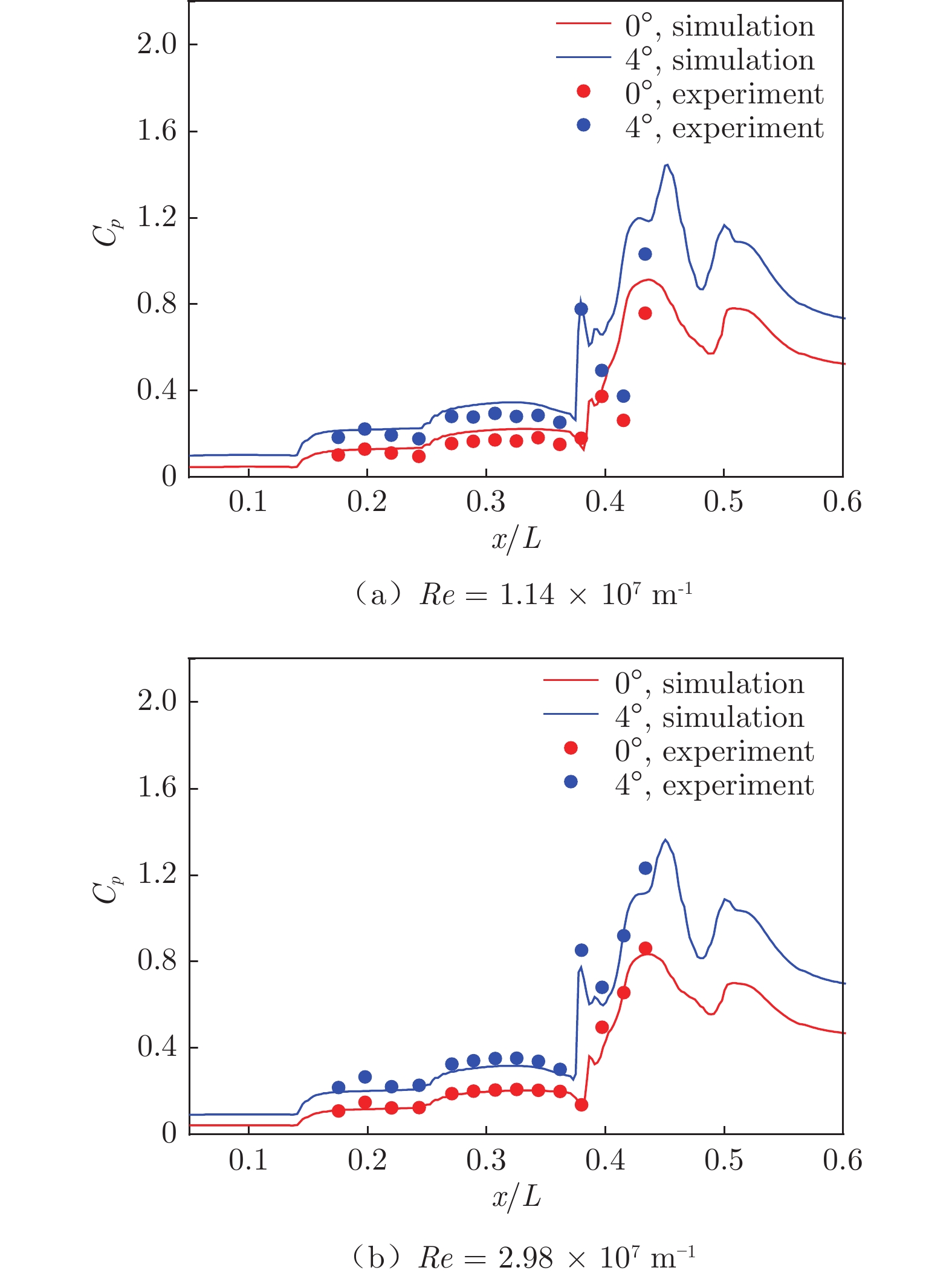
图10～12为飞行器内外流场大面积区域（包括压缩面、喉道和隔离段，x/L = 0.36之前为压缩面，之后为喉道）中心线上压力系数和热流值的对比。在所研究的试验条件下，沿流向压力系数Cp的仿真与试验结果符合较好，如图10所示。在x/L = 0.20之后，热流仿真与试验结果符合较好，如图11和12所示。因此，在所研究的试验条件下，本文采用的全湍流模型和数值方法对内外流一体化流场模拟和气动热预示比较可靠。
![]()
图 10 内外流场大面积区域压力系数仿真与试验对比Fig. 10 Comparison of simulation and experimental results of pressure coefficient![]()
图 11 内外流场大面积区域热流仿真与试验对比（α = 0°、4°）Fig. 11 Comparison of simulation and experimental results of heat flux (α = 0°、4°)![]()
图 12 内外流场大面积区域热流仿真与试验对比（α = 6°、8°）Fig. 12 Comparison of simulation and experimental results of heat flux (α = 6°、8°)当α = 0°、ReL = 1.14 × 107 m−1时，压缩面各测点热流仿真与试验的平均差异为22.3%，最大差异为46.4%，出现于压缩面结束位置（x/L = 0.36）。喉道热流仿真与试验的平均差异增大至43.5%，隔离段两者平均差异为31.8%，最大差异为50.3%，如图11（a）所示。从以上对比可以看出，沿流向热流差异增大，说明在干扰复杂的内流区域，仿真方法精度降低。当迎角从0°增大至6°时，喉道位置热流仿真与试验平均差异为19.6%，隔离段两者平均差异为50.4%，如图12（a）所示。结合迎角为0°和6°的喉道流场云图（图13）可以看出：小迎角条件下，喉道位置出现低压分离区，因此热流预示精度降低；大迎角条件下，隔离段位置激波串结构更加明显，热流仿真与试验一致性降低。
5 结 论
为评估气动热仿真方法在复杂模型中的预示精度，开展了气动热仿真与风洞试验一致性研究，重点对风洞试验流场条件下的激波后、Edney干扰和内流激波反射等气动热仿真与试验结果进行了比较，得到以下结论：
1）压缩面的热流仿真与试验结果符合较好，两者平均差异约为22.3%。喉道与隔离段的热流仿真与试验结果差异增大，内流区域的仿真精度降低，典型工况下喉道位置两者平均差异为43.5%，隔离段两者平均差异为31.8%。唇口的热流仿真与试验差异最大，可达到100%，出现于入射激波较强且入射激波与弓形激波中心相交的流场条件下。
2）沿流向热流仿真与试验差异增大的原因和解决措施，可分为4个方面：一是唇口热流与网格布局密切相关，本文对尖前缘热流计算进行了网格无关性研究，但是对于复杂的三维内外流一体模型，入射激波位置随空间的变化复杂，需进一步完善唇口及上游网格分布，可能有助于提升气动热仿真与试验的一致性；二是仿真方法对唇口和内流道等激波干扰区、喉道分离区等复杂流场的气动热模拟精度降低，需进一步改进数值方法，比如采用更接近真实条件的动量输运方程、高阶格式和LES等方法，分析各仿真模型和数值格式对复杂流动气动热模拟的误差源，建立不确定度评估方法；三是激波干扰位置流动结构具有非定常特征，尤其是对于斜激波与唇口激波中心交汇的位置，需要科学判断计算收敛性以及确定热流峰值；四是目前采用的气动热网格仿真点与试验测点“点对点”式一致性量化评估方法，尚不能准确代表空间分布模拟能力，尤其是对于复杂流动干扰区，需进一步完善气动热仿真与试验一致性评估方法。
致谢：本文风洞试验得到中国航天空气动力技术研究院第二研究所陈星、姚大鹏、邵忠杰等3位专家的大力支持。
-
![]()
图 1 内外流一体化气动热试验模型中心截面及热流测点位置示意图
Fig. 1 Illustration of symmetry surface for integrated forebody experimental model and heat flux sensor positions
![]()
图 2 气动热仿真数据与NAL HWT模型试验数据对比
Fig. 2 Comparison of non-dimensional heat flux with NAL HWT experiment interaction area
![]()
图 6 不同迎角下唇口中心截面的干扰流场云图
Fig. 6 Flow fields for inlet leading edge under typical attack angles
![]()
图 7 唇口热流仿真与试验对比（α = 0°、4°）
Fig. 7 Comparison of simulation and experimental results of dimensionless heat flux for inlet lip (α = 0°、4°)
![]()
图 8 唇口热流仿真与试验对比（α = 6°、8°）
Fig. 8 Comparison of simulation and experimental results of dimensionless heat flux for inlet lip (α = 6°、8°)
![]()
图 10 内外流场大面积区域压力系数仿真与试验对比
Fig. 10 Comparison of simulation and experimental results of pressure coefficient
![]()
图 11 内外流场大面积区域热流仿真与试验对比（α = 0°、4°）
Fig. 11 Comparison of simulation and experimental results of heat flux (α = 0°、4°)
![]()
图 12 内外流场大面积区域热流仿真与试验对比（α = 6°、8°）
Fig. 12 Comparison of simulation and experimental results of heat flux (α = 6°、8°)
表 1 风洞模拟流场参数表
Table 1 Experimental flow field parameter
试验编号 前室
总温/K前室
总压/MPaMa∞ ReL α/(°) 1 773 2.77 5.95 1.14 × 107 0 2 773 2.77 5.95 1.14 × 107 4 3 773 2.77 5.95 1.14 × 107 6 4 773 2.77 5.95 1.14 × 107 8 5 582 4.51 5.95 2.98 × 107 0 6 582 4.51 5.95 2.98 × 107 4 7 582 4.51 5.95 2.98 × 107 6 8 582 4.51 5.95 2.98 × 107 8 
下载: 导出CSV
表 2 唇口中心截面上无量纲峰值热流对比
Table 2 Comparison of simulation and experiment results of dimensionless heat flux for inlet lip at symmetry surface
试验编号 ReL α/(°) 无量纲峰值
热流（仿真）无量纲峰值
热流（试验）e 1 1.14 × 107 0 1.1 0.9 22.2% 2 1.14 × 107 4 1.1 0.9 22.2% 3 1.14 × 107 6 1.0 1.5 33.3% 4 1.14 × 107 8 1.9 1.7 11.7% 5 2.98 × 107 0 1.0 0.9 11.1% 6 2.98 × 107 4 1.0 0.8 25.0% 7 2.98 × 107 6 0.8 0.8 0 8 2.98 × 107 8 2.0 1.4 42.9%
下载: 导出CSV
-
[1] 乔文友, 余安远. 内转式进气道与飞行器前体的一体化设计综述[J]. 实验流体力学, 2019, 33(3): 43–59. DOI: 10.11729/syltlx20190028 QIAO W Y, YU A Y. Overview on integrated design of inward-turning inlet with aircraft forebody[J]. Journal of Experiments in Fluid Mechanics, 2019, 33(3): 43–59. doi: 10.11729/syltlx20190028
[2] 杨基明, 李祝飞, 朱雨建, 等. 激波的传播与干扰[J]. 力学进展, 2016, 46(1): 541–587. DOI: 10.6052/1000-0992-16-009 YANG J M, LI Z F, ZHU Y J, et al. Shock wave propagation and interactions[J]. Advances in Mechanics, 2016, 46(1): 541–587. doi: 10.6052/1000-0992-16-009
[3] 童福林, 段俊亦, 周桂宇, 等. 激波/湍流边界层干扰压力脉动特性数值研究[J]. 力学学报, 2021, 53(7): 1829–1841. DOI: 10.6052/0459-1879-21-094 TONG F L, DUAN J Y, ZHOU G Y, et al. Statistical characteristics of pressure fluctuation in shock wave and turbulent boundary layer interaction[J]. Chinese Journal of Theoretical and Applied Mechanics, 2021, 53(7): 1829–1841. doi: 10.6052/0459-1879-21-094
[4] 陈苏宇. 高超声速压缩拐角气动热环境研究[D]. 绵阳: 中国空气动力研究与发展中心研究生部, 2014. CHEN S Y. Investigation of aerothermal environment of hypersonic compression corners[D]. Mianyang: China Aerodynamics Research and Development Center Graduate School, 2014.
[5] 李素循, 倪招勇. 高超声速层流干扰流场研究[J]. 宇航学报, 2003, 24(6): 547–551. DOI: 10.3321/j.issn:1000-1328.2003.06.001 LI S X, NI Z Y. Investigation of laminar interactive flowfield in hypersonic flow[J]. Journal of Astronautics, 2003, 24(6): 547–551. doi: 10.3321/j.issn:1000-1328.2003.06.001
[6] WIETING A, HOLDEN M. Experimental study of shock wave interference heating on a cylindrical leading edge at Mach 6 and 8[C]//Proc of the 22nd Thermophysics Conference. 1987. doi: 10.2514/6.1987-1511
[7] HOLDEN M, MOSELLE J, WIETING A, et al. Studies of aerothermal loads generated in regions of shock/shock interaction in hypersonic flow[C]//Proc of the 26th Aerospace Sciences Meeting. 1988. doi: 10.2514/6.1988-477
[8] 潘沙, 田正雨, 冯定华, 等. 超燃冲压发动机唇口气动热计算研究与分析[J]. 航空动力学报, 2009, 24(9): 2096–2100. DOI: 10.13224/j.cnki.jasp.2009.09.030 PAN S, TIAN Z Y, FENG D H, et al. Computation and analysis of aeroheating of scramjet inlet cowl lip[J]. Journal of Aerospace Power, 2009, 24(9): 2096–2100. doi: 10.13224/j.cnki.jasp.2009.09.030
[9] 肖丰收, 李祝飞, 朱雨建, 等. 第Ⅳ类激波-激波干扰非定常性及其敏感因素分析[J]. 空气动力学学报, 2017, 35(1): 20–26. DOI: 10.7638/kqdlxxb-2015.0028 XIAO F S, LI Z F, ZHU Y J, et al. Numerical investigation on some key factors for the unsteady type Ⅳ shock-shock interaction[J]. Acta Aerodynamica Sinica, 2017, 35(1): 20–26. doi: 10.7638/kqdlxxb-2015.0028
[10] 张恩来, 李祝飞, 李一鸣, 等. 斜激波入射V形钝前缘溢流口激波干扰研究[J]. 实验流体力学, 2018, 32(3): 50–57. DOI: 10.11729/syltlx20180002 ZHANG E L, LI Z F, LI Y M, et al. Investigation on the shock interactions between an incident shock and a plate with V-shaped blunt leading edge[J]. Journal of Experiments in Fluid Mechanics, 2018, 32(3): 50–57. doi: 10.11729/syltlx20180002
[11] HOLDEN M S. Studies of scramjet performance in the LENS facilities[C]//Proc of the 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibition. 2000: 3604.
[12] 黎作武. NNLD算法在高超声速气动热计算中的确认与验证[C]//第七届全国流体力学学术会议论文摘要集. 2012: 126. [13] 张涵信. 关于 CFD 高精度保真的数值模拟研究[J]. 空气动力学学报, 2016, 34(1): 1–4. DOI: 10.7638/kqdlxxb-2015.0211 ZHANG H X. Investigations on fidelity of high order accurate numerical simulation for computational fluid dynamics[J]. Acta Aerodynamica Sinica, 2016, 34(1): 1–4. doi: 10.7638/kqdlxxb-2015.0211
[14] 姜振华, 阎超. 高超声速热流高精度数值模拟方法[J]. 北京航空航天大学学报, 2011, 37(12): 1529–1533. DOI: 10.13700/j.bh.1001-5965.2011.12.002 JIANG Z H, YAN C. High order accurate methods in numerical simulation of hypersonic heat transfer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(12): 1529–1533. doi: 10.13700/j.bh.1001-5965.2011.12.002
[15] HOLDEN M S. Ground test measurements of jet interaction effects on AIT interceptors at fully duplicated flight conditions[C]//Proc of the 8th DOD Electromagnetic Windows Symposium. 2000.
[16] 徐大军, 蔡国飙, 乐川. 吸气式高超声速飞行器气动热试验研究[J]. 宇航学报, 2006, 27(5): 1004–1009, 1095. DOI: 10.3321/j.issn:1000-1328.2006.05.037 XU D J, CAI G B, YUE C. Aeroheating experiment for airbreathing hypersonic vehicle[J]. Journal of Astronautics, 2006, 27(5): 1004–1009, 1095. doi: 10.3321/j.issn:1000-1328.2006.05.037
[17] 陈坚强. 国家数值风洞(NNW)工程关键技术进展[J]. 中国科学:技术科学, 2021, 51(11): 1326–1347. CHEN J Q. Advances in the key technologies of Chinese national numerical windtunnel project[J]. Scientia Sinica: Technologica, 2021, 51(11): 1326–1347.
[18] YAMAMOTO Y. Numerical and experimental aerothermo-dynamics of strong hypersonic shock-shock interactions[C]//Proc of the 8th AIAA/ASME Joint Thermophysics and Heat Transfer Conference. 2002. doi: 10.2514/6.2002-2891
[19] 贾居红. 临近空间高超声速气动热数值模拟研究[D]. 北京: 北京理工大学, 2016. JIA J H. Numerical study on hypersonic aerothermodynamic of near-space flight vehicle[D]. Beijing: Beijing Institute of Technology, 2016.
[20] 曾磊. 测热试验数据后处理方法及误差机理分析[D]. 绵阳: 中国空气动力研究与发展中心研究生部, 2012. ZENG L. Study on data processing method and error mechanism analysis of heat flux measurement in wind tunnel[D]. Mianyang: China Aerodynamics Research and Development Center Graduate School, 2012.
[21] 朱广生, 聂春生, 曹占伟, 等. 气动热环境试验及测量技术研究进展[J]. 实验流体力学, 2019, 33(2): 1–10. DOI: 10.11729/syltlx20180137 ZHU G S, NIE C S, CAO Z W, et al. Research progress of aerodynamic thermal environment test and measurement technology[J]. Journal of Experiments in Fluid Mechanics, 2019, 33(2): 1–10. doi: 10.11729/syltlx20180137
[22] 钱炜祺, 周宇, 邵元培. 表面热流辨识结果的误差分析与估计[J]. 空气动力学学报, 2020, 38(4): 687–693. DOI: 10.7638/kqdlxxb-2018.0185 QIAN W Q, ZHOU Y, SHAO Y P. Error analysis of surface heat flux estimation[J]. Acta Aerodynamica Sinica, 2020, 38(4): 687–693. doi: 10.7638/kqdlxxb-2018.0185
[23] MAVRIPLIS D J. Progress in CFD discretizations, algorithms and solvers for aerodynamic flows[C]//Proc of the AIAA Aviation 2019 Forum. 2019. doi: 10.2514/6.2019-2944
计量
- 文章访问数: 199
- HTML全文浏览量: 88
- PDF下载量: 27
