Experimental investigation on the flow-induced vibration of a riser subjected to the combination of internal liquid flow and external sheared flow
-
摘要:
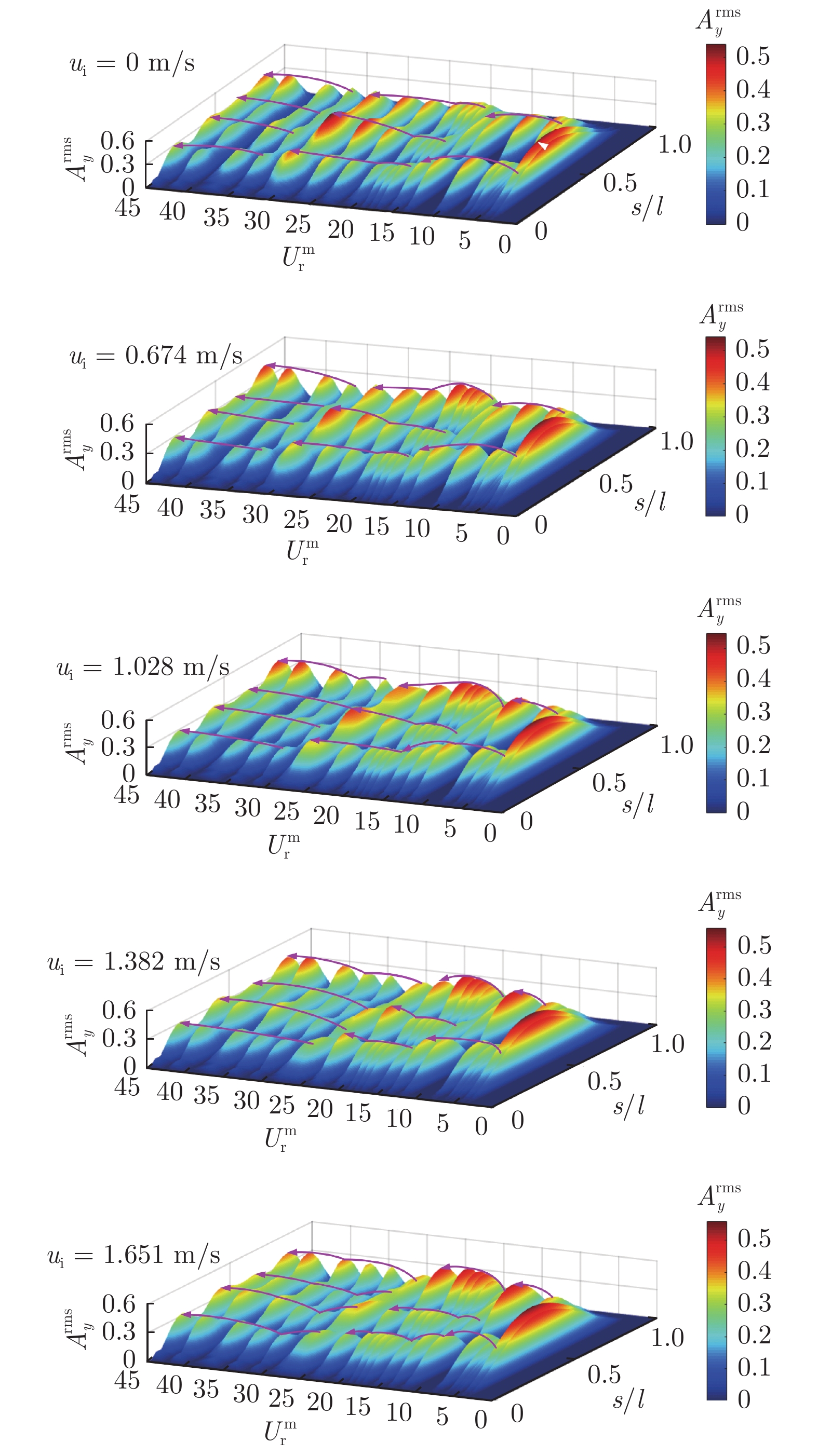
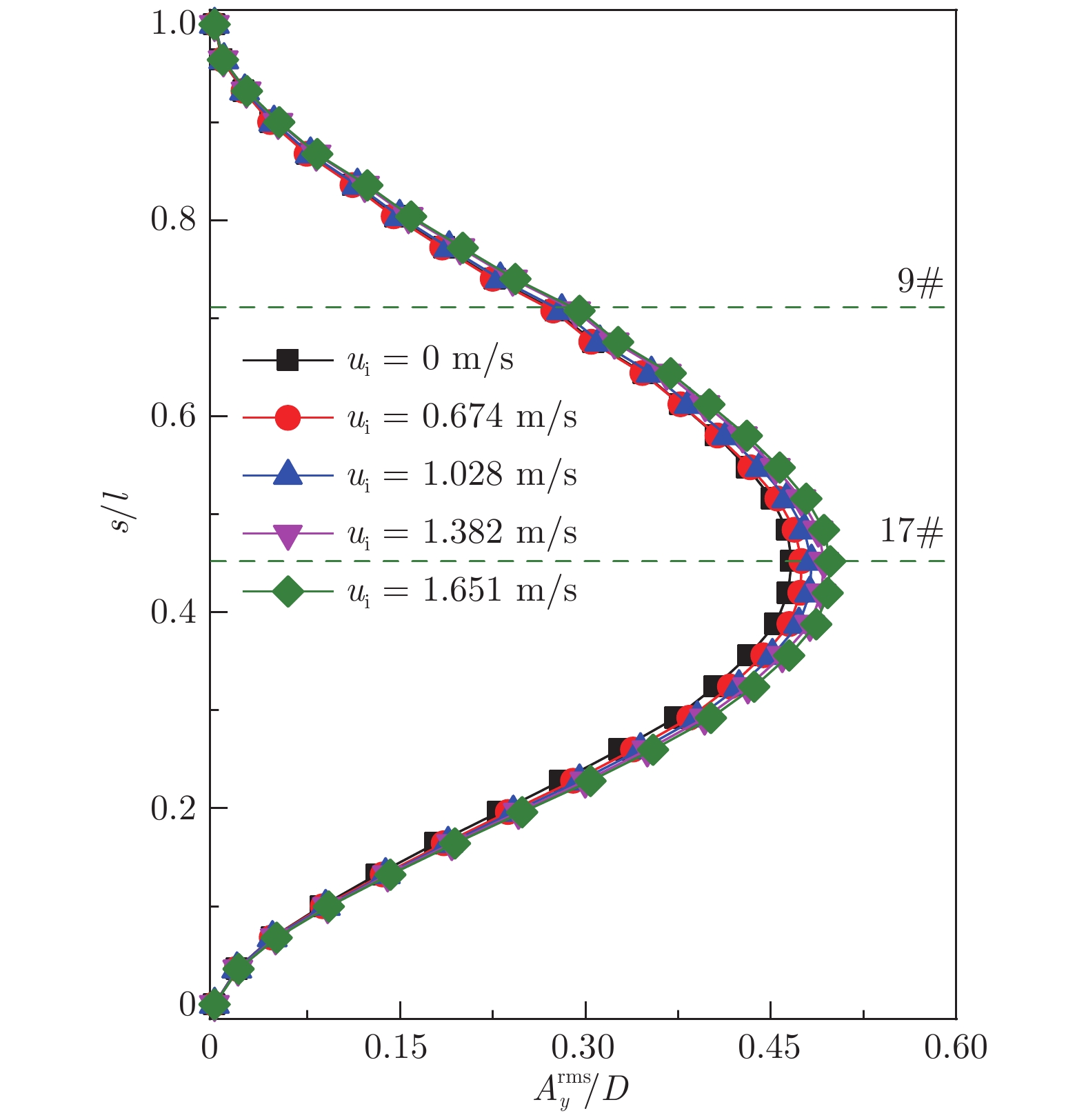
柔性立管广泛应用于海洋油气等矿产资源的输送，在内部流体与外部海流的夹击下极易产生复杂的振动响应，一旦发生疲劳失效，就会造成严重的环境污染。在循环水槽中开展了单相内流与非线性剪切外流耦合作用下悬链线型柔性立管的振动响应测试，采用高速摄像非介入测试方法捕捉了悬链线型柔性立管的振动位移。通过改变非线性剪切外流的约化速度（$U_{\text{\,r}}^{\text{m}}$ = 3.55～44.69）和内流流速（ui = 0.674～1.651 m/s），分析了内流流速对柔性立管振动响应的影响规律，剖析了不同流动工况下平面外振幅、振频的时空响应特性及振动模态的演变。实验结果表明：与纯外流激发的涡激振动相比，内流的存在使柔性立管的振幅增大，且振动模态转换发生在更低的约化速度，随着内流流速的增大，相邻模态间发生模态转换的临界约化速度越来越低；在本实验测试工况下，当柔性立管在纯外流作用下发生锁频振动时，振动模态没有发生改变，而在外流涡激振动处于模态过渡区时，内流的输送易使高阶模态在更低的约化速度时出现。
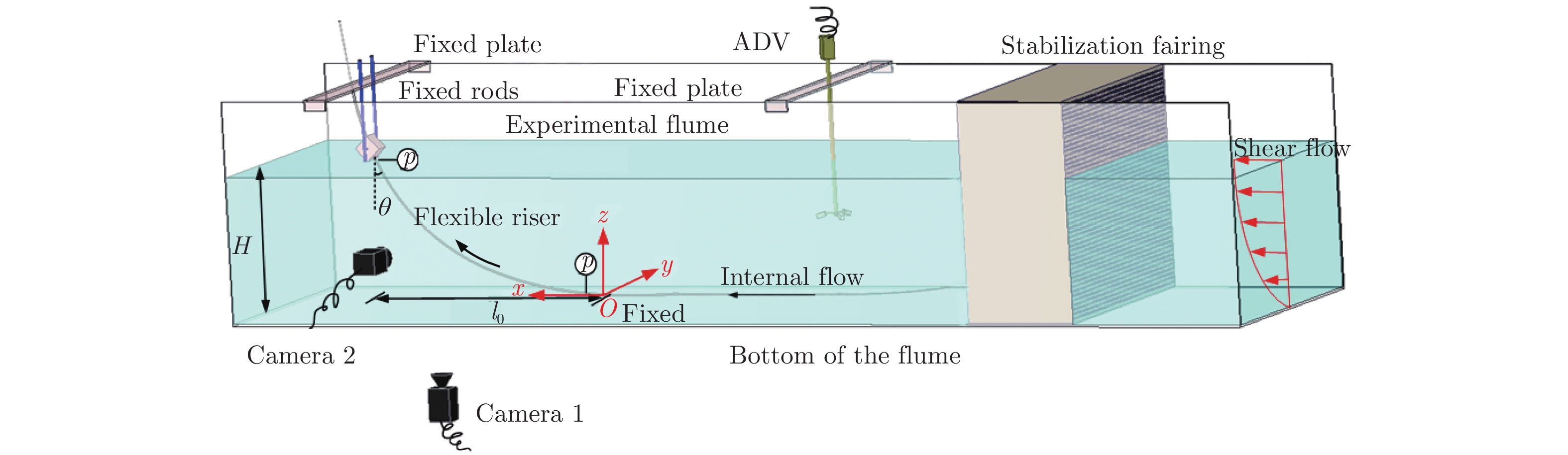
Abstract:Flexible risers which are commonly applied to transport submarine resources have been widely utilized in offshore engineering. The intricate Flow-Induced Vibration (FIV) of flexible risers is easily encountered with the presence of both internal and external flows. Once the riser fatigue failure occurs, it causes serious environmental pollution. In this work, a series of tests were conducted in a recirculating water flume to investigate the dynamic behavior of a flexible catenary riser under the combination of the internal liquid water flow and the external shear current. A non-intrusive high-speed imaging technique was employed to record the vibration displacement varying along the riser span. The reduced velocity and the internal flow velocity ranged from 3.55 to 44.69 and from 0.674 m/s to 1.651 m/s, respectively. The influence of the internal flow velocity on the dynamic response was examined. The experimental results including the spatial-temporal response amplitude and frequency as well as the mode evolution of out-of-plane were analyzed. The results show that the response is enhanced with increasing internal flow velocity except for the mode transition cases. In addition, the existence of the internal flow leads to the earlier occurrence of the mode transition. When the lock-in occurs in the vortex-induced vibration of the flexible riser, the amplitude of the flexible riser is magnified with increasing internal velocity, while the new mode response is not triggered. There is a new mode response occurring in the mode transition cases.
-
0 引言
低温风洞通过降低试验气体温度可以提高试验雷诺数，能够满足飞行器气动性能准确模拟对雷诺数的需求，是十分重要的飞行器气动性能地面模拟设备。试验气体降温过程中，低温风洞结构与气流间存在着不均匀热交换，结构局部易出现较大温度梯度，引发热变形，且受各类边界约束以及气动载荷的作用，导致结构应力超出许用范围，从而威胁设备运行安全。另外，风洞结构变形会引起风洞回路轴线偏离、气动型面变形和内部气流表面出现阶差等诸多问题，影响风洞的气动性能。因此，分析和控制低温环境下风洞结构的热变形是低温风洞研制的关键技术问题。
复杂结构的热变形分析通常采用试验测量和数值仿真等方法。相对而言，数值仿真能够准确、全面地反映结构温度场和应力场分布情况，为结构热力学特性优化提供可靠、充分的参考依据，且成本较低，分析周期较短。所以，基于数值仿真方法，国内外学者对低温结构的热力学特性开展了广泛研究。朱鸿梅[1-2]采用有限元方法，对冷却过程中非磁性低温杜瓦的螺纹粘接接头进行瞬态热应力仿真，分析了等效应力与冷却时间的变化关系。Kim、Kang[3-4]等对复合材料/铝环状试件的热力学特性进行了研究，并将低温热应力与有限元仿真结果作出对比分析。朱立伟[5]应用有限元分析软件分析了LNG船用超低温球阀在超低温条件下的应力特性，并提出改进应力集中的措施。上述研究均采用有限元分析方法，关注的是结构的热力学特性，而低温环境下考虑流固热耦合作用的热力学特性分析尚不多见。考虑流固热耦合作用的研究，也大多关注流体传热[6-7]，或温度变化较小的结构传热[8-9]。
本文以风洞典型结构部段--扩散段为研究对象，基于流固热耦合方法，建立低温风洞扩散段的流固热耦合仿真模型，重点分析低温下扩散段的换热特性，计算扩散段结构的温度及应力分布，并在风洞低温运行过程中对扩散段温度和应力进行测试研究。
1 试验装置
低温试验在中国空气动力研究与发展中心的0.3m跨声速低温风洞中进行，试验主要研究扩散段的热力学特性。低温风洞正常情况外壁面有保温层，风洞调试期间，壁面暂未加保温层，故本文计算按未加保温层考虑。风洞运行时，扩散段将气流动能恢复为压力能，以减少气流在扩散段下游各段的能量损失[10]。扩散段结构关于垂直中心面左右对称，由内流道、驻室、驻室进气管道和支座组成。4个支座均为滑动支座，通过双头螺柱压紧于绝热块上，从而限制结构在竖直方向的位移，同时保证低温工况下在水平方向可自由收缩。内流道中通入快速流动的低温氮气，使流场和结构得以快速降温。为降低驻室与内流道之间的温度梯度，需从风洞回路向驻室引入冷却气体，其温度与内流道中的氮气接近，但流速相对较小。结构外壁面直接与空气接触。扩散段模型如图 1所示。
2 计算方法
降温过程中，扩散段换热不均匀，导致局部存在温度梯度，引发热应力。本文采用流固热耦合方法，求解结构的温度分布；采用顺序热力耦合方法，求解结构的应力分布。
2.1 传热理论
传热有3种方式:导热、对流和热辐射。本文研究对象处于低温工况，可忽略辐射效应。
流体内部的传热涉及3个重要物理定律：质量守恒定律、动量守恒定律和能量守恒定律，此处不再赘述。
流体的管内流动状态取决于当地雷诺数Re，Re＞104时为完全湍流[11]。内流道入口雷诺数为2.96×106，采用标准k-ε两方程模型进行模拟。
本文中流体通过耦合界面与固体发生热交换，壁温是时间的函数，为第一类边界条件。
结构内部传热方式为导热，直角坐标系中的导热方程通常写作：
(1) 式中：
边界条件为第三类边界条件：
(2) 式中：Tw为固体壁面温度，Tf为膜层温度，即对流边界层中流体的温度。考虑热边界层对换热的影响，用T∞表示远场温度，Tf可用下式计算：
(3) 结构外壁面与大气传热方式为自然对流；内流道结构与流体之间的传热方式为强制对流。驻室腔体内氮气流速很低，与驻室壳体间的传热方式可视为自然对流。
等温水平长圆柱的大空间自然对流换热，可采用以下关联式[11]估算：
(4) 式中:Ra为瑞利数，Pr为普朗特数，要求Ra≤1012。
2.2 流固热耦合计算方法
多物理场耦合计算通常分为直接耦合法和间接耦合法。直接耦合是对问题涉及的所有数学物理方程进行联合求解，一般适用于较简单的物理问题。本文采用间接迭代耦合法，分别对流场和结构进行分析，再将耦合界面的物理量通过映射与差值[12-13]传递给外场进行计算，如此循环迭代。
采用多物理场代码耦合软件MpCCI，联合Abaqus与Fluent进行流固热耦合仿真。在结构与流场耦合界面上，交换的物理量为膜层温度Tf、换热系数h和壁温Tw。壁温由Abaqus计算，经MpCCI传入Fluent。耦合壁面的换热系数与膜层温度由Fluent计算，经MpCCI传入Abaqus。计算采用串行算法，即Abaqus收到Fluent传入的初始数据后开始迭代，经过固定耦合时间步长后，将计算得到的耦合量(节点温度)传入Fluent；Fluent收到数据后经相同时间步长的迭代，将计算得到的耦合量(换热系数与膜层温度)传入Abaqus，依此循环，典型串行算法的数据传递过程如图 2所示。
2.3 热应力计算
热应力是由于部件受热不均匀而存在温度差异，导致各处膨胀变形或收缩变形不一致，且相互制约而产生内应力。对各项同性材料，自由膨胀的变分量为:
(5) 式中：εx、εy、εz为沿X、Y、Z方向应变分量；α为线膨胀系数。
如果物体边界有约束条件，自由膨胀受到约束限制，微元体会产生热应力。根据线性应力原理和胡克定律，描述应力和应变关系的物理方程为：
(6) 
(7) 
(8) 
(9) 
(10) 
(11) 式中：E为材料杨氏模量；μ为泊松比；σx、σy、σz为沿X、Y、Z方向应力分量；G为材料剪切模量，G=2E(1+μ)；ΔT为从无应力状态开始的温差。
扩散段中温差较大区域为驻室与内流道的过渡区域，这也是应力分析重点关心的区域。
3 建立流固热耦合仿真模型
本节分别建立流体与结构传热模型，在MpCCI中设置相关耦合参数，联合Abaqus与Fluent进行流固热耦合分析。将结构温度场作为载荷导入Abaqus中，进行顺序热力耦合分析。
3.1 流体传热模型
扩散段内的流场比较复杂，对其做出以下几点简化。首先，驻室内气流压差小，且大部分位置气流速度低于1m/s，对换热能力的促进作用较小，因此以自然对流作为后期结构热固耦合的边界条件。流体传热模型中仅考虑内流道的流场，内流道壁面为耦合界面。其次，扩散段内流道实际入口气流较紊乱，速度分布复杂，此处简化为简单的均匀来流。最后，不考虑介质的摩擦损失以及介质的物性参数随温度的变化。
流体传热模型入口马赫数为0.2；入口温度随时间变化，通过Matlab对实测入口温度进行多项式拟合，并写入UDF，如图 3所示。出口边界设置为outflow；壁面边界条件设置为不滑移，温度由Abaqus传入。
湍流模型采用k-ε两方程模型，壁面函数采用标准壁面函数，要求第一层网格厚度位于对数律区域，且Y*>11.225。经Fluent计算后，调整第一层网格厚度，直到满足湍流模型对Y*的要求。
网格为六面体结构网格，数量为293 436，如图 4所示。为验证网格无关性，对以下工况--入口马赫数为0.2，入口流体温度为270K，壁面温度为300K--进行验证，对比壁面平均对流换热系数，结果如图 5所示。
3.2 结构传热模型
对结构作出以下几点简化。风洞扩散段是薄壁壳体，有限元采用实体单元对实际模型简化少，能较好反映实际结构，但厚度方向节点不易控制，网格质量不好，计算量大。因此本文采用壳体单元建模，可提高计算效率。此外，降温过程中，空气中的水蒸气会在扩散段外壁面凝华结霜，对传热会产生一定影响。建模中通过设置较小的对流换热系数来近似模拟，不考虑结霜过程。最后，不考虑支座处摩擦阻力对位移的约束。
扩散段结构关于垂直中心面左右对称，对于有限元计算，只需建立半模即可，如图 6所示。采用Abaqus前处理器对结构划分网格，并细化驻室与内流道交界处网格，保证壳单元厚度方向至少有5个积分点[14-15]，总网格数为19 714。传热分析采用传热单元DS4。结构传热分析中只需考虑模型的换热问题。初始温度设置为300K；外壁面自然对流换热系数可按公式(4)进行估算，驻室外表面不同截面处的直径、温度均变化较大，计算时采用算数平均值。降温末期，结构外表面结冰结霜会减弱传热效果，因此换热系数的取值应适当减小。结构外壁面换热系数取为5W/(m2·K)；驻室内冷却气体引自风洞回路，温度与内流道氮气温度接近，因此将内流道入口测量温度作为驻室气体温度。驻室内气流速度小，在大部分位置速度低于1m/s，因此简化为自然对流边界处理。自然对流换热系数通常在10W/(m2·K)以内，参照封闭腔内自然对流换热工况[16]下的换热水平，将驻室内换热系数取为3.5W/(m2·K)。
3.3 流固热耦合模型
在流固热耦合模型中，耦合界面为内流道壁面。总的降温时间为6400s，耦合物理量为流体温度、换热系数和固壁温度。
温度从300K降至110K，每秒钟温度下降0.03K。软件中，流固热耦合时间步长设置为1s。在该时间步长内，耦合量的变化都足够小，从而可准确反映瞬态过程中的换热特性。
3.4 结构应力模型
热应力分析中采用S4R壳体单元，支座处限制Y方向自由度，出口端面限制Z方向自由度，将传热分析得到的温度场作为温度载荷加载到应力分析步。
4 试验测试
测试系统包括低温电阻温度传感器、低温应变传感器、数据采集器和显示系统。
温度和应变传感器布置在驻室与内流道外壁面的水平位置，实时监测结构的温度与应力变化。粘贴传感器之前，先要对粘贴表面进行处理，保证传感器与表面的紧密贴合。然后在传感器与钢结构之间涂上刚性较好的低温胶，在传感器背面涂上弹性较好的防护胶。通过在测点附近粘贴补偿块的方式，消除温度变化造成的传感器误差。
数据采集仪型号为吉时利2701，将其与工控机箱串联，通过电脑显示器即可设置相关参数，实时监测结构的温度与应力变化。
试验中测点分布如图 7所示，其中T1~T13为温度测点。测点T1~T9位于驻室椎形体外表面水平母线上，测点T10位于冷气入口管道与驻室连接处附近，测点T11~T13位于冷气入口管道外壁；示意图中三角形代表应力测点S1，位于驻室与内流道连接处。在内流道、驻室靠近内表面处布置温度探针，监测与结构发生换热的气体温度。
降温时间为6400s，气流温度由300K降至130K。此间，结构表面会结霜。随后，风洞恢复常温，降温过程如图 8所示。
5 试验与仿真结果分析
本节首先将低温风洞试验温度测量结果与流固热耦合仿真结果进行对比，分析扩散段结构的传热特性。然后将低温风洞试验应力测量结果与顺序热力耦合仿真结果进行对比，分析结构应力状态。
5.1 耦合传热分析
由降温曲线的斜率可判断降温速率：0~2500s，温度均匀下降；2500~3400s，降温速率逐渐减慢；3400~4500s温度均匀下降；4500~4800s，降温速率突然变大，随后恢复之前的降温速率。
流固热耦合仿真计算得到结构在1000、2500、5000和6400s的温度场，如图 9所示。由温度分布可知，驻室与内流道过渡区域的温度梯度较大。驻室内气流速度低，换热效果差，且热量传导至温度较低的内流道需经过结构导热，以上原因导致驻室外壁温度明显高于内流道外壁温度。
测点T2位于内流道外壁，T4位于驻室与内流道过渡区域。通过对比发现，仿真曲线趋势与测量曲线保持一致，最大偏差为20K左右。2500~3400s，降温速率减慢，温度测量与仿真曲线的斜率也随时间减小，符合实际情况。4500~4800s，降温速率突然变大，在仿真曲线中可明显看到斜率增大，而实际测量曲线并未反映出该降温速率的变化，如图 10和11所示。
测点T7、T9位于驻室外壁面，由本节前面的分析可知该处降温速率较慢。实际测量发现，温度在250K以上，计算结果与试验数据吻合较好，如图 12和13所示。
测点T10位于驻室上，靠近冷气入口管道底部。测点T12位于冷气入口管道上。由于管道内气流速度较低，换热不充分，所以该处结构温度较高。试验测量与仿真计算偏差较小，在10K以内，如图 14和15所示。
总的来说，温度测量与仿真曲线吻合较好。最大偏差在20K以内，发生在降温末期。
5.2 结构应力分析
结构应力的大小与温度梯度成正比。由5.1节传热分析可知，驻室与内流道过渡区域应力较大。图 16为结构在1000、2500、5000和6400s时刻的应力分布。由应力分布可知，支座、法兰以及驻室与内流道过渡区域应力较大。由于采用壳体单元建模，支座、法兰处过于简化，可能导致应力计算不准确。
对比应力仿真曲线与结构降温曲线可知，应力变化与温度变化基本对应。在0~2500s，均匀降温，应力随时间增大；2500~3400s，降温速率逐渐减小，由于结构内部导热，局部温度梯度减小，热应力减小；3400~4500s，均匀降温，应力随时间增大；4500~4800s，降温速率突然变大后恢复，S1处应力曲线也出现一个凸起。
由图 17可知，应力仿真值与实际测量值吻合较好。最大偏差为10MPa左右，发生在降温末期。温度应力最大值121MPa出现在降温末期，在驻室与支座之间。使仿真与计算产生偏差的原因，可能有以下3点：(1)风洞回路中，低温氮气经过试验段后均匀性较差，导致结构传热不均匀；(2)降温末期，扩散段外结霜结冰，影响应力测量；(3)防护胶经过低温后粘合度下降，甚至出现脆裂。
![]()
图 17 降温过程测量与仿真应力变化曲线Fig. 17 Simulation and measuring curve of stress when cooling down通过仿真分析和试验测试，扩散段温度应力低于材料的许用应力(115MPa)，在低温和给定的试验温度变化条件下，扩散段结构是安全的。
6 结论
通过对低温风洞扩散段的数值计算与试验得出如下2点结论：
(1)采用壳体单元对风洞扩散段的结构进行有限元建模是可行的，可以减小计算规模。尽管局部位置可能过于简化，但应力计算值与仿真值基本在一个量级。
(2)利用第三方软件MpCCI联合Abaqus与Fluent进行流固热耦合仿真，得到结构的温度场分布；再将温度场作为载荷，利用Abaqus进行顺序热力耦合分析，求解结构的应力场。通过风洞低温试验测试结果表明，该方法能够准确反映低温风洞结构的热力学特性，可为低温风洞的结构安全性能优化提供可靠的仿真分析方法。
-
![]()
图 2 不同流速内流作用下柔性立管均方根振幅随约化速度的变化
Fig. 2 The three-dimensional visualization of the Root-Mean Squares (RMS) response amplitude with respect to s/l and the mean reduced velocity at different internal flow velocities
![]()
图 3 不同流速内流作用下柔性立管振动主导频率随约化速度的变化
Fig. 3 The dominant out-of-plane response frequency versus the reduced velocity
![]()
图 4 不同流速的内流作用下柔性立管各阶振动模态权重随外流约化速度的变化
Fig. 4 The modal weight variation of flexible riser response versus the reduced velocity at different internal velocities
![]()
图 5 $\text{U}_{\text{\,{{r}}}}^{\text{{{\,m}}}}$ = 3.55时内流流速对柔性立管均方根振幅响应的影响
Fig. 5 The influence of internal velocity on the response amplitude of flexible riser at $\text{U}_{\text{\,{{r}}}}^{\text{{{\,m}}}}$ = 3.55
![]()
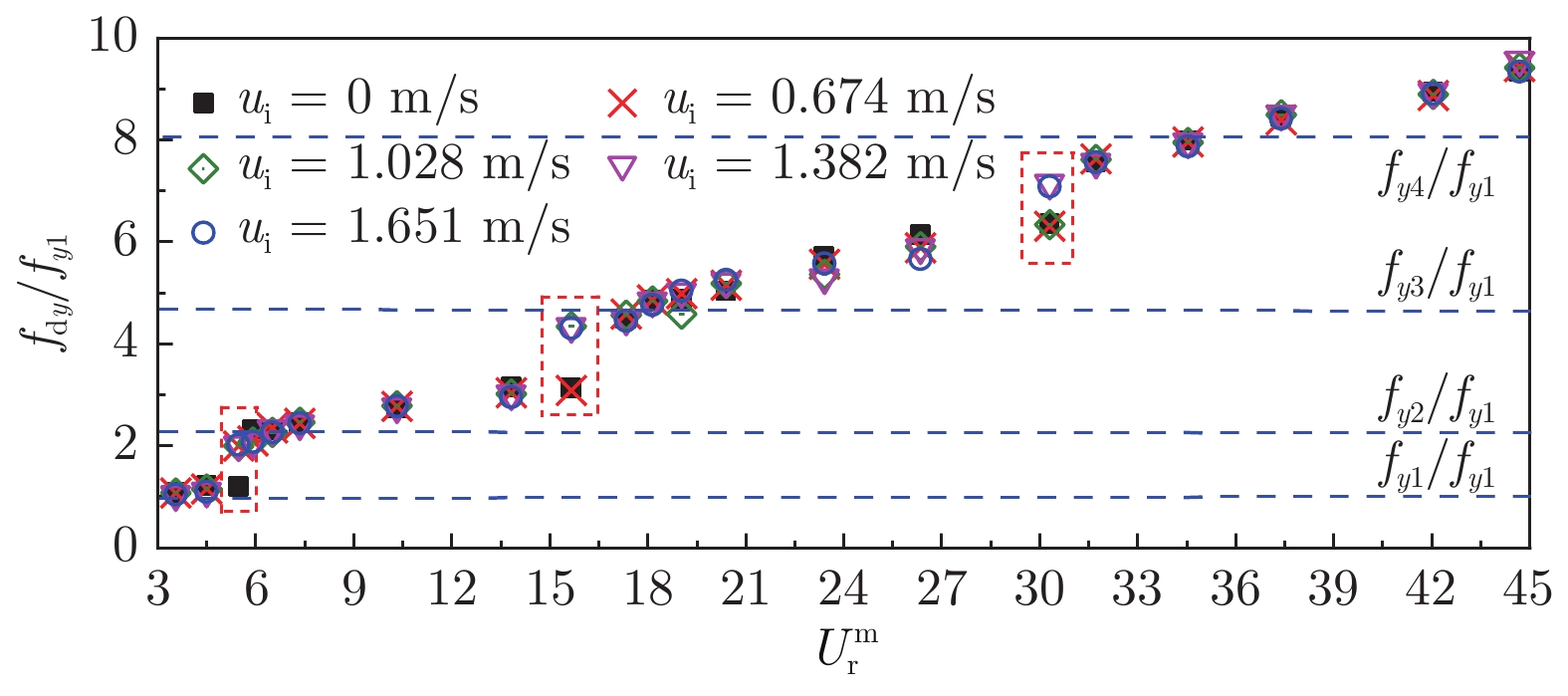
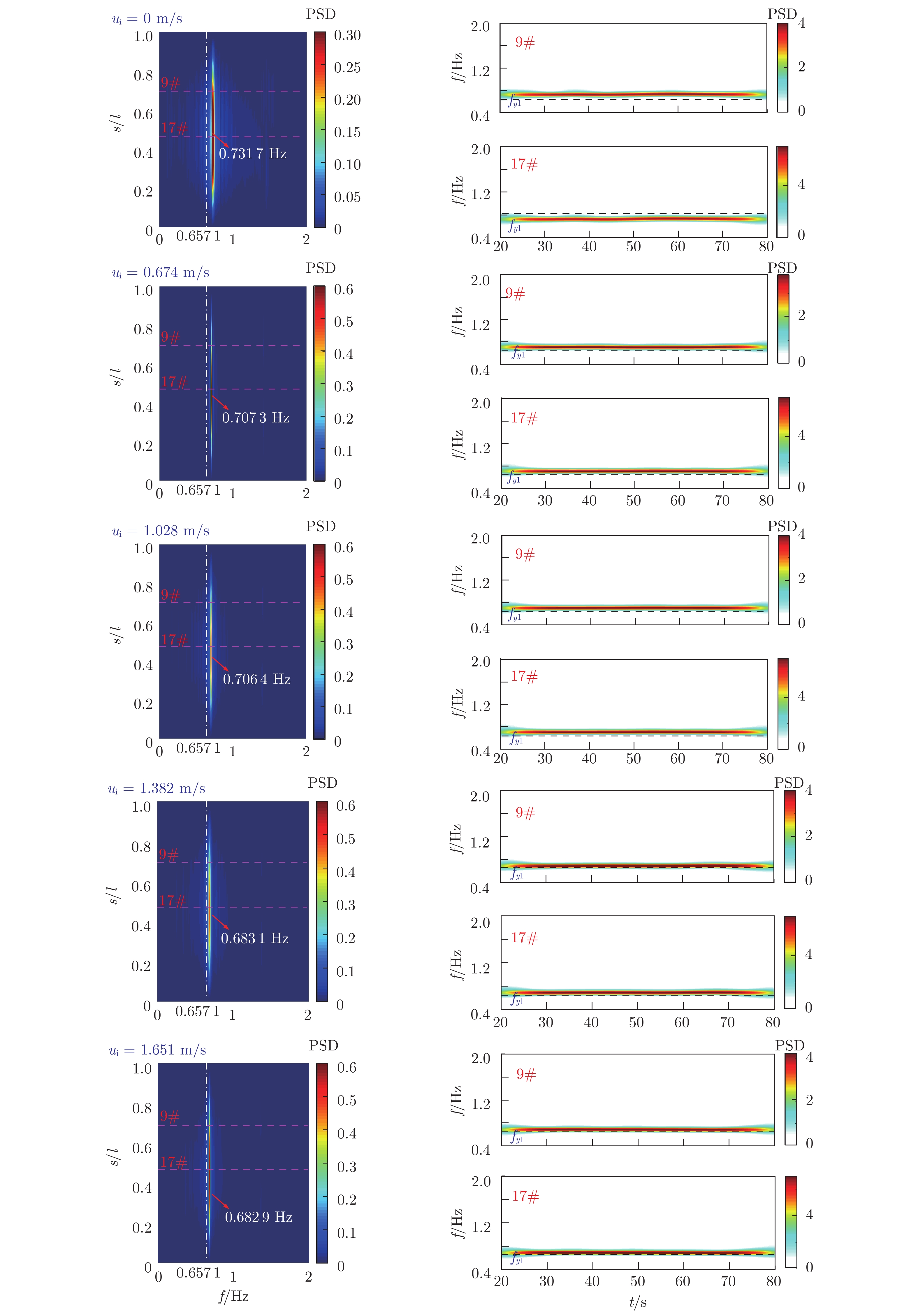
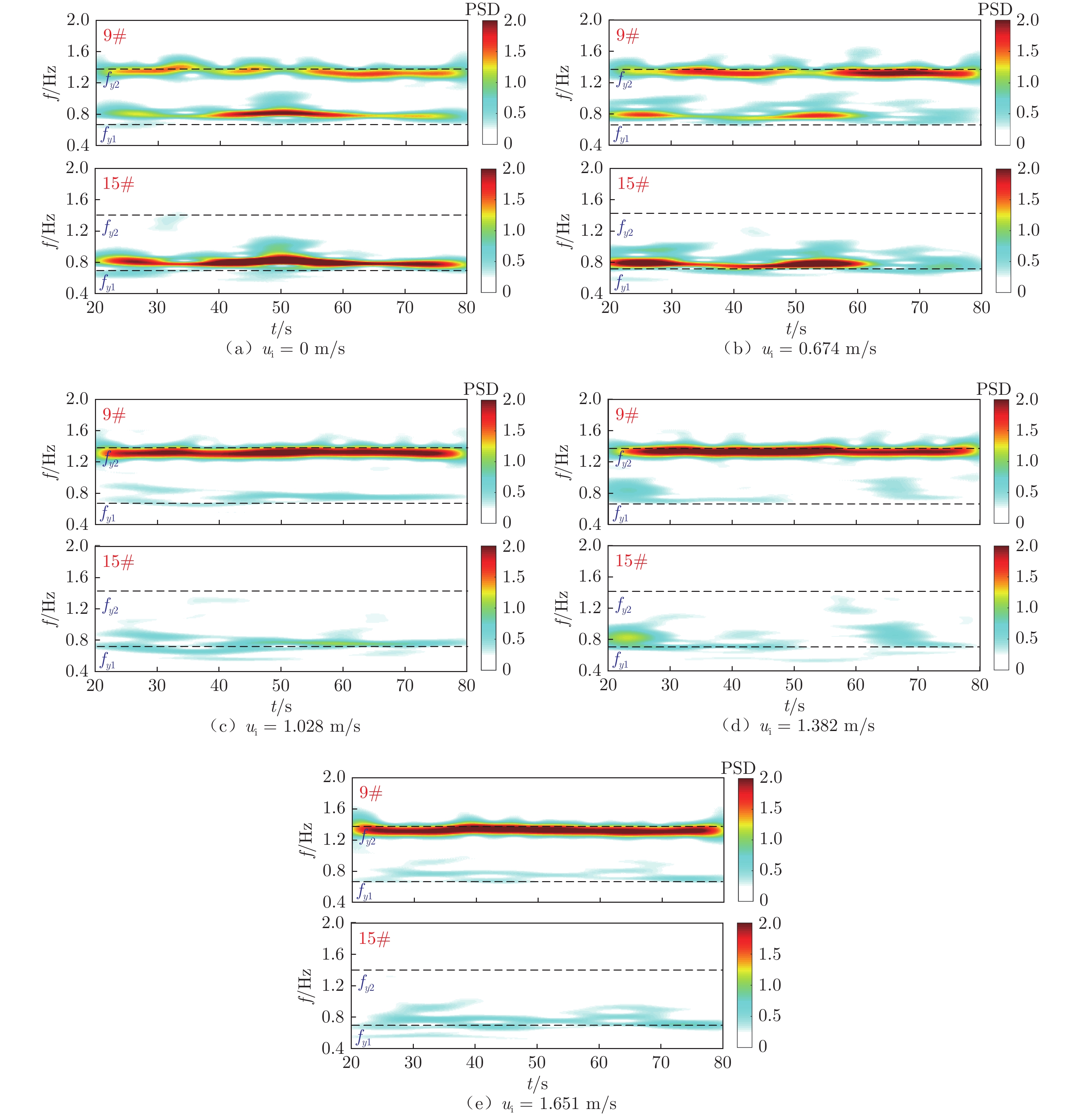
图 6 $\text{U}_{\text{\,{{r}}}}^{\text{{{\,m}}}}$ = 3.55时不同内流流速作用下柔性立管展向的频率分布及典型位置的时频变化
Fig. 6 The power spectra density distribution along the flexible riser span and wavelet time-frequency contours at typical positions of flexible at $\text{U}_{\text{\,{{r}}}}^{\text{{{\,m}}}}$ = 3.55 coupled with different internal velocities
![]()
图 7 $\text{U}_{\text{\,{{r}}}}^{\text{{{\,m}}}}$ = 5.47时内流流速对柔性立管均方根振幅响应的影响
Fig. 7 The influence of internal velocity on the response amplitude of flexible riser at $\text{U}_{\text{\,{{r}}}}^{\text{{{\,m}}}}$ = 5.47
![]()
图 8 $\text{U}_{\text{\,{{r}}}}^{\text{{{\,m}}}}$ = 5.47时不同内流流速作用下典型位置的时频变化
Fig. 8 Wavelet time-frequency contours at typical positions of flexible riser at $\text{U}_{\text{\,{{r}}}}^{\text{{{\,m}}}}$ = 5.47 coupled with different internal velocities
![]()
图 9 $\text{U}_{\text{\,{{r}}}}^{\text{{{\,m}}}}$ = 5.47时不同内流流速作用下柔性立管展向频率分布
Fig. 9 The power spectra density distribution along the flexible riser span at $\text{U}_{\text{\,{{r}}}}^{\text{{{\,m}}}}$ = 5.47 coupled with different internal velocities
表 1 柔性立管模型参数
Table 1 Parameters of the flexible riser model
参数 数值 单位 长度l 1000 mm 水平跨长l0 690 mm 外径D 8 mm 壁厚δ 1 mm 长径比l/D 125 弹性模量E 7.15 × 106 N/m2 单位长度质量m 0.0256 kg/m 质量比m* 1.073 
下载: 导出CSV
-
[1] HUERA-HUARTE F J, BEARMAN P W, CHAPLIN J R. On the force distribution along the axis of a flexible circular cylinder undergoing multi-mode vortex-induced vibrations[J]. Journal of Fluids and Structures, 2006, 22(6-7): 897–903. doi: 10.1016/j.jfluidstructs.2006.04.014
[2] CHAPLIN J R, BEARMAN P W, HUERA HUARTE F J, et al. Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current[J]. Journal of Fluids and Structures, 2005, 21(1): 3–24. doi: 10.1016/j.jfluidstructs.2005.04.010
[3] LEE L, ALLEN D. Vibration frequency and lock-in bandwidth of tensioned, flexible cylinders experiencing vortex shedding[J]. Journal of Fluids and Structures, 2010, 26(4): 602–610. doi: 10.1016/j.jfluidstructs.2010.02.002
[4] BOURGUET R, KARNIADAKIS G E, TRIANTAFYLLOU M S. Vortex-induced vibrations of a long flexible cylinder in shear flow[J]. Journal of Fluid Mechanics, 2011, 677: 342–382. doi: 10.1017/jfm.2011.90
[5] BOURGUET R, KARNIADAKIS G E, TRIANTAFYLLOU M S. Distributed lock-in drives broadband vortex-induced vibrations of a long flexible cylinder in shear flow[J]. Journal of Fluid Mechanics, 2013, 717: 361–375. doi: 10.1017/jfm.2012.576
[6] BOURGUET R, KARNIADAKIS G E, TRIANTAFYLLOU M S. Multi-frequency vortex-induced vibrations of a long tensioned beam in linear and exponential shear flows[J]. Journal of Fluids and Structures, 2013, 41: 33–42. doi: 10.1016/j.jfluidstructs.2012.07.007
[7] BOURGUET R. Vortex-induced vibrations of a flexible cylinder at subcritical Reynolds number[J]. Journal of Fluid Mechanics, 2020, 902: R3. doi: 10.1017/jfm.2020.676
[8] LIN K, WANG J S. Numerical simulation of vortex-induced vibration of long flexible risers using a SDVM-FEM coupled method[J]. Ocean Engineering, 2019, 172: 468–486. doi: 10.1016/j.oceaneng.2018.12.006
[9] LUCOR D, IMAS L, KARNIADAKIS G E. Vortex dislocations and force distribution of long flexible cylinders subjected to sheared flows[J]. Journal of Fluids and Structures, 2001, 15(3-4): 641–650. doi: 10.1006/jfls.2000.0366
[10] SARPKAYA T. Vortex-induced oscillations: a selective review[J]. Journal of Applied Mechanics, 1979, 46(2): 241–258. doi: 10.1115/1.3424537
[11] VANDIVER J K, ALLEN D, LI L. The occurrence of lock-in under highly sheared conditions[J]. Journal of Fluids and Structures, 1996, 10(5): 555–561. doi: 10.1006/jfls.1996.0037
[12] GRIFFIN O M, RAMBERG S E. Some recent studies of vortex shedding with application to marine tubulars and risers[J]. Journal of Energy Resources Technology, 1982, 104(1): 2–13. doi: 10.1115/1.3230377
[13] VANDIVER J K. Dimensionless parameters important to the prediction of vortex-induced vibration of long, flexible cylinders in ocean currents[J]. Journal of Fluids and Structures, 1993, 7(5): 423–455. doi: 10.1006/jfls.1993.1028
[14] BOURGUET R, LUCOR D, TRIANTAFYLLOU M S. Mono- and multi-frequency vortex-induced vibrations of a long tensioned beam in shear flow[J]. Journal of Fluids and Structures, 2012, 32: 52–64. doi: 10.1016/j.jfluidstructs.2011.05.008
[15] NEWMAN D J, KARNIADAKIS G E. A direct numerical simulation study of flow past a freely vibrating cable[J]. Journal of Fluid Mechanics, 1997, 344: 95–136. doi: 10.1017/s002211209700582x
[16] GAO Y, ZHANG Z Z, ZOU L, et al. Effect of boundary condition and aspect ratio on vortex-induced vibration response of a circular cylinder[J]. Ocean Engineering, 2019, 188: 106244. doi: 10.1016/j.oceaneng.2019.106244
[17] DUAN J L, ZHOU J F, YOU Y X, et al. Effect of internal flow on vortex-induced vibration dynamics of a flexible mining riser in external shear current[J]. Marine Structures, 2021, 80: 103094. doi: 10.1016/j.marstruc.2021.103094
[18] GUO H Y, LOU M, DONG X L. Experimental study on vortex-induced vibration of risers transporting fluid[C]//Proc of the Sixteenth International Offshore and Polar Engineering Conference. 2006.
[19] GUO H Y, WANG S Q, WU L, et al. Dynamic characteristics of marine risers conveying fluid[J]. China Ocean Engineering, 2000, 14(2): 153–160.
[20] MENG S, ZHANG X Q, CHE C D, et al. Cross-flow vortex-induced vibration of a flexible riser transporting an internal flow from subcritical to supercritical[J]. Ocean Engineering, 2017, 139: 74–84. doi: 10.1016/j.oceaneng.2017.04.039
[21] CHEN Z S, KIM W J, XIONG C B. Effect of upward internal flow on dynamics of riser model subject to shear current[J]. China Ocean Engineering, 2012, 26(1): 95–108. doi: 10.1007/s13344-012-0007-3
[22] GUO H Y, LOU M. Effect of internal flow on vortex-induced vibration of risers[J]. Journal of Fluids and Structures, 2008, 24(4): 496–504. doi: 10.1016/j.jfluidstructs.2007.10.002
[23] ZHU H J, HU J, GAO Y, et al. Spatial-temporal mode transition in vortex-induced vibration of catenary flexible riser[J]. Journal of Fluids and Structures, 2021, 102: 103234. doi: 10.1016/j.jfluidstructs.2021.103234
[24] ZHU H J, GAO Y, ZHAO H L. Experimental investigation of slug flow-induced vibration of a flexible riser[J]. Ocean Engineering, 2019, 189: 106370. doi: 10.1016/j.oceaneng.2019.106370
[25] ZHU H J, GAO Y, ZHAO H L. Coupling vibration response of a curved flexible riser under the combination of internal slug flow and external shear current[J]. Journal of Fluids and Structures, 2019, 91: 102724. doi: 10.1016/j.jfluidstructs.2019.102724
[26] ZHU H J, LIN P Z, GAO Y. Vortex-induced vibration and mode transition of a curved flexible free-hanging cylinder in exponential shear flows[J]. Journal of Fluids and Structures, 2019, 84: 56–76. doi: 10.1016/j.jfluidstructs.2018.10.009
[27] FAN D X, WANG Z C, TRIANTAFYLLOU M S, et al. Mapping the properties of the vortex-induced vibrations of flexible cylinders in uniform oncoming flow[J]. Journal of Fluid Mechanics, 2019, 881: 815–858. doi: 10.1017/jfm.2019.738
计量
- 文章访问数: 319
- HTML全文浏览量: 108
- PDF下载量: 66
