Infrared thermogram measurement experiment of hypersonic boundary-layer transition of a lifting body
-
摘要:
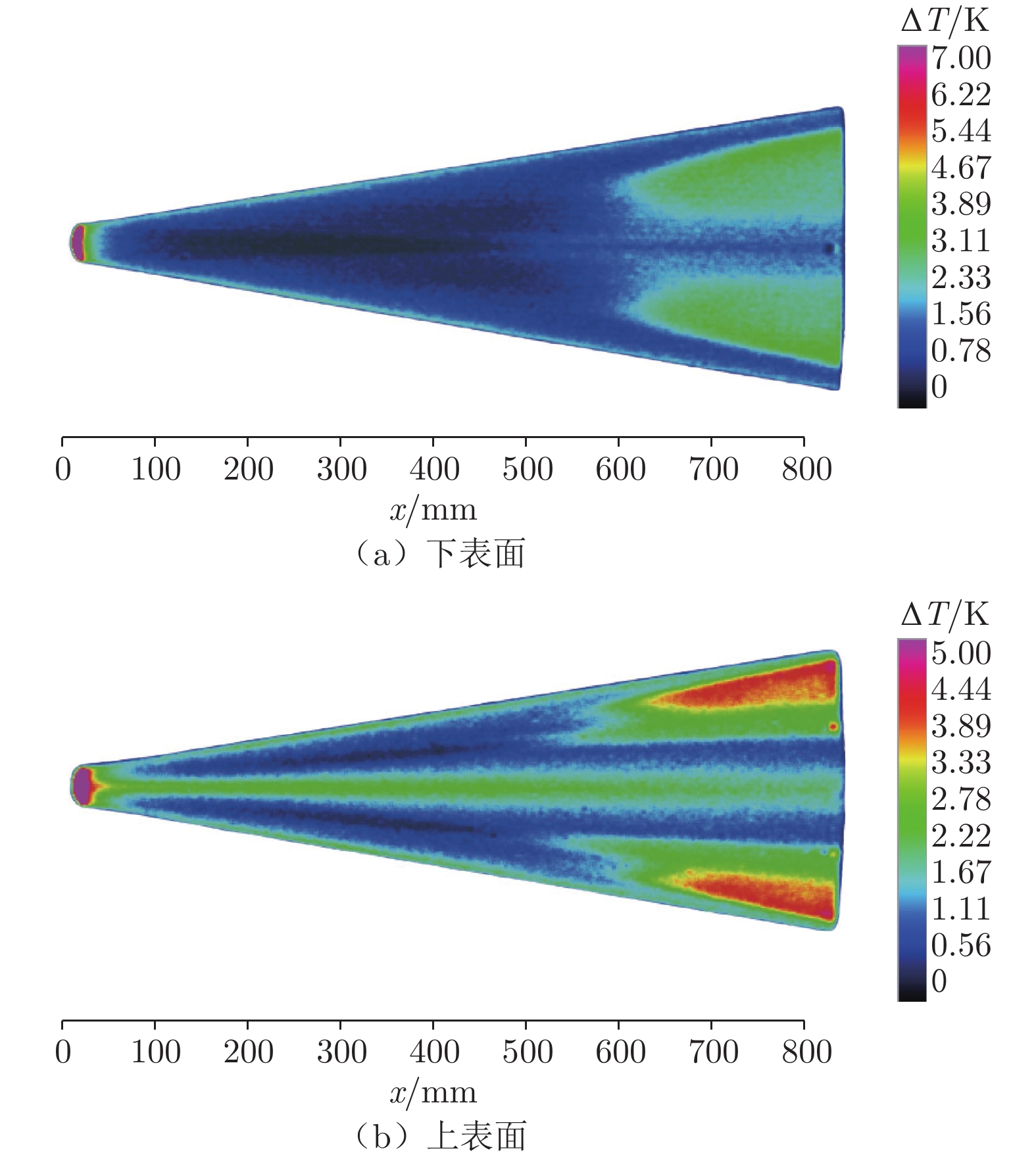
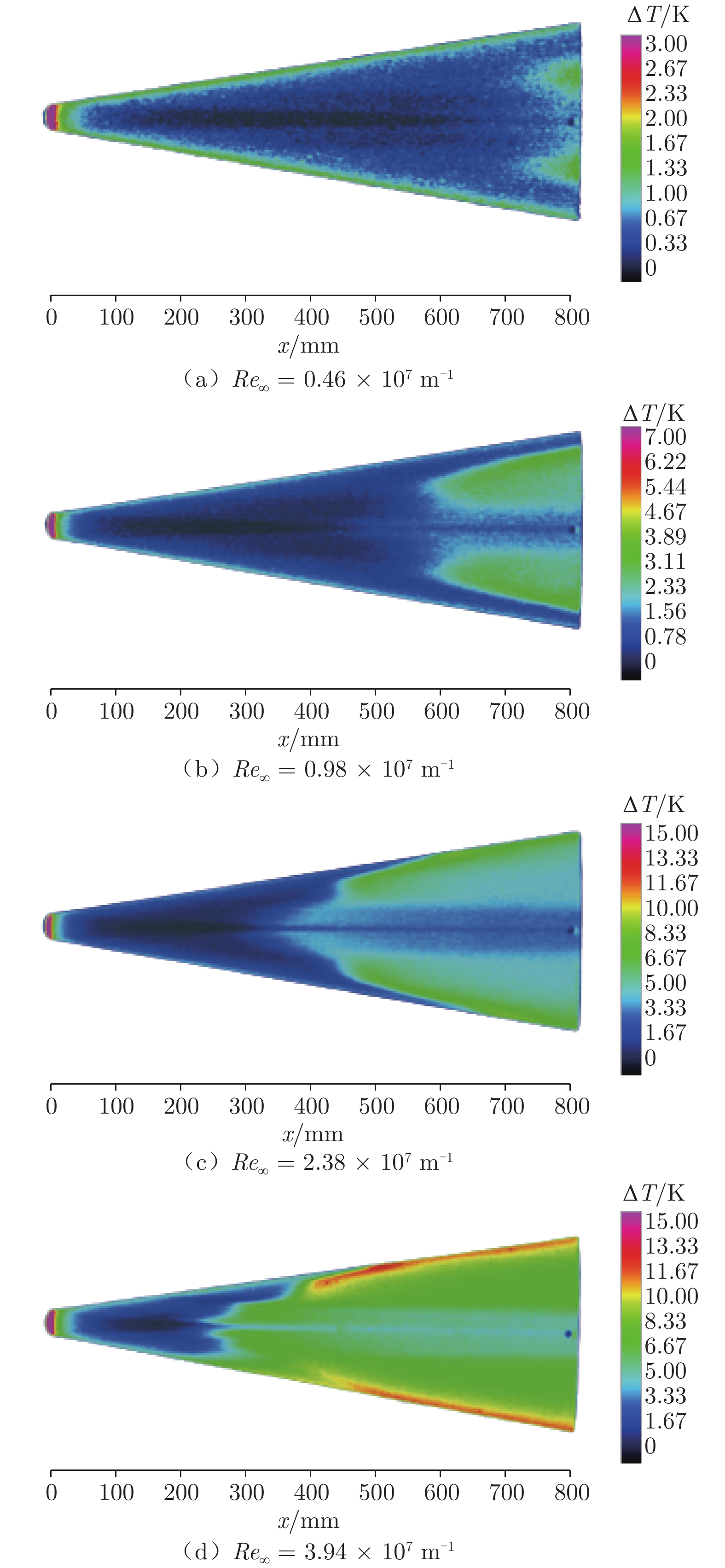
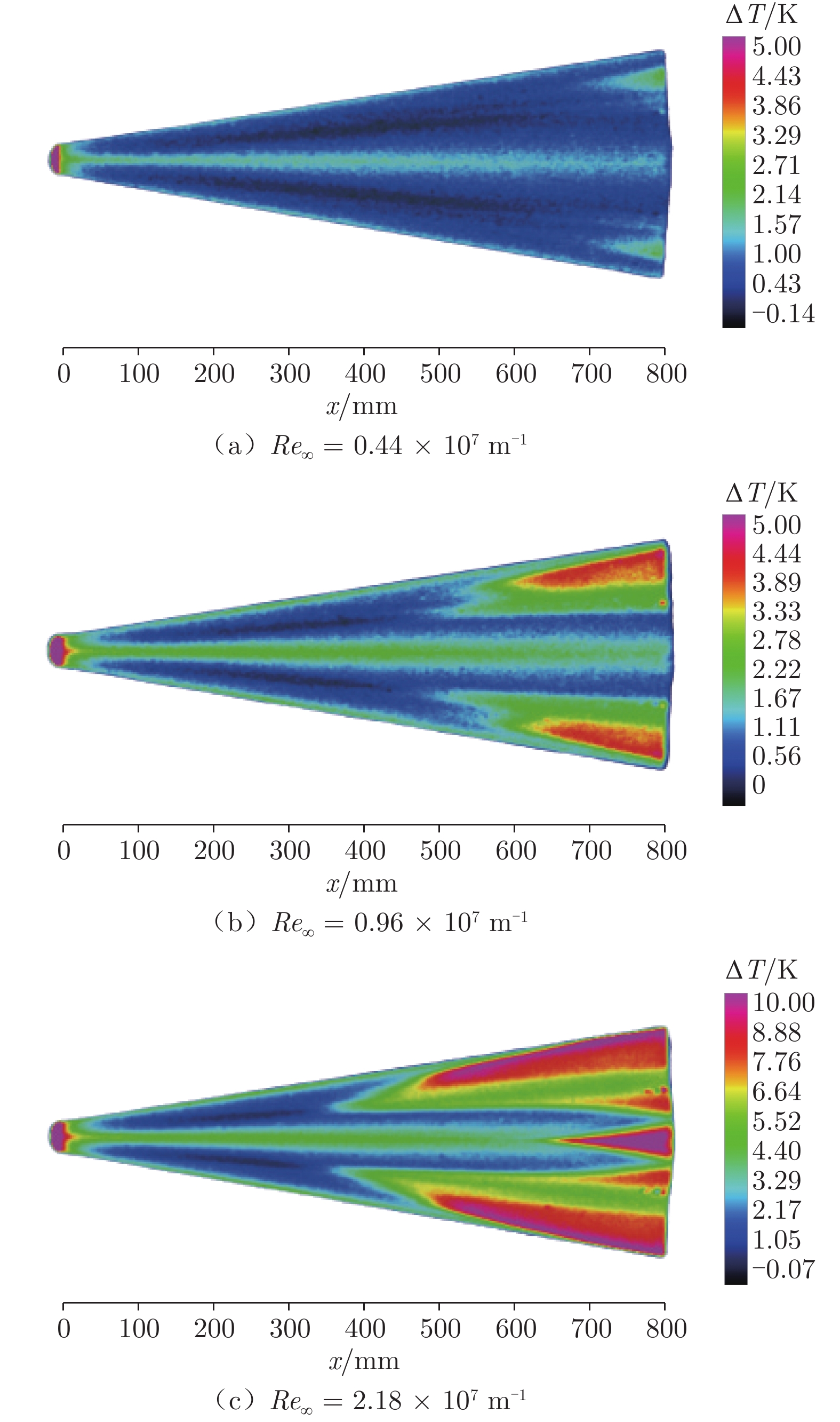
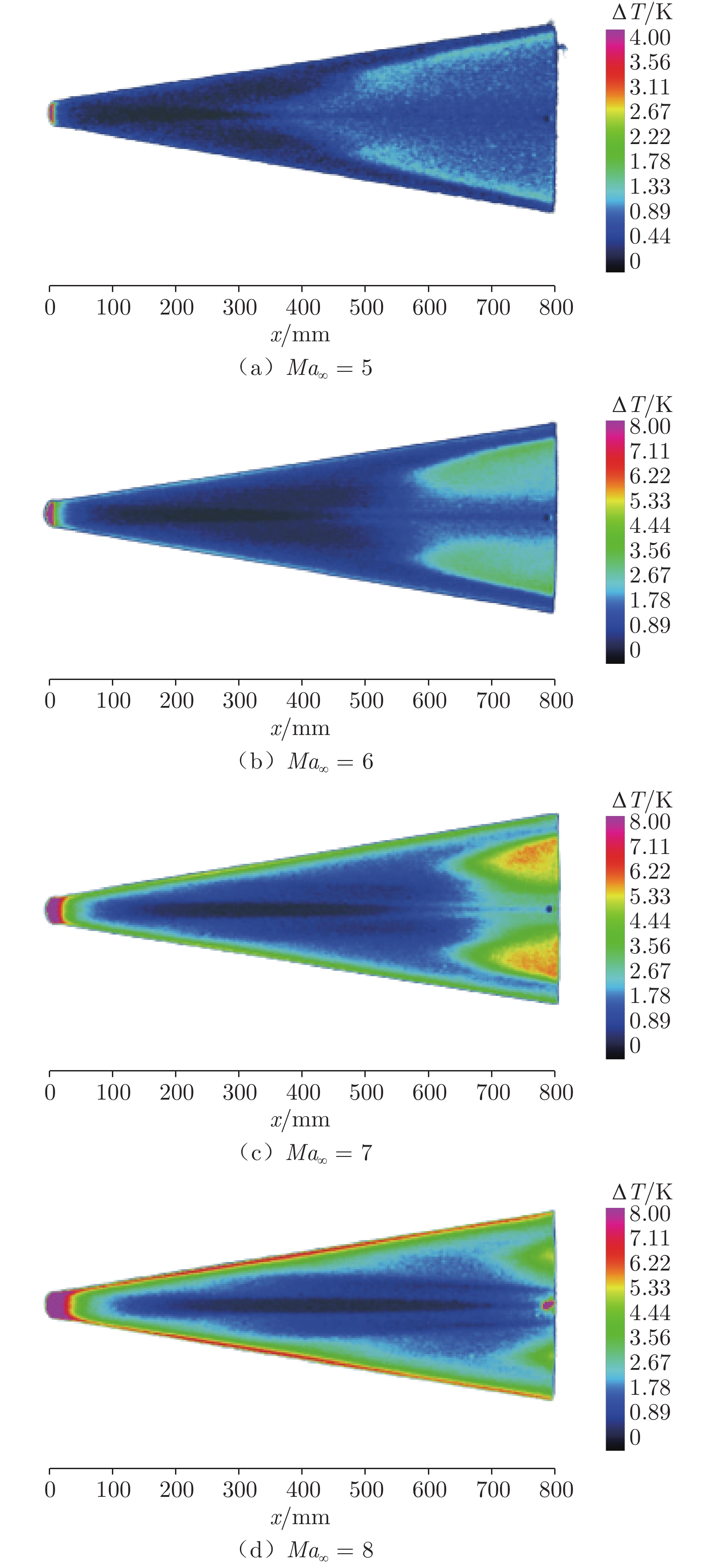
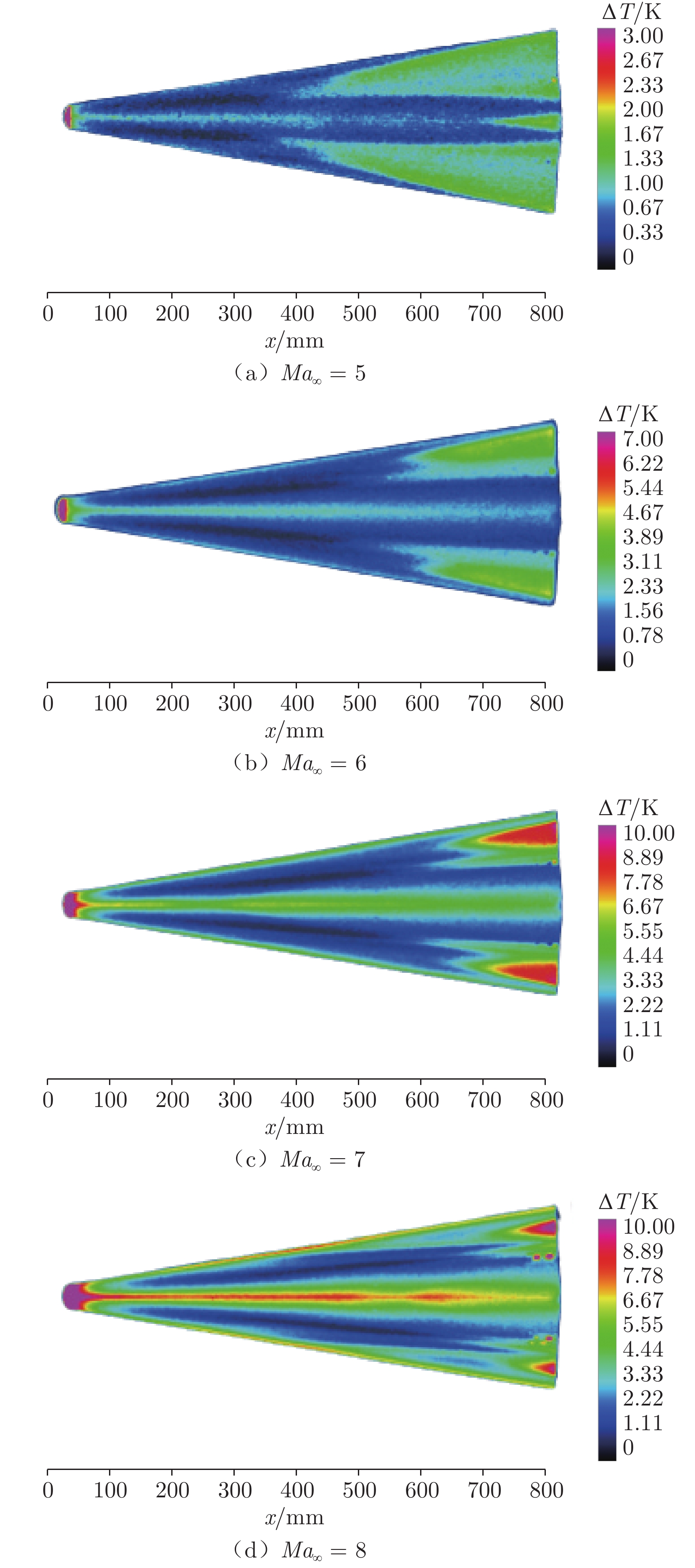
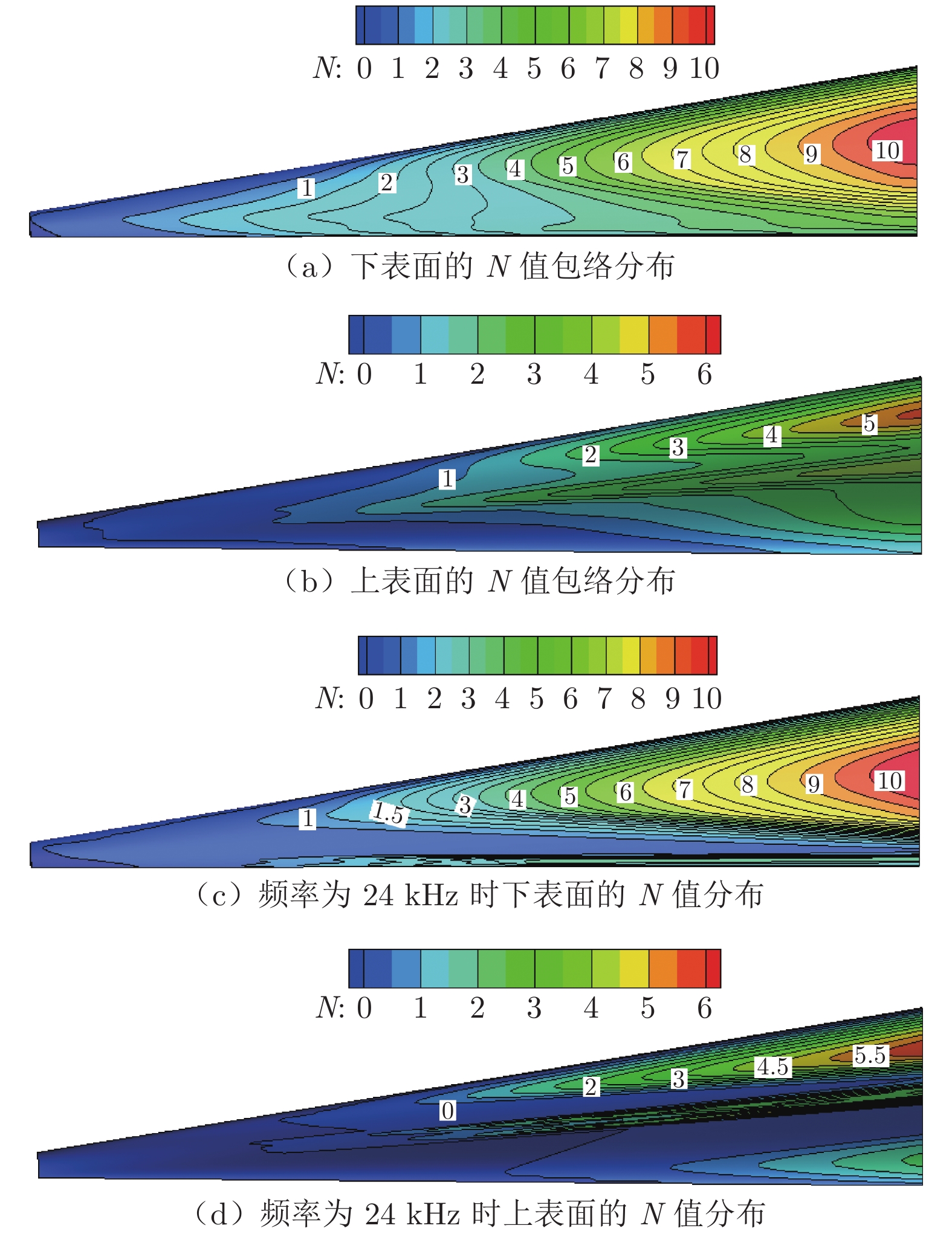
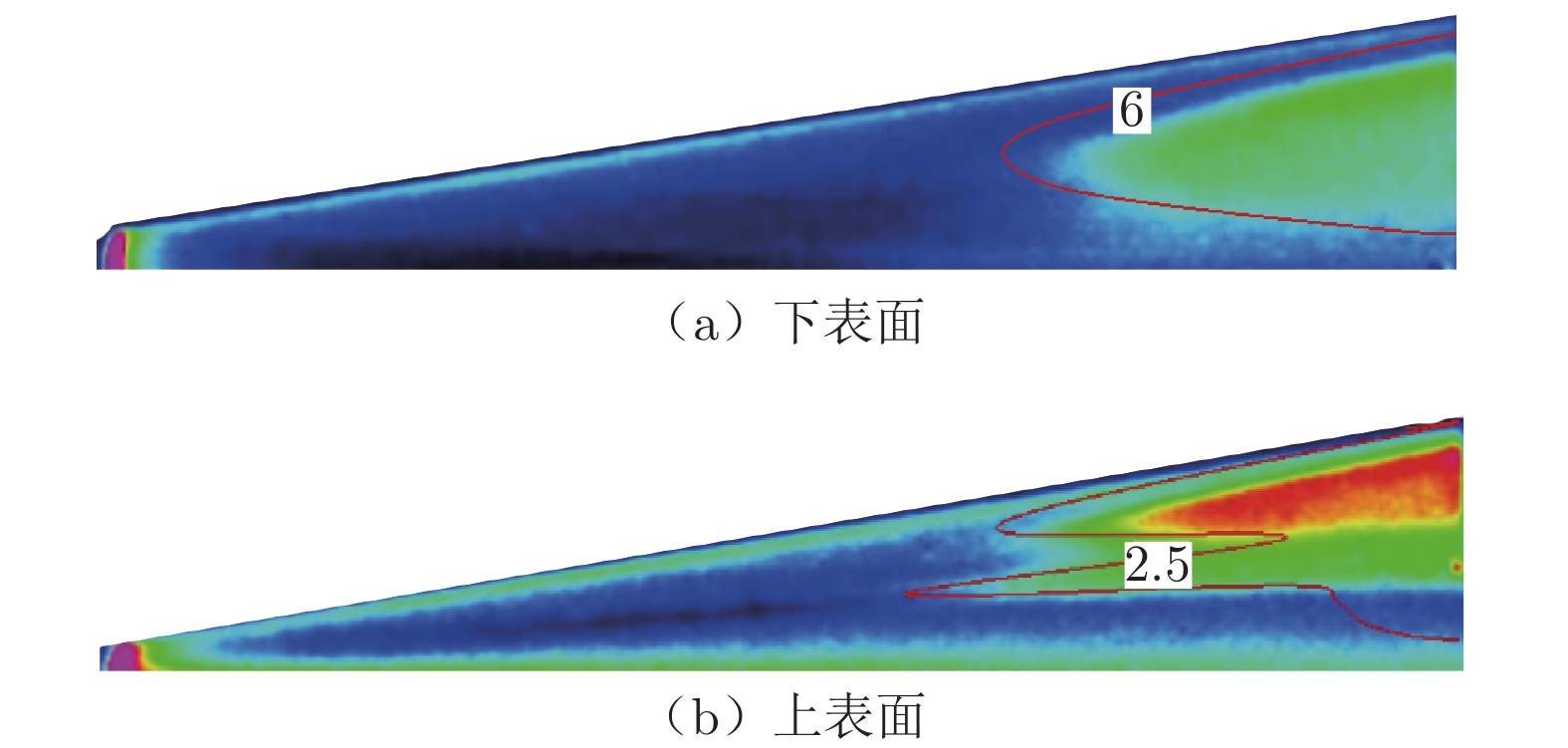
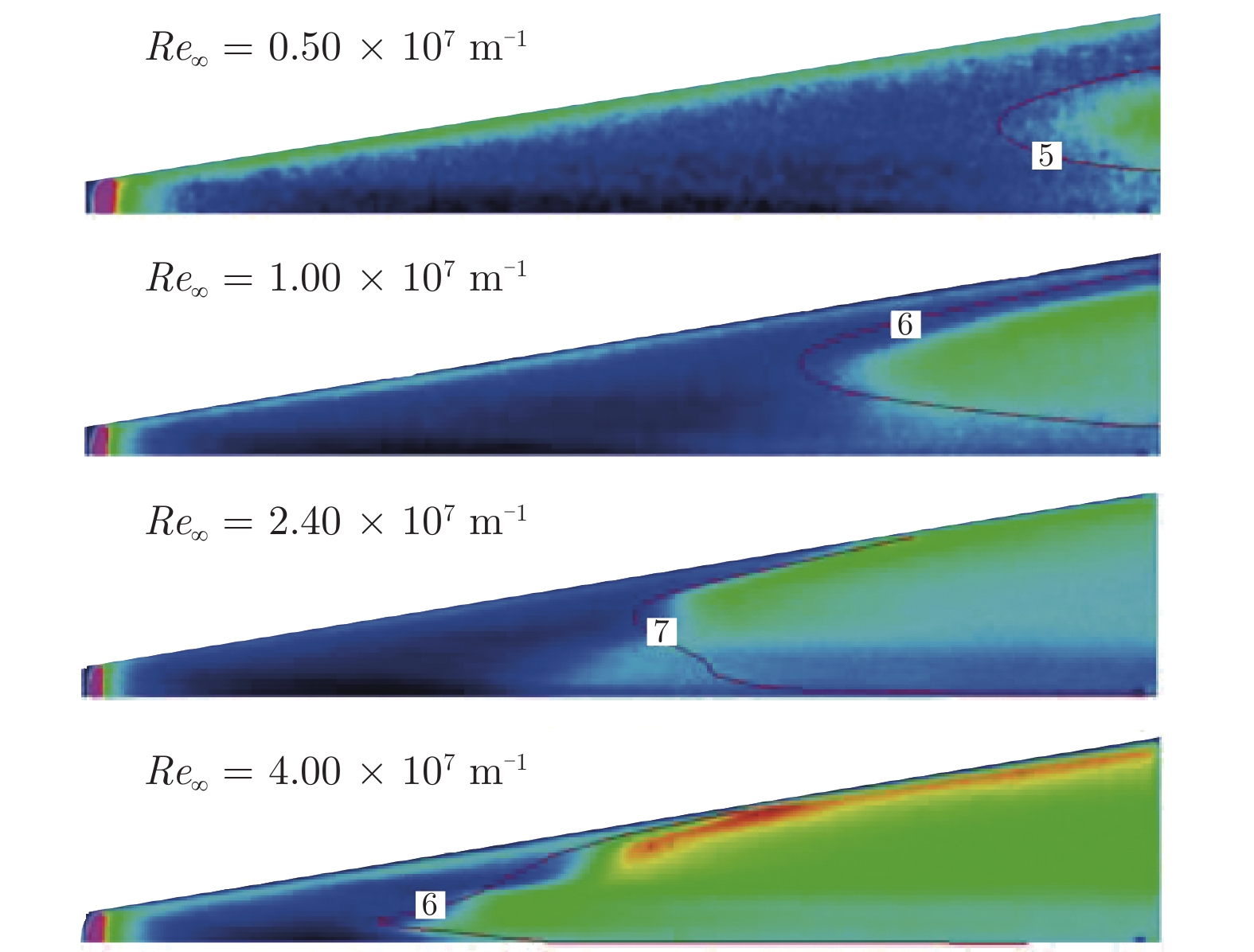
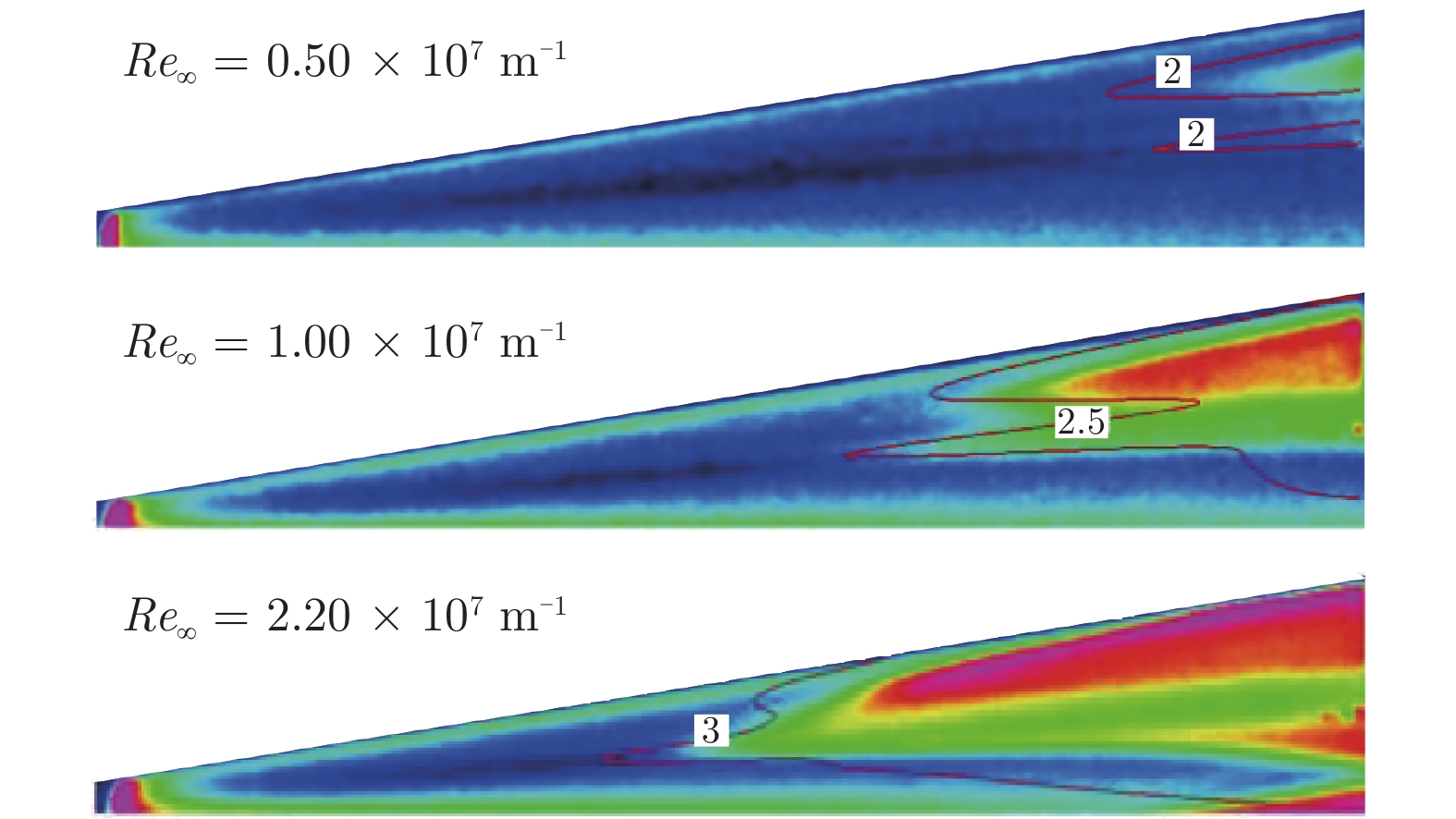
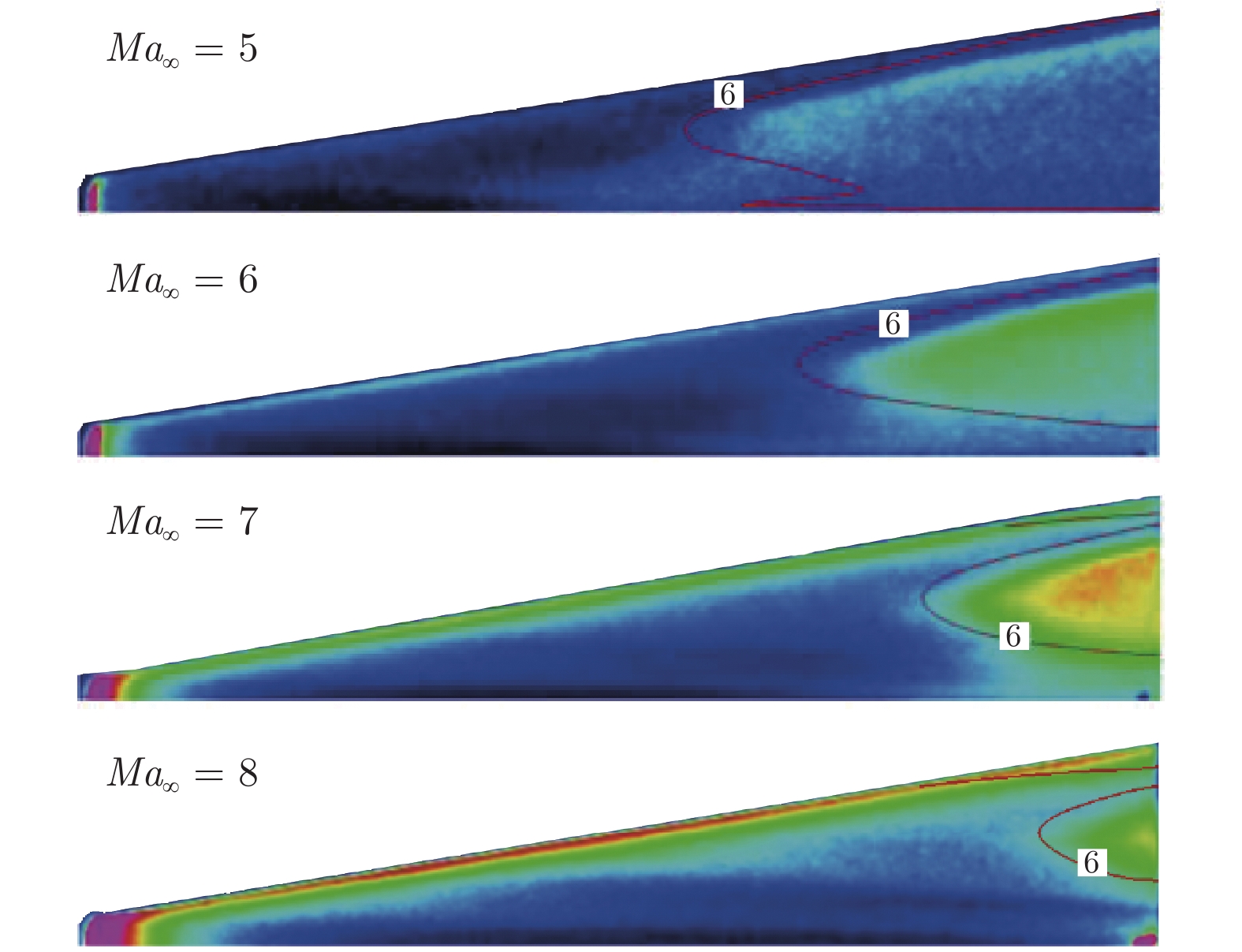
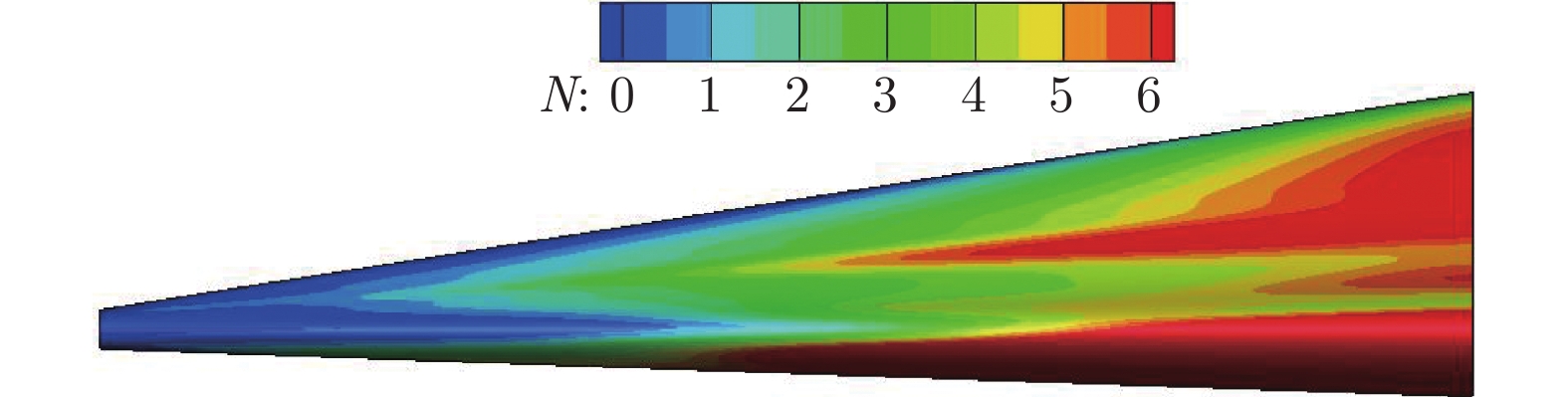
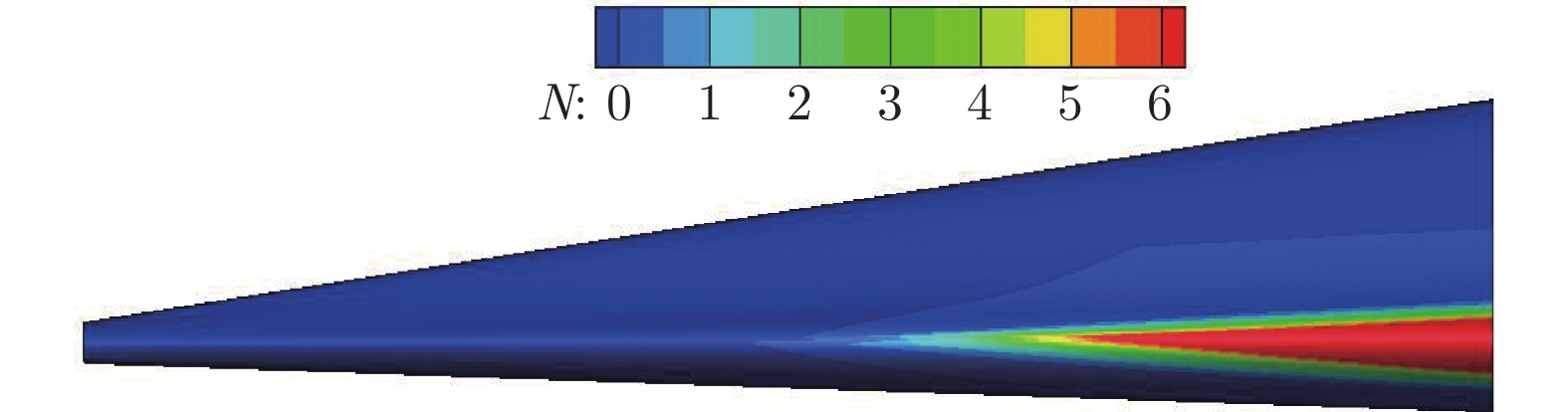
在常规高超声速风洞中，开展了针对升力体模型的边界层转捩红外测量实验，研究了不同单位雷诺数和马赫数对升力体边界层转捩的影响规律，并与eN方法计算结果进行了对比。实验模型长度为800 mm，来流单位雷诺数为0.46 × 107～3.94 × 107 m–1，马赫数为5～8，迎角为0°。通过大面积红外热图技术获得了模型表面温升分布，得到了边界层转捩阵面形状。实验结果表明：在升力体边界层中存在横流失稳和第二模态转捩；随着单位雷诺数增大，横流转捩效应增强，模型下表面和上表面温升增大，转捩阵面前移，转捩区域扩大；随着马赫数增大，横流转捩效应减弱，转捩位置后移，转捩区域显著减小；不同单位雷诺数和马赫数下的转捩N值比较接近，但上、下表面的转捩N值不同（下表面约为6，上表面约为2.5），侧缘在高单位雷诺数下会出现高频第二模态转捩。
Abstract:For a lifting body model, the boundary layer transition infrared thermogram measurement experiment was carried out in the conventional hypersonic wind tunnel, and the influence of different unit Reynolds number and Mach number on the lifting body boundary layer transition was studied, which was compared with the calculation results of the eN method. The length of the experimental model is 800 mm, the unit Reynolds number is 0.46 × 107 – 3.94 × 107 m–1, the Mach number is 5 – 8, and the angle of attack is 0°. The transition position and transition front of the boundary layer on the surface of the model are obtained by the large-area infrared thermogram technology. The analysis of the experimental results shows that there are crossflow instability and the second mode transition in the boundary layer of the lifting body. As the unit Reynolds number increases, the crossflow transition effect increases, the temperature rise on the lower and upper surfaces of the model increases, the transition front moves forward, and the transition area expands; as the Mach number increases, the crossflow transition effect gradually weakens and the transition position moves downstream, and the transition area significantly shrinks back. Moreover, the transition N factor at different Mach numbers and unit Reynolds numbers are relatively close, but the N factors of the upper and lower surfaces are different. The lower surface is about 6, and the upper surface is about 2.5. The high-frequency second mode transition occurs in the side edge at high unit Reynolds numbers.
-
Keywords:
- lifting body /
- hypersonic wind tunnel /
- boundary layer transition /
- infrared thermogram /
- eN method
-
0 引言
目前，要求地面试验设备完全模拟高超声速飞行环境是非常困难的，在一个试验设备上进行所有环境的模拟试验更是不可能的。因此，需要研制多种试验设备，以满足高超声速试验需求[1-5]。
常规高超声速风洞主要模拟参数是马赫数和雷诺数[6]，其他一些参数则主要通过高焓试验设备来模拟[7-8]。
在高超声速风洞运行中，气源不仅要维持风洞所必须达到的压力比，还需要满足雷诺数模拟的要求。一般来说，风洞的总压要足够高。如果风洞连续工作，高的压力比和高总压将使风洞消耗很大的动力，因而高超声速风洞多为暂冲式。
暂冲式常规高超声速风洞的运行方式是：气罐中的压缩空气经过加热系统达到所需温度，然后通过型面喷管，在试验段形成所需的高超声速流场，最后经由超声速扩散段升压后进入引射排气系统，排入大气，或经过冷却器进入真空系统，由真空泵系统排入大气。常规高超声速风洞一般加热温度在800K以下，主要是为了防止气流冷凝，不能真实模拟实际总温(马赫数6时达到1800K)，因此，开展发动机及飞行器一体化带动力试验还需要满足总温要求的高焓设备。
燃烧加热风洞是目前高超声速飞行器地面模拟试验尤其是带动力试验的主要设备。在过去的十几年间，中国空气动力研究与发展中心研制了不同尺度的脉冲燃烧风洞，探索了一体化飞行器设计、计算与试验技术[7-9]。在此基础上，发展了基于脉冲燃烧风洞的大尺度飞行器带动力一体化试验技术[10-11]，提出了一种基于一体化试验直接测力结果的飞行器和发动机性能评估方法。
由于采用燃烧加热方式，无论是采用氢燃料还是碳氢燃料，都会产生水蒸气(H2O)、二氧化碳(CO2)等燃烧产物，即形成所谓“污染”。污染组分将造成风洞试验气体物理化学属性与真实空气存在一定差异，导致地面试验难以完全模拟真实飞行状态下的所有来流参数，且给地面试验结果向真实飞行状态的外推带来不确定性。为了尽可能降低这种不确定性，地面试验一般需要慎重考虑试验来流与模拟对象环境之间的参数匹配问题：即通过有选择地调整污染来流的某些状态参数，使之逼近对应的真实飞行环境，同时放弃一些无法兼顾的非关键参数，以尽可能达到飞行器气动与推进性能的可靠模拟。
目前主要有两种模拟方式：对于气动力试验，一般采用静温、静压、马赫数模拟；对于发动机性能试验，也可以采用总焓、动压、马赫数模拟。
中国科技大学杨基明、罗喜胜等[12-13]通过典型升力体飞行器的试验和计算研究，证明污染组分使得斜激波波后参数相对纯净空气有一定变化，从而造成模型表面压力及模型的气动力有一定变化，但变化量较小。相对于纯净空气来流，污染空气来流时发动机推力、单位推力、比冲均有所下降。脉冲燃烧风洞采用氢氧燃烧加热，污染空气来流时推力性能下降相对较小，与纯净空气来流时较为接近。
西北工业大学宋文艳等[14]研究了H2O/CO2污染煤油燃料对超声速燃烧室的影响，认为污染对点火和超声速燃烧具有一定的抑制作用，污染组分的存在会导致燃烧室模态转换点发生变化。
谭宇等[15]在酒精燃烧和氢气燃烧两种加热方式的风洞设备上开展了匹配方案对超燃冲压发动机性能影响的试验研究，比较了两种目前较常用的气流参数匹配方案，结果表明：对于采用氢气燃烧加热方式的风洞设备，总焓动压马赫数(h0QM)匹配比静温静压马赫数(TPM)匹配能够获得更高的壁面静压和推力收益；对于采用酒精燃烧加热方式的风洞设备，两种匹配方案表现相当。
壁温比通常定义为模型壁面温度与恢复温度的比值。常规高超声速风洞来流温度较低，气流壁面恢复温度与壁面温度相差不大，接近于绝热状态；而燃烧加热脉冲风洞来流温度较高，风洞试验时间很短(300~600ms)，壁面温度基本保持常温，接近于等温状态，气流壁面恢复温度与试验模型表面温差较大，气流对壁面的加热效应明显。壁面温度条件会影响到高超声速边界层内的流动参数，进而影响到流场的波系结构和气动性能。壁温降低引起摩擦系数的增加和边界层厚度减小，使得激波边界层作用区域变小；同时，冷壁使得边界层内亚声速部分声速较低，马赫数更高。
为了评估真实飞行条件下的飞行器气动性能，需重点考虑壁温对燃烧加热脉冲风洞试验结果的影响。
本文采用不通气标模，在常规高超声速风洞以及两个不同尺度(Φ2.4m和Φ600mm)的脉冲燃烧风洞中开展对比测力试验，结合数值计算，研究脉冲燃烧风洞水凝结、雷诺数及壁温比对模型气动性能的影响规律。
1 试验模型
试验模型采用不通气标模。对应Φ2.4m脉冲燃烧风洞，试验模型为大不通气标模，采用背部支撑，如图 1所示；对应常规高超声速风洞和Φ600mm脉冲燃烧风洞，试验模型为1/5缩比的小不通气标模，采用尾部支撑，如图 2所示。
2 脉冲燃烧风洞水凝结影响研究
为了获得水凝结对脉冲燃烧风洞试验数据的影响，采用小不通气标模，在Φ600mm脉冲燃烧风洞开展不同总温条件下的对比试验研究，分析测力结果。
2.1 对比试验参数
对Φ600mm脉冲燃烧风洞喷管进行了试验配套改造，在来流总温、组分不同的条件下，保持风洞出口马赫数一致。以现有的Ma6喷管为基础(总温1500K)，设计制造总温为1200和1800K的喉道段，喷管出口马赫数与现有喷管一致。表 1为不通气高超标模试验参数(p0、T0分别为总压、总温，p、T分别为静压、静温)。
表 1 不同总温高超标模试验参数Table 1 Flow parameters of different T0 testsMa p0/MPa T0/K p/Pa T/K Re 6.0 4.5 1200 2368 162 7.08×106 6.0 5.1 1500 2398 210 4.98×106 6.0 5.8 1800 2374 263 3.61×106 2.2 试验结果
图 3、4给出了不通气高超标模的轴向力系数CA、法向力系数CN随迎角α变化的试验结果曲线。
![]()
图 3 高超标模不同总温试验CA~α曲线Fig. 3 CA~α graph of different T0 tests for the typical hypersonic model![]()
图 4 高超标模不同总温试验CN~α曲线Fig. 4 CN~α graph of different T0 tests for the typical hypersonic model试验表明：在总温1200~1800K试验状态下，最大轴向力系数差别为5.4%，说明水凝结对不通气高超标模的轴向力影响很小，约为5%左右。在-2°迎角时，总温1200K(有水凝结)试验状态的法向力系数较总温1500K减小了约40%；在0°~6°迎角下，法向力系数减小12%~5%，说明随着迎角的增加，模型下表面的凝结水蒸发，导致水凝结对法向力的影响减小。在-2°迎角时，总温1800K试验状态的法向力系数较总温1500K增加了约30%，说明总温1500K、-2°迎角状态在模型的下表面也发生了水凝结，导致模型下表面流场压力升高，法向力系数减小；而在其他迎角状态，总温1500K时并没有发生水凝结现象，因此法向力系数差别较小。
3 脉冲燃烧风洞雷诺数影响研究
3.1 对比试验参数
为了获得雷诺数对试验结果的影响，用不同尺度的不通气标模在Φ2.4m脉冲燃烧风洞和Φ600mm脉冲燃烧风洞进行对比试验，试验参数见表 2(CHIF：脉冲燃烧风洞)。
表 2 试验参数Table 2 Test parametersFacility Ma T0/K p0/MPa Φ2.4m CHIF 6 1575 4.76 Φ600mm CHIF 6 1500 4.61 3.2 试验和计算结果
图 5和6给出了大、小不通气标模在两个脉冲燃烧风洞的轴向力系数CA、法向力系数CN试验结果，同时也给出了两个模型按照对应风洞来流条件计算获得的气动力系数结果。
![]()
图 5 不通气标模轴向力系数计算和试验结果Fig. 5 Numerical and experimental axis force coefficients of the test model![]()
图 6 不通气标模法向力系数计算和试验结果Fig. 6 Numerical and experimental normal force coefficients of the test model计算结果表明：模型尺度对不通气标模的轴向力有一定影响，小不通气标模的轴向力略大于大不通气标模，相差约2%~5%。由于两个脉冲燃烧风洞模拟条件基本相同，试验时间也接近，因此这个差异可以解释为模型尺度(雷诺数)造成的：小不通气标模的雷诺数小于大不通气标模，因此轴向力略大。试验并未能够反映出雷诺数的影响，这可能是由于两个模型支撑方式不同以及试验测量误差掩盖了差异。
两个模型的法向力结果不一致，主要是由于支撑方式不同造成的。前期研究表明，腹部支撑对轴向力影响不大，但对法向力影响显著。
计算与试验结果符合较好，使计算和试验得到了相互验证。
4 脉冲燃烧风洞壁温比影响研究
采用小不通气标模，通过Φ600mm脉冲燃烧风洞及常规高超声速风洞的试验对比，结合数值计算，研究壁温比对脉冲燃烧风洞试验结果的影响。
4.1 对比试验参数
Φ600mm脉冲燃烧风洞与Φ1m常规高超声速风洞的试验流场存在总温、雷诺数、壁温比等方面的差异。假设壁温300K，风洞流场参数对比如表 3所示(HWT：常规高超声速风洞；Tratio为壁温比)。
表 3 Φ1m常规高超声速风洞与Φ600mm脉冲燃烧风洞流场参数Table 3 Test parameters of Φ1m hypersonic wind tunnel and Φ600mm combustion heated impulse facilityFacility Ma p0/MPa T0/K γ Re Tratio Φ1m HWT 6.0 3.00 500 1.40 2.62×107 5.17 Φ600mm CHIF 6.0 4.65 1560 1.36 4.10×106 1.49 4.2 试验和计算结果
脉冲燃烧风洞试验与计算结果表明：采用等温壁300K条件计算获得的阻力系数与试验数据比较接近，误差在6%以内；绝热壁计算阻力系数较等温壁300K计算小5%(迎角6°)~15%(迎角-2°)；不同壁温条件对升力系数的计算结果影响不大，与试验结果的误差分别在6%和8%以内；采用等温壁300K条件计算获得的结果与试验基本一致。图 7和8给出了脉冲燃烧风洞试验和计算的阻力系数CD及升力系数CL的对比曲线。
![]()
图 7 CD~α试验与计算结果对比(脉冲风洞，总温1500K)Fig. 7 CD~α comparison of numerical and experimental results from Φ600mm combustion heated impulse facility![]()
图 8 CL~α试验与计算结果对比(脉冲风洞，总温1500K)Fig. 8 CL~α comparison of numerical and experimental results from Φ600mm combustion heated impulse facility常规高超声速风洞试验和计算结果表明：不同壁温条件对计算结果影响不大，计算结果与试验符合较好，阻力误差在4%以内，升力误差在3%以内。图 9和10给出了相应的阻力系数和升力系数比较曲线。
![]()
图 9 CD~α试验与计算结果对比(常规高超声速风洞)Fig. 9 CD~α comparison of numerical and experimental results from Φ1m hypersonic wind tunnel![]()
图 10 CL~α试验与计算结果对比(常规高超声速风洞)Fig. 10 CL~α comparison of numerical and experimental results from Φ1m hypersonic wind tunnel通过试验验证，表明数值计算具有较高的可信度。为了进一步分析规律，采用数值计算分析了脉冲燃烧风洞与常规高超声速风洞阻力系数的数据相关性，如图 11所示。
![]()
图 11 CD~α计算与试验结果对比(脉冲燃烧风洞和常规高超声速风洞)Fig. 11 CD~α comparison of numerical and experimental results from combustion heated impulse facility and hypersonic wind tunnel(1) 脉冲燃烧风洞等温壁计算得到的阻力系数比常规高超声速风洞大7%(迎角6°)~17%(迎角-2°)，迎角越小，差异越大。这个差异由多方面因素导致，主要有雷诺数、比热比、壁温比等。
(2) 针对同一个模型，分别采用脉冲燃烧风洞和常规高超声速风洞的模拟参数计算(壁面都取绝热壁条件)，此时得到的结果差异应该排除了壁温比的影响，而反映了两个风洞模拟条件(如雷诺数、比热比)不同引起的变化量，计算获得的这一部分的影响量约为3%(迎角6°)~6%(迎角-2°)。
(3) 除去两个风洞模拟条件(如雷诺数、比热比)不同引起的阻力变化量，可得到壁温比的影响量约为4%(迎角6°)~12%(迎角-2°)，迎角越小，差异越大。
5 结论
通过脉冲燃烧风洞与常规高超声速风洞不通气高超标模对比试验和计算，得到如下结论：
(1) 脉冲燃烧风洞获得的气动力系数变化规律与常规高超声速风洞一致；
(2) 雷诺数、壁温比对阻力系数均有影响，其中壁温比影响显著，脉冲燃烧风洞获得的阻力系数明显大于常规高超声速风洞；
(3) 水凝结对不通气高超标模的轴向力影响较小，对法向力影响较大，且不同迎角状态影响量不同。
-
![]()
图 3 模型表面温升分布（Re∞ = 1.00 × 107 m–1）
Fig. 3 Surface temperature rise （Re∞ = 1.00 × 107 m–1）
![]()
图 10 不同雷诺数下的下表面的N等值线与风洞实验结果比较
Fig. 10 N-factor distribution compared with wind tunnel test at different Reynolds numbers on the lower surface
![]()
图 11 不同雷诺数下的上表面的N等值线与风洞实验结果比较
Fig. 11 N-factor distribution compared with wind tunnel test at different Reynolds numbers on the upper surface
![]()
图 12 不同马赫数下的下表面的N等值线与风洞实验结果比较
Fig. 12 N-factor distribution compared with wind tunnel test at different Mach numbers on the lower surface
![]()
图 13 不同马赫数下的上表面的N等值线与风洞实验结果比较
Fig. 13 N-factor distribution compared with wind tunnel test at different Mach numbers on the upper surface
![]()
图 15 侧缘第二模态N值分布（f =
1150 kHz）Fig. 15 N-factor distribution of second mode at side leading-edge （f =
1150 kHz）表 1 实验状态
Table 1 Test conditions
编号 Ma∞ Re∞ /m–1 α /(°) 研究内容 1 6 0.46 × 107～3.94 × 107 0 雷诺数对下表面、
上表面转捩的影响2 5～8 1.00 × 107 0 马赫数对下表面、
上表面转捩的影响
下载: 导出CSV
表 2 流场参数
Table 2 Parameters of flow field
Ma∞ p0
/MPaT0
/Kp∞
/PaT∞
/KRe∞
/m–1模型表面 5 0.50 381 988 64 0.99 × 107 下表面 6 0.51 485 339 60 0.46 × 107 下表面 6 1.11 487 726 60 0.98 × 107 下表面 6 2.78 492 1740 60 2.38 × 107 下表面 6 4.83 506 3030 61 3.94 × 107 下表面 7 2.45 610 608 57 1.04 × 107 下表面 8 4.4 724 436 52 0.99 × 107 下表面 5 0.52 387 1020 65 1.00 × 107 上表面 6 0.48 479 316 59 0.44 × 107 上表面 6 1.10 489 715 60 0.96 × 107 上表面 6 2.81 523 1780 64 2.18 × 107 上表面 7 2.47 609 613 57 1.05 × 107 上表面 8 4.37 733 433 53 0.97 × 107 上表面
下载: 导出CSV
-
[1] 陈坚强, 涂国华, 张毅锋, 等. 高超声速边界层转捩研究现状与发展趋势[J]. 空气动力学学报, 2017, 35(3): 311–337. CHEN J Q, TU G H, ZHANG Y F, et al. Hypersnonic boundary layer transition: what we know, where shall we go[J]. Acta Aerodynamica Sinica, 2017, 35(3): 311–337.
[2] 段毅, 姚世勇, 李思怡, 等. 高超声速边界层转捩的若干问题及工程应用研究进展综述[J]. 空气动力学学报, 2020, 38(2): 391–403. DOI: 10.7638/kqdlxxb-2020.0041 DUAN Y, YAO S Y, LI S Y, et al. Review of progress in some issues and engineering application of hypersonic boundary layer transition[J]. Acta Aerodynamica Sinica, 2020, 38(2): 391–403. doi: 10.7638/kqdlxxb-2020.0041
[3] 孙杭义, 陈喜兰, 罗月培, 等. 高超声速飞行器边界层转捩飞行实验项目地面试验进展[J]. 飞航导弹, 2020(6): 23–28. [4] 李强, 赵磊, 陈苏宇, 等. 展向凹槽及泄流孔对高超声速平板边界层转捩影响的试验研究[J]. 物理学报, 2020, 69(2): 024703. DOI: 10.7498/aps.69.20191155 LI Q, ZHAO L, CHEN S Y, et al. Experimental study on effect of transverse groove with/without discharge hole on hypersonic blunt flat-plate boundary layer transition[J]. Acta Physica Sinica, 2020, 69(2): 024703. doi: 10.7498/aps.69.20191155
[5] CASPER K M, BERESH S J, HENFLING J F, et al. Hypersonic wind-tunnel measurements of boundary-layer transition on a slender cone[J]. AIAA Journal, 2016, 54(4): 1250–1263. doi: 10.2514/1.J054033
[6] JULIANO T J, KIMMEL R L, WILLEMS S, et al. HIFiRE-1 boundary-layer transition: ground test results and stability analysis[C]//Proc of the 53rd AIAA Aerospace Sciences Meeting. 2015. doi: 10.2514/6.2015-1736
[7] 王文, 蒋华兵. 钝锥表面脉动压力风洞试验研究[J]. 装备环境工程, 2021, 18(3): 45–50. WANG W, JIANG H B. Wind tunnel test research on surface pressure fluctuations of a blunt cone[J]. Equipment Environmental Engineering, 2021, 18(3): 45–50.
[8] 陈久芬, 凌岗, 张庆虎, 等. 7°尖锥高超声速边界层转捩红外测量实验[J]. 实验流体力学, 2020, 34(1): 60–66. DOI: 10.11729/syltlx20180172 CHEN J F, LING G, ZHANG Q H, et al. Infrared thermography experiments of hypersonic boundary-layer transition on a 7° half-angle sharp cone[J]. Journal of Experiments in Fluid Mechanics, 2020, 34(1): 60–66. doi: 10.11729/syltlx20180172
[9] 易仕和, 刘小林, 牛海波, 等. 高超声速边界层流动稳定性实验研究[J]. 空气动力学学报, 2020, 38(1): 137–142. YI S H, LIU X L, NIU H B, et al. Experimental study on flow stability of hypersonic boundary layer[J]. Acta Aero-dynamica Sinica, 2020, 38(1): 137–142.
[10] 刘小林. 高超声速条件下圆锥边界层转捩相关实验研究[D]. 长沙: 国防科技大学, 2019. LIU X L. Experimental investigation of the hypersonic boundary layer transition on the cones[D]. Changsha: National University of Defense Technology, 2019.
[11] JULIANO T J, SCHNEIDER S P. Instability and transition on the HIFiRE-5 in a Mach 6 quiet tunnel[C]//Proc of the 40th Fluid Dynamics Conference and Exhibit. 2010. doi: 10.2514/6.2010-5004
[12] WHEATON B M, BERRIDGE D C, WOLF T D, et al. Boundary layer transition (BOLT) flight experiment overview[C]//Proc of the 2018 Fluid Dynamics Conference. 2018. doi: 10.2514/6.2018-2892
[13] BERRIDGE D C, McKIERNAN G, WADHAMS T P, et al. Hypersonic ground tests in support of the boundary layer transition (BOLT) flight experiment[C]//Proc of the 2018 Fluid Dynamics Conference. 2018. doi: 10.2514/6.2018-2893
[14] THOME J, DWIVEDI A, NICHOLS J W, et al. Direct numerical simulation of BOLT hypersonic flight vehicle[C]//Proc of the 2018 Fluid Dynamics Conference. 2018. doi: 10.2514/6.2018-2894
[15] MOYES A, KOCIAN T S, MULLEN C D, et al. Pre-flight boundary-layer stability analysis of BOLT geometry[C]//Proc of the 2018 Fluid Dynamics Conference. 2018. doi: 10.2514/6.2018-2895
[16] KOSTAK H, BOWERSOX R D, McKIERNAN G, et al. Freestream disturbance effects on boundary layer instability and transition on the AFOSR BOLT geometry[C]//Proc of the AIAA Scitech 2019 Forum. 2019. doi: 10.2514/6.2019-0088
[17] COOK D A, THOME J, NICHOLS J W, et al. Receptivity analysis of BOLT to distributed surface roughness using input-output analysis[C]//Proc of the AIAA Scitech 2019 Forum. 2019. doi: 10.2514/6.2019-0089
[18] BERRIDGE D C, KOSTAK H, McKIERNAN G, et al. Hypersonic ground tests with high-frequency instrumentation in support of the boundary layer transition (BOLT) flight experiment[C]//Proc of the AIAA Scitech 2019 Forum. 2019. doi: 10.2514/6.2019-0090
[19] BERRY S A, MASON M L, GREENE F, et al. LaRC aerothermodynamic ground tests in support of BOLT flight experiment[C]//Proc of the AIAA Scitech 2019 Forum. 2019. doi: 10.2514/6.2019-0091
[20] 高清, 李建华, 李潜. 升力体高超声速飞行器横向气动特性研究[J]. 实验流体力学, 2015, 29(1): 43–48. DOI: 10.11729/syltlx20130107 GAO Q, LI J H, LI Q. Study on lateral stability of hypersonic lifting-configurations[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(1): 43–48. doi: 10.11729/syltlx20130107
[21] LIU S S, YUAN X X, LIU Z Y, et al. Design and transition characteristics of a standard model for hypersonic boundary layer transition research[J]. Acta Mechanica Sinica, 2021, 37(11): 1637–1647. doi: 10.1007/s10409-021-01136-5
[22] 陈坚强, 涂国华, 万兵兵, 等. HyTRV流场特征与边界层稳定性特征分析[J]. 航空学报, 2021, 42(6): 124317. CHEN J Q, TU G H, WAN B B, et al. Characteristics of flow field and boundary-layer stability of HyTRV[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(6): 124317.
[23] 陈曦, 董思卫, 袁先旭, 等. 升力体（HyTRV）边界层全局稳定性分析[C]//第十九届全国激波与激波管学术会议论文集. 2020. [24] 罗纪生. 高超声速边界层的转捩及预测[J]. 航空学报, 2015, 36(1): 357–372. LUO J S. Transition and prediction for hypersonic boundary layers[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 357–372.
计量
- 文章访问数: 451
- HTML全文浏览量: 158
- PDF下载量: 107
