Simulation and fabrication of bionic sharkskin composite micro-nano wind resistance reduction structure
-
摘要:
仿生学与减阻技术的结合，为减阻开辟了重要的研究方向，在航空航天领域有着潜在的发展与应用前景。为提高降低风阻效果，本文对复合微纳减风阻结构进行了研究，基于仿生学原理，采用CFD仿真及激光微纳制造技术，建立了减阻结构组合模型，并在飞行器的大气传感器半球头体模型表面制造仿生鲨鱼皮复合微纳结构，即在仿生鲨鱼皮鳞片结构的基础上，通过激光干涉扫描二级微沟槽，以进一步提升减阻效果。采用CFD仿真与风洞实验相结合的方式，对减阻机理进行理论分析，完成了复合结构的微纳制造，减阻率最高可达10.3%。
Abstract:The combination of bionics and drag reduction technology has opened up an important research direction in the field of drag reduction, and has made a significant breakthrough. For better implementation to reduce the wind resistance effect, this paper studies the composite micro-nano drag reduction structure, according to the principle of bionics, through CFD simulation combined with the laser micro-nano fabrication technology. A combined model of drag reduction structure wad established. The flight vehicle air sensor head surface with bionic sharkskin composite micro-nano structures was manufactured by laser interference scanning on the basis of the bionic sharkskin scale structures, to further improve the drag reduction performance. Through the parallel simulation and wind tunnel test, the drag reduction mechanism was theoretically analyzed, and the composite structures were manufactured with a drag reduction rate of up to 10.3%.
-
Keywords:
- shark skin /
- drag reduction /
- wind tunnel testing /
- CFD flow field simulation /
- micro-nano structure /
- scale /
- bionic
-
0 引 言
经过长期自然选择，鲨鱼体表形成了大面积错位排布的微沟槽型鳞片[1]。以往研究证实，该微结构降低了游动阻力，提高了鲨鱼游速。基于仿生学原理，采用现有CFD仿真技术[2]和微纳制造技术[3]，可以制造出仿生鲨鱼皮结构，将其应用于飞行器减阻，能够有效提高飞行速度、降低能耗、延长续航时间。
目前，对仿生微纳减阻结构的研究主要集中于沟槽结构。Walsh[4]研究发现，三角形截面的沟槽结构减阻效果极佳，减阻率最高可达8%。SPEEDO公司生产的鲨鱼皮泳衣通过仿生鲨鱼皮微结构控制人体周围流场，使阻力降低7.5%左右[5]。刘志华等[6]对V型沟槽的研究表明，微沟槽尖峰具有扰流作用，其减阻率可达6.6%。田丽梅等[7]通过对仿生旋成体表面沟槽结构进行仿真计算发现，在44 m/s的速度下，棱纹结构可使旋成体总阻力降低11.12%。上述研究都证实了仿生微沟槽结构减阻的可行性。
本文在大量微纳减阻结构研究成果的基础上，采用CFD仿真与激光微纳制造相结合的方式，设计了仿生鲨鱼皮复合微纳减风阻结构，并在大气传感器半球头体模型表面完成了复合微纳结构的激光制备[8]。基于实验验证与减阻机理分析，对复合微纳结构进行了优化，使减风阻效果得到提升。
1 模型建立与理论分析
1.1 建立模型
1.1.1 建立鲨鱼皮鳞片结构模型
大量研究表明，鲨鱼皮鳞片结构具有很好的减阻效果，相关研究成果也证实了利用鲨鱼皮鳞片结构减阻的可行性。为了客观反映减阻效果及流体流动特性，根据鲨鱼皮鳞片的实际尺寸抽象出了单个鳞片的几何模型。单个鳞片及流场域参数如表1所示，其中，lc、ls分别为鳞片结构的横向长度和纵向长度，h1、h2分别为鳞片中间凸起的高度和两侧凸起的高度，Lx、Ly和Lz分别为计算域的流向长度、法向长度和展向长度。
表 1 实验模型参数Table 1 Experimental model parameterslc = ls h1 = h2 Lx Ly Lz 400 µm 150 µm 350 mm 350 mm 260 mm 采用作图软件UG构建了鲨鱼皮鳞片结构模型（图1），确定了鳞片排布组合方式，并在飞行器的大气传感器半球头体模型表面完成拼接覆盖（图2）。为尽可能在半球头体表面均匀铺满鳞片且不破坏鳞片间扰流的协同作用，基于计算结果将半球头体表面等分为6个区域，按照6个朝向呈放射状等距排列鳞片，每2个鳞片间距均为100 µm（图3）。
![]()
图 2 鲨鱼皮鳞片与半球头体排布组合整体图Fig. 2 Overall view of the combination of sharkskin scales and hemis-pherical head arrangement![]()
图 3 鲨鱼皮鳞片在半球头体表面的排布Fig. 3 The orientation of the scales on the surface of the hemispheric head1.1.2 确定二级微沟槽尺寸
仅依靠鲨鱼皮鳞片结构进行减阻，减阻效果有限。在鲨鱼皮鳞片结构减阻基础上，采用二级微沟槽构造增强减阻效果，即在鲨鱼皮鳞片结构上覆盖尺度更加微小的沟槽结构。基于丛茜等[9]对多种仿生非光滑沟槽减阻效果的验证，同时考虑来流条件下结构的稳定性，选取V型沟槽作为二级微沟槽结构。引入微沟槽无量纲深度h+和无量纲宽度s+进行计算，获得具有最佳减阻效果的临界条件[10]：
$$ {s^ + } = \frac{{s{v_\infty }}}{\nu }\sqrt {\frac{{{c_f}}}{2}} $$ (1) $$ {h^ + } = \frac{{h{v_\infty }}}{\nu }\sqrt {\frac{{{c_f}}}{2}} $$ (2) 式中：s为槽宽，h为槽深；v∞为风速；ν为气流的运动黏度；摩擦系数cf = 0.072(Re)$ ^{ - \frac{1}{5}} $。基于Walsh等的研究以及制造的可行性，选取具有最佳减阻效果的临界条件s+ = h+，即s = h = 10 µm。二级微沟槽结构如图4（a）所示。
![]()
图 4 二级微沟槽结构及其在鲨鱼皮鳞片结构上的排布（截面图）Fig. 4 Secondary microgrooves and the arrangement of secondary microgrooves on sharkskin scales (cross-sectional view)在气固两相绕流体动态模拟过程中[11-12]，为减缓速度梯度过大导致的湍流，将微沟槽截面设计为具有周期结构的类正弦状图形[13-14]。二级微沟槽则是在鳞片结构上进一步加工的微结构。为有效叠加两级微沟槽的减阻效果，微元区域需选取为包含鳞片和两鳞片间距在内的正方形区域（边长500 µm），且该区域所有二级微沟槽沿鳞片结构纵向开槽并贯穿整个鳞片表面，其截面如图4（b）所示。采用微元法仿真小区域微结构的气流流动过程，得出该区域的减阻率，继而通过积分表征出带有二级微沟槽结构的整个半球头体的减阻水平。
1.1.3 选择求解模型
在风洞实验过程中，气流在半球头体表面产生摩擦阻力和压差阻力，并具有一定黏附性。由于湍流的存在，半球头体受力不断变化。本文选取k–ω SST模型进行求解[15]，该模型对解的初始预测非常敏感，对边界层附近区域的网格划分也较为精细[16]，计算精度高，对壁面气流流动黏性和分离界限的计算尤其精细，在工业应用中较为普适。
1.2 理论分析
在一定速度来流条件下，飞行器表面会出现湍流，需采用N–S方程进行求解与分析。式（3）即为该过程的N–S方程，式（4）～（6）为分解到x、y、z方向的动量方程[17]：
$$ {\text{div }}{ {σ}} {\text{ = 0}} $$ (3) $$ \frac{{\partial {\boldsymbol{u}}}}{{\partial t}} + {\text{div}}( {{\boldsymbol{u}}{ {σ}} } ) = - \frac{1}{\rho }\frac{{\partial {\boldsymbol{p}}}}{{\partial x}} + {\boldsymbol{v}}{\text{div}}\left[ {{\text{grad}}( {\boldsymbol{u}} )} \right] $$ (4) $$ \frac{{\partial {\boldsymbol{v}}}}{{\partial t}} + {\text{div}}( {{\boldsymbol{v}}{ {σ}} } ) = - \frac{1}{\rho }\frac{{\partial {\boldsymbol{p}}}}{{\partial y}} + {\boldsymbol{v}}{\text{div}}\left[ {{\text{grad}}( {\boldsymbol{v}} )} \right] $$ (5) $$ \frac{{\partial {\boldsymbol{w}}}}{{\partial t}} + {\text{div}}( {{{{\boldsymbol{w}}{ {σ}}}} } ) = - \frac{1}{\rho }\frac{{\partial {\boldsymbol{p}}}}{{\partial z}} + {\boldsymbol{v}}{\text{div}}\left[ {{\text{grad}}( {\boldsymbol{w}} )} \right] $$ (6) 将x方向的动量方程进行速度与压力分解，并代入N–S方程，整理后可得：
$$ \frac{{\partial {\boldsymbol{U}}}}{{\partial t}} + {\rm{div}}( {{\boldsymbol{U}}{ {τ}} } ) + {\rm{div}}( {\overline {{{\boldsymbol{u}}'}{{ {σ}} '}} } ) = - \frac{1}{\rho }\frac{{\partial {\boldsymbol{P}}}}{{\partial x}} + {\boldsymbol{v}}{\rm{div}}\left[ {{\rm{grad}}( {\boldsymbol{U}})} \right] $$ (7) 式中：${ {σ}} $为气流的速度矢量；${\boldsymbol{u}}、{\boldsymbol{v}}、{\boldsymbol{w}} $分别为${ {σ}}$分解到x、y、z方向的速度矢量；${ {τ}}$和${\boldsymbol{U}} $分别为气流时均速度和x方向的时均速度；${\boldsymbol{p}} $和${\boldsymbol{P}} $分别为气流对目标体的压力和时均压力；${ {σ}}'$和$ {\boldsymbol{u}}' $分别为气流脉动速度和x方向气流脉动速度；ρ为流体密度。
可以看到，式（7）增加了一个附加项$ \operatorname{div}(\overline{{\boldsymbol{u}} '{ {σ}}'}) $，即雷诺应力项。同理，其他两个方向也都增加了一个雷诺应力项。雷诺应力项的出现引起了湍流现象，说明该项即为湍流产生的条件[18]。
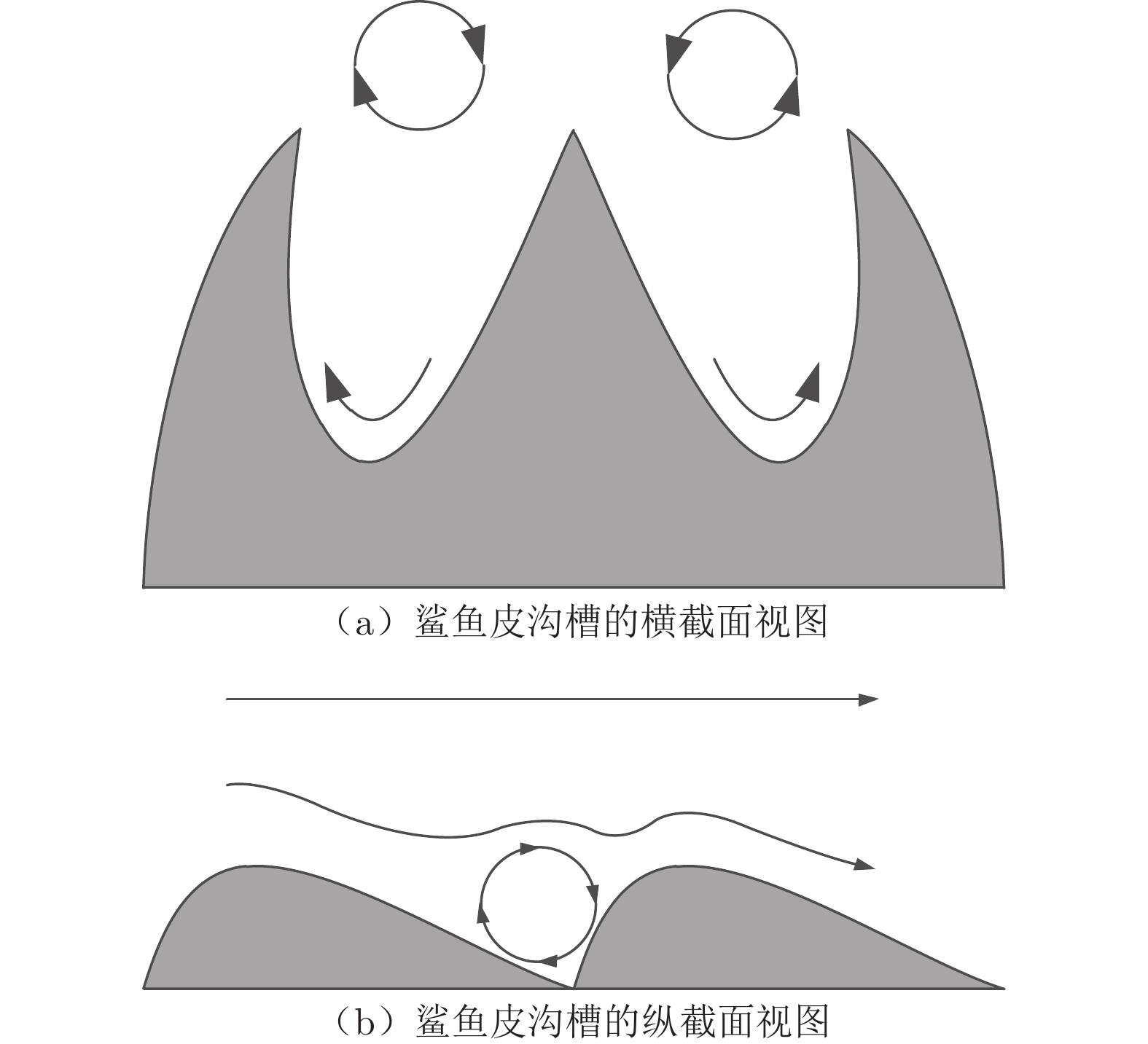
半球头体表面的速度梯度很大，因而涡量很大，这也是流场中旋涡形成的主要原因，边界层分离会导致旋涡的周期性脱落。图5（a）和（b）为仿生鲨鱼皮横、纵截面的气流流动视图，沟槽内回转的涡流受到鲨鱼皮鳞片凸起的阻碍，产生“二次涡”，减弱了微结构表面与低速条带相关联的涡流强度，抑制了低速条带的形成，并削弱了低速气流运动的不稳定性，即低速条带缓慢向上提升的过程被减弱，流体微团间的动量交换降低，从而达到减阻效果[19-20]。
2 实验与讨论
为更好地进行对比分析，将光滑半球头体与覆盖仿生鲨鱼皮鳞片结构的半球头体置于同一流场域中，在相同条件下进行仿真，风洞检测模型如图6所示。严格设定边界条件，将左右壁面定义为对称边界，上下表面无滑移，流体介质设置为空气，出入口设置为速度入口、压力出口。
![]()
图 6 光滑半球头体风洞检测模型和覆盖仿生鲨鱼皮鳞片的半球头体风洞检测模型Fig. 6 Wind tunnel detection model of smooth hemispheric head and wind tunnel inspection models of hemispherical cephalic bodies covered with bionic sharkskin scales网格划分是有限元处理的关键[21]，网格质量决定了仿真结构正确与否。在CFD仿真过程中，覆盖于半球头体表面的每个仿生鲨鱼皮鳞片都需要极高精度的网格划分进行表征。由于计算机CPU、GPU运行速度有限，为提高计算速度及效率，将半球头体对称均分为24份，取其中之一代替整体进行风洞实验的仿真。图7为仿生鲨鱼皮的网格划分，总网格数为34300011，实体离散化节点7262815个，网格最小尺寸为10 µm，平均网格质量达0.88，网格质量良好，有助于计算收敛。
网格划分完成后进行仿真计算，根据空气阻力系数公式（8）进行求解：
$$ C = \frac{{2F}}{{\rho v_\infty ^2A}} $$ (8) 式中，C为空气阻力系数，F为阻力，ρ为空气密度，A为迎风面积，v∞为风速。
针对覆盖仿生鲨鱼皮鳞片的半球头体和对照组光滑半球头体，分别求解150 km/h（41.67 m/s）和160 km/h（44.44 m/s）风速下的阻力及阻力系数。当迭代曲线收敛后，根据积分原理还原出整个模型的受力情况，最后采用式（9）求得减阻率：
$$ {\text{Δ}} C = \frac{{\left| {{C_1} - {C_0}} \right|}}{{{C_0}}} $$ (9) 由仿真计算（计算方法详见文献[22]）结果得到阻力值及阻力系数，如表2所示，2个风速下的减阻率分别为16.9%和18.4%。
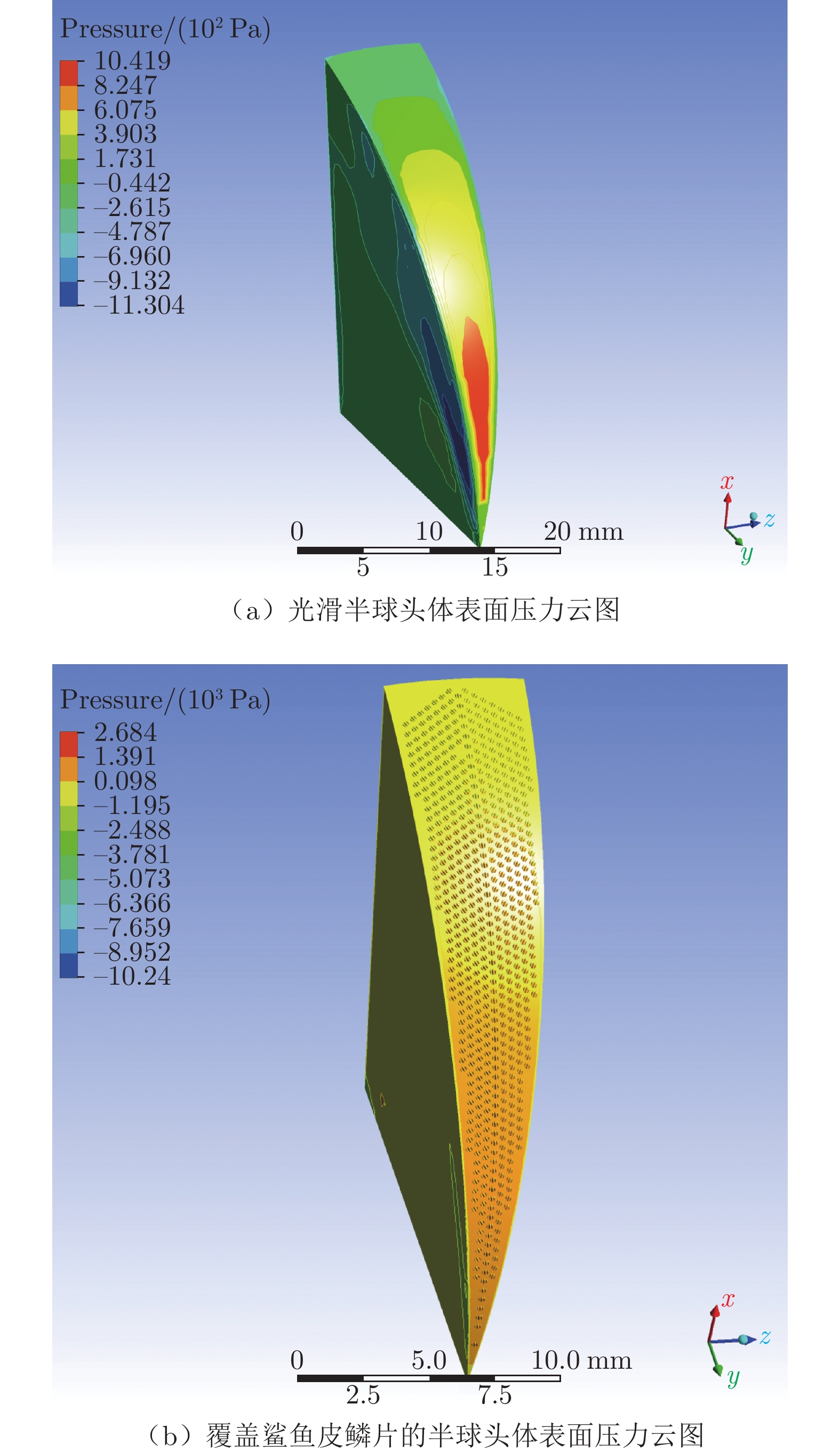
表 2 CFD仿真参数Table 2 CFD simulation parameter样品 v∞/(km·h–1) F/N C ΔC 光滑半球头体 150 1.499 0.413 － 覆盖鳞片的半球头体 150 1.245 0.343 16.9% 光滑半球头体 160 1.731 0.419 － 覆盖鳞片的半球头体 160 1.407 0.342 18.4% 由式（8）可知，当空气密度、迎风面积和风速均相同时，阻力系数与阻力线性相关，两者趋势相同。迭代曲线稳定并收敛后，同一风速下覆盖仿生鲨鱼皮鳞片的半球头体的迭代次数比光滑半球头体明显减少。微结构的存在使迭代曲线更快收敛。为更直观地表征减阻效果，通过后处理得到光滑半球头体与覆盖仿生鲨鱼皮鳞片的半球头体同一位置的压力云图和速度矢量云图，如图8～10所示。
![]()
图 8 光滑半球头体y = 0处的速度矢量云图及局部放大图Fig. 8 The velocity vector cloud of the smooth hemispheric head aty = 0 and an enlarged version![]()
图 9 覆盖鳞片的半球头体y = 0处的速度矢量云图及局部放大Fig. 9 Velocity vector cloud image of hemispherical head covered by sharkskin structure at y = 0 and an enlarged version![]()
图 10 同一部分半球头体的压力云图Fig. 10 Pressure cloud images of the same part of hemispheric cephalic body由图8和9可知，在半球头体前端，具有一定速度的气流在垂直方向（y方向）受到半球头体阻滞，瞬时速度降为0，全部动压转变为静压，在迎角微小的前端，存在一个较大正压区。图8中光滑球头体表面的边界层很薄，与之相比，由于鳞片的存在，图9中边界层厚度明显增大，混合层厚度减小，结合等高线对应数值跨度可以看到来流速度明显降低。
对比图10（a）与（b）可以看到：1/24光滑半球头体表面压力云图颜色明显分层，表明压力损失较大；而覆盖仿生鲨鱼鳞片的半球头体表面压降变化不明显，无明显压力损失，受力更加均匀，受力最大的正压区阻力也明显降低，可见仿生鲨鱼皮鳞片实现了很好的减阻效果。
在相同边界条件下对带有二级微沟槽的微元区域仿真计算，得到稳定的阻力系数为1.896 × 10−9，而光滑微元区域的阻力系数为1.986 × 10−9，减阻率为4.5%。经计算，两模型在风速为150和160 km/h时的雷诺数分别为2.7 × 106和2.9 × 106，且壁面第一层网格单元的y＋均集中于0.8～2.0之间，进一步证明了边界层网格划分的合理性。
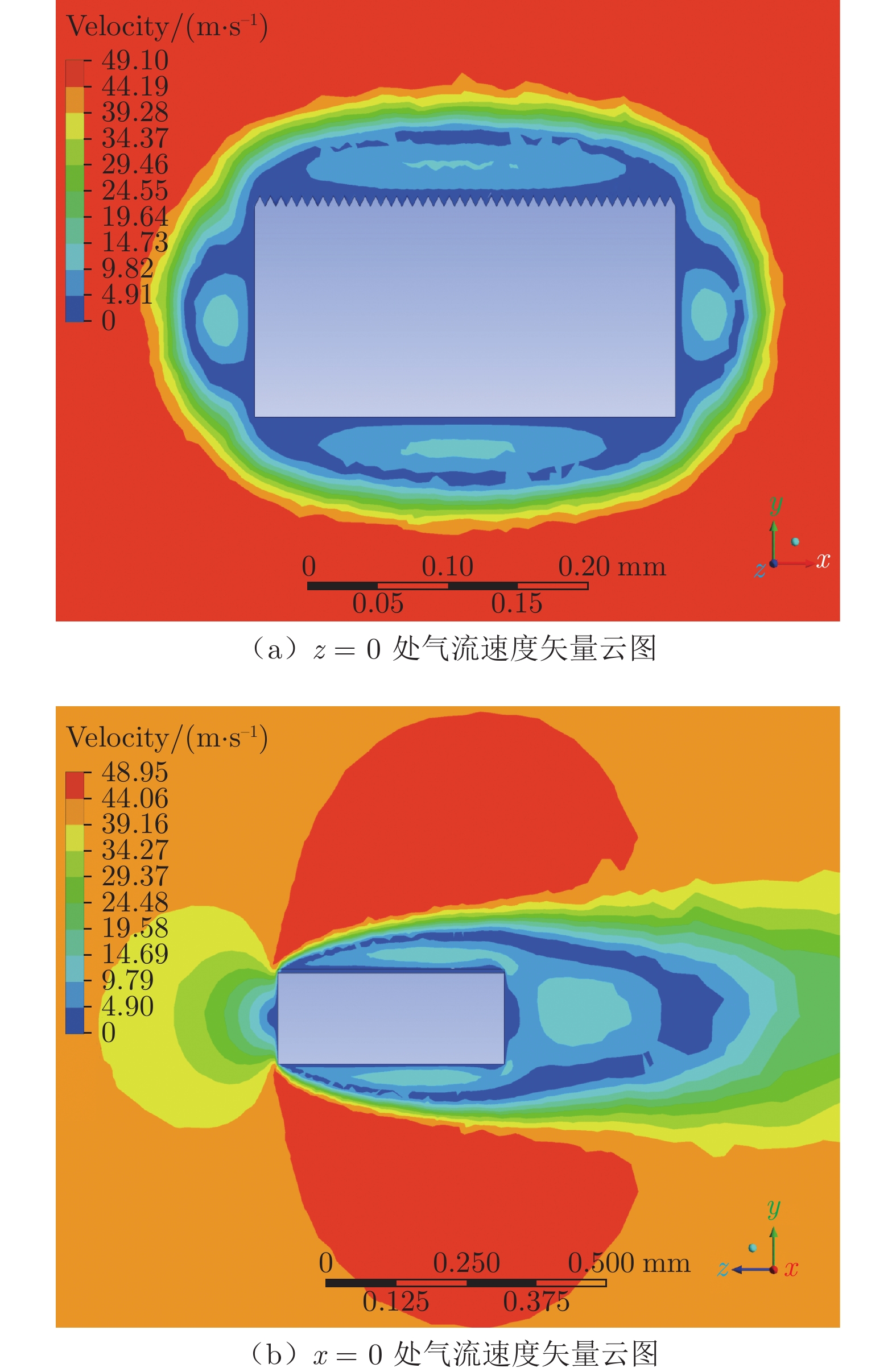
经后处理，得到微元区域二级微沟槽气流速度矢量云图，如图11所示。从x = 0、z = 0截面的云图可以看出：二级微沟槽近壁区边界层厚度明显大于光滑表面对应区域，且有增厚趋势；混合层厚度变薄，湍流被削弱，壁面速度梯度降低，同时压力也明显降低，从而导致阻力降低，实现了减阻效果。
![]()
图 11 二级微沟槽区域气流速度矢量云图Fig. 11 Velocity vector cloud diagram of airflow in the element region of secondary groove基于仿真结果，按照设定尺寸对半球头体表面进行激光微纳加工，制造了一批成型钛合金（TC4）半球头样件并作预处理[23]。实验中使用了3个半球头体样件：表面光滑的半球头体样件A作为对照组；以相同工序在样件B和C表面激光扫描仿生鲨鱼皮微结构；进一步加工样件C，通过激光干涉加工二级微沟槽，形成复合结构。图12和13为制备完成后各样件表面微结构的SEM电镜图。
最后，通过风洞实验验证减阻效果。以压力传感器实时记录阻力值，并实时计算出减阻率，结果如表3所示。当风速为150 km/h时，与对照组样件A相比，样件B的阻力降低了8.7%，样件C的阻力降低了10.3%。半球头体表面的仿生鲨鱼皮结构及复合减阻结构均表现出了优秀的减阻性能。
表 3 风洞实验参数表Table 3 Parameters of wind tunnel experiment样品 v∞/(km·h–1) F/N C ΔC 光滑表面样件A 150 1.386 0.3823 － 非光滑表面样件B 150 1.266 0.3491 8.7% 非光滑表面样件C 150 1.243 0.3430 10.3% 光滑表面样件A 160 1.565 0.3804 － 非光滑表面样件B 160 1.442 0.3504 7.9% 非光滑表面样件C 160 1.407 0.3419 10.1% 对比表2和3可以发现：在残差精度范围内，覆盖微结构的样件的阻力系数风洞实验与仿真结果一致，验证了仿真方法的可行性。由此可见，减阻率出现偏差，原因在于光滑半球头体。对比表2和3的数据发现，光滑半球头体受力的仿真结果与实际检测结果存在偏差。从光滑半球头体风洞实验结果可知，微观角度的真实物体表面并非绝对光滑，其无规则的微观结构会导致阻力的变化。理想化模型无需考虑机械能转化和内能消耗，简化了流动过程，并能客观精确地反映流动特性。因此，可以认为仿真计算与风洞实验得到的规律一致。
![]()
图 13 激光扫描仿生鲨鱼皮鳞片加激光干涉加工二级微沟槽Fig. 13 Laser scanning and laser interference processing secondary groove3 结 论
1）仿生鲨鱼皮与二级微沟槽的复合结构具有很好的减阻效果。在仿生鲨鱼皮鳞片结构基础上均匀覆盖更小尺度的二级微沟槽结构，能够延长“二次涡”的回旋路径，降低沟槽底部气流速度梯度，减小气流对壁面的黏附力，削弱来流强度，增大边界层厚度，进一步提升减阻效果。
2）仿真结果与风洞实验结果一致。复合微纳减阻结构的减阻率可达10.3%，验证了仿真方法的可行性。仿真方法可以替代一部分风洞实验预测及评估减阻效果，从而降低成本、提高效率。
本文采用仿真与风洞实验手段进行研究，以验证结果的可靠性。受风洞实验条件所限，仅对当前所能达到的最高风速（即非常临近的2个风速条件150和160 km/h）进行了仿真与实验。在后续工作中，亟待在更高风速和不同来流方向条件下开展复合微纳减阻结构的减阻效果研究。
-
![]()
图 2 鲨鱼皮鳞片与半球头体排布组合整体图
Fig. 2 Overall view of the combination of sharkskin scales and hemis-pherical head arrangement
![]()
图 3 鲨鱼皮鳞片在半球头体表面的排布
Fig. 3 The orientation of the scales on the surface of the hemispheric head
![]()
图 4 二级微沟槽结构及其在鲨鱼皮鳞片结构上的排布（截面图）
Fig. 4 Secondary microgrooves and the arrangement of secondary microgrooves on sharkskin scales (cross-sectional view)
![]()
图 6 光滑半球头体风洞检测模型和覆盖仿生鲨鱼皮鳞片的半球头体风洞检测模型
Fig. 6 Wind tunnel detection model of smooth hemispheric head and wind tunnel inspection models of hemispherical cephalic bodies covered with bionic sharkskin scales
![]()
图 8 光滑半球头体y = 0处的速度矢量云图及局部放大图
Fig. 8 The velocity vector cloud of the smooth hemispheric head aty = 0 and an enlarged version
![]()
图 9 覆盖鳞片的半球头体y = 0处的速度矢量云图及局部放大
Fig. 9 Velocity vector cloud image of hemispherical head covered by sharkskin structure at y = 0 and an enlarged version
![]()
图 10 同一部分半球头体的压力云图
Fig. 10 Pressure cloud images of the same part of hemispheric cephalic body
![]()
图 11 二级微沟槽区域气流速度矢量云图
Fig. 11 Velocity vector cloud diagram of airflow in the element region of secondary groove
![]()
图 13 激光扫描仿生鲨鱼皮鳞片加激光干涉加工二级微沟槽
Fig. 13 Laser scanning and laser interference processing secondary groove
表 1 实验模型参数
Table 1 Experimental model parameters
lc = ls h1 = h2 Lx Ly Lz 400 µm 150 µm 350 mm 350 mm 260 mm 
下载: 导出CSV
表 2 CFD仿真参数
Table 2 CFD simulation parameter
样品 v∞/(km·h–1) F/N C ΔC 光滑半球头体 150 1.499 0.413 － 覆盖鳞片的半球头体 150 1.245 0.343 16.9% 光滑半球头体 160 1.731 0.419 － 覆盖鳞片的半球头体 160 1.407 0.342 18.4%
下载: 导出CSV
表 3 风洞实验参数表
Table 3 Parameters of wind tunnel experiment
样品 v∞/(km·h–1) F/N C ΔC 光滑表面样件A 150 1.386 0.3823 － 非光滑表面样件B 150 1.266 0.3491 8.7% 非光滑表面样件C 150 1.243 0.3430 10.3% 光滑表面样件A 160 1.565 0.3804 － 非光滑表面样件B 160 1.442 0.3504 7.9% 非光滑表面样件C 160 1.407 0.3419 10.1%
下载: 导出CSV
-
[1] DOMEL A G, SAADAT M, WEAVER J C, et al. Shark skin-inspired designs that improve aerodynamic performance[J]. Journal of the Royal Society, Interface, 2018, 15(139): 20170828. doi: 10.1098/rsif.2017.0828
[2] 李黎明. ANSYS有限元分析实用教程[M]. 北京: 清华大学出版社, 2005. [3] WANG Y H, ZHANG Z B, XU J K, et al. One-step method using laser for large-scale preparation of bionic superhydro-phobic & drag-reducing fish-scale surface[J]. Surface and Coatings Technology, 2021, 409: 126801. doi: 10.1016/j.surfcoat.2020.126801
[4] WALSH M J. Turbulent boundary layer drag reduction using riblets[C]//AIAA 20th Aerospace Sciences Meeting. 1982. doi: 10.2514/6.1982-169
[5] SANDERS R H, RUSHALL B, TOUSSAINT H, et al. Bodysuit yourself: but first think about it[J]. Journal of Turbulence, 2001, S/3(138): 201–212.
[6] 刘志华, 董文才, 夏飞. V型沟槽尖峰形状对减阻效果及流场特性影响的数值分析[J]. 水动力学研究与进展:A辑, 2006, 21(2): 223–231. DOI: 10.3969/j.issn.1000-4874.2006.02.011 LIU Z H, DONG W C, XIA F. The effects of the tip shape of V-groove on drag reduction and flow field characteristics by numerical analysis[J]. Journal of Hydrodynamics:Series A, 2006, 21(2): 223–231. doi: 10.3969/j.issn.1000-4874.2006.02.011
[7] 田丽梅, 任露泉, 刘庆平, 等. 仿生非光滑旋成体表面减阻特性数值模拟[J]. 吉林大学学报(工学版), 2006, 36(6): 908–913. DOI: 10.3969/j.issn.1671-5497.2006.06.016 TIAN L M, REN L Q, LIU Q P, et al. Numerical simulation on drag reduction characteristic around bodies of revolution with bionic non-smooth surface[J]. Journal of Jilin University(Engineering and Technology Edition), 2006, 36(6): 908–913. doi: 10.3969/j.issn.1671-5497.2006.06.016
[8] DENG Z F, YANG Q, CHEN F, et al. Fabrication of large-area concave microlens array on silicon by femtosecond laser micromachining[J]. Optics Letters, 2015, 40(9): 1928–1931. doi: 10.1364/OL.40.001928
[9] 丛茜, 封云, 任露泉. 仿生非光滑沟槽形状对减阻效果的影响[J]. 水动力学研究与进展:A辑, 2006, 21(2): 232–238. DOI: 10.3969/j.issn.1000-4874.2006.02.012 CONG Q, FENG Y, REN L Q. Affecting of riblets shape of nonsmooth surface on drag reduction[J]. Journal of Hydrodynamics:Series A, 2006, 21(2): 232–238. doi: 10.3969/j.issn.1000-4874.2006.02.012
[10] STANFORD B, IFJU P, ALBERTANI R, et al. Fixed membrane wings for micro air vehicles: experimental charac-terization, numerical modeling, and tailoring[J]. Progress in Aerospace Sciences, 2008, 44(4): 258–294. doi: 10.1016/j.paerosci.2008.03.001
[11] HU C L, WANG X D, WANG G Y, et al. The structures of unsteady cavitation shedding flow around an axisymmetric body with a blunt headform[J]. Journal of Mechanical Science and Technology, 2018, 32(1): 199–210. doi: 10.1007/s12206-017-1221-y
[12] JIANG X X, XU Y Q, WANG C, et al. Numerical simulations of gas-particle flow behavior created by low-level rotary-winged aircraft flight over particle bed[J]. Applied Mathematics and Mechanics, 2019, 40(3): 397–406. doi: 10.1007/s10483-019-2449-9
[13] OEFFNER J, LAUDER G V. The hydrodynamic function of shark skin and two biomimetic applications[J]. The Journal of Experimental Biology, 2012, 215(Pt 5): 785–795. doi: 10.1242/jeb.063040
[14] FUAAD P A, PRAKASH K A. Enhanced drag-reduction over superhydrophobic surfaces with sinusoidal textures: a DNS study[J]. Computers & Fluids, 2019, 181: 208–223. doi: 10.1016/j.compfluid.2019.01.022
[15] MENTER F. Zonal two equation k-ω turbulence models for aerodynamic flows[R]. AIAA-93-2906, 1993. doi: doi.org/10.2514/6.1993-2906
[16] BOROUCHAKI H, LAUG P, GEORGE P L. Parametric surface meshing using a combined advancing-front genera-lized Delaunay approach[J]. International Journal for Numerical Methods in Engineering, 2000, 49(1-2): 233–259. doi:10.1002/1097-0207(20000910/20)49:1/2<233::AID-NME931>3.0.CO;2-G
[17] VERSTEEG H, MALALASEKERA W. An introduction to computational fluid dynamics: the finite volume method[M]. Apache Junction: World Publishing Corporation, 1995.
[18] YANG D D, YU A, JI B, et al. Numerical analyses of ventilated cavitation over a 2-D NACA0015 hydrofoil using two turbulence modeling methods[J]. Journal of Hydro-dynamics, 2018, 30(2): 345–356. doi: 10.1007/s42241-018-0032-7
[19] RASTEGARI A, AKHAVAN R. The common mechanism of turbulent skin-friction drag reduction with superhydro-phobic longitudinal microgrooves and riblets[J]. Journal of Fluid Mechanics, 2018, 838: 68–104. doi: 10.1017/jfm.2017.865
[20] ZHANG L, SHAN X B, XIE T. Active control for wall drag reduction: methods, mechanisms and performance[J]. IEEE Access, 2020, 8: 7039–7057. doi: 10.1109/ACCESS.2020.2963843
[21] STRANG G, FIX G. An analysis of the finite element method[M]. Englewood: Prentice-Hall, 1973.
[22] CHEN D K, CUI X X, CHEN H W. Dual-composite drag-reduction surface based on the multilayered structure and mechanical properties of tuna skin[J]. Microscopy Research and Technique, 2021, 84(8): 1862–1872. doi: 10.1002/jemt.23743
[23] LIU R, CHI Z D, CAO L, et al. Fabrication of biomimetic superhydrophobic and anti-icing Ti6Al4V alloy surfaces by direct laser interference lithography and hydrothermal treatment[J]. Applied Surface Science, 2020, 534: 147576. doi: 10.1016/j.apsusc.2020.147576
-
期刊类型引用(3)
1. 于飞洋，伍名裘，关伟. 整流罩的气动特性与力学性能研究. 电子机械工程. 2025(01): 52-57 . 
百度学术
2. 徐成宇，王永华，焦远东，于化东，弯艳玲，张倩. 仿生鲨鱼皮表面的快速制备和减阻性能研究. 表面技术. 2025(05): 72-82 . 百度学术
3. 张浩，李政恒，李茂林，赵智超，邵玉彬. 壁面微沟槽管道高聚物溶液流动减阻仿真研究. 山东建筑大学学报. 2024(06): 55-62 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 1151
- HTML全文浏览量: 331
- PDF下载量: 113
- 被引次数: 4
