Wind tunnel experimental study on aerodynamics and noise based on the influence of automobile rearview mirror shapes
-
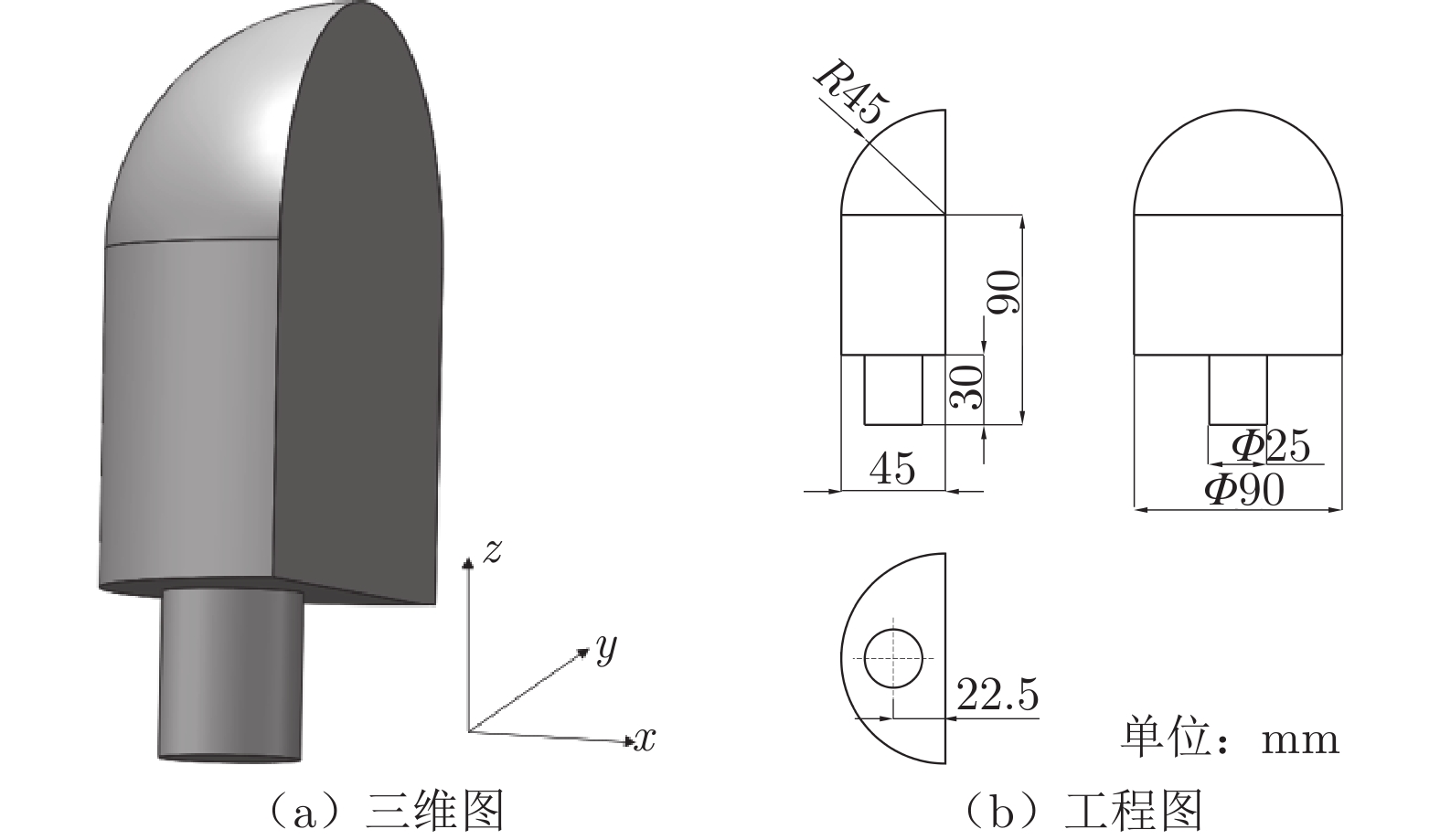
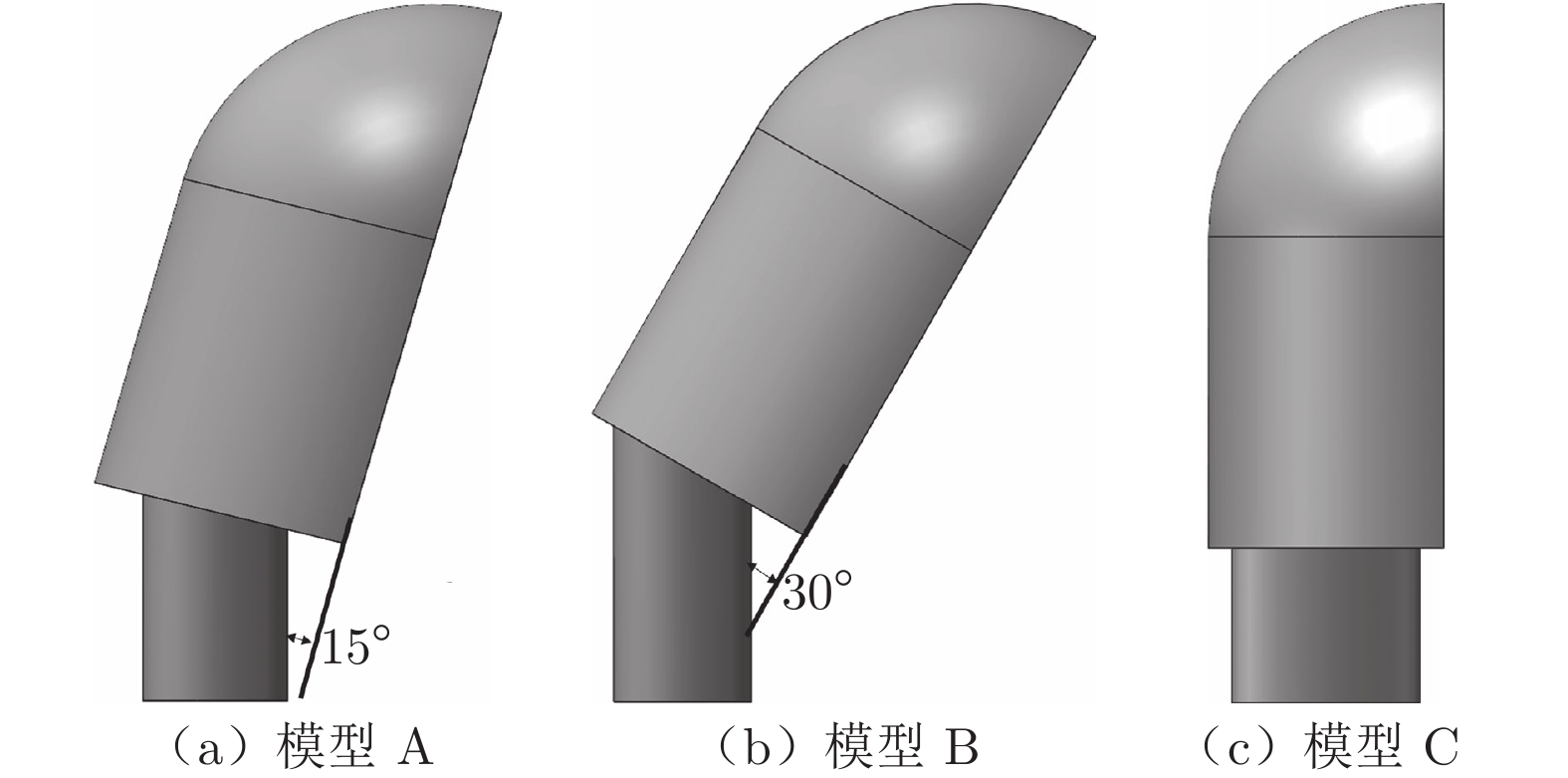
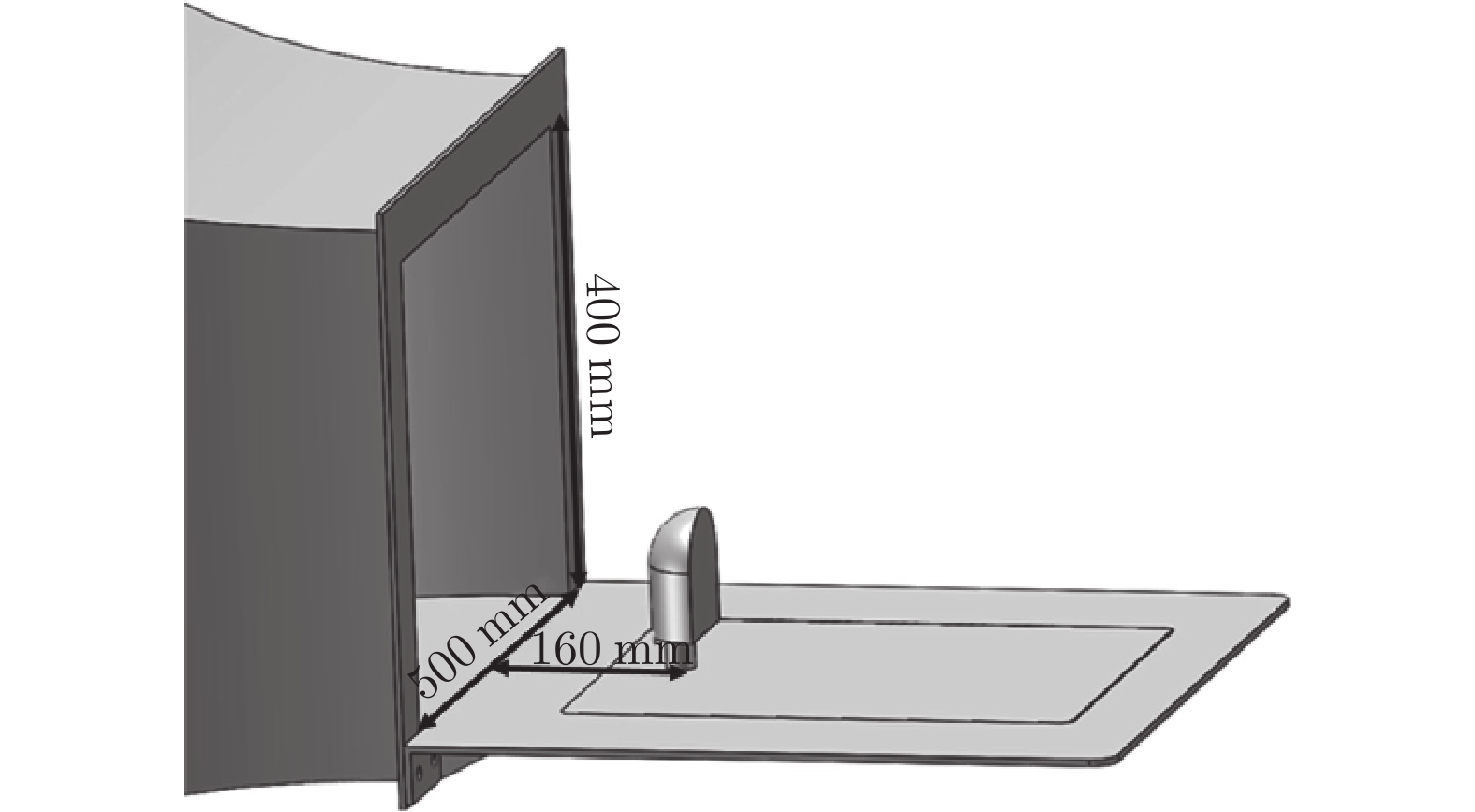
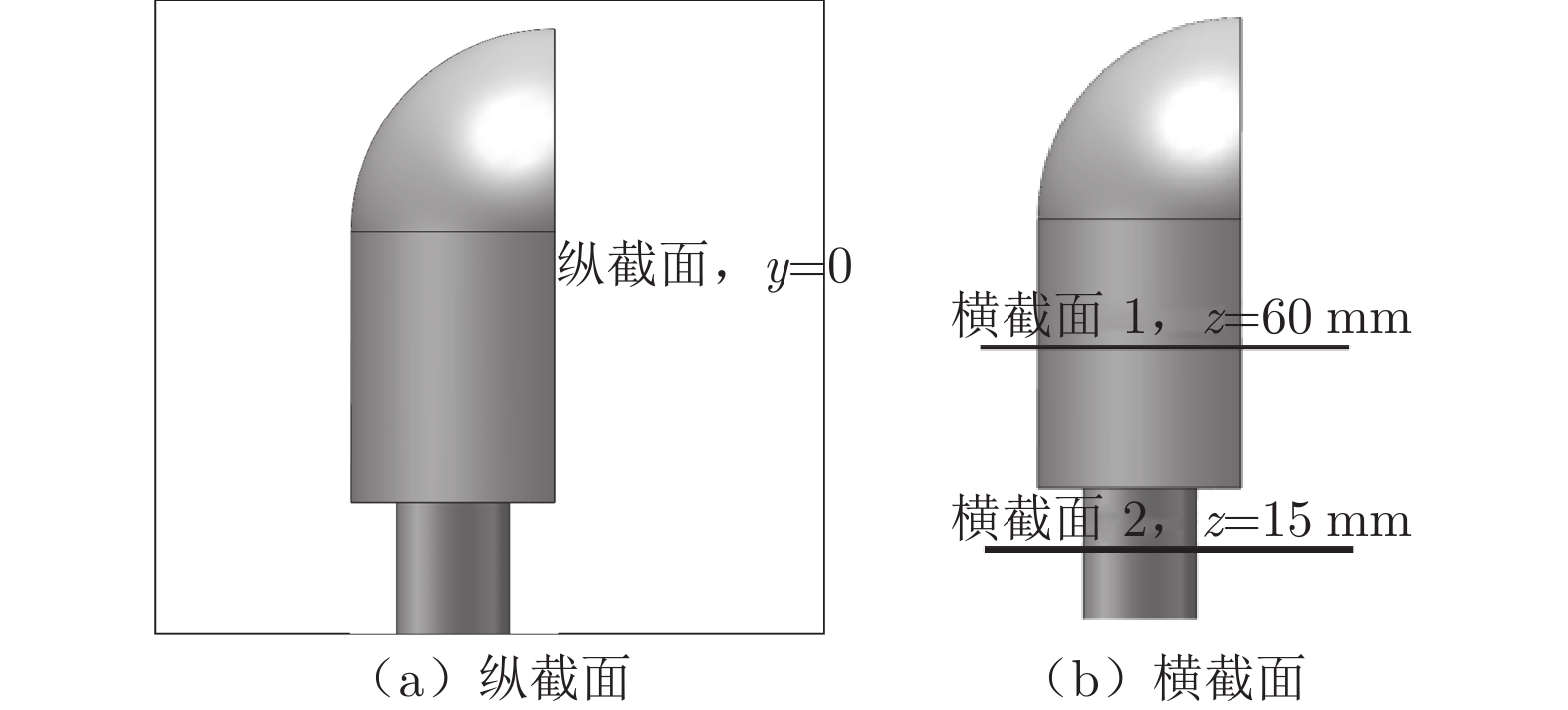
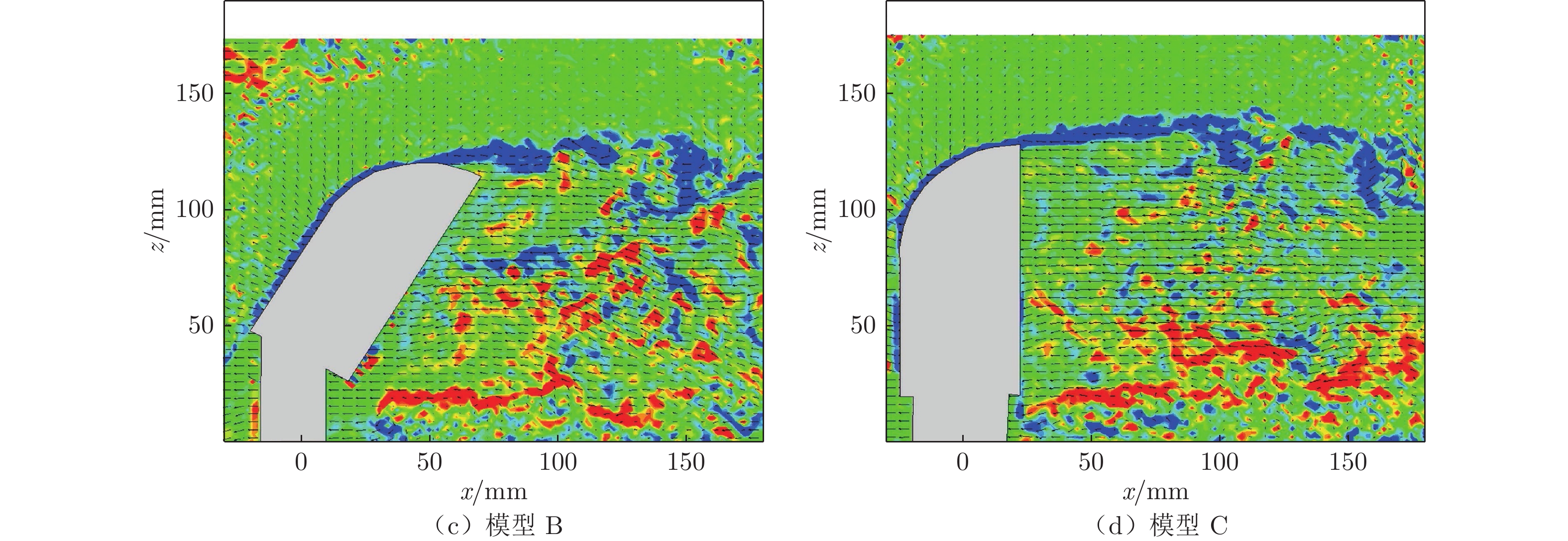
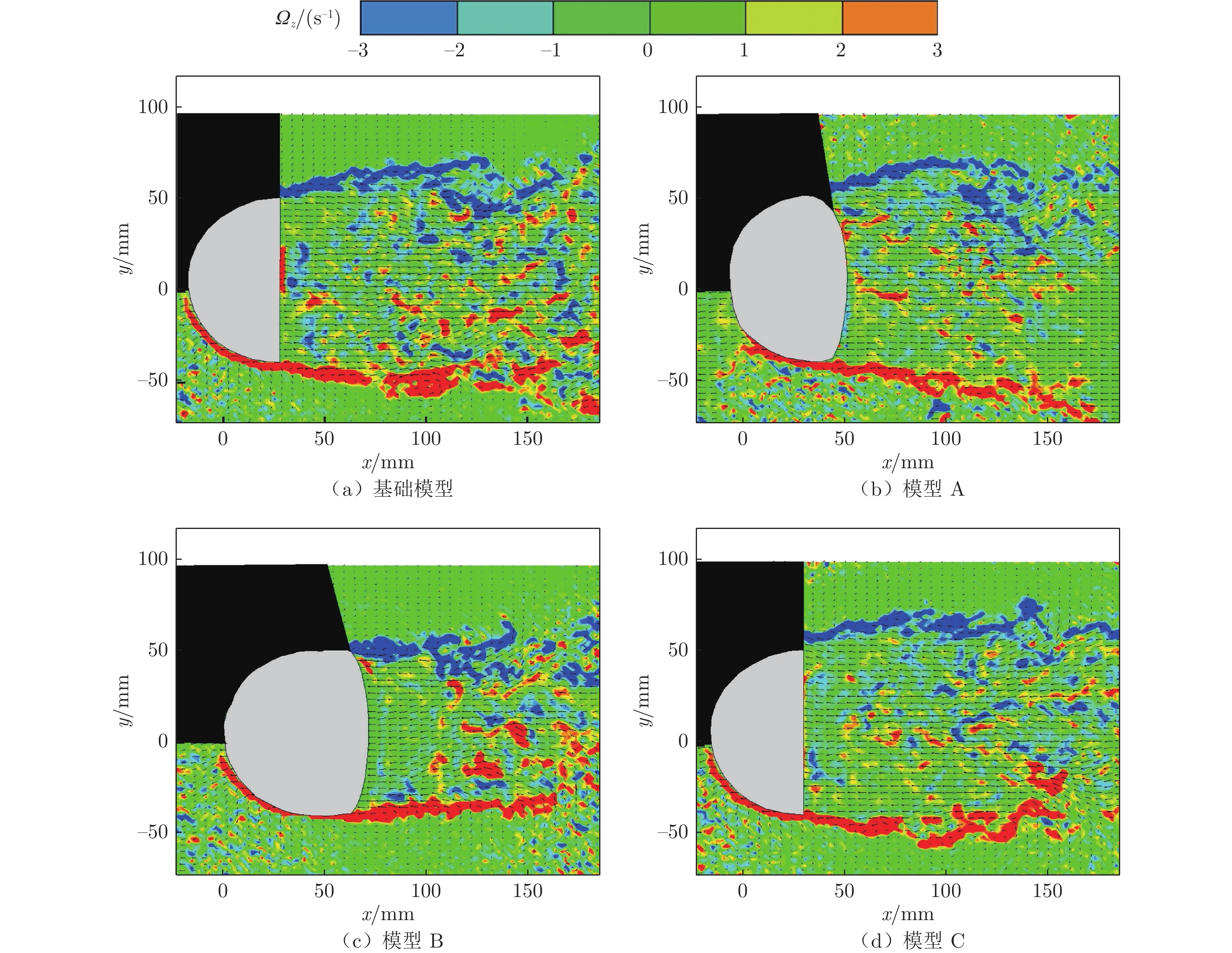
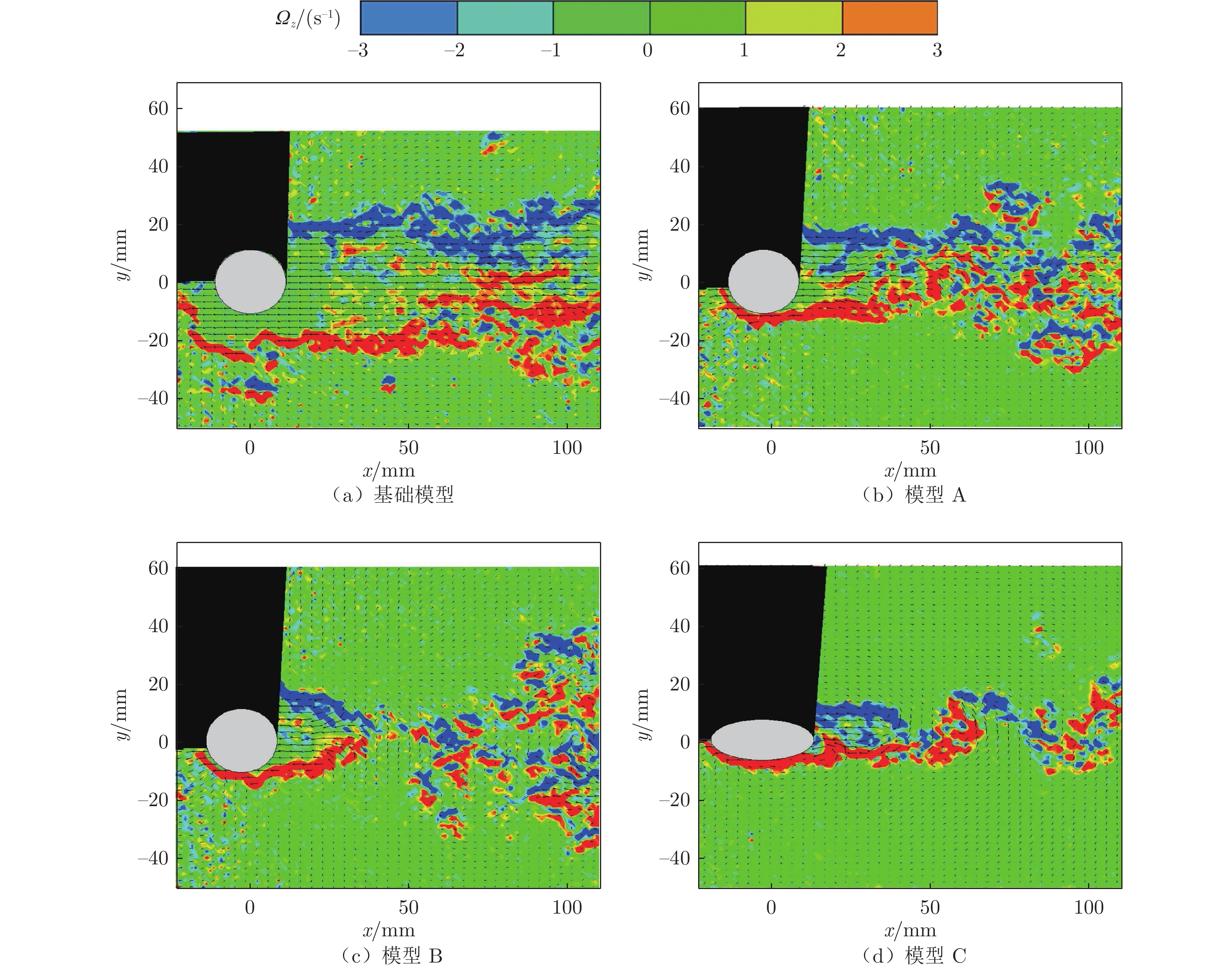
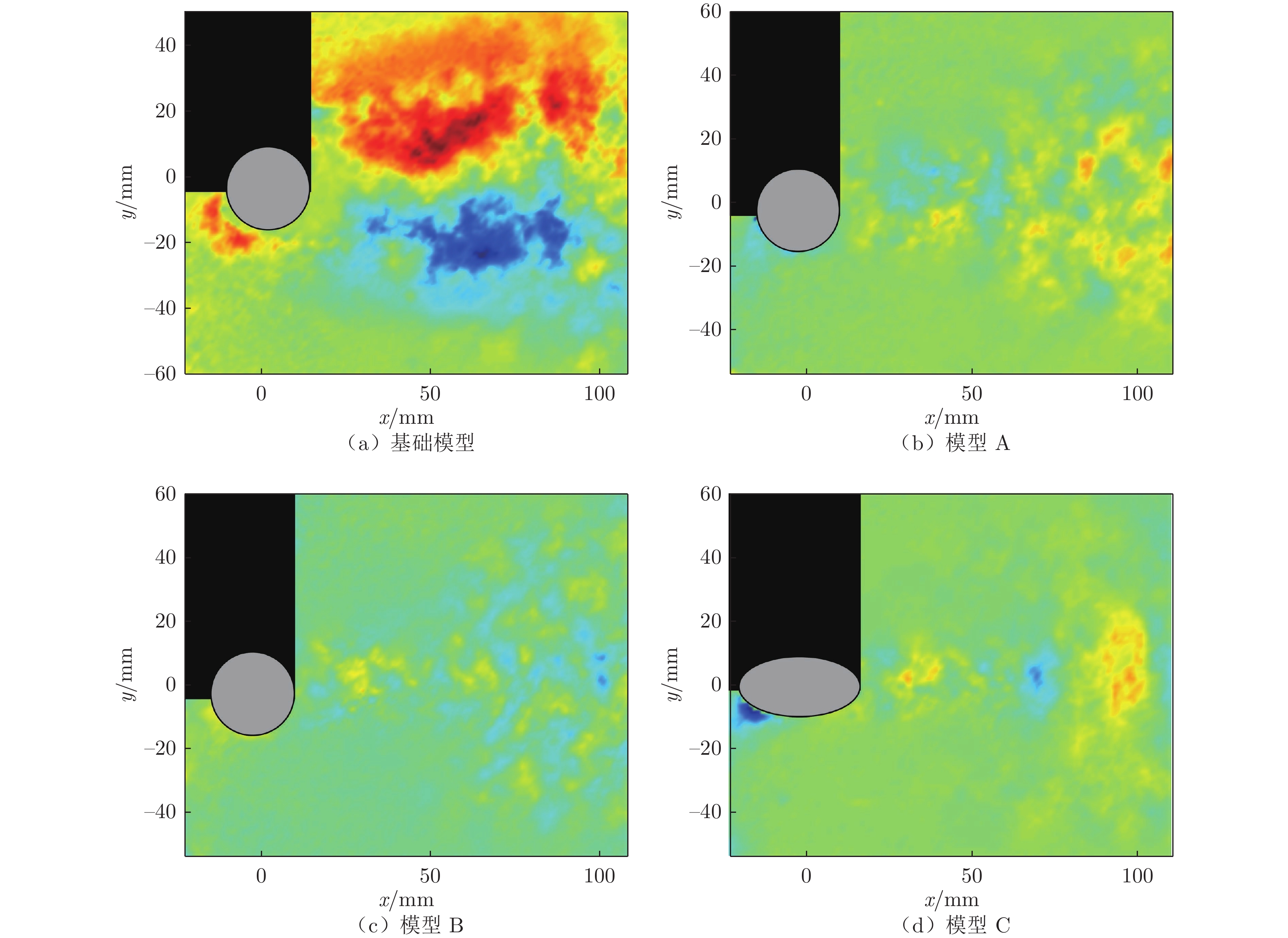
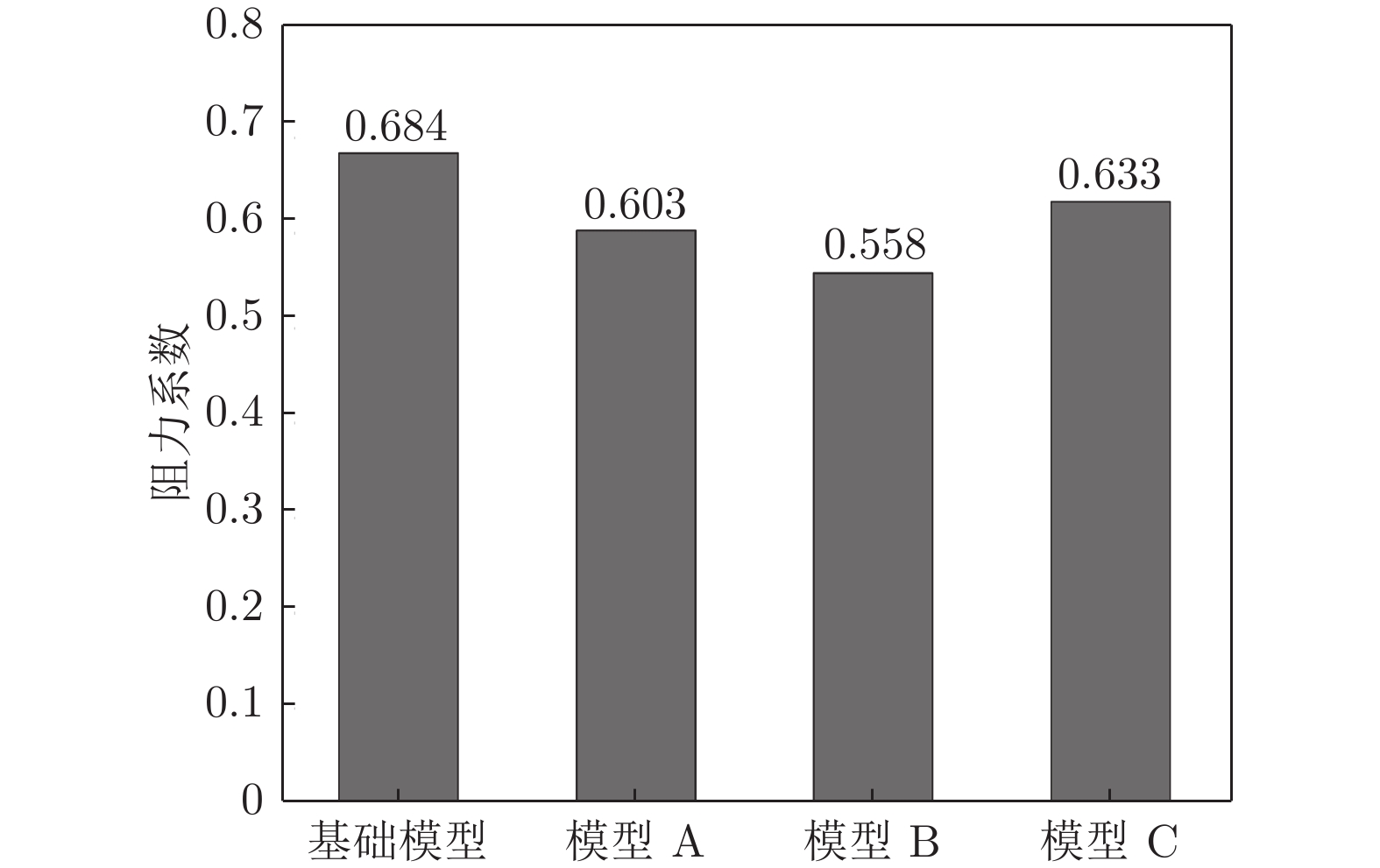
摘要: 为降低由汽车后视镜带来的气动噪声，本文以一简化汽车外后视镜模型为基础模型，提出3个不同造型改进方案：A造型模型镜身倾斜15°；B造型模型镜身倾斜30°；C造型模型将原圆柱形底座改为椭柱形底座。对4款造型外后视镜模型进行风洞实验研究，分析流场、空气阻力和壁面脉动压力随造型改变的规律。气动特性（流场和阻力）采用粒子图像测速仪 (PIV) 和六分量动态天平测量，声学特性采用壁面麦克风对侧窗平板的湍流脉动进行测量。研究结果表明：3个造型改进方案均可在不同程度上改善外后视镜尾迹区域流场品质，有效降低空气阻力和气动噪声。其中B模型阻力系数较基础模型降低18.4%，壁面脉动压力总声压级在中低频段可降低4.6 dB；C模型可降低阻力系数7.5%，总声压级可降低4.3 dB。Abstract: To reduce the aerodynamic noise caused by automobile rearview mirrors, a simplified rearview mirror model was taken as the research object, and three different modeling improvement schemes were proposed: model A tilts the mirror body at 15°; model B tilts the mirror body at 30°; model C changes the cylindrical base to an elliptical base. Wind tunnel experiments were carried out on the models to analyze the variation rules of the flow field, drag, and wall pressure fluctuation with the change of the model. The particle image velocimetry (PIV) and six-component balance were used to measure the aerodynamic characteristics including the flow field and drag, and the wall microphone was applied to measure the acoustic characteristics. The results show that all three schemes can improve the flow quality in the wake area of the rearview mirror, effectively reducing the drag and the generation of aerodynamic noise. Compared to the base model, the drag coefficient and the overall sound pressure level of the wall pressure fluctuation of model B can be reduced by 18.4% and 4.6 dB in the low-mid frequency range. For model C, the corresponding results are 7.5% and 4.3 dB, respectively. The research results are beneficial for engineers in the aerodynamic and acoustic design of automobile rearview mirrors.
-
0 引言
激波干扰现象，因其产生的激波、剪切层、膨胀波、超声速射流以及伴随的旋涡和湍流等复杂流动结构，不仅是高超声速飞行器研究与发展过程中需要重点关注的空气动力学问题之一，也是困扰工程应用的一大难题[1, 2]。以斜激波与圆柱/圆球弓形激波之间的相互作用为典型模型，根据激波干扰位置和激波强度不同，Edney[3]总结出6种具有普适性的激波干扰类型(Ⅰ~Ⅵ类)。其中，第Ⅳ类激波干扰因其产生的超声速射流冲击壁面会带来严峻的热/力载荷而受到设计和研究人员的广泛关注[4-7]。在某些情况下，激波干扰产生的超声速射流高度弯曲，不会直接冲击壁面，这种激波干扰被称为第Ⅳa类[8]。
高超声速进气道流动存在多种形式的激波干扰现象，尤其以设计工况下前体激波入射进气道唇口[9]形成的激波干扰最为突出。针对前体激波与二元进气道唇口弓形激波的干扰问题，Wieting等[10]进行了系统性研究，获得了丰富的压力和热流数据。近年来，前缘高度后掠的内转式进气道[11-13]逐渐成为研究热点之一。然而，其普遍采用的V形溢流口(唇口)与二元进气道唇口具有明显的区别。最近，Xiao等[14]在不考虑前体激波的情况下，将内转式进气道溢流口简化为V形钝前缘，研究发现：在一定的几何参数下，V形钝前缘自身就会形成类似于Edney第Ⅳ类激波干扰的流动结构。显然，当前体激波入射V形钝前缘溢流口时，将产生更加复杂的波系结构，很可能加剧溢流口的气动热。
另一方面，根据来流条件的不同，进气道会出现亚额定、额定和超额定等3种工作状态[15]。针对二元进气道的研究表明[16-17]：在超额定状态下，前体激波入射在唇口内部，当前体激波与唇口激波发生Edney第Ⅱ类激波干扰时，形成的亚声速区可能导致进气道局部不起动。相对而言，内转式进气道唇口更加复杂，前体激波与其相互作用的研究尚未见系统报道，亟需针对性的机理揭示，以补充认识上的不足。
采用完整的内转式进气道对V形溢流口激波干扰特性进行研究，不仅会耗费大量的计算和实验资源，更会带来多种复杂因素的影响。抓住内转式进气道V形溢流口的主要流动特征，有侧重地进行简化，继而揭示其流动机理和关键影响因素，当属高效简洁的研究方式。因此，本文将内转式进气道V形溢流口简化为V形钝前缘平板。鉴于内转式进气道的前体激波为复杂的三维曲面激波，为便于准确描述和控制，本文暂不考虑入射激波的展向曲率，而是采用简化的斜激波，以突出V形钝前缘溢流口自身带来的主要特征。继而采用激波风洞实验和数值模拟相结合的方法，揭示入射激波与V形钝前缘溢流口相对位置变化引起的激波干扰形态演变，以期为内转式进气道溢流口设计提供有价值的参考。
1 实验和计算方法
1.1 实验设备和模型
V形钝前缘平板由较长的平直段和交叉位置倒圆部分组成，如图 1所示。交叉位置倒圆半径R=6.5mm，前缘钝化半径r=2mm，前缘扩张角β=48°。前缘平直段的长度L=31r，以使其产生的脱体激波充分发展。以V形前缘驻点位置为坐标原点，定义流向为x方向，平板展向为z方向，垂直于平板方向为y方向。
为了更加清楚地观察波系结构，对V形钝前缘平板实验模型进行了2.5倍放大。实验在中国科学技术大学的KDJB330反射型激波风洞[18-20]中进行。实验来流马赫数为6，静压为891Pa，静温为101K。纹影系统采用Z字形光路布置，如图 2所示。通过高速摄影记录流场纹影图像, 拍摄帧率为15000Hz，曝光时间为2μs。入射斜激波由气流偏转角为12°的斜劈产生，斜劈流向长度为200mm，展向宽度为260mm。为了获得丰富的流场信息，考虑到模型对光路的遮挡，分别从平行于平板(z方向，见图 2)和垂直于平板(y方向，见图 3)2个方向对流场进行拍摄。通过前后移动斜劈的方式，改变入射斜激波与V形钝前缘溢流口的相对位置。为了便于分析，斜激波入射位置采用不考虑激波干扰时无粘斜激波在平板上的入射点坐标。
1.2 计算方法
数值计算采用Fluent软件求解Navier-Stokes方程，并使用具有二阶精度的格式离散。对流通量采用AUSM格式，湍流模型采用k-ω SST模型，气体分子粘性采用Sutherland公式，气体定压比热使用CHEMKIN温度多项式进行计算。对于V形钝前缘平板流场的计算，由于来流和几何的对称性，为了节省计算资源，采用1/4计算域进行模拟。采用结构化六面体网格，计算域及局部网格如图 4和5所示，近壁面采用等比加密，壁面y+ < 1，总网格量约3000万。有斜激波入射时的计算域如图 6所示，此时六面体网格总数在5000万左右。为了与风洞实验进行对比，来流条件设置与实验一致。在数值模拟中监视各方程残差，监测出口位置的流量及质量平均马赫数、驻点位置的壁面压力和热流量。待残差收敛并且各监测参数稳定，认为流场收敛。
![]()
图 6 斜激波入射V形钝前缘平板计算域Fig. 6 Computational domain of the V-shaped blunt leading edge plate with shock incidence由于三维流动的复杂性，数值模拟获得的流场结构难以直接与具有光路积分效应的实验纹影进行对比。为此，本文按照纹影法的原理对数值模拟流场进行处理。如为了获得z方向穿过全流场的数值纹影，将流场沿z方向划分为k个等间距的区域，假设每个小区域内的流场参数沿z方向均匀分布，则经过流场的光线偏转角εx由式(1)[21]得到：
(1) 式中，n为折射率，ξ1和ξ2分别为光线进入流场和离开流场位置的z坐标。由此获得的光强变化可以与z方向穿过流场的实验纹影进行直观对比。
2 结果与分析
V形钝前缘自身的三维绕流会导致复杂的激波干扰，因此在研究斜激波入射V形钝前缘平板激波干扰前，有必要对V形钝前缘基本波系结构进行研究。
2.1 V形钝前缘平板基本流场
从y方向拍摄的流场纹影与流场x-z对称面数值纹影的对比如图 7(a)所示，可以看到数值模拟较好地捕捉到了基本的波系结构。图 7(b)为上半部分波系结构的示意图，其中DS代表V形钝前缘斜直段产生的脱体激波，BS代表V形前缘交叉位置形成的弓形激波，脱体激波DS入射弓形激波BS，相交于三波点T，在三波点位置产生透射激波TS和滑移线Σ。脱体激波DS波后的超声速气流在V形前缘交叉倒圆位置被压缩，压缩波汇聚形成弯曲激波CS。透射激波TS与弯曲激波CS发生异侧激波干扰，形成马赫杆MS。激波BS以及马赫杆MS波后气流均为亚声速，而透射激波TS波后气流为超声速，超声速气流在亚声速区域之间不断地压缩和膨胀，交替出现激波和膨胀波，形成超声速射流结构。超声速射流沿壁面运动，在驻点前发生碰撞，并卷起形成反向旋转的涡对结构。涡对结构与弓形激波BS相互作用，使得弓形激波波面向上游凸起，并出现Kink。将脱体激波DS视为入射激波，则V形钝前缘激波干扰结构与Edney第Ⅴ类激波干扰类似。流场中存在射流失稳和剪切层脱涡等流动过程，数值模拟虽然不能捕捉这些非定常过程，但能够刻画基本波系结构，流动的非定常性没有显著影响本文对波系干扰类型的研究。
为了探讨流场波系的三维结构，从z方向也进行了纹影拍摄。使用本文1.2节所描述的三维流场后处理方法得到的数值纹影与实验纹影图像进行了对比，如图 8(a)所示。由于流场的三维性，在z方向纹影图像上可以看到3道激波，从左到右依次为弓形激波BS上凸起的激波面(Bulge)、弓形激波BS和弯曲激波CS。图 8(b)进一步定量比较了数值模拟与实验获得的激波BS及其凸起的激波面的位置。结果表明：激波BS的位置符合较好，而凸起的激波面(Bulge)略有差别。这是由于激波BS相对稳定，而凸起的激波面受涡对结构的影响(见图 7)，具有一定的非定常性。整体而言，数值模拟与实验纹影吻合较好，可用于本文后续的激波干扰研究。
图 9比较了相同钝化半径下二维圆柱产生的弓形激波和V形钝前缘平板弓形激波。其中，Δ1和Δ2分别代表V形钝前缘和圆柱弓形激波的脱体距离，V形钝前缘弓形激波由x-y对称面的数值模拟给出，圆柱产生的弓形激波形状由Billig[22]公式给出，而弓形激波面上声速点位置的激波角β*由以下公式[23]给出：
(2) ![]()
图 9 V形钝前缘脱体激波与圆柱脱体激波对比Fig. 9 Comparison between the bow shock of the cylinder and V-shaped blunt leading edge式中，Ma∞为来流马赫数, γ为气体比热比。从图 9可以看出，由于自身的激波干扰，V形钝前缘交叉位置弓形激波的脱体距离较大，并且驻点前存在大范围的亚声速区。进一步采用马赫数为5.95的等值面给出V形钝前缘平板的三维激波结构(图 10)，可以看出：前缘脱体激波DS和弓形激波BS均为三维曲面激波，并且BS波面有较大范围的凸起。这表明V形钝前缘弓形激波的近正激波区域较大，当斜激波与弓形激波干扰时，出现第Ⅲ和第Ⅳ类干扰的范围更大[24]。
2.2 斜激波入射V形钝前缘溢流口激波干扰流场
当入射斜激波距离V形溢流口上游较远时，对应于亚额定工况下内转式进气道前体激波与唇口激波相交于唇口外的情况。图 11(a)为斜激波无粘入射平板位置坐标为x/r=-10.5时的流场纹影图片，图 11(b)为波系示意图。斜激波IS从平板下侧入射弓形激波BS超声速区域，发生同侧激波相交，出现Edney第Ⅵ类激波干扰。激波相互作用导致弓形激波的激波角减小，入射激波干扰后形成透射激波TS和剪切层Σ。
![]()
图 11 斜激波入射x/r=-10.5流场波系结构Fig. 11 Shock structure of the flowfield with the shock incidence at x/r=-10.5向下游移动斜劈，当斜激波无粘入射位置为x/r=-3时，斜激波入射在V形前缘驻点前的亚声速区，此时对应于内转式进气道额定工况下前体激波入射唇口的情况。仅从z方向拍摄纹影时，由于模型遮挡，难以获得干扰点附近激波干扰形态。因此，需要结合y方向的纹影来判断干扰类型。从图 12(a)流场z方向的纹影可以看出, 入射斜激波IS分为了两道斜激波，分别为IS和IS′。其中，IS′是入射斜激波IS与V形钝前缘的脱体激波DS干扰产生的透射激波。IS′入射V形前缘平板壁面形成反射激波RS，而入射斜激波IS与弓形激波BS的干扰点被模型遮挡。从图 12(b)流场y方向的纹影可以看到，在驻点前存在两道弓形激波BS和BS′。结合图 12(a)和(b)两个方向的纹影，推测激波干扰类型可能为Edney第Ⅳ类激波干扰，其流场结构如图 13所示。此时，由于斜激波IS入射，原有的弓形激波BS转变为通过透射激波TS连接的两段弓形激波BS和BS′，并伴随着超声速射流的产生，该流场结构很复杂，将在2.3节进一步分析。因此，在内转式进气道额定工况下，前体激波入射溢流口驻点前亚声速区域，可能带来复杂的激波干扰流场，对进气道流动带来负面影响。
![]()
图 12 入射位置x/r=-3流场纹影Fig. 12 Schlieren images of the flowfield with the shock incidence at x/r=-3![]()
图 13 入射位置x/r=-3流场示意图Fig. 13 Schematic of the flowfield with the shock incidence at x/r=-3进一步向下游移动斜劈，使得斜激波无粘入射位置为x/r=0.2，此时对应于内转式进气道超额定状态下前体激波入射溢流口内部的情况。流场纹影如图 14(a)所示，图 14(b)为其流场示意图。入射激波IS与弓形激波BS干扰形成的剪切层Σ并没有撞击壁面，而是形成一种有别于经典的Edney第Ⅲ类激波干扰的结构。其原因在于：V形钝前缘脱体激波DS与弓形激波BS干扰形成的脱体距离和亚声速区域较大，使得发生第Ⅲ类激波干扰的区域增大[23]。
![]()
图 14 入射位置x/r=0.2流场纹影Fig. 14 Schlieren images of the flowfield with the shock incidence at x/r=0.2当斜激波无粘入射位置为x/r=3时，斜激波与弓形激波BS的超声速区域干扰，流场纹影如图 15(a)所示，流场如图 15(b)所示。入射斜激波IS与弓形激波BS相交，形成长度较短的马赫杆MS、透射激波TS以及剪切层Σ1和Σ2。这种由Edney第Ⅱ类激波干扰形成的亚声速区，可能会带来进气道局部不起动[16-17]，应避免出现。
![]()
图 15 入射位置x/r=3流场纹影Fig. 15 Schlieren images of the flowfield with the shock incidence at x/r=32.3 斜激波/弓形激波第Ⅳ类激波干扰流场分析
当斜激波入射V形钝前缘时，三维波系干扰的情况如图 16所示(这里采用斜激波在上)。根据激波位置和特点，可能会出现3种干扰情况：第一种是入射斜激波IS与脱体激波DS相交，第二种是入射斜激波IS与弓形激波BS相交，第三种是入射斜激波与激波BS和DS的交线相交。鉴于三维激波干扰的复杂性，为了深入理解斜激波入射V形前缘时的激波干扰流场，本节以斜激波无粘入射壁面位置坐标为x/r=-5时作为典型工况，结合数值模拟进行分析。与入射位置为x/r=-3的工况(图 12)相比，此时激波干扰点位置更接近BS的正激波部分。
![]()
图 16 斜激波入射V形钝前缘三维流场示意图Fig. 16 Schematic of the shock interaction flowfield of the V-shaped blunt leading edge with shock incidence图 17(a)采用流向截面和展向对称面(z/r=0)展示了斜激波IS与V形钝前缘波系干扰三维结构的演化情况。其中，流向截面的马赫数云图仅显示了一半流场，而展向对称面通过马赫数等值线显示。在x/r=-5截面上(局部放大见图 17(b))，入射斜激波IS与脱体激波DS的较弱部分发生异侧相交，形成Edney第Ⅰ类干扰，产生的透射激波TS相对于激波IS向DS激波面偏折。在x/r=-2.5截面上(局部放大见图 17(c))，入射斜激波IS与脱体激波DS的较强部分发生异侧相交，形成Edney第Ⅱ类激波干扰，并产生马赫杆MS，此时的透射激波TS1入射钝前缘壁面。图 17沿流向发展的波系结构表明：由于入射斜激波IS与前缘脱体激波DS相交处DS激波强度的变化，激波干扰类型由Edney第Ⅰ类转变为第Ⅱ类。而在V形钝前缘溢流口处，如图 17(a)中的蓝色线框所示，入射激波IS与弓形激波BS发生干扰并产生超声速射流，这一区域的流场结构将在图 18中进行分析说明。
![]()
图 17 斜激波与V形溢流口波系干扰Fig. 17 Shock interactions between IS and the V-shaped blunt leading edge![]()
图 18 入射激波作用下V形钝前缘交叉倒圆位置激波干扰流场Fig. 18 Shock interactions near the crotch of the V-shaped blunt leading edge with shock incidence在斜激波入射条件下，多股气流共同汇集在V形钝前缘交叉位置，形成更加复杂的三维激波干扰流场。图 18给出了V形钝前缘交叉位置z/r=0和y/r=-0.4两个正交截面上的流场结构。从z/r=0截面可以看出，入射斜激波与弓形激波BS干扰后，形成通过透射激波TS4连接的两段弓形激波BS和BS′以及超声速射流。该超声速射流并未直接入射壁面，而是发生高度弯曲沿壁面方向溢流，此干扰类型是第Ⅳ a类干扰。而y/r=-0.4截面展示了斜激波IS同时与弓形激波BS和脱体激波DS发生多波系干扰的情况，由于IS与DS干扰已经形成了马赫杆MS(见图 17(c))，MS再与弓形激波BS干扰形成透射激波TS3以及超声速射流区域。可见，入射激波IS、弓形激波BS与脱体激波DS三者之间的干扰互相耦合。
将数值模拟流场沿y方向进行三维纹影处理，如图 19(a)所示，与图 19(b)给出的实验纹影图像符合较好。从三维纹影结果中可以看到，V形钝前缘溢流口弓形激波BS被分为两道激波BS和BS′。实验纹影图像与数值计算结果相互印证了斜激波与V形钝前缘弓形激波发生了第Ⅳa类激波干扰。
![]()
图 19 y方向实验纹影与CFD三维纹影对比Fig. 19 Comparison between the experimental schlieren and the three-dimensional numerical schlieren viewing from the y direction3 结论
通过简化构型对内转式进气道V形钝前缘溢流口激波干扰特性进行了研究，得到以下结论：
(1) V形钝前缘自身形成的激波干扰，导致其驻点前弓形激波的脱体距离较大，波后存在大范围的亚声速区，因此在估算内转式进气道溢流口激波脱体距离时，需慎用圆柱脱体激波距离计算公式。
(2) 斜激波入射在V形钝前缘驻点前弓形激波接近正激波的位置时，发生Edney第Ⅳa类激波干扰。此时，入射激波与弓形激波BS的干扰以及弓形激波BS与脱体激波DS的干扰互相耦合，形成多处超声速射流区域。因此，在内转式进气道额定工况下，前体激波入射V形溢流口驻点前亚声速区域可能带来复杂的流场结构，在实际应用中应当予以关注。
(3) 当斜激波入射在V形钝前缘弓形激波亚声速区的声速点附近时，出现一种有别于Edney第Ⅲ类激波干扰的波系结构，此时干扰产生的剪切层未入射壁面。
(4) 入射斜激波与V形钝前缘脱体激波DS、弓形激波BS的超声速区域干扰时的形态与Edney第Ⅰ、Ⅱ、Ⅵ类激波干扰类似，其中第Ⅱ类干扰形成的马赫杆后局部亚声速区域，可能造成内转式进气道局部不起动。
鉴于V形溢流口三维流动的复杂性，在激波干扰引起的气动热以及三维前体激波入射方面，还有待进一步的细致研究。
-
![]()
图 3 基础模型与模型C底部支撑柱横截面的差异
Fig. 3 Diagram of difference between baseline model and model C on a cross-section of the support column
![]()
图 11 不同模型在监测点3、4的频谱对比图
Fig. 11 Spectrum comparison map of monitoring points 3 and 4 in different models
![]()
图 12 不同模型在监测点10、11的频谱对比图
Fig. 12 Spectrum comparison map of monitoring points 10 and 11 in different models
![]()
图 13 不同模型在监测点17、18的频谱对比图
Fig. 13 Spectrum comparison map of monitoring points 17 and 18 in different models
![]()
图 17 纵截面涡强及矢量场分布对比图
Fig. 17 Comparison of vortex intensity and vector field distribution in longitudinal section
![]()
图 18 横截面1涡强及矢量场分布对比图
Fig. 18 Comparison of vortex intensity and vector field distribution in cross section 1
![]()
图 19 横截面2涡强及矢量场分布对比图
Fig. 19 Comparison of vortex intensity and vector field distribution in cross section 2
![]()
图 20 横截面2上POD第一模态y方向分布对比图
Fig. 20 Comparison of first POD mode （mode-1） associated with the vertical fluctuating for flows over four models
![]()
图 21 模型C横截面2的POD第二模态及矢量场分布对比图
Fig. 21 Second POD mode （mode-2） associated with the streamwise and vertical fluctuating for flows over model C
![]()
图 22 4个模型在横截面2上的POD模态动能百分比
Fig. 22 Percentage of kinetic energy held by the POD modes for the four models on the cross section-2
表 1 第一排3个监测点总声压级对照表
Table 1 Comparison table of overall sound pressure level of three monitoring points in the first row
单位：dB 监测点 3 4 5 背景压力 115.6 111.9 114.6 基础模型 127.4 126.4 127.6 模型 A 125.4 124.8 126.1 模型 B 124.3 123.8 124.7 模型 C 123.2 123.4 123.3 
下载: 导出CSV
表 2 第二排3个监测点总声压级对照表
Table 2 Comparison table of overall sound pressure level of three monitoring points in the second row
单位：dB 监测点 10 11 12 背景压力 113.4 112.7 113.8 基础模型 126.7 125.0 126.9 模型 A 124.3 124.7 125.7 模型 B 122.8 123.5 124.1 模型 C 122.1 123.1 122.8
下载: 导出CSV
表 3 第三排3个监测点总声压级对照表
Table 3 Comparison table of overall sound pressure level of three monitoring points in the third row
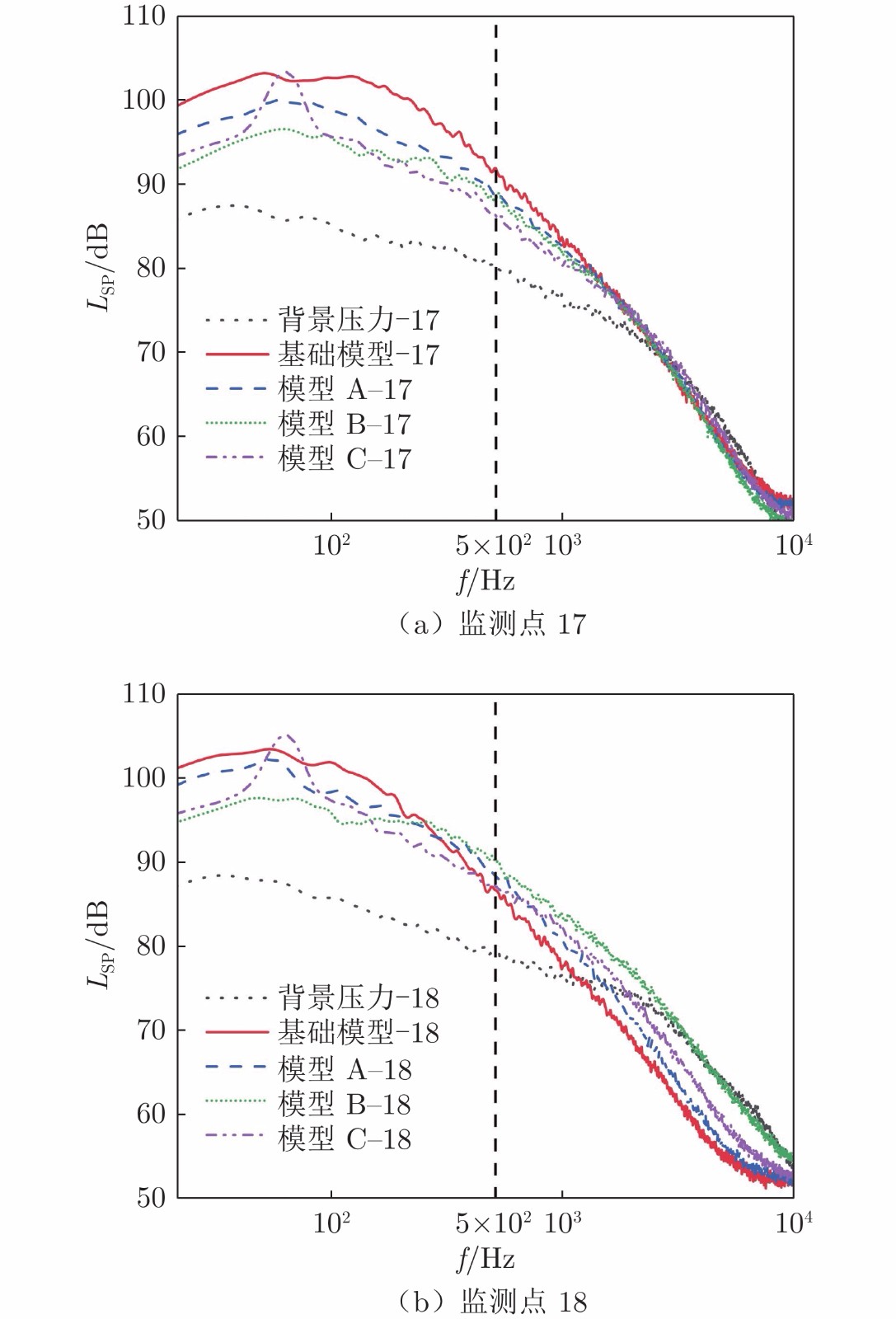
单位：dB 监测点 17 18 19 背景压力 112.5 113.0 113.8 基础模型 126.5 124.4 126.3 模型 A 122.7 122.9 123.3 模型 B 120.5 122.1 121.3 模型 C 121.2 122.5 122.0
下载: 导出CSV
表 4 各改进模型与基础模型总声压级在不同频率范围内的差值
Table 4 Overall sound pressure level differences between the modified models and the generic simple model
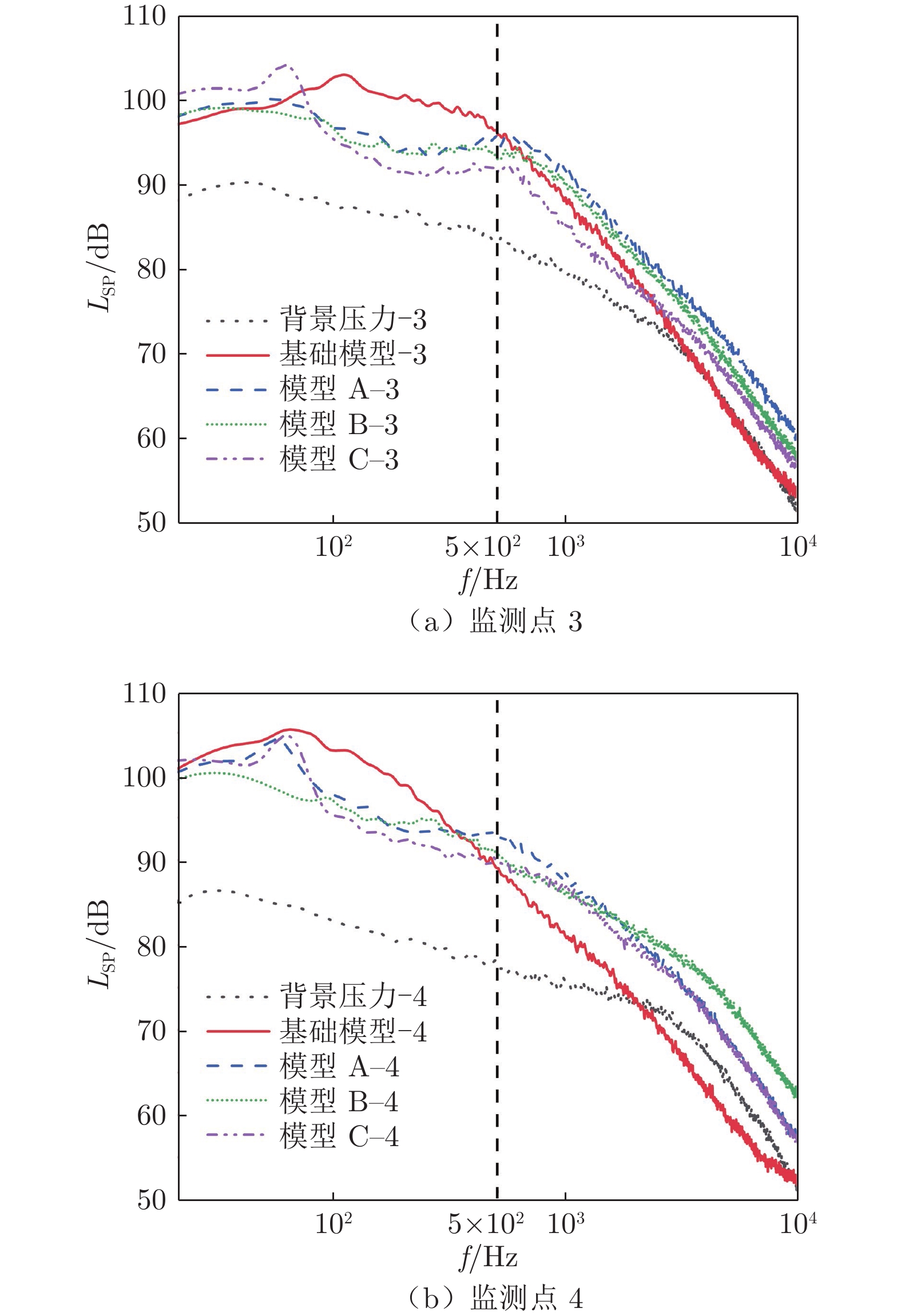
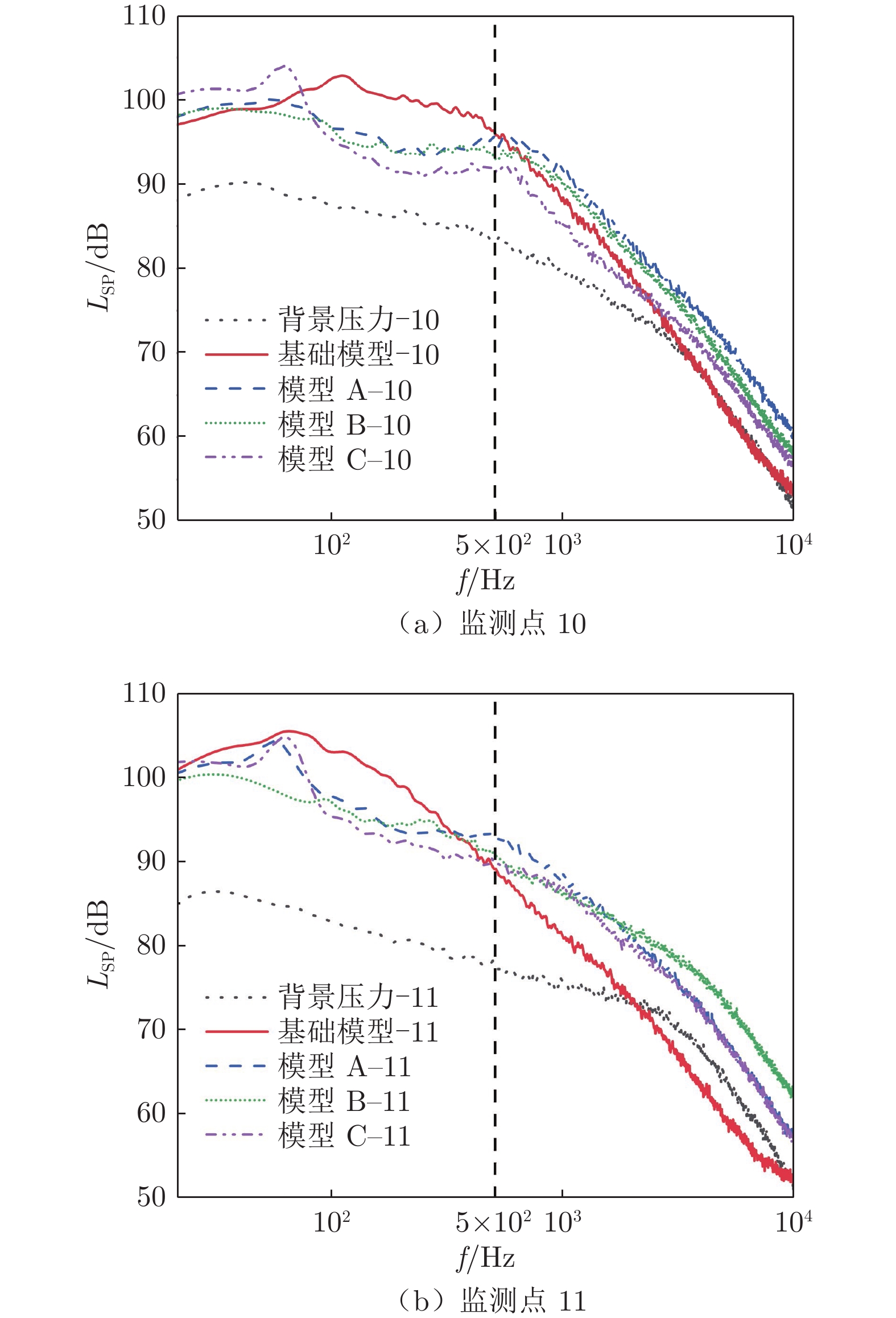
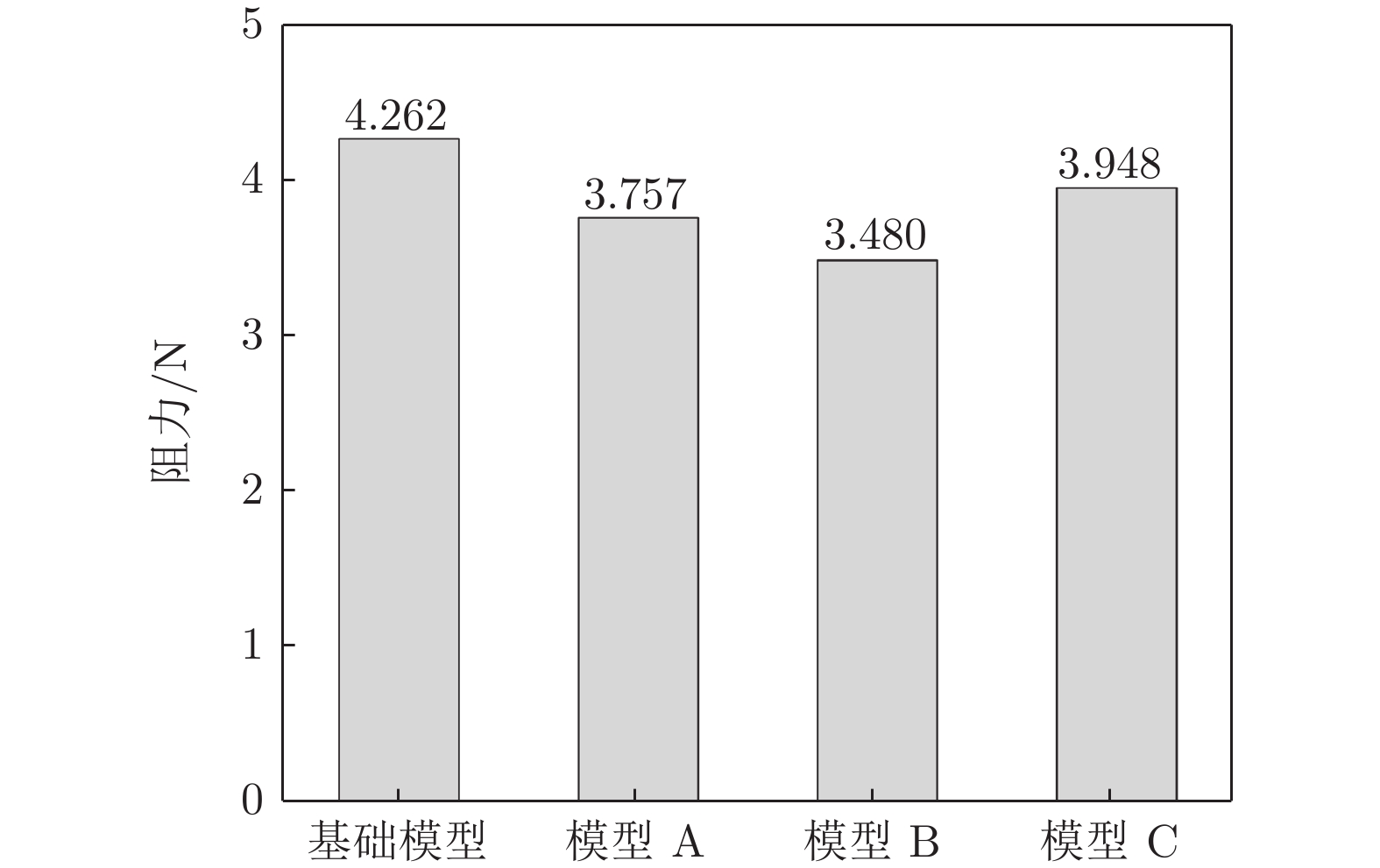
单位：dB 20～500 Hz频段 20～104 Hz频段 ΔLsp1（模型 A−基础模型） −3.0 −1.9 ΔLsp2（模型 B−基础模型） −4.6 −3.3 ΔLsp3（模型 C−基础模型） −4.3 −3.7
下载: 导出CSV
表 5 模型阻力实验值
Table 5 Test values of models drag
单位：N 实验次数 基础模型 模型 A 模型 B 模型 C 1 4.229 3.733 3.489 3.911 2 4.257 3.739 3.478 3.930 3 4.262 3.768 3.476 3.953 4 4.277 3.760 3.479 3.965 5 4.287 3.784 3.480 3.983 均值 4.262 3.757 3.480 3.948
下载: 导出CSV
-
[1] BUCHHEIM R, DOBRZYNSKI W, MANKAU H, et al. Vehicle interior noise related to external aerodynamics[J]. International Journal of Vehicle Design, 1982, 3(4): 398–410. doi: 10.1504/IJVD.1982.061286
[2] HUCHO W, SOVRAN G. Aerodynamics of road vehicles[J]. Annual Review of Fluid Mechanics, 1993, 25: 485–537. doi: 10.1146/annurev.fl.25.010193.002413
[3] 沈钰贵, 陆森林, 孟新. 高速汽车侧窗气流噪声模拟[J]. 机械设计与制造, 2012(7): 125–127. DOI: 10.3969/j.issn.1001-3997.2012.07.046 SHEN Y G, LU S L, MENG X. Simulation on aerodynamic noise of automobile’s side window at high speed[J]. Machinery Design & Manufacture, 2012(7): 125–127. doi: 10.3969/j.issn.1001-3997.2012.07.046
[4] OETTLE N, MANKOWSKI O, SIMS-WILLIAMS D, et al. Evaluation of the aerodynamic and aeroacoustic response of a vehicle to transient flow conditions[J]. SAE International Journal of Passenger Cars - Mechanical Systems, 2013, 6(1): 389–402. doi: 10.4271/2013-01-1250
[5] GRAHS T, OTHMER C. Evaluation of aerodynamic noise generation: parameter study of a generic side mirror evaluating the aeroacoustic source strength[C]//European Conference on Computational Fluid Dynamics. 2006.
[6] KIM D, KIM M, SAREDI E, et al. Robotic PTV study of the flow around automotive side-view mirror models[J]. Experimental Thermal and Fluid Science, 2020, 119: 110202. doi: 10.1016/j.expthermflusci.2020.110202
[7] KATO Y. Numerical simulations of aeroacoustic fields around automobile rear-view mirrors[J]. SAE International Journal of Passenger Cars - Mechanical Systems, 2012, 5(1): 567–579. doi: 10.4271/2012-01-0586
[8] LI Q L, YANG Z G, WANG Y G, et al. Experimental and numerical studies on aerodynamic noise of automotive rear view mirror[J]. Noise Control Engineering Journal, 2011, 59(6): 613. doi: 10.3397/1.3657481
[9] MOHAMUD O M, JOHNSON P. Broadband noise source models as aeroacoustic tools in designing low NVH HVAC ducts[C]//Proc of the SAE Technical Paper Series, 400 Commonwealth Drive. 2006. doi: 10.4271/2006-01-1192
[10] CHEN K H, JOHNSON J, DIETSCHI U, et al. Automotive mirror wind noise simulations and wind tunnel measurements[C]//Proc of the 14th AIAA/CEAS Aeroacoustics Conference (29th AIAA Aeroacoustics Conference). 2008. doi: 10.2514/6.2008-2906
[11] WALKER R, WEI W. Optimization of mirror angle for front window buffeting and wind noise using experimental methods[C]//Proc of the SAE Technical Paper Series Commonwealth Drive. 2007. doi: 10.4271/2007-01-2401
[12] YAO H D, DAVIDSON L, CHRONEER Z. Investigation of interior noise from generic side- View mirror using incompressible and compressible solvers of DES and LES[C]//Proc of the SAE Technical Paper Series, 400 Commonwealth Drive. 2018. doi: 10.4271/2018-01-0735
[13] 王雪钊. 后视镜优化对某轿车气动噪声的影响研究[D]. 镇江: 江苏大学, 2019. WANG X Z. Research on the influence of the wing mirror optimization on aerodynamic noise of A car[D]. Zhenjiang: Jiangsu University, 2019.
[14] 刘红光, 陆森林. 高速车辆气流噪声计算方法[J]. 交通运输工程学报, 2002, 2(2): 41–44. DOI: 10.3321/j.issn:1671-1637.2002.02.010 LIU H G, LU S L. Calculation method of the aerodynamic noise around high speed vehicles[J]. Journal of Traffic and Transportation Engineering, 2002, 2(2): 41–44. doi: 10.3321/j.issn:1671-1637.2002.02.010
[15] 谢超, 谷正气, 杨振东, 等. 不同RANS/LES混合模型的汽车气动噪声分析[J]. 汽车工程, 2015, 37(4): 440–445, 459. DOI: 10.3969/j.issn.1000-680X.2015.04.012 XIE C, GU Z Q, YANG Z D, et al. Analysis on vehicle aerodynamic noise with different hybrid RANS/LES models[J]. Automotive Engineering, 2015, 37(4): 440–445, 459. doi: 10.3969/j.issn.1000-680X.2015.04.012
[16] 陈鑫, 冯晓, 沈传亮, 等. 车外后视镜造型对气动噪声影响的实验研究[J]. 汽车工程, 2017, 39(2): 206–213. DOI: 10.19562/j.chinasae.qcgc.2017.02.014 CHEN X, FENG X, SHEN C L, et al. An experimental study on the effects of exterior rearview mirrors styling on aerodynamic noise[J]. Automotive Engineering, 2017, 39(2): 206–213. doi: 10.19562/j.chinasae.qcgc.2017.02.014
[17] 陈鑫, 王宁, 沈传亮, 等. 后视镜造型对前侧窗气动噪声的影响[J]. 吉林大学学报(工学版), 2020, 50(2): 426–436. DOI: 10.13229/j.cnki.jdxbgxb20180867 CHEN X, WANG N, SHEN C L, et al. Effect of rearview mirror modeling on aerodynamic noise of front window[J]. Journal of Jilin University (Engineering and Technology Edition), 2020, 50(2): 426–436. doi: 10.13229/j.cnki.jdxbgxb20180867
[18] 李启良, 杜文海, 王毅刚, 等. 基于主动射流的汽车后视镜区域气动噪声控制[J]. 同济大学学报(自然科学版), 2019, 47(8): 1195–1200. DOI: 10.11908/j.issn.0253-374x.2019.08.017 LI Q L, DU W H, WANG Y G, et al. Aerodynamic noise control of automobile rear view mirror based on active jet[J]. Journal of Tongji University (Natural Science), 2019, 47(8): 1195–1200. doi: 10.11908/j.issn.0253-374x.2019.08.017
[19] 姜豪, 赖万虎, 张思文, 等. 汽车后视镜气动噪声优化研究[J]. 汽车工程, 2020, 42(1): 121–126. DOI: 10.19562/j.chinasae.qcgc.2020.01.018 JIANG H, LAI W H, ZHANG S W, et al. Research on aeroacoustic optimization of vehicle rearview mirror[J]. Automotive Engineering, 2020, 42(1): 121–126. doi: 10.19562/j.chinasae.qcgc.2020.01.018
[20] LI Y Q, LIU Y Y, DING Z Y. Numerical simulation on the impact of the bionic structure on aerodynamic noises of sidewindow regions in vehicles[J]. Journal of Vibroengineering, 2018, 20(2): 1257–1271. doi: 10.21595/jve.2017.18779
[21] TAIRA K, BRUNTON S L, DAWSON S T M, et al. Modal analysis of fluid flows: an overview[J]. AIAA Journal, 2017, 55(12): 4013–4041. doi: 10.2514/1.J056060
计量
- 文章访问数: 310
- HTML全文浏览量: 79
- PDF下载量: 49
