Reconstruction of turbulent fields based on super-resolution reconstruction method
-
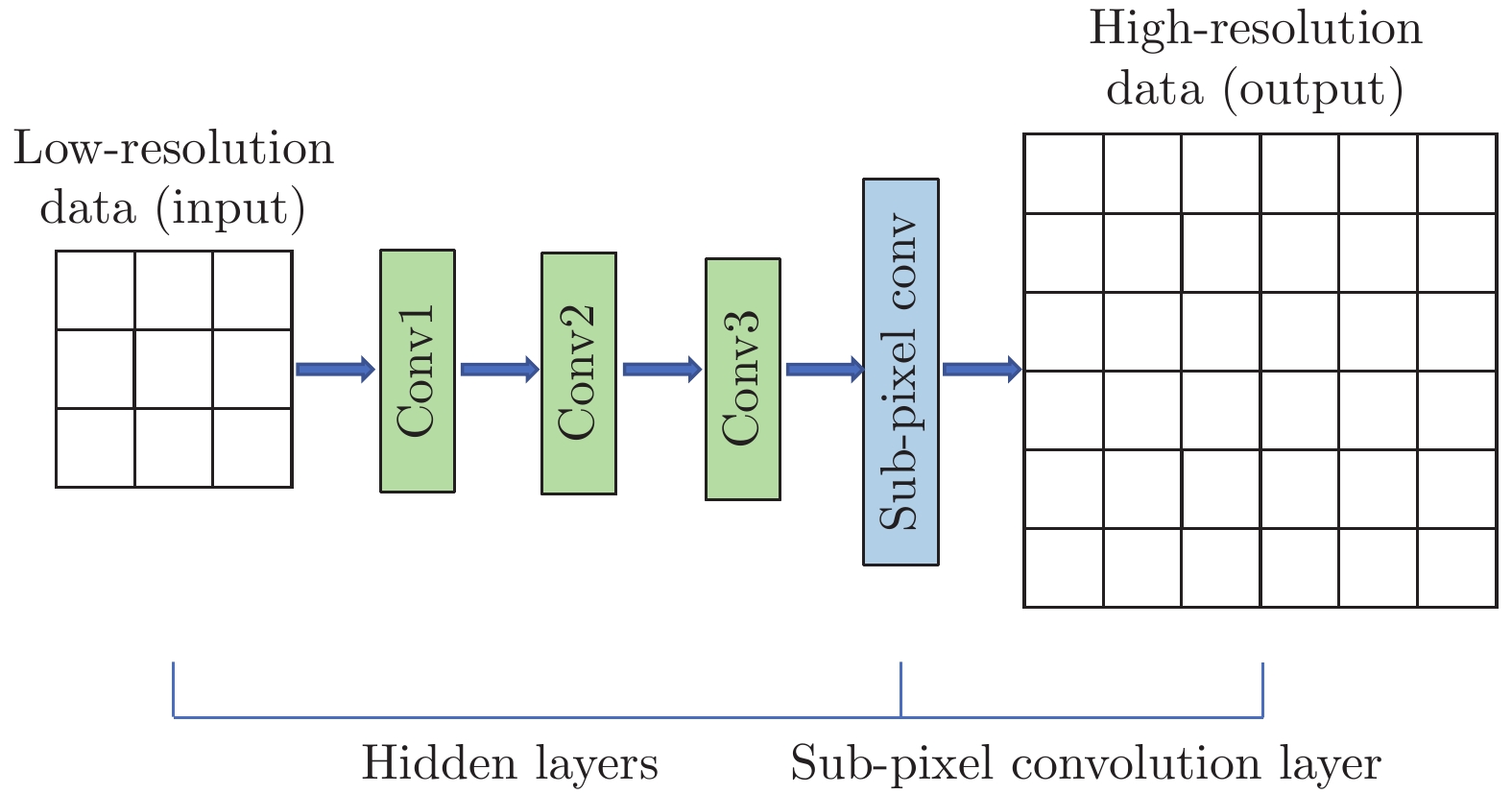
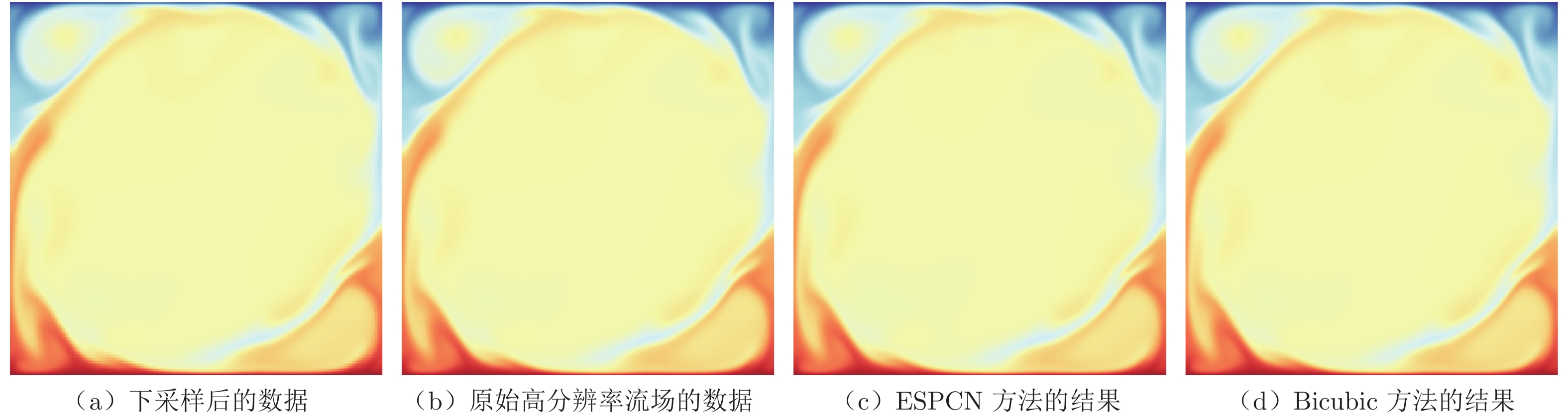
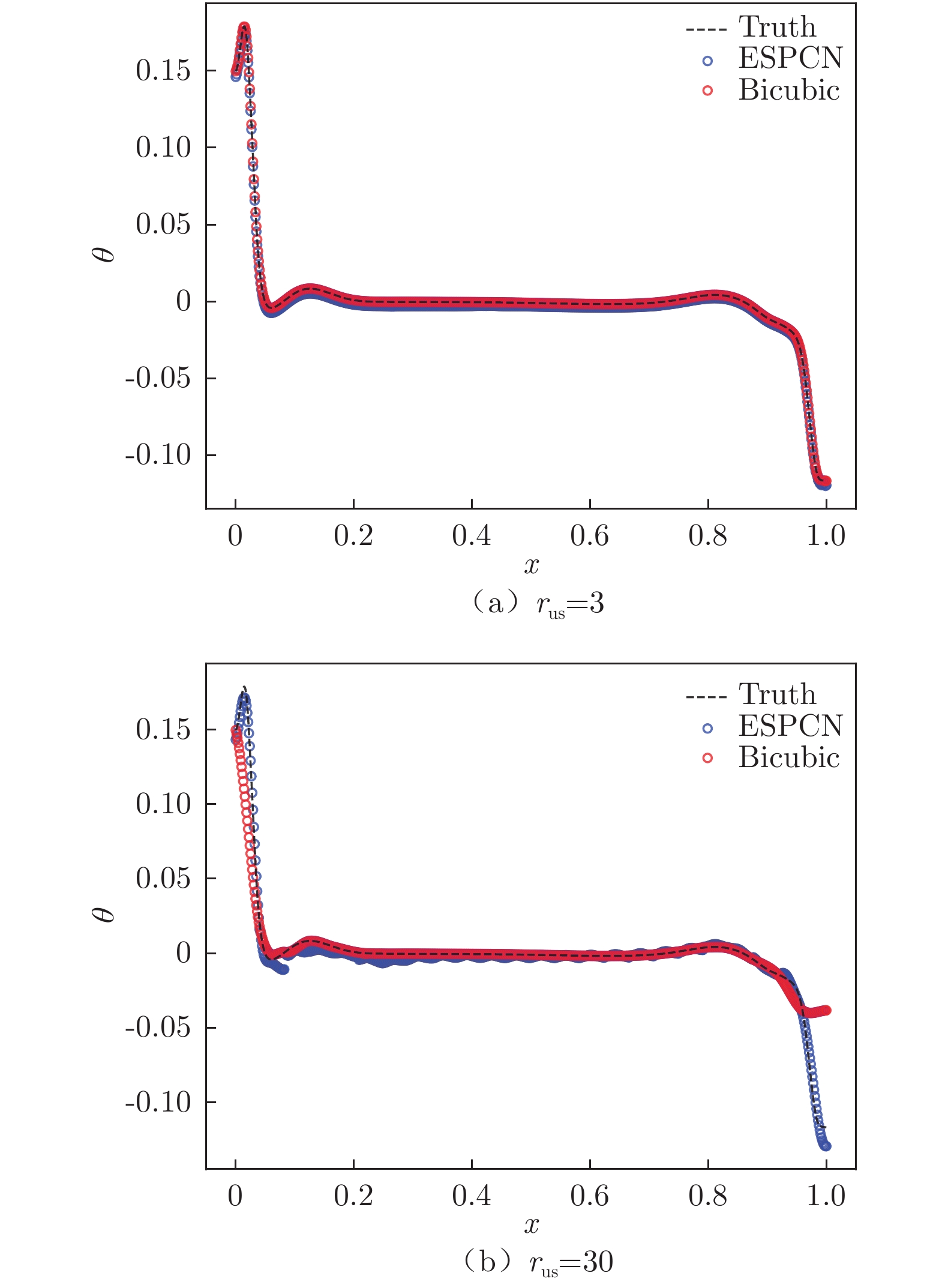
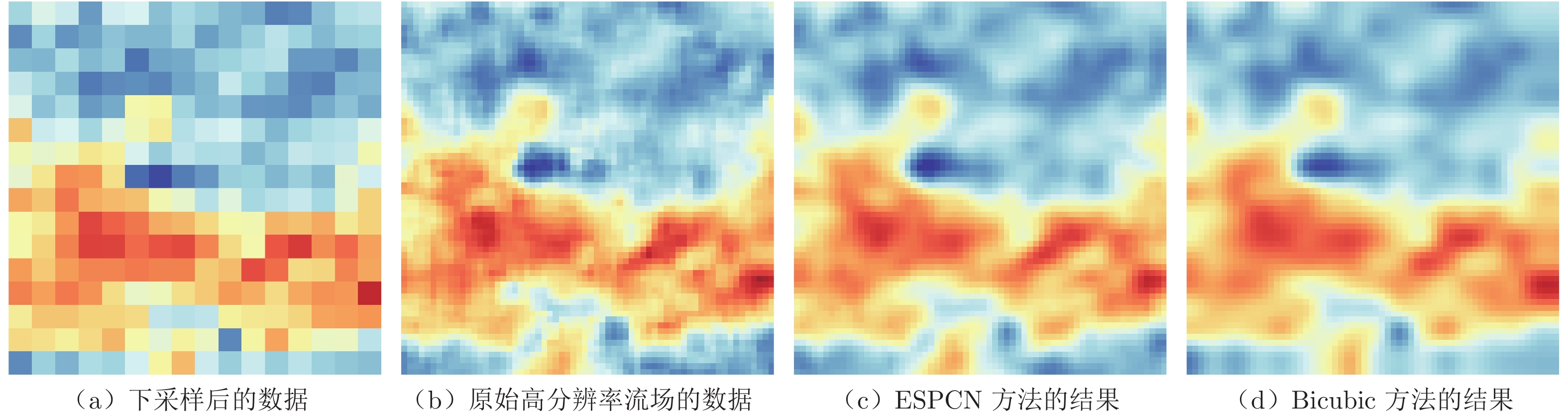
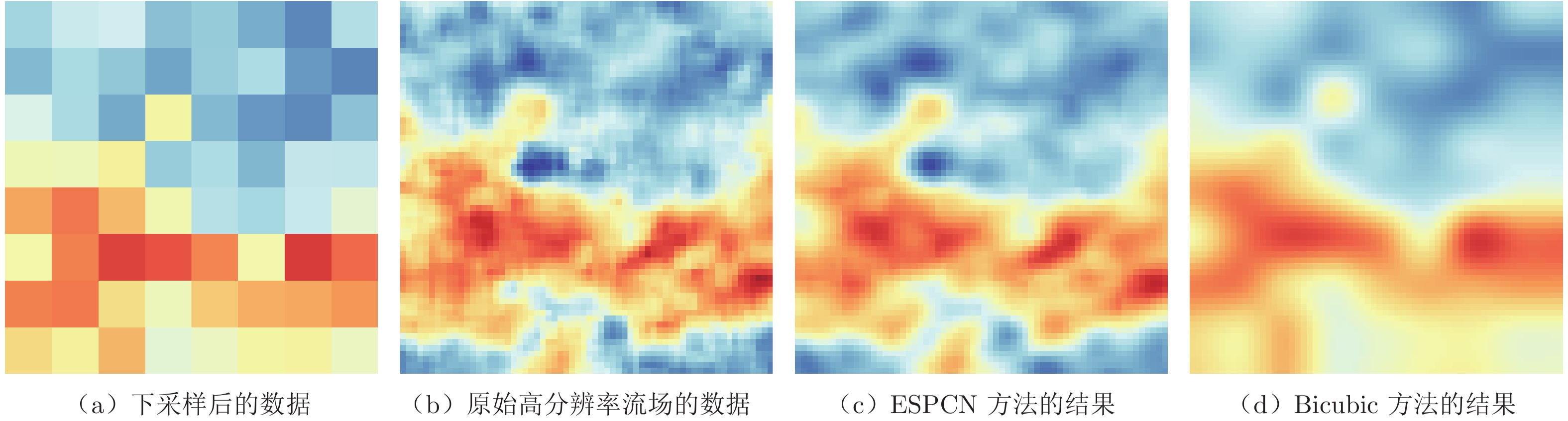
摘要: 从低分辨率流场数据中获取精细流场信息具有重要的研究意义。基于卷积神经网络的超分辨率重构方法是近年来发展的一种较为有效的精细流场重构方法。本文采用高效亚像素卷积神经网络（Efficient Sub-Pixel Convolutional Neural Network，ESPCN），对Rayleigh–Bénard（RB）对流的数值模拟数据和湍流边界层（Turbulent Boundary Layer，TBL）的实验测量数据进行了超分辨率重构，并与双三次插值方法（Bicubic Interpolation）的重构结果进行对比。对比结果表明：在较小的下采样比下，ESPCN方法和Bicubic方法的重构精度相当；在较大的下采样比下，ESPCN方法的重构精度明显优于Bicubic方法。此外，ESPCN方法对数据梯度较大区域的超分辨率重构效果优于Bicubic方法。Abstract: It is an important issue to obtain detailed flow fields from limited flow fields data. The convolutional-neural-networks-based super-resolution reconstruction methods developed in recent years are effective methods to obtain detailed flow fields. The efficient sub-pixel convolutional neural network（ESPCN） method is used to reconstruct Rayleigh–Bénard（RB） convection numerical simulation data and turbulent boundary layer（TBL） experimental measured data, and obtain high resolution flow fields data. The reconstructed high resolution flow fields data obtained using ESPCN is then compared to the results from the traditional super-resolution reconstruction method, the bicubic interpolation method. The results indicate that the flow fields reconstructed by the ESPCN method and the bicubic method agree well with the original high-resolution flow fields data when the down-sampling ratio is small. But, when the down-sampling ratio is large, the accuracy of the flow fields reconstructed by the ESPCN method is significantly better than that constructed by the bicubic method. In addition, the ESPCN method has a better performance than the bicubic method in areas with large gradients.
-
0 引言
0.6m×0.6m连续式跨声速风洞（以下简称0.6m风洞）为国内首座具备负压实验能力的连续式跨声速风洞,试验马赫数范围为0.2~1.6，压力范围为20~250kPa(绝对压力)，具有3个试验段，该风洞通过阀门控制系统实现常压、增压和降压运行，其中增压、常压运行通过调节进排气系统实现，降压运行通过调节抽真空系统实现。
风洞的总压调节能力及精度是风洞的一个重要技术指标，对提高试验效率和试验数据精准度具有重 要作用。目前，国内连续式跨声速风洞数量较少，NF-6风洞作为国内首座连续式跨声速风洞，其马赫数范围较窄，试验工况相对较少[1- 2]。目前国内外风洞对马赫数控制方法描述较多，而对连续式风洞总压控制及马赫数和总压的耦合关系描述较少[3-11]。暂冲式风洞压力控制通过主调压阀和引射器调压阀等实现[9-11]，而0.6m连续式风洞压力主要通过进排气和抽真空阀门/泵组合来实现，且总压调节受马赫数调节手段影响，可借鉴的内容较少。各种改进的模糊PID控制方法在风洞中尤其是马赫数或风速控制的应用较多[12-13]，文献[13]对某暂冲式风洞主气流压力控制原理进行了简单分析，并引入模糊控制概念，总压控制精度达到0.5%，因此本文拟采用模糊PID来进行总压控制，但其控制参数大幅跳动时容易导致控制器输出跳动，进而导致压力波动，因而需要结合0.6m连续式风洞压力特性对控制算法进行优化。
0.6m风洞阀门系统结构见图 1。
不同于现有其他风洞，该风洞压力调节系统具有以下特性：
(1) 总压调节手段多，包含9台阀门和3台泵，不同的压力工况采用不同的阀门组合进行控制。
(2) 压力控制范围广，从绝对压力20kPa至250kPa，涉及常压、增压、负压3种不同的工况，且试验过程中可连续变总压、连续变马赫数和连续变迎角[14]。
(3) 压力控制精度要求高，设计指标为0.2%(常压和增压)[15]。
(4) 作为大型连续式风洞的引导性风洞，风洞运行过程中迎角、二喉道、压缩机转速、驻室抽气流量等随时需要调节，这些因素都对总压有较大影响，从而导致压力场波动较大，需要总压控制策略具备很强的适应能力[14-15]。
本文主要研究内容为：分析0.6m连续式风洞的压力控制特性，摸索多试验工况、宽压力调节范围下具有较好适应性的压力控制策略，并结合控制对象特性通过对模糊PID算法分段变参数的方式进行改进，并实施该风洞的压力控制，为风洞控制策略优化及试验效率的提高奠定基础，同时为后续的大型风洞建设积累经验。
1 风洞总压和马赫数耦合特性
连续式跨声速风洞主要通过调节进气/排气/抽真空阀门的开度来实现总压的调节，由于总压和马赫数在调节时相互耦合，致使调节难度加大，且调节时间较长，经过分析，总压和马赫数调节手段的耦合关系如图 2所示。
其中，G1(s)至G9(s)分别为每种控制量的传递函数，Gab(s)为总压对马赫数的影响函数，Gba(s)为马赫数对总压的影响函数，Ga(s)为总压控制传递函数，Gb(s)为马赫数控制传递函数。
为提高总压控制精度并减少调节稳定时间，理论上需要对总压和马赫数进行解耦控制，但目前总压和马赫数的解耦算法在工程应用中较少，更多是通过控制策略的优化并尽可能减少耦合的方式，因此，本系统设计时将多种马赫数调节手段调节时对总压的影响作为总压控制的扰动对待，同时风洞马赫数控制策略设计时减少总压和马赫数的耦合。0.6m风洞总压控制主要通过调节相应的调节阀开度实现，因此需首先建立调节阀开度和风洞总压的关系。对于可压缩流体，理想情况下，流量Q和压力之间关系为[16]：
(1) 其中，β为缩流处截面等效直径与管道截面等效直径之比； E为与流速有关的系数；A为缩流处截面积；ρ为密度；Q为体积流量； p1为入口静压；p2为出口静压，近似等于大气压；ε为流体膨胀系数。
同时，对于抛物线特性[17]的调节阀，在理想情况下其流量和阀门开度之间满足下式：
(2) 其中，Qmax为流经阀门的最大流量，R为阀门的可调比，为流经阀门的最大流量和最小流量的比值，国内调节阀R一般取为30或50，l/L为阀门开度的百分比。
由式(1)和(2)可得调节阀开度和静压的关系，而风洞总压由静压和动压组成，进而得到调节阀开度和风洞总压之间的关系：
(3) 
(4) 
(5) 
(6) 其中，p0为总压，f1(n)为风速和压缩机转速的函数关系，考虑到稳定段气流速度较低，可忽略不计，f2(α,r,l,m)为马赫数调节对总压的影响量，a为迎角变化梯度，r为压缩机静叶角，l为二喉道位移，m为驻室抽气量。
由此可见，连续式风洞总压影响因素包括：马赫数调节方式、气流介质密度（由风洞内总压和总温确定）、调节阀开度、气源压力等，本文重点对气源压力、阀门开度、压缩机转速和目标总压进行考虑以设计总压控制策略。
2 总压控制策略
为保证总压控制精度并确保风洞运行安全，考虑到PID算法具有结构简单、稳定性好、工作可靠、调整方便的优点，但同时存在自适应能力差的缺点，因此拟采用模糊PID算法，其对压力波动有较强适应性，但由于该连续式风洞压力范围较广，且不同目标压力区间下压力特性不同，若单纯采用模糊PID进行控制，可能导致不同压力工况参数匹配度较差，从而带来震荡或超调，因此该连续式风洞总压控制的核心算法采用分段变参数加模糊PID控制。
结合该连续式跨声速风洞压力变化规律，以及连续式风洞运行时压缩机充气密封系统将向风洞洞体内漏气的特性，为节省气源耗气量，确定该风洞总压控制策略为：
(1) 当工况为常压（控制压力目标在大气压至105kPa）时，由于压缩机充气密封往洞体漏气，因此仅利用排气调节阀进行总压控制；
(2) 当工况为增压（控制压力目标大于105kPa）时，通过预置进气阀开度和调节排气阀进行总压控制；
(3) 当工况为负压（控制压力目标低于94kPa）时，开启真空泵，通过预置进气调节阀开度、开启真空泵和调节抽真空调节阀进行总压控制；
(4) 当压缩机转速大幅上升或下降时，压力会大幅波动，通过计算目标转速和当前转速误差以及转速误差变化率，对参与调节的阀门采用分段限幅跟随调节的方式，以减少积分饱和和超调，同时为减少总压和马赫数耦合，变马赫数时采用多阶梯升压缩机转速的控制方式。
(5) 压力调节过程中，进气阀预置开度与气源压力和目标压力满足调试确定的函数关系，排气主调阀进行压力粗调（0.2%以上），待压力稳定后由排气辅调阀精调（0.2%以下至0.04%）。
3 分段变参数加模糊变参数PID算法
3.1 模糊PID控制算法
模糊PID控制算法以常规PID控制为基础，系统首先计算被控量的误差e和误差变化率ec作为二维模糊控制器的输入变量，然后通过模糊化、模糊控制规则推理、解模糊得到KP，KI和KD的修正量，在控制过程中在线实时整定PID各参数，其原理已经非常成熟，这里不再累述。
3.2 分段变参数加模糊变参数PI算法
由于风洞总压控制范围较宽，在不同的压力区间，风洞的总压特性不同，尤其当总压较高时(p0≥200kPa)，风洞排气调节阀开度增大后总压下降明显，同时目前调节阀存在响应时间及执行速度较慢的问题，当压力快速变化时阀门的调节速度跟不上“节奏”，因此若不根据压力控制范围对控制参数进行调整，而仍使用常压时的基准调节参数，必然导致PID算法适应性差，产生较大的超调。因此，以模糊自适应PID为基础，增加目标总压作为输入变量，首先根据目标总压进行分段，基于不同的总压控制目标结合简单PI调试规律初步确定PI参数基准值，尔后由模糊算法进行变参数控制，以提高不同试验状态的自适应能力，原理框图见图 3。
![]()
图 3 分段变参数加模糊PID控制框图Fig. 3 Block diagram of valve control system using segmented parameter and fuzzy PID3.3 模糊控制参数及规则表
阀门控制系统中，将计算出的目标压力、实际压力和给定压力的误差e和误差变化率ec作为模糊控制器的输入变量，PI控制器的2个参数KP、KI的修正量ΔKP、ΔKI作为输出变量。误差e基本论域取[-0.75，0.75]，其偏差变化率ec的基本论域取[-0.5，0.5]，输出变量ΔKP、ΔKI基本论域分别取为[-0.5，0.5]、[-1.5，1.5]，E、EC、ΔKP、ΔKI分别是输入变量e、ec、输出变量ΔKP、ΔKI所对应的模糊语言变量。E、EC、ΔKP、ΔKI都分别取7个模糊子集，其中NB、NM、NS、ZO、PS、PM、PB分别代表负大、负中、负小、零（又分成正零ZP、负零ZN）、正小、正中、正大。模糊语言变量选择三角隶属函数。
调试过程先摸索出不同压力区间段的大体P、I参数，同时为防止控制输出突跳，将控制参数进行拟合处理后再作为模块控制的输入，见式7。
(7) 式中KP、KI为分段后基准比例系数和积分系数，p为目标压力。根据不同目标压力分段，能有效缩小适合当前目标压力的基准P、I值范围，基准P、I波动范围缩小，也就缩小了最终的P、I参数波动的绝对值，进而避免了控制参数大幅跳动的问题。
表 1给出了结合风洞压力特性的分段变参数模糊PID控制规则表。 PID的实时控制参数是在基准P、I参数的基础加上模糊算法得到的P、I参数增量。
表 1 阀门控制系统
Table 1
E EC NB NM NS 0 PS PM PB NB PB/NL PB/NL PB/NM PB/NM PB/NS PS/0 PS/0 NM PB/NB PB/NB PB/NM PB/NS PB/NS 0/0 0/0 NS PM/NM PM/NM PM/NS PS/NS 0/0 NS/PS NS/PS ZP PS/NS PS/NS PS/NS 0/0 NS/PS NM/PM NM/PM ZN NP/PS NP/PS PS/NS 0/0 NS/PS PM/PS PM/PS PS NS/NS NS/NS 0/0 NS/PS NS/PS PM/PS PM/PS PM 0/0 0/0 NS/PS NM/PS NM/PM PB/NB PB/NB PB PS/0 PS/0 NM/PS NM/PM NM/PM PB/NL PB/NL 3.4 进气阀门开度预置
由于连续式风洞有大量用于气密封的空气往洞内泄露，因此常压时采用气密封漏气加排气阀调节的方式（进气阀关闭）；而在增压时尤其高目标压力段，当压力欠压时，若仅通过气密封漏气的方式进行补气则速度过慢，需通过进气阀门对风洞进行补气，调试时为尽量减少气源压力波动对总压控制的影响，结合阀门性能曲线，减少气源消耗，进气阀以一个相对固定的进气量往风洞灌气，进气阀预置开度与气源压力和目标压力满足下列函数关系：
(8) 
(9) 
(10) 4 软件流程设计
程序设计时首先基于模块化编程方法，将阀门和泵进行组合以实现不同压力工况控制，风洞运行时，根据工况命令调用不同的模块，以满足多种工况下阀门开关组合的控制逻辑需求，并通过压力控制模块实现闭环控制，压力闭环由阀门系统PLC 315实现，风洞主控系统和阀门控制系统通过Profinet工业以太网进行通信，阀门控制系统软件流程见图 4。
5 试验验证
为测试控制算法性能，对变总压、变马赫数、变迎角等不同工况均进行了调试，迎角范围为-4°～14°，图 5和6列举了不同工况下的典型测试结果，其中图 5为风洞在常压和增压工况下变马赫数变迎角调试结果，图 6为负压20kPa变马赫数变迎角试验结果。
![]()
图 6 20kPa变马赫数变迎角调试结果Fig. 6 The debug result with varying Mach numbers and attack angles at the pressure of 20kPa由图 5和6可见，趋于稳态后，常压100kPa时，总压最大值100.071，最小值99.923，平均值100.002，按
6 结论
经过试验验证，可以得出以下结论：
（1） 利用分段变参数加模糊PID控制方法实现了0.6m风洞总压精确控制，总压控制精度优于设计指标要求，该控制方法对较宽压力范围或调节阀性能比较敏感的风洞压力控制是有效的；
（2） 如果进一步提高各调节阀的控制精度及响应速度，总压控制精度和稳定速度将进一步提升；
（3） 本文在0.6m风洞探讨的风洞总压控制策略可为后续大型风洞及其他连续式风洞的压力控制方法提供参考。
下一步还将重点对总压和马赫数之间，不同马赫数调节手段与总压控制之间的耦合关系等方面展开更深入的研究。
-
![]()
图 2 下采样比为3的RB系统温度场数据的超分辨率重构结果
Fig. 2 The super-resolution reconstruction result of the temperature field data of the RB system with rus=3
![]()
图 3 下采样比为30的RB系统温度场数据的超分辨率重构结果
Fig. 3 The super-resolution reconstruction result of the temperature field data of the RB system with rus=30
![]()
图 4 RB系统中心线温度数据剖面的超分辨率重构结果
Fig. 4 Comparison of the results of the temperature profile of the horizontal centerline of the RB system temperature field data
![]()
图 5 RB系统瞬时温度场数据PDF分布的超分辨率重构结果
Fig. 5 Comparison of PDF results of instantaneous temperature field data of the RB system temperature field data
![]()
图 7 下采样比为4的TBL流向速度数据的超分辨率重构结果
Fig. 7 The super-resolution reconstruction result of the TBL streamwise velocity with the down-sampling rus =4
![]()
图 8 下采样比为8的TBL流向速度数据的超分辨率重构结果
Fig. 8 The super-resolution reconstruction result of the TBL streamwise velocity with the down-sampling rus =8
表 1 不同下采样比的MSE
Table 1 MSE with different down-sampling rus
rus=3 rus=10 rus=20 rus=30 ESPCN 4.02×10–6 4.58×10–6 2.41×10–5 3.08×10–5 Bicubic 6.97×10–6 1.95×10–4 7.11×10–4 1.39×10–3 
下载: 导出CSV
表 2 不同下采样比的MSE
Table 2 MSE with different down-sampling rus
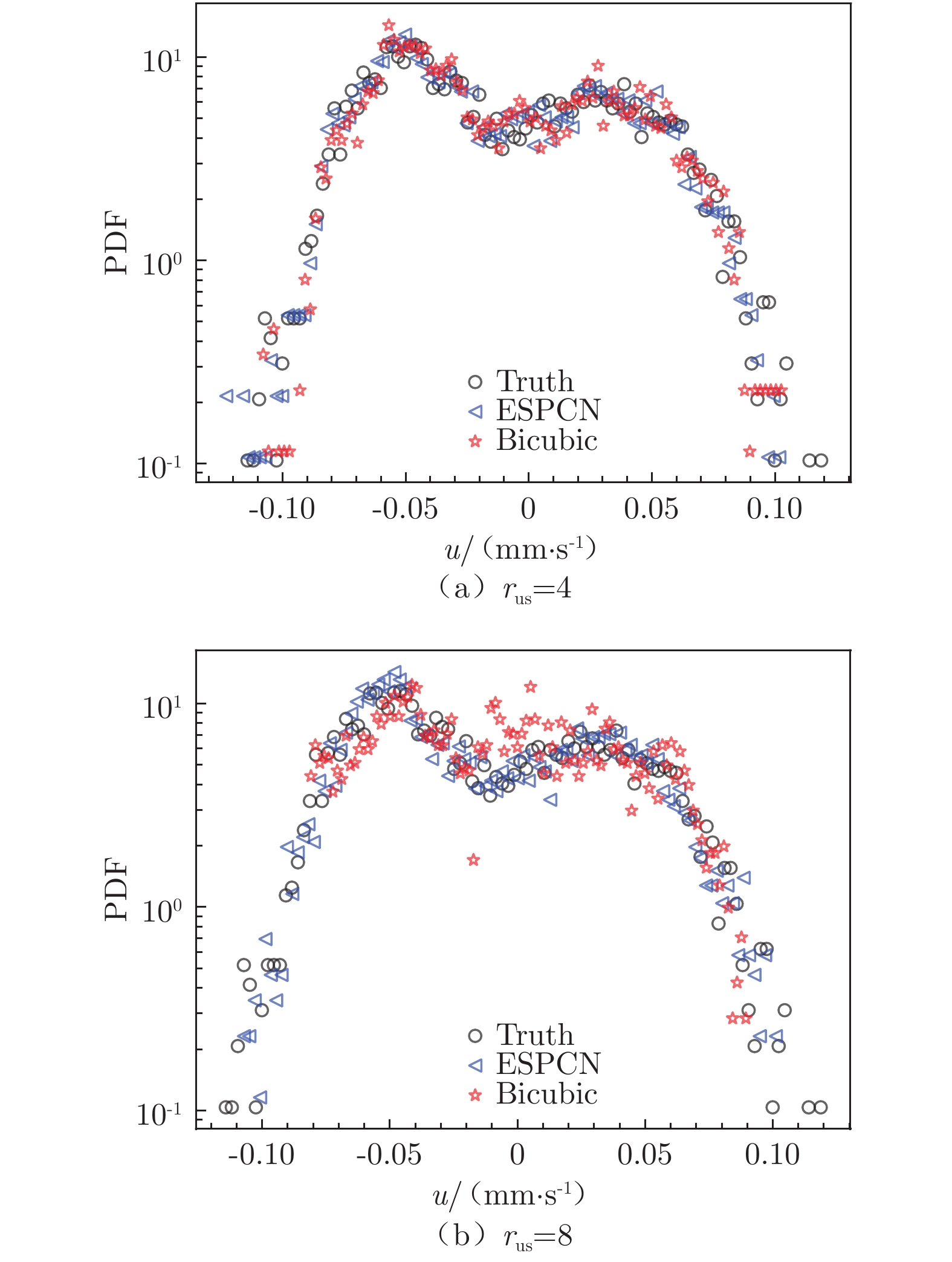
rus =2 rus =4 rus =8 ESPCN 1.63×10–4 4.32×10–4 7.00×10–4 Bicubic 1.60×10–4 7.16×10–4 3.62×10–3
下载: 导出CSV
-
[1] ADRIAN R J. Twenty years of particle image velocimetry[J]. Experiments in Fluids,2005,39(2):159-169. doi: 10.1007/s00348-005-0991-7
[2] WANG Z J,FIDKOWSKI K,ABGRALL R,et al. High-order CFD methods: current status and perspective[J]. International Journal for Numerical Methods in Fluids,2013,72(8):811-845. doi: 10.1002/fld.3767
[3] 郭中州,何志强,赵文文,等. 高效非结构网格变形与流场插值方法[J]. 航空学报,2018,39(12):126-137. DOI: 10.7527/S1000-6893.2018.22411 GUO Z Z,HE Z Q,ZHAO W W,et al. Efficient mesh deformation and flowfield interpolation method for unstruc-tured mesh[J]. Acta Aeronautica Et Astronautica Sinica,2018,39(12):126-137. doi: 10.7527/S1000-6893.2018.22411
[4] TÖLKE J,KRAFCZYK M. Second order interpolation of the flow field in the lattice Boltzmann method[J]. Computers & Mathematics With Applications,2009,58(5):898-902. doi: 10.1016/j.camwa.2009.02.012
[5] DRUAULT P,GUIBERT P,ALIZON F. Use of proper orthogonal decomposition for time interpolation from PIV data[J]. Experiments in Fluids,2005,39(6):1009-1023. doi: 10.1007/s00348-005-0035-3
[6] GUNES H,RIST U. Spatial resolution enhancement/smoothing of stereo-particle-image-velocimetry data using proper-orthogonal-decomposition-based and Kriging inter-polation methods[J]. Physics of Fluids,2007,19(6):064101. doi: 10.1063/1.2740710
[7] ROESGEN T. Optimal subpixel interpolation in particle image velocimetry[J]. Experiments in Fluids,2003,35(3):252-256. doi: 10.1007/s00348-003-0627-8
[8] DUNLOP G R. A rapid computational method for improve-ments to nearest neighbour interpolation[J]. Computers & Mathematics With Applications,1980,6(3):349-353. doi: 10.1016/0898-1221(80)90042-5
[9] BLU T,THÉVENAZ P,UNSER M. Linear interpolation revitalized[J]. IEEE Transactions on Image Processing,2004,13(5):710-719. doi: 10.1109/tip.2004.826093
[10] CARLSON R E,FRITSCH F N. Monotone piecewise bicubic interpolation[J]. SIAM Journal on Numerical Analysis,1985,22(2):386-400. doi: 10.1137/0722023
[11] DONG C, LOY C C, HE K M, et al. Learning a deep convolutional network for image super-resolution[C]//Computer Vision – ECCV 2014, 2014: 184-199. doi: 10.1007/978-3-319-10593-2_13
[12] DONG C,LOY C C,HE K M,et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2016,38(2):295-307. doi: 10.1109/TPAMI.2015.2439281
[13] DONG C, LOY C C, TANG X O. Accelerating the super-resolution convolutional neural network[C]//Computer Vision – ECCV 2016, 2016: 391-407. doi: 10.1007/978-3-319-46475-6_25
[14] SHI W Z, CABALLERO J, HUSZÁR F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]// Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. 2016: 1874-1883. doi: 10.1109/CVPR.2016.207
[15] LEDIG C, THEIS L, HUSZÁR F, et al. Photo-realistic single image super-resolution using a generative adversarial network[C]// Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. 2017: 105-114. doi: 10.1109/CVPR.2017.19
[16] HE C X,WANG P,LIU Y Z. Sequential data assimilation of turbulent flow and pressure fields over aerofoil[J]. AIAA Journal,2021,60(2):1091-1103. doi: 10.2514/1.J060697
[17] DENG Z W,CHEN Y J,LIU Y Z,et al. Time-resolved turbulent velocity field reconstruction using a long short-term memory(LSTM)-based artificial intelligence framework[J]. Physics of Fluids,2019,31(7):075108. doi: 10.1063/1.5111558
[18] 谢晨月,袁泽龙,王建春,等. 基于人工神经网络的湍流大涡模拟方法[J]. 力学学报,2021,53(1):1-16. DOI: 10.6052/0459-1879-20-420 XIE C Y,YUAN Z L,WANG J C,et al. Artificial neural network-based subgrid-scale models for large-eddy simula-tion of turbulence[J]. Chinese Journal of Theoretical and Applied Mechanics,2021,53(1):1-16. doi: 10.6052/0459-1879-20-420
[19] XIE C Y,WANG J C,LI H,et al. Artificial neural network mixed model for large eddy simulation of compressible isotropic turbulence[J]. Physics of Fluids,2019,31(8):085112. doi: 10.1063/1.5110788
[20] LI K,KOU J Q,ZHANG W W. Unsteady aerodynamic reduced-order modeling based on machine learning across multiple airfoils[J]. Aerospace Science and Technology,2021,119:107173. doi: 10.1016/j.ast.2021.107173
[21] 张伟伟,寇家庆,刘溢浪. 智能赋能流体力学展望[J]. 航空学报,2021,42(4):524689-524689. DOI: 10.7527/S1000-6893.2020.24689 ZHANG W W,KOU J Q,LIU Y L. Prospect of artificial intelligence empowered fluid mechanics[J]. Acta Aeronautica et Astronautica Sinica,2021,42(4):524689-524689. doi: 10.7527/S1000-6893.2020.24689
[22] WERHAHN M,XIE Y,CHU M Y,et al. A multi-pass GAN for fluid flow super-resolution[J]. Proceedings of the ACM on Computer Graphics and Interactive Techniques,2019,2(2):1-21. doi: 10.1145/3340251
[23] FUKAMI K,FUKAGATA K,TAIRA K. Super-resolution reconstruction of turbulent flows with machine learning[J]. Journal of Fluid Mechanics,2019,870:106-120. doi: 10.1017/jfm.2019.238
[24] FUKAMI K,FUKAGATA K,TAIRA K. Machine-learning-based spatio-temporal super resolution reconstruction of turbulent flows[J]. Journal of Fluid Mechanics,2021,909:A9. doi: 10.1017/jfm.2020.948
[25] LIU B,TANG J P,HUANG H B,et al. Deep learning methods for super-resolution reconstruction of turbulent flows[J]. Physics of Fluids,2020,32(2):025105. doi: 10.1063/1.5140772
[26] DENG Z W,HE C X,LIU Y Z,et al. Super-resolution reconstruction of turbulent velocity fields using a generative adversarial network-based artificial intelligence framework[J]. Physics of Fluids,2019,31(12):125111. doi: 10.1063/1.5127031
[27] BAI K,LI W,DESBRUN M,et al. Dynamic upsampling of smoke through dictionary-based learning[J]. ACM Transactions on Graphics,2021,40(1):1-19. doi: 10.1145/3412360
[28] GAO H,SUN L N,WANG J X. Super-resolution and denoising of fluid flow using physics-informed convolutional neural networks without high-resolution labels[J]. Physics of Fluids,2021,33(7):073603. doi: 10.1063/5.0054312
[29] KIM H,KIM J,WON S,et al. Unsupervised deep learning for super-resolution reconstruction of turbulence[J]. Journal of Fluid Mechanics,2021,910:A29. doi: 10.1017/jfm.2020.1028
[30] SCHRÖDER A,GEISLER R,STAACK K,et al. Eulerian and Lagrangian views of a turbulent boundary layer flow using time-resolved tomographic PIV[J]. Experiments in Fluids,2011,50(4):1071-1091. doi: 10.1007/s00348-010-1014-x
-
期刊类型引用(8)
1. 邓海均，熊波，罗新福，洪少尊，李强，王伟仲，刘俊. 跨声速风洞中使用短轴探管测量试验段核心流马赫数影响研究. 南京航空航天大学学报. 2022(02): 225-232 . 
百度学术
2. 邓海均，熊波，罗新福，洪少尊，李腾骥，张利波，韩新峰. 连续式跨声速风洞短轴探管设计与试验. 航空动力学报. 2022(06): 1171-1180 . 百度学术
3. 郭良斌，余振东，吴永良，李宁. 暂冲实验气源两级调压阀串联调压的参数设计及测试. 机床与液压. 2021(07): 1-7+21 . 百度学术
4. 陈吉明，吴盛豪，廖达雄，裴海涛，吕金磊，熊波. 0.6 m连续式跨声速风洞流场品质改进试验研究. 南京航空航天大学学报. 2021(02): 236-242 . 百度学术
5. 陈海峰，黄叙辉，凌忠伟，马列波，秦建华. 0.6米暂冲式跨超声速风洞控制系统研制. 自动化与仪器仪表. 2021(04): 35-39 . 百度学术
6. 邓海均，熊波，罗新福，洪少尊，刘奇，蒲泓宇，刘为杰. 跨声速风洞试验段马赫数静压探针移测方法初探. 西北工业大学学报. 2021(04): 786-793 . 百度学术
7. 陈旦，杨孝松，李刚，郭守春，陈天毅. 连续式风洞总压和调节阀相关性研究及其应用. 西北工业大学学报. 2020(02): 325-332 . 百度学术
8. 陈旦，张永双，李刚，郭守春，沈牟. 一种连续式跨声速风洞总压控制方法设计. 实验流体力学. 2019(06): 65-71 . 本站查看
其他类型引用(2)
计量
- 文章访问数: 2099
- HTML全文浏览量: 332
- PDF下载量: 208
- 被引次数: 10
