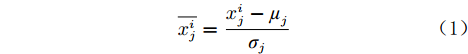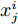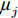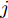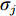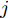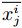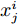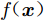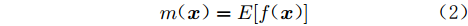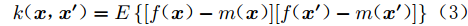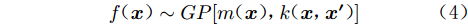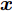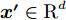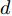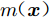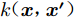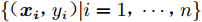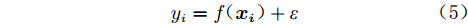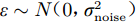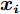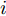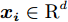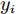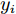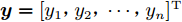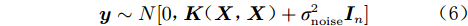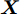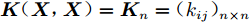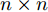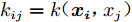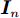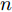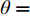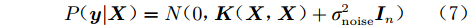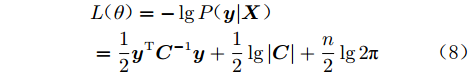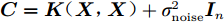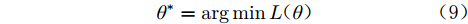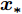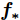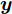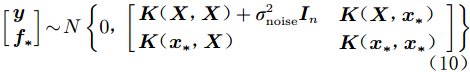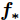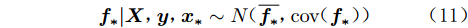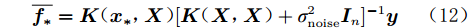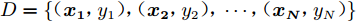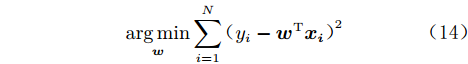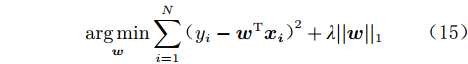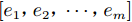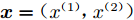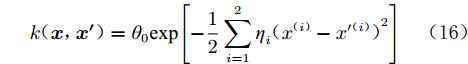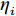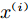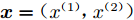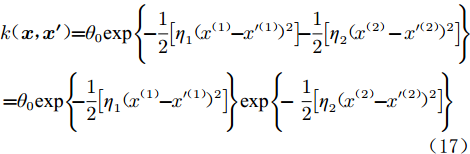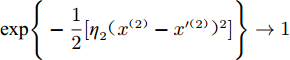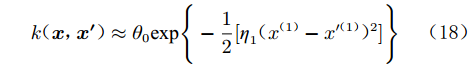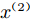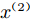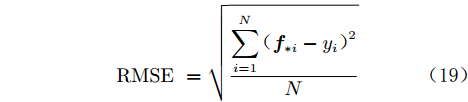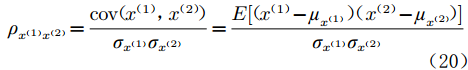Predictive analysis of flow control in high-speed complex flow field based on machine learning
-
摘要: 流动控制激励器是主动流动控制技术的核心,其设计水平和工作性能直接决定了主动流动控制的应用效果和应用方向。为了获得流动控制激励器的作用规律,需要大量实验研究激励参数对控制效果参数的影响,实验代价较大。利用逆向等离子体合成射流激波控制实验数据,采用机器学习中的高斯过程回归模型,获得激励器参数(头锥直径、腔体体积、放电电容、出口直径)到控制效果参数(最大脱体距离)的映射规律,对比多种核函数下高斯过程回归的预测效果,采用特征重要性分析方法分析激励器参数对控制效果参数的影响程度。结果表明:对于小样本问题,采用2次多项式核函数Poly2的高斯过程回归预测精度最高。在特征重要性分析上,头锥直径对最大脱体距离的影响程度最大;其次是放电电容和腔体体积,2个参数的影响相近;出口直径影响最小。本文工作可为高速复杂流场流动控制实验中激励器各项参数的设置提供一定参考。Abstract: The flow control actuator is the core of the active flow control technology. The design level and performance of actuator directly determine the application direction and effect of active flow control. In order to obtain the action law of the flow control actuator, a large number of experiments are needed to study the influence of excitation parameters on control effect parameters, and the experimental cost is large. In this paper, the experimental data of jet shock control in reverse plasma synthesis are used, and the Gaussian process regression model in machine learning is used to obtain the mapping law from the actuator parameters (head cone diameter, cavity volume, discharge capacitance and outlet diameter) to the control effect parameters (maximum out of body distance). We compare the prediction effects of Gaussian process regression under various kernel functions, and analyze the influence of actuator parameters on control effect parameters by using the characteristic importance analysis method. The results show that for this small sample problem, Gaussian process regression with the quadratic polynomial kernel function Poly2 obtains the highest accuracy; in characteristic importance analysis, the head cone diameter has the greatest influence on the maximum separation distance, followed by discharge capacitance and cavity volume. The influence of these two parameters is similar, and the influence of the outlet diameter is the least. The work of this paper can provide some guidance for the setting of various parameters of the actuator in the flow control experiment of the high-speed complex flow field.
-
Keywords:
- active flow control /
- exciter /
- machine learning /
- Gaussian process /
- feature importance analysis
-
0 引 言
流动控制技术是流体力学研究的前沿和热点之一,高效的流动控制系统能够显著提高飞行器动力性能、节约大量燃料、降低碳排放。流动控制技术主要分为被动控制和主动控制2种方式。被动控制[1]不需要额外的能量,具有控制简单、易于实现、设计制造成本低的特点。主动控制[2]则是引入辅助能量的控制方式。主动流动控制技术发展的核心问题是研制高性能的流动控制激励器[3],在不同的应用条件和控制目的下,对激励器的工作性能要求也有所不同,因此获得激励器工作性能参数变化规律,对激励器优化设计和实际应用意义重大。
在激励器工作性能参数研究实验中,传统的方法需要对每个工况参数设置不同数值,通过大量的对比实验来研究各个不同参数对实验结果的影响程度,需耗费大量的时间和资源。机器学习[4]的快速发展为流动控制技术提供了新的发展方向。Minelli等[5]通过遗传算法实现了高雷诺数钝体绕流开环控制的最优参数预测。Ren等[6]采用格子Boltzmann方法求解器第一次还原了层流条件下的控制效果,并对湍流条件下圆柱绕流减阻进行了探究。Rabault等[7]使用近端策略优化方法完成了圆柱减阻的闭环主动控制。侯宏等[8]在边界层转捩的主动控制中使用了神经网络模型构建了抽吸速度和边界层转捩位置之间的映射关系。这些基于机器学习的主动流动控制技术都取得了比较理想的效果,但其中分析激励器参数对控制效果参数影响的工作较少。因此,本文重点通过已有实验数据研究激励器参数和控制效果参数之间的关系,分析影响控制效果参数的重要因素,指导实验中激励器参数的设置。
本文从有限的实验数据(样本容量小于30)中挖掘数据之间的关系,属于小样本机器学习问题[9]。在机器学习中对小样本问题的处理一般有3个步骤:1)使用不易过拟合的模型(如非参数化模型);2)简化问题,采用特征重要性分析方法,若存在重要性较弱的特征,可将其删除;3)交叉验证(适用于小样本数据集的模型验证方法)。
高斯过程回归(Gaussian Process Regression,GPR)是一种非参数化机器学习模型,已广泛应用于小样本的非线性问题。罗亦泳等[10]构建了基于GPR的GPS高程转换模型,将GPR与其他拟合模型进行对比,通过将17个GPS点划分为不同比例的训练和测试数据集,分析了不同比例的训练数据集对不同GPS高程转换模型精度的影响。罗亦泳[11]将64期大坝变形观测数据划分为50期训练数据和14期测试数据,通过GPR构建了大坝变形预测模型,并建立了预测结果的方差及置信区间的估计方法,对预测结果进行了可靠性分析。孙斌等[12]为了提高风速预测的精度,采用了一种基于GPR的风速预测模型,并将GPR与支持向量机、最小二乘支持向量机和BP神经网络进行了比较。这些工作均证明了GPR模型能够成功地对小样本回归问题进行建模,具有较好的推广性。
特征重要性分析是分析监督学习中不同输入参数对输出参数影响程度的方法,可获得重要特征参数,降低数据中冗余信息的干扰,改善模型的性能。常用的方法包括卷积神经网络、LASSO回归、自动关联确定(Automatic Relevance Determination,ARD)和随机森林(Random Forest,RF)等。张韶辉等[13]利用LASSO回归分析筛选出了与冠心病密切相关的血脂指标。黄梅等[14]在分类挖掘中采用了基于随机森林的特征重要性分析方法。刘鑫童[15]基于深度卷积神经网络对甲状腺超声图像进行了系统分析并提取了重要特征。Sun等[16]使用spalart allmaras湍流模型生成的训练数据对ANN湍流模型进行训练,使用optimal brain surgeon算法确定输入特征的相关性。已有的这些工作表明:通过特征重要性分析,有效提高了研究者对有监督学习问题的理解;有针对性地利用好重要特征,可以提高模型预测精度。通过特征重要性分析,删除重要性较弱的特征适用于小样本问题中样本容量小于特征维度的情况,而本文数据的样本容量大于特征维度,满足高斯过程回归模型对样本数量的要求,因此本文保留所有特征,重点分析不同激励器参数对控制效果参数的影响程度。
为了验证小样本机器学习中模型的泛化性能,通常采用交叉验证方法将原始数据集划分为训练集和测试集,避免为追求高准确率而在训练集上产生过拟合,保证模型在样本外数据上的预测准确率。训练集和测试集数据的不同划分,会使模型准确率发生明显的变化,为了消除这一变化因素,通常采用K折交叉验证实现模型验证。胡伟杰等[17]通过GPR对180个样本采用5折交叉验证,预测了导弹气动性能,对比了不同数据划分比例下GPR模型的预测结果和稳定性。高赫等[18]基于GPR对2578个样本采用了5折交叉验证,控制了连续式风洞马赫数,采用了随机划分数据集与分组划分数据集2种策略进行建模。Nematzadeh等[19]采用不同的机器学习算法作为分类器,对原始乳腺癌和预后性威斯康辛乳腺癌进行分类,利用K折交叉验证对不同机器学习算法进行了乳腺癌分类比较分析。
在超声速条件下,本文利用逆向等离子体合成射流流动控制技术[20]进行半球体激波控制实验[21]。实验数据包括15个样本,每个样本的参数包括控制对象参数(头锥直径)、主动激励参数(腔体体积、电极间距、放电电容、出口直径、击穿电压)和控制效果参数(最大脱体距离)。每个样本的电极间距和击穿电压都是相同的,回归模型无法学习这2个参数与最大脱体距离的映射关系,故实验中不考虑该参数。采用GPR[22]学习得到激励器参数(头锥直径、腔体体积、放电电容、出口直径)到控制效果参数(最大脱体距离)的映射规律,利用K折交叉验证中的留一交叉验证法评估GPR模型的预测结果,采用特征重要性分析方法分析各激励器参数对最大脱体距离的影响程度,分析激励器参数影响程度与控制效果预测精度的关系。本文工作对激励器控制对象参数和主动激励参数实验设计具有一定参考价值。
1 研究方案
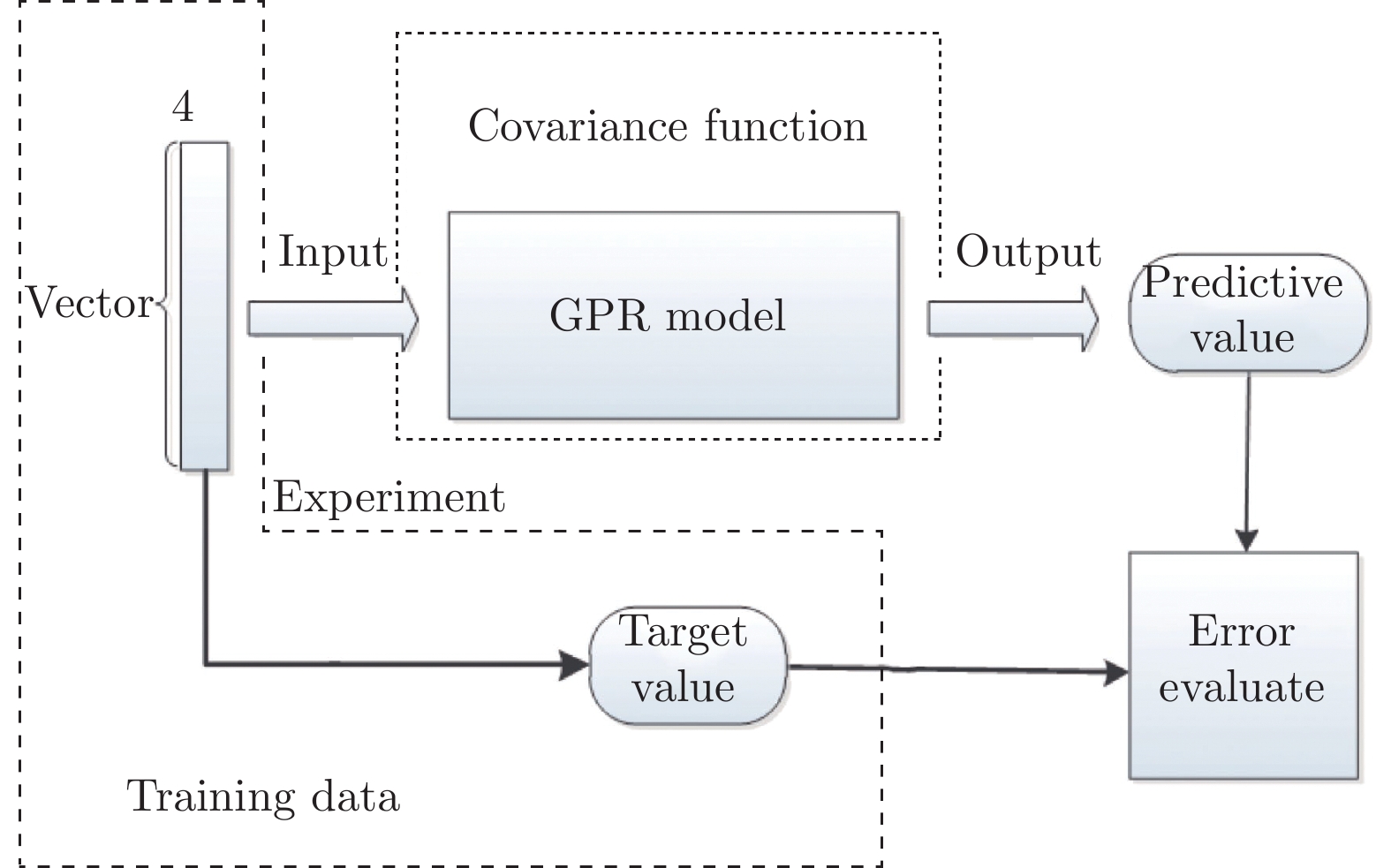
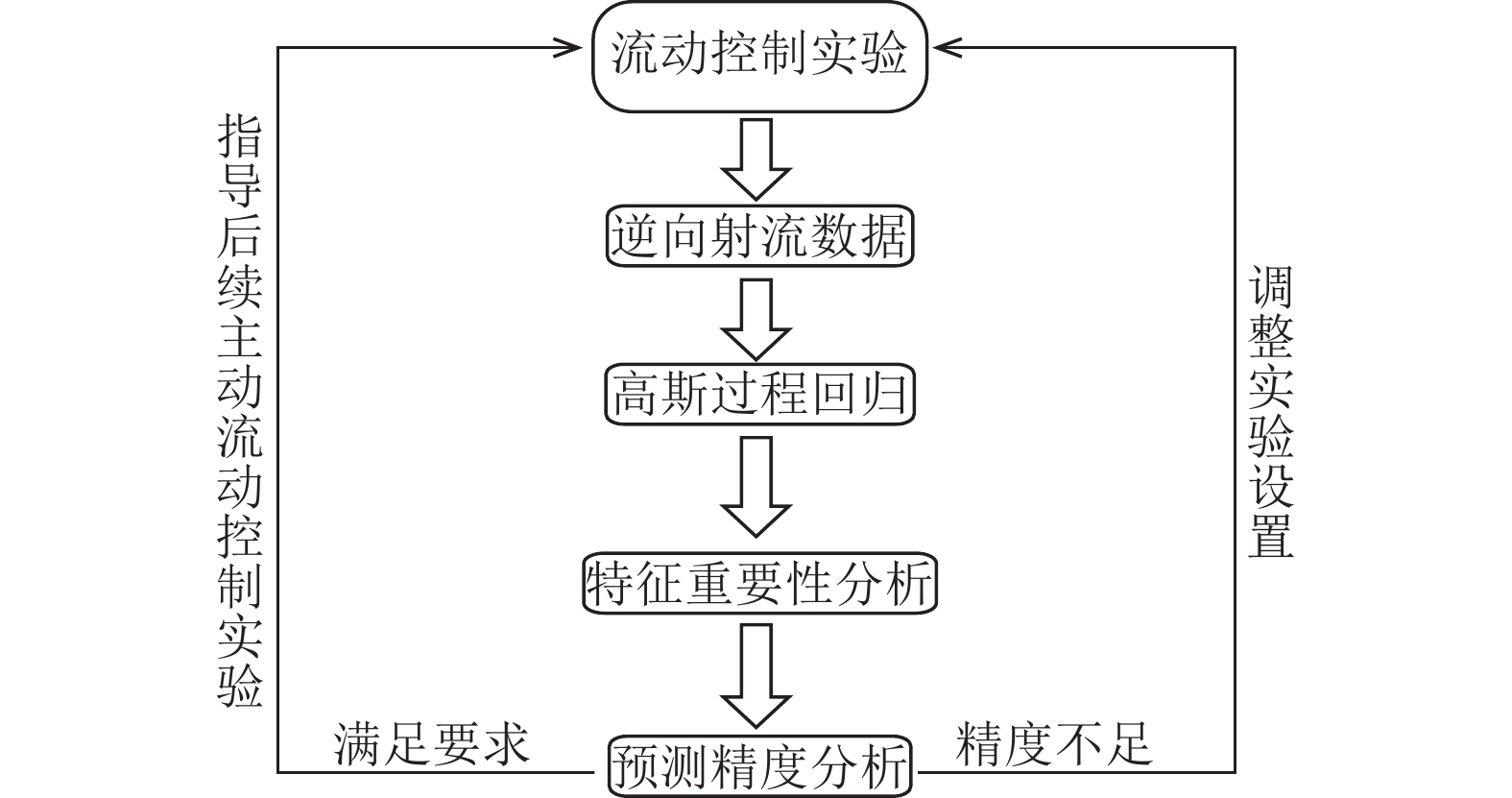
本文研究方案(图1)可分为4部分:第1部分是工程实验环节,使用逆向等离子体合成射流流动控制技术,设置不同的激励器参数进行实验,获得不同参数组合对应的控制效果,并对各个参数属性值进行标准化处理;第2部分使用高斯过程回归对数据进行建模,得到重要的激励器参数与控制效果参数之间的映射关系;第3部分采用特征重要性分析对各个激励器参数进行特征重要性排序;第4部分使用建立好的回归模型对控制效果参数进行预测,并评估模型的预测性能,分析激励器参数影响程度与控制效果预测精度的关系。若预测精度不足,则需要重新调整实验设置,根据激励器参数影响程度和控制效果预测精度的关系增加实验样本;若预测精度满足要求,则可用于指导后续主动流动控制实验。
1.1 实验数据
如表1所示,实验采集的数据包含控制对象参数(头锥直径)、主动激励参数(腔体体积、电极间距、放电电容、出口直径、击穿电压)和控制效果参数(最大脱体距离)。激励器头锥直径会影响等离子体合成射流的速度和流场结构。激励器腔体体积[23]是影响射流流场特性的重要结构参数,反映激励器工作气体质量,决定腔内气体温度及压力的变化,并最终影响流场发展及射流速度。电极间距[24]是造成不同等离子体分布的关键结构参数,不同电极间距下外电场分布形态和数值的差异是形成2种典型分布(类弥散和离散通道)模式的直接原因。放电电容[25]与等离子体合成射流速度呈正相关:大电容产生更多的能量沉积,实现腔体的充分加热,可产生速度更大的等离子体射流和强度更大的前驱激波;小电容所产生的等离子体射流流场内压缩波数增加,前驱激波强度减弱。出口直径[25]会影响等离子体合成射流的速度和耗散时间,且与前驱激波的强度呈正相关。激励器工作击穿电压[23]与激励器所处环境压强呈正相关,与放电频率呈负相关。
表 1 实验数据Table 1 Experimental data序号 头锥直径/mm 腔体体积/mm3 电极间距/mm 放电电容/nF 出口直径/mm 击穿电压/kV 最大脱体距离/mm 1 50 1500 3.5 80 5.0 5.2 14.7 2 50 1500 3.5 160 5.0 5.2 16.1 3 50 1500 3.5 640 5.0 5.2 14.5 4 50 1500 3.5 320 5.0 5.2 13.3 5 50 1500 3.5 320 9.0 5.2 14.3 6 50 1500 3.5 320 1.5 5.2 17.5 7 50 1500 3.5 640 3.0 5.2 21.8 8 50 1500 3.5 640 7.0 5.2 16.2 9 50 1500 3.5 640 9.0 5.2 16.9 10 30 1500 3.5 640 5.0 5.2 12.6 11 70 1500 3.5 640 5.0 5.2 23.5 12 50 3000 3.5 640 5.0 5.2 15.7 13 50 500 3.5 640 5.0 5.2 18.7 14 50 250 3.5 640 5.0 5.2 20.8 15 50 1500 3.5 640 5.0 5.2 14.1 在一个开有出口孔缝的小腔体内放电产生等离子体,通过加热腔内气体使等离子体增压膨胀并高速喷出,产生速度高达数百米每秒的高能射流,即等离子体合成射流。射流锋面前方有一道呈球对称的结构,为前驱激波的强压缩波。前驱激波与射流出口孔缝之间的距离即为脱体距离。当高能射流达到最大长度时,前驱激波与射流出口孔缝之间达到最大脱体距离。拍摄等离子体合成射流流场的发展过程,截取高能射流达到最大长度时的一帧图像作为最大脱体距离图像,如图2所示。通过在图像中测量前驱激波最远点与射流出口孔缝2个像素点之间的距离得到本研究所需的最大脱体距离。
将控制对象参数和主动激励参数作为高斯过程回归模型的输入、控制效果参数作为高斯过程回归模型的输出,其参数设置同表1。图2即显示了一组控制效果参数的实验结果。
在将数据输入机器学习的模型之前,为避免参数数值范围不同对建模效果产生影响,需要将数据进行标准化处理。标准化公式为:
$$ \overline {x_j^i} = \frac{{x_j^i - {\mu _j}}}{{{\sigma _j}}} $$ (1) 式中,
$ x_j^i $ 是第$ i $ 个样本的第$ j $ 个特征,$ {\mu _j} $ 是第$ j $ 个特征的均值,$ {\sigma _j} $ 是第$ j $ 个特征的标准差,$ \overline {x_j^i} $ 是$x_j^i$ 标准化后的结果。1.2 基于GPR的控制效果参数预测模型
本文针对激励器控制效果预测的小样本回归问题,提出了基于高斯过程回归的预测模型,模型框架如图3所示。以逆向等离子体合成射流实验为例,输入为4维参数向量(头锥直径、放电电容、腔体体积和出口直径)。首先将4维参数向量作为输入数据输入到GPR模型中训练模型,然后将GPR模型输出的预测值与实验获得的最大脱体距离真实值进行对比,使用误差评估方法计算最大脱体距离的真实值与预测值之间的误差,得到GPR模型的预测精度。本文的样本数为15,特征维度为4,满足使用高斯过程回归模型的最低样本容量要求[26]。
1.2.1 GPR的模型假设
高斯过程可视为定义在函数
$f( {\boldsymbol{x}} )$ 上的一个分布,其性质由均值函数和协方差函数决定:$$ m({\boldsymbol{x}}) = E[f({\boldsymbol{x}})] $$ (2) $$ k({\boldsymbol{x}},{{\boldsymbol{x'}}}) = E\left\{[f({\boldsymbol{x}}) - m({\boldsymbol{x}})][f({{\boldsymbol{x'}}}) - m({{\boldsymbol{x'}}})]\right\} $$ (3) $$ f({\boldsymbol{x}})\sim GP[m({\boldsymbol{x}}),k({\boldsymbol{x}},{{\boldsymbol{x'}}})] $$ (4) 式中:
${\boldsymbol{ x }}$ 、${{\boldsymbol{x'}}} \in {{\boldsymbol{{\rm{{R}}}}}^d}$ ,为$ d $ 维输入向量;$m({\boldsymbol{x}})$ 为均值函数;$k({\boldsymbol{x}},{{\boldsymbol{x'}}})$ 为协方差函数。假设训练集为
$\left\{ {({{\boldsymbol{x_i}}},{y_i})|i = 1,\cdots,n} \right\}$ ,n为训练集样本数。对于回归问题,模型如下:$$ {y_i} = f({{\boldsymbol{x_i}}}) + \varepsilon $$ (5) 式中:
$\varepsilon \sim N(0,\sigma _{{\rm{noise}}}^2)$ 为高斯噪声;${{\boldsymbol{x_i}}}$ 为第$ i $ 个输入向量,${{\boldsymbol{x_i}}} \in {{\rm{R}}^d}$ ;$ {y_i} $ 为对应的观测值,${y_i} \in {{\boldsymbol{{\rm{R}}}} }$ 。为计算方便,将$ {y}_{i} $ 中心化,均值设置0,这时所有观测值构成的列向量${\boldsymbol{y }}= {[{y_{1}},{y_2},\cdots,{y_n}]^{\rm{T}}}$ 的先验概率分布为:$$ {\boldsymbol{y}}\sim N[0,{\boldsymbol{K}}({\boldsymbol{X}},{\boldsymbol{X}}) + \sigma _{{\rm{noise}}}^2{{\boldsymbol{I}}_n}] $$ (6) 式中:
${\boldsymbol{ X }}$ 为特征矩阵,矩阵中每一行代表一个输入向量;${\boldsymbol{K}}({\boldsymbol{X}},{\boldsymbol{X}}) = {{\boldsymbol{K}}_n} = ({k_{ij}})_{ n \times n }$ 为$ n \times n $ 阶对称正定协方差矩阵,矩阵元素${k_{ij}} = k({{\boldsymbol{x_i}}},{x_j})$ ;${{\boldsymbol{I}}_n}$ 为$ n $ 阶单位矩阵。1.2.2 GPR的训练
假设一个协方差函数的超参数集合为
$ \theta = \{ {\theta _i}\} _{i = 1}^m $ ,$ m $ 为超参数的数量,通常采用极大似然法确定$ \theta $ 的最优值。观测值${\boldsymbol{ y }}$ 的边缘概率分布为:$${ P}({\boldsymbol{y}}|{\boldsymbol{X}}) = N(0,{\boldsymbol{K}}({\boldsymbol{X}},{\boldsymbol{X}}) + \sigma _{{\rm{noise}}}^2{{\boldsymbol{I}}_n}) $$ (7) 通过式(7)可以得到训练集的负对数边际似然函数为:
$$ \begin{split}& L( \theta ) = - \lg P( {{\boldsymbol{y}}|{\boldsymbol{X}}} ) \\& = \frac{1}{2}{{\boldsymbol{y}}^{\rm{T}}}{{\boldsymbol{C}}^{ - 1}}{\boldsymbol{y}} + \frac{1}{2}\lg |{\boldsymbol{C}}| + \frac{n}{2}\lg 2\pi \end{split} $$ (8) 式中,
${\boldsymbol{C}} = {\boldsymbol{K}}({\boldsymbol{X}},{\boldsymbol{X}}) + \sigma _{{\rm{noise}}}^2{{\boldsymbol{I}}_n}$ ,$|{\boldsymbol{C}}|$ 为矩阵${\boldsymbol{C }}$ 的行列式。GPR模型的优化目标为:$$ {\theta ^*} = \arg \min L(\theta ) $$ (9) 计算
$ L(\theta ) $ 关于各超参数$ {\theta _i} $ 的偏导数,然后采用共轭梯度下降法等优化算法迭代更新超参数来最小化$ L(\theta ) $ 。1.2.3 协方差函数的选择
本文使用的协方差函数有Polynomial(Poly)核、Squared exponential isotropic(SEiso)核、Squared exponential automatic relevance determination(SEard)核、Stationary+Matern(SM)核和Additive(Add)核[27]。
Poly是一种非标准核函数,比较适用于正交归一化后的数据。根据平方指数协方差函数的超参数取值,可以分为2种核函数:当向量对应的各个维度带宽取值相同时,得到的核函数就是各向同性的平方指数核,即SEiso核;当向量对应的各个维度带宽取值不同时,得到的核函数就是各向异性的平方指数核,即SEard核。SM协方差函数是将多种单一的核函数相加构成的复杂协方差函数。Add作为加性协方差函数,在输入向量的各个维度定义基本的协方差函数。
1.2.4 GPR的预测
对于测试集中的一个样本
${{\boldsymbol{x_*}}}$ ,其对应的预测值${{\boldsymbol{f_*}}}$ 与观测值${\boldsymbol{y}}$ 的联合先验分布为:$$ \left[ \begin{gathered} {\boldsymbol{ y}} \\ {{\boldsymbol{f_*}}} \\ \end{gathered} \right] \sim N\left\{ {0,\left[ \begin{gathered} {\boldsymbol{K}}({\boldsymbol{X}},{\boldsymbol{X}}) + \sigma _{{\rm{noise}}}^2{{\boldsymbol{I}}_n}\begin{array}{*{20}{c}} {}& {{\boldsymbol{K}}({\boldsymbol{X}},{{\boldsymbol{x_ *}} })} \end{array} \\ {\boldsymbol{ K}}({{\boldsymbol{x_ * }}},{\boldsymbol{X}})\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{} \end{array}}&{} \end{array}\begin{array}{*{20}{c}} {}& {\;{\boldsymbol{K}}({{\boldsymbol{x_ * }}},{{\boldsymbol{x_ *}} })} \end{array} \\ \end{gathered} \right]} \right\} $$ (10) 通过式(10)和一些矩阵运算,可以得到预测值
${{\boldsymbol{f_*}}}$ 的条件概率分布为:$$ {{\boldsymbol{f_*}}}|{\boldsymbol{X}},{\boldsymbol{y}},{{\boldsymbol{x_*}}}\sim N(\overline {{{\boldsymbol{f_*}}}},{{\rm{cov}}} ({{\boldsymbol{f_*}}})) $$ (11) 式中:
$$ \overline {{{\boldsymbol{f_*}}}} = {\boldsymbol{K}}({{\boldsymbol{x_*}}},{\boldsymbol{X}}){[{\boldsymbol{K}}({\boldsymbol{X}},{\boldsymbol{X}}) + \sigma _{{\rm{noise}}}^2{{\boldsymbol{I}}_n}]^{ - 1}}{\boldsymbol{y}} $$ (12) $$ \begin{split} {\mathop{\rm {cov}}} ( {{{\boldsymbol{f_*}}}} ) =&{\boldsymbol{ K}}( {{{\boldsymbol{x_*}}},{{\boldsymbol{x_*}}}} ) - {\boldsymbol{K}}( {{{\boldsymbol{x_*}}},{\boldsymbol{X}}} ) \times \\& {\left[ {{\boldsymbol{K}}( {{\boldsymbol{X}},{\boldsymbol{X}}} ) + {{\boldsymbol{I}}_n}} \right]^{ - 1}}{\boldsymbol{K}}( {{\boldsymbol{X}},{{\boldsymbol{x_*}}}} ) \end{split} $$ (13) 式(12)为预测值,式(13)为预测的方差,可以评估预测的不确定度。
1.3 特征重要性分析
本文使用的特征重要性分析[28]方法有LASSO回归、随机森林和自动关联确定。不同的特征重要性分析方法的准则不同,通过综合比较多种特征重要性分析方法的结果,增加分析结果的置信程度。
1.3.1 LASSO回归
数据集
$D = \{ ({{\boldsymbol{x_1}}},{y_1}),({{\boldsymbol{x_2}}},{y_2}),\cdots,({{\boldsymbol{x_N}}},{y_N})\}$ ,其中N为数据集样本数。考虑最简单的线性回归模型,以平方误差作为损失函数,则优化目标为:$$ \mathop {\arg \min }\limits_{\boldsymbol{w}} \sum\limits_{i = 1}^N {{{({y_i} - {{\boldsymbol{w}}^{\rm{T}}}{{\boldsymbol{x_i}}})}^2} } $$ (14) 式中,w为权重向量。当样本特征很多而样本数相对较少时,式(14)很容易陷入过拟合。为了缓解过拟合问题,对式(14)引入L1正则:
$$ \mathop {\arg \min }\limits_{\boldsymbol{w}} \sum\limits_{i = 1}^N {{{({y_i} - {{\boldsymbol{w}}^{\rm{T}}}{{\boldsymbol{x_i}}})}^2} + \lambda ||{\boldsymbol{w}}|{|_1}} $$ (15) 式中,
$ \lambda > 0 $ ,为正则化参数。式(15)为LASSO的优化目标[29]。LASSO采用L1正则,可以产生稀疏解(w许多分量为0)。根据这一特性进行特征选择,权重绝对值大的分量对结果的影响大。1.3.2 随机森林
随机森林[30]是以决策树[31]为基学习器构建的模型。RF可以用于特征重要性分析,计算特征重要性的方法主要有2种:
1)采用平均不纯度减少准则
通过不纯度能够确定节点,即最优条件。一个森林能够计算每个特征平均减少的不纯度,并把平均减少的不纯度作为特征重要性分析的值。
2)采用平均准确性减少准则
RF在构建每一棵基决策树时,使用bootstrap的方式对样本进行有放回采样,因此每次都会有一些样本不参与决策树的构建,这些样本即为袋外数据(out of bag data),可以利用这些数据进行特征重要性评估。对于RF中的每一棵基决策树,先利用袋外数据进行测试得到测试误差,然后将这些测试数据
$[{e_1},{e_2},\cdots,{e_m}]$ 的某个特征顺序打乱(改变测试样本特征值)再得到m个测试误差,将其作为该特征的重要性。若一个特征发生改变对预测结果影响很大,则说明该特征比较重要。1.3.3 自动关联确定
假设输入空间是二维,
${\boldsymbol{x}} = ({ x^{(1)}},{ x^{(2)}})$ ,ARD核的形式为:$$ k({\boldsymbol{x}},{{\boldsymbol{x'}}}) = {\theta _0}\exp \Bigg[ { - \frac{1}{2}\sum\limits_{i = 1}^2 {{\eta _i}{{({{{x^{(i)}} }}- {x'{^{(i)}}})}^2}} } \Bigg] $$ (16) 可以看出,随着特定
$ {\eta _i} $ (对输入空间距离的伸缩变换参数)的减小,函数受输入变量${{x^{(i)}}}$ 的影响变小。将${\boldsymbol{x}} = ({x^{(1)}},{x^{(2)}})$ 代入式(16)得到 :$$\begin{split}& k({\boldsymbol{x}}, {{\boldsymbol{x'}}}) = {\theta _0}\exp \Bigg\{ - \frac{1}{2} \left[{\eta _1}{( {x^{(1)}} - x'^{(1)} )^2}\right] - \frac{1}{2} \left[{\eta _2}{( {x^{(2)}} - x'^{(2)} )^2}\right] \Bigg\} \\& = {\theta _0}\exp \Bigg\{ - \frac{1}{2} \left[{\eta _1}{( {x^{(1)}} - x'^{(1)} )^2}\right] \Bigg\}\exp \Bigg\{ - \frac{1}{2} \left[{\eta _2}{( {x^{(2)}} - x'^{(2)} )^2}\right] \Bigg\} \\\end{split} $$ (17) 假设
$ {\eta _2} $ 很小,则$\exp \Bigg\{ - \dfrac{1}{2}[{\eta _2}{({x^{(2)}} - x'^{(2)})^2}]\Bigg\} \to 1$ ,即:$$ k({\boldsymbol{x}},{{\boldsymbol{x'}}}) \approx {\theta _0}\exp \Bigg\{ - \frac{1}{2}[{\eta _1}{({x^{(1)}} - x'^{(1)})^2}]\Bigg\} $$ (18) 此时核函数的取值几乎不受输入变量
${x^{(2)}}$ 的影响,说明${x^{(2)}}$ 对最终输出的影响不大。利用ARD协方差函数的这个性质,可以判断出不同特征对结果的影响大小,并且整个过程无需人为干预,模型可自适应地从数据中学得这种关系。2 实验结果及分析
2.1 预测性能评估
采用均方根误差(RMSE)作为训练和测试误差:
$${\rm{ RMSE }}= \sqrt {\frac{{\displaystyle\sum\limits_{i = 1}^N {{{({\boldsymbol{f}}_{*i} - {{{y}}_i})}^2}} }}{N}} $$ (19) 模型验证采用K折交叉验证,其本质是创建一系列训练集和测试集,先计算模型在每个测试集上的准确率,再计算平均值。具体步骤如下:1)将原始数据集划分为相等的K部分;2)将第1部分作为测试集,其余作为训练集;3)训练模型,计算模型在测试集上的准确率;4)每次用不同的部分作为测试集,重复步骤2)和3) K次;5)将平均准确率作为最终的模型准确率。留一交叉验证法是K折交叉验证的一个特例,将数据子集划分的数量与样本数相同(K=N),每次只留一个样本用于测试,这种方法适用于小样本的情况。由于本文属于小样本问题,且样本的参数取值跨度很大,参数的分布密度较低,因此采用原始数据的4个激励器参数特征、15个样本进行留一交叉验证实验,即每次选取14个样本作为训练数据,留一个样本来评估模型预测的结果,重复实验15次,取15次实验结果的平均RMSE评价模型性能。
不同核函数的训练均方根误差盒状图如图4所示,测试误差均值如表2所示。由图4可知,SM和Add核训练误差明显比其他核函数低,表明其对训练数据的拟合程度更好。但由表2可知,这2种核函数的测试误差明显高于其他核函数,而二次多项式核函数Poly2虽然在训练数据集上误差高于SM和Add核,但在测试数据集上获得了最高的预测精度。这是由于SM和Add核所含超参数较多,在样本数较少的情况下容易产生过拟合。多项式核、SEiso核和SEard核都只含有2个超参数,在小样本训练的情况下具有较好的泛化性能。
表 2 测试数据集上GPR不同核函数对应的预测RMSE均值Table 2 Mean RMSE for models with different kernel functions of GPR on test data set核函数 RMSE Poly2 2.4178$ \pm $2.5498 Poly3 2.4198$ \pm $2.5531 Poly4 2.4208$ \pm $2.5498 SEiso 2.4985$ \pm $2.5869 SEard 2.6906$ \pm $2.5919 SM 13.7693$ \pm $2.5546 Add 4.3876$ \pm $2.0921 2.2 相关性分析
2.2.1 皮尔逊相关系数
皮尔逊相关系数[32]可以衡量2个变量(x(1),x(2))的线性相关程度,其值介于−1和1之间,计算公式如下:
$$\; {\rho _{x^{(1)} x^{(2)}}} = \frac{{{{\rm{cov}}} ( x^{(1)}, x^{(2)} )}}{{{\sigma _{x^{(1)}}}{\sigma _{x^{(2)}}}}} = \frac{{E[( x^{(1)} - {\mu _{x^{(1)}}})(x^{(2)} - {\mu _{x^{(2)}}} )]}}{{{\sigma _{x^{(1)}}}{\sigma _{x^{(2)}}}}} $$ (20) 式中,μ为样本均值,σ为标准差。通过计算逆向射流数据不同特征和最大脱体距离之间的皮尔逊相关系数,得到如图5所示的相关性热图。可以看出,头锥直径、放电电容与最大脱体距离相关性较强,且呈正相关;腔体体积、出口直径与最大脱体距离呈负相关,且出口直径与最大脱体距离之间的线性相关性最弱。
2.2.2 特征重要性分析
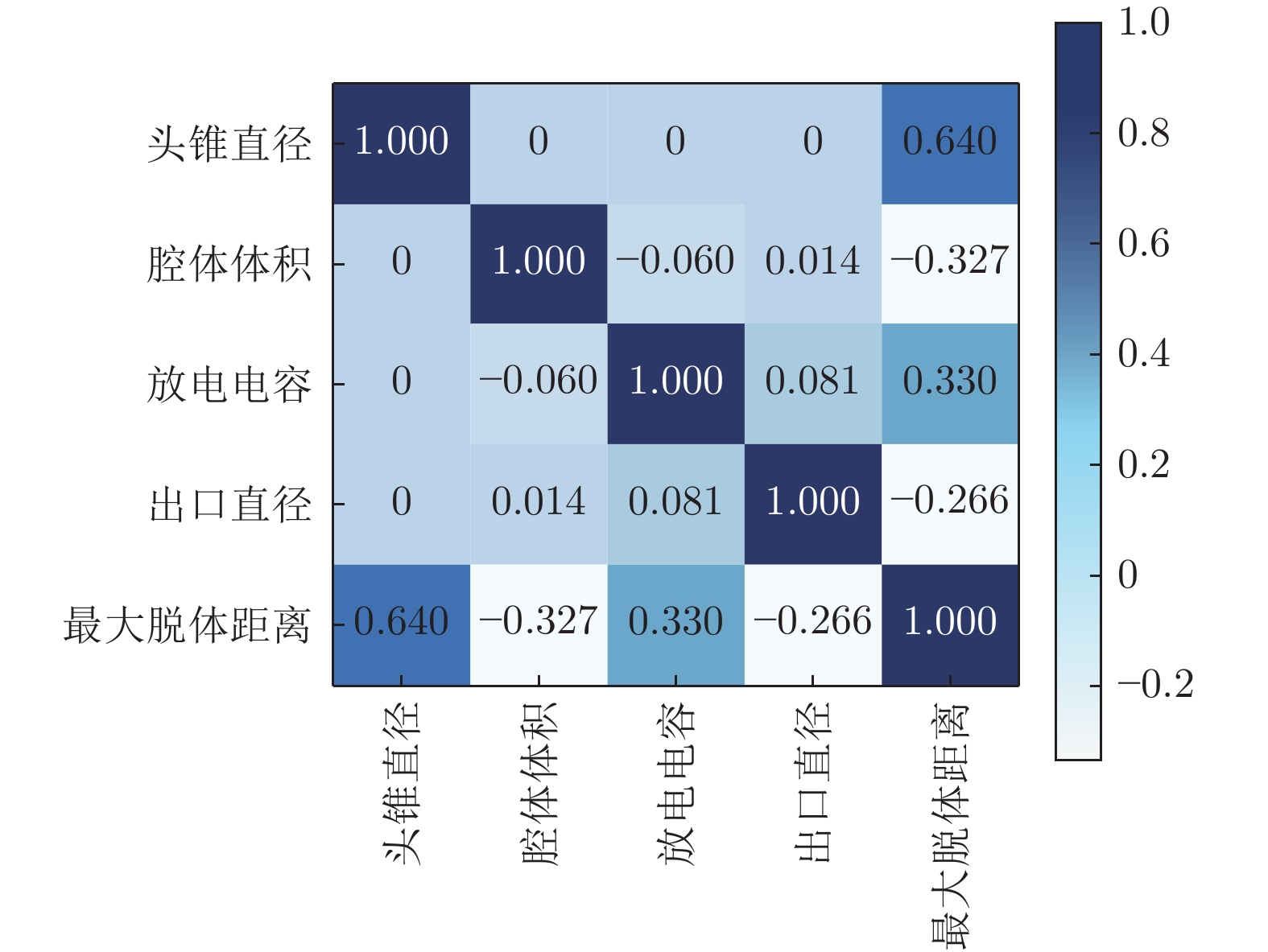
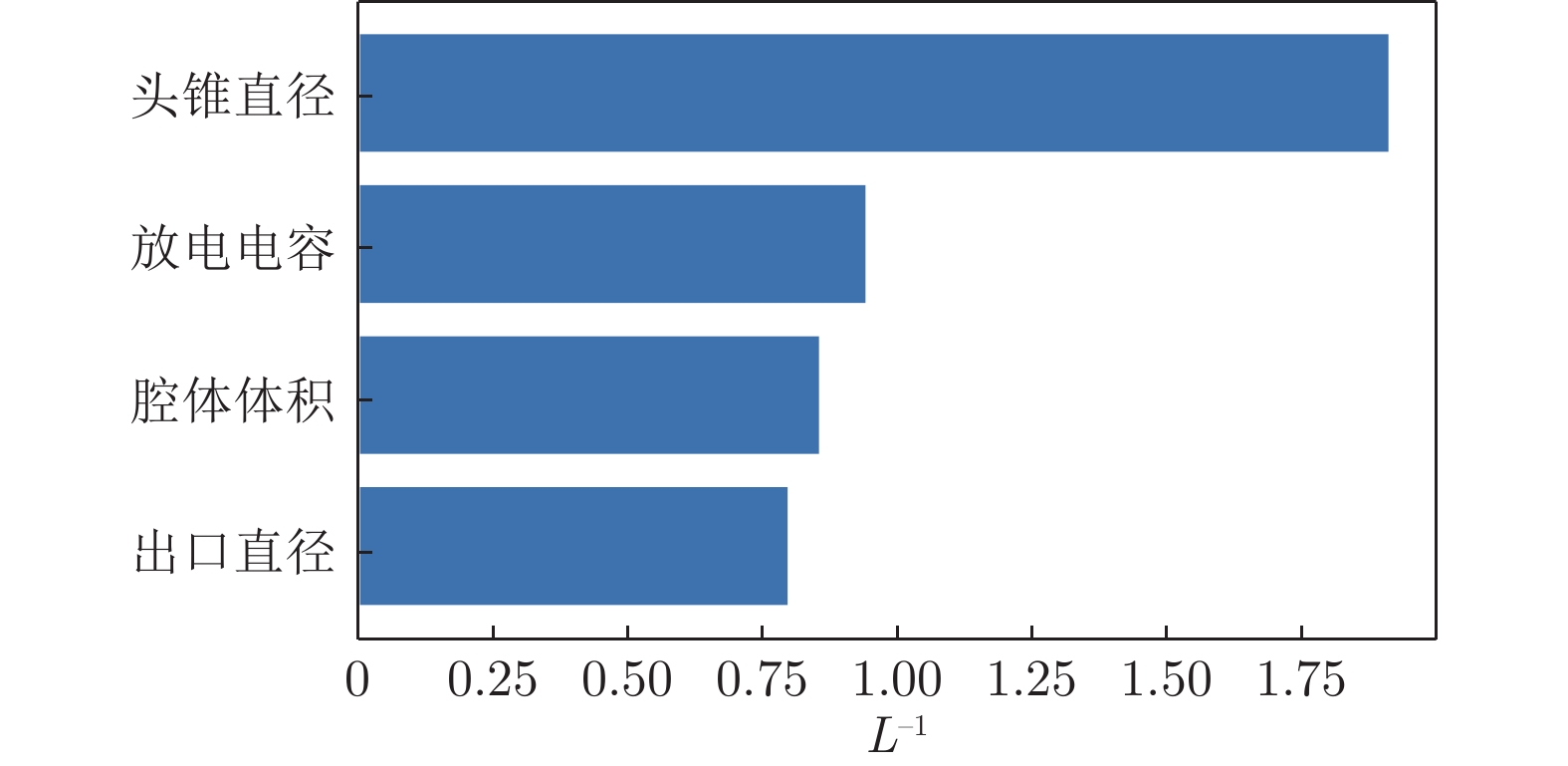
通过皮尔逊相关系数可以初步得出各个特征与最大脱体距离之间的线性相关性,但复杂流场的头锥直径、腔体体积、放电电容、出口直径与最大脱体距离之间并不是简单的线性关系。为了进一步挖掘它们之间的关系,利用ARD、LASSO、RF这3种特征重要性分析方法得到各个特征的重要性,如图6~8所示。
ARD核函数自适应可以确定重要特征的特点,通过高斯过程回归得到各个维度的带宽L(归一化后),L越大,则特征对结果的影响越小。定义特征重要性为L–1。由图6可知,头锥直径对结果的影响最大,出口直径对结果的影响最小。这也从某种角度为后期实验指明了方向:对结果影响较小的特征,实验过程中的采样数量可以尽量少;相反,对结果影响较大的特征,实验过程中的采样数量可以尽量多。这样可以最大限度地减少实验次数,增加数据的多样性,从有限的数据中挖掘尽可能多的有用信息。
由皮尔逊相关系数可知,头锥直径、腔体体积、放电电容和出口直径之间无明显的线性相关性,所以此时可以利用LASSO来分析特征重要性。将LASSO的正则化参数设为0.1,得到各个特征权重的绝对值。从图7可以看出,利用LASSO得到的特征重要性分析结果与ARD方法的结果完全一致。
RF有2种计算特征重要性的方式,在本实验中采用平均准确性减少准则,因为平均不纯度减少准则对取值个数较多的特征存在一定的偏好,会使特征重要性估计不准确。由于本文只有4个特征,所以在训练RF时并没有引入属性扰动,为了增加结果的稳定性,将基决策树的个数设为100。由图8可知,与前述2种方法一样,RF的结果也是头锥直径对最大脱体距离影响最大,而出口直径对最大脱体距离影响最小。
上述特征重要性分析方法针对实验样本的参数进行,而样本的数量有限,因此实验结果只适用于样本的参数取值范围(头锥直径30~70 mm,腔体体积250~3000 mm3,放电电容80~640 nF,出口直径1.5~9.0 mm)。 由特征重要性分析结果可知:相对而言,头锥直径对最大脱体距离影响最大;其次是腔体体积和放电电容,这2个参数对最大脱体距离的影响相差不大;出口直径影响最小。
2.3 特征与预测结果的关系分析
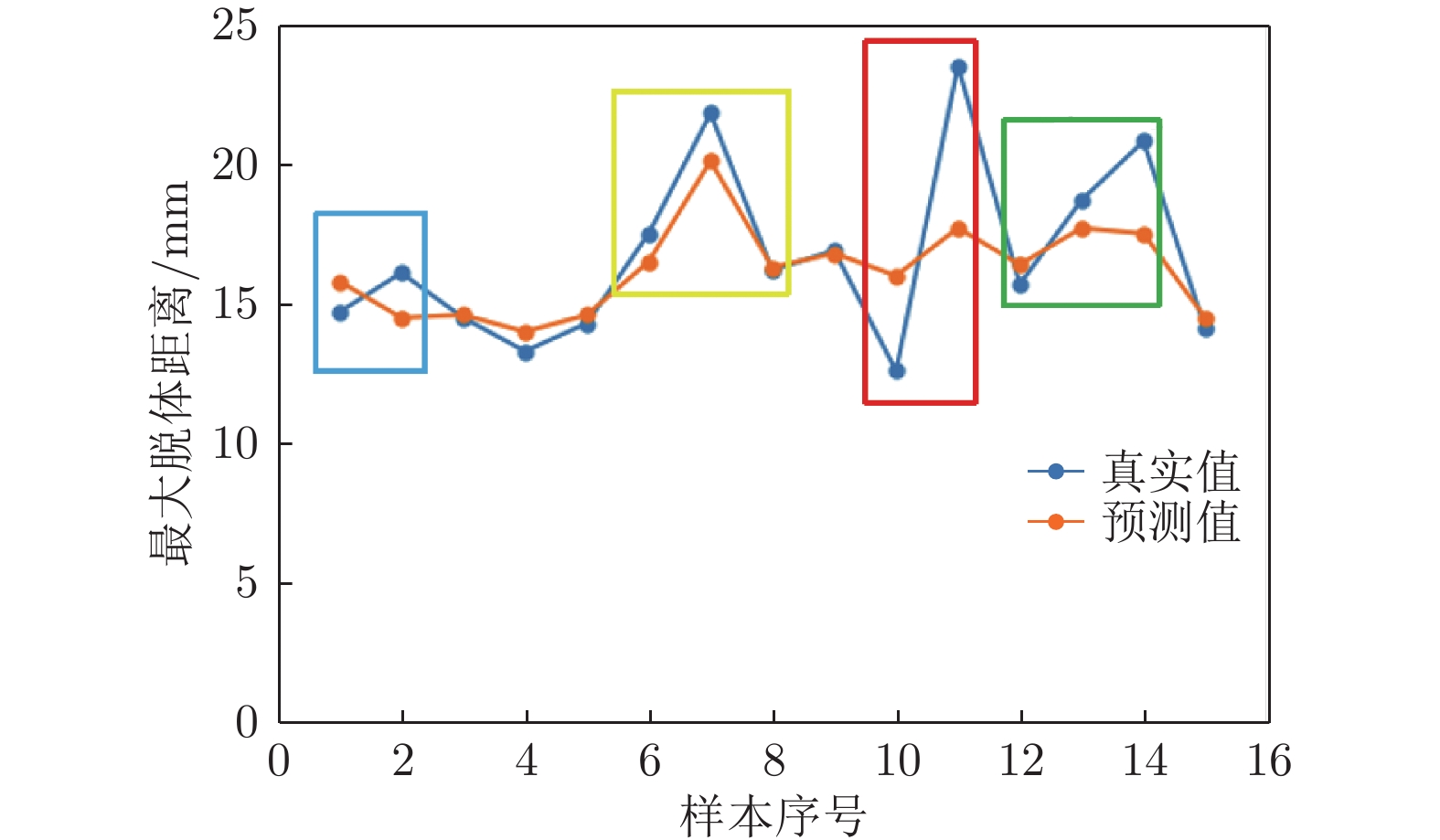
图9和表3显示了最大脱体距离的预测结果,其中红框、绿框和蓝框标注出了预测不够准确的样本。对应表3中的实验数据可以发现,红色方框中样本的头锥直径分别为30和70 mm,蓝色方框中样本的放电电容分别为80和160 nF,绿色方框中样本的腔体体积分别为3000、500和250 mm3。头锥直径作为最大脱体距离最重要的影响特征,放电电容和腔体体积作为次重要的特征,实验数据在这3个特征上分布密度较低,导致模型的预测不够准确。对比发现黄框中样本的预测相对准确(真实值与预测值误差的均值最小),对应于采样密度较低的出口直径。由于出口直径是重要性最小的特征,因此对最大脱体距离预测精度的影响较小。除颜色框中的样本外,其余样本在各个特征维度上的分布密度较大,因此预测结果均较为准确。根据以上分析,为提高模型预测精度,设计实验时应加大对控制效果参数影响较大的激励器参数的设置密度,减少对控制效果参数影响较小的激励器参数的设置密度,以减少实验次数,最大程度利用实验资源。
表 3 实验数据及预测结果Table 3 Experimental data and prediction results
3 结 论
1)使用逆向等离子体合成射流激波控制实验数据对激励器参数和控制效果参数之间的映射关系进行建模,建立了高斯过程回归模型。对比多种核函数下高斯过程回归的预测效果,采用二次多项式核函数Poly2的高斯过程回归预测效果最好,因此对于样本量少的数据集,使用“简单”的核函数能够得到更为准确的预测结果。
2)采用3种特征重要性分析方法(ARD、LASSO、RF)分析各个激励器参数特征对最大脱体距离的影响程度,结果发现头锥直径对最大脱体距离的影响程度最大,放电电容和腔体体积的影响次之且相近,出口直径的影响最小。
3)对结果影响比较大的特征(如头锥直径、放电电容和腔体体积)应增加其采样数量;反之,对结果影响较小的特征(如出口直径)可以减少其采样数量,以减少实验次数。
4)本文提出的应用于逆向等离子体合成射流激波控制实验的控制效果分析方法,也适用于工程设计中其他类似控制问题研究。通过对少量实验数据内隐含的激励器参数和控制效果参数之间的映射关系建模,并对激励器参数进行重要性分析,可以得到合理的实验参数设置方式,提高实验效率和控制效果预测精度。
-
表 1 实验数据
Table 1 Experimental data
序号 头锥直径/mm 腔体体积/mm3 电极间距/mm 放电电容/nF 出口直径/mm 击穿电压/kV 最大脱体距离/mm 1 50 1500 3.5 80 5.0 5.2 14.7 2 50 1500 3.5 160 5.0 5.2 16.1 3 50 1500 3.5 640 5.0 5.2 14.5 4 50 1500 3.5 320 5.0 5.2 13.3 5 50 1500 3.5 320 9.0 5.2 14.3 6 50 1500 3.5 320 1.5 5.2 17.5 7 50 1500 3.5 640 3.0 5.2 21.8 8 50 1500 3.5 640 7.0 5.2 16.2 9 50 1500 3.5 640 9.0 5.2 16.9 10 30 1500 3.5 640 5.0 5.2 12.6 11 70 1500 3.5 640 5.0 5.2 23.5 12 50 3000 3.5 640 5.0 5.2 15.7 13 50 500 3.5 640 5.0 5.2 18.7 14 50 250 3.5 640 5.0 5.2 20.8 15 50 1500 3.5 640 5.0 5.2 14.1 表 2 测试数据集上GPR不同核函数对应的预测RMSE均值
Table 2 Mean RMSE for models with different kernel functions of GPR on test data set
核函数 RMSE Poly2 2.4178$ \pm $2.5498 Poly3 2.4198$ \pm $2.5531 Poly4 2.4208$ \pm $2.5498 SEiso 2.4985$ \pm $2.5869 SEard 2.6906$ \pm $2.5919 SM 13.7693$ \pm $2.5546 Add 4.3876$ \pm $2.0921 表 3 实验数据及预测结果
Table 3 Experimental data and prediction results

-
[1] BEN-GIDA H,STEFANINI J,STALNOV O,et al. Application of passive flow control techniques to attenuate the unsteady near wake of airborne turrets in subsonic flow[J]. Aerospace Science and Technology,2021,119:107129. doi: 10.1016/J.AST.2021.107129
[2] 战培国,程娅红,赵昕. 主动流动控制技术研究[J]. 航空科学技术,2010,21(5):2-6. DOI: 10.3969/j.issn.1007-5453.2010.05.001 ZHAN P G,CHENG Y H,ZHAO X. A review of active flow control technology[J]. Aeronautical Science and Technology,2010,21(5):2-6. doi: 10.3969/j.issn.1007-5453.2010.05.001
[3] 王林,罗振兵,夏智勋,等. 高速流场主动流动控制激励器研究进展[J]. 中国科学(技术科学),2012,42(10):1103-1119. DOI: 10.1360/ze2012-42-10-1103 WANG L,LUO Z B,XIA Z X,et al. Review of actuators for high speed active flow control[J]. SCIENTIA SINICA Technologica,2012,42(10):1103-1119. doi: 10.1360/ze2012-42-10-1103
[4] BISHOP C . Pattern recognition and machine learning[M]. Germany: Springer, 2006.
[5] MINELLI G,DONG T,NOACK B R,et al. Upstream actuation for bluff-body wake control driven by a genetically inspired optimization[J]. Journal of Fluid Mechanics,2020,893:A1. doi: 10.1017/JFM.2020.220
[6] REN F,RABAULT J,TANG H. Applying deep reinforce-ment learning to active flow control in weakly turbulent conditions[J]. Physics of Fluids,2021,33(3):037121. doi: 10.1063/5.0037371
[7] RABAULT J,KUCHTA M,JENSEN A,et al. Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control[J]. Journal of Fluid Mechanics,2019,865:281-302. doi: 10.1017/JFM.2019.62
[8] 侯宏,杨建华. RBF网络用于边界层转捩中抽吸流优化控制[J]. 航空学报,2002,23(6):556-559. DOI: 10.3321/j.issn:1000-6893.2002.06.003 HOU H,YANG J H. Plant identification in active control of laminar boundary-layer transition by suction using RBF neural network[J]. Acta Aeronautica ET Astronautica Sinica,2002,23(6):556-559. doi: 10.3321/j.issn:1000-6893.2002.06.003
[9] 卢俊峰, 龚小庆. 统计学[M]. 杭州: 浙江工商大学出版社, 2020. [10] 罗亦泳,姚宜斌,张立亭,等. 基于高斯过程的GPS高程转换模型[J]. 测绘通报,2015(11):11-14,59. LUO Y Y,YAO Y B,ZHANG L T,ET AL. GPS height transformation model based on Gaussian process[J]. Bulletin of Surveying and Mapping,2015(11):11-14,59.
[11] 罗亦泳. 基于高斯过程的大坝变形预测模型[J]. 浙江工业大学学报,2016,44(5):543-546. DOI: 10.3969/j.issn.1006-4303.2016.05.015 LUO Y Y. A Gaussian process based model for predicting deformations of dams[J]. Journal of Zhejiang University of Technology,2016,44(5):543-546. doi: 10.3969/j.issn.1006-4303.2016.05.015
[12] 孙斌,姚海涛,刘婷. 基于高斯过程回归的短期风速预测[J]. 中国电机工程学报,2012,32(29):104-109,5. SUN B,YAO H T,LIU T. Short-term wind speed forecasting based on gaussian process regression model[J]. Proceedings of the CSEE,2012,32(29):104-109,5.
[13] 张韶辉,苏强,赵永亮,等. 基于LASSO回归对冠心病相关血脂指标的筛选[J]. 中国综合临床,2021,37(2):148-153. DOI: 10.3760/cma.j.cn101721-20200807-00060 ZHANG S H,SU Q,ZHAO Y L,et al. Screening of lipid parameters in coronary artery disease based on Lasso regression[J]. Clinical Medicine of China,2021,37(2):148-153. doi: 10.3760/cma.j.cn101721-20200807-00060
[14] 黄梅,朱焱. 基于随机森林特征重要性的K-匿名特征优选[J]. 计算机应用与软件,2020,37(3):266-270. DOI: 10.3969/j.issn.1000-386x.2020.03.045 HUANG M,ZHU Y. K-anonymity feature optimization based on the importance of random forest features[J]. Computer Applications and Software,2020,37(3):266-270. doi: 10.3969/j.issn.1000-386x.2020.03.045
[15] 刘鑫童. 深度卷积神经网络在甲状腺超声图像中的分类研究[D]. 银川: 宁夏大学, 2018. LIU X T. Classification of deep convolution neural networks in thyroid ultrasound images[D]. Yinchuan: Ningxia Univer- sity, 2018.
[16] SUN L,AN W,LIU X J,et al. On developing data-driven turbulence model for DG solution of RANS[J]. Chinese Journal of Aeronautics,2019,32(8):1869-1884. doi: 10.1016/J.CJA.2019.04.004
[17] 胡伟杰,黄增辉,刘学军,等. 基于自动核构造高斯过程的导弹气动性能预测[J]. 航空学报,2021,42(4):289-302. HU W J,HUANG Z H,LIU X J,et al. Missile aerodynamic performance prediction of Gaussian process through auto-matic kernel construction[J]. Acta Aeronautica ET Astro-nautica Sinica,2021,42(4):289-302.
[18] 高赫,刘学军,郭晋,等. 基于高斯过程回归的连续式风洞马赫数控制[J]. 空气动力学学报,2019,37(3):480-487. DOI: 10.7638/kqdlxxb-2019.0018F GAO H,LIU X J,GUO J,et al. Mach number control of continuous wind tunnel based on Gaussian process regre-ssion[J]. Acta Aerodynamica Sinica,2019,37(3):480-487. doi: 10.7638/kqdlxxb-2019.0018F
[19] NEMATZADEH Z, IBRAHIM R, SELAMAT A. Compa-rative studies on breast cancer classifications with k-fold cross validations using machine learning techniques[C]//Proc of the 2015 10th Asian control conference (ASCC). IEEE, 2015: 1-6. doi: 10.1109/ASCC.2015.7244654
[20] 宗豪华,吴云,宋慧敏,等. 等离子体合成射流的理论模型与重频激励特性[J]. 航空学报,2015,36(6):1762-1774. ZONG H H,WU Y,SONG H M,et al. Analytical model and repetitive working characteristics of plasma synthetic jet[J]. Acta Aeronautica ET Astronautica Sinica,2015,36(6):1762-1774.
[21] 李铮, 史志伟, 魏晨瑶, 等. 高超声速流场中等离子体合成射流激励器逆向喷流激波控制研究[C]//第十届全国流体力学学术会议论文摘要集. 2018. [22] PRESS M. Approximation methods for Gaussian process regression[J]. MIT Press,2007,14(2):333-350.
[23] 王林,夏智勋,罗振兵,等. 两电极等离子体合成射流激励器工作特性研究[J]. 物理学报,2014,63(19):194702. DOI: 10.7498/aps.63.194702 WANG L,XIA Z X,LUO Z B,et al. Experimental study on the characteristics of a two-electrode plasma synthetic jet actuator[J]. Acta Physica Sinica,2014,63(19):194702. doi: 10.7498/aps.63.194702
[24] 姜慧,邵涛,章程,等. 不同电极间距下纳秒脉冲表面介质阻挡放电分布特性[J]. 电工技术学报,2017,32(2):33-42. JIANG H,SHAO T,ZHANG C,et al. Distribution cha-racteristics of nanosecond-pulsed surface dielectric barrier discharge at different electrode gaps[J]. Transactions of China Electrotechnical Society,2017,32(2):33-42.
[25] 王林,罗振兵,夏智勋,等. 三电极等离子体合成射流激励器工作特性参数影响实验[J]. 气体物理,2017,2(6):1-8. WANG L,LUO Z B,XIA Z X,et al. Experimental study of the parameters influence on flow characteristic of the three-electrode plasma synthetic jet actuator[J]. Physics of Gases,2017,2(6):1-8.
[26] RASMUSSEN C E, WILLIAMS C K I. Gaussian processes for machine learning[M]. America: the MIT press, 2005. doi: 10.7551/MITPRESS/3206.001.0001
[27] 徐冲,刘保国,刘开云,等. 基于组合核函数的高斯过程边坡角智能设计[J]. 岩土力学,2010,31(3):821-826. DOI: 10.3969/j.issn.1000-7598.2010.03.028 XU C,LIU B G,LIU K Y,et al. Slope angle intelligent design based on gaussian process with combinatorial kernel function[J]. Rock and Soil Mechanics,2010,31(3):821-826. doi: 10.3969/j.issn.1000-7598.2010.03.028
[28] 王娟,慈林林,姚康泽. 特征选择方法综述[J]. 计算机工程与科学,2005,27(12):68-71. DOI: 10.3969/j.issn.1007-130X.2005.12.024 WANG J,CI L L,YAO K Z. A survey of feature selection[J]. Computer Engineering and Science,2005,27(12):68-71. doi: 10.3969/j.issn.1007-130X.2005.12.024
[29] 刘晓宁. 基于LASSO特征选择的方法比较[J]. 安徽电子信息职业技术学院学报,2014,13(1):26-30. DOI: 10.3969/j.issn.1671-802X.2014.01.009 LIU X N. Comparison of feature selection methods based on lasso[J]. Journal of Anhui Vocational College of Electronics & Information Technology,2014,13(1):26-30. doi: 10.3969/j.issn.1671-802X.2014.01.009
[30] 李欣海. 随机森林模型在分类与回归分析中的应用[J]. 应用昆虫学报,2013,50(4):1190-1197. DOI: 10.7679/j.issn.2095-1353.2013.163 LI X H. Using “random forest” for classification and regression[J]. Chinese Journal of Applied Entomology,2013,50(4):1190-1197. doi: 10.7679/j.issn.2095-1353.2013.163
[31] 徐鹏,林森. 基于C4.5决策树的流量分类方法[J]. 软件学报,2009,20(10):2692-2704. DOI: 10.3724/SP.J.1001.2009.03444 XU P,LIN S. Internet traffic classification using C4.5 decision tree[J]. Journal of Software,2009,20(10):2692-2704. doi: 10.3724/SP.J.1001.2009.03444
[32] BENESTY J, CHEN J D, HUANG Y T, et al. Pearson correlation coefficient[M]//Noise reduction in speech pro-cessing. Berlin Heidelberg: Springer Berlin Heidelberg, 2009: 1-4. doi: 10.1007/978-3-642-00296-0_5
-
期刊类型引用(3)
1. 汤依唯,李超,苏彩虹. 高超声速飞行器上升段边界层转捩的参数影响分析. 气体物理. 2024(06): 11-20 .  百度学术
百度学术
2. 吴里银,张扣立,李晨阳,李清廉. 超声速气流中液体横向射流空间振荡分布建模. 实验流体力学. 2018(04): 20-30 .  本站查看
本站查看
3. 叶友达,张涵信,蒋勤学,张现峰. 近空间高超声速飞行器气动特性研究的若干关键问题. 力学学报. 2018(06): 1292-1310 .  百度学术
百度学术
其他类型引用(2)






 下载:
下载: