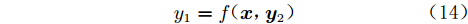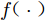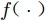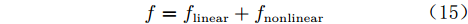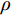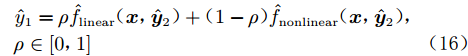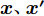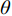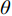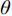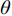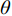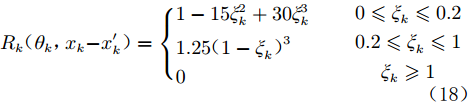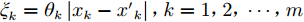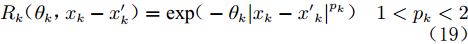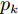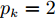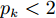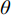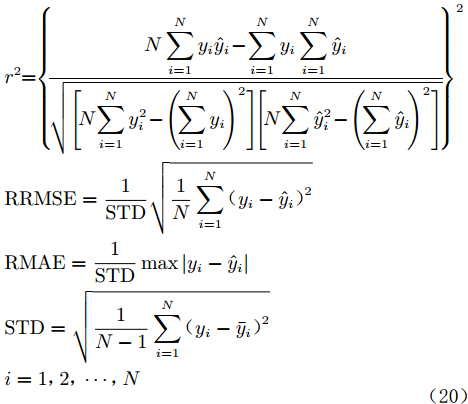Comparison of machine learning data fusion methods applied to aerodynamic modeling of rocket first stage with grid fins
-
摘要: 机器学习数据融合方法可帮助降低飞行器气动数据库建立的成本，加快研制进度，目前已经成为飞行器设计方法领域越来越活跃的研究方向，但其在工程复杂问题方面的应用研究并不充分。将多种常见变可信度数据融合模型应用于运载火箭子级栅格舵落区控制的工程项目，在开展部分工况的风洞试验基础上，结合少量的CFD数值模拟结果，研究相关函数和不同模型预测完整工况气动特性数据的差异性。通过对比加法标度函数修正模型、Co-Kriging模型、分层Kriging模型和多可信度神经网络模型等4种不同的数据融合模型发现：高斯指数相关函数对气动建模问题的适应性更好；Co-Kriging模型对气动数据的内插表现最好；分层Kriging模型对内插的预测精度较高，外插效果不理想；多可信度神经网络模型在外插区域能获得更光滑、合理的预测结果。Abstract: Machine learning data fusion method has attracted significant attention recently in aerodynamic database construction since it makes a trade-off between high prediction accuracy and low fitting cost by fusing samples of different fidelities. But the research on methods for complex engineering project is not sufficient. In this paper, several commonly used variable-fidelity models （VFMs） of data fusion are applied to the control law design in the rocket first stage landing area control project with grid fins. Based on wind tunnel tests of partial test states, combined with CFD simulation results, VFMs successfully predict the whole aerodynamic characteristics of grid fins. Here, our objective is to compare the performances of these four VFM methods （AS-MFS, Co-Kriging, HK, MFNN） and the results show that: Gaussian exponential function is more suitable for aerodynamic modeling problems; Co-Kriging has the best performance in the interpolation of aerodynamic data; HK model has high prediction accuracy for interpolation but has poor performance for extrapolation; MFNN model can obtain smoother and more reasonable results in the extrapolation region.
-
Keywords:
- variable-fidelity model /
- aerodynamic modeling /
- data fusion /
- grid fin /
- machine learning
-
0 引 言
飞行器气动设计的核心工作之一是提供准确、完备的气动特性数据，其中最为重要的是冻结外形气动特性数据，国外一般称为“设计气动数据库”。然而，对于流动条件变化复杂的高超声速飞行器，建立设计气动数据库通常需要开展规模庞大和复杂的风洞试验和CFD计算，导致气动研制经费和进度难以控制[1-2]。因此工程应用迫切需要发展新的方法降低气动数据库建立成本。
近年来，随着数字化飞行器设计技术的发展，研究人员在人工智能技术与空气动力学结合方面开展了诸多有益的尝试与探索[3]。其中具有代表性的机器学习方法已经成为最主流的人工智能实现方式，被广泛应用于飞行器多源气动数据融合与建模。机器学习方法可以快速预测不同工况下飞行器的气动特性，对建立完备的气动数据库、降低飞行器设计成本以及提升飞行器综合性能具有重要意义[4-5]。
变可信度融合模型是机器学习方法中的代表性方法[1, 6-9]。它是一种针对小样本数据的监督式机器学习方法[2]，其核心思想是先利用大量的低可信度（成本低、精度差）数据去近似气动特性的变化趋势，再融合高可信度（成本高、精度好）数据进行修正，实现对未知状态下气动特性的高精度预测。目前常用的变可信度融合模型大致可以分为以下4类[6, 8]：
1）基于标度函数的修正模型
基于标度函数的修正模型是在低可信度模型基础上，以相加、相乘或两者混合的方式引入标度函数，从而构建高可信度模型的近似模型。Haftka[10]和Chang等[11]最早提出了乘法标度函数的修正方法，通过缩放比例系数可使低可信度模型在局部近似于高可信度分析的结果。Alexandrov等[12-13]将其与置信域法结合，提出了一阶加法和乘法标度函数，并应用于翼型和机翼的优化设计之中，显著降低了计算成本。舒乐时等[14]和Park等[15]建立了更符合全局模型变化趋势的差异函数，提高了变可信度模型的预测精度。Wang[16]提出了一种基于最小二乘法的加法标度函数构造方法，提高了模型的泛化能力。杜涛等[1]提出了一种针对变可信度模型的自适应预处理技术，解决了加法标度函数修正模型在原始数据绝对值较小情况下出现数据失真的问题。韩忠华等[17]改善了混合标度函数修正方法，并引入了梯度等信息，进一步提高了模型的预测精度。
2）空间映射模型
该方法最早由Bandler在1994年提出[18]，Bandler建立了高、低设计空间的映射关系，使低可信度函数的局部特性能够逼近高可信度函数。而后Robinson等[19]提出了一种改进的空间映射方法，并应用于扑翼的气动建模与优化中。Jonsson等[20]也将此方法应用于跨声速机翼的气动优化设计中。空间映射模型最主要的特点是允许高、低可信度模型的设计空间维数不一致，并且适用于高可信度样本较少的高维建模问题[8]。
3）Co-Kriging类模型
Co-Kriging是在Kriging模型基础上发展起来的一类针对多可信度数据的高斯回归模型，被认为是一种浅层机器学习方法[21]。其基于贝叶斯理论，通过建立自回归模型将多种精度的数据进行融合，利用交叉协方差来衡量不同精度数据间的相关性。Kennedy和O’Hagan[22]首次将其应用于工程科学领域，提出了经典的KOH模型。之后，该模型的算法理论被不断改进，包括采用多项式缩放系数[23-24]、引入更多不同可信度层数据[25-26]、建模样本非嵌套化[27]等。韩忠华[28]和 Zimmermann等[29]提出了一种能够避免复杂交叉协方差计算的Co-Kriging模型。此外，韩忠华等[30]还提出了一种通用性更强、建模更加简洁的分层Kriging模型（Hierarchical kriging，HK）。该模型的基本思想是以大量的低可信度数据建立全局趋势模型，通过少量的高可信度样本进行修正，最终建立起高精度的预测模型。HK方法的后续改进研究可以参阅文献[6]和[8]。
4）多可信度神经网络模型
多可信度神经网络模型（Multi-Fidelity Neural Network，MFNN）采用最新发展的深度学习技术，先根据低可信度样本建立神经网络模型，再将低可信度模型的预测值和高可信度样本同时作为高可信度神经网络的输入，最后根据输出的预测值与高可信度样本标签值之间的差异来构建损失函数，迭代训练模型参数。Meng等[31]在MFNN模型的基础上提出了多可信度贝叶斯神经网络[32]，该方法可提供模型预测值的均方误差。何磊等[33]将MFNN网络应用于亚声速翼型的气动特性建模。张鑫帅等[34]则将MFNN网络应用于翼型与翼身组合体的气动优化设计。
虽然变可信度融合模型理论与算法在近十年已取得了长足的进步，但现有方法的泛化能力仍明显不足，大多数模型还停留在实验室研究阶段，缺乏工程研制中复杂应用场景的适应性研究[6]。
2019年，在我国首次开展的在役火箭子级落区控制项目中，由于飞行操态较多，跨越马赫数范围广，气动研制工作面临经费和进度的双重压力。本文作者所在团队首次尝试引入变可信度融合模型技术，在解决了4项关键算法和技术问题、提升了模型在复杂工程问题中的适应性，利用加法标度函数修正模型和HK模型学习了项目部分风洞试验及CFD计算结果后，预测了全部工况的气动特性，按时建立了飞行气动数据库，并大幅降低了风洞试验和数值仿真的需求[2]。2019年7月，飞行搭载试验取得成功，预测结果的正确性获得了验证。
本文是上述研究工作的继续。在应用中作者发现相关函数和模型的选择对预测结果的正确性和质量有较大影响，因此，本文将深入研究影响机理，进一步发掘变可信度融合模型在工程复杂场景中应用的鲁棒性和适应性。除文献[2]中的加法标度函数修正模型和HK模型外，本文还将额外对比2种变可信度融合模型—Co-Kriging模型和MFNN模型。这4种变可信度融合模型几乎代表了当前主流的气动融合建模思路。通过对建模结果的对比分析，讨论不同相关函数和模型的工程适应性，并给出变可信度融合模型的使用建议。
1 变可信度模型理论与算法
1.1 基本假设
对于一个
$m$ 维的建模问题，假设存在通过不同来源或不同精度的分析模型得到的高、低可信度样本数据集：$$ \begin{split}& {{\boldsymbol{S}}_1} = {（{\boldsymbol{x}}_1^{（1）}，{\boldsymbol{x}}_1^{（2）}，\cdots，{\boldsymbol{x}}_1^{（{n_1}）}）^{\text{T}}} \in {\mathbb{R}^{{n_1} \times m}} \\& {{\boldsymbol{S}}_2} = {（{\boldsymbol{x}}_2^{（1）}，{\boldsymbol{x}}_2^{（2）}，\cdots，{\boldsymbol{x}}_2^{（{n_2}）}）^{\text{T}}} \in {\mathbb{R}^{{n_2} \times m}} \end{split} $$ (1) 以及对应的响应值：
$$ \begin{split}& {{\boldsymbol{y}}_1} = {[{y_1}（{\boldsymbol{x}}_1^{（1）}），{y_1}（{\boldsymbol{x}}_1^{（2）}），\cdots，{y_1}（{\boldsymbol{x}}_1^{（{n_1}）}）]^{\text{T}}} \in {\mathbb{R}^{{n_1}}} \\& {{\boldsymbol{y}}_2} = {[{y_2}（{\boldsymbol{x}}_2^{（1）}），{y_2}（{\boldsymbol{x}}_2^{（2）}），\cdots，{y_2}（{\boldsymbol{x}}_2^{（{n_2}）}）]^{\text{T}}} \in {\mathbb{R}^{{n_2}}} \end{split} $$ (2) 其中，下标“1”表示高可信度，“2”表示低可信度；
$ {n}_{1}和{n}_{2} $ 分别为高、低可信度样本点个数，$\mathbb{R} $ 为实数集。变可信度模型构建中所需要解决的核心问题是如何有效地融合高、低精度分析模型的数据，使预测结果能更逼近真实的高精度结果。下面将介绍4种常见的变可信度融合模型理论。
1.2 加法标度函数修正模型
基于加法标度函数修正的变可信度融合模型（Additive Scaling Function Based Multi-fidelity Surrogate Model，AS−MFS）是一种以低可信度模型为基础、通过加法标度函数的方式引入高可信度数据辅助构建高可信度分析模型的近似模型，具体的公式推导可参见文献[8]。在AS-MFS中，标度函数
$\delta （{\boldsymbol{x}}）$ 定义为高可信度样本点${\boldsymbol{x}}_1^{（i）}$ 处高、低可信度分析模型输出响应间的差值：$$ \delta （{\boldsymbol{x}}_1^{（i）}） = {y_1}（{\boldsymbol{x}}_1^{（i）}） - {y_2}（{\boldsymbol{x}}_1^{（i）}） $$ (3) 通过分别取高可信度样本点集合
$ {{\boldsymbol{S}}_1} = {（{\boldsymbol{x}}_1^{（1）}}， {{\boldsymbol{x}}_1^{（2）}，\cdots，} {{\boldsymbol{x}}_1^{（{n_1}）}）^{\text{T}}} $ 和标度函数因子集合$ { {δ}} = {（{\delta _1}，{\delta _2}，\cdots，} {{\delta _{{n_1}}}）^{\text{T}}} $ 作为输入和输出来构建加法标度函数$\hat \delta （{\boldsymbol{x}}）$ 。于是，AS-MFS模型的最终预估值为：$$ {\hat y_1}（{\boldsymbol{x}}） = {\hat y_2}（{\boldsymbol{x}}） + \hat \delta （{\boldsymbol{x}}） $$ (4) 由于概念直观且模型简洁，AS-MFS已成为标度函数修正模型中最常用的方法，被广泛应用于工程问题的建模和设计过程中[8]。
1.3 Co-Kriging模型
本文选用的Co-Kriging模型来自文献[29]。假设模型预估值为已知样本响应值的线性加权：
$$ {\hat y_1}（{\boldsymbol{x}}） = {{ {λ}}}_1^{\text{T}}{{\boldsymbol{y}}_1} + {{ {λ}}}_2^{\text{T}}{{\boldsymbol{y}}_2} $$ (5) 其中，
${{ {λ}}}$ 是权重系数。为了寻找最优的权重系数，在满足无偏估计的情况下最小化$\hat y（ {\boldsymbol{x}} ）$ 的均方误差：$$ \begin{split}& \min \;\;{\rm{MSE}}\left[ {{{\hat y}_1}{\text{（}}{\boldsymbol{x}}{\text{）}}} \right] = E\left[ {{{{\text{（}}{{ {λ}}}_1^{\text{T}}{{\boldsymbol{Y}}_1} + {{ {λ}}}_2^{\text{T}}{{\boldsymbol{Y}}_2}-{Y_1}{\text{）}}}^2}} \right] \\& {\text{s}}{\text{.t}}.\;\;E（{{ {λ}}}_1^{\text{T}}{{\boldsymbol{Y}}_1} + {{ {λ}}}_2^{\text{T}}{{\boldsymbol{Y}}_2}） = E（ {{Y_1}} ） \end{split}$$ (6) 为了降低模型的复杂程度，文献[29]假设高、低可信度数据具有相同的过程方差
${\delta}^2 $ 。同时为了描述不同可信度数据之间的相关性，额外引入了一个模型超参数$\gamma \in \left[ {0，1} \right]$ ，于是通过拉格朗日乘子法可将公式（6）转为矩阵形式：$$\begin{split}& \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{R}}^{（11）}}}&{\gamma {{\boldsymbol{R}}^{（12）}}}&{\boldsymbol{1}}&{\boldsymbol{0}} \\ {\gamma {{\boldsymbol{R}}^{（21）}}}&{{{\boldsymbol{R}}^{（22）}}}&{\boldsymbol{0}}&{\boldsymbol{1}} \\ {{{\boldsymbol{1}}^{\text{T}}}}&{{{\boldsymbol{0}}^{\text{T}}}}&0&0 \\ {\boldsymbol{0}}&{{{\boldsymbol{1}}^{\text{T}}}}&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{ {λ}}}_1}} \\ {{{{ {λ}}}_2}} \\ {{{{\mu _1}} \mathord{\left/ {\vphantom {{{\mu _1}} {2{\sigma ^2}}}} \right. } {2{\sigma ^2}}}} \\ {{{{\mu _2}} \mathord{\left/ {\vphantom {{{\mu _2}} {2{\sigma ^2}}}} \right. } {2{\sigma ^2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{r}}_1}（{\boldsymbol{x}}）} \\ {\gamma {{\boldsymbol{r}}_2}（{\boldsymbol{x}}）} \\ 1 \\ 0 \end{array}} \right]\\ \end{split}$$ (7) 经过推导可得，Co-Kriging模型的预估值表达式为：
$$ \begin{split}& {\hat {y_1}}（{\boldsymbol{x}}） = {{ {φ}}^{\rm{T}}}{{\tilde {{{ {β}}}} }} + {{\boldsymbol{r}}^{\rm{T}}}（{\boldsymbol{x}}）{{\boldsymbol{R}}^{ - 1}}（{{{\tilde {{\boldsymbol{y}}}}}_{\boldsymbol{s}}} - {{{\boldsymbol{F}}\tilde {{{ {β}}}} }}）， \\& { {φ}} = \left[ \begin{array}{l} 1\\ 0 \end{array} \right]，\tilde { {β}} = \left[ \begin{array}{l} {{\tilde \beta }_1}\\ {{\tilde \beta }_2} \end{array} \right] = {（{{{\boldsymbol{F}}^{\rm{T}}}{{\boldsymbol{R}}^{ - 1}}{\boldsymbol{F}}} ）^{ - 1}}{{\boldsymbol{F}}^{\rm{T}}}{{\boldsymbol{R}}^{ - 1}}{{\tilde {\boldsymbol{y}}}_{\boldsymbol{s}}}，\\& {\boldsymbol{r}} = \left[ \begin{array}{l} {{\boldsymbol{r}}_1}（{\boldsymbol{x}} ）\\ \gamma {{\boldsymbol{r}}_2}（{\boldsymbol{x}} ） \end{array} \right]，{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{R}}^{（{11} ）}}}&{\gamma {{\boldsymbol{R}}^{（{12} ）}}}\\ {\gamma {{\boldsymbol{R}}^{（{21} ）}}}&{{{\boldsymbol{R}}^{（{22} ）}}} \end{array}} \right]，\\& {{\tilde {\boldsymbol{y}}}_{\boldsymbol{s}}} = \left[ \begin{array}{l} {{\boldsymbol{y}}_1}\\ {{\boldsymbol{y}}_2} \end{array} \right]，{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{1}}&{\boldsymbol{0}}\\ {\boldsymbol{0}}&{\boldsymbol{1}} \end{array}} \right]\\[-12pt] \end{split} $$ (8) 1.4 分层Kriging模型
韩忠华等[30]于2012年提出了分层Kriging模型，它是对传统Kriging模型理论的进一步发展。首先，针对低可信度数据集建立Kriging模型：
$$ {\hat y_2}（{\boldsymbol{x}}） = {\beta _{{2}}} + {\boldsymbol{r}}_2^{\text{T}}（{\boldsymbol{x}}）{\boldsymbol{R}}_2^{ - 1}（{{\boldsymbol{y}}_2} - {\beta _{{2}}}{\boldsymbol{F}}） $$ (9) 其次，假设在高可信度样本点处存在静态随机过程：
$$ Y（{\boldsymbol{x}}） = {\beta _1}{\hat y_2}（{\boldsymbol{x}}） + Z（{\boldsymbol{x}}） $$ (10) 其中，Z（x）表示均值为0、差为
$\sigma ^2 $ 的静态随机过程。这里低可信度Kriging模型的预估值$ {\hat y_2}（{\boldsymbol{x}}） $ 与常数缩放因子${\beta _1}$ 的乘积代替了原先的常数回归项，成为高可信度模型的全局趋势模型。与Kriging模型类似，可推得HK模型的均方误差为：$$ {\rm{MSE}}\left[ {\hat y（{\boldsymbol{x}}）} \right]{\text{ = }}E\left[ {{{（{{\lambda}^{\text{T}}}{{\boldsymbol{Y}}_S} - Y（{\boldsymbol{x}}））}^2}} \right] $$ (11) 并满足如下无偏估计的条件：
$$ E\left[ {\sum\limits_{i = 1}^n {{\lambda ^{（i）}}Y（{{\boldsymbol{x}}^{（i）}}）} } \right] = E\left[ {Y（{\boldsymbol{x}}）} \right] $$ (12) 最终，HK模型的预估值可表示为：
$$ {\hat y_1}（{\boldsymbol{x}}） = {\beta _1}{\hat y_2}（{\boldsymbol{x}}） + {{\boldsymbol{r}}^{\text{T}}}（{\boldsymbol{x}}）{{\boldsymbol{R}}^{ - 1}}（{{\boldsymbol{y}}_1} - {\beta _1}{\boldsymbol{F}}） $$ (13) 1.5 多可信度神经网络模型
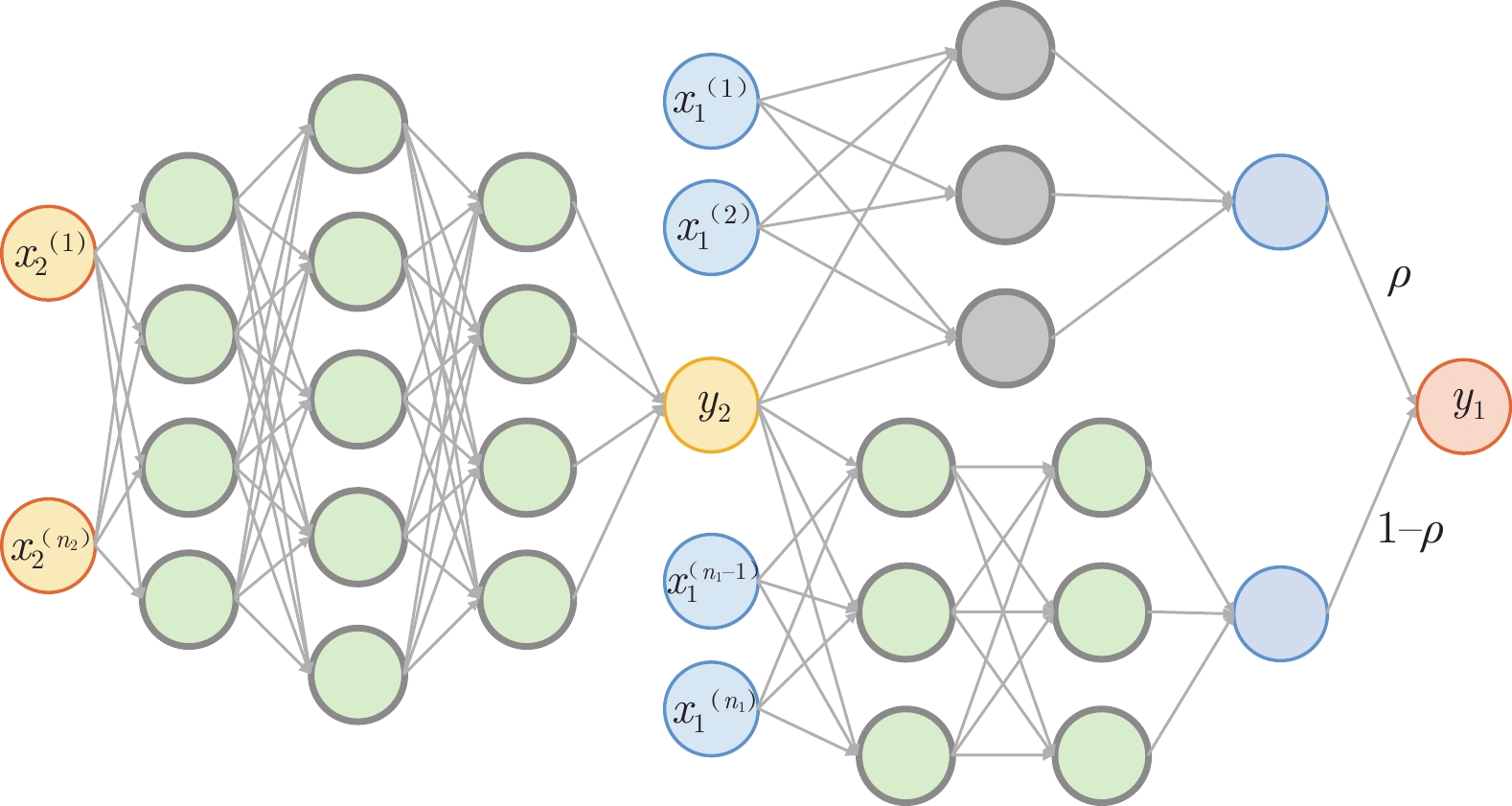
除了基于贝叶斯理论的变可信度模型，近年来新发展了一种基于深度学习的多可信度神经网络模型（MFNN），其模型结构如图1所示，具体推导过程可以参阅文献[31]。
假设高、低可信度数据之间的关系可以表示为：
$$ {y_1} = f（{\boldsymbol{x}}，{{\boldsymbol{y}}_2}） $$ (14) 其中，
$f（ \cdot ）$ 表示数据从低可信度层到高可信度层的映射关系。一般认为在高、低可信度数据层均存在线性和非线性相关性，于是映射函数$f（ \cdot ）$ 可拆为两部分：$$ f = {f_{{\text{linear}}}} + {f_{{\text{nonlinear}}}} $$ (15) 为了描述高、低可信度数据间线性和非线性相关性的程度，引入超参数缩放因子
$\;\rho $ ，于是MFNN模型的预估值表达式为：$$\begin{split}& {\hat y_1} = \rho {\hat f_{{\rm{linear}}}}（{\boldsymbol{x}}，{{{\hat {\boldsymbol{y}}}}_2}） + （1 - \rho ）{\hat f_{{\rm{nonlinear}}}}（{\boldsymbol{x}}，{{{\hat {\boldsymbol{y}}}}_2}），\\& \rho \in [0，1] \end{split}$$ (16) 2 在栅格舵气动建模与预测上的应用和比较
2.1 模型训练样本集
预测对象为在役火箭的一子级，如图2所示，其级间段设计了4片对称分布的栅格舵，对再入过程的俯仰、偏航和滚转通道进行气动操纵。本文将以俯仰通道气动特性为研究对象，输入变量为马赫数、攻角（α）和俯仰舵偏角。
![]()
项目以风洞试验（图3）为主，辅以少量CFD计算（图4）。由于进度和经费的原因，风洞试验和CFD计算的结果并不充分。亚声速和跨声速条件的试验成本低、进度快，均开展了试验；马赫数大于4的状态未开展试验，最终仅开展了所需工况的54%，如表1所示。理论上，风洞试验状态比CFD计算更加接近飞行器表面真实的流动状态，因此，本文将风洞试验数据视为高可信度数据，而CFD计算结果是低可信度辅助数据。
![]()
![]()
亚声速段时，火箭一子级带栅格舵外形的俯仰力矩在0°攻角附近为静稳定配平点，而超声速段变为不稳定配平点（图5），跨声速段容易出现显著的壅塞现象。栅格舵的俯仰力矩表现出远比轴向力和法向力复杂的变化特性。这种特性能够代表工程应用的复杂场景，因此本文将俯仰力矩特性的气动建模与预测作为主要研究对象。
从气动数据集中筛选出不同舵偏角、马赫数、攻角（输入数据）与俯仰力矩系数（输出数据），得到不同舵偏角下的310组风洞试验数据和96组CFD计算数据，其空间分布情况如图6所示，4个舵偏角从上往下依次为–20°、–10°、0°和10°。从图中可以看出：高可信度风洞试验数据（绿色球体）主要集中在跨声速段，缺少高超声速段数据（马赫数4以上）；而CFD计算数据（红色方块）覆盖了全马赫数工况，但缺少大攻角下（攻角15°以上）俯仰力矩数据。
![]()
图 5 火箭一子级带栅格舵外形跨声速段和超声速段俯仰力矩特性Fig. 5 Pitching moment characteristics of rocket first stage with grid fins in the transonic and supersonic regimes![]()
图 6 栅格舵俯仰力矩系数数据集空间分布情况Fig. 6 Pitching moment data set of rocket first stage with grid fins2.2 模型训练的关键问题
本文采用4种变可信度融合模型对俯仰力矩系数进行建模与预测。下面先对模型训练过程中出现的一些关键问题进行分析和讨论。
2.2.1 相关函数的选择与影响
除了MFNN模型，其余3种变可信度融合模型均基于高斯过程回归理论。高斯过程回归—本文特指Kriging模型—是一种使用高斯过程先验对数据进行插值分析的模型。它通常包含不超过两层的非线性特征变换，因而被认为是一种浅层的机器学习模型[3, 21]。文献[2]中，我们发现相关函数R和模型超参数训练对Kriging模型的预测效果影响很大。相关函数又称为“核函数”，是一类仅与样本点空间距离相关的光滑函数，满足距离为0时等于1、距离无穷大时等于0，且相关性随着距离的增大而减小。对于一个
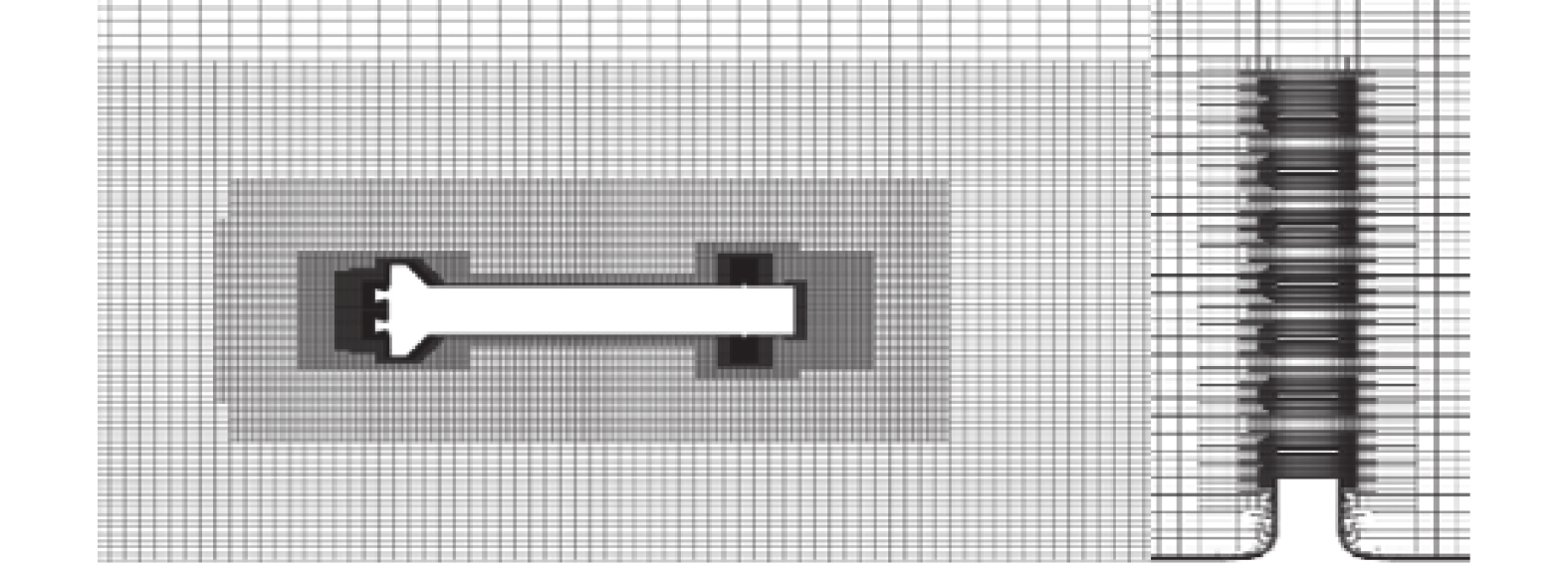
$m$ 维的建模问题，相关函数一般具有如下的形式：$$ R（{\boldsymbol{x}}，{\boldsymbol{x'}}） = \prod\limits_{k = 1}^m {{R_k}（{\theta _k}，{x_k} - {x'_k}）} $$ (17) 其中，
${\boldsymbol{x}}、{\boldsymbol{x'}}$ 为设计空间中任意两个不同位置，$\theta $ 为待定的模型超参数。一般来说，带有$\theta $ 的相关函数可以更好地反映不同变量在该维空间上的变化尺度，通过训练$\theta $ 可以提高Kriging模型对非线性函数的拟合能力。另外，还有一类不带$\theta $ 的相关函数，如薄板样条函数，它们往往对非线性函数的拟合较差，而对线性函数的拟合较好。目前常用的带
$\theta $ 的相关函数包括三次样条函数和高斯指数函数[35]。本节将着重考察这两种相关函数对预测效果的影响。三次样条函数的解析表达式为：
$$ {R_k}（{\theta _k}，{x_k} - {x'_k}） = \left\{ {\begin{array}{*{20}{l}} {1 - 15\xi _k^2 + 30\xi _k^3} \\ {1.25{{（1 - {\xi _k}）}^3}} \\ 0 \end{array}} \right. \begin{array}{*{20}{c}} \quad {0 \leqslant {\xi _k} \leqslant 0.2} \\ \quad {0.2 \leqslant {\xi _k} \leqslant 1} \\ \quad {{\xi _k} \geqslant 1} \end{array} $$ (18) 其中，
${\xi _k} = {\theta _k}\left| {{x_k} - {{x'}_k}} \right|，k = 1，2，\cdots，m$ 。该函数二阶可导，在光滑性和鲁棒性方面能取得很好的折中[7]。高斯指数函数的解析表达式为：
$$ {R_k}（{\theta _k}，{x_k} - {x'_k}） = \exp （ - {\theta _k}{\left| {{x_k} - {{x'}_k}} \right|^{{p_k}}}）\quad 1 < {p_k} < 2 $$ (19) 其中，
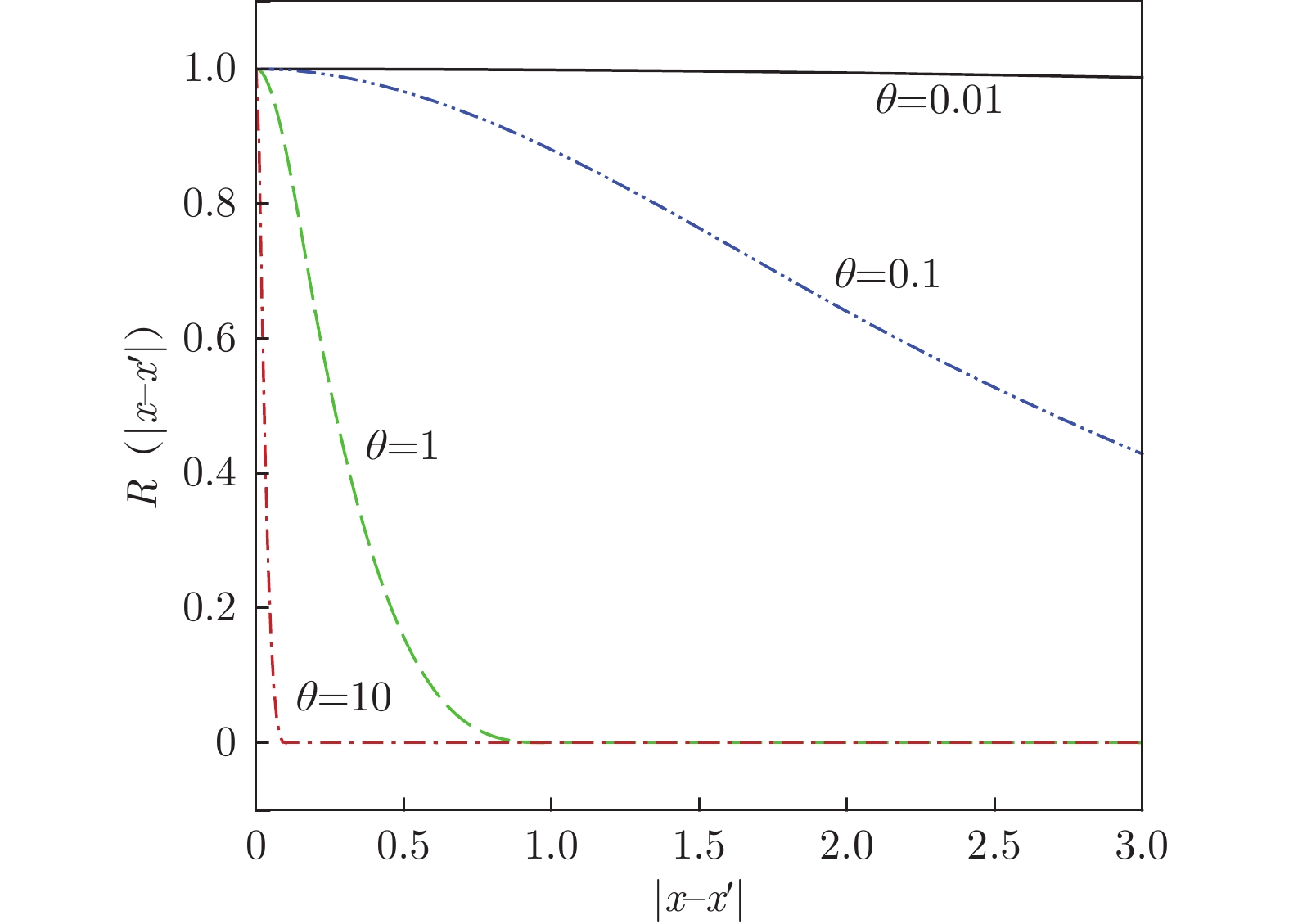
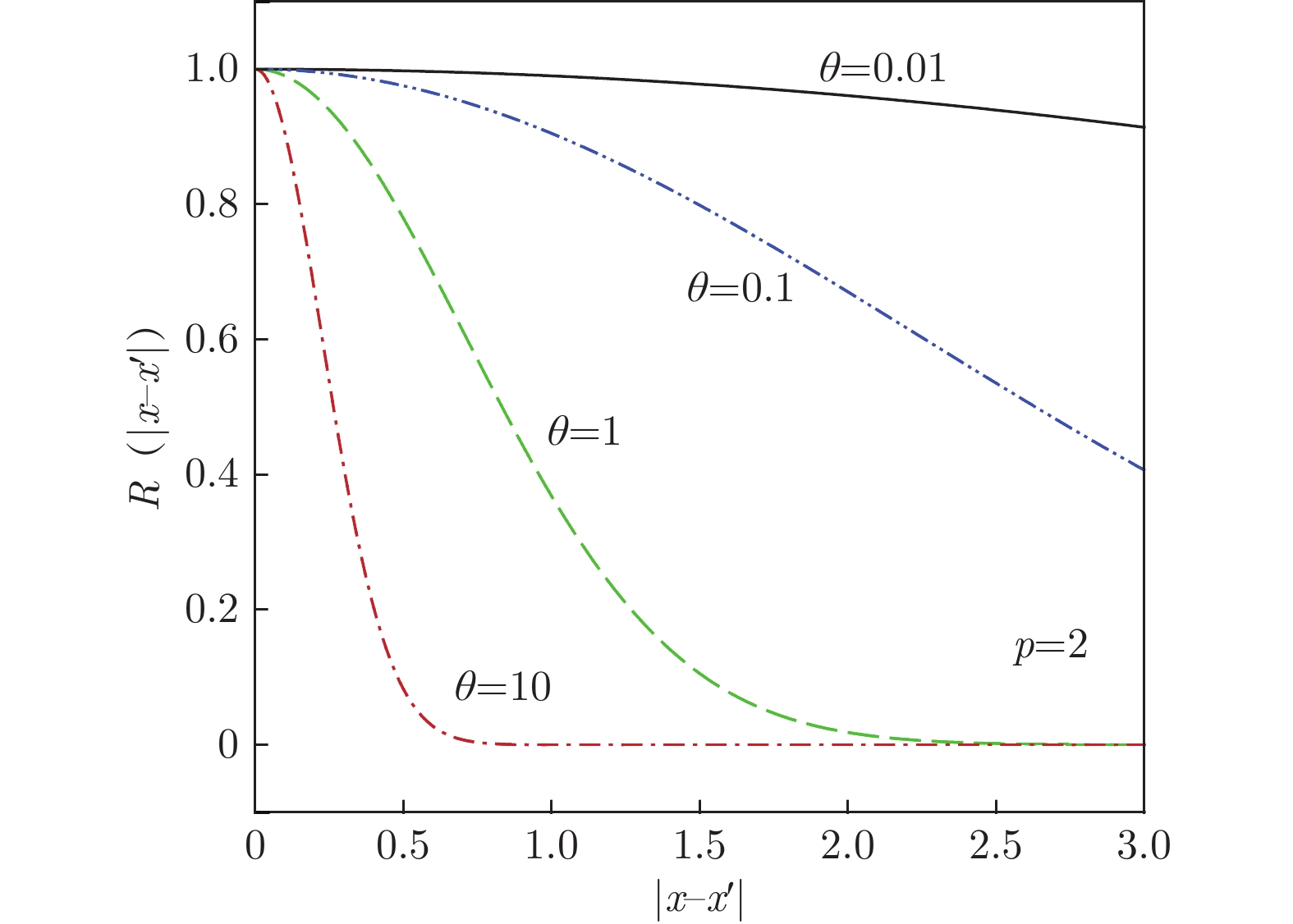
$ {p_k} $ 为相关函数光滑程度的各向异性参数。$ {p_k} = 2 $ 时，相关函数无穷阶次可导；$ {p_k} < 2 $ 时，相关函数一阶可导。图7、8分别为超参数
$\theta $ 取不同值时三次样条函数和高斯指数函数的变化情况。从图中可以看到，随着$\theta $ 的增大，相关函数曲线逐渐变“陡峭”，这意味着较大的$\theta $ 会缩小作用范围。$\theta $ 取值相同时，对比三次样条函数和高斯指数函数（p = 2），可以发现：三次样条函数随样本空间距离的变化更剧烈，并且当样本空间距离大到一定程度时，二者的相关性消失。文献[35]将这类样本局部性影响较大而全局性影响较小的相关函数称为“紧支撑性函数”。图9展示了$\theta $ = 1时高斯指数函数取随参数p的变化情况。可以看到，随着参数p的增大，相关函数在样本距离较小的情况下过渡得更为平缓。为了保持这种光滑的过渡性，本文限制高斯指数函数参数p的取值范围为[1.5，2]，且参数p与超参数$\theta $ 都可以通过最大似然估计的方法优化得到[7]。![]()
图 8 不同超参数下的高斯指数函数变化（p = 2）Fig. 8 Influence of θ on the Gauss correlation function with p = 2![]()
图 9 不同参数p时的高斯指数函数变化（θ = 1）Fig. 9 Influence of index p on the Gauss correlation function with θ = 1上文通过理论分析解释了两种相关函数的差异性，下面将其应用于栅格舵的俯仰力矩参数建模问题，考察不同相关函数对预测效果的影响情况。本文以舵偏角
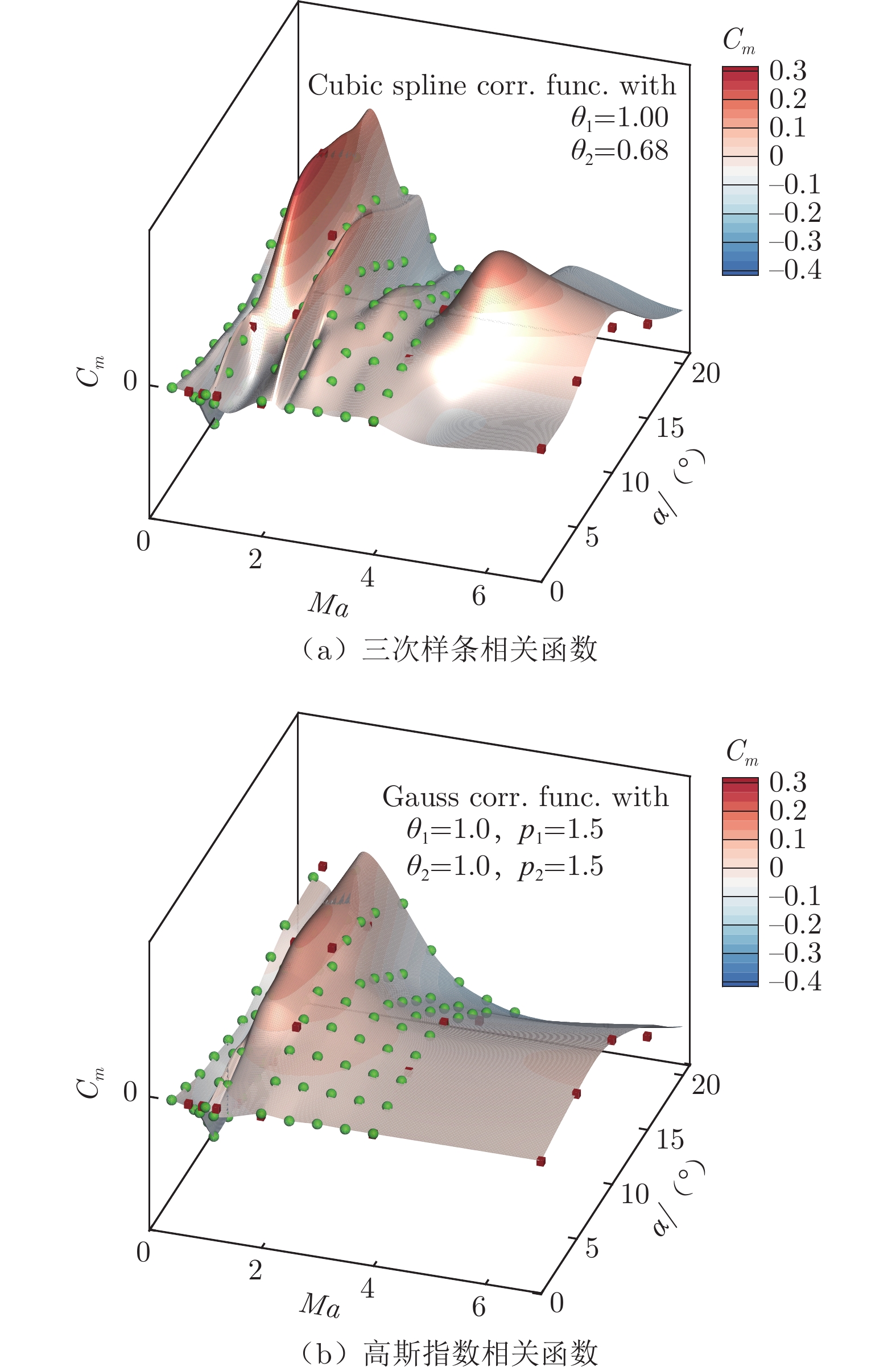
$\psi $ =0°时的俯仰力矩系数建模为例。需要说明的是，当俯仰舵无偏转时，共有100组风洞试验数据和24组CFD计算数据；模型的第一维输入是马赫数，第二维输入是攻角。为在同一标准下进行对比，首先将两种相关函数的超参数优化范围均限制在[0.001，1.0]。图10为HK模型采用不同相关函数的预测结果对比。从图中可以看到，采用紧支撑性较强的三次样条函数时，预测曲面变得不光滑，在离样本点较远的区域出现波浪型“隆起”现象；而采用高斯指数函数时，整个预测曲面在设计空间内的变化都较为光滑。
![]()
图 10 基于不同相关函数的HK模型对俯仰力矩系数建模结果对比（超参数优化范围受限制）Fig. 10 Comparison of predicted pitching moment coefficients via HK model based on different correlation functions （with optimization boundaries for hyperparameters）然后，解除对超参数优化范围的限制，基于最大似然估计理论对超参数进行彻底优化，得到优化后的超参数及俯仰力矩系数预测结果，如图11所示。从图中可以看到：采用三次样条作为相关函数时，优化后超参数的第一维数值较大，反映在预测曲面上，俯仰力矩系数预测值沿马赫数方向出现了过拟合现象；而采用高斯指数函数时，预测模型未出现明显的过拟合现象。造成这一现象的原因是：三次样条函数的紧支撑性使得其在
$\theta $ 较大时样本的影响域很小（图7），一旦预测点稍微偏离样本点，就无法获取样本响应值的相关信息，预测值将迅速靠近模型自身的常数回归项。在HK模型的外插区域，由于缺少高可信度风洞数据，采用高斯指数函数的模型预测曲面出现了小范围凹坑与鼓包。根据马赫数无关性原理，该现象不符合实际的物理规律。这也从侧面反映出：并不是模型的超参数优化得越彻底，预测效果就会越好；而是需要结合建模问题本身，给出合理的优化空间。![]()
图 11 基于不同相关函数的HK模型对俯仰力矩系数建模结果对比（超参数优化范围不作限制）Fig. 11 Comparison of predicted pitching moment coefficients via HK model based on different correlation functions （with no optimization boundaries for hyperparameters）本文将超参数的优化范围限制在[0.001，1.0]，再对比不同变可信度高斯回归模型采用这两种相关函数的俯仰力矩系数预测曲线，截取了攻角为10°的结果，如图12所示。从图中可以看到：采用三次样条作为相关函数时，3种变可信度模型的预测曲线均出现了不同程度的“振荡”现象；而采用高斯指数函数时，模型预测曲线变化较为光滑，更符合物理规律。图12充分显示了相关函数对预测结果的重要性。在后续的分析中，选用高斯指数函数作为AS-MFS模型、Co-Kriging模型和HK模型的相关函数。
![]()
图 12 采用两种相关函数的不同变可信度模型对俯仰力矩系数建模的结果对比Fig. 12 Comparison of predicted pitching moment coefficients via different variable-fidelity model based on the two correlation functions2.2.2 预测结果的检验方法
如何评估最终建立的变可信度融合模型的预测精度，是研究人员最关心、也是其在工程问题中取得成功应用的关键性问题之一[2]。本文沿用文献[2]提出的检验方法：交叉验证与物理规律检验相结合。交叉验证，即屏蔽一小部分试验数据，将其设定为未知，然后与模型预测进行比较。气动特性数据并非毫无规律可言，而是需要满足客观存在的物理规律，例如Oswatitsch高超马赫数无关性原则。这些规律可以帮助研究人员对气动模型进一步确认预测结果[2]。
鉴于项目数据空间分布的特殊性，高可信度风洞试验结果仅分布在马赫数4以下的状态（图6）。本文将马赫数区间分成两段，分别采用交叉验证和物理规律检验的方法。具体而言：
1）对马赫数小于4的内插区域，由于存在高可信度样本数据，因此随机屏蔽一小部分风洞试验数据点作为测试集，计算相关系数（r2）、相对均方根误差（RRMSE）和相对最大绝对误差（RMAE） 3个指标来表征模型的预估精度。其中，r2和RRMSE用来表征模型的全局预测精度，且r2越接近1、RRMSE越接近0，模型全局预测越精确；RMAE用来表征模型的局部预测精度，且RMAE越接近0，模型局部预测越精确。3个指标的计算公式如下：
$$ \begin{split}& {r^2} = {\left\{ {\frac{{N\displaystyle\sum\limits_{i = 1}^N {{y_i}{{\hat y}_i}} - \displaystyle\sum\limits_{i = 1}^N {{y_i}} \displaystyle\sum\limits_{i = 1}^N {{{\hat y}_i}} }}{{\sqrt {\left[ {N \displaystyle\sum\limits_{i = 1}^N {y_i^2} - {{\left( {\displaystyle\sum\limits_{i = 1}^N {{y_i}} } \right)}^2}} \right] \left[ {N \displaystyle\sum\limits_{i = 1}^N {\hat y_i^2} - {{\left( {\displaystyle\sum\limits_{i = 1}^N {{{\hat y}_i}} } \right)}^2}} \right]} }}} \right\}^2} \\& {\rm{RRMSE}} = \frac{1}{{{\rm{STD}}}}\sqrt {\frac{1}{N}\displaystyle\sum\limits_{i = 1}^N {{{（ {{y_i} - {{\hat y}_i}} ）}^2}} } \\& {\rm{RMAE}} = \frac{1}{{{\rm{STD}}}}\max \left| {{y_i} - {{\hat y}_i}} \right| \\& {\rm{STD}} = \sqrt {\frac{1}{{N - 1}}\displaystyle\sum\limits_{i = 1}^N {{{（ {{y_i} - {{\bar y}_i}} ）}^2}} }\\& i = 1，2，\cdots，N \end{split} $$ (20) 其中，N为测试集中的样本个数。需要说明的是，N的值不宜过大，否则会导致需要被屏蔽的高可信度风洞试验数据过多，从而减少参与气动建模的高可信度样本数据，造成模型预测精度的损失。综合考虑后，从310组高可信度样本里抽取了30组样本作为测试集。
2）对于马赫数大于4的外插区域，由于缺乏风洞试验数据，无法采用交叉验证方法进行精度评估，因而采用物理规律进行检验。需要说明的是，火箭一子级带栅格舵外形的飞行搭载试验取得了成功，其在再入启控的过程中经历了外插段的高马赫数区间，也从侧面间接说明了采用变可信度融合模型进行外插的正确性和有效性。后续研究工作中将发展对外插结果的直接验证方法。
2.3 模型的预测结果及对比
本节采用2.1小节介绍的4种变可信度融合模型分别对–20°、–10°、0°和10°舵偏角下栅格舵的俯仰力矩系数进行建模。表2为各舵偏角下的样本个数分布情况。
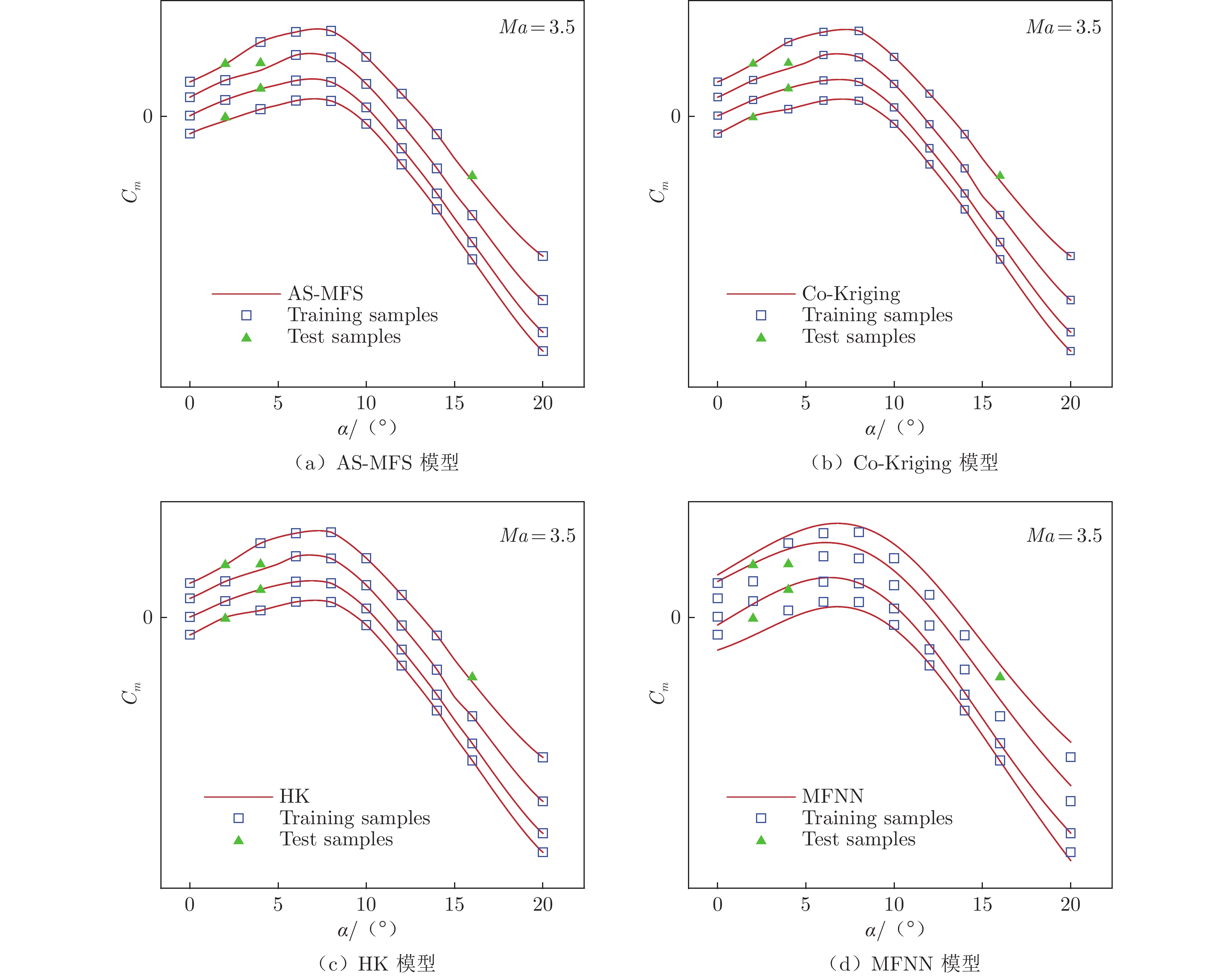
表 2 不同舵偏角下样本分布情况Table 2 Data sets for different elevator deflections of grid fins舵偏角 –20° –10° 0° 10° 总计 训练集样本个数 85 55 85 55 280 测试集样本个数 5 5 15 5 30 图13为采用高斯指数相关函数的AS-MFS模型、Co-Kriging模型、HK模型和MFNN模型在马赫数[0.4，4]区间内对俯仰力矩系数的内插结果对比。从图中可以看到，AS-MFS模型、Co-Kriging模型和HK模型的预测结果较为接近，均比较光滑，各舵偏角对应的预测曲面近似平行且相互隔开，不存在交叉现象。MFNN模型预测的俯仰力矩系数在跨声速、大攻角区域有较高的隆起现象；在跨声速区，–20°和–10°舵偏角下的俯仰力矩系数有明显的交叉现象。图14为马赫数为3.5时采用交叉验证方法检验不同模型预测结果的对比情况。从图中可以看到，Co-Kriging模型和HK模型的预测值与测试点吻合最好，且二者精度较为接近。AS-MFS模型的预测精度稍弱于前两种模型。由于AS-MFS、Co-Kriging模型和HK模型为插值模型，因此预测曲线均精确通过了训练样本；而MFNN的预测结果较差，且由于它是拟合模型，因此未精确通过训练样本。此外，表3还展示了采用交叉验证方法计算的模型精度指标对比情况。可以看到，在–20°、0°和10°舵偏角下，Co-Kriging模型的3项精度指标均优于其他3种模型。在–10°舵偏角下，Co-Kriging模型除RRMSE指标稍弱于HK模型外，其他2项精度指标仍为最佳。这表明Co-Kriging模型在栅格舵俯仰力矩系数的内插预测上具备一定的精度优势。HK模型的精度指标仅次于Co-Kriging模型，也表现出了较强的预测能力。在4种模型中，MFNN模型预测结果的3项指标均最差，俯仰力矩系数的预测误差较大。
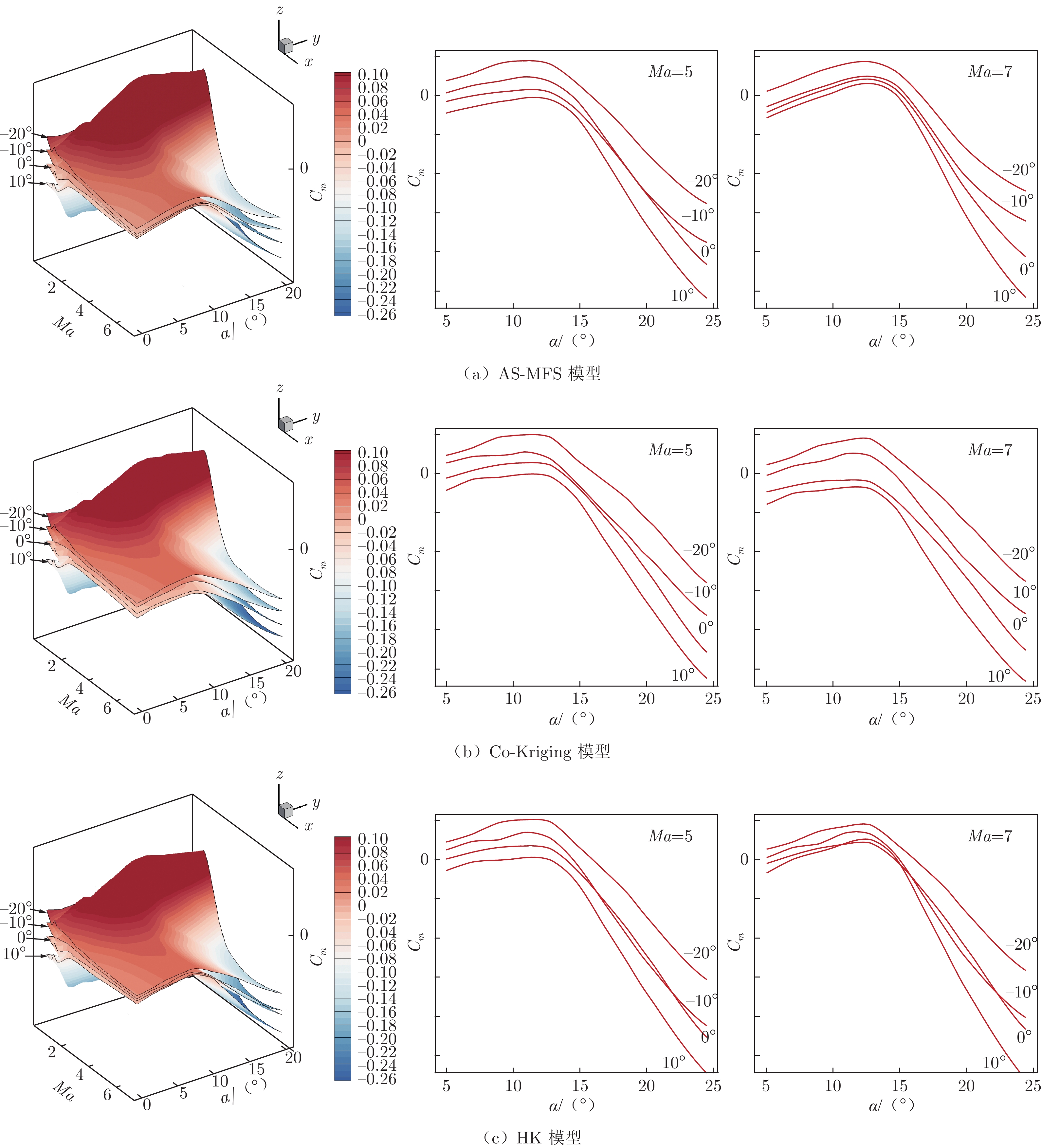
表 3 针对俯仰力矩系数建模不同模型精度指标对比Table 3 Comparison of different accuracy indicators for pitching moment coefficients via different VFMs舵偏角 模 型 r2 RRMSE RMAE -20° AS-MFS 0.997148 0.050151 0.080148 Co-Kriging 0.999482 0.024037 0.035985 HK 0.998572 0.040432 0.073526 MFNN 0.949331 0.433717 0.722283 -10° AS-MFS 0.941375 0.328419 0.535310 Co-Kriging 0.953788 0.324708 0.455177 HK 0.938108 0.317452 0.462085 MFNN 0.842811 0.756029 1.124043 0° AS-MFS 0.989935 0.146836 0.245788 Co-Kriging 0.996639 0.068603 0.109666 HK 0.993100 0.104178 0.183757 MFNN 0.985395 0.117386 0.326321 10° AS-MFS 0.988510 0.097516 0.179175 Co-Kriging 0.995607 0.060434 0.101578 HK 0.994743 0.066439 0.101578 MFNN 0.970473 0.175599 0.318173 ![]()
图 13 不同变可信度模型对俯仰力矩系数建模内插结果对比Fig. 13 Comparison of predicted pitching moment coefficients via different VFMs![]()
图 14 不同变可信度模型在马赫数为3.5时俯仰力矩系数预测结果的交叉验证对比Fig. 14 Comparison of cross validation for predicted pitching moment coefficients via different VFMs at Mach 3.5图15为4种变可信度模型的外插预测结果对比，其中单独截取了马赫数为5和7下的俯仰力矩系数随攻角变化结果进行展示。从图中可以看到，AS-MFS模型和MFNN模型的外插曲面最光滑，相比之下，Co-Kriging模型和HK模型外插曲面的光滑程度略微下降，存在少量凹坑。在马赫数为5的状态下，AS-MFS模型预测的0°和–10° 舵偏角下的俯仰力矩系数曲线在攻角14°附近有部分重叠，HK模型的俯仰力矩系数曲线在2个舵偏角下则存在交叉现象。Co-Kriging模型和MFNN模型不同舵偏角下的俯仰力矩系数曲线均无交叉现象。在马赫数为7的状态下，HK模型预测的2个舵偏角下的俯仰力矩系数曲线仍然交叉，而其余3种模型的预测结果较好，符合基本物理规律。需要注意的是，在0°攻角、0°舵偏角状态下，俯仰力矩系数理论上过零点，但AS-MFS模型和Co-Kriging模型预测值在马赫数为5和7状态下整组预测曲线均向下略微偏移，俯仰力矩系数未能过零点；而HK模型和MFNN模型预测值在该状态时经过了零点，符合客观物理规律。考虑到HK模型预测结果存在交叉现象，因此可以认为MFNN模型在俯仰力矩系数外插时的预测效果更好。
![]()
图 15 不同变可信度模型对俯仰力矩系数建模外插结果对比Fig. 15 Comparison of predicted pitching moment coefficients via different VFMs综上所述，Co-Kriging模型对栅格舵俯仰力矩系数的内插有着较为良好的表现，而采用MFNN模型可以在外插区域得到相对更加光滑、合理的预测结果。
3 结 论
本文将机器学习数据融合方法应用于在役火箭一子级栅格舵落区控制项目的气动研制中，在开展部分工况风洞试验的基础上，结合少量的CFD计算结果，预测获得了设计所需的完整气动特性数据。通过对比4种变可信度融合模型对栅格舵俯仰力矩气动特性的预测结果，得出结论如下：
1）针对栅格舵气动建模等全局预测问题，选用高斯指数函数作为高斯过程回归类机器学习模型的核函数，可以获得更光滑、鲁棒性更好的预测结果；合理的超参数优化范围可以进一步提高模型的预测精度。
2）对于栅格舵俯仰力矩系数的内插，Co-Kriging模型可以获得相对较好的预测结果，模型的泛化能力更强。
3）HK模型在俯仰力矩系数内插时表现出较强的预测能力，但在外插时效果不理想，不同舵偏角下存在不合理的交叉现象。
4）采用MFNN模型在高马赫数下对俯仰力矩系数外插时可以获得更为光滑、合理的预测结果，但在内插时的预测误差较大。
5）总体而言，内插的预测可信度更高，外插的风险较大，还需要开展更多的研究工作。
后续将继续探索变可信度模型与气动特性建模的深度融合，考虑改进现有的模型理论与算法，建立融入人工经验或物理认知的变可信度新模型，进一步提高气动特性预测的智能化水平。同时，发展对外插结果的直接验证方法，更全面系统地评估不同机器学习融合模型的性能，为工程人员提供技术参考。
-
![]()
![]()
![]()
![]()
图 5 火箭一子级带栅格舵外形跨声速段和超声速段俯仰力矩特性
Fig. 5 Pitching moment characteristics of rocket first stage with grid fins in the transonic and supersonic regimes
![]()
图 6 栅格舵俯仰力矩系数数据集空间分布情况
Fig. 6 Pitching moment data set of rocket first stage with grid fins
![]()
图 8 不同超参数下的高斯指数函数变化（p = 2）
Fig. 8 Influence of θ on the Gauss correlation function with p = 2
![]()
图 9 不同参数p时的高斯指数函数变化（θ = 1）
Fig. 9 Influence of index p on the Gauss correlation function with θ = 1
![]()
图 10 基于不同相关函数的HK模型对俯仰力矩系数建模结果对比（超参数优化范围受限制）
Fig. 10 Comparison of predicted pitching moment coefficients via HK model based on different correlation functions （with optimization boundaries for hyperparameters）
![]()
图 11 基于不同相关函数的HK模型对俯仰力矩系数建模结果对比（超参数优化范围不作限制）
Fig. 11 Comparison of predicted pitching moment coefficients via HK model based on different correlation functions （with no optimization boundaries for hyperparameters）
![]()
图 12 采用两种相关函数的不同变可信度模型对俯仰力矩系数建模的结果对比
Fig. 12 Comparison of predicted pitching moment coefficients via different variable-fidelity model based on the two correlation functions
![]()
图 13 不同变可信度模型对俯仰力矩系数建模内插结果对比
Fig. 13 Comparison of predicted pitching moment coefficients via different VFMs
![]()
图 14 不同变可信度模型在马赫数为3.5时俯仰力矩系数预测结果的交叉验证对比
Fig. 14 Comparison of cross validation for predicted pitching moment coefficients via different VFMs at Mach 3.5
![]()
图 15 不同变可信度模型对俯仰力矩系数建模外插结果对比
Fig. 15 Comparison of predicted pitching moment coefficients via different VFMs
表 1 俯仰特性风洞试验情况[2]
Table 1 Fundamental state for wind tunnel experiment on pitching moment characteristics[2]
马赫数 0.4 0.8 0.9 1 1.15 2 2.5 3 3.5 4 5 6 7 车次数 7 7 7 2 7 7 2 2 7 1 0 0 0 
下载: 导出CSV
表 2 不同舵偏角下样本分布情况
Table 2 Data sets for different elevator deflections of grid fins
舵偏角 –20° –10° 0° 10° 总计 训练集样本个数 85 55 85 55 280 测试集样本个数 5 5 15 5 30
下载: 导出CSV
表 3 针对俯仰力矩系数建模不同模型精度指标对比
Table 3 Comparison of different accuracy indicators for pitching moment coefficients via different VFMs
舵偏角 模 型 r2 RRMSE RMAE -20° AS-MFS 0.997148 0.050151 0.080148 Co-Kriging 0.999482 0.024037 0.035985 HK 0.998572 0.040432 0.073526 MFNN 0.949331 0.433717 0.722283 -10° AS-MFS 0.941375 0.328419 0.535310 Co-Kriging 0.953788 0.324708 0.455177 HK 0.938108 0.317452 0.462085 MFNN 0.842811 0.756029 1.124043 0° AS-MFS 0.989935 0.146836 0.245788 Co-Kriging 0.996639 0.068603 0.109666 HK 0.993100 0.104178 0.183757 MFNN 0.985395 0.117386 0.326321 10° AS-MFS 0.988510 0.097516 0.179175 Co-Kriging 0.995607 0.060434 0.101578 HK 0.994743 0.066439 0.101578 MFNN 0.970473 0.175599 0.318173
下载: 导出CSV
-
[1] 杜涛,陈闽慷,李凰立,等. 变精度模型(VCM)的自适应预处理方法研究[J]. 空气动力学学报,2018,36(2):315-319. DOI: 10.7638/kqdlxxb-2016.0040 DU T,CHEN M K,LI H L,et al. Research on adaptive preconditioning method for variable complexity model[J]. Acta Aerodynamica Sinica,2018,36(2):315-319. doi: 10.7638/kqdlxxb-2016.0040
[2] 杜涛,许晨舟,王国辉,等. 人工智能气动特性预测技术在火箭子级落区控制项目的应用[J]. 宇航学报,2021,42(1):61-73. DOI: 10.3873/j.issn.1000-1328.2021.01.007 DU T,XU C Z,WANG G H,et al. The application of aerodynamic coefficients prediction technique via artificial intelligence method to rocket first stage landing area control project[J]. Journal of Astronautics,2021,42(1):61-73. doi: 10.3873/j.issn.1000-1328.2021.01.007
[3] 张天姣,钱炜祺,周宇,等. 人工智能与空气动力学结合的初步思考[J]. 航空工程进展,2019,10(1):1-11. ZHANG T J,QIAN W Q,ZHOU Y,et al. Preliminary thoughts on the combination of artificial intelligence and aerodynamics[J]. Advances in Aeronautical Science and Engineering,2019,10(1):1-11.
[4] 唐志共,王文正,陈功,等. 气动模型在现代气动试验设计中的应用研究[J]. 空气动力学学报,2017,35(2):172-176. DOI: 10.7638/kqdlxxb—2015.0190 TANG Z G,WANG W Z,CHEN G,et al. Research on the application of aerodynamic models in modern design of aerodynamic experiments[J]. Acta Aerodynamica Sinica,2017,35(2):172-176. doi: 10.7638/kqdlxxb—2015.0190
[5] SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD vision 2030 study: A path to revolutionary computational aerosciences[R]. NASA/CR-2014-218178, 2014.
[6] 韩忠华,许晨舟,乔建领,等. 基于代理模型的高效全局气动优化设计方法研究进展[J]. 航空学报,2020,41(5):25-65. HAN Z H,XU C Z,QIAO J L,et al. Recent progress of efficient global aerodynamic shape optimization using surrogate-based approach[J]. Acta Aeronautica et Astronautica Sinica,2020,41(5):25-65.
[7] 韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报,2016,37(11):3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization: a review of recent progress[J]. Acta Aeronautica et Astronautica Sinica,2016,37(11):3197-3225.
[8] 周奇,杨扬,宋学官,等. 变可信度近似模型及其在复杂装备优化设计中的应用研究进展[J]. 机械工程学报,2020,56(24):219-245. DOI: 10.3901/JME.2020.24.219 ZHOU Q,YANG Y,SONG X G,et al. Survey of multi-fidelity surrogate models and their applications in the design and optimization of engineering equipment[J]. Journal of Mechanical Engineering,2020,56(24):219-245. doi: 10.3901/JME.2020.24.219
[9] 何开锋,钱炜祺,汪清,等. 数据融合技术在空气动力学研究中的应用[J]. 空气动力学学报,2014,32(6):777-782. DOI: 10.7638/kqdlxxb—2014.0072 HE K F,QIAN W Q,WANG Q,et al. Application of data fusion technique in aerodynamics studies[J]. Acta Aerodynamica Sinica,2014,32(6):777-782. doi: 10.7638/kqdlxxb—2014.0072
[10] HAFTKA R T. Combining global and local approximations[J]. AIAA Journal,1991,29(9):1523-1525. doi: 10.2514/3.10768
[11] CHANG K J,HAFTKA R T,GILES G L,et al. Sensitivity-based scaling for approximating structural response[J]. Journal of Aircraft,1993,30(2):283-288. doi: 10.2514/3.48278
[12] ALEXANDROV N M,DENNIS J E,LEWIS R M,et al. A trust-region framework for managing the use of approximation models in optimization[J]. Structural Optimization,1998,15(1):16-23. doi: 10.1007/BF01197433
[13] ALEXANDROV N, NIELSEN E, LEWIS R, et al. First-order model management with variable-fidelity physics applied to multi-element airfoil optimization[C]//Proc of the 8th Symposium on Multidisciplinary Analysis and Optimization. 2000. doi: 10.2514/6.2000-4886
[14] SHU L S,JIANG P,SONG X G,et al. Novel approach for selecting low-fidelity scale factor in multifidelity metamodeling[J]. AIAA Journal,2019,57(12):5320-5330. doi: 10.2514/1.j057989
[15] PARK C,HAFTKA R T,KIM N H. Low-fidelity scale factor improves Bayesian multi-fidelity prediction by reducing bumpiness of discrepancy function[J]. Structural and Multidisciplinary Optimization,2018,58(2):399-414. doi: 10.1007/s00158-018-2031-2
[16] WANG S,LIU Y,ZHOU Q,et al. A multi-fidelity surrogate model based on moving least squares: fusing different fidelity data for engineering design[J]. Structural and Multidisciplinary Optimization,2021,64(6):3637-3652. doi: 10.1007/s00158-021-03044-5
[17] HAN Z H,GÖRTZ S,ZIMMERMANN R. Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function[J]. Aerospace Science and Technology,2013,25(1):177-189. doi: 10.1016/j.ast.2012.01.006
[18] BANDLER J W,BIERNACKI R M,CHEN S H,et al. Space mapping technique for electromagnetic optimization[J]. IEEE Transactions on Microwave Theory and Techniques,1994,42(12):2536-2544. doi: 10.1109/22.339794
[19] ROBINSON T D,ELDRED M S,WILLCOX K E,et al. Surrogate-based optimization using multifidelity models with variable parameterization and corrected space mapping[J]. AIAA Journal,2008,46(11):2814-2822. doi: 10.2514/1.36043
[20] JONSSON E, LEIFSSON L, KOZIEL S. Aerodynamic optimization of wings by space mapping[C]//Proc of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. 2013. doi: 10.2514/6.2013-780
[21] 何磊,钱炜祺,汪清,等. 机器学习方法在气动特性建模中的应用[J]. 空气动力学学报,2019,37(3):470-479. DOI: 10.7638/kqdlxxb—2019.0033 HE L,QIAN W Q,WANG Q,et al. Applications of machine learning for aerodynamic characteristics modeling[J]. Acta Aerodynamica Sinica,2019,37(3):470-479. doi: 10.7638/kqdlxxb—2019.0033
[22] KENNEDY M,O'HAGAN A. Predicting the output from a complex computer code when fast approximations are available[J]. Biometrika,2000,87(1):1-13. doi: 10.1093/biomet/87.1.1
[23] QIAN P Z G,WU C F J. Bayesian hierarchical modeling for integrating low-accuracy and high-accuracy experiments[J]. Technometrics,2008,50(2):192-204. doi: 10.1198/004017008000000082
[24] LE GRATIET L,GARNIER J. Recursive co-kriging model for design of computer experiments with multiple levels of fidelity[J]. International Journal for Uncertainty Quantification,2014,4(5):365-386. doi: 10.1615/int.j.uncertaintyquantification.2014006914
[25] XIAO M Y,ZHANG G H,BREITKOPF P,et al. Extended Co-Kriging interpolation method based on multi-fidelity data[J]. Applied Mathematics and Computation,2018,323:120-131. doi: 10.1016/j.amc.2017.10.055
[26] ZAYTSEV A. Reliable surrogate modeling of engineering data with more than two levels of fidelity[C]//Proc of the 2016 7th International Conference on Mechanical and Aerospace Engineering （ICMAE）. 2016: 341-345. doi: 10.1109/ICMAE.2016.7549563
[27] ZHOU Q,WU Y D,GUO Z D,et al. A generalized hierarchical co-Kriging model for multi-fidelity data fusion[J]. Structural and Multidisciplinary Optimization,2020,62(4):1885-1904. doi: 10.1007/s00158-020-02583-7
[28] HAN Z H,GÖRTZ S. Alternative cokriging method for variable-fidelity surrogate modeling[J]. AIAA Journal,2012,50(5):1205-1210. doi: 10.2514/1.J051243
[29] ZIMMERMANN R, HAN Z H. Simplified cross-correlation estimation for multifidelity surrogate cokriging models[J]. Advances and Applications in Mathematical Sciences, 2010.
[30] HAN Z H,GÖRTZ S. Hierarchical kriging model for variable-fidelity surrogate modeling[J]. AIAA Journal,2012,50(9):1885-1896. doi: 10.2514/1.J051354
[31] MENG X H,KARNIADAKIS G E. A composite neural network that learns from multi-fidelity data: application to function approximation and inverse PDE problems[J]. Journal of Computational Physics,2020,401:109020. doi: 10.1016/j.jcp.2019.109020
[32] MENG X H,BABAEE H,KARNIADAKIS G E. Multi-fidelity Bayesian neural networks: Algorithms and applications[J]. Journal of Computational Physics,2021,438:110361. doi: 10.1016/j.jcp.2021.110361
[33] HE L,QIAN W Q,ZHAO T,et al. Multi-fidelity aerodynamic data fusion with a deep neural network modeling method[J]. Entropy (Basel, Switzerland),2020,22(9):1022. doi: 10.3390/e22091022
[34] ZHANG X S,XIE F F,JI T W,et al. Multi-fidelity deep neural network surrogate model for aerodynamic shape optimization[J]. Computer Methods in Applied Mechanics and Engineering,2021,373:113485. doi: 10.1016/j.cma.2020.113485
[35] SATRIA P P,RIZKI Z L,SHIMOYAMA K. Gaussian process surrogate model with composite kernel learning for engineering design[J]. AIAA Journal,2020,58(4):1864-1880. doi: 10.2514/1.J058807
-
期刊类型引用(4)
1. 宁晨伽，吴继飞，李国帅，张伟伟. 面向民机标模的宽域高雷诺数小样本气动建模方法研究. 空气动力学学报. 2024(08): 60-76+34 . 
百度学术
2. 刘汉宇，张耘隆，张津泽，胡彦辰，袁赫. 基于风洞试验数据和仿真融合修正的气动特性预示技术. 导弹与航天运载技术(中英文). 2023(02): 97-101+136 . 百度学术
3. 杜涛，牟宇，杨建民，李君，胡彦辰. CZ-2C子级落区栅格舵的气动设计实践及发展展望. 导弹与航天运载技术(中英文). 2023(03): 20-26 . 百度学术
4. 包为民. 可重复使用运载火箭技术发展综述. 航空学报. 2023(23): 8-33+3 . 百度学术
其他类型引用(3)
计量
- 文章访问数: 1660
- HTML全文浏览量: 478
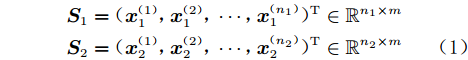
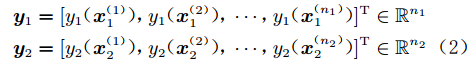
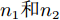
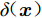
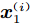
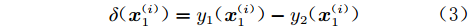
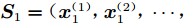
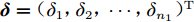
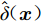
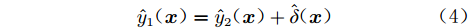
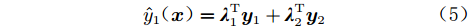
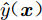
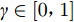
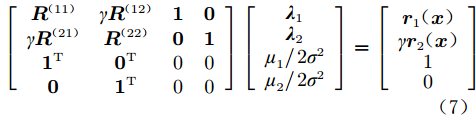
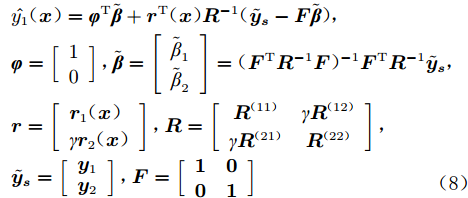
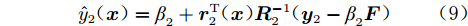
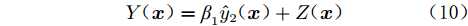
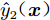
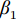
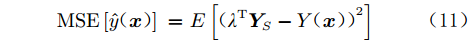
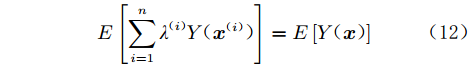
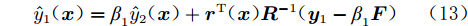
- PDF下载量: 109
- 被引次数: 7
