0   引　言

动导数即动态稳定性导数，是气动力和力矩关于角速度的导数，是飞行器气动性能设计、控制系统和总体设计中必不可少的气动参数^[1]。

从20世纪60年代开始，国内外空气动力研究机构就开展了动导数风洞试验技术研究，基于不同尺寸、不同速域的风洞研制了不同形式的动导数试验设备^[2-13]。美国在低速动导数测量技术（天平系统、模型和支撑系统设计、数据采集和处理等）方面发展较早，成熟度较高，试验模型尺寸大（可达3 m量级），始终处于国际领先水平^[14-16]。

我国常用的低速动导数试验系统大多基于3 m量级风洞建立，模型机翼展长及机身长度均小于1.5 m，在保证斯特劳哈尔数与真机一致的前提下，动导数试验的风速（一般为30 m/s左右）低于常规测力试验的风速^[17]。同时，动导数试验系统需要进行模型强迫振荡运动驱动及运动的传递，试验机构不同于常规测力试验机构，模型姿态角依靠转盘角和振荡机构耦合调节，一般存在机构复杂等问题。

为更好地发挥4 m量级低速风洞的试验能力，本文针对大型飞行器研制对高精度动导数数据的获取需求，开展增大试验模型尺寸、提高试验风速、优化设计振荡运动机构与模型姿态角机构等动导数试验技术研究，在FL–51风洞建立了2.5 m量级模型的强迫振荡动导数试验系统，具备俯仰、偏航、滚转、升沉及侧移等5种振荡模态，试验能力全面，可以获取飞机气动性能分析所需的主要动导数。针对试验模型尺寸及试验风速增大带来的负载增大问题，试验系统采用液压摆动马达和液压缸直接输出谐波运动并驱动运动部件和试验模型，设计了独立的迎角和侧滑角机构，具有驱动设备结构紧凑、驱动能力强、运动传递间隙小、运动控制精度高等特点，适于进行尺寸2.0～2.5 m模型的低速动导数试验。角振荡试验系统的结构形式与常规测力试验系统相近，兼顾进行常规测力试验的能力，可提高动导数试验数据与静态气动力试验数据之间的相关性。

1   试验系统

1.1   风洞

FL–51风洞是一座单回路低速风洞，具有开口和闭口试验段，试验段截面为矩形。动导数试验系统是基于开口试验段研发的，开口试验段的截面尺寸为4.5 m（宽） × 3.5 m（高），长度为6.5 m。空风洞最大风速为85 m/s。

1.2   角振荡动导数试验装置

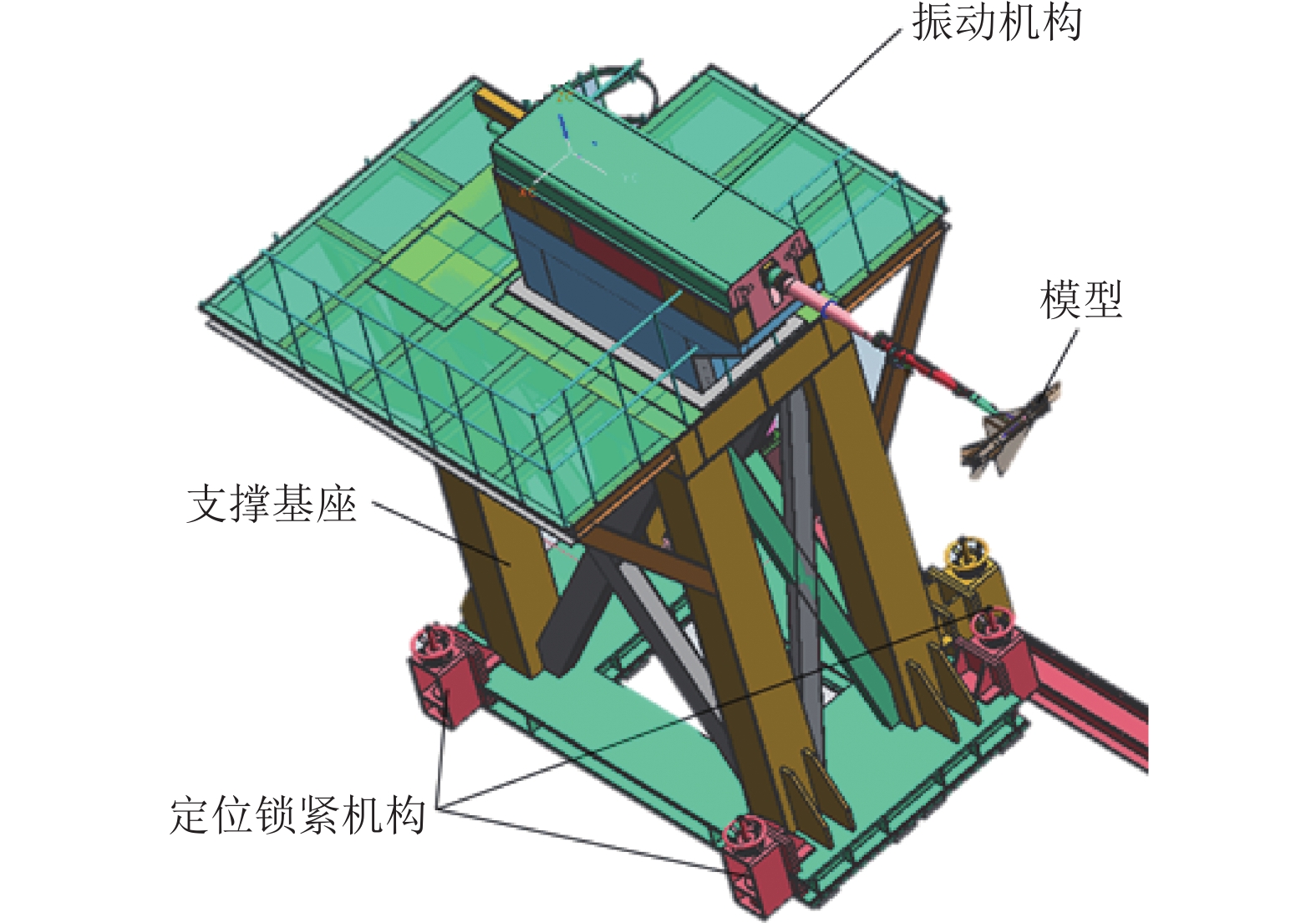
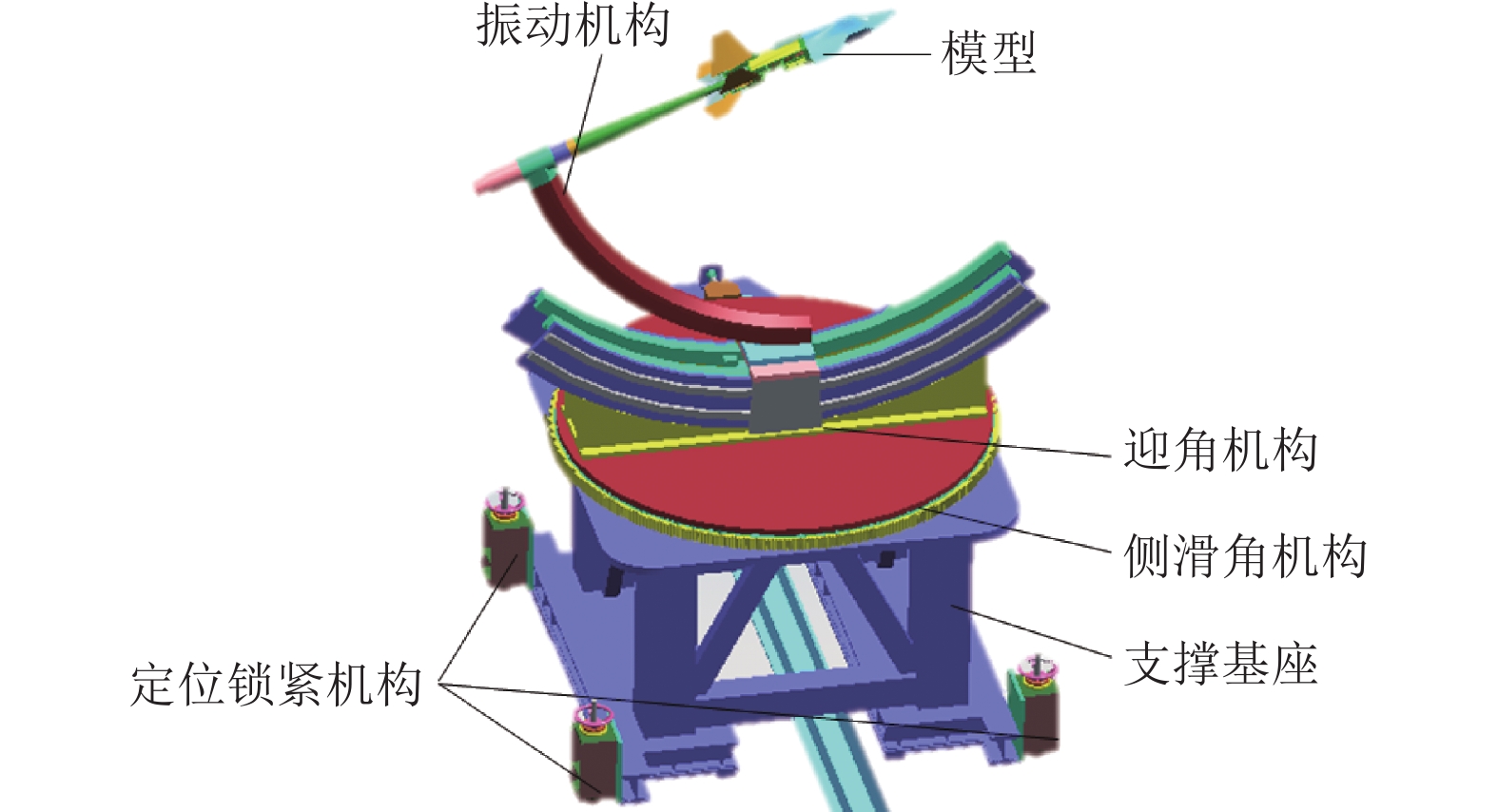
角振荡动导数试验装置如图1所示。装置整体质量为32 t，具有独立的支撑基座，可采用“气浮+牵引车”的方式在地面移动。支撑基座四角设有定位和锁紧机构，可将试验装置定位并锁紧于地面。装置具有独立解耦的迎角和侧滑角机构，避免了传统动导数试验系统中模型姿态角由转盘角和振荡机构耦合调节的问题，提高了系统结构的对称性，更适用于大尺寸模型动导数试验。

图  1  角振荡动导数试验装置示意图

Fig.  1  Angular oscillation dynamic derivatives test device

下载: 全尺寸图片 幻灯片

侧滑角机构安装于支撑基座上平面，采用“直径3 m的外齿式回转轴承+电机减速器”的结构形式，该形式结构简单、运行平稳、控制精度高。侧滑角β的范围为−40°～40°。迎角机构安装于侧滑角机构的回转轴承上，采用“弧形导轨+滑块+电机减速器”的结构形式。为保证系统的刚度和强度，迎角机构采用并列双导轨形式，导轨回转半径3 m，回转中心位于试验段中心水平面内，距地面高度5.5 m。迎角机构采用伺服电机驱动齿轮转动，带动2个滑块在弧形导轨上移动，实现模型迎角α在−36°～36°范围内变化。

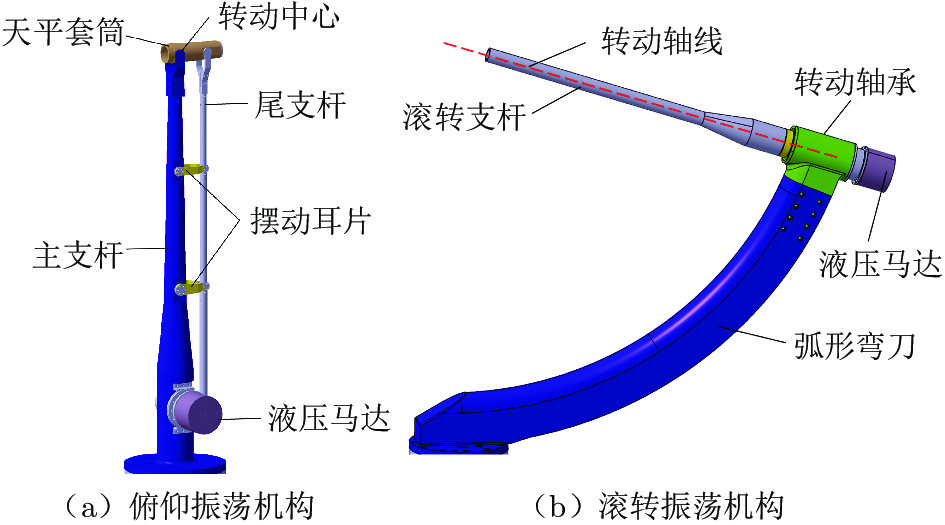
角振荡机构包括俯仰、偏航、滚转等3个相互独立的机构，可分别安装于迎角机构上，安装接口统一。对模型振荡运动过程中的惯性载荷、气动载荷进行总体估算，驱动扭矩需在2000 N·m左右。经过对液压马达和伺服电机、减速器进行调研，发现液压马达在整体结构尺寸、安装便捷程度上优于“伺服电机+减速器”，可直接安装于主支杆和弧形弯刀末端，且不会对流场带来较大干扰。如图2所示，本文角振荡机构采用液压摆动马达直接驱动，产生谐波振荡运动，偏航振荡机构、滚转振荡机构的马达出轴通过张紧套直接与偏航支杆和滚转支杆紧固连接，产生绕振荡轴线的角运动，俯仰振荡机构的马达出轴通过张紧套与摆动耳片紧固连接，摆动耳片带动尾支杆产生上下运动，尾支杆的顶端推拉天平套筒的尾端产生绕转动中心的角运动。角振荡机构振幅A = 1°～10°，频率f = 0.5 ～2.5 Hz。

图  2  角振荡机构示意图

Fig.  2  Schematic of angular oscillation mechanism

下载: 全尺寸图片 幻灯片

角振荡运动驱动及传递形式的特点如下^[18-19]：

1）运动传递环节少。传统动导数试验机构通常采用伺服电机作为驱动动力源，由于电机的输出扭矩不足，往往需要采用减速器、齿轮齿条、凸轮机构等机械部件将电机的连续转动转化为谐波振荡并传递至模型端。本文采用液压摆动马达作为驱动动力源，其输出扭矩在3000 N·m以上，满足对振荡装置、模型强迫振荡运动的驱动需求；而且液压摆动马达可直接输出任意连续波形的运动，无需减速器、齿轮齿条、凸轮机构等部件，大大减少了运动传递环节，振荡机构更加简洁，对模型附近流场干扰小，更适合在气动力试验中使用。

2）运动传递间隙小。取消了减速器、齿轮齿条、凸轮机构等部件，极大地改善了振荡机构运动传递环节中的间隙，有利于提高系统刚性和运动控制精度，进而有助于提升动导数试验数据的质量。

3）电磁干扰小。采用液压驱动的形式，在天平及信号线缆附近没有伺服电机带来的电磁干扰，有利于提升信号采集及信号传输的质量。

对角振荡动导数试验装置进行了动力学特性模态分析，表1给出了前6阶模态分析结果，各阶模态频率均在16 Hz以上，表明角振荡试验装置的前6阶模态固有频率均避开了角振荡运动频率。同时，在保证试验天平及模型刚度的前提下，可以尽量减小质量，以减小对试验系统整体动力学特性的影响，避免设备发生共振问题。

表  1  角振荡动导数试验装置模态分析结果

Table  1  Modal analysis results of angular oscillation test device

模态阶数	频率/Hz
1	16.06
2	19.35
3	34.29
4	37.62
5	46.83
6	48.91

下载: 导出CSV 

| 显示表格

1.3   平移振荡动导数试验装置

平移振荡动导数试验装置如图3所示。装置整体质量22 t，具有独立支撑基座，可采用“气浮+牵引车”方式在地面移动。支撑基座四角设有定位和锁紧机构，可将试验装置定位及锁紧于地面。

图  3  平移振荡动导数试验装置示意图

Fig.  3  Schematic of translational oscillation dynamic derivatives test device

下载: 全尺寸图片 幻灯片

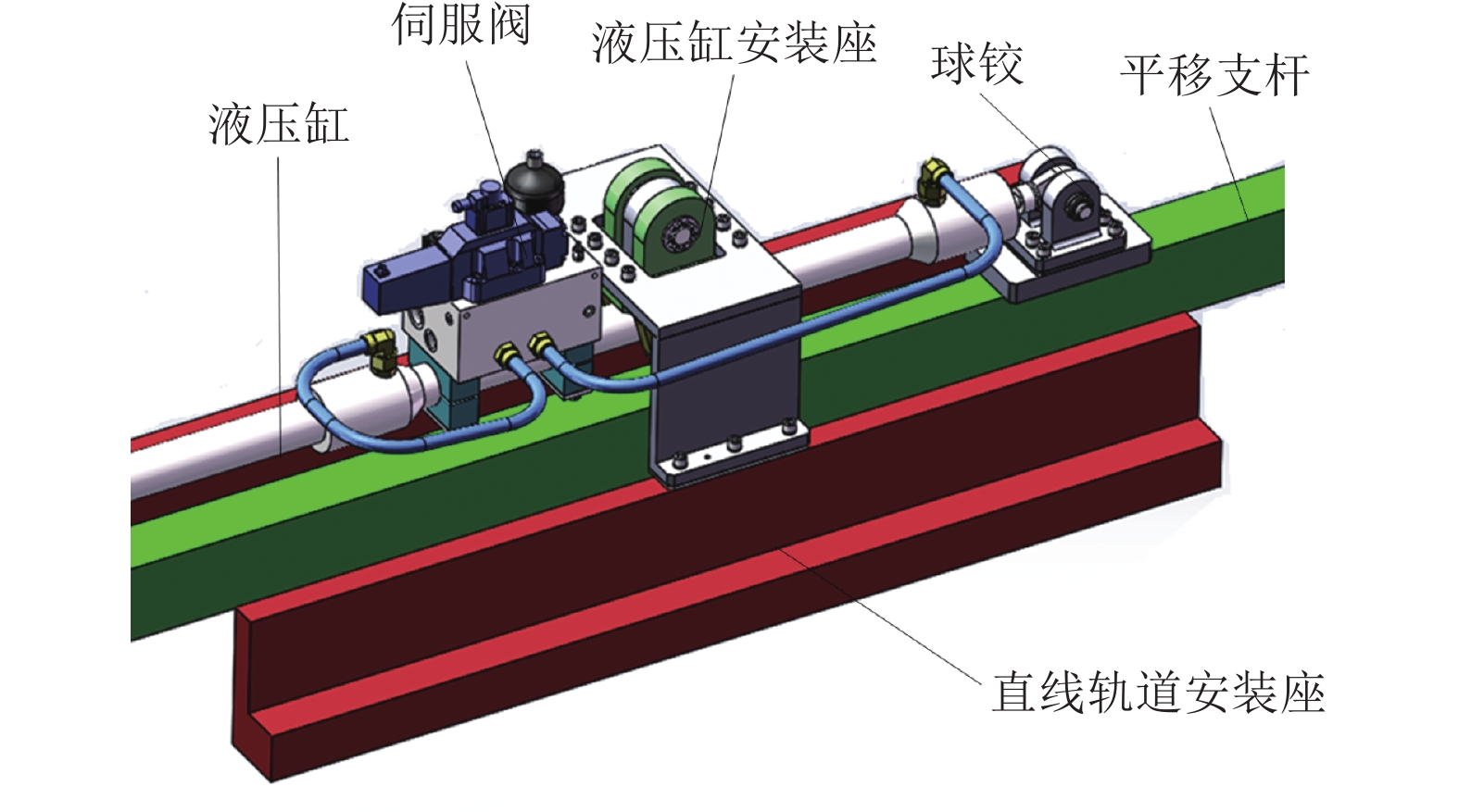
平移振荡机构安装于支撑基座上，由伺服液压缸、直线轨道、轨道安装座、平移运动支杆等组成，如图4所示。液压缸可产生任意连续波形的运动，其外缸通过特制的、具有一定角自由度的安装座固定于支撑基座上，内缸则通过球铰与平移支杆连接，带动平移支杆沿直线轨道进行平移运动。模型正装时为侧移振荡模态，模型侧装时为升沉振荡模态。平移振荡机构的驱动及运动传递形式与角振荡机构类似，也同样具有运动传递环节少、运动传递间隙小、电磁干扰小等特点。平移振荡机构振幅A = 0.06～0.35 m，频率f = 0.5～2.5 Hz。

图  4  平移振荡机构示意图

Fig.  4  Schematic of translational oscillation mechanism

下载: 全尺寸图片 幻灯片

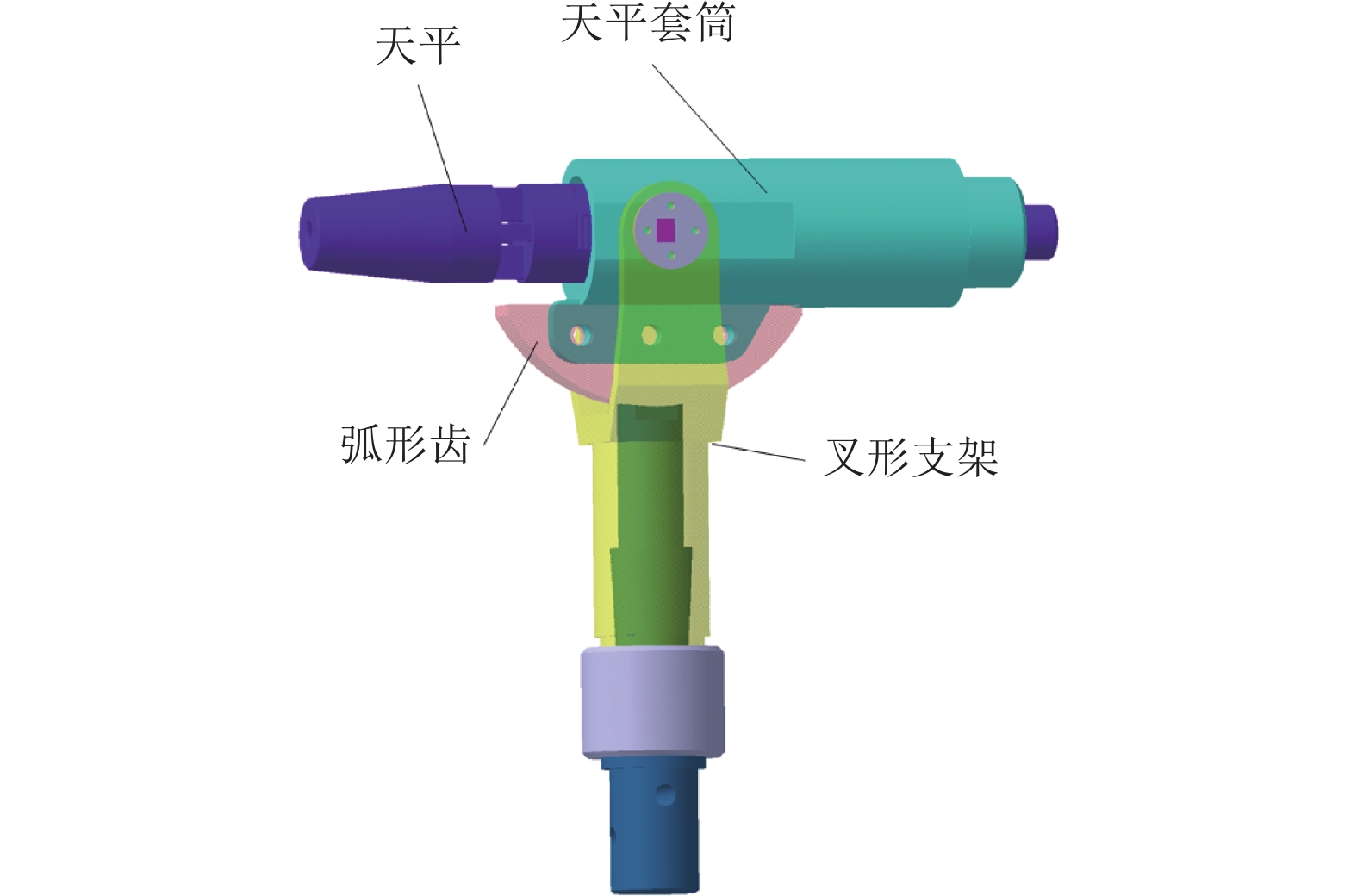
平移振荡动导数试验装置的迎角机构安装于平移支杆末端。迎角机构为手动的变角度头（如图5所示），通过弧形齿带动天平套筒绕转心转动，实现迎角变化，迎角调节梯度Δα = 2°。侧滑角通过平移支杆滚转角的变化来调节，同样为手动形式。平移振荡动导数试验装置的迎角范围α = −36°～36°，侧滑角范围β = −40°～40°。

图  5  平移振荡变角度头示意图

Fig.  5  Schematic of translational oscillation variable angle rig

下载: 全尺寸图片 幻灯片

对平移振荡试验装置进行了动力学特性模态分析，表2给出了前6阶模态分析结果，各阶模态频率均在23 Hz以上，表明平移振荡试验装置的前6阶模态固有频率均避开了平移振荡运动频率。

表  2  平移振荡试验装置模态分析结果

Table  2  Modal analysis results of translational oscillation test device

模态阶数	频率/Hz
1	23.16
2	32.82
3	35.36
4	98.11
5	99.55
6	117.61

下载: 导出CSV 

| 显示表格

1.4   控制、采集系统

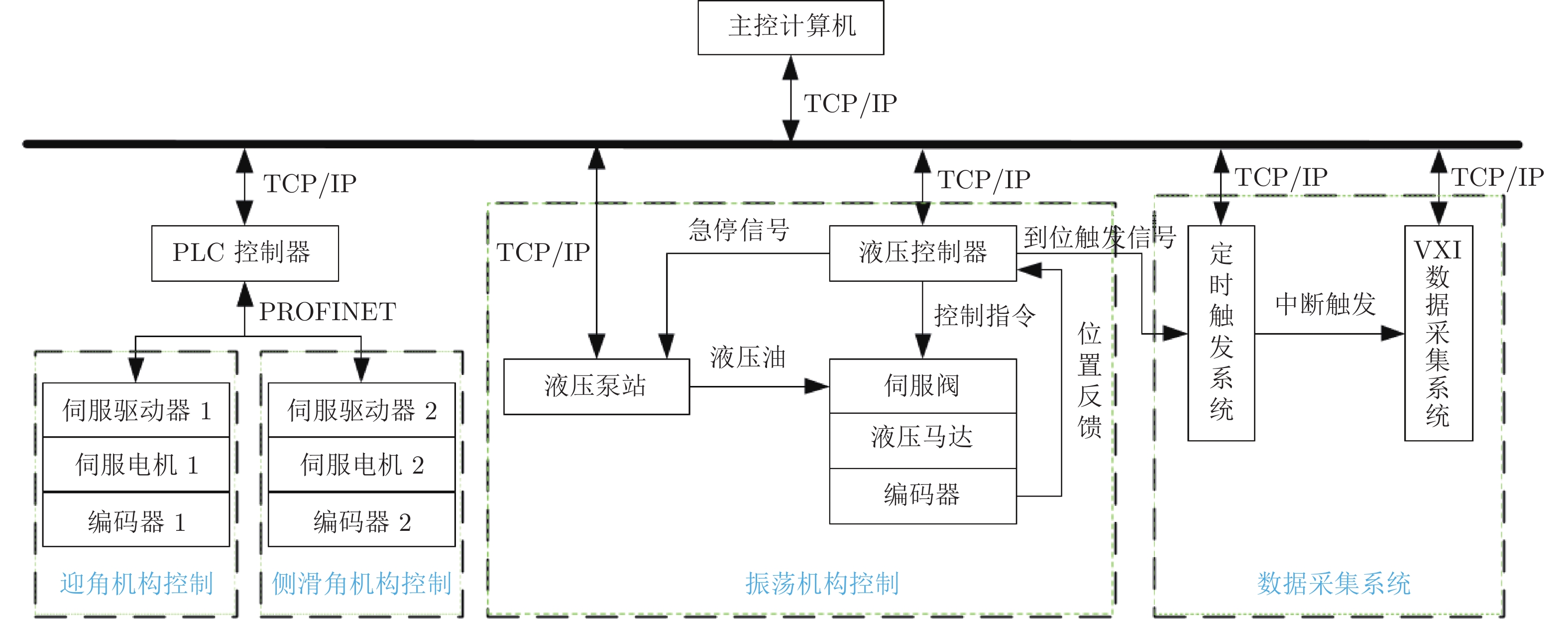
角振荡系统的控制、采集系统原理如图6所示。控制系统主要实现3种模态振荡机构、迎角机构及侧滑角机构的高精度位置伺服控制功能，由主控计算机、PLC控制器、伺服驱动器、伺服电机、液压控制器、伺服阀、液压马达、编码器和液压泵站等组成。其中，迎角机构和侧滑角机构由电机伺服系统驱动，进行点对点的定位运动，实现试验模型迎角和侧滑角的改变；振荡机构由电液伺服系统驱动，进行给定运动指标的谐波振荡运动，从而驱动试验模型进行强迫运动。

图  6  控制、数据采集系统原理图

Fig.  6  Schematic of control and acquisition system

下载: 全尺寸图片 幻灯片

采集系统由定时触发系统和数据采集系统组成。其中，定时触发系统基于FPGA硬件架构开发，具有时钟周期精准、响应频率高和稳定性好等优点，数据采集系统基于VXI总线开发，采样频率高且稳定性好。

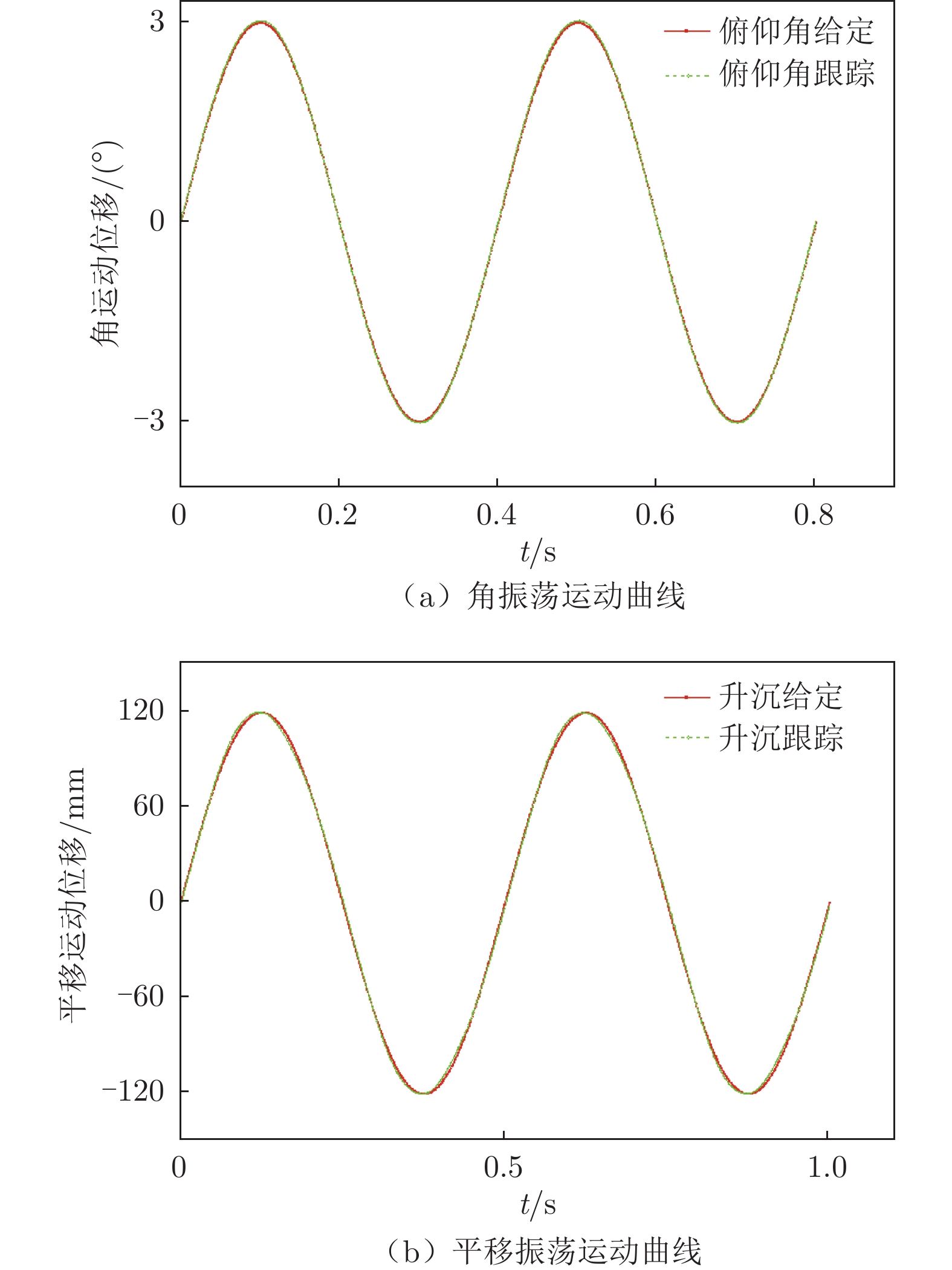
试验过程中，当振荡机构达到设定的运动指标后、第一次经过振荡平衡位置时，液压控制器向定时触发系统输出到位触发信号；定时触发系统接收信号后，根据试验频率及单周期采集点数，自动按照等时间间隔向数据采集系统发送中断触发脉冲信号，触发数据采集系统进行数据采集，试验采集点数由单周期采集点数及采集周期数确定；数据采集系统对天平数据信号和振荡机构实时位置信号进行同步采集存储。数据采集系统包括CT–400型VXI主机箱、零槽控制器、1413C采集板卡及SCP信号调理模块，具有程控滤波功能。滤波截止频率为2、10、100和1500 Hz，低速动导数试验时通常采用10 Hz滤波截止频率。

按照角振荡动导数和平移振荡动导数的运动指标，分别对2套装置（角振荡动导数试验装置、平移振荡动导数试验装置）的性能指标进行运动调试。图7给出了典型运动指标下的实际运动曲线与标准正弦曲线的对比，表3和4分别为角振荡和平移振荡运动曲线与给定标准信号之间的差异。通过分析可知，2套装置的幅频/相频特性以及动态特性均表现优秀，满足动导数试验的要求。

图  7  谐波振荡运动曲线

Fig.  7  Harmonic oscillation movement curve

下载: 全尺寸图片 幻灯片

表  3  角振荡运动曲线与给定标准信号的差异

Table  3  Differences between angular oscillation motion curve and given standard signal

振幅/(°)	频率/Hz	幅值差/(°)	相位差/(°)
3	0.5	0.015	0.13
3	1.0	0.020	0.16
3	1.5	0.025	0.16
3	2.0	0.032	0.07
3	2.5	0.040	0.05

下载: 导出CSV 

| 显示表格

表  4  平移振荡运动曲线与给定标准信号的差异

Table  4  Differences between translational oscillation motion curve and given standard signal

振幅/m	频率/Hz	幅值差/m	相位差/(°)
0.12	0.5	0.0014	1.48
0.12	1.0	0.0021	1.1
0.12	1.5	0.0028	0.70
0.12	2.0	0.0031	0.3
0.12	2.5	0.0032	0.04

下载: 导出CSV 

| 显示表格

控制、采集系统具有以下特点：

1）模型运动近端的角度编码器或直线位移传感器可直接测量模型实际振荡运动的位置信号，并参与运动的闭环控制；

2）伺服液压系统自动化程度高，运动参数可通过试验运转计划直接读取并自动调整，运动控制精准，且可产生任意连续波形运动；

3）定时触发系统能够自动获取试验参数，自动改变中断触发脉冲信号的时间间隔，且由于时钟周期精准度高，能够实现对采集系统的精准触发。

1.5   试验原理

以俯仰振荡为例，当模型作振幅为θ₀、圆频率为ω的正弦振荡时：

Δα为迎角增量，t为时间，θ、q、$ \dot q $、$ \dot \alpha $分别为俯仰角位移、俯仰角速度、俯仰角加速度、迎角角速度。

以俯仰力矩为例，建立气动力数学模型如下：

模型力矩方程如下：

式中：M_z(t)为气动力矩，${M}_{z {\text{Ⅰ}}}(t) $为惯性力矩，${M}_{z {\text{Ⅱ}}}(t) $为强迫力矩；δ为强迫力矩${M}_{z {\text{Ⅱ}}}(t) $与位移θ的相位差。无风时，M_z(t) = 0，式（5）可写为：

式中下标“w”代表无风试验。有风时，式（5）可写为：

下标“y”表示有风试验。式（8）和（7）相减，可得：

将式（4）、（6）代入式（9）得：

从式（10）可得到以下2个等式：

进行无量纲化，可得：

式中，ρ为空气密度，v为试验风速，S为模型参考面积，c_A为模型平均气动弦长，K = ωc_A/(2v)。

其他导数的推导过程类似。

2   典型验证试验与结果分析

2.1   动态标模试验

为验证试验系统数据准度，采用1 m量级动态标模进行试验验证（如图8所示）。该标模由国内多家空气动力研究单位联合设计，具有典型四代机布局及气动力特征，并基于国内多座低速风洞建立了较为完整的气动力数据体系（2016年发布标模）。

图  8  1 m量级动态标模验证试验照片

Fig.  8  Verification test of standard dynamic model

下载: 全尺寸图片 幻灯片

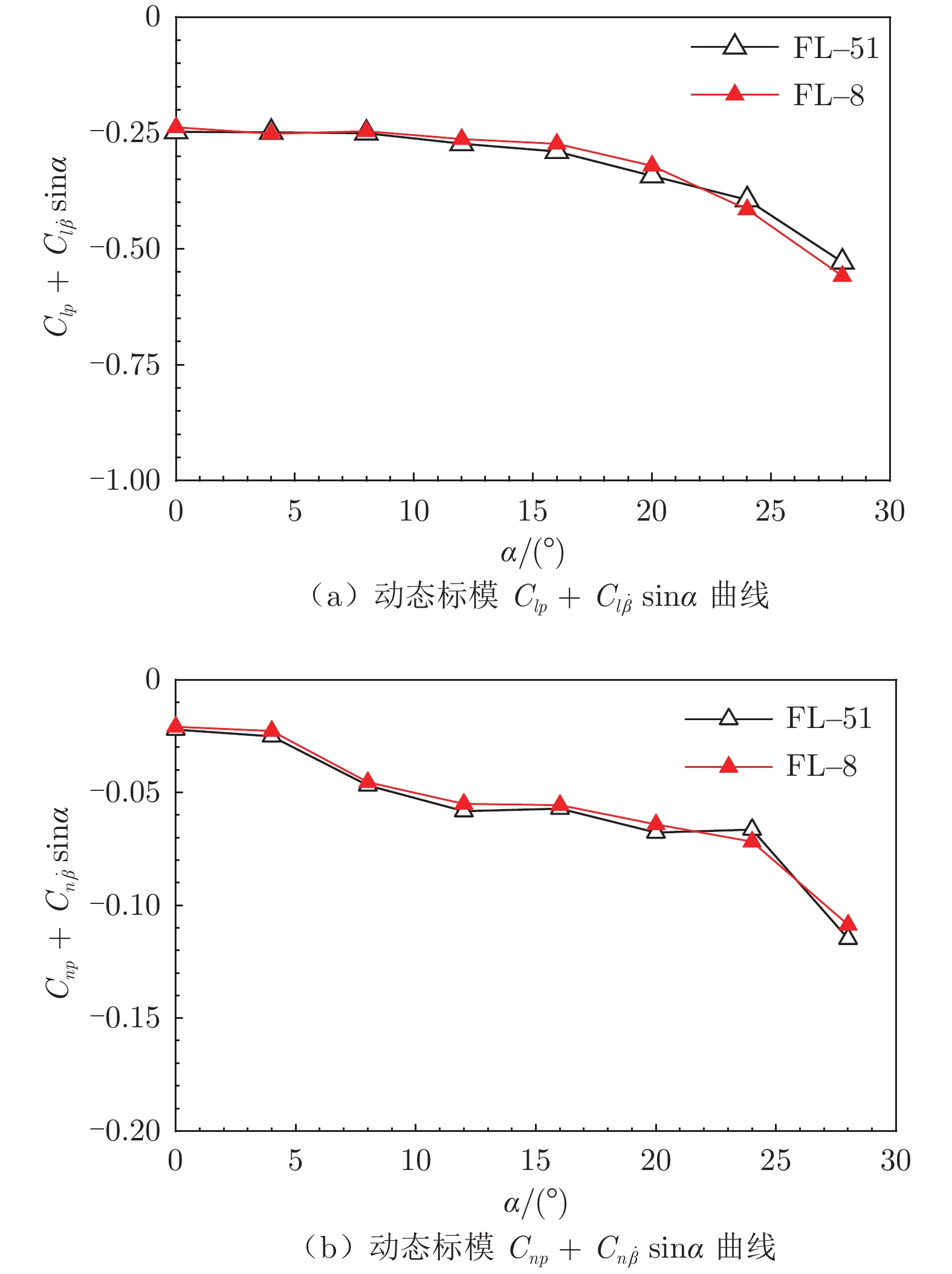
本文研究的动导数试验系统中只有滚转振荡模态具有可更换小尺寸模型的支杆，且各振荡模态的运动驱动、传递、控制和采集等环节的技术方法和设备类似或一致，因此，仅进行了滚转振荡模态下的验证试验。图9给出了滚转振荡模态下的滚转力矩复合动导数$ {C_{lp}} + {C_{l\dot \beta }}\sin \alpha $、偏航力矩复合交叉动导数$ {C_{np}} + {C_{n\dot \beta }}\sin \alpha $的重复性曲线（$ {C_l} $为滚转力矩系数，$ {C_n} $为偏航力矩系数）。基于FL–51风洞动导数试验系统得到的试验数据与标模在FL–8风洞中得到的试验数据一致性较好，表明FL–51风洞动导数试验系统的数据准度满足使用要求。

图  9  1 m量级动态标模滚转振荡试验对比曲线

Fig.  9  Comparison curve of rolling oscillation test of standard dynamic model

下载: 全尺寸图片 幻灯片

2.2   某翼身融合布局模型动导数试验

采用某翼身融合布局飞机低速动导数试验模型进行了试验，如图10所示。模型翼展为2.4 m，适合采用本文试验系统进行动导数试验，可以验证系统的试验能力以及模型尺寸、试验风速增大后的数据精度。模型采用“铝合金骨架+碳纤维蒙皮”的结构形式，由前机身、中机身、机翼、后机身、尾翼等组成，主要几何参数如表5所示。

图  10  翼身融合布局飞机动导数试验照片

Fig.  10  Dynamic derivatives test photos of wing-body model

下载: 全尺寸图片 幻灯片

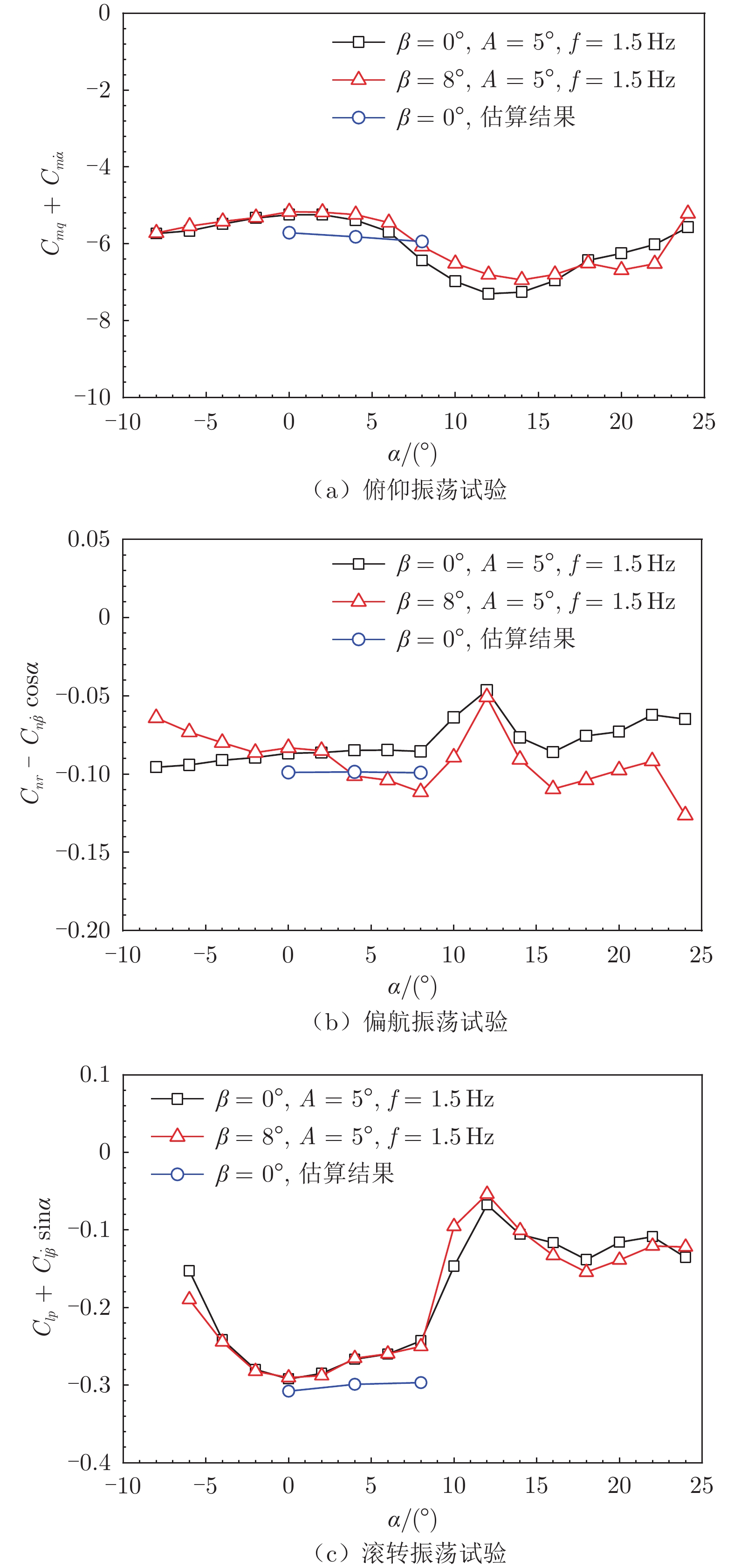
表  5  翼身融合布局飞机动导数试验模型参数

Table  5  Dynamic derivative test model parameters of wing-body

参数	值
模型比例	1∶15
参考面积S/m2	1.072
平均气动弦长cA/m	0.691
展长b/m	2.4

下载: 导出CSV 

| 显示表格

针对翼身融合布局模型进行了滚转、俯仰、偏航等3个角振荡模态的动导数试验，试验风速范围为40～55 m/s，试验雷诺数最高达到2.6 × 10⁶。图11给出了各复合动导数曲线，其中包括对各阻尼动导数的估算结果。可以看出，在小迎角范围内，各动导数基本呈现出线性规律，其量值与估算结果相近。随着迎角增大，动导数出现大幅波动，但基本保持阻尼状态。图11（b）为翼身融合布局模型的偏航力矩复合动导数随迎角变化的曲线，可以看出偏航力矩复合动导数的阻尼较小，原因主要在于该布局“V”形尾翼的夹角较大，尾翼对飞机气动力矩和稳定性的作用主要集中于纵向。

图  11  翼身融合布局飞机动导数试验曲线

Fig.  11  Dynamic derivatives test results of wing-body model

下载: 全尺寸图片 幻灯片

针对翼身融合布局模型进行了重复性试验，以各试验迎角下数据的均方根误差与算术平均值之比作为相对重复性精度，表6给出了复合动导数的相对重复性精度。可以看出，在整个试验迎角范围内，俯仰力矩复合动导数和偏航力矩复合动导数的重复性精度在3%以内，滚转力矩复合动导数重复性精度在1%以内，试验数据精度较好。

表  6  动导数重复性精度

Table  6  Dynamic derivatives repeatability accuracy

α/(°)	$ ({C}_{mq} + {C}_{m\dot{\alpha }}) $/%	$ ({C}_{lp} + {C}_{l\dot{\beta }}\mathrm{sin}\alpha ) $/%	$ ({C}_{nr}-{C}_{n\dot{\beta }}\mathrm{cos}\alpha ) $/%
0	1.0	0.2	0.4
8	0.4	0.4	0.3
16	0.4	1.0	1.0
20	1.7	0.3	2.0
24	2.9	0.1	2.8

下载: 导出CSV 

| 显示表格

试验系统有利于数据精度提高的因素如下：

1）模型尺寸约为3 m量级风洞动导数试验系统模型尺寸的2倍，试验风速约为1.5倍，模型质量得到有效控制，提高了气动载荷在总载荷中的占比；

2）强迫运动传递过程间隙小，模型运动精准度较高。

3   结　论

在4.5 m × 3.5 m低速风洞开口试验段开展了2.5 m量级模型动导数试验技术研究，得到如下结论：

1）4.5 m × 3.5 m低速风洞动导数试验系统振荡模态齐全，可实现2.5 m量级模型动导数试验。

2）试验系统迎角、侧滑角及运动机构实现了独立解耦。

3）试验系统采用液压马达和液压缸直接驱动运动部件，通过液压伺服系统的控制直接实现强迫谐波运动的产生以及振幅、频率的高精度自动控制，驱动结构紧凑、驱动能力强、运动传递间隙小。

4）本文建立的动导数试验系统，其数据重复性精度在3%以内，适合进行大型飞行器的低速动导数试验。