基于深度神经网络的流场时空重构方法

韩仁坤; 刘子扬; 钱炜祺; 王文正; 陈刚

doi:10.11729/syltlx20210124

基于深度神经网络的流场时空重构方法

韩仁坤^{1, 3,},
刘子扬¹,
钱炜祺³,
王文正³,
陈刚^{1, 2, ,}

1.
西安交通大学航天航空学院陕西省先进飞行器服役环境与控制重点实验室，西安　710049
2.
机械结构强度与振动国家重点实验室，西安　710049
3.
中国空气动力研究与发展中心，绵阳　621000

详细信息

作者简介:
韩仁坤: （1995—），男，河南商丘人，博士研究生。研究方向：非线性流固耦合系统深度学习降阶模型。通信地址：陕西省西安市咸宁西路28号西安交通大学兴庆校区航天航空学院（710049）。E-mail：hanrenkun@stu.xjtu.edu.cn

通讯作者:
陈刚: E-mail： aachengang@mail.xjtu.edu.cn

中图分类号: V211.79
计量
- 文章访问数: 1923
- HTML全文浏览量: 661
- PDF下载量: 238
出版历程
- 收稿日期: 2021-11-09
- 修回日期: 2022-01-11
- 录用日期: 2022-03-17
- 网络出版日期: 2022-07-11
- 刊出日期: 2022-07-03

Spatio-temporal reconstruction method of flow field based on deep neural network

HAN Renkun^{1, 3,},
LIU Ziyang¹,
QIAN Weiqi³,
WANG Wenzheng³,
CHEN Gang^{1, 2, ,}

1.
Shaanxi Key Laboratory of Environment and Control for Flight Vehicle, School of Aerospace Engineering, Xi’an Jiaotong University, Xi’an　710049, China
2.
State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an　710049, China
3.
China Aerodynamics Research and Development Center, Mianyang　621000, China

摘要

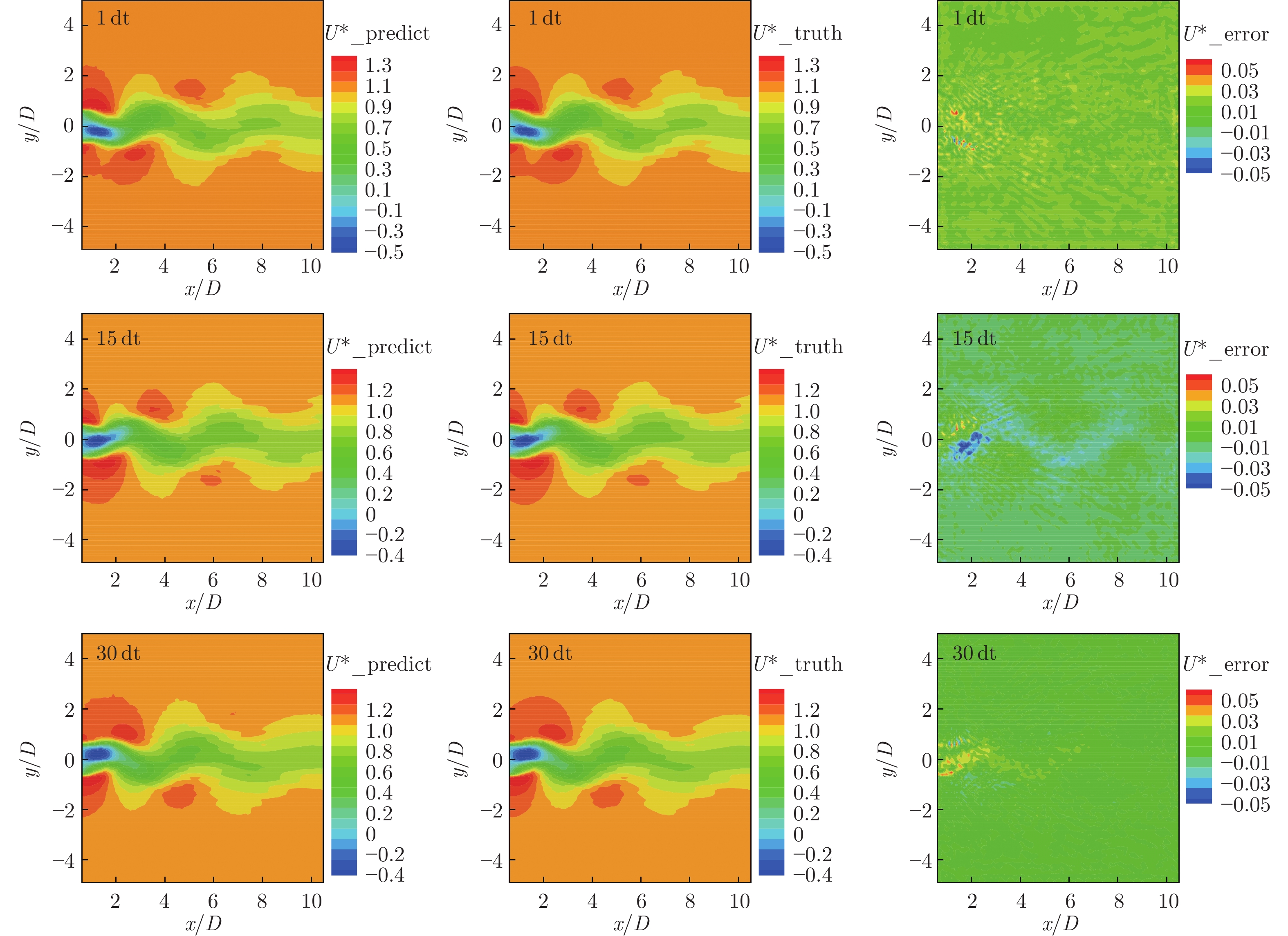
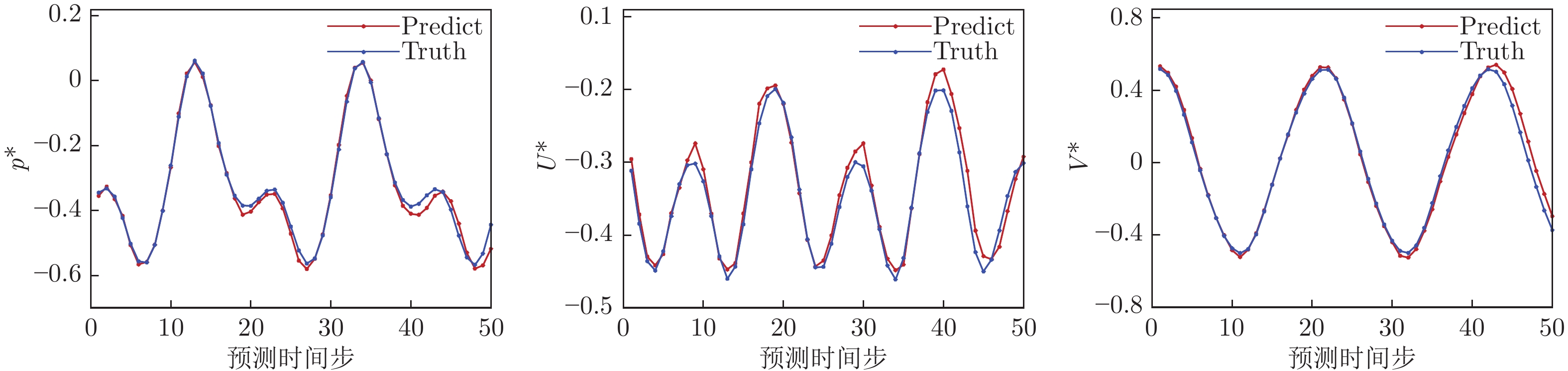
摘要: 针对流场粒子图像测速实验中时间和空间高分辨率测量代价高的问题，研究了数据驱动的流场时空重构方法。为了对实验测得的低分辨率数据进行时空高分辨率重构，提出了一种基于深度神经网络的流场时空重构方法，并构建了一种基于卷积神经网络和长短时记忆神经网络的混合深度神经网络。该混合深度神经网络能够学习流场的时空演化特征，训练完成后可实现对实验数据的时空高分辨率重构。测试结果表明：只进行流场空间高分辨率重构时，重构出的流场与真实流场之间的均方根误差为0.0065左右，流场数据点数是原来的51倍；同时进行流场时间和空间高分辨率重构时，重构出的流场与真实流场之间的均方根误差可保持在0.065左右，流场时间维度的密度是原来的5倍，可极大提高实验效率，节约实验成本。
- 深度神经网络 /
- 高分辨率 /
- 重构 /
- 时空特征
Abstract: The flow field PIV measurement method cost a lot, but the measurement results have low spatial and temporal resolution. The spatio-temporal reconstruction method of flow field based on experimental and numerical simulation data is studied. In order to realize the high-resolution spatio-temporal reconstruction of the experimentally measured low-resolution data, a flow field spatio-temporal reconstruction method based on deep neural network is proposed. A hybrid deep neural network based on convolutional neural network and long-short-term memory neural network is constructed. This hybrid deep neural network is trained to learn the spatio-temporal evolution features of the flow field. After the training is completed, it can be used to reconstruct the experimental data into spatio-temporal high-resolution results. The test results show that when the spatial high-resolution reconstruction is performed alone, the mean square error between the reconstructed flow field and the ground truth flow field is about 0.0065, and the number of data points is 51 times more than that of the input field. When the flow field is reconstructed to high resolution in time and space at the same time, the mean square error be maintained at about 0.065, and the density in the time dimension is 5 times more than that of the input field. It is proved that this method can greatly improve the efficiency of the experiment and save the cost of the experiment.
- deep neural network /
- high resolution /
- reconstruction /
- spatio-temporal features

HTML全文

图 1 空间重构深度神经网络结构示意图

Fig. 1 Structure of deep neural network for spatial reconstruction

下载: 全尺寸图片幻灯片

图 2 长短时记忆神经网络的神经元结构图

Fig. 2 Sketch of neuron structure in LSTM

下载: 全尺寸图片幻灯片

图 3 流场时空重构数据流动示意图

Fig. 3 Sketch of data flow in flow field spatio-temporal reconstruction method

下载: 全尺寸图片幻灯片

图 4 深度神经网络结构示意图

Fig. 4 Sketch of deep neural network structure

下载: 全尺寸图片幻灯片

图 5 结构化网格

Fig. 5 Structured grid

下载: 全尺寸图片幻灯片

图 6 空间高分辨率流场重构结果与数值模拟结果对比

Fig. 6 Comparison of spatial high-resolution reconstruction results and numerical simulation results

下载: 全尺寸图片幻灯片

图 7 流场重构值与真实值对比散点图

Fig. 7 Scatter of comparison between reconstructed flow field value and ground truth flow field value

下载: 全尺寸图片幻灯片

图 8 无校正时不同时间步流场重构结果与数值模拟结果对比

Fig. 8 Comparison of flow field reconstruction results without correction and numerical simulation results at different time steps

下载: 全尺寸图片幻灯片

图 9 不同校正方法持续预测结果均方根误差对比

Fig. 9 Comparison of the RMSE between different correction methods

下载: 全尺寸图片幻灯片

图 10 使用混合数据校正时不同时间步流场重构结果与数值模拟结果对比

Fig. 10 Comparison of flow field reconstruction results corrected with proportional mixing data and numerical simulation results at different time steps

下载: 全尺寸图片幻灯片

图 11 特定位置流场变量演化对比

Fig. 11 Comparison of evolution of flow field variables at specific locations

下载: 全尺寸图片幻灯片

表 1 深度神经网络结构参数

Table 1 Details of the structure parameters in the hybrid deep neural network

层名	卷积核尺寸/滑动步长	输出尺寸
Conv 1	3×3/1	3×14×14×3
Conv 2	3×3/1	3×14×14×8
Conv 3	3×3/1	3×14×14×16
Conv 4	3×3/2	3×7×7×32
Conv 5	3×3/1	3×7×7×64
Conv 6	3×3/1	3×7×7×64
LSTM	3×3/1	1×7×7×64
DeConv 1	3×3/1	1×7×7×64
DeConv 2	3×3/2	1×13×13×64
DeConv 3	3×3/1	1×13×13×32
DeConv 4	3×3/2	1×25×25×32
DeConv 5	3×3/1	1×25×25×16
DeConv 6	3×3/2	1×50×50×16
DeConv 7	3×3/1	1×50×50×8
DeConv 8	3×3/2	1×100×100×8
DeConv 9	3×3/1	1×100×100×3

下载: 导出CSV

参考文献(23)

[1]	ADRIAN R J. Multi-point optical measurements of simultaneous vectors in unsteady flow—a review[J]. International Journal of Heat and Fluid Flow,1986,7(2):127-145. doi: 10.1016/0142-727X(86)90062-7
[2]	王福君,王洪平,高琪,等. 鱼游动涡结构PIV实验研究[J]. 实验流体力学,2020,34(5):20-28. DOI: 10.11729/syltlx20200039 WANG F J,WANG H P,GAO Q,et al. PIV experimental study on fish swimming vortex structure[J]. Journal of Experiments in Fluid Mechanics,2020,34(5):20-28. doi: 10.11729/syltlx20200039
[3]	王昕. 面向非定常流场的实时自适应PIV测量技术研究[D]. 武汉: 华中科技大学, 2017. WANG X. Research of real-time adaptive PIV measurement technique oriented to unsteady flow field[D]. Wuhan: Huazhong University of Science and Technology, 2017.
[4]	LECUN Y,BENGIO Y,HINTON G. Deep learning[J]. Nature,2015,521(7553):436-444. doi: 10.1038/nature14539
[5]	KRIZHEVSKY A,SUTSKEVER I,HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM,2017,60(6):84-90. doi: 10.1145/3065386
[6]	SAINATH T N, MOHAMED A R, KINGSBURY B, et al. Deep convolutional neural networks for LVCSR[C]//Proc of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing. 2013: 8614-8618. doi: 10.1109/ICASSP.2013.6639347
[7]	XIONG H Y,ALIPANAHI B,LEE L J,et al. RNA splicing: The human splicing code reveals new insights into the genetic determinants of disease[J]. Science,2015,347(6218):1254806. doi: 10.1126/science.1254806
[8]	LING J L,KURZAWSKI A,TEMPLETON J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance[J]. Journal of Fluid Mechanics,2016,807:155-166. doi: 10.1017/jfm.2016.615
[9]	RAISSI M,YAZDANI A,KARNIADAKIS G E. Hidden fluid mechanics: learning velocity and pressure fields from flow visualizations[J]. Science,2020,367(6481):1026-1030. doi: 10.1126/science.aaw4741
[10]	叶舒然,张珍,王一伟,等. 基于卷积神经网络的深度学习流场特征识别及应用进展[J]. 航空学报,2021,42(4):524736. YE S R,ZHANG Z,WANG Y W,et al. Progress in deep convolutional neural network based flow field recognition and its applications[J]. Acta Aeronautica et Astronautica Sinica,2021,42(4):524736.
[11]	HUI X Y,BAI J Q,WANG H,et al. Fast pressure distribution prediction of airfoils using deep learning[J]. Aerospace Science and Technology,2020,105:105949. doi: 10.1016/j.ast.2020.105949
[12]	王怡星,韩仁坤,刘子扬,等. 流体力学深度学习建模技术研究进展[J]. 航空学报,2021,42(4):225-244. WANG Y X,HAN R K,LIU Z Y,et al. Progress of deep learning modeling technology for fluid mechanics[J]. Acta Aeronautica et Astronautica Sinica,2021,42(4):225-244.
[13]	SEKAR V,JIANG Q H,SHU C,et al. Fast flow field prediction over airfoils using deep learning approach[J]. Physics of Fluids,2019,31(5):057103. doi: 10.1063/1.5094943
[14]	JIN X W,CHENG P,CHEN W L,et al. Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder[J]. Physics of Fluids,2018,30(4):047105. doi: 10.1063/1.5024595
[15]	HAN R K,WANG Y X,ZHANG Y,et al. A novel spatial-temporal prediction method for unsteady wake flows based on hybrid deep neural network[J]. Physics of Fluids,2019,31(12):127101. doi: 10.1063/1.5127247
[16]	惠心雨,袁泽龙,白俊强,等. 基于深度学习的非定常周期性流动预测方法[J]. 空气动力学学报,2019,37(3):462-469. DOI: 10.7638/kqdlxxb-2019.0003 HUI X Y,YUAN Z L,BAI J Q,et al. A method of unsteady periodic flow field prediction based on the deep learning[J]. Acta Aerodynamica Sinica,2019,37(3):462-469. doi: 10.7638/kqdlxxb-2019.0003
[17]	FUKAMI K,FUKAGATA K,TAIRA K. Super-resolution reconstruction of turbulent flows with machine learning[J]. Journal of Fluid Mechanics,2019,870:106-120. doi: 10.1017/jfm.2019.238
[18]	LAGEMANN C,LAGEMANN K,MUKHERJEE S,et al. Deep recurrent optical flow learning for particle image velocimetry data[J]. Nature Machine Intelligence,2021,3(7):641-651. doi: 10.1038/s42256-021-00369-0
[19]	朱浩然,高琪,王洪平,等. 基于机器学习方法的三维粒子重构技术[J]. 实验流体力学,2021,35(3):88-93. DOI: 10.11729/syltlx20200141 ZHU H R,GAO Q,WANG H P,et al. Particle reconstruction of volumetric particle image velocimetry with strategy of machine learning[J]. Journal of Experiments in Fluid Mechanics,2021,35(3):88-93. doi: 10.11729/syltlx20200141
[20]	蔡声泽,许超,高琪,等. 基于深度神经网络的粒子图像测速算法[J]. 空气动力学学报,2019,37(3):455-461. DOI: 10.7638/kqdlxxb—2019.0042 CAI S Z,XU C,GAO Q,et al. Particle image velocimetry based on a deep neural network[J]. Acta Aerodynamica Sinica,2019,37(3):455-461. doi: 10.7638/kqdlxxb—2019.0042
[21]	GUO C Y,FAN Y W,HAN Y,et al. Deep-learning-based liquid extraction algorithm for particle image velocimetry in two-phase flow experiments of an object entering water[J]. Applied Ocean Research,2021,108:102526. doi: 10.1016/j.apor.2021.102526
[22]	YU C D,FAN Y W,BI X J,et al. Deep particle image velocimetry supervised learning under light conditions[J]. Flow Measurement and Instrumentation,2021,80:102000. doi: 10.1016/j.flowmeasinst.2021.102000
[23]	ABADI M, AGARWAL A, BARHAM P, et al. TensorFlow: Large-scale machine learning on heterogeneous systems[EB/OL]. [2021-11-22]. https://arxiv.org/pdf/1603.04467.pdf/.