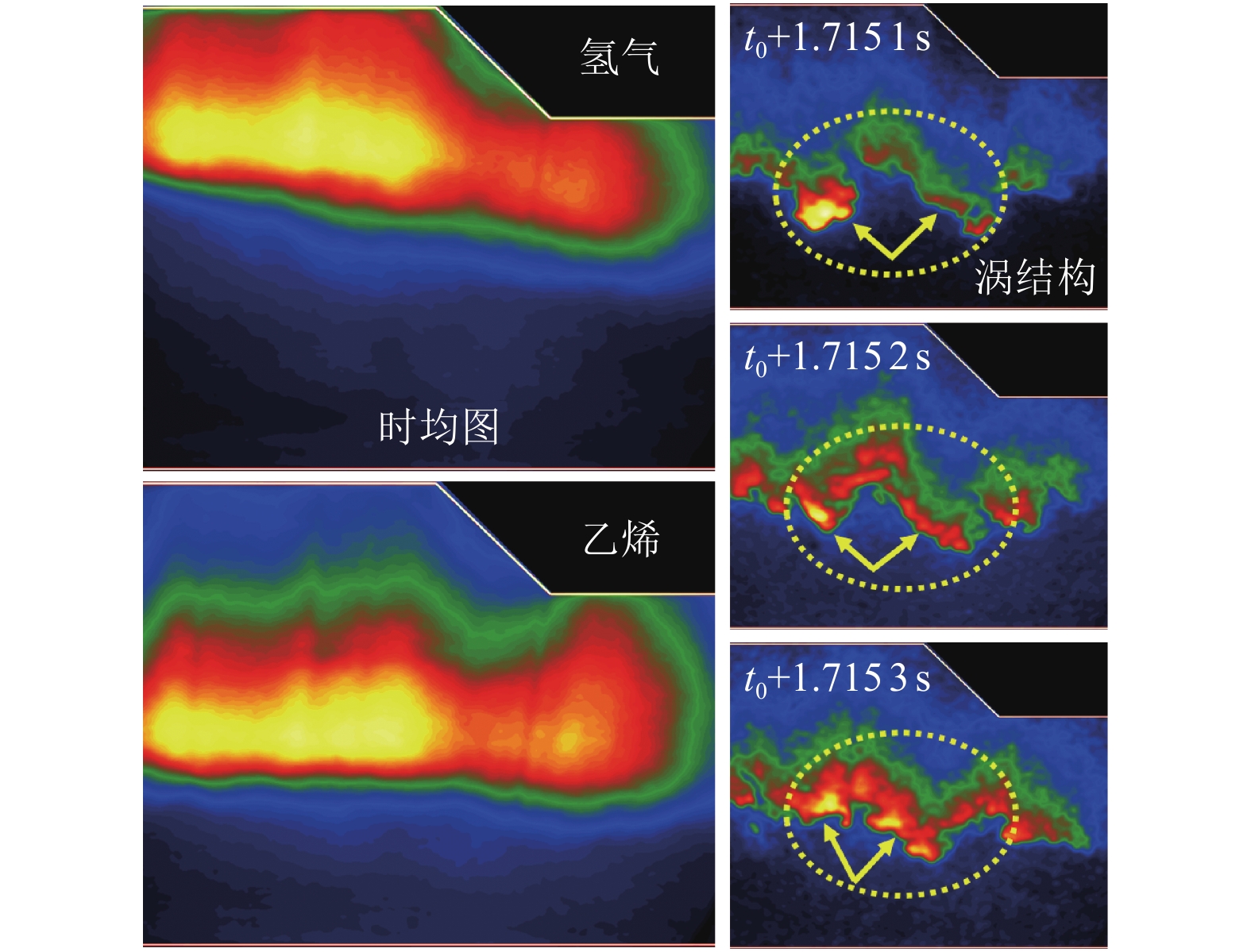
10 kHz OH-PLIF imaging measurement of a scramjet combustor
-
-
0 引 言
燃气涡轮是航空发动机和地面燃气轮机的主要热端部件,直接承受来自燃烧室高温燃气的冲刷。其中来流燃气的湍流度是影响涡轮叶片热负荷和传热冷却特性的决定性因素之一[1],提高来流的湍流度会显著增强叶片表面的对流换热系数并影响其分布,对发动机性能和寿命的影响不容忽视,湍流度的准确测量和预估具有特别重要的现实意义[2-5]。
常见的湍流度的测量方法包括粒子图像测速(PIV)、激光多普勒测速(LDV)、核磁共振成像测速(MRV)、多孔探针测速等,Chemnitz等[6]在高速叶栅风洞内比较了PIV与恒温热线风速仪(CTA)在湍流度测量方面的差异,发现两者的平均测量偏差在0.4%以内,而有限的偏差可能是由于探头的几何结构导致的;Olivier等[7]在完全湍流的管道内,分别利用LDV和PIV测量了声波速度分量的振幅和相位,并成功与Minotti等[8]的实验结果互相验证;夏振炎等[9]采用3维LDV获取了湍射流上游的时均和脉动速度场分布,探究了脉动速度分量、平均流速、射流宽度、雷诺应力的规律性变化;Ligęza等[10]在研究湍流能量谱时,提出确定CTA带宽分布的间接方法,并揭示其对于湍流能量谱分布的影响;Lien等[11]采用多孔探针进行了湍流度和表面摩擦系数的研究,发现在湍流场内,只要探头的尺寸足以浸入到边界层内,则探头几何形状的影响可以忽略不计。
尽管湍流度对涡轮叶片表面传热和温度分布特性具有显著影响,但在中高温叶栅实验台上准确测量燃机特征工况下的湍流强度,依然存在较高难度,Wicksall等[12]在
1350 ℃条件下的旋流稳定燃烧器内开展流动特性的研究,但燃烧产生的高光强宽频带可见光对相机光学元器件的使用带来很高的要求;Zhang和Glezer[13,14]设计可以在1200 ℃以上环境下使用的热通量探针,再利用滞止点的传热关系推导湍流度,但是该方法会对流场产生不可避免的干扰,同时测量误差相对较高。机理研究表明,在湍流场中具有相关结构的两个变量间的关系,可以通过随机预估(Stochastic Estimation,SE)获取,Adrain[15]首次提出采用条件平均的方法获取两个相关变量之间的关系,并借助该关系实现对未知量的预估;随后,Adrain和Guezennec[16,17]相继通过实验的方法,利用多点测量预估了湍流速度场分布;Naguib等[18]则通过对壁面脉动压力的测量,首次在湍流边界层内建立了脉动压力与脉动速度的线性随机预估(LSE)和二次随机预估(QSE)关系;之后,Murray和Ukeiley[19]在二维凹腔内分别利用LES和QSE预估速度分布,并与数值仿真结果进行对比,发现LSE可以较为准确地预估流场的整体结构,同时QSE可以捕捉涡结构随时间演变的细节;而后,Hudy[20]通过在轴对称的后台阶模型中采用LSE,也成功实现了对流动细节的解析。
综合以上,国内外各位学者通过对凹腔、后台阶等经典模型的研究,利用LSE和QSE方法实现了对流场结构的研究,在这些经典模型中,由于流场结构的特殊性,压力脉动与速度脉动之间很容易建立起较高的相关性,但在更一般的湍流叶栅风洞中,相关程度往往较低[21],随机预估方法的准确性和适用性还有待进一步的研究。
本文将从LSE的角度出发,利用抽吸式叶栅风洞实验系统,组合湍流栅格,搭建一套高湍流度叶栅风洞实验平台,利用热线风速仪和麦克风,分别获取主流脉动速度和通道内壁面的脉动压力,并建立二者的关联,利用相关特性实现对湍流度的预估,对比预估结果与测量结果,证实LSE对湍流度预估的准确性,在低马赫数(Ma < 0.3)范围内为燃机特征工况下湍流度测量方案的研究提供新的思路。
1 实验原理
在创建相关系数${r_{u'p'}}$时,首先需要在已知的流场中同时获取脉动压力与脉动速度的信号序列,在基于单点连续测量的脉动压力与脉动速度关联性的求解中,脉动压力与脉动速度信号的测点位置固定,通过数据采集卡连续高频对脉动速度与脉动压力信号进行同步采样。根据Adrain和Guezennec提出的观点,脉动压力与预估脉动速度之间的关系可以利用泰勒级数展开,其二阶表达式为:
$$ \begin{gathered} \tilde u({x_0} + {\text{Δ}} x,{y_0} + {\text{Δ}} y,{{\textit{z}}_0} + {\text{Δ}} {\textit{z}},t + {\text{Δ}} t) \\ = A({\text{Δ}} x,{\text{Δ}} y,{\text{Δ}} {\textit{z}},{\text{Δ}} t;{x_0};{y_0};{{\textit{z}}_0})p'({x_0},{y_0},{{\textit{z}}_0},t) \\ + B({\text{Δ}} x,{\text{Δ}} y,{\text{Δ}} {\textit{z}},{\text{Δ}} t;{x_0};{y_0};{{\textit{z}}_0})p{'^2}({x_0},{y_0},{{\textit{z}}_0},t) \\ + O(p{'^3}) \\ \end{gathered} $$ (1) $({x_0},{y_0},{z_0})$为实验段内的脉动压力测量点的位置坐标,t为同步测量脉动压力与脉动速度的时刻,${\text{Δ}} x$,${\text{Δ}} y$,${\text{Δ}} z$为三个方向上获取的脉动速度与脉动压力测量点之间的距离,具体取值见表1,${\text{Δ}} t$代表时间的滞后量,其值由脉动速度与脉动压力的关联度分布得出,$p'$表示压力的脉动值,A为线性预估系数,B为二次预估系数,在线性预估方法中,B = 0,A的表达式通过将脉动速度测量值与预估值之间的误差平方最小化获得,即:
表 1 麦克风与热线的相对位置Table 1 The position of the microphones relative to the hot wire序号 △x/mm △y/mm △z/mm 1 0 0 34.5 2 50 0 34.5 3 100 0 34.5 4 150 0 34.5 $$ E({e^2}) = \left\langle {{{\left\{ \begin{gathered} \tilde u({x_0} + {\text{Δ}}x,{y_0} + {\text{Δ}}y,{{\textit{z}}_0} + {\text{Δ}}{\textit{z}},t + {\text{Δ}}t) \\ - u'({x_0} + {\text{Δ}}x,{y_0} + {\text{Δ}}y,{{\textit{z}}_0} + {\text{Δ}}{\textit{z}},t + {\text{Δ}} t) \\ \end{gathered} \right\} }^2}} \right\rangle $$ (2) 在满足$\dfrac{{\partial E({e^2})}}{{\partial A}} = 0$ 的条件下,可得A的表达式如下:
$$ \begin{aligned} A & = \frac{\left\langle u^{\prime} \left(x_0 + {\text{Δ}} x, y_0 + {\text{Δ}} y, z_0 + {\text{Δ}} z, t+{\text{Δ}} t\right) \cdot p^{\prime} \left(x_0, y_0, z_0, t\right)\right\rangle}{\left\langle p^{\prime}\left(x_0, y_0, z_0, t\right) \cdot p^{\prime}\left(x_0, y_0, z_0, t\right)\right\rangle} \\ & =\frac{r_{u^{\prime} p^{\prime}}}{p_{\mathrm{rms}}^{\prime 2}} \end{aligned} $$ (3) ${r_{u'p'}}$即为测量获得脉动速度与脉动压力二者间的相关系数,$p{'_{{\text{rms}}}}$为脉动压力的均方根,$\left\langle {\;} \right\rangle $表示各样本测量结果取平均。因此,当通过相关系数获取脉动压力与速度之间的预估系数A后,便通过测量得到的脉动压力预估出脉动速度,采用的预估脉动速度的公式为:
$$ \tilde u = \frac{{{r_{u'p'}}}}{{p_{rms}^{\prime 2}}}p' $$ (4) 在获取一段脉动压力序列后,便可估算出脉动速度的序列。由于相关系数存在量纲,在判断两组向量之间是否存在相关性的时候,将无量纲化的相关系数${R_{u'p'}}$作为判断相关程度的直接依据,${R_{u'p'}}$的表达式为:
$$ \begin{aligned} {R_{u'p'}} & =\frac{{\sum\limits_{i = 1}^n {({u_i} - \bar u)({p_i} - \bar p)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{({u_i} - \bar u)}^2}} } \sqrt {\sum\limits_{i = 1}^n {{{({p_i} - \bar p)}^2}} } }} \\&= \frac{{\dfrac{1}{n} \cdot \sum\limits_{i = 1}^n {(u{'_i}p{'_i})} }}{{\sqrt {\dfrac{1}{n}\sum\limits_{i = 1}^n {u{'_i}^2} } \sqrt {\dfrac{1}{n}\sum\limits_{i = 1}^n {p{'_i}^2} } }} \end{aligned}$$ (5) 其中$ \sqrt {\dfrac{1}{n}\sum\limits_{i = 1}^n {u{'_i}^2} } = u{'_{rms}} $,$ \sqrt {\dfrac{1}{n}\sum\limits_{i = 1}^n {p{'_i}^2} } = p{'_{rms}} $, $ \dfrac{1}{n} \cdot \sum\limits_{i = 1}^n {(u{'_i}p{'_i})} = {r_{u'p'}}$,因此${R_{u'p'}} = \dfrac{{{r_{u'p'}}}}{{u{'_{rms}}p{'_{rms}}}}$。
实验过程中发现,在${R_{u'p'}}$较低的情况下,由公式(4)计算得到的预估脉动速度,比实际测得的脉动速度偏低,而如果将无量纲系数${R_{u'p'}}$引入到表达式的分母位置中,由于${R_{u'p'}}$是介于0~1之间的数,便可以将预估脉动速度放大到原结果的$1/{R_{u'p'}}$倍,提高该公式的准确性,推导过程如下:
在公式(5)中,$R_{u^{\prime} p^{\prime}}=\dfrac{r_{u^{\prime} p^{\prime}}}{u_{r m s}^{\prime} p_{r m s}^{\prime}}$,因此
$$ r_{u^{\prime} p^{\prime}}=R_{u^{\prime} p^{\prime} }{u_{r m s}^{\prime}} p_{r m s}^{\prime} $$ (6) 将公式(6)带入公式(4)内,得到:
$$ \tilde u = \frac{{{R_{u'p'}}u{'_{rms}}p{'_{rms}}}}{{p_{rms}^{'2}}}p' $$ (7) 当预测多个样本的平均脉动速度时,可以采用脉动速度的均方根代替脉动速度,因此$p' = p{'_{rms}}$,将其带入到(7)中,可以得到
$$ \tilde u = {R_{u'p'}} \cdot u{'_{rms}} $$ (8) 此时,若在分母位置存在无量纲系数${R_{u'p'}}$,公式(8)便可以转化为
$$ \tilde u = u{'_{rms}} $$ (9) 其中$\tilde u$是预估得到的速度脉动,$u{'_{rms}}$是热线多次采样计算出来的脉动速度的均方根,两者存在统计学意义上的相等。
因此,修正后的线性预估公式为:
$$ \tilde u = \frac{{{r_{u'p'}}}}{{{R_{u'p'}}p_{rms}^{\prime2}}}p' $$ (10) 同理,在关联度较高,比如在${R_{u'p'}} = 1$的情况下,修正公式(10)自动转变为原公式(4),保证预估关系的可靠性。
2 实验方案
抽吸式叶栅风洞实验台上通过增设湍流栅格来提高实验段的湍流度(如图1),其实验段如图2所示,由于其流向位置处于叶栅段正前方,截面尺寸270 mm × 69 mm,基于叶片轴向弦长的特征雷诺数为1.2 × 104~4.3 × 104,在实验段上壁面伸入热线探针,使得热线测点处于流道中心位置;在实验段下壁面沿流向布置脉动压力传感器,同时在风洞外侧布置参考传感器以获取环境参考信号。
图3是抽吸式叶栅风洞内脉动压力与脉动速度测量实验系统,通过在实验段前方布置湍流栅格,可以将通道内湍流度提高至约5%~13%。利用数据采集卡将脉动压力信号、脉动速度信号以及皮托管获得的主流速度信号、温度传感器获取的温度信号同步传输到计算机中进行数据存储和处理。由于采用热线风速仪获取瞬时速度,热线风速仪的测速范围可以满足本方法在燃烧室下游与进口导叶上游之间区域的测速需要,而更高速度条件下,便需要采用更先进的高速高频测速技术。叶栅风洞实验段的结构和流动参数如表2、表3所示:
表 2 抽吸式叶栅风洞实验段结构参数Table 2 Structure parameters of the test section of the suction type cascade wind tunnel特征结构 参数 轴向弦长Cax 50.18 mm 叶高/轴向弦长S/Cax 1.369 栅距/轴向弦长P/Cax 1.346 进气角θ1 0° 出气角θ2 76.5° 表 3 抽吸式叶栅风洞实验段流动参数Table 3 Flow parameters of the test section of the suction type cascade wind tunnel特征流动 参数 进口雷诺数Rein 1.2 × 104~4.3 × 104 进口流速vin 3.76 m/s~12.75 m/s 湍流度Tu 5%~13% 温度T 20℃ 脉动压力传感器采用AWA14426电容式压力场测量传声器,该传声器灵敏度较高,频响性能较好,非线性失真小,测量频率范围3.15 hz~20 khz,响应范围25 dB~161 dB,相应脉动压力测量范围在3.56 × 10−4 Pa~
2244 Pa,满足实验测试要求,并且出厂前提供每台传声器的标准校核曲线,曲线表明传感器的灵敏度在实验范围内基本保持稳定,测量误差不高于0.4 dB。传感器外径为1/2英寸,在抽吸式叶栅风洞内,沿流向每隔50 mm布置一处传感器,沿流程共布置4处以获取剪切层发展变化对脉动压力的影响。实验用单线恒温热线风速仪测量实验通道中心位置处的瞬时速度,热线的感应长度约1.5 mm,直径为5 um,测速范围为0.5~100 m/s。每次使用前利用皮托管进行校核,测量点的数据利用King’s Law拟合出实验曲线,并保证相对误差在 ± 1%以内。热线风速仪固定在坐标架上,可沿流向(x方向)及高度方向(y方向)移动。当热线正对来流方向时,由于热线本身无法识别瞬时速度的方向,所测结果为xz平面内瞬时合速度的大小,在各向同性的叶栅风洞内部,速度脉动的大小与热线测量结果的维度关系不大,因此可以使用二维合速度脉动的大小$u'$和通道底面脉动压力$p'$构建相关系数,获取脉动速度和脉动压力的相关性。同时注意到,风洞中安装和不安装热线时通道底面脉动压力测量结果基本没有变化,这表明热线的存在对实验结果没有显著影响。
气流温度由Pt100热电阻一体化温度变送器测量(测温范围0-100℃,输出范围0-10 V),用于对热线测量的输出电压进行修正。
实验中的数据采集卡为NI-USB-6343BNC数据采集卡,它可提供16路差分BNC模拟输入,最高采样率为5 × 105 Hz,而实验过程中采样率为
5000 Hz(初步实验表明流动信号最高频率不高于2000 Hz),更高采样率的数据采集证明信号无失真。除通道底面的脉动压力传感器外,在风洞实验段侧壁面上也布置了一个脉动压力传感器,用来获取实验段底面脉动压力传感器采集到的环境噪音。3 误差分析
本实验中,误差来源于热线风速仪、温度传感器、脉动压力传感器和数据采集卡,其不确定度分别为1%、0.3%、0.3%和3.1%,采样的不确定度与采样次数密切相关,计算方法为:
$$ U = \frac{1}{{\sqrt M }} $$ 其中M为采样次数,实验中取M =
1024 ,因此得到数据采集卡的不确定度为3.1%。脉动速度的测量不确定度由热线风速仪、温度传感器和数据采集卡的不确定度组成,而脉动压力传感器的测量不确定度则由脉动压力传感器和数据采集卡的不确定度组成,根据测量不确定度的合成公式:
$$ U = \sqrt {\sum\limits_{i = 1}^n {U_i^2} } $$ 计算得到脉动速度和脉动压力的测量误差分别为3.27%和3.11%。
通过不确定度传递公式[22]:
$$ {U_{Tu}} = \sqrt {{{(\frac{{\partial Tu}}{{\partial \tilde u}})}^2}{U_{\tilde u}}^2 + {{(\frac{{\partial Tu}}{{\partial p'}})}^2}{U_{p'}}^2} $$ 进而得到湍流度预估值的不确定度为4.22%。
4 结果与讨论
4.1 脉动速度与脉动压力的频谱特性
为了验证实验方法的准确性,实验首先在下吹式低速风洞内展开,由于风扇桨叶的扰动,使得风洞内存在大尺度的涡流结构,脉动速度与脉动压力之间具备更高的相关性。
图4展示了流向位置布置2处脉动压力传感器获取的功率谱密度(Power Spectrum Density,PSD)分布,其中P1为实验段上游的脉动压力传感器获取的脉动压力信号,而P2则为下游信号。其中边界层内压力脉动的频率范围主要集中在10~30 hz内,峰值为20 hz,同时上游信号的功率谱密度强于下游,这可能是由于下吹式风洞特点导致的。在下吹式风洞内,上游信号更接近风洞桨叶,受到来流的扰动作用更加明显,因此上游传感器获取的信号强度更高。对于环境参考信号P0,其峰值强度低于通道内部测量信号峰值强度值的1%,因此在本实验中,忽略了环境噪声对于实验测量带来的影响。
图5为热线获取的脉动速度信号的功率谱密度分布。可以看出在20 hz处存在速度脉动的峰值强度,因此可以推测存在特征频率为20 hz的涡流结构,同时通过观察脉动压力信号与脉动速度信号的相干性(Coherence)分布,发现在20 hz处,脉动速度与脉动压力信号之间高度相干,这也为证明两者间存在相关性提供了依据。
在抽吸式风洞内,图6展示了不同来流速度下,脉动压力传感器获取的脉动压力信号的频谱分布。来流雷诺数分别为2.0 × 104和3.0 × 104的工况,其中P1~P4分别表示沿流向分布的第1~4个脉动压力传感器信号。孔板栅格后壁面边界层内的压力脉动主要集中在15~40 hz频率范围内,在30 hz附近存在脉动压力信号的峰值。随着流速的提高,在73 hz附近脉动压力信号的第2峰值强度有所提升,这可能是随着来流速度的进一步提高,边界层内流动不稳定性进一步增强导致的。
不同来流速度下参考脉动压力信号的功率谱密度分布(图7),其对应的来流速度与图6一致。P0代表参考脉动压力传感器获取的脉动压力信号,由图7可以看出随着流速提高,参考脉动压力信号强度也在提升,同时看出在参考信号中,信号的主要频率依旧在30 hz附近,这表明流动信号与环境信号在本实验中存在高度耦合的情况,但环境信号强度依旧很弱,峰值强度约为流动信号峰值强度的0.1%。
不同来流速度下,主流脉动速度的功率谱密度分布如图8所示,与下吹式低速风洞内获得结果不同,脉动速度的功率谱密度分布没有明显的峰值,表明在实验段内,虽然湍流度可以达到5%以上,但主流内以均匀各向同性分布的小尺度的涡为主,不存在含有特征频率的大尺度涡结构,这将为建立脉动速度和脉动压力的关联性带来困难。在图9中,30 hz附近脉动压力信号与脉动速度信号之间的最大相干性大约在0.4~0.5左右,相比于下吹式低速风洞内0.8左右的相干性有显著降低。
图10展示了圆孔栅格内,来流雷诺数为
30000 时,底面脉动压力传感器获取信号的频谱图,其中P1~P4分别代表通道内部沿程布置的4个脉动压力传感器获得的信号,而P0则是位于风洞壁面以外的参考信号。与孔板栅格的情况类似,剪切层的发展对于脉动压力信号强度有显著影响,越接近风洞下游,脉动压力信号强度越高,同时明显看出,相同来流速度下,圆孔栅格后的脉动压力信号强度高于孔板栅格,但参考脉动压力信号的强度变化不大。图11为圆孔栅格内脉动速度的功率谱密度分布图,在图中所示频率范围内,并没有出现频率的峰值,与孔板栅格类似,这表明在圆孔栅格后,尽管湍流强度比孔板栅格高,但是其涡分布依旧呈现很强的均匀各向同性的特点,没有特征尺度的涡流结构存在,同时与测量脉动压力信号的相干性也比较低,最高仅有0.2左右,这也从侧面反映出为脉动压力与脉动速度之间的相关性将会受到削弱。
4.2 脉动速度与脉动压力的相关性
在下吹式低速风洞内,脉动速度信号和脉动压力信号同步测量,获取了
1024 组样本内的数据进行统计平均,得到了脉动速度和脉动压力信号的关联度分布曲线和相应的时间滞后性如图12所示。图中最大关联度约为0.39,所对应的脉动压力信号滞后于脉动速度信号约为0.0108 s。在抽吸式叶栅风洞内,开展脉动压力信号与脉动速度信号的相关性分析。图13展示了孔板栅格内,自由来流雷诺数为
60000 的条件下,获取的脉动压力与脉动速度的关联度分布,在滞后时间为0.0054 s时,可以取得最大关联度0.12。图14为相同来流雷诺数条件下,圆孔栅格内的脉动压力与脉动速度关联度分布,在脉动压力滞后于脉动速度
0.0032 s时,取得最大关联度为0.057。可以发现,在圆孔栅格后,脉动压力与脉动速度之间的关联度更小,而湍流强度更大,这表明均匀各向同性湍流强度的提高可能是导致关联度降低的原因。4.3 脉动速度测量值与预估值对比分析
图15展示了基于修正后的关联函数,得到的预估速度脉动与测量速度脉动之间的分布关系,预估速度脉动的变化趋势与测量速度脉动基本保持一致,关联函数可以较为准确的捕捉通道内大尺度的速度脉动,然而实际速度脉动的变化往往存在尺度小、不稳定性强的特点,因此脉动压力传感器无法准确预估脉动速度的微小变化,同时小尺度的速度脉动,也会在通道内流动发展的过程中不断耗散,因而带来一定的估计误差。
图16为孔板栅格后抽吸式叶栅风洞内测量获取的脉动速度与利用线性相关函数获取的预估脉动速度之间的对比。与下吹式低速风洞内结果一致,预估值与测量值在整体趋势上保持一致,不同的是在小风洞内,速度脉动的频率更高,不稳定性更强,采用线性相关获取的速度脉动很难准确捕获脉动速度的细微变化。但是利用修正后的预估关系式,发现在对
1024 组样本获取的预估结果进行统计平均后,预估脉动速度的值为0.4225 m/s,而测量获取脉动速度的值为0.4135 m/s,相对误差约为2.18%。在圆孔栅格后获取的测量速度脉动与预估速度脉动之间的对比如图17所示,与孔板栅格相比,明显观察到脉动速度的幅值进一步扩大,同时预估速度脉动对于测量速度脉动的预估精确度有所降低,对于更小尺度的脉动速度的预估更加困难,但总体趋势两者依旧相符。从定量角度看,预估速度脉动的平均值为
1.1041 m/s,而测量平均值为1.0787 m/s,相对误差为2.35%。5 结 论
本实验在布置湍流栅格的叶栅风洞内,开展壁面脉动压力与主流脉动速度相关性的研究,分别采用麦克风和热线风速仪同步获取脉动压力和脉动速度值,基于线性随机的方法预估主流速度脉动和湍流度,主要结论如下:
1)下吹式风洞内脉动压力信号存在20 hz附近的峰值频率,抽吸式叶栅风洞峰值频率在30 hz左右,随着来流速度的增大,脉动压力信号强度提升,且位于剪切层发展下游的脉动压力传感器获取的信号强度更高;
2)孔板栅格后,脉动速度与脉动压力的最大关联度约为
0.1173 ,圆孔栅格后最大关联度约为0.0561 ,相比于下吹式低速风洞内0.2648 的最大关联度均有显著降低;3)湍流栅格的存在破坏了叶栅风洞内的涡流结构,形成均匀各向同性的小尺度涡,是导致脉动速度与脉动压力相干性和关联度降低的主要原因;
4)基于修正后的线性随机预估表达式,叶栅风洞内预估脉动速度与测量脉动速度基本保持一致,两者相对误差控制在5%以内,为中高温环境下开展相关研究提供了新的思路。
-
期刊类型引用(2)
1. 付在国,冯文杰,王子婧,刘斌. 发动机进口旋转部件的三维积冰数值模拟(英文). Transactions of Nanjing University of Aeronautics and Astronautics. 2023(06): 663-677 .  百度学术
百度学术
2. 刘宇,秦梦婕,王强,易贤. 含盐海水飞沫的结冰风洞试验相似准则. 航空学报. 2023(S2): 303-313 .  百度学术
百度学术
其他类型引用(0)






 下载:
下载: