Investigation on artificial intelligence for the prediction of aeroacoustic performances and controlling parameters optimization of aircraft
-
摘要: 多参数多条件下的精准气动特性数据是进行飞行器快速设计、系统完善、性能评估、指标考核的基本前提和根本保证。基于人工智能的深度学习技术与流体力学交叉融合已成为当前发展趋势，并在湍流模型改造、系统理论建模、气动数据预测、控制参数优化、复杂流场重构等方面得到成功应用。为最大限度发挥深度学习的强大表征能力，围绕内埋弹舱作战运用和智能优化设计需求，构建了弹舱空腔气动特性多场载荷数据库，采用基于数据驱动的深度学习方法，建立了耦合因素影响下的空腔气动/声学特性智能分析深度前馈神经网络模型，实现了有限约束条件下的空腔气动/声学特性快速预测，并引入随机搜索和贝叶斯超参数优化方法增强了模型鲁棒性，为空腔噪声有效控制模型快速优化设计提供了数据基础和方法途径。Abstract: Accurate aerodynamic characteristic data under different conditions is the prerequisite and fundamental guarantee for the fast design of a flight vehicle, the improvement of a control system, the evaluation of performances and performance appraisal. The cross synthesis between the machine learning technology （ML） based on deep neural network （DNN） and fluid mechanics is developing fast and has achieved remarkable progresses in the modification of turbulence models, modeling of systems, prediction of the aerodynamic and aeroacoustic characteristics, optimization of control parameters and reconstruction of the flow field. To effectively apply the powerful representative capability of DNN, according to the demand of intelligent optimization and design of weapon bays, this paper first established a database of aerodynamic loads for flows past cavities and then built deep forward neural network model for the prediction of aerodynamic loads. To enhance the robustness of the model, random search and Bayesian optimization are introduced during the training of the model. Numerical results show that the trained DNN model is able to predict the aerodynamic loads and aeroacoustic characteristics accurately and efficiently, which provides a useful tool for the prediction and control of the aeroacoustic characteristics of the cavity.
-
-
![]()
图 4 多输入–多输出的深度人工神经网络模型
Fig. 4 Deep artificial neural network with multiple inputs and outputs
![]()
图 5 空腔载荷智能模型算法训练流程
Fig. 5 Flowchart for the training of the deep forward neural network models for the prediction of cavity loads
![]()
图 7 训练集内不同马赫数下空腔静压系数试验值与模型预测值对比
Fig. 7 Comparison of static pressure coefficients along the symme-tric lines at the bottom of the cavity between the experimental data and the results predicted by the DNN model in the training data sets
![]()
图 8 测试集内空腔底部对称线上静压系数试验值与模型预测值对比
Fig. 8 Comparison of static pressure coefficients along the symme-tric lines at the bottom of the cavity between the experimental data and the results predicted by the DNN model in the test data sets
![]()
图 9 训练集内不同马赫数下空腔声压级试验值与模型预测值对比
Fig. 9 Comparison of SPL along the symmetric lines at the bottom of the cavity between the experimental data and the results predicted by the DNN model in the training data sets
![]()
图 10 测试集内空腔声压级试验值与模型预测值对比
Fig. 10 Comparison of static pressure coefficients along the symme-tric lines at the bottom of the cavity between the experimental data and the results predicted by the DNN model in the test data sets
![]()
图 11 马赫数0.6、迎角–4°时，训练集内不同位置上的噪声频率特性
Fig. 11 Comparison of spectrum at different positions of the cavity at Ma=0.6 and
$\alpha $ =–4° between the experimental data and the results predicted by the DNN model in the training data sets![]()
图 12 马赫数1.5、迎角–4°时，测试集内不同位置上的噪声频率特性
Fig. 12 Comparison of spectrum at different positions of the cavity at Ma=0.6 and
$\alpha $ =–4° between the experimental data and the results predicted by the DNN model in the test data sets![]()
图 13 Ma=1.5时，前缘锯齿噪声控制神经网络模型预测声压级对比
Fig. 13 Comparison of SPL between the experimental data and the results predicted by the DNN model for cavity flows at Ma=1.5 with leading-edge serrations noise control
![]()
图 14 齿角固定为60o时不同底高和齿高参数空间内最大声压级降幅值
Fig. 14 Maximum decrease of SPL with different h and e
![]()
图 15 前缘锯齿参数优化前后腔内声压级对比
Fig. 15 Comparison of SPL for cavity flows with original leading-edge serrations control and optimized serrations control
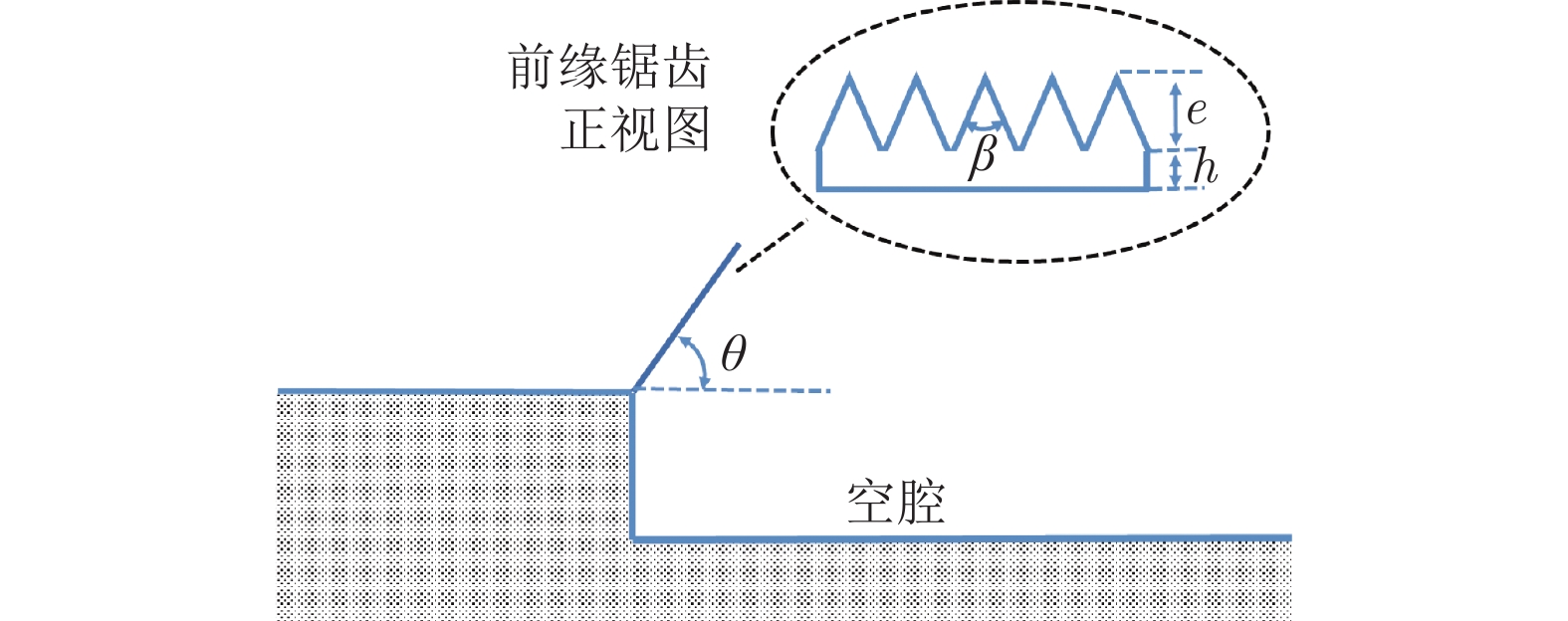
表 1 不同前缘锯齿流动控制装置几何参数
Table 1 Different geometric parameters of the leading-edge serra-tions for flow control
组别 底高h/mm 齿高e/mm 齿角β/（°） 1 4.27 3.46 60 2 6.00 1.73 60 3 6.00 6.93 60 4 0 3.00 30 5 0 3.00 45 6 0 3.00 60 7 1.00 2.00 30 8 1.00 2.00 45 9 1.00 2.00 60 10 0 1.00 45 11 0 1.70 45 12 0.40 2.00 45 13 1.40 2.00 45 14 2.10 2.00 45 
下载: 导出CSV
表 2 深度神经网络模型超参数范围
Table 2 Ranges of hyper-parameters in DNN model
nlayer nneural βeff 3～10 8～50 10–3
下载: 导出CSV
表 3 静压智能预测模型的训练集和测试集
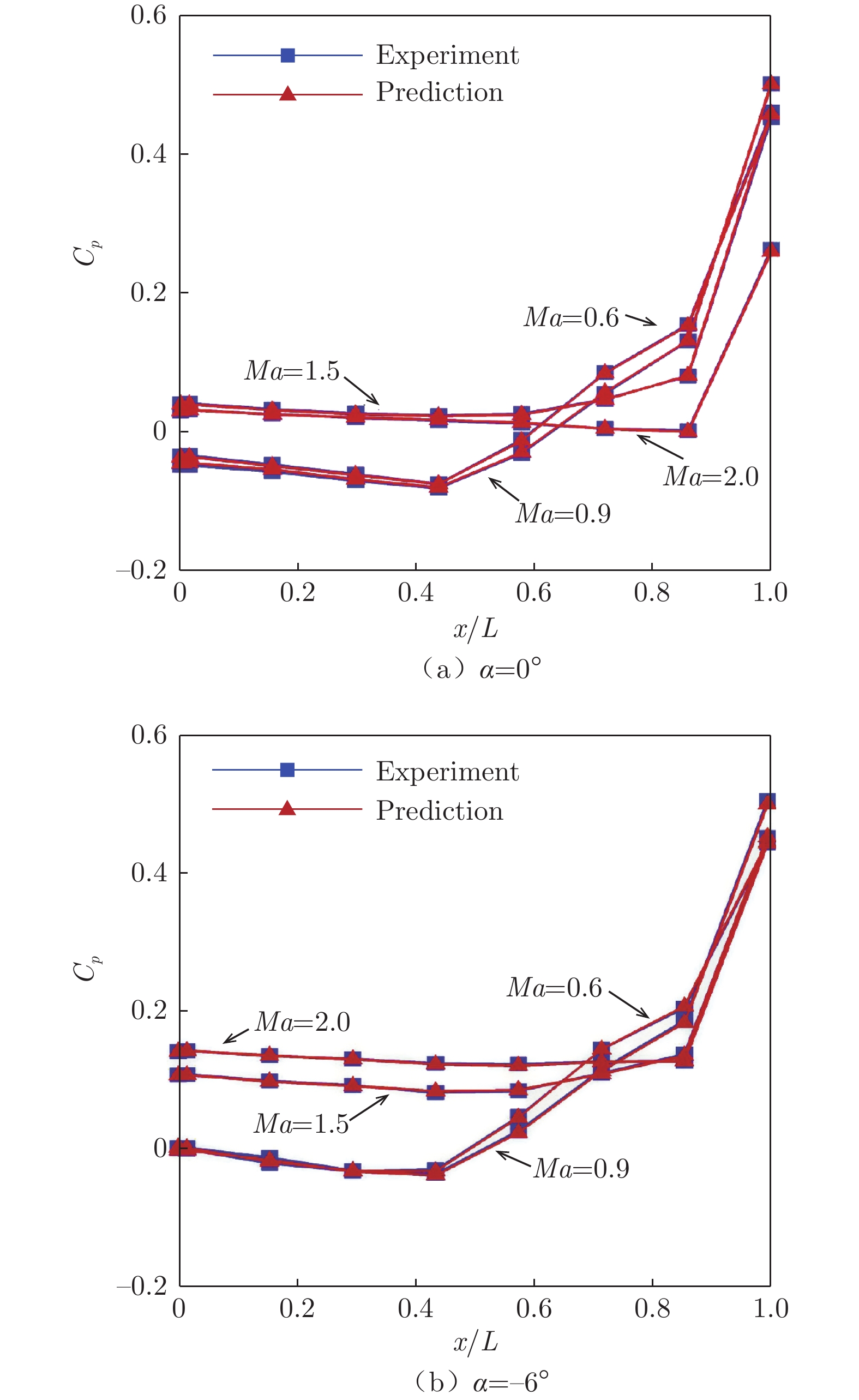
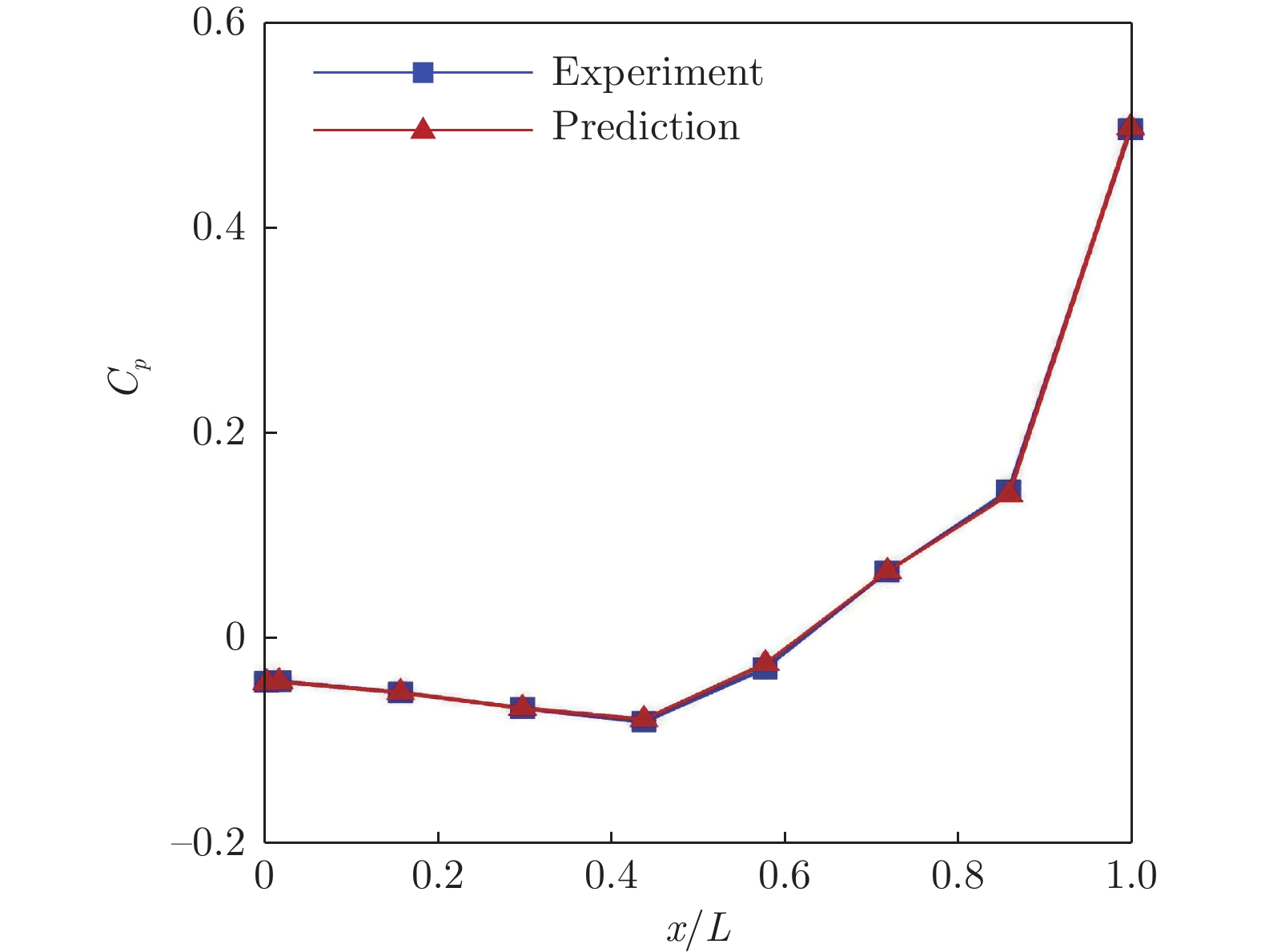
Table 3 Training and test sets for the prediction model of the static pressure coefficient
马赫数 迎角α/（°） 训练集 0.6 –6，–4，–2，0，2 0.9 –6，–4，0，2 1.5 –6，–4，–2，0，2 2.0 –6，–4，–2，0，2 测试集 0.9 –2
下载: 导出CSV
表 4 声压级智能预测模型的训练集和测试集
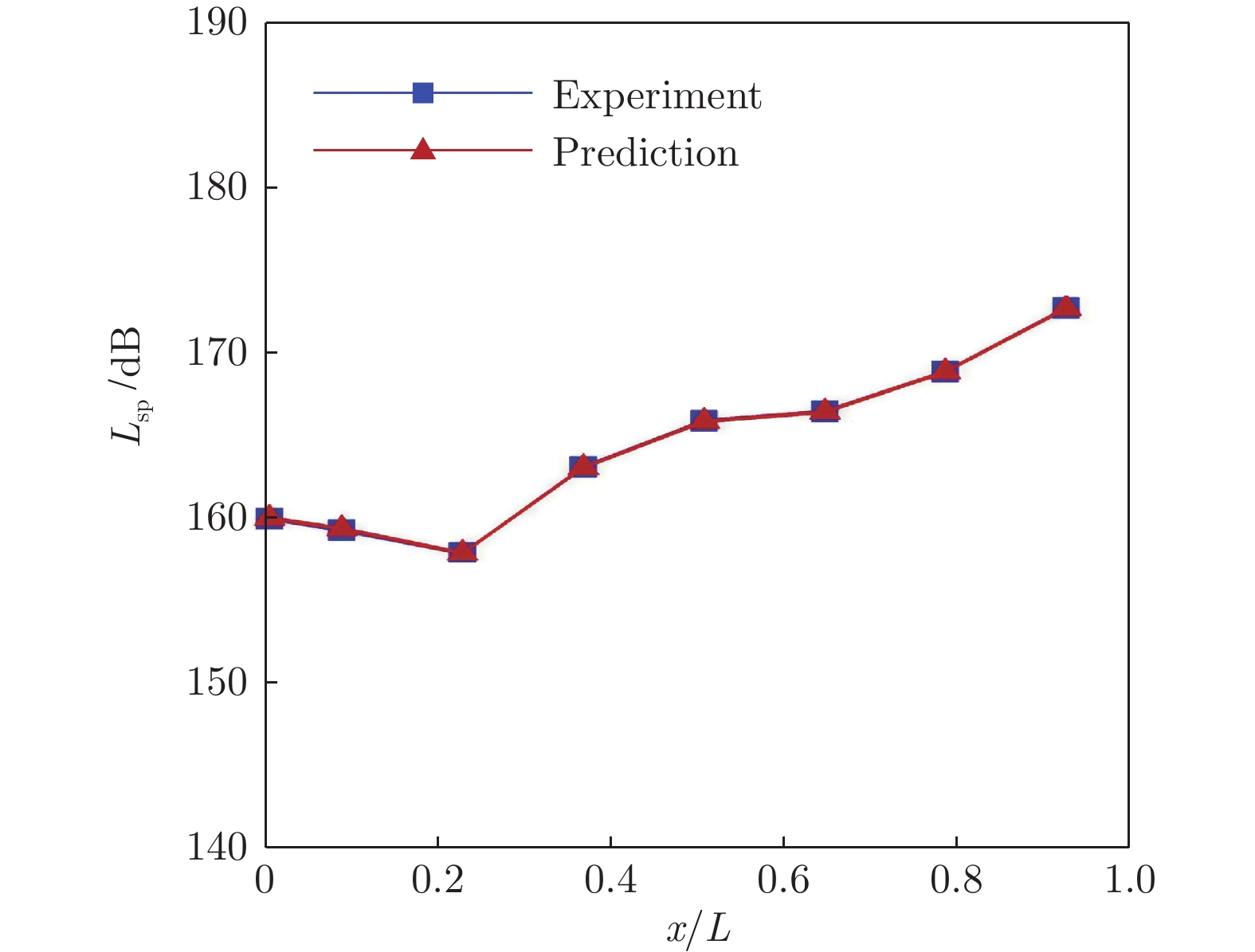
Table 4 Training and test sets for the prediction model of the sound pressure level
马赫数 迎角α/（°） 训练集 0.6 –6，–4，–2，0，2 0.9 –6，–2，0，2 1.5 –6，–4，–2，0，2 2.0 –6，–4，–2，0，2 测试集 0.9 –4
下载: 导出CSV
表 5 频谱智能预测模型的训练集和测试集
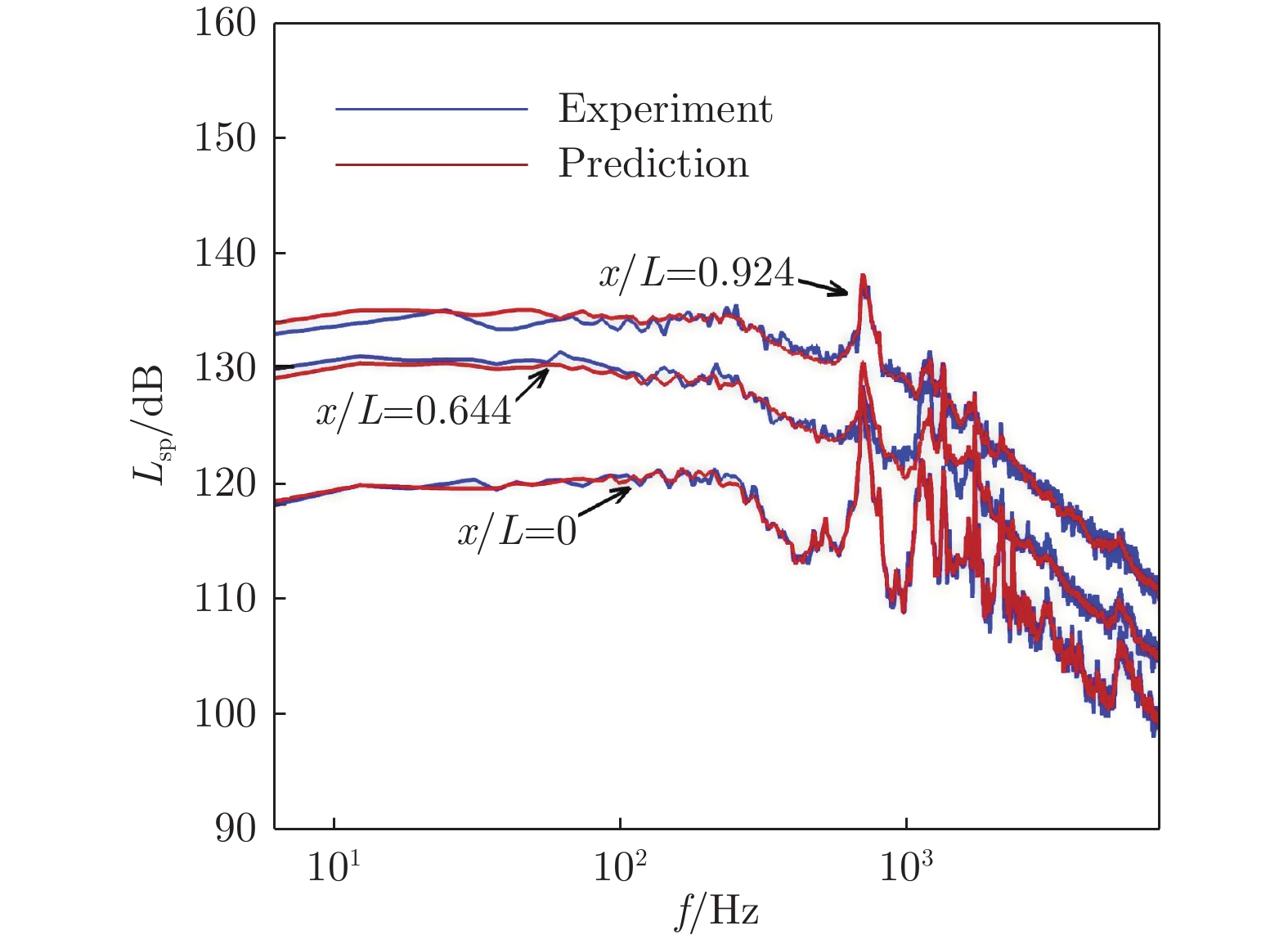
Table 5 Training and test sets for the prediction model of sound spectrum
马赫数 迎角α/（°） 训练集 0.6 –6，–4，–2，0，2 0.9 –6，–4，–2，0，2 1.5 –6，–2，0，2 2.0 –6，–4，–2，0，2 测试集 1.5 –4
下载: 导出CSV
表 6 前缘锯齿噪声控制试验参数及智能预测模型的训练集
Table 6 Training sets for the prediction model of SPL with leading-edge serrations for noise control
底高h/mm 齿高e/mm 齿角β/（°） 迎角α/（°） 4.27 3.46 60 –4，–2，2 6.00 1.73 60 –6，–2，0，2 6.00 6.93 60 –6，–4，–2，0，2 0 3.00 30 –4，–2，0，2 0 3.00 45 –2，0，2 0 3.00 60 –6，–2，0，2 1.00 2.00 30 –6，–2，0 1.00 2.00 45 –6，–4，–2，0 1.00 2.00 60 –6，–4，–2，0，2 0 1.00 45 –6，–4，–2 0 1.70 45 –6，–4，–2，0，2 0.40 2.00 45 –4，–2，0，2 1.40 2.00 45 –6，–4，–2，0，2 2.10 2.00 45 –4，–2，0，2
下载: 导出CSV
表 7 前缘锯齿噪声控制试验参数及智能预测模型的测试集
Table 7 Test sets for the prediction model of SPL with leading-edge serrations for noise control
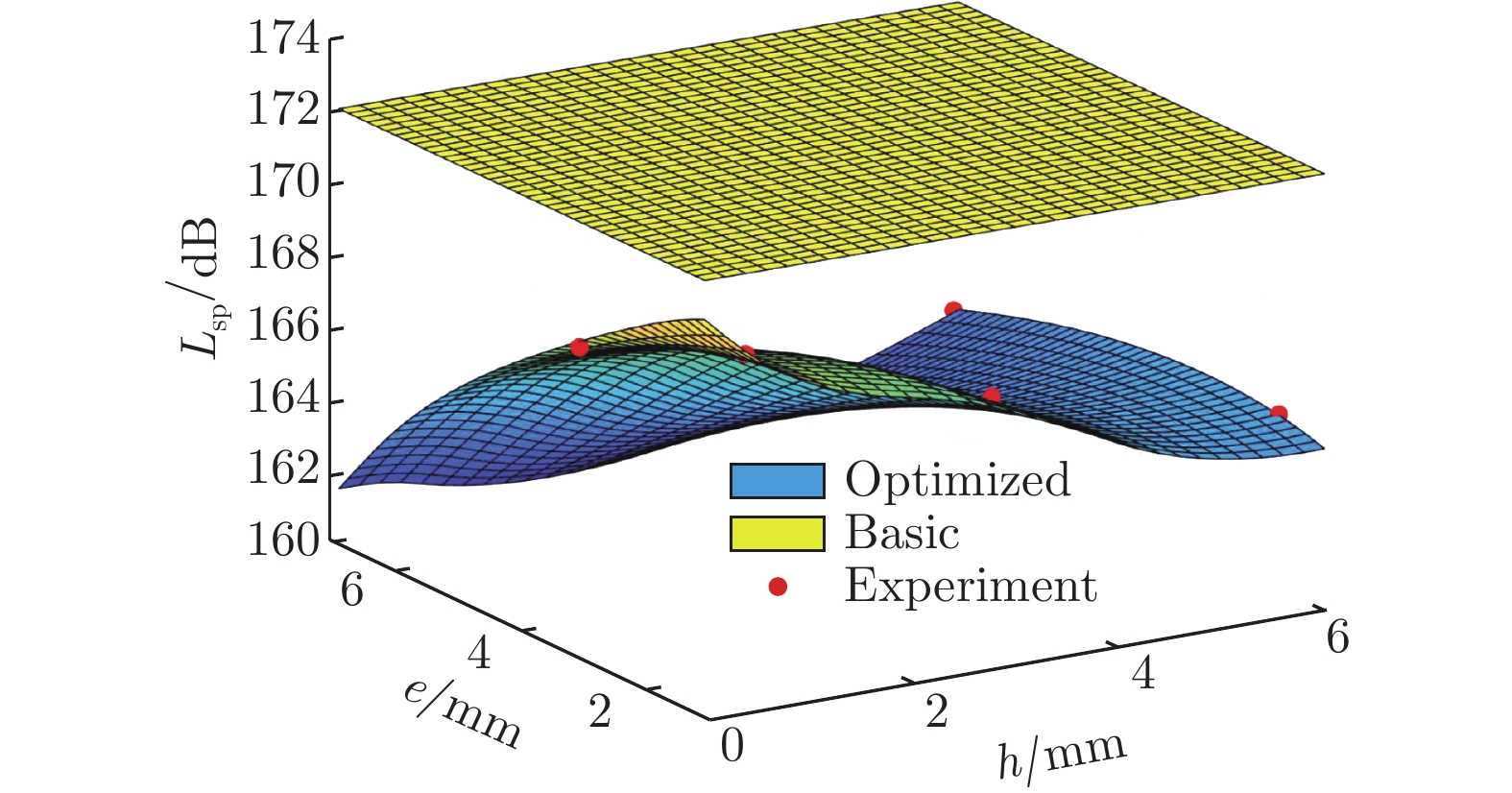
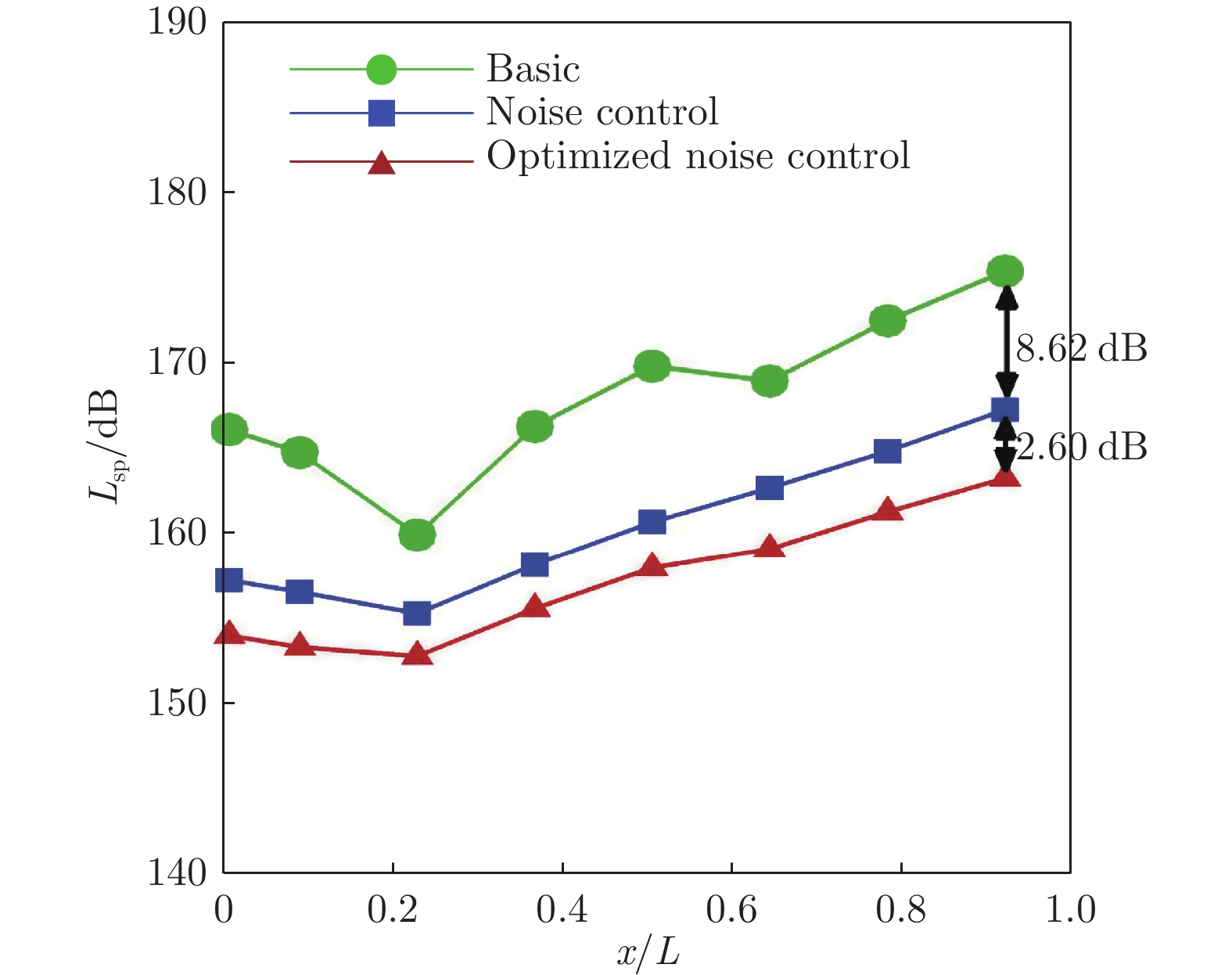
底高h/mm 齿高e/mm 齿角β/（°） 迎角α/（°） 4.27 3.46 60 –6，0 6.00 1.73 60 –4 0 3.00 30 –6 0 3.00 45 –4，–6 0 3.00 60 –4 1.00 2.00 30 –4，2 1.00 2.00 45 2 0 1.00 45 –2，2 0.40 2.00 45 –6 2.10 2.00 45 –6
下载: 导出CSV
表 8 不同迎角下前缘锯齿结构优化后的参数及其噪声控制效果
Table 8 Optimized geometrical parameters for the leading-edge serrations and its noise control result
马赫数 迎角
α/（°）原声压级
下降值
Lsp/dB优化结构参数 优化后的
声压级
Lsp/dBh/mm e/mm β/（°） 1.5 2 –9.69 1.80 6.85 60 –12.34 0 –8.62 2.00 6.85 60 –11.22 –2 –7.59 2.20 6.85 60 –10.23 –4 –7.44 2.20 6.85 60 –10.04 –6 –7.94 2.40 6.85 60 –10.57
下载: 导出CSV
-
[1] 汪清,钱炜祺,丁娣. 飞机大迎角非定常气动力建模研究进展[J]. 航空学报,2016,37(8):2331-2347. DOI: 10.7527/S1000-6893.2016.0072 WANG Q,QIAN W Q,DING D. A review of unsteady aerodynamic modeling of aircrafts at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica,2016,37(8):2331-2347. doi: 10.7527/S1000-6893.2016.0072
[2] 蔡金狮. 飞行器系统辨识[M]. 北京: 宇航出版社, 1995. [3] LIN G F, LAN C, BRANDON J. A generalized dynamic aerodynamic coefficient model for flight dynamics applica-tions[R]. AIAA-97-3643, 1997. doi: 10.2514/6.1997-3643
[4] ALLWINE D, STRAHLER J, LAWRENCE D, et al. Non-linear modeling of unsteady aerodynamics at high angle of attack[R]. AIAA 2004-5275, 2004. doi: 10.2514/6.2004-5275
[5] GOMAN M, KHRABROV A. State-space representation of aerodynamic characteristics of an aircraft at high angels of attack[R]. AIAA-92-4651-CP, 1992. doi: 10.2514/6.1992-4651
[6] JEONG S, CHIBA K, OBAYASHI S. Data mining for aero-dynamic design space[R]. AIAA-2005-5079, 2005. doi: 10.2514/6.2005-5079
[7] KUMANO T, JEONG S, OBAYASHI S, et al. Multi-disciplinary design optimization of wing shape for a small jet aircraft using kriging model[R]. AIAA-2006-932, 2006. doi: 10.2514/6.2006-932
[8] CHIBA K,OBAYASHI S. Data mining for multidisciplinary design space of regional-jet wing[J]. Journal of Aerospace Computing,Information,and Communication,2007,4(11):1019-1036. doi: 10.2514/1.19404
[9] LING J L,KURZAWSKI A,TEMPLETON J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance[J]. Journal of Fluid Mechanics,2016,807:155-166. doi: 10.1017/jfm.2016.615
[10] XIAO H,WU J L,WANG J X,et al. Quantifying and reducing model-form uncertainties in Reynolds-averaged Navier-Stokes simulations: a data-driven,physics-informed Bayesian approach[J]. Journal of Computational Physics,2016,324:115-136. doi: 10.1016/j.jcp.2016.07.038
[11] WANG Z J, LI J L, LAN C E, et al. Estimation of unsteady aerodynamic models from flight test data[R]. AIAA 2001-4017, 2001. doi: 10.2514/6.2001-4017
[12] WANG Z J, LAN E, BRANDON J. Estimation of lateral-directional unsteady aerodynamic models from flight test data[R]. AIAA 2002-4626, 2002. doi: 10.2514/6.2002-4626
[13] LUI H F S,WOLF W R. Construction of reduced-order models for fluid flows using deep feedforward neural networks[J]. Journal of Fluid Mechanics,2019,872:963-994. doi: 10.1017/jfm.2019.358
[14] ROWLEY C W,WILLIAMS D R. Dynamics and control of high-Reynolds-number flow over open cavities[J]. Annual Review of Fluid Mechanics,2006,38:251-276. doi: 10.1146/annurev.fluid.38.050304.092057
[15] BIAN S Y,DRISCOLL J F,ELBING B R,et al. Time resolved flow-field measurements of a turbulent mixing layer over a rectangular cavity[J]. Experiments in Fluids,2011,51(1):51-63. doi: 10.1007/s00348-010-1025-7
[16] CROOK S D,LAU T C W,KELSO R M. Three-dimensional flow within shallow, narrow cavities[J]. Journal of Fluid Mechanics,2013,735:587-612. doi: 10.1017/jfm.2013.519
[17] LIU X F,KATZ J. Vortex-corner interactions in a cavity shear layer elucidated by time-resolved measurements of the pressure field[J]. Journal of Fluid Mechanics,2013,728:417-457. doi: 10.1017/jfm.2013.275
[18] TUERKE F,SCIAMARELLA D,PASTUR L R,et al. Frequency-selection mechanism in incompressible open-cavity flows via reflected instability waves[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics,2015,91(1):013005. doi: 10.1103/PhysRevE.91.013005
[19] DIX R E, BAUER R C. Experimental and predicted acoustic amplitudes in a rectangular cavity[R]. AIAA-2000-0472, 2000. doi: 10.2514/6.2000-472
[20] STALLINGS R L, WILCOX F J Jr, et al. Experimental cavity pressure distributions at supersonic speeds[R]. NASA TP-2683, 1987.
[21] SAROHIA V. Experimental investigation of oscillations in flows over shallow cavities[C]//Proc of the 14th Aerospace Sciences Meeting. 1976. doi: 10.2514/6.1976-182
[22] TAM C K W,BLOCK P J W. On the tones and pressure oscillations induced by flow over rectangular cavities[J]. Journal of Fluid Mechanics,1978,89(2):373-399. doi: 10.1017/s0022112078002657
[23] 杨党国,李建强,罗新福,等. 弹穴流动特性高速风洞试验研究[J]. 实验流体力学,2006,20(4):33-39. DOI: 10.3969/j.issn.1672-9897.2006.04.006 YANG D G,LI J Q,LUO X F,et al. Investigation on flowing characteristics of the internal weapon cavity in wind tunnel[J]. Journal of Experiments in Fluid Mechanics,2006,20(4):33-39. doi: 10.3969/j.issn.1672-9897.2006.04.006
[24] 杨党国,范召林,李建强,等. 弹舱流动特性数值模拟及风洞试验研究[J]. 空气动力学学报,2009,27(3):378-383. DOI: 10.3969/j.issn.0258-1825.2009.03.021 YANG D G,FAN Z L,LI J Q,et al. Studies on flow characteristics of cavity by numerical simulation and wind tunnel test[J]. Acta Aerodynamica Sinica,2009,27(3):378-383. doi: 10.3969/j.issn.0258-1825.2009.03.021
[25] 杨党国. 内埋式武器弹舱流动特性研究[D]. 绵阳: 中国空气动力研究与发展中心, 2006. [26] 杨党国,吴继飞,罗新福. 零质量射流对开式空腔气动噪声抑制效果分析[J]. 航空学报,2011,32(6):1007-1014. DOI: 11-1929/V.20110324.1201.007 YANG D G,WU J F,LUO X F. Investigation on suppression effect of zero-net-mass-flux jet on aerodynamic noise inside open cavities[J]. Acta Aeronautica et Astronautica Sinica,2011,32(6):1007-1014. doi: 11-1929/V.20110324.1201.007
[27] 杨党国,范召林,李建强,等. 后壁倒角对空腔噪声的抑制效果[J]. 实验流体力学,2010,24(5):22-25. DOI: 10.3969/j.issn.1672-9897.2010.05.005 YANG D G,FAN Z L,LI J Q,et al. Suppression effect of rear-face angle of cavity on aerodynamic noise[J]. Journal of Experiments in Fluid Mechanics,2010,24(5):22-25. doi: 10.3969/j.issn.1672-9897.2010.05.005
[28] 周方奇,杨党国,王显圣,等. 前缘直板扰流对高速空腔的降噪效果分析[J]. 航空学报,2018,39(4):128-138. DOI: 10.7527/S1000-6893.2017.21812 ZHOU F Q,YANG D G,WANG X S,et al. Effect of leading edge plate on high speed cavity noise control[J]. Acta Aeronautica et Astronautica Sinica,2018,39(4):128-138. doi: 10.7527/S1000-6893.2017.21812
[29] 刘俊,杨党国,王显圣,等. 基于URANS与DDES方法的空腔近场噪声数值研究[J]. 振动与冲击,2016,35(20):154-159. DOI: 10.13465/j.cnki.jvs.2016.20.025 LIU J,YANG D G,WANG X S,et al. Numerical simulation of near-field cavity noise by URANS and DDES[J]. Journal of Vibration and Shock,2016,35(20):154-159. doi: 10.13465/j.cnki.jvs.2016.20.025
[30] 刘俊,杨党国,王显圣,等. 湍流边界层厚度对三维空腔流动的影响[J]. 航空学报,2016,37(2):475-483. DOI: 10.7527/S1000-6893.2015.0112 LIU J,YANG D G,WANG X S,et al. Effect of turbulent boundary layer thickness on a three-dimensional cavity flow[J]. Acta Aeronautica et Astronautica Sinica,2016,37(2):475-483. doi: 10.7527/S1000-6893.2015.0112
[31] TENNEY A S, GLAUSER M N, LEWALLE J, et al. A deep learning approach to jet noise prediction[R]. AIAA 2018-1736, 2018. doi: 10.2514/6.2018-1736
[32] VLACHAS P R,BYEON W,WAN Z Y,et al. Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences,2018,474(2213):20170844. doi: 10.1098/rspa.2017.0844
[33] PAWAR S,RAHMAN S M,VADDIREDDY H,et al. A deep learning enabler for nonintrusive reduced order model-ing of fluid flows[J]. Physics of Fluids,2019,31(8):085101. doi: 10.1063/1.5113494
计量
- 文章访问数: 1843
- HTML全文浏览量: 292
- PDF下载量: 136
