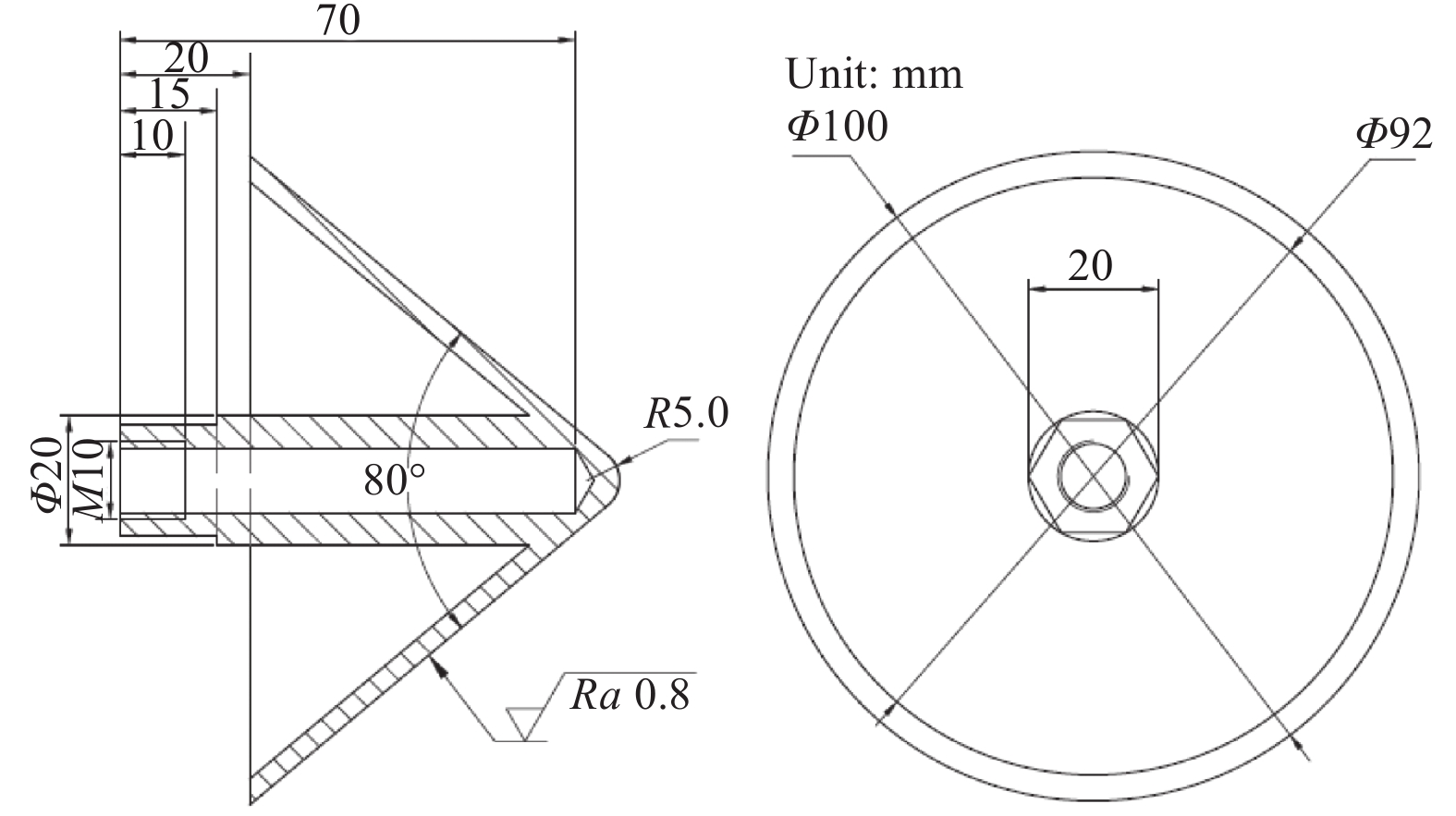
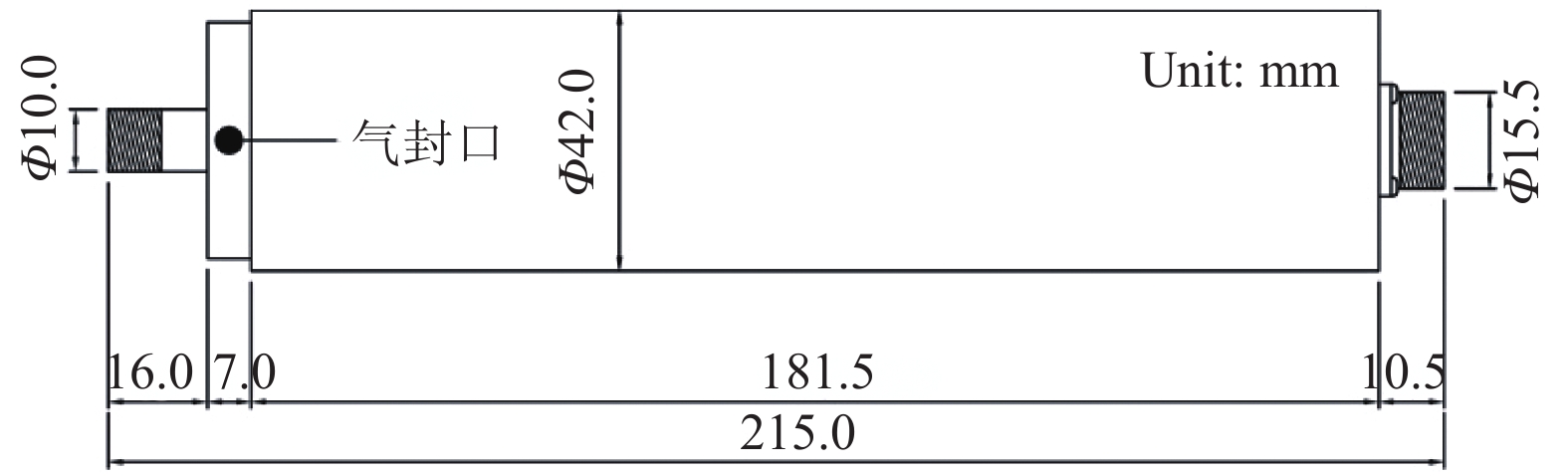
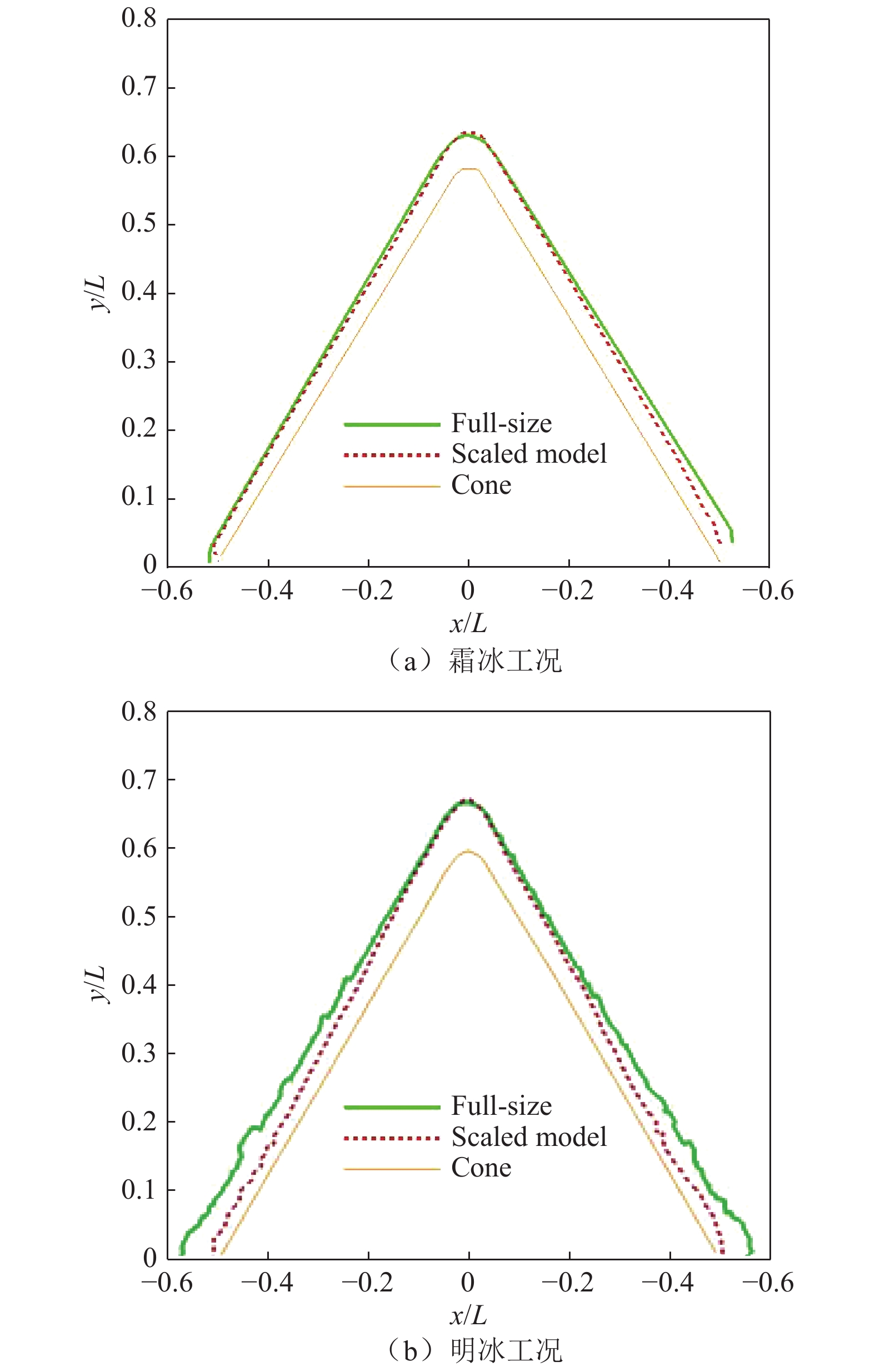
Abstract: In order to verify the scaling law of a rotating cone, a study on a rotating cone icing was carried out, and the icing scaling law of the rotating cone was derived. Taking a cone with a bottom diameter of 100 mm and cone angle of 80° as the full size model, and a cone with a bottom diameter of 50 mm and cone angle of 80° as the scaled model, the ice wind tunnel tests were carried out under different conditions. The ice shape on the surface of the cone was obtained by image method and processed in a dimensionless manner. Then the ice shape of the full size model was compared with that of the scaled model. The results show that, for glaze ice the ice shape of the front half of the cone on the full size and scaled models is in good agreement, but it is not in good agreement at the back half of the cone, and for rime ice the ice shape is in fairly good agreement on the full size and scaled models. The reasons are discussed, and suggestions are put forward for improvement.