Aeroelastic correction for nonlinear aerodynamic data in wind tunnel tests
-
摘要:
介绍了一种在静气弹分析中引入CFD数据进行风洞数据非线性段弹性修正的方法。将多个迎角的CFD数据作为外部气动力引入NASTRAN静气弹分析，计算不同迎角（升力）区间内的气动导数并得到分段弹刚比，积分得到未变形模型的气动特性曲线。对大展弦比翼身组合体模型在不同动压和马赫数下的风洞试验结果进行弹性修正，结果表明：该方法显著提高了升力和力矩曲线非线性段的修正精度；在风洞试验的迎角范围内，与动压外插结果吻合，升力和力矩的最大误差不超过0.015和0.005；不同马赫数和动压下的修正结果表明该方法具有广泛的适用性，能够兼顾效率和精度，具有大规模应用的潜力。
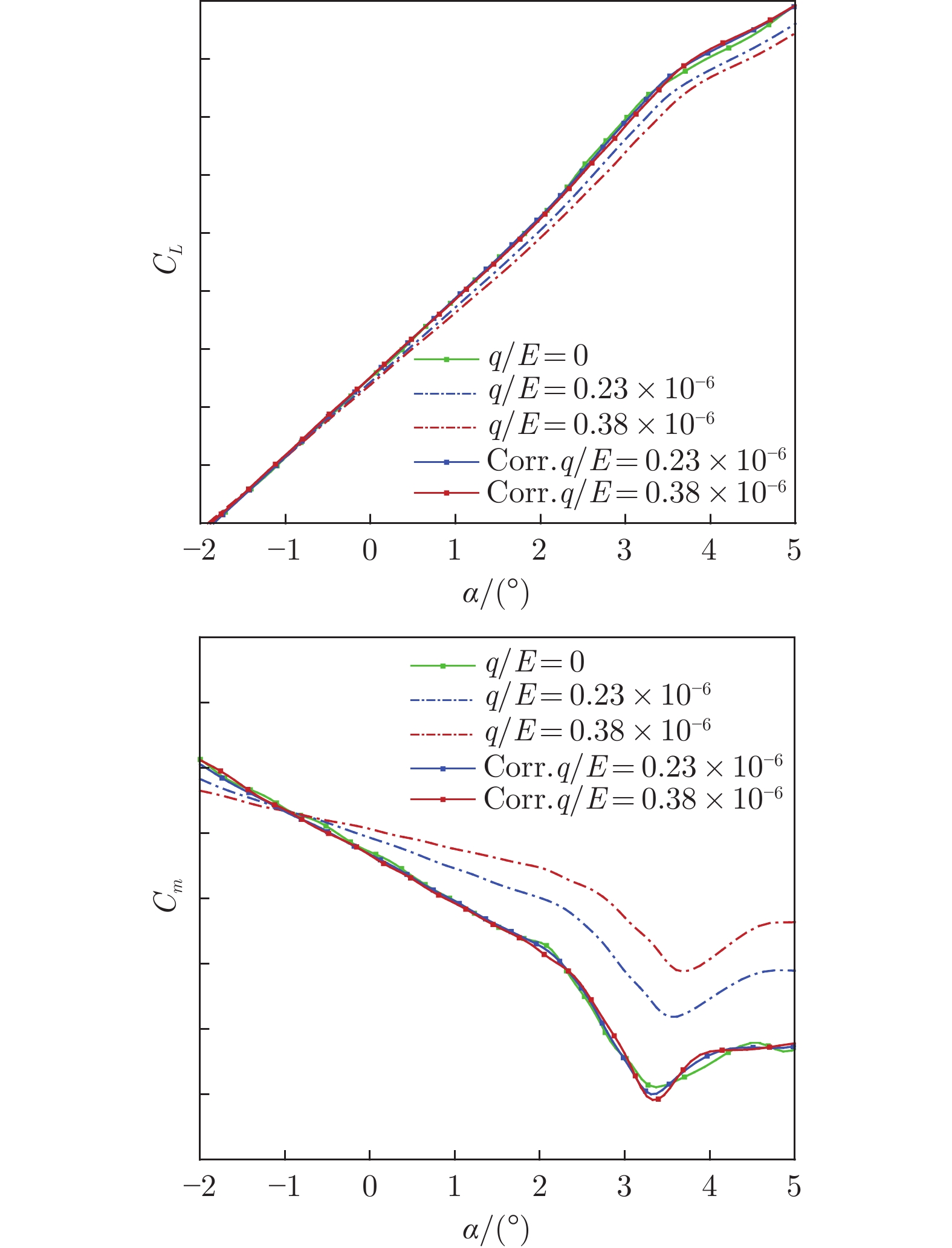
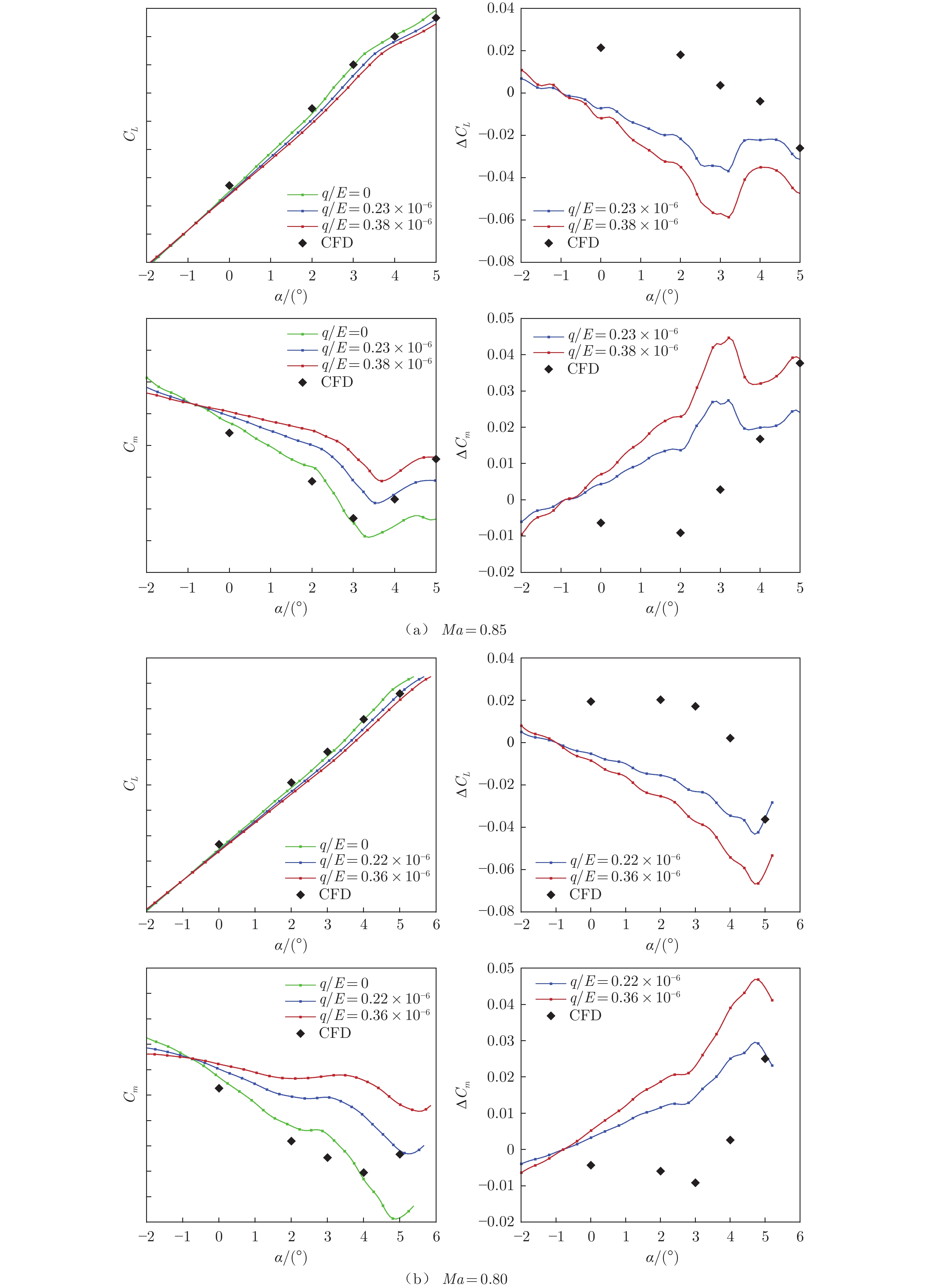
Abstract:A correction method for model deformation effects in wind tunnel tests is developed based on NASTRAN static aeroelastic analysis integrated with CFD data. Flexible To Rigid Ratio (FTR) of longitudinal aerodynamic derivatives for different angles of attack are calculated by NASTRAN with CFD correction, which is used to obtain aerodynamic characteristics of the undeformed model. Corrected aerodynamic characteristics of a high-aspect-ratio wingbody model under different circumstances of Mach number and dynamic pressure suggest that the proposed method largely improves the correction in the nonlinear part of CL and Cm curve. A minor discrepancy exists between corrected data and extrapolated results at different dynamic pressures, which is at most 0.015 for CL and 0.005 for Cm respectively. Moreover, the method is robust enough to gain accurate corrected results under different circumstances and efficient enough for large scale application in aircraft design.
-
0 引言
燃烧是发动机中燃料能量转换的主要形式，准确地描述燃烧过程，从而得到精确的燃烧数值模拟结果, 可以高效指导发动机的设计与实验。实际应用中，发动机中的燃烧大多是湍流的，燃烧与湍流之间的相互作用机理复杂，使得湍流燃烧数值模拟成为了重要的研究课题。
随着计算机能力的提升，大涡模拟(Large Eddy Simulation, LES)逐渐成为湍流燃烧数值模拟的重要研究手段。在湍流燃烧LES中需要使用燃烧模型来封闭标量方程中的化学反应源项。目前精度较高的燃烧模型，如小火焰模型[1-5]、线性涡模型[6-7]、基于概率密度函数的模型[8-12]、条件矩模型[13-14]、加厚火焰面模型[5, 15]、涡耗散模型[16]和部分预混反应器模型[17]等，均需要借助详细的化学反应机理来描述燃烧时的复杂反应过程，如燃烧场中的局部熄火和再燃、化学反应速率随压力的非线性变化、低温化学反应的影响、污染物排放等。
化学反应机理是指描述化学过程的基元反应的集合。在燃烧时，燃料分解产生大量化学分子和自由基，称为组分，组分间最基本的化学反应为基元反应。要准确模拟燃烧过程，所需的化学反应机理的规模是巨大的，可以包含数量成百上千的组分和基元反应[18]。而且化学反应组分常微分方程组(Ordinary Differential Equations，ODEs)通常是刚性的，如果使用常规的显式格式求解，为了计算稳定必须使用极小的时间步长。常见的解决方法是使用基于隐式格式的刚性求解器，如DVODE[19]和DASSL[20]等。因此，在湍流燃烧LES中，求解化学反应方程的时间常占据主要部分[21]。
化学反应机理规模的增加将导致化学反应源项计算量的迅速增长。应用小火焰类燃烧模型，如FGM(Flamelet Generated Manifolds)或FPV(Flamelet/Progress-Variable)等，可以通过预先建表的方法回避在线求解化学反应问题，类似的还有PRISM(Piecewise Reusable Implementation of Solution Mapping)[22]、RS-HDMR(Random Sampling-High Dimensional Model Representation)[23-24]等映射方法。相比于直接使用总包反应机理，此类方法虽然在一定程度上考虑了详细化学反应机理的作用，但化学反应表中的变量数量严重受限于计算机内存空间，当燃烧的工况不处于预先存储结果的工况范围内时，就会缺乏灵活性和适应性，与直接在线求解化学反应相比准确性较低。为了降低直接求解化学反应的计算时间，虽然可以使用在线的建表方法，如ISAT(In Situ Adaptive Tabulation)[25-29]，但是，ISAT方法对内存需求仍较大，并且在线建表的速度快慢也依赖于直接积分的求解速度。而提高直接求解的计算效率，可以通过使用化学反应机理简化或采用高效的积分求解器来实现。
对于不同的燃烧问题，反应机理的组分和基元反应并不都是活跃的，可能仅仅其中的某一部分是重要的，而其他部分的反应速率则可以忽略不计。因此，研究人员发展了许多化学反应机理简化方法，如敏感性分析法[30-32]、准稳态假设法[33]、局部平衡法[33]、计算奇异摄动法[34]、ILDM(Intrinsic Low Dimensional Manifold)法[35]和DRG(Direct Relation Graph)法[36]及其衍生算法，如DRGEP(Directed Relation Graph Error Propagation)方法[37]、PFA(Path Flux Analysis)[38-40]、EFA(Element Flux Analysis)[41-43]和GPS(Global Pathway Selection)方法[44]等。
上述反应机理简化方法需要在流场计算前完成，并在计算过程中直接使用预先简化好的反应机理。为了保证简化机理的准确性，这种预先简化的机理常包含了较多的组分。然而，对于同一燃烧场中的不同时刻或当地，反应机理可以进一步简化。因此研究人员发展了一类动态自适应化学法(Dynamic Adaptive Chemistry，DAC)[39, 45-48]，可以在计算过程中动态简化化学反应机理。动态简化主要基于DRG、PFA或GPS算法，因为这些方法能以较小的额外时间花费完成机理简化。DAC方法已应用于多种简单模型的燃烧计算，如HCCI(Homogeneous Charge Compression Igni-tion)模型[47, 49]、部分预混搅拌反应器模型[27, 50-52]、自着火问题和一维火焰传播[48, 53-54]等。
DAC方法也在不断地改进，并与其他简化方法耦合应用。为了进一步降低机理简化本身所占用的时间，Sun等[55]提出了自相关动态自适应化学(Correlated Dynamic Adaptive Chemistry，CoDAC)方法。该方法将具有相近状态的不同空间位置和时间节点网格点进行归类后统一处理，这与分区模型和CA(Cell Agglomeration)方法[56-57]的思想相同，自相关技术有效地降低了化学反应机理简化所需要的计算时间。Oluwole等[54]发展了一种DSRR(Decoupled Species and Reaction Reduction)简化方法，相比于DRG简化，具有同等的简化计算速度并提供了改进的误差控制方法。DSRR的显著优点是不需要指定初始组分，但简化结果可能会导致元素不守恒[54]。Xie等[58]提出的TSRA(Time-Scale and Jacobian-aided Rate Analysis)将组分分为活跃的(Active)、直接耦合的(Directly coupled)和不重要的(Inconsequential)3类，通过迭代计算来保证元素守恒。此外，DAC方法和ISAT方法结合，构成TDAC(Tabulated Dynamic Adaptive Chemistry)[27, 51, 59-60]方法，可以进一步提高化学反应计算速度。除了将DAC和ISAT二者结合，Xie等[60]提出的DAAM(Dynamic Adaptive Acceleration Method)可以根据DAC和ISAT的计算耗时自动选择二者之中较快的方法进行计算。最后，分区方法或CA方法也可以和DAC及ISAT结合[52, 61-62]，实现更高效的计算。
通过提高求解器计算效率也可以加速化学反应求解，如使用外推法[63]，点隐式求解器[64]、带预处理的Krylov求解器[65]、刚性去除法[66]和基于多时间尺度(MTS，Multi-Timescale Method)分析的混合多时间尺度(HMTS，Hybrid Multi-Timescale Method)法[67]，HMM(Heterogeneous Multiscale Method)方法[68]和AHI(Adaptive Method for Hybrid Integra-tion)[69]方法等。
求解化学反应常微分方程组，除了使用广泛应用的显式或隐式格式外，还可以使用指数格式积分方法(Exponential Integrator)[70]。这种方法构造含有Jacobian矩阵指数函数形式的积分格式，其优势在于可以使用显式大步长时间推进得到稳定的计算结果，适用于刚性常微分方程问题和振荡系统问题。因此，指数格式被广泛应用于金融与统计学[71]、正则化理论[72]、电磁场模拟[73]及浅水方程模拟[74]等领域。在指数积分方法中，需要计算Jacobian矩阵的指数函数。在多种计算矩阵指数函数的方法[75]中通用性较好、计算效率较高的方法是收缩乘方和Padé近似[76]方法。然而，这种方法所需的计算量与矩阵维数的3次方成正比，因此适用于较小规模的矩阵，对于大型矩阵，尤其是大型稀疏矩阵，其计算效率很低。一种广泛采用的解决方法是利用Krylov子空间近似[77]，将原问题投影到其Krylov子空间，从而实现降维，减少问题规模[74, 78-81]。Krylov子空间近似也常被应用于GMRES (Generalized Minimum Residual)算法和BiCGSTAB (Biconjugate Gradient Stabilized)算法等线性方程组求解方法中。
在燃烧数值模拟中，刚性化学反应问题也适合用指数格式求解。Bisetti[82]和Curtis等[83]的研究表明, 四阶指数积分格式和Krylov子空间近似方法可应用于求解自着火和HCCI的化学反应机理。然而，四阶指数积分格式每步需要计算3次矩阵指数函数，计算量较大。Niesen和Wright[79]发展了一种自适应时间步长和Krylov子空间大小的算法:Phipm算法。该求解器已被应用于自着火问题数值模拟，与DVODE求解器相比，显著提高了化学反应求解效率[84]。
为了研究湍流燃烧数值模拟中化学反应机理计算的加速方法，本文阐述了DAC和指数格式在湍流燃烧数值模拟中的应用情况。首先，探讨了DAC在湍流燃烧数值模拟中的加速效果。然后，考察了Krylov子空间近似的指数格式求解湍流-化学反应系统的加速效果。
1 动态化学反应机理简化在燃烧数值模拟中的应用
Liu等[21, 85]使用53组分/325反应的GRI-Mech 3.0反应机理和基于PFA的CoDAC简化方法对Sandia Flame D进行了LES数值模拟。Sandia Flame D是美国Sandia国家实验室发展的经典湍流射流火焰，由主射流、值班射流和空气伴流组成，其中主射流由25%甲烷和75%空气组成，值班射流为甲烷-空气燃烧后的平衡产物。具体参数可见Barlow等[86]的研究。数值模拟结果如图 1所示，通过对比发现，使用CoDAC简化的LES计算结果与未使用简化得到的结果符合得很好，表明使用CoDAC可以准确模拟非预混湍流火焰特性。使用CoDAC后，LES中化学反应计算时间总体下降了29%，化学反应速率的求解仍然占据总求解时间的主要部分。Yang等[64, 87-89]同样使用基于PFA的CoDAC方法简化化学反应计算，并结合CoTran方法降低组分输运系数的计算。对湍流预混火焰的DNS模拟[64]结果表明, 简化方法的加速因子可以达到2.7，在湍流非预混火焰的DNS模拟[89]中可以达到4.0。CoDAC简化方法也被用于模拟实验室尺度湍流火焰Sandia Flame D[87]和Flame E[88]的LES，使用的反应机理为20组分/84反应的简化机理，该反应机理是通过对GRI-Mech3.0机理使用GPS简化后获得的。该研究对比了有限速率化学模型和小火焰/进度变量方法，结果表明，2种模型都较好地反映了实验结果的变化趋势，但使用有限速率化学模型和CoDAC简化相比于FPV模型，可以得到更准确的统计结果。
![]()
DAC还被应用于超声速燃烧数值模拟中。Wu等[90]对比了DAC、TDAC方法和骨架机理在超声速燃烧室数值模拟中的表现。结果表明DAC和TDAC可以准确模拟燃烧室的特性和火焰结构，而骨架机理不能准确预测火焰的稳定特性。在计算效率方面，在57组分/269反应的UCSD反应机理的基础上使用DAC可以获得与使用30组分/143反应的骨架机理同等的加速效果，而在DAC的基础上使用TDAC可以将计算效率再提高1倍。
在实际燃烧设备的数值模拟中，DAC方法也得到了应用，Li等[59]对比研究了TDAC方法和5种不同的化学反应机理简化方法：DRG、DRGEP、Contino等的DAC方法[91]、PFA和EFA。研究使用非定常雷诺平均方法(URANS)数值模拟了DJHC(Delft Jet-in-Hot-Coflow)燃烧器的燃烧特性，结果表明DRGEP、DAC和EFA方法比DRG和PFA方法准确。对于小规模反应机理，TDAC方法中的制表方法贡献了主要的计算加速，而对于大规模反应机理，DAC简化起了主要作用。Zhou和Lu等[92-93]使用URANS和LES方法模拟了Spray H正庚烷湍流喷雾火焰，结果表明使用DAC的加速因子可达到2.0。在化工应用方面，Huang等[94]使用基于DRG的DAC方法模拟了石英玻璃反应炉的SiCl4/H2/O2燃烧系统，加速因子为2.2。
DAC在内燃机数值模拟中受到了广泛关注，DAC方法及其他多种化学反应机理简化方法被应用于加速计算。Shi等[95]使用基于DRGEP的DAC进行了DI(Direct-Injection)发动机的二维数值模拟，并改进了确定初始组分的方法。计算速度的对比表明，在多维发动机数值模拟中的DAC简化加速效果不如在单区绝热发动机模型模拟中显著，但仍有效加速了化学反应计算。对于34组分和61组分的正庚烷反应机理，计算时间分别节省了30%和50%。Contino等[91]使用TDAC模拟了HCCI发动机的燃烧过程，加速因子可高达500.0，而对于柴油发动机，加速因子在9.0左右。Xie等[60]将DAAM方法用于PCCI(Premixed Charge Compression Ignition)发动机的数值模拟，模拟结果显示DAAM相比于ISAT方法使计算加速了50%，其计算效率也高于ISAT-DAC方法，且数值模拟的准确性处于同一水平。此外，DAC和ISAT方法也可以和CA方法联合[61-62]，在分区的基础上再进行DAC简化或ISAT建表，可以进步一提高计算速度。Zhou等[61]的研究表明，对于约40个组分的反应机理，CA联合DAC的方法可以使计算加速一倍，而对于约140个组分的反应机理，加速因子可达到9.0左右。
DAC在湍流燃烧数值模拟中的加速效果不尽相同，其影响因素是多方面的：
(1) DAC简化的加速效果与数值模拟结果误差是相关的，用户所能容忍的误差越大，DAC简化能实现的加速就越大。误差的调节方式与DAC中具体应用的简化方法有关，如DRG、DRGEP、PFA等通过简化阈值调节，合理阈值的大小还根据所使用简化机理的不同而不同，最终的误差需要通过结果来验证；而DSRR则通过给定容许误差来调节。
(2) 加速效果与燃烧特性有关。Liu等[21]的研究表明，对于燃烧反应不活跃的情况，如自着火过程发生前的慢速反应区域和自着火完成后的平衡区域，以及一维预混火焰面上游的未燃区和火焰面下游的已燃区，燃烧过程中活跃的组分数较小，使用DAC简化可以显著降低局部简化机理中的组分，从而大大提高计算速度。而对于反应较为剧烈的区域(如自着火时刻或火焰锋面处)，化学反应过程复杂，涉及组分多，因此DAC简化产生的局部简化机理规模较大，甚至与输入的反应机理规模相当，此时DAC的加速效果不明显。
(3) 加速效果与输入反应机理有关，应用规模越大的反应机理通常能获得越明显的加速效果。例如Wu等[90]的研究表明，同等网格数量的情况下，对于57组分、75组分和111组分的反应机理，DAC的加速因子分别为1.9、2.2和2.5。
在实际应用中，DAC如果与其他加速手段耦合，加速效果也会受到影响。例如DAC方法与ISAT方法耦合时[51]，DAC的加速效果随ISAT误差阈值的增大而略有降低。在湍流燃烧的并行计算中，化学反应计算的并行方式也对DAC的加速效果有较大影响。Liu等[21]的研究表明，由于并行LES中化学反应的计算效率受火焰面附近处理器核心的计算效率控制，在并行计算中，化学反应求解完成后，核与核之间需要进行一次同步并通信，然后再进行下一步计算，因此总体的化学反应计算时间由各个核心中最慢的决定。例如，图 2所示是不同核心上的化学反应计算时间tODE, p，可以看到不同计算区域中的tODE, p差别很大，火焰反应区附近的tODE, p显著高于其他反应活性较低的区域。放大图 2(a), 显示出最高的tODE, p出现在火焰中r=d, 10d < x < 25d的区域。这正是湍流-化学相互作用最强烈的区域，湍流火焰中的局部熄火和再燃频繁发生。CoDAC和DAC的主要区别在于是否进行自相关算法运算。图 2(d)所示是当地各个网格点上的简化机理中通过PFA算法得到而不是通过自相关算法得到的占比ϕPFA, p，分布结果同样表明在火焰反应区附近自相关算法带来的计算加速效果不明显。在自着火的模拟结果中(如图 3所示)，同样可以发现在反应活跃的点火时刻，计算时间也出现了显著升高的现象。因此，要进一步提高计算效率，一方面应平衡处理器之间的计算效率，如使用x2f_mpi算法[96]等；另一方面，可以发展更高效的化学反应积分方法，从而提高整体计算效率。
![]()
图 2 在各处理器核心上的(a) ODE时间(tODE, p)以及(b) ODE时间、(c)温度T、(d) PFA占比(ϕPFA, p)和(e)简化机理中组分数(NS)的局部放大视图[21]Fig. 2 Contour plot of (a) ODE time on each processor (tODE, p) together with zoom-in view of (b) ODE time on each processor, (c) temperature T, (d) percentage of cells performing PFA (ϕPFA, p) and (e) number of selected species in locally reduced mechanism (NS) [21]![]()
2 Krylov子空间近似的指数积分格式
对于如下的燃烧化学反应常微分方程问题：
(1) 二阶的指数积分格式可以表示为[70]：
(2) 式中ϕ表示包括温度和组分质量分数在内的微分方程变量，ωk表示各个变量的化学反应速率，h为时间步长，当时间步长较短时可认为Jacobian矩阵Jk=∂ωk/∂ϕk是近似恒定的，矩阵的φ函数定义为：
(3) 此时，常微分方程的求解变成了对一般形式为φ1(τA)v的向量的求解，其中A为在n×n维实空间Rn×n中的矩阵，v为在n维实空间Rn中的向量。
当n很大时，φ函数的计算需要巨大的计算量，利用Krylov子空间的性质，组合φ1(τA)v可以方便地在更小的m维Krylov子空间中得到近似。Krylov子空间是由向量序列v, Av, A2v, …, Am-1v张成的空间，构造Krylov子空间的算法称为Arnoldi算法[77]。原向量φ1(τA)v在Krylov子空间中的近似可以表示为[77]：
(4) 式中β=‖v‖，Vm=(v1, v2, …, vm)为Krylov子空间的基向量，Hm为上Hessenberg矩阵，是原矩阵A在Krylov子空间中的投影，e1和em分别表示第1维和第m维单位向量。当矩阵A在Krylov子空间中投影为Hm时，Hm的特征值称为Ritz值，随着m的增加，收敛于原矩阵A模最大的特征值。这一重要性质使Krylov子空间广泛应用于近似求解矩阵特征值问题[97]。通过近似式(4)，原n维问题降为m维问题，使指数格式求解所需的计算量显著降低。
Bisetti[82]使用四阶Rosenbrock指数格式exp4[98]计算了火焰的自着火过程，结果表明, 尽管使用大时间步长时非线性系统刚性很大，但指数格式方法仍是稳定的。Curtis等[83]对比了CPU和GPU计算时exp4和expbr43指数积分格式的计算效率，结果表明2种指数积分格式在CPU和GPU上都慢于隐式求解器CVODE和Radau-IIA。然而，四阶指数积分格式每推进1个时间步长需要计算3次矩阵指数函数。而矩阵指数函数的计算十分耗时，为了实现加速计算，应尽量减少计算次数。因此，刘再刚等[84]使用二阶指数格式，如式(2)，并引入Schur分解方法有效控制了算法的舍入误差[99]，发展了用于加速燃烧化学反应计算的指数积分求解器。
指数格式算法的计算效率可以使用简单的燃烧模型来估计。带配对混合(Pairwise mixing)的局部搅拌反应器(Partially-Stirred Reactor, PaSR)是一个假设的反应器[100]。这种反应器可以用于模拟湍流燃烧数值模拟中的小尺度混合和反应过程，常用于检验燃烧化学反应计算方法和ISAT方法的准确性和计算效率。模拟使用的燃料和参数与Liu等[21]的研究相同，PaSR入流由3部分组成，分别为甲烷、甲烷-空气燃烧后的平衡产物以及空气，并分别对应Sandia Flame系列火焰的主射流、值班射流和空气伴流。在Liu等[21]的研究中，CoDAC在PaSR模拟中得到了与LES模拟相近的加速结果，表明了PaSR能合理估计LES的计算效率。对于燃烧化学反应问题，还可以同时使用一些加速算法。CoDAC简化应用于指数格式可以减少算法中矩阵A和v的维数，SpeedCHEM(SC)库[101]中的稀疏矩阵算法和解析Jacobian矩阵算法可以降低矩阵存储所需的内存空间，并加速Jacobian矩阵和Arnoldi算法中矩阵-向量乘法Av的计算。MTS方法[69]可以分离刚性问题中的刚性部分和非刚性部分，从而降低刚性方程组的数量。在指数格式中，作用与CoDAC相同，可以减少算法中矩阵A和v的维数。Liu等[99]将指数积分格式与SC库、CoDAC简化和MTS方法结合，并与DVODE求解器的计算结果作了详细对比，不同的组合算例列于表 1。
表 1 使用不同加速方法的算例设置Table 1 Simulated cases for different acceleration methods加速方法\求解器 DVODE 指数格式 Non R - SC As Bs SC + CoDAC Asc Bsc SC+MTS Asm Bsm SC + CoDAC + MTS Ascm Bscm 图 4所示是分别使用GRI-Mech 3.0[102]和USC Mech Ⅱ[103](111组分/784反应)计算得到的结果。图中的加速因子和误差均以表 1中的参考工况R为基准，加速因子和误差的详细定义可参考文献[99]。从图中可以看出，在同等精度并同时采用了SC的情况下，使用指数格式的计算速度均显著快于使用隐式格式求解器DVODE，并且加速效果显著优于使用DVODE结合3种加速算法。但指数格式结合CoDAC和MTS加速算法时，不仅计算精度下降，计算效率也有所下降。从图 5可以看出，效率下降主要是由CoDAC和MTS带来的额外开销导致的。因此只使用含SC的指数格式可以得到最佳的加速效果。
![]()
图 4 使用反应机理(a)GRI-Mech 3.0[102]和(b)USC Mech Ⅱ[103]得到的表 1中算例的加速因子γ与最大平均相对误差ε的关系。Xsc(εr)，Xsm(α)和Xscm(εr, α)表示表 1所列工况算例，括号中的数值εr和α分别表示CoDAC简化阈值和MTS安全因子[99]Fig. 4 The speedup factor γ as functions of maximum averaged relative error ε for the cases in Table 1 with (a) GRI-Mech 3.0[102] and (b) USC Mech Ⅱ [103]. Xsc (εr), Xsm(α) and Xscm(εr, α) represent the cases in Table 1 and numbers εr and α in the parentheses represent the reduction threshold of CoDAC and the safety factor of MTS, respectively[99]![]()
指数格式的加速效果一方面来源于大步长显式时间推进的优势，另一方面是由于与Krylov子空间近似的降维效果。从图 6中可以看到，Krylov子空间的大小增长速度远低于刚性方程组规模的增速。由此可知，在化学反应计算中应用指数格式在保证计算精度的同时可以显著提高计算速度。因此，其在燃烧LES中有很好的应用前景。指数格式求解器直接求解化学反应方程组，如果与查表类加速方法，如ISAT相结合，可以进一步降低化学反应计算时间，从而实现快速高精度的湍流燃烧数值模拟，从而使得详细化学反应机理用于实际发动机燃烧室湍流燃烧数值模拟成为可能，并以此指导湍流燃烧研究和燃烧器设计与实验。
![]()
3 结论
在湍流燃烧数值模拟中使用详细化学反应机理可以显著提高燃烧反应计算精度，但是由此导致的计算量激增是阻碍大规模高精度燃烧数值模拟的主要因素之一。在计算过程中动态、自适应地进行化学反应机理简化可以获得一定的加速效果。然而，在并行燃烧数值模拟中，由于燃烧场中火焰反应区域的分布不均匀，处理器核心的负载极度不平衡，且核心之间需要进行必要的同步通信，加速效果在很大程度上不能充分发挥。相比之下，使用刚性求解器得到的加速将直接作用于每个处理器核心，更有利于整体计算效率提高。相比于常见的隐式格式以及CoDAC和MTS加速方法，在同等精度下，Krylov子空间近似的指数积分格式对化学反应计算的加速效果更为显著，加速主要来源于指数格式的显式大时间步推进能力和Krylov子空间近似的降维效果。
为了进一步提高化学反应的求解速度，首先，可行的方法是以高效积分求解器为基础，紧密结合查表类方法，互相弥补2种方法的不足：用查表代替重复性计算，用高效积分补充表中的元素。其次，使用自适应网格以及自适应平衡处理器核心负载的算法，可以有效避免计算资源的空闲，提高整体计算效率。最后，燃烧化学反应的求解涉及的浮点数运算密集，较适合使用图形处理器架构进行运算，这也是燃烧数值模拟加速的一个发展方向。
-
![]()
图 1 使用偶极子网格切割的CFD表面网格
Fig. 1 CFD surface mesh cut by the DLM panels uncut CFD mesh and cut CFD mesh
![]()
图 3 计算模型与风洞测量变形结果对比
Fig. 3 Comparison of displacement and rotation between NASTRAN model and wind tunnel measurement
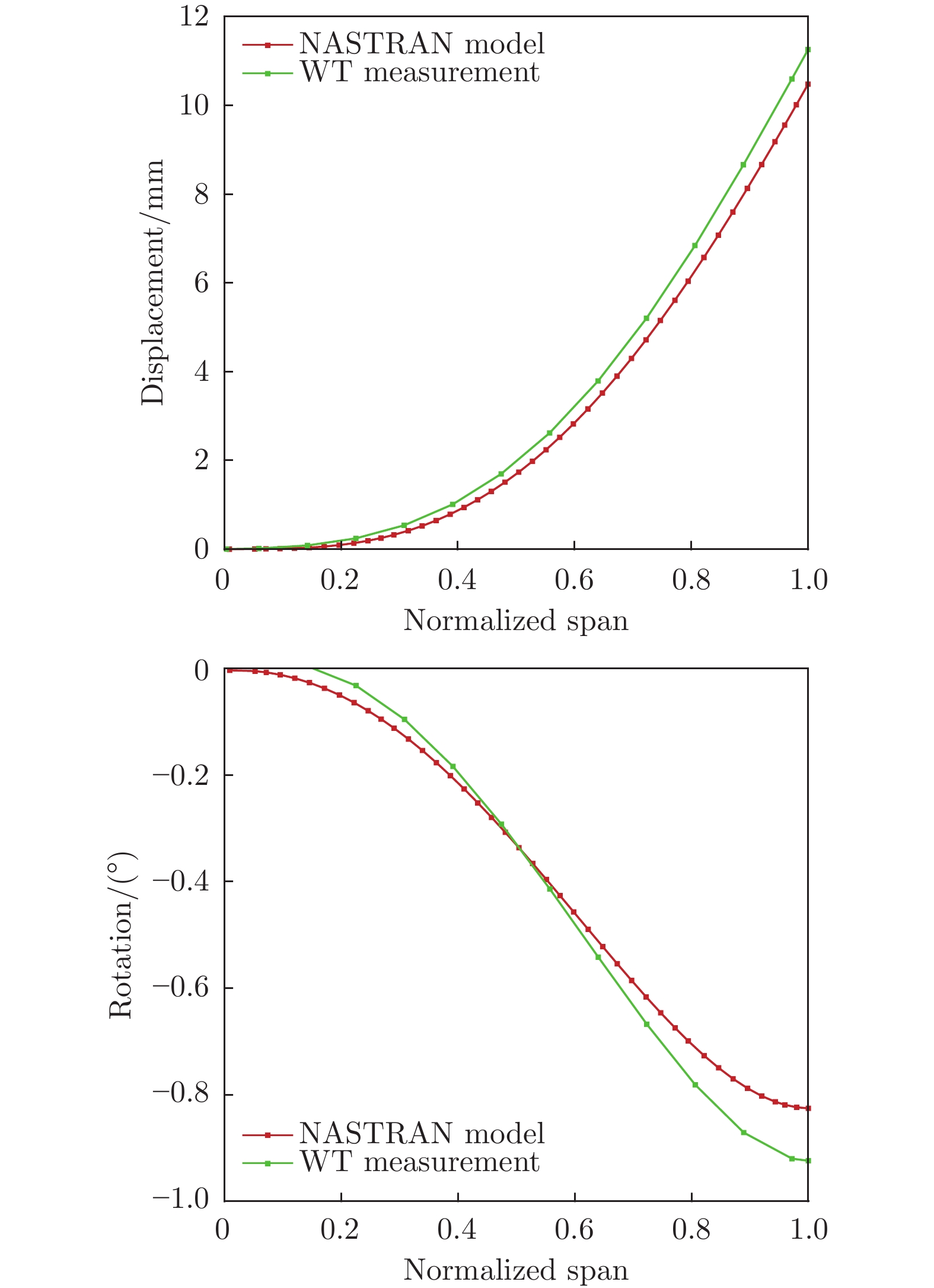
表 1 计算模型与风洞测量变形结果对比
Table 1 Comparison of displacement and rotation between NASTRAN model and wind tunnel measurement
翼尖变形 风洞测量 计算模型 误差 位移/mm 11.2592 10.4803 0.7789 扭转角/(°) − 0.9240 − 0.8255 0.0984 
下载: 导出CSV
表 2 Ma = 0.85工况下CL–α曲线修正误差
Table 2 Deviation of corrected CL–α curve at Ma = 0.85
q/E =
0.38 × 10−6Ave. ΔCL Advantage Max ΔCL Advantage Fixed KCL 0.0075 — 0.0245 — Piecewise KCL 0.0055 −26.7% 0.0137 −44.2%
下载: 导出CSV
表 3 Ma = 0.80工况下CL–α曲线修正误差
Table 3 Deviation of corrected CL–α curve at Ma = 0.80
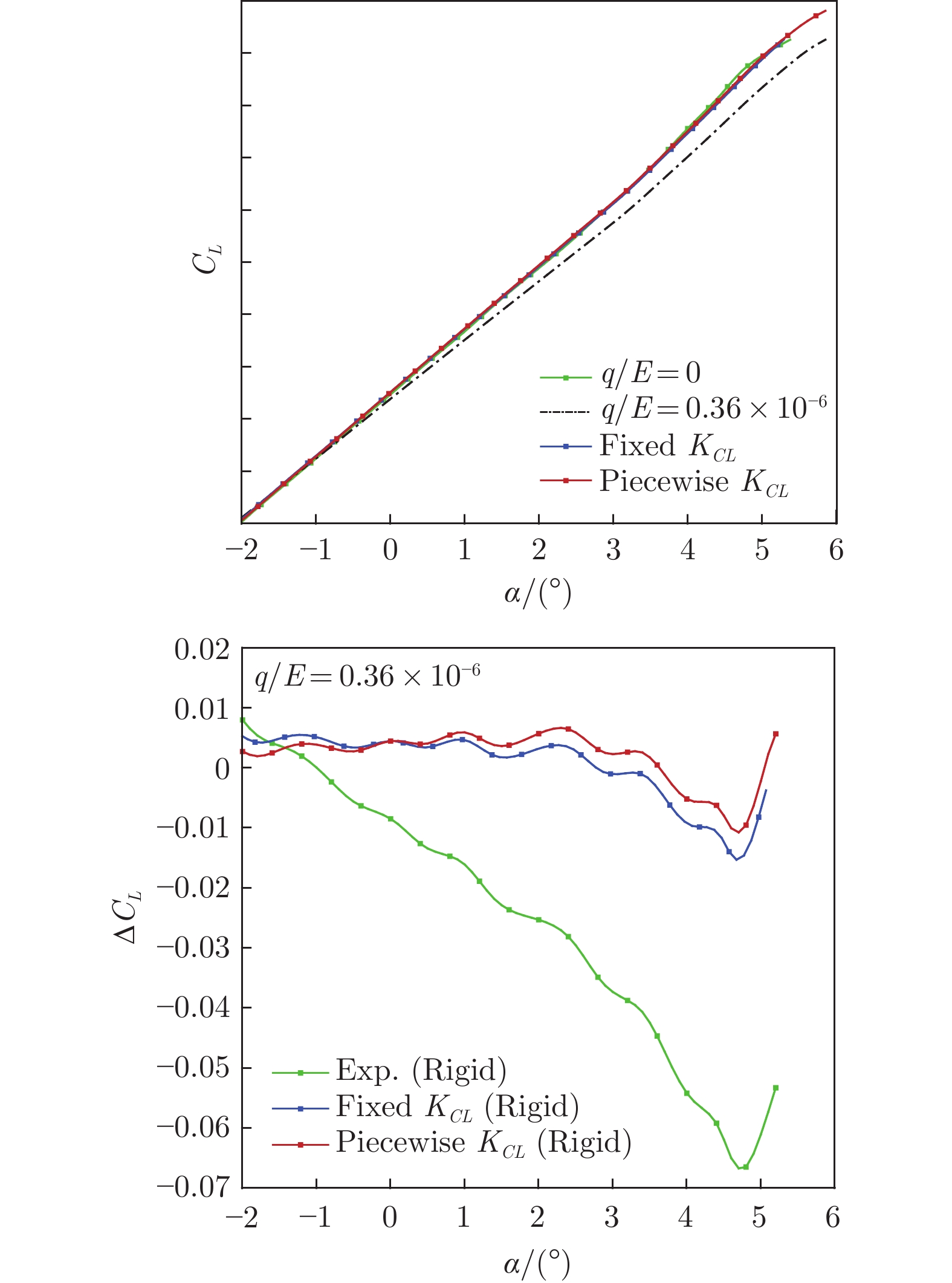
q/E =
0.36 × 10−6Ave. ΔCL Advantage Max ΔCL Advantage Fixed KCL 0.0047 — 0.0153 — Piecewise KCL 0.0043 −8.9% 0.0108 −29.7%
下载: 导出CSV
表 4 Ma = 0.85工况下Cm–α曲线修正误差
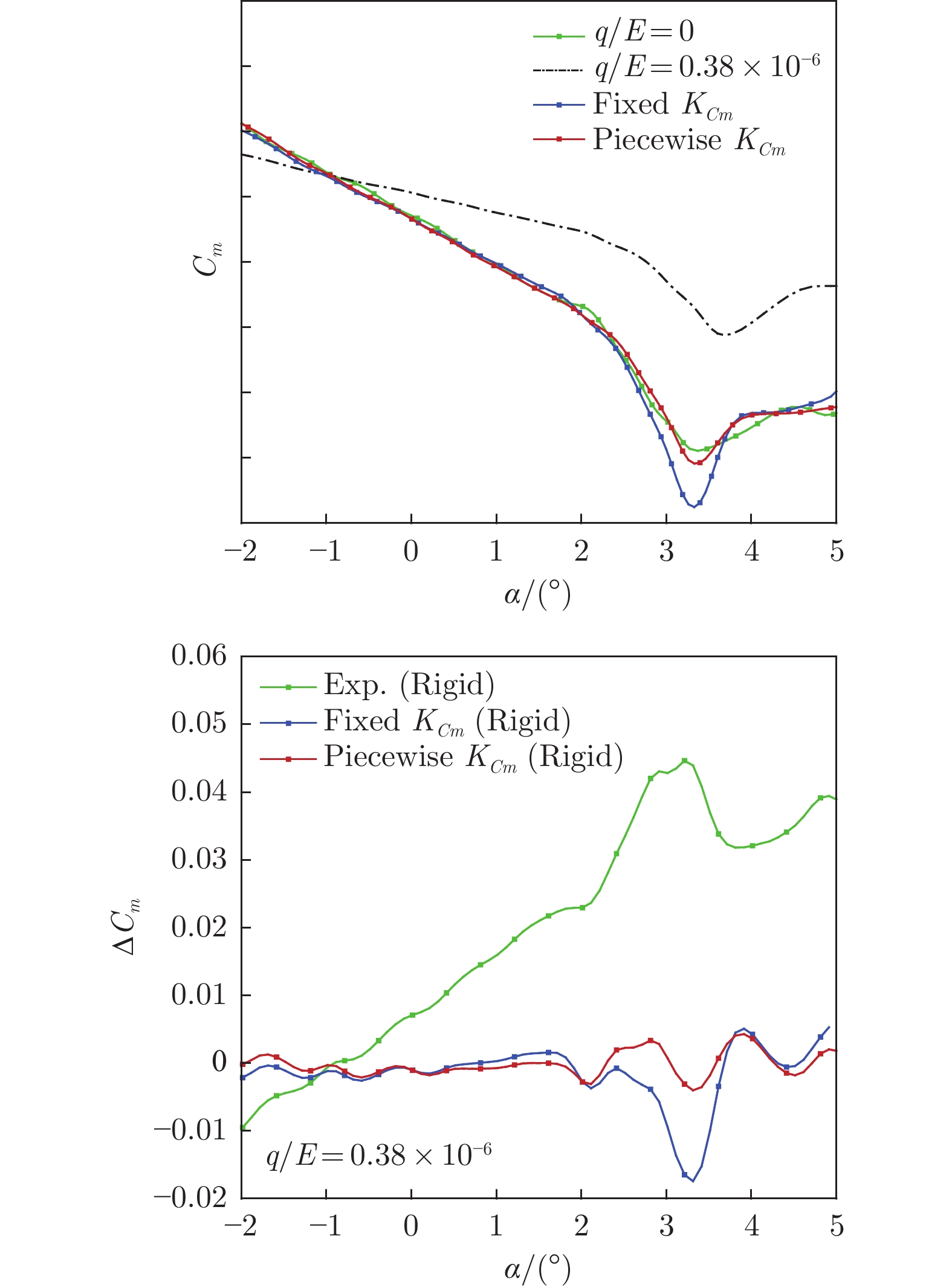
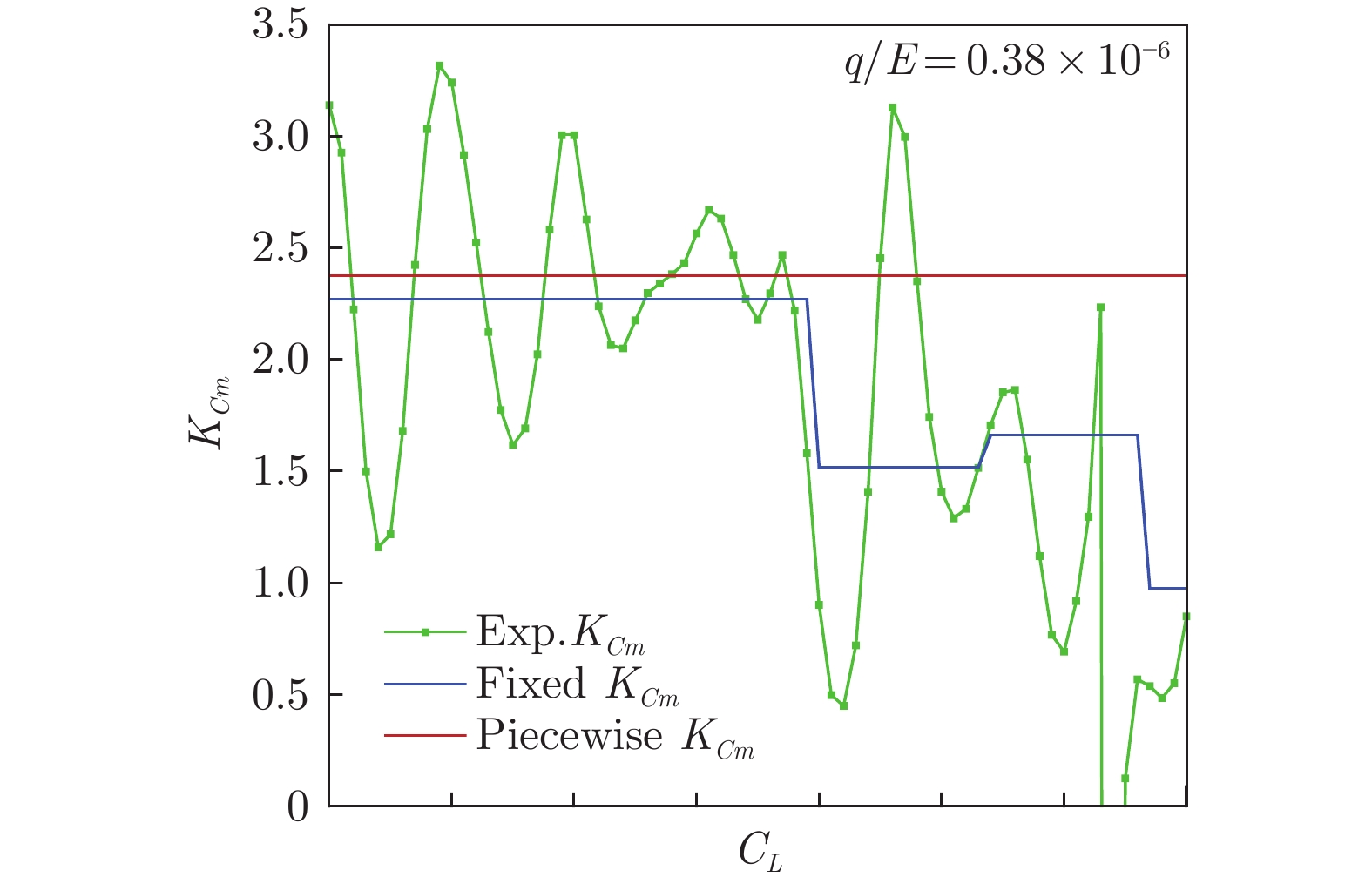
Table 4 Deviation of corrected Cm–α curve at Ma = 0.85
q/E =
0.38 × 10−6Ave. ΔCm Advantage Max ΔCm Advantage Fixed KCm 0.0030 — 0.0174 — Piecewise KCm 0.0014 −53.7% 0.0043 −75.5%
下载: 导出CSV
表 5 Ma = 0.80工况下Cm–α曲线修正误差
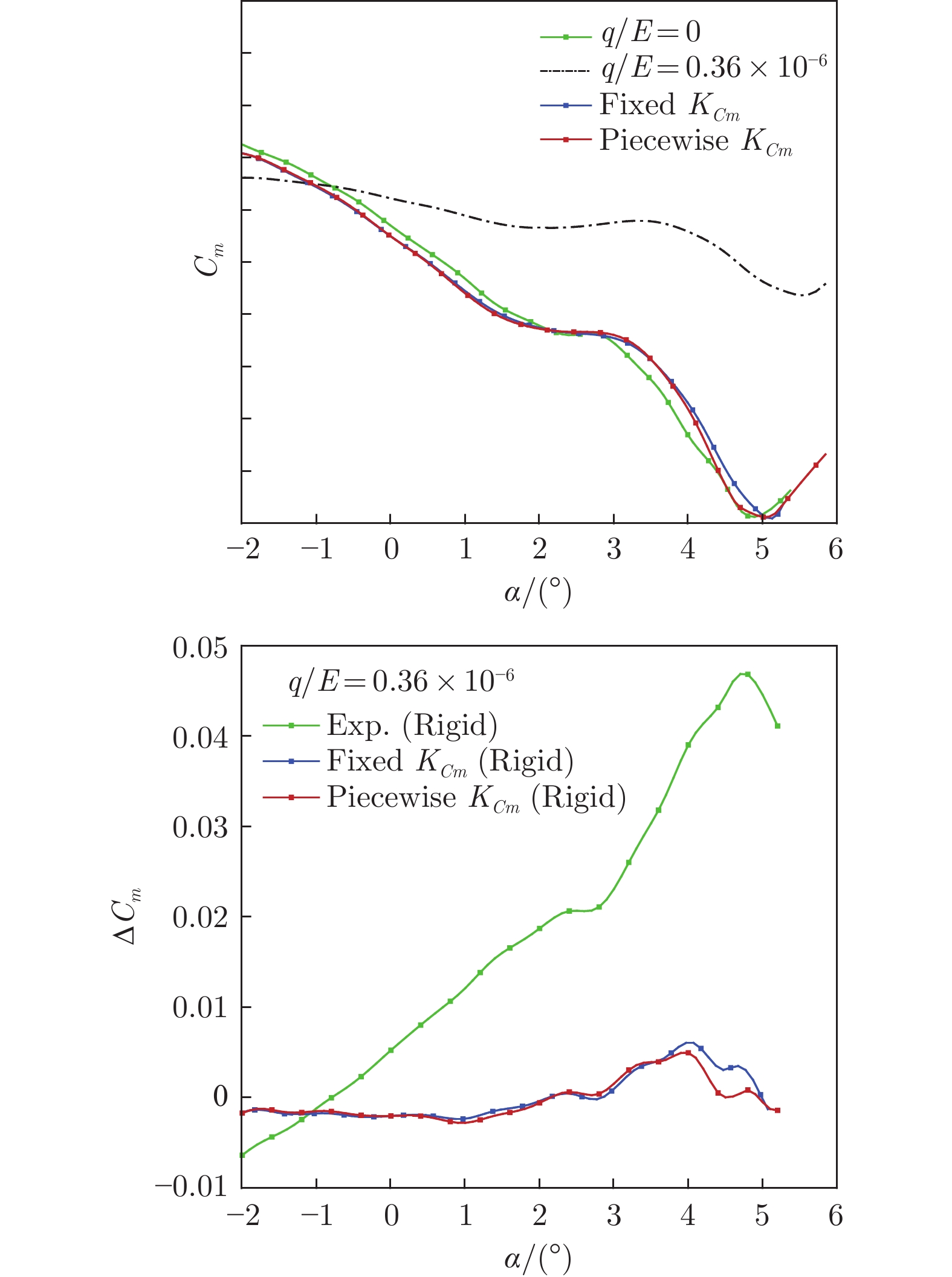
Table 5 Deviation of corrected Cm–α curve at Ma = 0.80
q/E =
0.38 × 10−6Ave. ΔCm Advantage Max ΔCm Advantage Fixed KCm 0.0021 — 0.0061 — Piecewise KCm 0.0018 −12.0% 0.0050 −18.1%
下载: 导出CSV
表 6 Ma = 0.85工况下的弹性修正一致性
Table 6 Consistency of elastic correction at Ma = 0.85
Ave. ΔCL Max ΔCL Ave. ΔCm Max ΔCm Discrepancy 0.0030 0.0078 0.0008 0.0024
下载: 导出CSV
表 7 计算步骤表
Table 7 Main procedure of correction
编号 计算步骤 计算资源 每个算例
耗时1 CFD计算，迎角0°、2°、3°、4°、5°，
多重网格计算5000 步16核CPU工作站 4 h 2 CFD数据映射至气动面元 移动工作站 5 min 3 生成各迎角（升力）区间修正矩阵 移动工作站 5 min 4 NASTRAN静气弹分析 移动工作站 5 min
下载: 导出CSV
-
[1] KEYE S, RUDNIK R. Aero-elastic simulation of DLR’s F6 transport aircraft configuration and comparison to experimental data[C]//Proc of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition. 2009: 580. doi: 10.2514/6.2009-580
[2] 刘大伟, 熊贵天, 刘洋, 等. 宽体客机高速风洞试验数据修正方法[J]. 航空学报, 2019, 40(2): 16–31. DOI: 10.7527/S1000-6893.2018.22205 LIU D W, XIONG G T, LIU Y, et al. Method of test data correction for wide-body aircraft in high speed wind tunnel[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(2): 16–31. doi: 10.7527/S1000-6893.2018.22205
[3] BENEDICT K A, HEDGES L, ROBINSON A, et al. Inclusion of aeroelastic twist into the CFD analysis of the twin-engine NASA common research model[C]//Proc of the 52nd Aerospace Sciences Meeting. 2014: 0251. doi: 10.2514/6.2014-0251
[4] KEYE S, BRODERSEN O, RIVERS M B. Investigation of aeroelastic effects on the NASA common research model[J]. Journal of Aircraft, 2014, 51(4): 1323–1330. doi: 10.2514/1.C032598
[5] RIVERS M, HUNTER C, CAMPBELL R. Further investigation of the support system effects and wing twist on the NASA common research model[C]//Proc of the 30th AIAA Applied Aerodynamics Conference. 2012: 3209. doi: 10.2514/6.2012-3209
[6] YASUE K, SAWADA K. CFD-aided evaluation of Reynolds number scaling effect accounting for static model deformation[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2012, 55(5): 321–331. doi: 10.2322/tjsass.55.321
[7] BALLMANN J. Experimental Analysis of high Reynolds Number structural Dynamics in ETW[C]//Proc of the 46th AIAA Aerospace Sciences Meeting and Exhibition. 2008: 841. doi: 10.2514/6.2008-841
[8] BIANCOLINI M E, CELLA U, GROTH C, et al. Static aeroelastic analysis of an aircraft wind-tunnel model by means of modal RBF mesh updating[J]. Journal of Aerospace Engineering, 2016, 29(6): 04016061. doi: 10.1061/(asce)as.1943-5525.0000627
[9] CELLA U, BIANCOLINI M E. Aeroelastic analysis of aircraft wind-tunnel model coupling structural and fluid dynamic codes[J]. Journal of Aircraft, 2012, 49(2): 407–414. doi: 10.2514/1.C031293
[10] VRCHOTA P, PRACHAŘ A. Using wing model deformation for improvement of CFD results of ESWIRP project[J]. CEAS Aeronautical Journal, 2018, 9(2): 361–372. doi: 10.1007/s13272-018-0286-3
[11] 王艺坤, 史爱明. 机翼风洞试验模型CFD静气动弹性修正研究[J]. 科学技术与工程, 2012, 12(15): 3685–3688. DOI: 10.3969/j.issn.1671-1815.2012.15.032 WANG Y K, SHI A M. Static aeroelastic correction for wind tunnel results of wing model with CFD[J]. Science Technology and Engineering, 2012, 12(15): 3685–3688. doi: 10.3969/j.issn.1671-1815.2012.15.032
[12] 夏生林, 赵利霞, 唐克兵, 等. CFD技术在静气动弹性修正计算中的研究与应用[C]// 第十一届全国空气弹性学术交流会会议论文集. 2009: 310-315. XIA S L, ZHAO L X, TANG K B, et al. The investigation and application of the technique of CFD simulation to static aeroelasticity correction[C]//Proc of the 11th Academic Conference of Aeroelasticity. 2009: 310-315.
[13] LIU D W, XU X, LI Q, et al. Ispravak učinaka deformacije modela za superkritično krilo u transoničkom vjetrenom tunelu[J]. Tehnicki Vjesnik, 2017, 24(6): 1647–1655. doi: 10.17559/tv-20160525142932
[14] 孙岩, 张征宇, 邓小刚, 等. 风洞模型静弹性变形对气动力影响研究[J]. 空气动力学学报, 2013, 31(3): 294–300. DOI: 10.3969/j.issn.1672-9897.2011.03.013 SUN Y, ZHANG Z Y, DENG X G, et al. Static aeroelastic effects of wind tunnel model on aerodynamic forces[J]. Acta Aerodynamica Sinica, 2013, 31(3): 294–300. doi: 10.3969/j.issn.1672-9897.2011.03.013
[15] SUN Y, WANG Y T, RONCH A, et al. A fast correction method of model deformation effects in wind tunnel tests[J]. Aerospace, 2018, 5(4): 125. doi: 10.3390/aerospace5040125
[16] GIBSON T. Investigation of wind tunnel model deformation under high Reynolds number aerodynamic loading[C]//Proc of the 40th AIAA Aerospace Sciences Meeting & Exhibition. 2002: 424. doi: 10.2514/6.2002-424
[17] 赵卓林, 张家齐, 徐港, 等. 一种基于CFD的增压风洞试验数据刚体修正方法[J]. 飞机设计, 2019, 39(6): 31–34. DOI: 10.19555/j.cnki.1673-4599.2019.06.007 ZHAO Z L, ZHANG J Q, XU G, et al. A correction study on pressurized wind tunnel results based on CFD[J]. Aircraft Design, 2019, 39(6): 31–34. doi: 10.19555/j.cnki.1673-4599.2019.06.007
[18] GIESING J P, KALMAN T P, RODDEN W P. Correction factory techniques for improving aerodynamic prediction methods[R]. NASA-CR-144967, 1976.
[19] WIESEMAN C D. Methodology for matching experimental and computational aerodynamic data[R]. NASA-TM-100592, 1988.
[20] 严德, 杨超, 万志强. 应用气动力修正技术的静气动弹性发散计算[J]. 北京航空航天大学学报, 2007, 33(10): 1146–1149. DOI: 10.3969/j.issn.1001-5965.2007.10.004 YAN D, YANG C, WAN Z Q. Static Aeroelastic divergence analysis by introducing correction techniques of aerodynamic data[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(10): 1146–1149. doi: 10.3969/j.issn.1001-5965.2007.10.004
[21] MORENO R, NARISETTI R, VON KNOBLAUCH F, et al. A modification to the enhanced correction factor technique to correlate with experimental data[C]//Proc of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. 2015: 1421. doi: 10.2514/6.2015-1421
-
期刊类型引用(5)
1. 胡喆，张军，倪章松，苏文，许德军，黄丹. 磁浮飞行风洞动模型系统振动特性仿真研究. 振动与冲击. 2025(02): 143-150+198 . 
百度学术
2. 聂少军，汪运鹏，王春，姜宗林. 激波风洞测力信号的频域数据深度学习建模分析方法. 振动与冲击. 2023(13): 296-302+315 . 百度学术
3. 聂少军，汪运鹏. 基于时频变换的激波风洞天平信号分析与处理. 力学学报. 2022(01): 232-243 . 百度学术
4. 王南天，王雄，孙鹏，许晓斌，邹琼芬. 连续变迎角试验数据自适应分段拟合滤波方法. 北京航空航天大学学报. 2021(06): 1145-1151 . 百度学术
5. 聂少军，王粤，汪运鹏，赵敏，隋婧. 循环神经网络在智能天平研究中的应用. 力学学报. 2021(08): 2336-2344 . 百度学术
其他类型引用(3)
计量
- 文章访问数: 183
- HTML全文浏览量: 73
- PDF下载量: 18
- 被引次数: 8
