Experimental study on drag reduction of L-shaped bluff body by AC-DBD plasma actuation
-
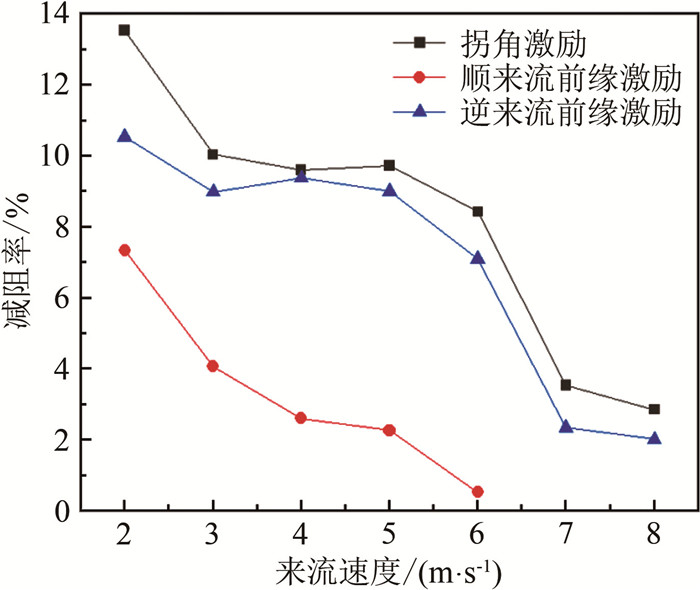
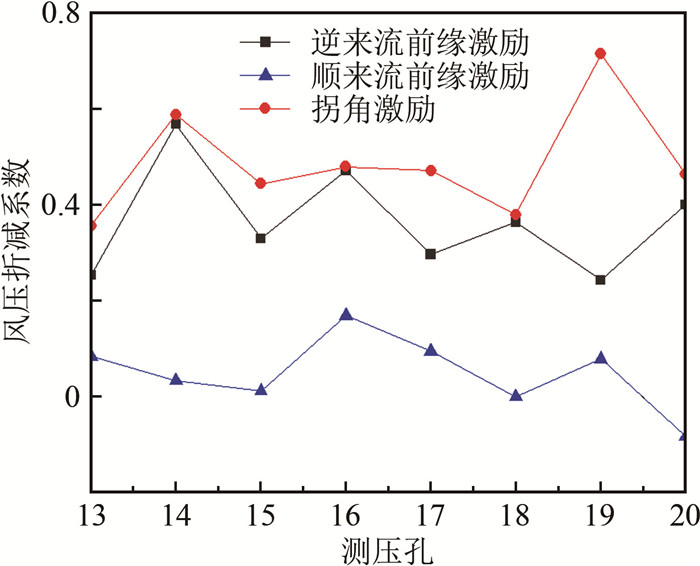
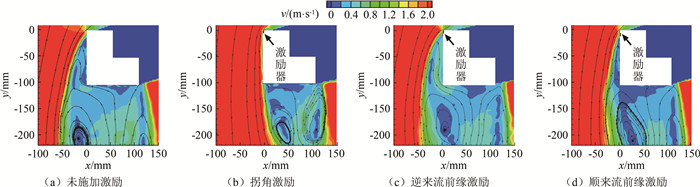
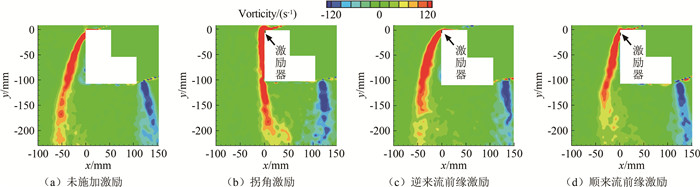
摘要: 等离子体流动控制是一种应用广泛的主动流动控制技术。为进一步研究其机理、拓展其应用范围,针对L形截面钝体模型,采用3种AC-DBD(介质阻挡放电)等离子体激励器布置形式,比较了施加激励后的减阻效果,并对减阻机理进行了研究。实验在南京航空航天大学0.8 m低速直流风洞中进行(风向角0°、来流速度2~8 m/s),激励器布置形式为顺来流前缘激励、逆来流前缘激励和拐角激励。研究结果表明:不同来流速度下,等离子体激励器对L形截面钝体都有一定的减阻效果,且减阻效果随流速增大而降低;拐角激励减阻效果最佳,逆来流前缘激励次之,顺来流前缘激励最差;通过流场分析,说明了激励器布置形式变化产生了不同的扰动效果;不同的流动控制机理是影响减阻效果的关键因素。Abstract: Plasma flow control is a widely used active flow control method. In order to further expand the application scope and understand the actuation mechanism, three kinds of AC-DBD (Dielectric Barrier Discharge) plasma actuator layout forms are used to compare the drag reduction capabilities of the L-shaped model after actuation, and the drag reduction mechanism is studied. The experiment is carried out in a low-speed DC wind tunnel, with a wind direction angle of 0°, and a wind speed of 2-8 m/s. These different actuators layout forms are the plasma actuator placed close to the leading edge along the incoming flow direction, the plasma actuator placed close to the leading edge against the incoming flow direction, and the plasma actuator arranged at the corner, respectively. Research shows that plasma actuators under different wind speed conditions have a certain control effect on drag reduction of bluff bodies, and the control ability decreases with the increase of wind speed. The plasma actuator placed in the corner produces the best control effect, and the drag reduction rate can reach more than 13% at low speed. The plasma actuator placed close to the leading edge against the incoming flow direction produces a similar effect. The drag reduction rate of the plasma actuator near the leading edge along the inflow direction can only reach about 7% at most. By analyzing the flow field, it is shown that the change of layout position produces different disturbance effects. Different flow control mechan-isms are the key factors affecting the actuation effect.
-
0 引 言
随着“工业4.0”和“中国制造2025”的提出,增材制造技术在航空、航天和汽车等领域的应用不断深入,以铝合金为代表的轻质合金材料需求快速增长。铝合金具有资源丰富、密度低、比强度较高的优点。2019年SmarTech报告指出,2018年增材制造铝合金粉出货量增长43%,且未来10年将以每年近50%的速度增长。
增材制造要求铝合金粉末具有粒径集中度高(15~53 μm和53~150 μm)、球形度高、含氧量低、无卫星粉和空心粉等特性。金属液体雾化是增材制造用金属粉末的主要制备方式[1],主要基于气雾化、等离子体旋转电极雾化[2-3]和等离子体雾化[4]等原理。采用这些方法制备的金属粉末粒径大、粒径分布宽、球形度差且含有卫星粉和空心粉,无法为增材制造提供高性能粉末。与气雾化和旋转电极雾化相比,采用转盘雾化技术制备的金属粉末具有粒径小、粒径集中度高、球形度高、无卫星粉和空心粉、成本低廉等优势,更加适用于增材制造。
受限于高温热烧蚀,转盘雾化技术目前主要应用于制备低温锡粉和功能材料等,转盘雾化制备铝合金及更高温度合金粉末的相关实验研究仍在开展之中。20世纪90年代,佐藤富雄等[5-7]采用钼盘片制备了铝镁锆合金粉末,后又进一步分析了粉末高温酸化特性[8]。Angers等研究了转盘表面涂层技术[9]并采用倒置转盘雾化技术制备了2024铝合金粉末[10],研究了AZ91镁合金在转盘雾化中产生的不规则颗粒[11]。Labrecque等[12]也对倒置转盘离心雾化制备镁合金技术进行了研究。陈振华等[13-14]提出了金属熔体多级快速凝固过程成粉理论并制取了铝锌合金粉末。温树德[15]基于转盘雾化技术研究了铅和铝雾化,并对8640钢进行了试探性雾化。Öztürk等[16-18]基于带鳍片转盘,采用喷嘴冷却转盘方法研究了锡、铝等金属的雾化技术。Eslamian等[19]在采用转盘离心雾化6061铝合金的过程中添加碳化硅粉末,形成了金属基复合粉末。刘英杰等[20]采用转盘雾化法制备了AlSi10Mg铝合金粉末,并对粉末各项性能和3D打印结构件性能进行了测试。Plookphol等[21]分析了转盘离心雾化制备SAC305粉末的影响参数。Zhang和Zhao[22-25]研究了离心雾化转杯几何形状和关键工艺参数对锡粉粒径和分布的影响并对金属液体的流动发展进行了分析。Alejandra等[26]研究了向雾化颗粒吹气对离心雾化制备铜粉的影响。王东祥等[27-30]分析了转盘雾化的若干流体力学问题,并采用熔融铝进行了离心雾化高温相似试验研究。从现有研究成果看,转盘雾化制备铝合金粉末技术目前仍处于实验室研究阶段,以制备少量样品和分析粉末性能为主,转盘表面金属液体的流体动力学问题研究和系统的粉末粒径分布规律研究较少。
本文基于独立开发的一套高温转盘雾化制粉实验装置,针对1060纯铝和AlSi10Mg铝合金,研究金属液体的铺展流动特征,分析流量、转速、盘径和转盘表面构型等对金属粉末性能的影响规律,基于线性回归理论分析得到粒径公式,以期为铝合金粉末的转盘离心雾化制备提供理论和技术支撑。
1 实验材料和方法
1.1 实验材料
采用1060纯铝和AlSi10Mg铝合金作为实验材料,化学成分见表1和2,表3和4分别列出了两者的物理性质(表中温度为实验中熔融铝液温度)。
表 1 1060纯铝的化学成分(%)Table 1 Chemical composition of 1060 pure aluminum (%)Al Fe Si Cu Zn V Mn Mg Ti 99.6 0.35 0.25 0.05 0.05 0.05 0.03 0.03 0.03 表 2 AlSi10Mg铝合金的化学成分(%)Table 2 Physical properties of 1060 pure aluminum (%)Al Si Zn Mg Fe Mn Ti Cu Ni Sn Pb else 9.70 0.60 0.50 0.50 0.40 0.10 0.07 0.05 0.05 0.05 注:“else”表示铝合金中除其他化学成分外,其余皆为Al的含量。 表 3 1060纯铝的物理性质Table 3 Physical properties of 1060 pure aluminumTemperature
/KDensity
/(g·cm−3)Viscosity
/(Pa·s)Surface tension
coefficient /(N·m−1)1150 2.310 0.926 × 10−3 0.843 1.2 高温转盘雾化制粉实验装置
本文基于现有研究积累,开发了一套高温转盘雾化制粉实验装置(图1和2)。该装置主要由加热炉、坩埚(内有塞杆)、转盘、高速电机、雾化室、真空泵、循环水冷系统(包括冷却水池、水泵、冷却水管道等)、氮气充装及循环冷却系统(含氮气钢瓶、风机、冷却风嘴及相关管道等)、集粉罐、高清摄像机、计算机等组成。加热炉为电阻式,电压380 V,最高温度1200 ℃,温度误差 ± 1 ℃。坩埚、塞杆都为石墨材质,坩埚容积8.8 L,塞杆头部为锥面,与坩埚下底面内锥孔配合密封。雾化室直径2.5 m,高度3.5 m,上半部为圆柱体,下半部为80°倒锥体。高速电机为标准电主轴,采用变频器控制转速,最高转速6 × 104 r/min。雾化室壁面为夹层冷却结构,以循环冷却水增压冷却。水泵为不锈钢多级离心泵(上海雨洲泵业制造有限公司,32CDLF4–160型),流量4 m3/h。
为防止粉末氧化并提高球形度,雾化室内部为惰性气体环境:先以真空泵将雾化室抽真空,再充入高纯氮气至微正压。真空泵为旋片式(上海万经泵业制造有限公司,2X–100型),极限压力6 × 10−2 Pa。采用标准40 L钢瓶供应氮气(体积分数99.9%),减压后充入雾化室并保持微正压100 Pa,防止外部空气进入。为快速冷却飞离转盘边缘的金属液滴,同时防止转盘上表面热量经转轴向下传递至高速电机内部,设计了一路氮气循环冷却系统,对转盘和转轴周围液滴进行冷却。冷却氮气采用高压风机(浙江亚士霸电机有限公司,HG–3000型,最大风压38 kPa,流量318 m3/h)增压。雾化室侧壁开了2个标准视窗(视窗直径约90 mm),视窗外安装2台高清摄像机,视频信号通过网线传输至计算机进行实时显示和存储。雾化室下部安装了收集粉末的集粉罐。
1.3 不同构型的转盘设计
转盘是雾化制粉装置的核心部件,需承受高温金属液体的持续冲刷,应具有耐高温、耐熔蚀的特性;为保证金属液体与转盘充分接触,转盘上表面应具有良好的润湿性;为防止金属液体的热量沿转轴向下传递至高速电机内部,转盘还应具有低热导率。本文设计了平面、锥面和弧面等3种构型的转盘(图3),用以研究不同构型转盘的雾化性能。为保证润湿性及耐高温、耐熔蚀特性,转盘以耐高温、耐熔蚀的复合材料制作,并进行了提高润湿性的加工处理。转盘具体参数见后文实验结果介绍。
1.4 转盘雾化实验
实验中,将雾化室抽真空至压力100 Pa以下,然后充入体积分数99.9%的氮气至微正压100 Pa(表压)。向坩埚中投入一块铝锭(直径80 mm,长150 mm),加热炉升温至880 ℃,铝锭完全熔化为铝液。启动高速电机至设定转速,拔出塞杆,铝液垂直流下至转盘中心,迅速沿盘面铺展流动至转盘边缘,高速甩出雾化为液滴。液滴在表面张力作用下收缩为球形并在飞行过程中与氮气快速对流换热,凝固为粉末,最终下落汇集至集粉罐中。图4为转盘雾化制备球形铝粉实验的典型照片。从图中可以看到:亮红色的高温铝液在铺展过程中与转盘发生热传递,使得转盘升温变红;转盘周围布满大量凝固后飘落的铝粉。
1.5 粉末取样及筛分处理
受水跃或沉积层的影响,部分铝液并非均匀铺展于盘面,而是斜向飞溅而出,形成大片铝渣或铝丝。研究者普遍认为铝渣或铝丝不属于离心雾化产物,需以筛网将其过滤,收集粒径750 μm以下的粉末进行统计分析。采用二分器从收集的粉末中取出50 g样品进行筛分,将各筛网上的粉末收集至样品瓶并精确称重,基于筛下质量百分比计算粉末累积质量分数。
使用的分析测试仪器包括:扫描电子显微镜(Hitachi SU1510,二次电子分辨率3.0 nm);粉末二分器(国标3 mm × 32格,浙江欣锴实验仪器设备有限公司);机械振筛机(河南亚创机械设备有限公司,YC–200型);标准分样筛(直径200 mm,60、100、150、300、400目,上海言锦筛网加工厂);高精度电子秤(3000 ± 0.02 g)。
2 实验结果与讨论
2.1 转盘表面铝液铺展流动形貌表征
图5为雾化实验结束后转盘上表面的照片(实验转速分别为18000、24000、30000 r/min)。以18000 r/min转速的转盘为例(图6):在直径25 mm范围内,铝膜铺覆稀疏且非常薄,命名为“光洁区(clean area)”;在直径25~44 mm范围内,转盘表面铺覆了薄薄的铝层,手触有磨砂感,命名为“磨砂区(frosted area)”。在直径44 ~48 mm范围内,磨砂层上表面又覆了一层非常薄的铝膜,命名为“铺展区(spreading area)”;“铺展区”之外(直径大于48 mm)即为常见的“沉积层区(deposit layer area)”。
从图5和6可以看到:越靠近转盘边缘,沉积层越厚(可达1~2 mm);在部分实验中,甚至还出现了沉积层上又覆一层沉积层的“二次沉积”现象;随着转速升高,“磨砂区”范围扩大,在部分实验中,沉积层出现了螺旋棱或径向棱,相关研究认为该现象可能是由转盘和氮气的对流换热所造成的:转盘边缘处的金属液膜较薄,加热量小于冷却量,液膜更容易降温凝固并累积。
沉积层容易造成离心雾化过程中出现“水跃”,产生较大的铝渣,降低粉末收集率,因此实验中应尽量减少沉积层。在转盘雾化实验中,由于铝液流动不够充分且在转盘停止后易迅速凝固为尺寸较大的铝渣,难以观察转盘表面各典型区域,导致相关研究较少,因此,转盘表面各典型区域的产生原因还亟待开展进一步的研究分析。
图7为转速30000 r/min的实验结束后的转盘照片。从图中可以看到转盘边缘存在许多“锯齿”(约420个),雾化液滴就是在这些锯齿点位上形成。该实验现象与佐藤富雄等[6]的研究结果一致。
2.2 粉末微观形貌表征
选取粒径在15~53 μm之间的1060纯铝和AlSi10Mg合金铝粉末分析微观形貌。图8为粉末的扫描电镜图片。图9[20]给出了典型的气雾化制备的AlSi10Mg合金铝粉末形貌进行对比。从图中可以看出,在同样的惰性气体环境下,转盘雾化粉末的球形度好、表面光洁、大小均匀、无卫星粉,而气雾化粉末中充满了大小不一的卫星粉。造成这种差异的主要原因在于:在气雾化制粉过程中,液体被气流破碎为大小不一的液滴,在湍流和旋涡作用下,发生多次碰撞和黏附,小颗粒和大颗粒液滴团聚为卫星粉;而在转盘雾化制粉过程中,液体从转盘中心向边缘铺展、分散流动,在转盘边缘雾化为液滴后,沿转盘切线方向飞出,继续在雾化室内分散运动,而雾化室内氮气比较稳定,液滴在飞行过程中不易碰撞和团聚,避免了卫星粉的出现。卫星粉会导致粉末流动性变差,在增材制造中产生孔隙缺陷。因此,转盘雾化制备的粉末球形度和流动性更好,非常适合增材制造。
2.3 粉末粒径分布分析
从某次典型实验(转速39900 r/min,转盘直径59 mm)制备的1060纯铝粉中取样50 g进行数据分析,得到该样品的粒径分布曲线,如图10所示(左侧纵坐标为差分分布,右侧为累积分布)。为表征粉末的粒径集中度,采用单峰Extreme函数对差分曲线进行拟合分析,函数表达式如下:
$$ \begin{split}& y = {y_0} + A{e^{( - {e^{ - z}} - z + 1)}} \\& z = (x - {x_c})/w \end{split} $$ (1) 式中:x、y分别为横、纵坐标;z为计算中间值;xc为中心点横坐标;y0为偏移量;A为幅值;w为宽度。
从图中可以看到,实验数据峰值出现在105.7 μm处。Extreme函数拟合曲线的y0 = 0.08343,A = 0.44052,中心xc = 102.18724,宽度w = 9.27,说明该样品粒径分布非常窄。0~150 μm累积分布为83.04%,对应增材制造中使用的15~53 μm(选择性激光熔化SLM,Selective Laser Melting)和53~150 μm(激光近净成型LENS,Laser Engineered Net Shaping)这2个区间,说明转盘雾化制备的粉末粒径分布非常符合增材制造的要求。
2.4 分裂模式对粒径分布的影响
在转盘离心雾化过程中,由于液体流速和转盘转速不同,液体存在3种分裂模式,即直接滴状分裂(DDF)、丝状分裂(LD)和膜状分裂(FD)[32],如图11所示。
随着液体流速增大,分裂模式逐渐由DDF模式向LD模式和FD模式变化。Champagne等[33-34]发现,对于各种金属(如Al、Cu和Zn),DDF模式下液滴的最终形状为球形,而LF模式下更易形成椭球形状。从DDF模式到LF模式和LF模式到FD模式的转变流量公式[34]为:
$$ {Q_t} = \frac{{K{\sigma ^{0.88}}{D^{0.68}}}}{{{\mu ^{0.17}}{\omega ^{0.6}}{\rho ^{0.71}}}} $$ (2) 式中:D为转盘直径,单位m;ω为转速,单位rad/s;ρ为密度,单位kg/m3;σ为表面张力,单位N/m;μ为动力学黏性系数,单位Pa·s;K为常数(从DDF向LD转变时,K = 0.07;从LD向FD转变时,K = 1.33)。从式(2)可以看出:当转速ω增大、转盘直径D减小时,转变流量Qt降低,有利于从DDF模式过渡到LF模式,并最后过渡到FD模式。
为研究不同分裂模式对雾化效果的影响,采用不同孔径的坩埚导液管来控制铝液流量。图12为相同条件下(转速18000 r/min,转盘直径59 mm,转盘为弧面盘(弧面半径90 mm),加热温度880 ℃)、金属流量Q分别为5.33和1.23 mL/s的1060纯铝粉的粒径差分分布和累积分布。从粒径分布曲线(红色和黑色曲线)可以看到:与大流量(5.33 ml/)粉末相比,小流量(1.23 mL/s)粉末的粒径分布曲线更窄,即小流量粉末粒径集中度更高,细粉末含量也更高。从粒径累积分布曲线(蓝色和绿色曲线)可以看到:小流量下0~150 μm粉末的质量分数为63.3%,粉末中位径d50 = 137.1 μm;大流量的0~150 μm粉末含量为51.52 %,中位径d50 = 151.3 μm。
结合表3中1060纯铝的物理性质,根据式(2)可以计算得到不同转速下DDF模式向LD模式转变的临界流量Q1和LD模式向DD模式转变的临界流量Q2,如表5所示。从表中可以看到,对于上文转速18000 r/min、转盘直径59 mm的实验,Q1 = 1.28 mL/s。实验中的小流量1.23 mL/s低于临界流量Q1,属于DDF模式;而大流量5.33 mL/s处于Q1和Q2之间,属于LD模式。
表 5 离心分裂模式转变临界流量Table 5 Centrifugal atomization critical flow rate at different speedsω/(r·min−1) D/mm Q1 /(mL·s−1) Q2 /(mL·s−1) 6000 59 2.47 46.93 12000 59 1.63 30.97 18000 59 1.28 24.28 24000 59 1.08 20.43 本节实验得到的数据表明,DDF模式下的液滴中位径小于LD模式(即小流量下的中位径更小),粒径分布也更窄,这与Champagne的分裂模式理论一致。因此,在其他条件相同时,采用较小流量使分裂模式变为DDF模式,能够获得更小的粉末中位径和更高的细粉率。
2.5 中位径影响参数规律
转盘雾化粉末的中位径与液体密度、表面张力、转速、转盘直径等参数相关。Walton等[35]给出了计算离心雾化粉末中位径d50的公式:
$$ {d_{50}} = 3.8{\left( {\frac{\sigma }{{\rho D{\omega ^2}}}} \right)^{0.5}} $$ (3) Labrecque等[12]结合体积流量的影响,给出了AZ91镁合金离心雾化粉末中位径的理论公式:
$$ {d_{50}} = 4.27 \times {10^6} \cdot \frac{1}{{{\omega ^{0.95}}}} \cdot \frac{1}{{{D^{0.61}}}} \cdot {\left( {\frac{\sigma }{\rho }} \right)^{0.42}} \cdot {Q^{0.12}} $$ (4) Champagne等[36]提出了预测离心雾化粉末中位径的公式:
$$ {d_{50}} = \frac{{3.65{Q^{0.06}}}}{{\omega {D^{0.58}}}}{\left( {\frac{\sigma }{\rho }} \right)^{0.46}} $$ (5) Dunkley等[37]给出了球形液滴中位径计算公式:
$$ {d_{50}} = {\left( {\frac{{6\sigma }}{{\rho {\omega ^2}R}}} \right)^{0.5}} $$ (6) Tornberg[38]提出了一个中位径理论公式:
$$ {d_{50}} = \sqrt {\frac{{4.8\sigma }}{{\rho {\omega ^2}R\left[ {1 - {{\left( {\omega R} \right)}^{0.93}}\mu } \right]}}} $$ (7) 国为民等[39]认为,熔化的薄层液态金属雾化为极小的液滴瞬间抛出时,所受的离心力理论上与表面张力相等。离心雾化粉末中位径的理论公式[39]为:
$$ {d_{50}} = \sqrt {\frac{{12\sigma }}{{\rho {\omega ^2}D}}} $$ (8) 以上各式中:R为转盘半径,单位m;Q为金属液体流量,单位m3/s。
以上理论模型虽然不尽相同,但液滴中位径的变化规律基本一致,在液体物性参数固定的情况下,都是随着转速和转盘直径的增大而减小;对于不同的液体,密度越大、表面张力越小,中位径越小。
2.5.1 不同转速对中位径的影响
在其他参数固定(加热温度880 ℃,转盘直径60 mm,弧面半径90 mm,金属流量5.33 mL/s)的情况下,分别进行了转速为6000、12000、18000、24000 r/min的离心雾化实验,4个转速对应的中位径d50分别为266.8、179.0、147.7、116.0 μm。图13为实验值与理论公式(3)~(8)的计算值对比。从图中可以看到,各曲线的整体趋势都是中位径随转速增大而减小:当转速在10000 r/min以下时,理论计算值明显大于实验值,Champagne公式的计算值更接近实验值;当转速在10000 r/min以上时,实验值位于各计算值之间,国为民(Guo)和Labrecque公式的计算值与实验值吻合较好。
实验刚开始时,转盘初始温度较低,铝液会迅速在转盘表面凝结,使转盘动平衡变差,若此时转盘转速较高,极易导致转盘剧烈振动甚至损坏。为保护转盘和电极,在实验中采用了逐渐增大转盘转速直至实验所需转速的方式。因此,高转速实验条件下制备的粉末中会掺混一部分较低转速下产生的相对较粗的粉末,降低了高转速实验条件下的细粉率,导致通过实验得到的d50值偏大,而实际高转速下的d50相对较小,与理论计算值更为接近。针对这一问题,需要进一步改进实验方法和分析手段来进行验证。
2.5.2 不同转盘直径对粉末中位径的影响
在其他参数固定(加热温度880℃,转盘弧面半径90 mm,金属流量2.94 mL/s,转速24000 r/min)的情况下,针对直径40、50、60 mm的转盘进行实验,将实验值与理论计算值进行对比,结果如图14所示。可以看到,粉末中位径的实验值和计算值都呈现出随转盘直径增大而减小的规律:直径为40 mm时,中位径为123.4 μm,与Tornberg公式的计算值最为接近;直径为50和60 mm时,中位径分别为96.4和86.5 μm,与Champagne公式的计算值最为接近。
2.5.3 不同转盘构型对粉体中位径的影响
在其他参数固定(加热炉温度880 ℃,转盘直径60 mm,转速24000 r/min,流量2.94 mL/s)的情况下,基于图3中的3种转盘构型,分别针对平面盘、12°锥面盘、弧面盘A(弧面半径90 mm)和弧面盘B(弧面半径80 mm)进行实验。对实验得到的粉末进行取样和筛分,分别统计d10、d50和d90(粒径累计分布为10%、50%、90%时对应的粒径),结果如图15所示。从图中可以看到:在4种转盘构型下,d10都约为54.0 μm,而d50、d90的差异较大;弧面盘B的d50最小(85.5 μm),平面盘的d50最大(99.8 μm);12°锥面盘的d90最小(197.8 μm),弧面盘A的d90最大(257.6 μm)。因此,若需要粒径非常小的粉末,可以采用d50最小的弧面盘B(弧面半径80 mm);若需绝大部分粉末都较细,可以采用d90最小的12°锥面盘。
2.5.4 中位径线性拟合公式
通过量纲分析可知,粉末中位径d50与雾化参数[σ/(ρDω2)]0.5成线性关系。图16给出了1060纯铝粉的中位径d50实验值随雾化参数[σ/(ρDω2)]0.5的变化情况及线性拟合曲线。中位径线性回归拟合公式为:
$$ {d_{50}} = 3.22{\left( {\frac{\sigma }{{\rho D{\omega ^2}}}} \right)^{0.5}} $$ (9) 拟合曲线的截距为0,拟合斜率为3.22,标准误差为0.102,表明中位径与雾化参数线性关系良好。
3 结 论
本文开展了转盘雾化制备铝合金粉末的实验研究,得到如下结论:
1)铝液在转盘表面铺展流动的过程中,存在“光洁区”“磨砂区”“铺展区”和“沉积层区”等4个典型区域。
2)液体流量降低,会使转盘雾化分裂模式由丝状分裂向直接滴状分裂转变,能够降低粉末中位径并提高细粉率。
3)在本文实验的平面、锥面和弧面转盘中,弧面盘的d50最小,锥面盘的d90最小。
4)1060纯铝粉的中位径d50与雾化参数(σ/ρDω2)0.5的线性关系良好,通过线性回归拟合,提出了一个新的中位径理论公式。
致谢:本文实验操作得到了技术人员樊志勇的帮助,扫描电镜实验得到了雷现奇老师的帮助,特此致谢。
-
表 1 实验工况表
Table 1 Experimental conditions
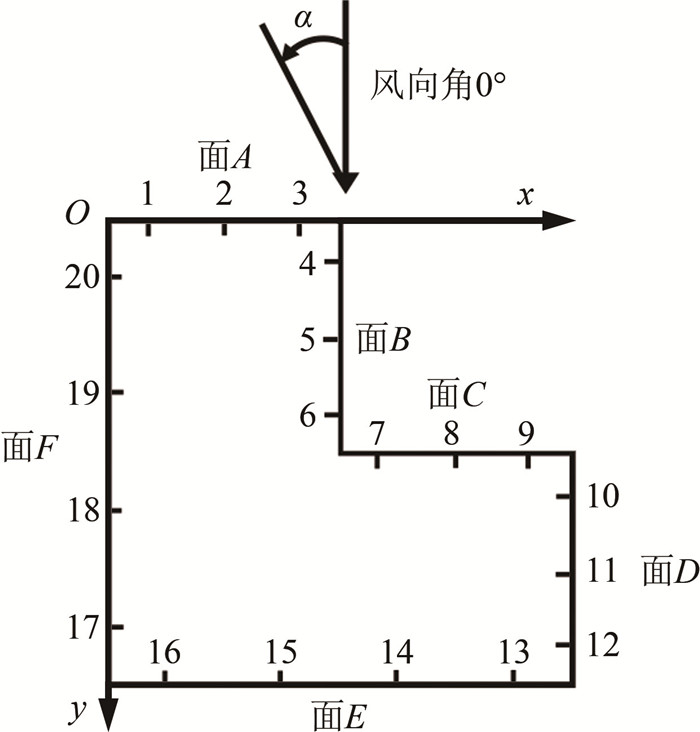
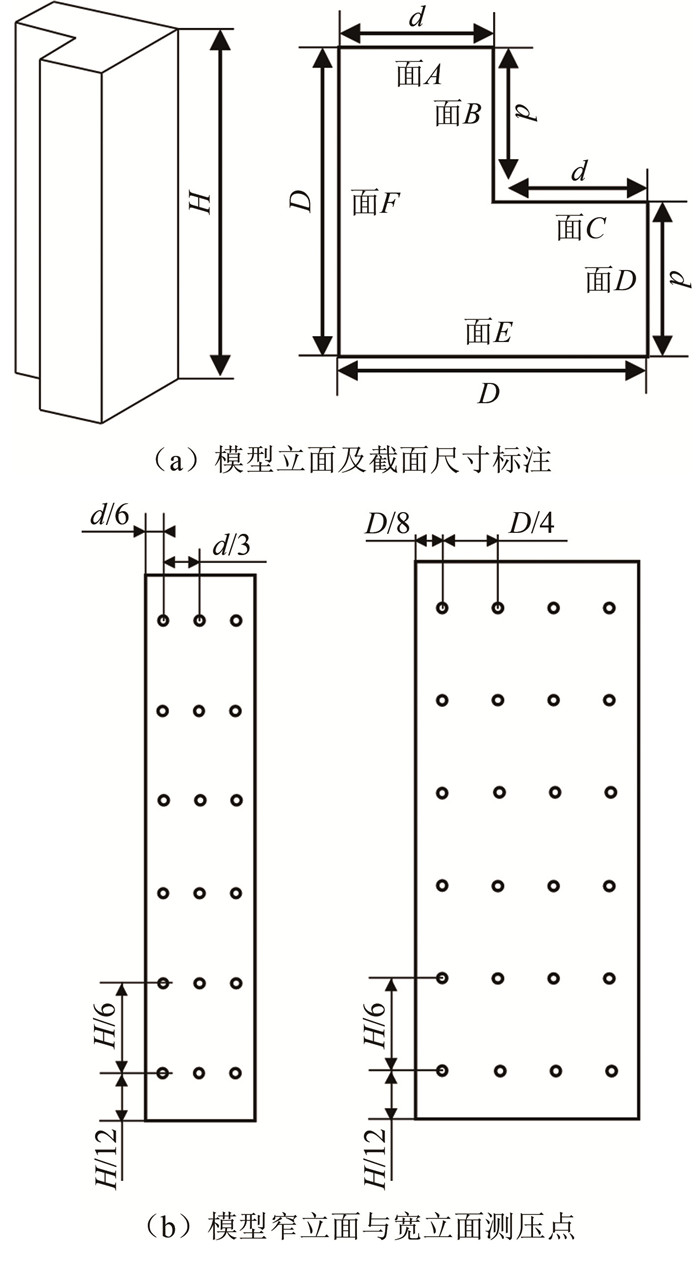
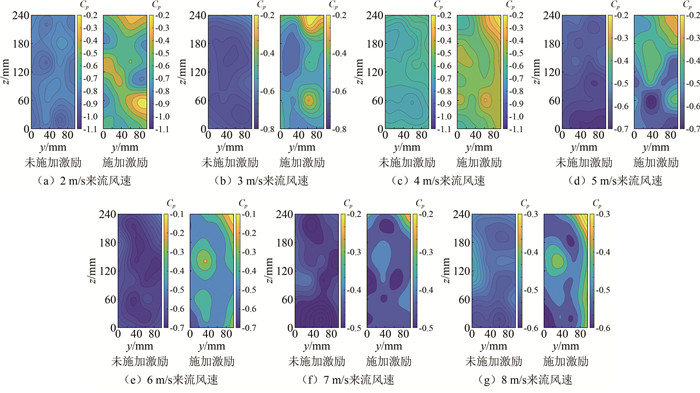
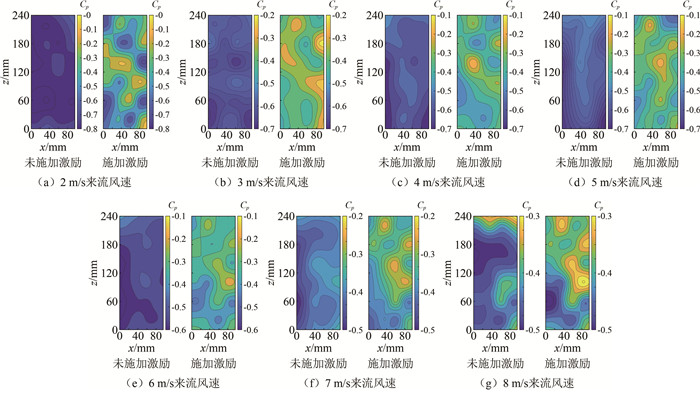
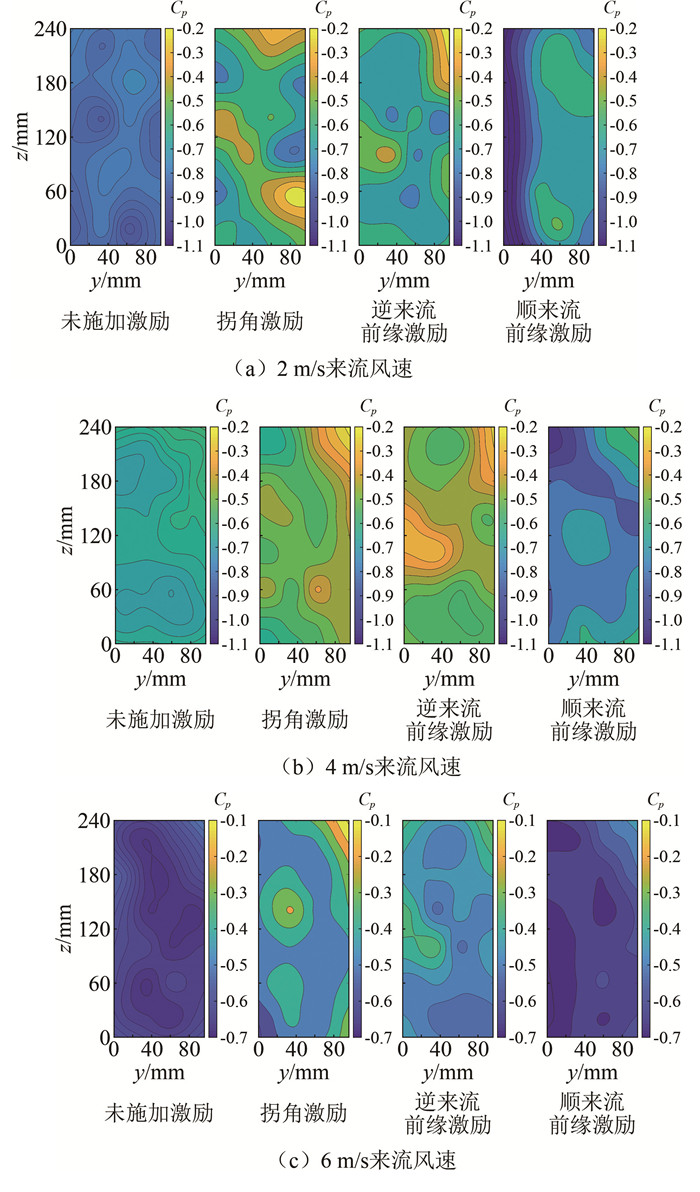
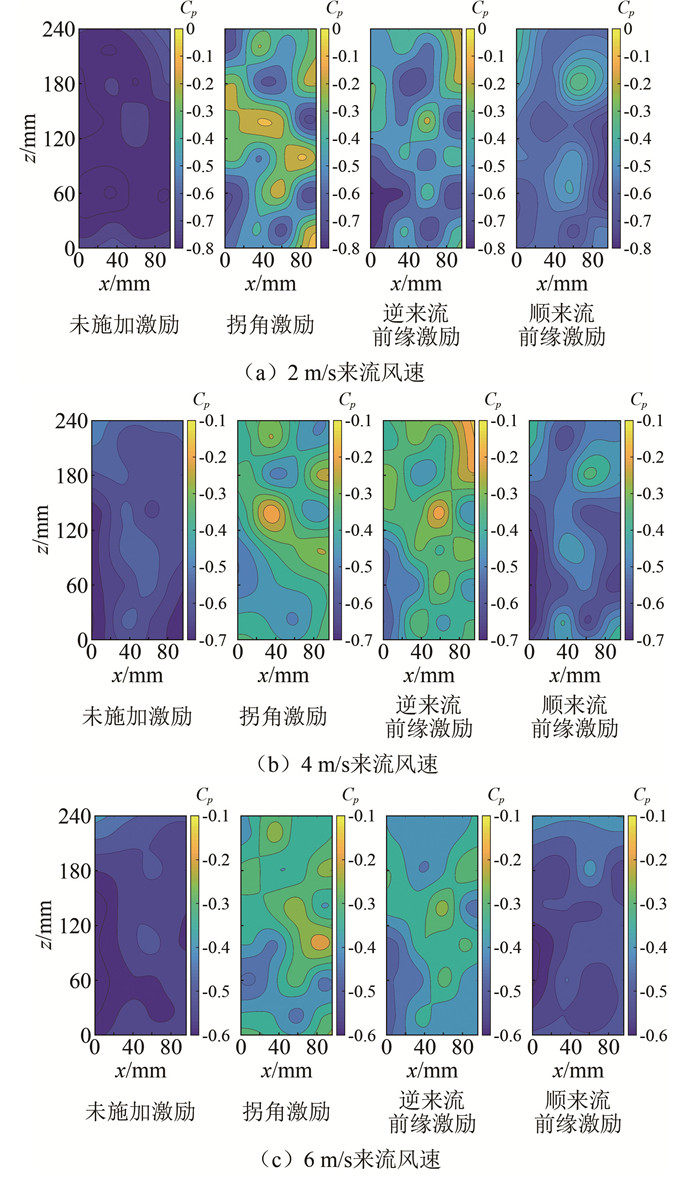
激励器布置形式 风向角/(°) 来流速度/(m·s-1) 顺来流前缘激励 0 2, 3, 4, 5, 6 逆来流前缘激励 0 2, 3, 4, 5, 6, 7, 8 拐角激励 0 2, 3, 4, 5, 6, 7, 8 -
[1] 吴瑾, 夏逸鸣, 张丽芳. 土木工程结构抗风设计[M]. 北京: 科学出版社, 2007. [2] SIMIU E, YEO D H. Wind effects on structures: modern structural design for wind[M/OL]. 4th ed. New Jersey: Wiley-Blackwell, 2019: 55-71. [2020-08-19]. https://onlinelibrary.wiley.com/doi/book/10.1002/9781119375890.doi: 10.1002/9781119375890
[3] KENNEDY J, NERI E, BENNETT G J. The reduction of main landing gear noise[C]//Proc of the 22nd AIAA/CEAS Aeroacoustics Conference. 2016 doi: 10.2514/6.2016-2900
[4] DIPANKAR A, SENGUPTA T K, TALLA S B. Suppression of vortex shedding behind a circular cylinder by another control cylinder at low Reynolds numbers[J]. Journal of Fluid Mechanics, 2007, 573: 171-190. doi: 10.1017/s002211200600382x
[5] BAO Y, TAO J. The passive control of wake flow behind a circular cylinder by parallel dualplates[J]. Journal of Fluids and Structures, 2013, 37: 201-219. doi: 10.1016/j.jfluidstructs.2012.11.002
[6] MARUTA E, KANDA M, SATO J. Effects on surface roughness for wind pressure on glass and cladding ofbuildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74-76: 651-663. doi: 10.1016/S0167-6105(98)00059-2
[7] TANAKA H, TAMURA Y, OHTAKE K, et al. Experimental investigation of aerodynamic forces and wind pressures acting on tall buildings with various unconventional configurations[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 107-108: 179-191. doi: 10.1016/j.jweia.2012.04.014
[8] 张耀春, 秦云, 王春刚. 洞口设置对高层建筑静力风荷载的影响研究[J]. 建筑结构学报, 2004, 25(4): 112-117, 123. DOI: 10.3321/j.issn:1000-6869.2004.04.018 ZHANG Y C, QIN Y, WANG C G. Research on the influence of openings to static wind load of highrise buildings[J]. Journal of Building Structures, 2004, 25(4): 112-117, 123. doi: 10.3321/j.issn:1000-6869.2004.04.018
[9] 顾明, 王凤元, 全涌, 等. 超高层建筑风荷载的试验研究[J]. 建筑结构学报, 2000, 21(4): 48-54. DOI: 10.14006/j.jzjgxb.2000.04.007 GU M, WANG F Y, QUAN Y, et al. Experimental study on dynamic wind loads on super-tall buildings[J]. Journal of Building Structures, 2000, 21(4): 48-54. doi: 10.14006/j.jzjgxb.2000.04.007
[10] 张正维, 全涌, 顾明, 等. 凹角对方形截面高层建筑基底气动力系数的影响研究[J]. 土木工程学报, 2013, 46(7): 58-65. DOI: 10.15951/j.tmgcxb.2013.07.017 ZHANG Z W, QUAN Y, GU M, et al. Effects of corner recession modification on aerodynamic coefficients of square high-rise buildings[J]. China Civil Engineering Journal, 2013, 46(7): 58-65. doi: 10.15951/j.tmgcxb.2013.07.017
[11] BANDI E K, KIM Y, YOSHIDA A, et al. Aerodynamic characteristics of triangular-section tall buildings with different helical angles[C]//Proc of the ICWE13-International Conference on Wind Engineering'13. 2011.
[12] 战培国, 程娅红, 赵昕. 主动流动控制技术研究[J]. 航空科学技术, 2010, 21(5): 2-6. DOI: 10.3969/j.issn.1007-5453.2010.05.001 ZHAN P G, CHENG Y H, ZHAO X. A review of active flow controltechnology[J]. Aeronautical Science and Technology, 2010, 21(5): 2-6. doi: 10.3969/j.issn.1007-5453.2010.05.001
[13] FENG L H, WANG J J, PAN C. Effect of novel synthetic jet on wake vortex shedding modes of a circular cylinder[J]. Journal of Fluids and Structures, 2010, 26(6): 900-917. doi: 10.1016/j.jfluidstructs.2010.05.003
[14] 王佳, 邓飞, 张衡. 壁面振动对流场特性影响的数值模拟预报[J]. 声学技术, 2013, 32(4, Pt. 2): 76-79. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-SXJS201308001022.htm WANG J, DENG F, ZHANG H. The numerical simulation forecast of the characteristic on wall oscillation to the flow field[J]Technical Acoustics, 2013, 32(4, Pt. 2): 76-79. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-SXJS201308001022.htm
[15] 董宇飞, 魏中磊. 流线型轴对称钝体尾迹特性及其声激励控制[J]. 力学学报, 1999, 31(6): 682-693. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB199906006.htm DONG Y F, WEI Z L. Experimental investigation of the wake of axisymmetric bluff body and its control by means of acoustic forcing[J]. Acta Mechanica Sinica, 1999, 31(6): 682-693. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB199906006.htm
[16] 张立启. 三维圆柱绕流与涡激振动的行波壁控制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019. ZHANG L Q. Study on traveling wave wall control method of flow around the three-dimensional cylinder and vortex induced vibration[D]. Harbin: Harbin Institute of Technology, 2019. doi: 10.27061/d.cnki.ghgdu.2019.002261
[17] 郑朝荣, 张耀春. 高层建筑风荷载减阻的吸气方法数值研究[J]. 应用基础与工程科学学报, 2010, 18(1): 80-90. DOI: 10.3969/j.issn.1005-0930.2010.01.010 ZHENG C R, ZHANG Y C. Numerical investigation of the wind-load reduction for a high-rise building by suction[J]. Journal of Basic Science and Engineering, 2010, 18(1): 80-90. doi: 10.3969/j.issn.1005-0930.2010.01.010
[18] 张洪福. 超高层建筑横风向风致效应定常吸气控制[D]. 哈尔滨: 哈尔滨工业大学, 2013. ZHANG H F. Steady suction for controlling Across-wind-induced effects of super High-risebuildings[D]. Harbin: Harbin Institute of Technology, 2013.
[19] SHTENDEL T, SEIFERT A. Three-dimensional aspects of cylinder drag reduction by suction and oscillatoryblowing[J]. International Journal of Heat and Fluid Flow, 2014, 45: 109-127. doi: 10.1016/j.ijheatfluidflow.2013.10.009
[20] 史志伟, 杜海, 李铮, 等. 等离子体流动控制技术原理及典型应用[J]. 高压电器, 2017, 53(4): 72-78. DOI: 10.13296/j.1001-1609.hva.2017.04.013 SHI Z W, DU H, LI Z, et al. Mechanism and applications of plasma flow control technology[J]. High Voltage Apparatus, 2017, 53(4): 72-78. doi: 10.13296/j.1001-1609.hva.2017.04.013
[21] WANG J J, CHOI K S, FENG L H, et al. Recent developments in DBD plasma flow control[J]. Progress in Aerospace Sciences, 2013, 62: 52-78. doi: 10.1016/j.paerosci.2013.05.003
[22] 龙玥霄, 李华星, 孟宣市. AC和NS等离子体激励对细长前体分离涡流场的控制[J]. 航空工程进展, 2014, 5(3): 358-363. DOI: 10.16615/j.cnki.1674-8190.2014.03.014 LONG Y X, LI H X, MENG X S. Flow control over a slender forebody using AC and NS-DBD plasmaactuators[J]. Advances in Aeronautical Science and Engineering, 2014, 5(3): 358-363. doi: 10.16615/j.cnki.1674-8190.2014.03.014
[23] 孟宣市, 杨泽人, 陈琦, 等. 低雷诺数下层流分离的等离子体控制[J]. 航空学报, 2016, 37(7): 2112-2122. DOI: 10.7527/S1000-6893.2015.0244 MENG X S, YANG Z R, CHEN Q, et al. Laminar separation control at low Reynolds numbers using plasmaactuation[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(7): 2112-2122. doi: 10.7527/S1000-6893.2015.0244
[24] 聂万胜, 程钰锋, 车学科. 介质阻挡放电等离子体流动控制研究进展[J]. 力学进展, 2012, 42(6): 722-734. DOI: 10.6052/1000-0992-11-161 NIE W S, CHENG Y F, CHE X K. A review on dielectric barrier discharge plasma flowcontrol[J]. Advances in Mechanics, 2012, 42(6): 722-734. doi: 10.6052/1000-0992-11-161
[25] 吴云, 李应红. 等离子体流动控制研究进展与展望[J]. 航空学报, 2015, 36(2): 381-405. DOI: 10.7527/S1000-6893.2014.0246 WU Y, LI Y H. Progress and outlook of plasma flow control[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(2): 381-405. doi: 10.7527/S1000-6893.2014.0246
[26] 马力群, 冯立好. 放置于驻点的合成射流控制圆柱涡脱落模式的实验研究[J]. 中国科学(技术科学), 2013, 43(2): 208-219. DOI: 10.1007/s11431-012-5074-4 MA L Q, FENG L H. Experimental investigation on control of vortex shedding mode of a circular cylinder using synthetic jets placed at stagnationpoints[J]. Scientia Sinica Technologica, 2013, 43(2): 208-219. doi: 10.1007/s11431-012-5074-4
[27] 孙卫威. 等离子体流动控制技术在低矮建筑物应用的研究[D]. 长沙: 湖南大学, 2017. SUN W W. The application research of plasma flow control technology on low rise buildings[D]. Changsha: Hunan University, 2017.
[28] 郑朝荣, 张耀春. 吸气方法在高层建筑风荷载减阻中的应用[J]. 工程力学, 2009, 26(z1): 51-56. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX2009S1016.htm ZHENG C R, ZHANG Y C. Application of the suction method to reduce the wind load on high-rise building[J]. Engineering Mechanics, 2009, 26(z1): 51-56. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX2009S1016.htm
-
期刊类型引用(1)
1. 蒋丹丹,张浩然. 试飞中的扰流板安全分析研究. 科技与创新. 2024(05): 163-165 .  百度学术
百度学术
其他类型引用(2)






 下载:
下载: