Wind tunnel test of blade number effect on icing distribution of vertical axis wind turbine
-
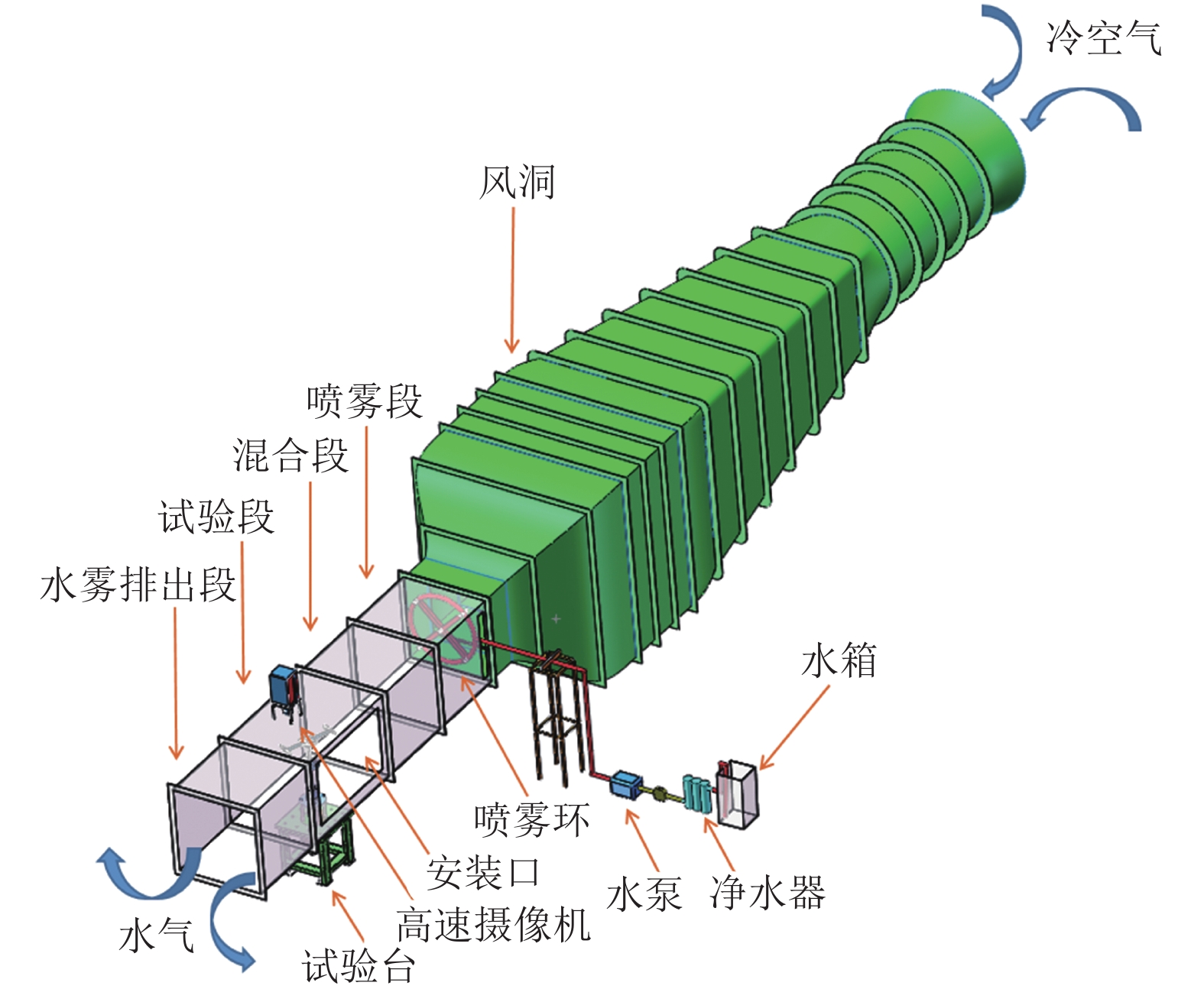
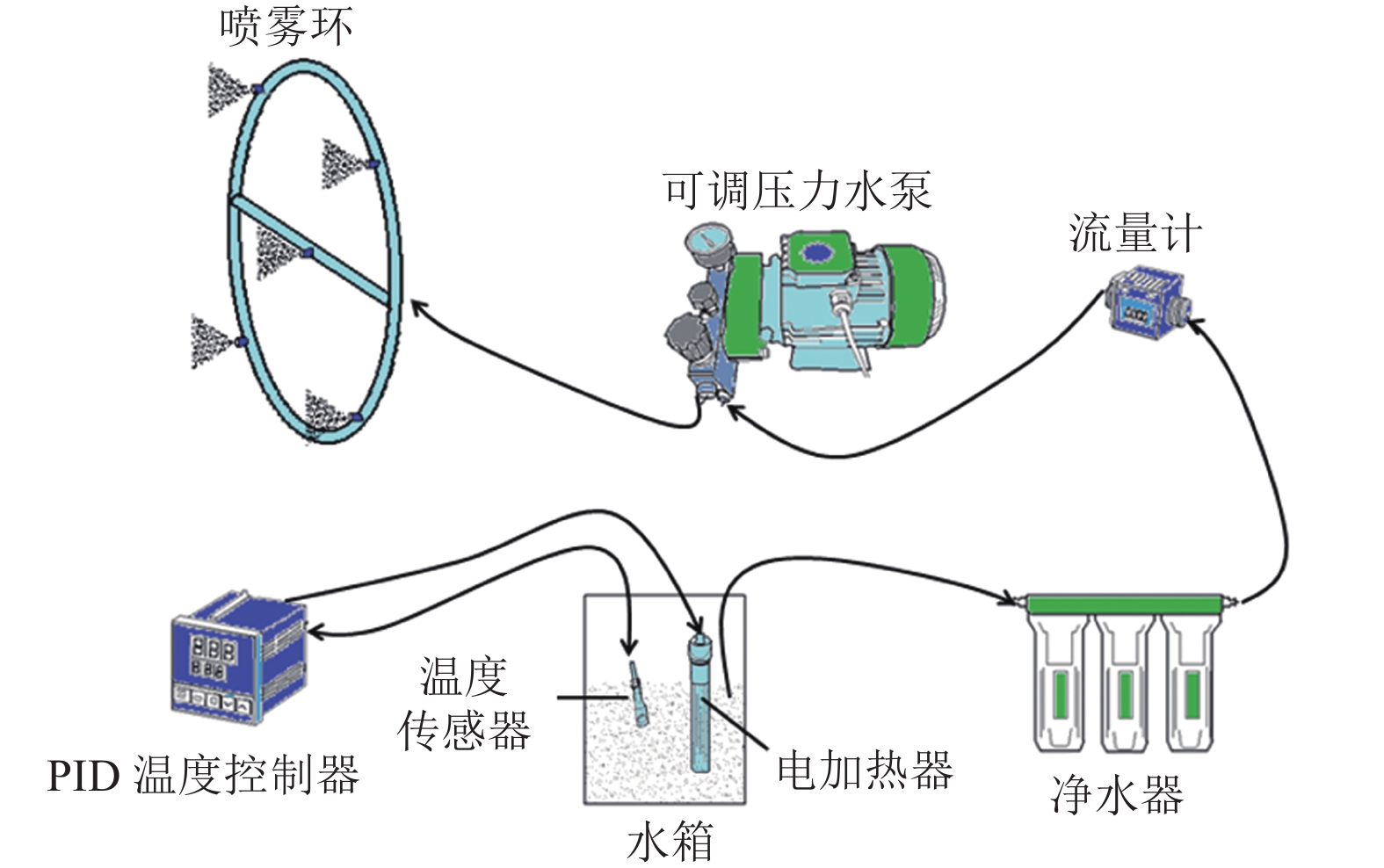
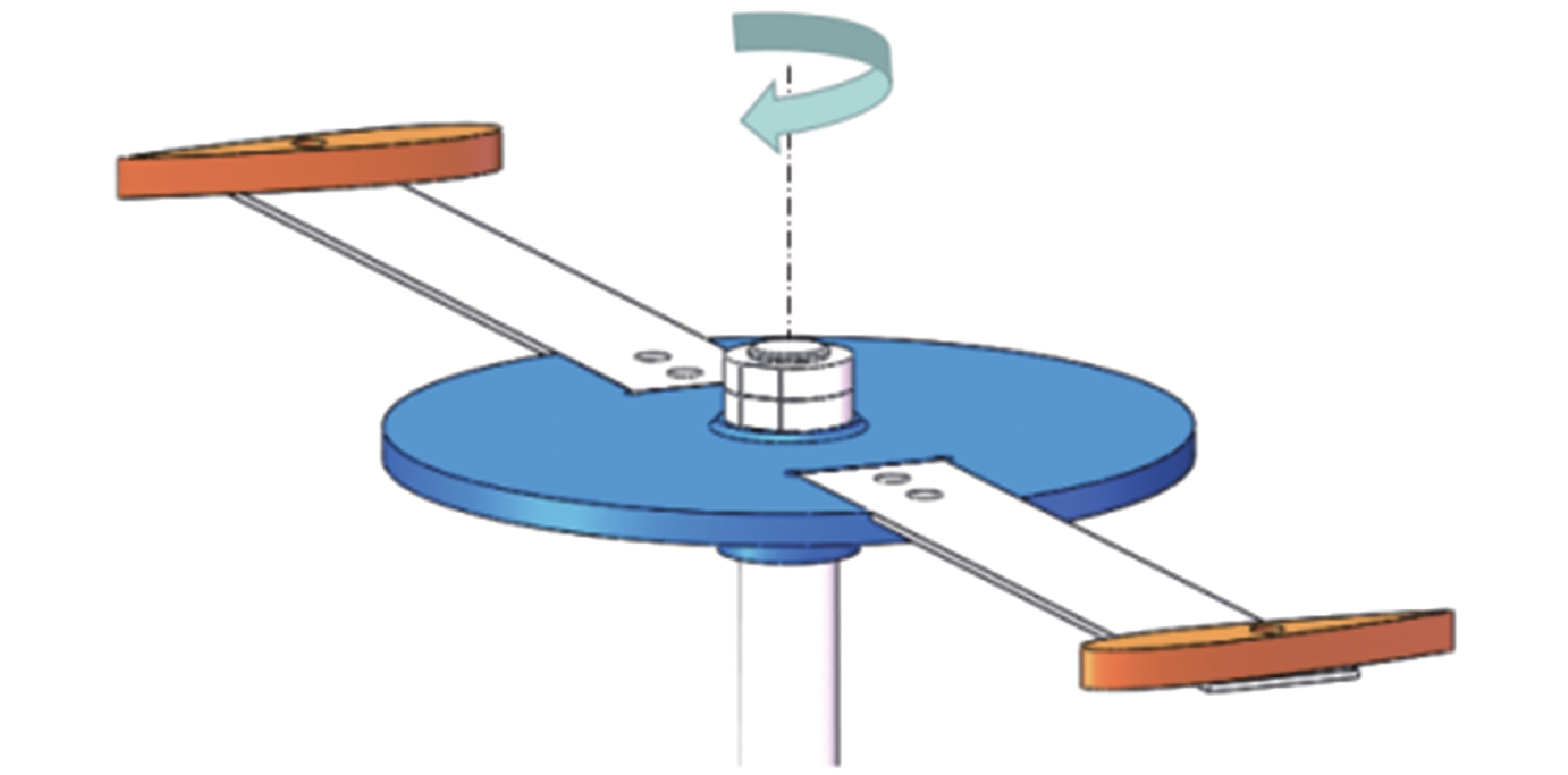
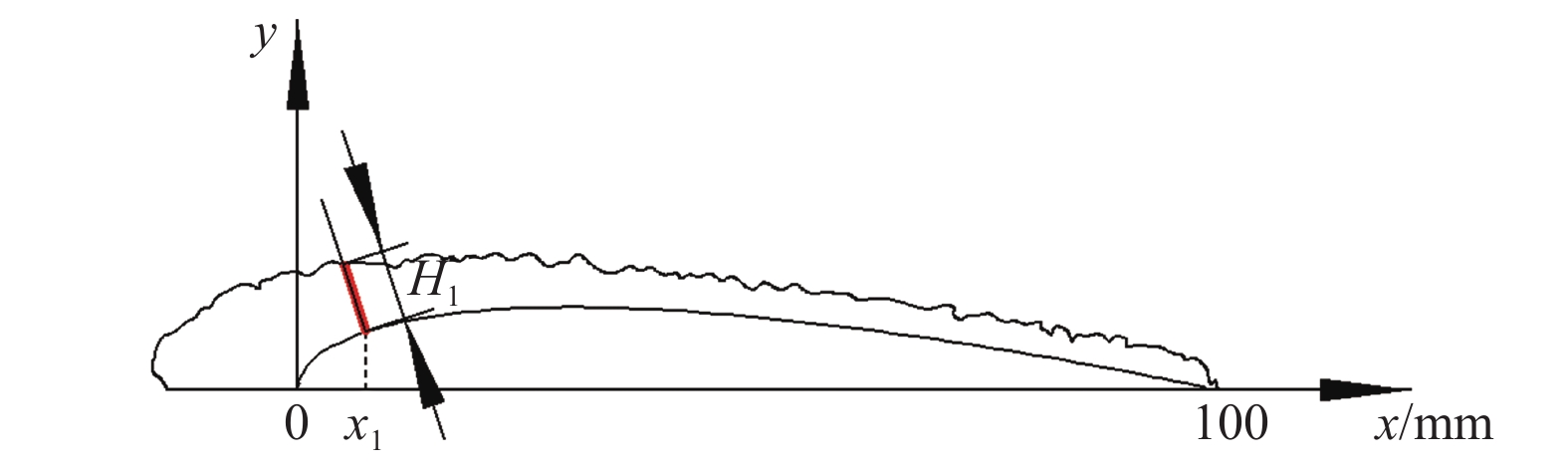
摘要: 风力机叶片表面结冰会降低其气动性能和发电效率。本文研究了旋转状态下叶片数对垂直轴风力机叶片表面结冰分布的影响;搭建了利用自然低温的结冰风洞试验系统;测试了3种叶片数(1、2、4)、3种尖速比(0.2、0.6、1.0)条件下的叶片结冰分布情况。结果表明:在不同尖速比下,叶片数对垂直轴风力机叶片表面结冰分布规律影响显著,叶片内外表面的结冰总体呈现非对称分布特点;随着叶片数增加,叶片表面冰层厚度呈先增后减的变化趋势;在叶片前缘弦长10%区域内,冰层厚度增幅显著大于叶片其他部位;随尖速比增大,叶片前缘冰层厚度显著大于叶片其他部位,叶片前缘内外表面的冰层厚度差值呈递增的变化趋势。研究结果可为风力机叶片防/除冰技术提供参考。Abstract: Icing on the surface of wind turbine blades can reduce the turbine’s aerodynamic characteristics and power generation efficiency. In this paper, the effect of the number of blades on the icing distribution on the blade surface of a vertical axis wind turbine is studied. A natural low temperature icing wind tunnel experiment system was built to test the icing distribution of three groups of blades (1, 2, 4) under three tip speed ratios (0.2, 0.6, 1.0). The results show that the number of blades has a significant effect on the distribution of icing on the blade surface of the vertical axis wind turbine under different tip speed ratios, and the icing distribution on the inner and outer surfaces of the blade is asymmetric. With the increase of the number of blades, the thickness of the ice layer on the surface of the blades increases first and then decreases. In the 10% area at the leading edge of the chord, the increase of the thickness of the ice layer is significantly greater than that at other parts of the blade. With the increase of the tip speed ratio, the thickness of the ice layer on the leading edge of the blade is significantly larger than that at other parts of the blade, and the thickness difference of the ice layer between the inner and outer surface on the leading edge of the blade increases gradually. The research results can provide a reference for the anti-icing and de-icing technology of wind turbine blades.
-
Keywords:
- vertical axis wind turbine /
- icing /
- wind tunnel test /
- blade /
- tip speed ratio
-
0 引言
FL-12风洞作为主力风洞承担着大量重要试验任务,其中包括进气道、吹气流动控制、引射短舱和TPS等多项试验,这些试验任务都需要供气控制系统输送稳定、可控的气流到试验模型,并要达到优于±3g/s的绝对控制精度,同时要求流量调节范围大、稳定时间短,因此实现流量宽范围快速精确控制是供气试验最为基础和关键的环节[1-3]。
目前模拟调节阀的高精度阀门定位器死区0.1%,综合误差0.5%[4],达不到试验要求的流量控制精度,而且在实际工况中其工作流量特性随着试验模型的变化而变化,同时存在死区、调节滞后严重、调节范围不宽、密封件易磨损等问题,因此无法满足当前供气试验要求。
与模拟调节阀相比,数字阀具有可调范围宽、控制精度高、响应速度快、结构简单、鲁棒性强、可靠性高等特点[5-7],目前数字阀主要分为PWM(脉冲宽度调制)数字阀和PCM(脉冲编码调制)数字阀[8-9]。PWM数字阀也称高速开关式数字阀,通过调节PWM信号的占空比来控制阀的平均流量,但是数字阀的流量和得失电时间存在一定的矛盾。PCM数字阀是将开关阀按照一定规律的排列组合(二进制、斐波那契数列等)实现对流量的控制,但是离散化的形式会导致流量输出的不连续性,同时小口径喷嘴的加工难度较高,进退阶时波动较大,频繁切换阀会造成冲击和噪声,缩短低位开关阀的寿命。
为解决PWM数字阀流量和得失电时间的矛盾和PCM数字阀的流量不连续性和低位开关阀的寿命问题,本文设计了PCM+PWM数字阀。该数字阀通过PCM数字阀提供基准流量,PWM数字阀在基准流量的基础上再进行调节,其中PCM数字阀采用多路文丘里喷嘴与开关阀按照二进制规律排列组合而成,PWM数字阀由单路小口径文丘里喷嘴与高频开关阀组成。
1 数字阀的设计指标和设计方案
1.1 设计指标
依据试验任务需求,FL-12风洞供气控制系统中数字阀设计的主要技术指标:(1) 阀前压力范围:6.0~8.0MPa;(2) 阀后压力范围:0.1~6.0MPa;(3) 流量控制范围:0.1~6.0kg/s;(4) 绝对控制精度:≤±3g/s;(5) 稳定控制时间:≤30s。
1.2 设计方案
本文中设计的数字阀由13位半PCM数字阀+ PWM数字阀,共计16路喷嘴和16路开关阀组成。图 1为数字阀支路示意图,气流依次通过喷嘴、高压金属软管、电磁阀后流出,系统先通过开关不同位的电磁阀来控制每路管道的通断以达到组合出不同流量的目的,当流量输出值与给定值的差值进入预先设定的误差带内,则停止动作PCM数字阀,由PWM数字阀通过脉宽调制控制。在实际流量控制中,PCM数字阀起到量程调节作用,PWM数字阀起到精细调节作用。
2 数字阀设计的关键技术
2.1 喷嘴的选择与设计
为使喷嘴流量特性不受后端试验模型状态变化及背压影响,采用了临界流喷嘴。临界流喷嘴主要包括临界流标准喷嘴和临界流文丘里喷嘴,其中临界流标准喷嘴结构如图 2所示。如果保持喷嘴入口压力p1和温度T1不变,使其出口压力p2逐渐减小,则通过喷嘴的气体流量qm将逐渐增加。当出口压力下降至pc时,通过喷嘴的流量将达到最大值,气体流速为当地声速,再继续降低出口压力,通过喷嘴的流量将不再增加,流速也保持声速不变。将喷嘴出口的流速达到声速的压力pc称为临界压力,pc/p1称为临界压力比,通过喷嘴的流量(qm)max称为临界流量[10]。
对于空气(γ=1.4),可以通过公式1计算得到临界压力比为0.528。由于数字阀前压力一般稳定在8MPa,因此要保证“恒流”特性不变,出口压力p2必须低于临界压力4.224MPa,显然无法满足最大出口压力为6MPa的设计要求,而且压力损耗太大。

(1) 为使出口压力得到恢复,采用喉道后面带扩压管的临界流文丘里喷嘴,其出口压力高低与其扩散段尺寸有关[11]。根据JJG620-2008《临界流文丘里喷嘴》,可以计算出最大背压比p2/p1与扩散段面积比A2/A*的对应参数表(见表 1),其中p1为入口压力,p2为出口压力,A*为喉道面积,A2为扩散段出口面积。
表 1 临界流文丘里喷嘴的最大允许背压比表(γ=1.4)Table 1 Maximum allowable back pressure ratio of the critical flow Venturi-type nozzleA2/A* p2/p1 A2/A* p2/p1 1.1 0.6863 1.9 0.8495 1.2 0.7376 2.0 0.8554 1.3 0.7701 2.5 0.8743 1.4 0.7930 3.0 0.8842 1.5 0.8101 3.5 0.8900 1.6 0.8233 4.0 0.8937 1.7 0.8339 5.0 0.8981 1.8 0.8424 10.0 0.9038 依据表 1,选择喷嘴扩散段面积比为4.0,在理想条件下,当出口压力低于0.8937倍入口压力,即可达到临界状态,喷嘴喉道流速为声速,流量由入口压力、入口温度与喉道面积唯一确定。依据圆环形喉道临界流文丘里喷嘴设计准则[12],喷嘴的结构设计如图 3所示。
2.2 喉道面积的分配
PCM数字阀的喷嘴喉道面积按照二进制规律排列,通过这些不同的喉道可以组合不同喉道面积,组合喉道面积范围在所有喉道面积之和与最小喉道面积之间,最小分辨率是最小喉道面积,因此设计足够小的喉道面积就可以解决定位精度的问题,设计足够多的位数就可以解决流量调节范围的问题。
PCM数字阀的设计工况是入口压力为8.0MPa,入口温度为20℃,流量为6.0kg/s,在最大允许背压比范围内,根据公式(2) 可得PCM数字阀需要的喉道总面积为3.176cm2。

(2) 式中:p1为喷嘴入口压力(Pa);T1为喷嘴入口温度(K);A*为喉道面积(m2)。
经计算,将喉道总面积按照13位半二进制分配,各喷嘴喉道面积分配值及工作流量分配值如表 2所示。
表 2 PCM数字阀各喷嘴喉道面积及对应流量计算表Table 2 Nozzle throat area and calculated flow value of the PCM digital valveBit位 临界流量/(kg·s-1) 喷嘴喉道面积/cm2 喉道通径/mm 1 0.00059332 0.00031416 0.2000 2 0.0011866 0.00062832 0.2828 3 0.0023733 0.0012566 0.4000 4 0.0047466 0.0025133 0.5657 5 0.0094932 0.0050265 0.8000 6 0.018986 0.010053 1.1314 7 0.037973 0.020106 1.6000 8 0.075945 0.040212 2.2627 9 0.15189 0.080425 3.2000 10 0.30378 0.16085 4.5255 11 0.60756 0.3217 6.4000 12 1.2151 0.6434 9.0510 13 2.4303 1.2868 12.8000 13半 1.2151 0.6434 9.0510 合计 6.075 3.2170 实际设计PCM数字阀总喉道面积为3.217cm2,在不考虑喷嘴加工误差的情况下,其喉道面积分辨率(定位精度)为1/10239,在设计工况下对应的最小流量为0.6g/s。
PWM喷嘴喉道面积的选取需依据试验流量精度要求(±3g/s),并充分考虑裕量,预设误差带为±6g/s,可在表 2中选取喉道口径0.8mm的喷嘴作为PWM数字阀的喷嘴。
2.3 电磁阀参数计算与型号选择
流量系数CV是电磁阀主要的计算参数,表征为阀门流通能力大小,根据设计工况,并按照公式(3) 进行计算,结果如表 3所示。

(3) 表 3 电磁阀流量系数计算与型号选择Table 3 Magnetic valve flow coefficient calculation and model selectionBit位 计算流量系数/(m3·h-1) 电磁阀流量系数/(m3·h-1) 电磁阀阀座口径/mm 电磁阀型号 PWM 0.02892 0.05 8.0 2/943 1 0.00195 0.13 2.0 A5232 2 0.00390 0.13 2.0 A5232 3 0.00781 0.13 2.0 A5232 4 0.01563 0.13 2.0 A5232 5 0.03125 2.0 8.0 B4623 6 0.0625 2.0 8.0 B4623 7 0.12501 2.0 8.0 B4623 8 0.25003 2.0 8.0 B4623 9 0.50005 2.0 8.0 B4623 10 1.00010 2.0 8.0 B4623 11 2.00021 8.0 25.0 A4625 12 4.00042 8.0 25.0 A4625 13 7.99895 20.0 32.0 A4827 13半 4.00042 8.0 25.0 A4625 式中:Q为标准状态下最大流量,Nm3/h;G为空气比重,为1.1kg/Nm3; T为气体温度, ℃; p1为入口压力, kg/cm2; p2为出口压力, kg/cm2; Δp=p1-p2, kg/cm2。
PCM数字阀的开关阀采用德国GSR二位二通系列的电磁阀, PWM数字阀的高频开关阀采用德国GSR 2/943,该阀动作频率可达1kHz,具有脉宽调制功能,线性流量控制。为使各喷嘴入口压力、温度等条件一致,入口压力稳定,出口压力满足喷嘴喉道气流为声速流要求,电磁阀的流量系数尽量选大,以减小工作压力降,同时需要一定容积的阀体/管道作为稳定段,增加喷嘴入口压力的稳定性[13]。
由于电磁阀不同口径的开关时间存在一定差异,其口径不大于25mm时阀门开关时间约为0.1s,而口径为32mm时阀门开关时间长达0.44s。为了减少各阀门在时间上的差异,增加阀门切换过程中的稳定性,电磁阀的口径都选用25mm以内的。口径32mm的电磁阀则由2个口径25mm的电磁阀组合替代,因此13位半的PCM数字阀具有15个支路,再加上PWM数字阀,共计16个支路。
3 流量控制策略
3.1 供气控制系统
供气控制系统的高压气源来自12~22MPa的高压储气罐,经减压阀降低至稳定的8MPa,再通过数字阀输出试验需要的流量值。在数字阀后端有高精度的文丘里流量计实时监测和反馈输出的流量值,从而组成闭环控制系统,如图 4所示。
3.2 流量调节运算方法
供气控制系统采用了微分前置非线性PID流量调节运算方法,其控制量通过数字阀完成,实现主管路流量的控制。该运算方法首先根据主管路流量给定与流量反馈完成PID运算,然后通过PID运算结果和数字阀气流入口总压总温,计算数字阀阀位偏差,将此偏差作为数字阀阀位补偿值重新调整阀位,从而调整主管路流量输出值,当流量输出值与给定值的差值进入预先设定的误差带内(±6g/s),则停止动作PCM数字阀,由PWM数字阀通过脉宽调制控制。该运算的微分前置环节可对供气管道及管道设备(数字阀后的供气管道、空气换热器、空气过滤器等)容积造成的流量滞后进行补偿,缩短调节过渡过程时间,增加系统稳定性;比例和积分环节的运算律按照大误差小比例、小积分增益,以及小误差大比例、大积分增益的控制策略构建。
4 调试与应用
4.1 调试
FL-12风洞供气控制系统的数字阀安装示意图如图 5所示。
在调试中,需要在不同流量、不同试验模型状态的情况下,多次调整PID运算的比例增益、积分增益和调节微分增益等参数,使流量控制达到最佳状态。表 4给出了流量闭环控制的测试结果,当给定流量1.2、2.4、3.55和4.67kg/s时,系统流量控制的最大绝对误差分别为1.9、2.2、2.5和2.6g/s,最大相对误差分别为0.15%、0.09%、0.07%、和0.06%。调试数据表明,该套数字阀的流量控制精度能够满足设计指标±3g/s,同时能够实现宽范围的流量调节,且效果平稳,重复性好,可靠性高。
表 4 流量闭环控制的测试结果(单位:kg/s)Table 4 Test results of the flow closed loop control给定流量 1.2 2.4 3.55 4.67 均值流量 1.2012 2.3984 3.5518 4.6688 最大流量 1.2019 2.4022 3.5525 4.6720 最小流量 1.1996 2.3979 3.5480 4.6674 极差 0.0023 0.0043 0.0045 0.0046 最大绝对误差 0.0019 0.0022 0.0025 0.0026 最大相对误差 0.15% 0.09% 0.07% 0.05% 4.2 应用
数字阀在供气控制系统中调试完成后,开展了数十项供气试验。其中以某型飞机进气道试验为例,本次试验的供气流量为1.0和3.2kg/s,流量控制调节过程曲线和稳态过程曲线分别如图 6和7所示。
当供气流量为1.0kg/s时,流量稳定时间为15s,最大绝对误差为1.8g/s,最大相对误差为0.15%;当供气流量为3.2kg/s时,流量稳定时间为16s,最大绝对误差为2.7g/s,最大相对误差为0.08%。
5 结论
大量的供气试验结果表明,采用13位半PCM数字阀和PWM数字阀组合的数字阀在FL-12风洞供气控制系统中的应用是成功的,全面达到了设计指标。其控制精度高、响应时间短、调节范围宽和可靠稳定等特点,为风洞供气试验提供了强有力的支撑。
-
表 1 试验条件
Table 1 Experimental condition
试验条件 数值 温度 T/℃ –12~–14 尖速比 λ 0.2, 0.6, 1.0 风速 U/(m·s–1) 4 叶片数 B 1, 2, 4 液态水含量 LWC/(g·m–3) 0.58 水滴平均直径 MVD/μm 50 试验时间 t/min 15 拍摄间隔 Δt/min 5 表 2 试验方案
Table 2 Experimental scheme
工况 尖速比 λ 叶片数 B 1 0.2 1 2 0.2 2 3 0.2 4 4 0.6 1 5 0.6 2 6 0.6 4 7 1.0 1 8 1.0 2 9 1.0 4 -
[1] 战培国. 国外寒冷地区风力机结冰问题研究[J]. 航空科学技术,2016,27(2):1-6. DOI: 10.3969/j.issn.1007-5453.2016.02.001 ZHAN P G. Review of the wind turbine icing in overseas cold regions[J]. Aeronautical Science & Technology,2016,27(2):1-6. doi: 10.3969/j.issn.1007-5453.2016.02.001
[2] 朱胜兵. 大型风力机叶片结冰对其模态影响的研究[D]. 长沙: 湖南大学, 2018. ZHU S B. Modal analysis on large wind turbine and its blade characterized by ice accumulation[D]. Changsha: Hunan University, 2018.
[3] LI Y,TAGAWA K,FENG F,et al. A wind tunnel experimental study of icing on wind turbine blade airfoil[J]. Energy Conversion and Management,2014,85:591-595. doi: 10.1016/j.enconman.2014.05.026
[4] 王晓东,于佳鑫,房代宝,等. 随机风况下风力机翼型结冰对气动特性的影响研究[J]. 风机技术,2020,62(2):59-66. WANG X D,YU J X,FANG D B,et al. Investigations on the influence of icing on aerodynamics of wind turbine airfoil under stochastic wind conditions[J]. Chinese Journal of Turbomachinery,2020,62(2):59-66.
[5] 陈红星. 薄覆冰状态下小型风力发电机叶片模态试验研究[D]. 呼和浩特: 内蒙古农业大学, 2019. CHEN H X. Modal test of small wind turbine blades under thin ice cover[D]. Hohhot: Inner Mongolia Agricultural University, 2019.
[6] 胡良权,陈进格,沈昕,等. 结冰对风力机载荷的影响[J]. 上海交通大学学报,2018,52(8):904-909. HU L Q,CHEN J G,SHEN X,et al. Load of wind turbine affected by icing[J]. Journal of Shanghai Jiao Tong University,2018,52(8):904-909.
[7] GAO L Y,LIU Y,HU H. An experimental investigation of dynamic ice accretion process on a wind turbine airfoil model considering various icing conditions[J]. International Journal of Heat and Mass Transfer,2019,133:930-939. doi: 10.1016/j.ijheatmasstransfer.2018.12.181
[8] BLASCO P,PALACIOS J,SCHMITZ S. Effect of icing roughness on wind turbine power production[J]. Wind Energy,2017,20(4):601-617. doi: 10.1002/we.2026
[9] ETEMADDAR M,HANSEN M O L,MOAN T. Wind turbine aerodynamic response under atmospheric icing conditions[J]. Wind Energy,2014,17(2):241-265. doi: 10.1002/we.1573
[10] 易贤,周志宏,杜雁霞,等. 考虑相变时间效应的结冰试验相似参数[J]. 实验流体力学,2016,30(2):14-19. DOI: 10.11729/syltlx20160016 YI X,ZHOU Z H,DU Y X,et al. An icing scaling parameter with the effects of phase change time[J]. Journal of Experiments in Fluid Mechanics,2016,30(2):14-19. doi: 10.11729/syltlx20160016
[11] 易贤,郭龙,符澄,等. 结冰风洞试验段水滴分布特性分析[J]. 实验流体力学,2016,30(3):2-7. DOI: 10.11729/syltlx20160034 YI X,GUO L,FU C,et al. Analysis of water droplets distribution in the test section of an icing wind tunnel[J]. Journal of Experiments in Fluid Mechanics,2016,30(3):2-7. doi: 10.11729/syltlx20160034
[12] 周志宏,易贤,桂业伟,等. 考虑水滴动力学效应的结冰试验相似准则[J]. 实验流体力学,2016,30(2):20-25. DOI: 10.11729/syltlx20160013 ZHOU Z H,YI X,GUI Y W,et al. Icing scaling law with the dynamic effects of water droplets[J]. Journal of Experiments in Fluid Mechanics,2016,30(2):20-25. doi: 10.11729/syltlx20160013
[13] 李维浩,李伟斌,易贤,等. 考虑动力学效应的结冰试验相似准则修正方法[J]. 实验流体力学,2020,34(3):97-103. DOI: 10.11729/syltlx20190166 LI W H,LI W B,YI X,et al. A correction method of icing testing scaling law with dynamic effects[J]. Journal of Experiments in Fluid Mechanics,2020,34(3):97-103. doi: 10.11729/syltlx20190166
[14] LI Y,WANG S L,LIU Q D,et al. Characteristics of ice accretions on blade of the straight-bladed vertical axis wind turbine rotating at low tip speed ratio[J]. Cold Regions Science and Technology,2018,145:1-13. doi: 10.1016/j.coldregions.2017.09.001
[15] 李岩,孙策,郭文峰,等. 利用自然低温的旋转叶片结冰风洞试验系统设计[J]. 实验流体力学,2018,32(2):40-47. DOI: 10.11729/syltlx20170073 LI Y,SUN C,GUO W F,et al. Design of icing wind tunnel experiment system for rotating blades by using natural low temperature[J]. Journal of Experiments in Fluid Mechanics,2018,32(2):40-47. doi: 10.11729/syltlx20170073







 下载:
下载: