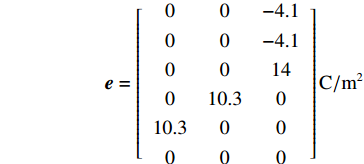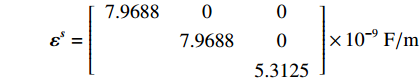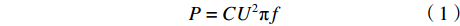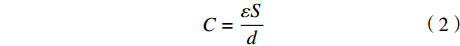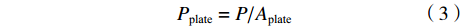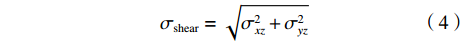Research on the influence of the piezoelectric ceramics layout on de-icing effect
-
摘要: 用仿真与实验的方式研究了压电陶瓷除冰技术在复合材料上的应用。通过有限元仿真研究了在能耗相等的前提下压电陶瓷布局（数目、间距）对除冰效果的影响，并进行了冷环境下除冰实验。仿真结果表明：按合理的布局方式，将尺寸较大的单块压电陶瓷分成尺寸较小的多块时，会有比大尺寸单块压电陶瓷更好的除冰效果；随着压电陶瓷间距的减小，除冰效果进一步增强。实验结果表明：增大压电陶瓷输入功率可以较大程度缩短除冰时间；将尺寸较大的单个压电陶瓷分成尺寸较小的4块后，相同能耗下除冰效果增强；减小压电陶瓷之间的的间距后，除冰时间进一步缩短。Abstract: The piezoelectric de-icing method is studied by simulation and experiment on a composite plate. The effect of piezoelectric ceramic layout (number, spacing) on the de-icing effect under the same energy consumption is studied by finite element simulation. The de-icing experiments are done under cold environment condition. The results show that when the piezoelectric ceramics with larger dimension are divided into smaller pieces according to a certain layout, the de-icing effect becomes better than that with large size single piezoelectric ceramic. As the spacing of the piezoelectric ceramics decreases, the deicing effect is further enhanced. The experimental results show that the de-icing time can be greatly shortened by increasing the input power of actuators. After dividing the large piezoelectric ceramics into four smaller ones, the de-icing effect is enhanced with the same energy consumption. The de-icing time is further shortened after the spacing of the piezoelectric ceramics is reduced.
-
0 引 言
飞机飞过云层时，云层中聚积的过冷水滴会与飞机外表面发生撞击，水滴撞击后会迅速在飞机表面结冰[1-2]。冰层在机翼前缘表面聚积会改变飞机的气动特性，使飞机的阻力增大、升力降低，严重时会引发飞机失控而坠毁[3]。为了避免飞机因为结冰而造成损失，发展防除冰技术就显得十分重要。到目前为止，国内外研究人员发展了多种防除冰技术，主要有3大类：液体防除冰技术、热力学防除冰技术和机械除冰技术[4]。其中，热力学类的电热防除冰技术和机械类的电脉冲除冰技术已经在飞机上有所应用[5]。
尽管这些技术都能达到防除冰的目的，但是它们都有各自明显的缺点，例如能耗过高以及给飞机增加了额外的重量[6]。热力学防除冰方法中，每平方米的待防护结构表面就需要高达10 kW的功耗[7]。因此，发展一种低能耗、小质量、小体积的防除冰技术就显得尤为重要。
压电除冰技术首先由国外学者提出，并受到广泛的关注。压电除冰技术利用压电材料的逆压电效应[8]，通过安置在结构表面的压电作动器（最常用的为压电陶瓷[9-10]）的激振，引起待除冰结构振动，从而在结构与冰层交界面产生剪切应力，当剪切应力超过冰层与结构表面之间的黏附强度（大气中的水结的冰为0.05～0.50 MPa）[11-13]，冰层就会从结构表面脱落。国内研究者也对压电除冰技术在飞机机翼与风力机叶片上的应用进行了研究[14-17]。谭海辉等[18-19]研究了风力机叶片超声波除冰理论与方法，提出风力机叶片压电除冰的最佳方案。Wang等[20]利用铌酸锂材料制成的压电作动器进行了复合材料风力机叶片上的除冰研究，分别给出了冰层厚度与除冰时间、能耗的关系式。Daniliuk等[11]分析了不同材料的超声作动器在金属和复合材料结构上的除冰效果。文献[21]研究了翼型内表面压电陶瓷的可贴范围。文献[22]的研究表明，在压电除冰系统中，单个压电陶瓷尺寸的选择与振型的波长有关。但是在实际除冰系统中，为了取得最佳除冰效果，需要在1个位置放置多块压电陶瓷，而关于压电陶瓷布局选择的研究还比较欠缺。针对这一问题，本文在1个波峰或波谷布置多个压电陶瓷，对压电陶瓷的尺寸与间距对除冰效果的影响进行研究。
近年来，复合材料在航空和风力机行业大量应用，纤维增强复合材料是复合材料中应用最广泛的一种[23-24]。本文所研究的结构为玻璃纤维增强环氧树脂复合材料，其中基体材料为环氧树脂，增强材料为玻璃纤维。
1 单个压电陶瓷的有效面积对除冰效果的影响
1.1 复合材料平板的模态分析
对尺寸为300 mm×200 mm×2 mm的复合材料平板进行模态分析，材料的物理参数如表1所示。其中E为杨氏模量，ν为泊松比，G为剪切模量，下标x、y、z分别表示长度、宽度、厚度3个方向。平板的纤维铺层共有8层，每一层的厚度为0.25 mm，纤维的铺设角度如图1所示。提取平板的前六阶模态，其位移振型如图2所示。由图2可以看出，平板的前六阶振型都呈现沿平板长度方向的“波峰-节点-波谷”分布，且节点位置的位移为0 ，波峰/波谷位置位移较大，这说明除冰模态选择时，应使冰层处于波峰/波谷的位置。
表 1 复合材料的物理参数Table 1 Physical parameters of composite materialsDensity/（kg·m–3） Ex /Pa Ey /Pa Ez /Pa νxy νxz νyz Gxy /Pa Gxz /Pa Gyz /Pa 2000 5.00×1010 8.00×109 8.00×109 0.30 0.30 0.40 5.00×109 5.00×109 3.85×109 在压电除冰有限元分析时，往往认为模型中积冰的位置位于平板的中间[25-26]。这就需要选择平板中间位置为波峰的某一阶模态，即奇数阶的模态。在用压电陶瓷驱动平板振动时，为了获得更好的激振效果，应将压电陶瓷布置在波峰/波谷的位置。为了有较多的位置安装压电陶瓷，在奇数阶的模态中选取平板的第五阶模态为除冰模态（波峰/波谷总数为5，可布置5处压电陶瓷），由图2可以看出第五阶固有频率为955.62 Hz。
1.2 单个压电陶瓷不同有效面积下的谐响应分析
对“平板-冰层-压电陶瓷”结构进行谐响应分析。冰层尺寸为20 mm×20 mm×1 mm，位于平板的中间波峰位置。冰层的密度为919 kg/m3、泊松比为0.33、杨氏模量为8.58×109 Pa。
压电陶瓷为PZT8，密度为7600 kg/m3，刚度cE、压电常数e、介电常数εs矩阵表示如下：
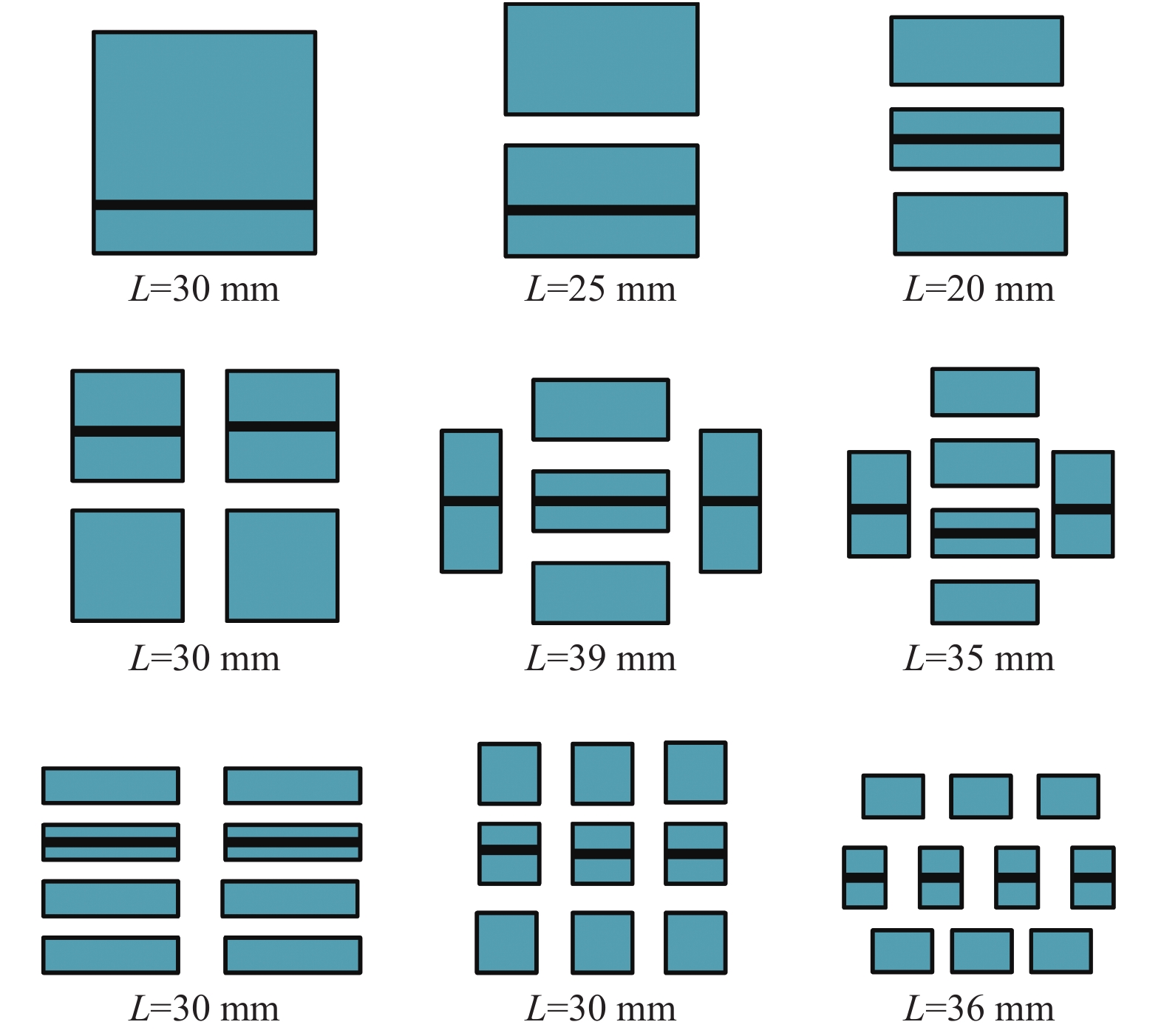
$$\;{{\boldsymbol{c}}^{\boldsymbol{E}}} = \left[\! {\begin{array}{*{20}{c}} {14.9}&{8.11}&{8.11}&0&0&0 \\ {}&{14.9}&{8.11}&0&0&0 \\ {}&{}&{13.2}&0&0&0 \\ {}&{}&{}&{3.13}&0&0 \\ {}&{}&{}&{}&{3.13}&0 \\ {}&{}&{}&{}&{}&{3.4} \end{array}}\! \right] \times {10^{10}} \; {\rm{N}}/{{\rm{m}}^{2}}$$ $${\boldsymbol{e}} = \left[ {\begin{array}{*{20}{c}} 0&0&{ - 4.1} \\ 0&0&{ - 4.1} \\ 0&0&{14} \\ 0&{10.3}&0 \\ {10.3}&0&0 \\ 0&0&0 \end{array}} \right]{\rm{C}}/{{\rm{m}}^{2}}$$ $${{\boldsymbol{\varepsilon}} ^{\boldsymbol{s}}} = \left[ {\begin{array}{*{20}{c}} {7.9688}&0&0 \\ {}&{7.9688}&0 \\ {}&{}&{5.3125} \end{array}} \right] \times {10^{ - 9}}\;{\rm{F}}/{{\rm{m}}}$$ 为了分析单个压电陶瓷的有效面积（压电陶瓷与结构的接触面积）对除冰效果的影响，在压电陶瓷总有效面积为900 mm2的前提下，将其分成了不同尺寸、不同数目的小块压电陶瓷，分别进行谐响应分析。单个压电陶瓷尺寸及其有效面积如表2所示，不同数目的压电陶瓷布局如图3所示，图中L表示不同布局下压电陶瓷的总长度（即图中不同布局下黑线的总长）。
表 2 不同数目的压电陶瓷的尺寸表（厚度为2 mm）Table 2 Dimensions of different numbers of piezoelectric ceramics （thickness is 2 mm）Number of
piezoelectric ceramicsLength/
mmWidth/
mmEffective area of
single piezoelectric ceramic/mm2Total effective
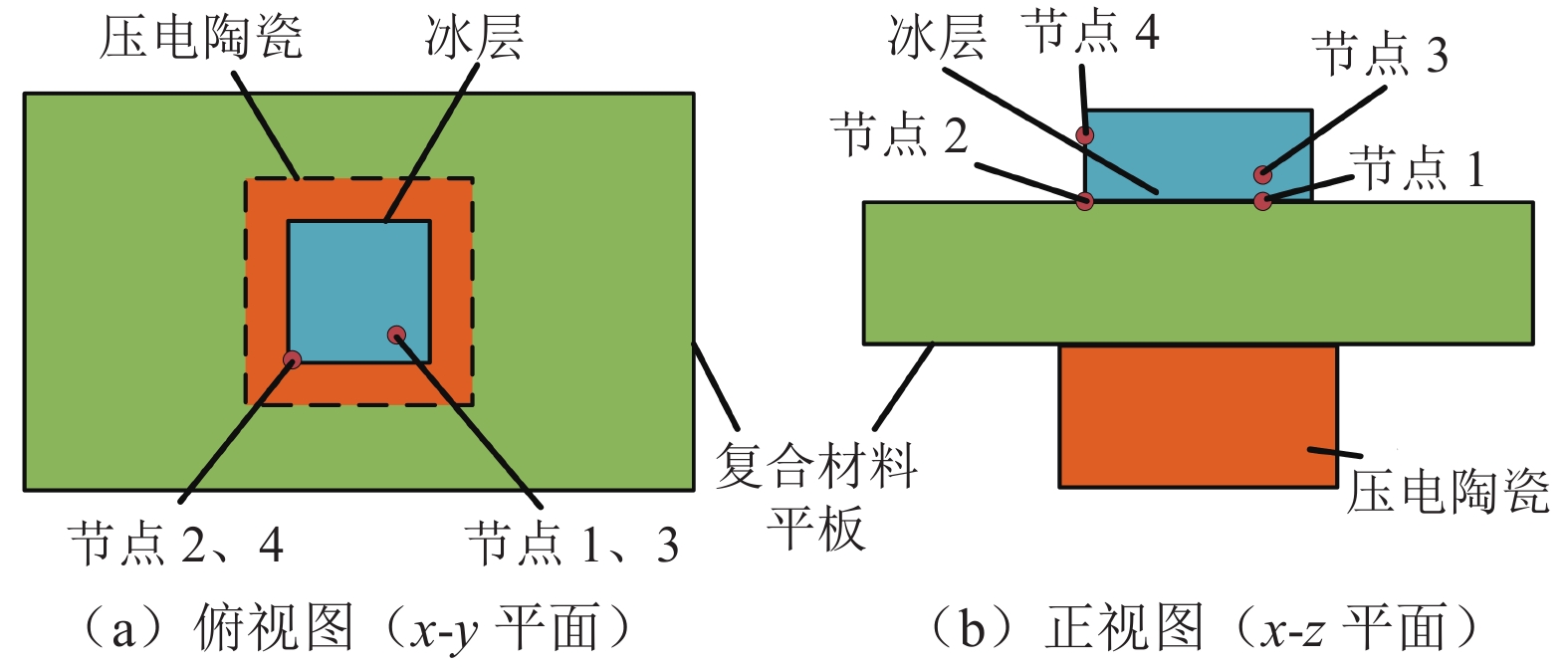
area/mm21 30.0 30.0 900.0 900.0 2 25.0 18.0 450.0 900.0 3 20.0 15.0 300.0 900.0 4 15.0 15.0 225.0 900.0 5 15.0 12.0 180.0 900.0 6 15.0 10.0 150.0 900.0 8 15.0 7.5 112.5 900.0 9 10.0 10.0 100.0 900.0 10 10.0 9.0 90.0 900.0 选取了“平板-冰层-压电陶瓷”模型中的4个节点来观察谐响应结果，通过这4个节点的位移来判断激振效果的强弱。节点的位置如图4所示，节点1、2位于冰层与平板交界面上，节点3、4位于冰层内部。模型中的坐标原点位于平板内部中心位置，4个节点的坐标分别是（5，–5，1）、（–10，–10，1）、（5，–5，1.5）、（–10，–10，1.8），单位为mm。
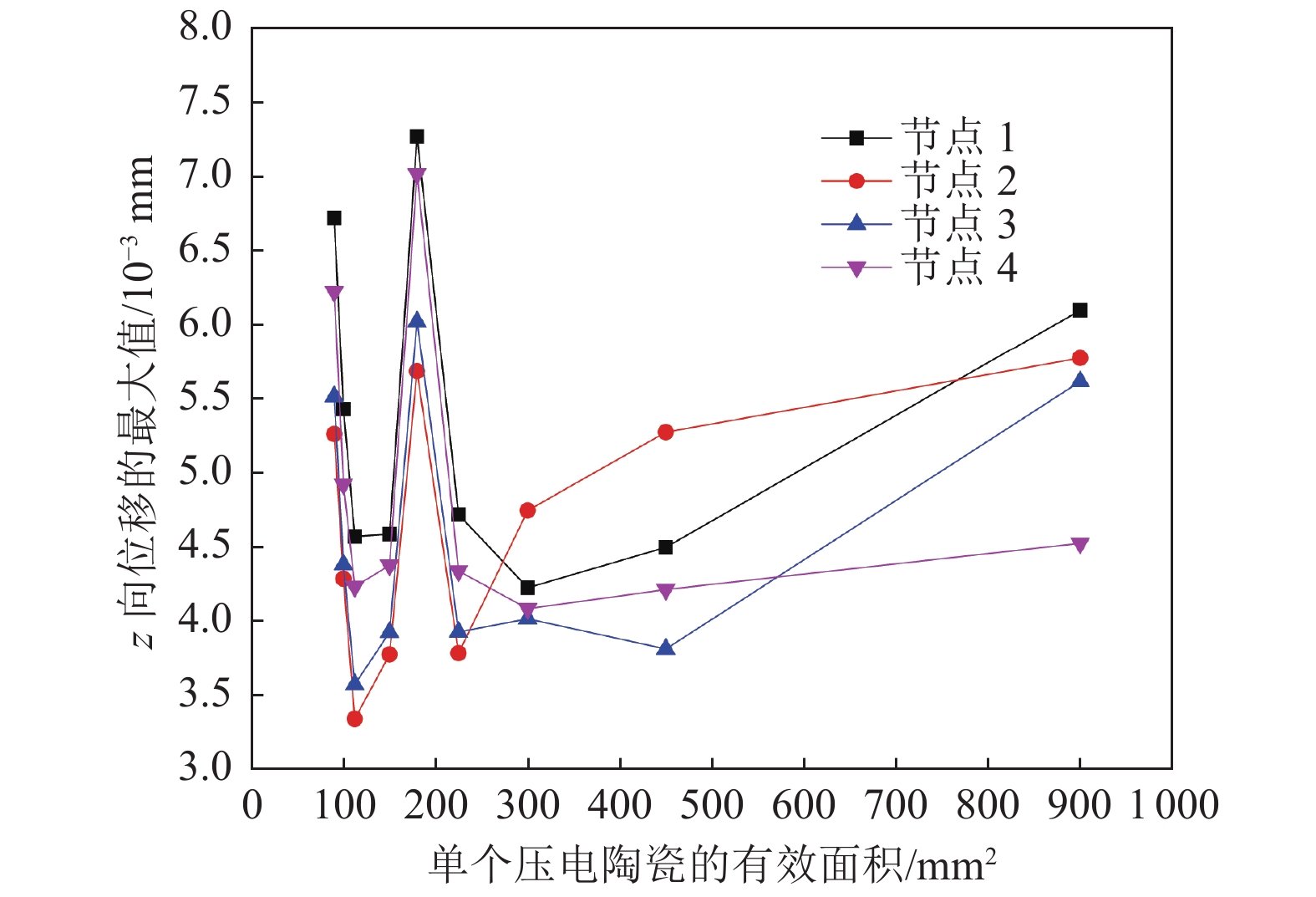
采用完全法谐响应分析，设置的频率范围为905～1005 Hz，共100个载荷步，激励电压为200 V，阻尼系数设置为0.01。4个节点在频率范围内的z向位移最大值随单个压电陶瓷面积的变化曲线如图5所示。
![]()
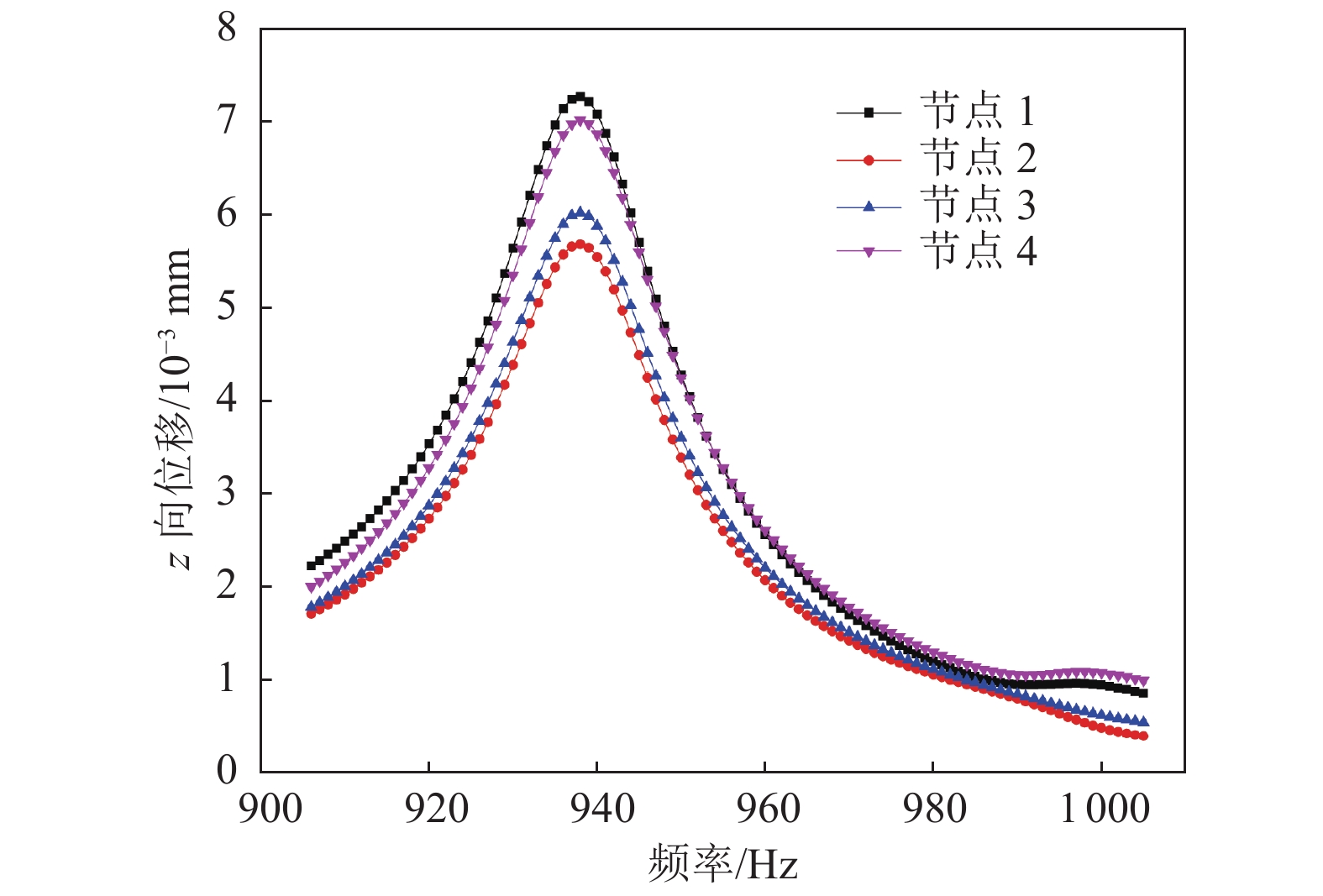
图 5 节点最大位移随单个压电陶瓷有效面积的变化曲线Fig. 5 The curve of the maximum displacements of nodes varying with the effective area of single piezoelectric ceramic由图5可见，单个压电陶瓷与平板的有效接触面积为180 mm2，即大压电陶瓷被分成尺寸相等的5小块时，有比整块大压电陶瓷更好的激振效果（总接触面积和能耗不变的前提下，压电陶瓷由完整1块改为小尺寸5块时，节点位移的最大值平均增大了 17.43%）。这是由于压电陶瓷的刚度远大于复合材料平板的刚度，在平板振动时陶瓷会对其产生抑制作用。当使用1块尺寸较大的完整压电陶瓷时，与陶瓷接触的整个平板区域受到抑制，而当陶瓷分成小块时，这种抑制作用相对分散。压电陶瓷的数目为5时的节点位移-频率曲线如图6所示，由图可知激振效果最佳的频率接近平板结构的第五阶固有频率。
2 压电陶瓷间距对除冰效果的影响
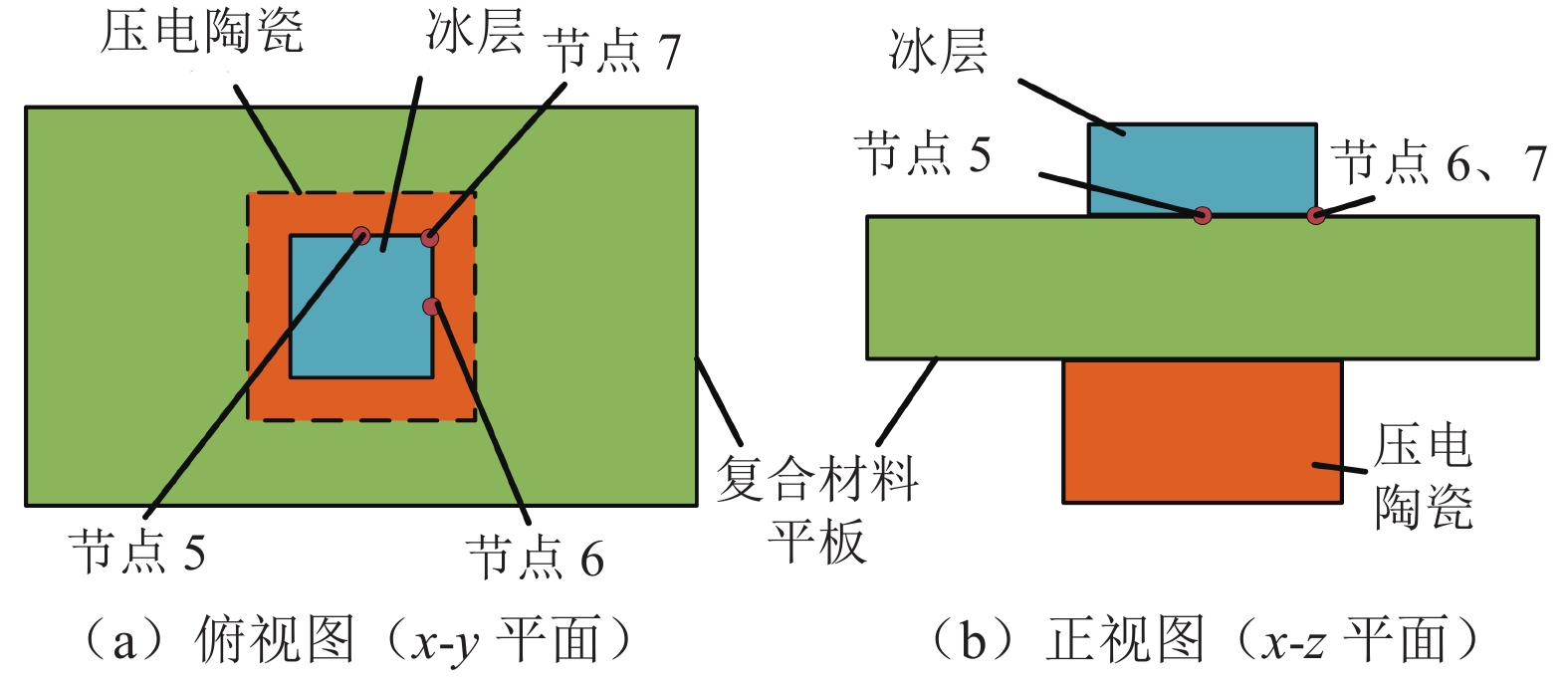
在平板振型的1个波峰/波谷处、单个压电陶瓷尺寸为180 mm2的前提下，分析了压电陶瓷的间距对激振效果和除冰效果的影响。在改变5块压电陶瓷的间距后，通过另外3个位于冰层与平板交界面上的节点的最大位移来分析压电陶瓷间距对激振效果的影响，节点的位置如图7所示，3个节点的坐标分别是（0，10，1）、（10，0，1）和（10，10，1），单位为mm。改变压电陶瓷间距后的节点最大位移变化情况如图8所示。
随着压电陶瓷间距的增大，节点的最大位移逐渐减小。这表明：在平板振型的1个波峰或波谷的位置布置多个压电陶瓷时，压电陶瓷的间距越小，除冰效果越好。这是因为和压电陶瓷的尺寸与间距相比，平板上由激振产生的位移是极小的；压电陶瓷的间距越大，振动在叠加前传递的距离就越大，因结构阻尼而产生的损耗也越大，而这些损耗就会使平板原本较小的位移进一步减小，从而降低除冰效果。
3 压电陶瓷最佳布局下除冰效果验证
为了检验1、2节中所述的布局规律能否在低能耗的前提下达到除冰效果，在长宽比不同的两块复合材料平板上进行了仿真验证，计算了相应条件下单位面积复合材料平板上的能耗。压电陶瓷的功率可以由下式计算：
$$P = C {U^2} {\text{π}} f$$ (1) 式中，U为电压峰值，f为频率，C为压电陶瓷电容，可由下式求得：
$$C = \frac{{\varepsilon S}}{d}$$ (2) 式中，ε为介电常数，S为压电陶瓷与平板接触的有效面积，d为压电陶瓷厚度。平板单位面积上的功率为：
$${P_{\text{plate}}} = {P / {{A_{\text{plate}}}}}$$ (3) 其中Aplate为平板待防护面积。
3.1 长宽比1.5的平板除冰效果验证
在参数如1.1节所述的复合材料平板上进行了低频与高频下的除冰效果验证，平板的长宽比为1.5。冰层与平板交界面上的剪切应力为[12]：
$${\sigma _{{\rm{shear}}}} = \sqrt {\sigma _{xz}^2 + \sigma _{yz}^2} $$ (4) 3.1.1 低频下的除冰效果验证
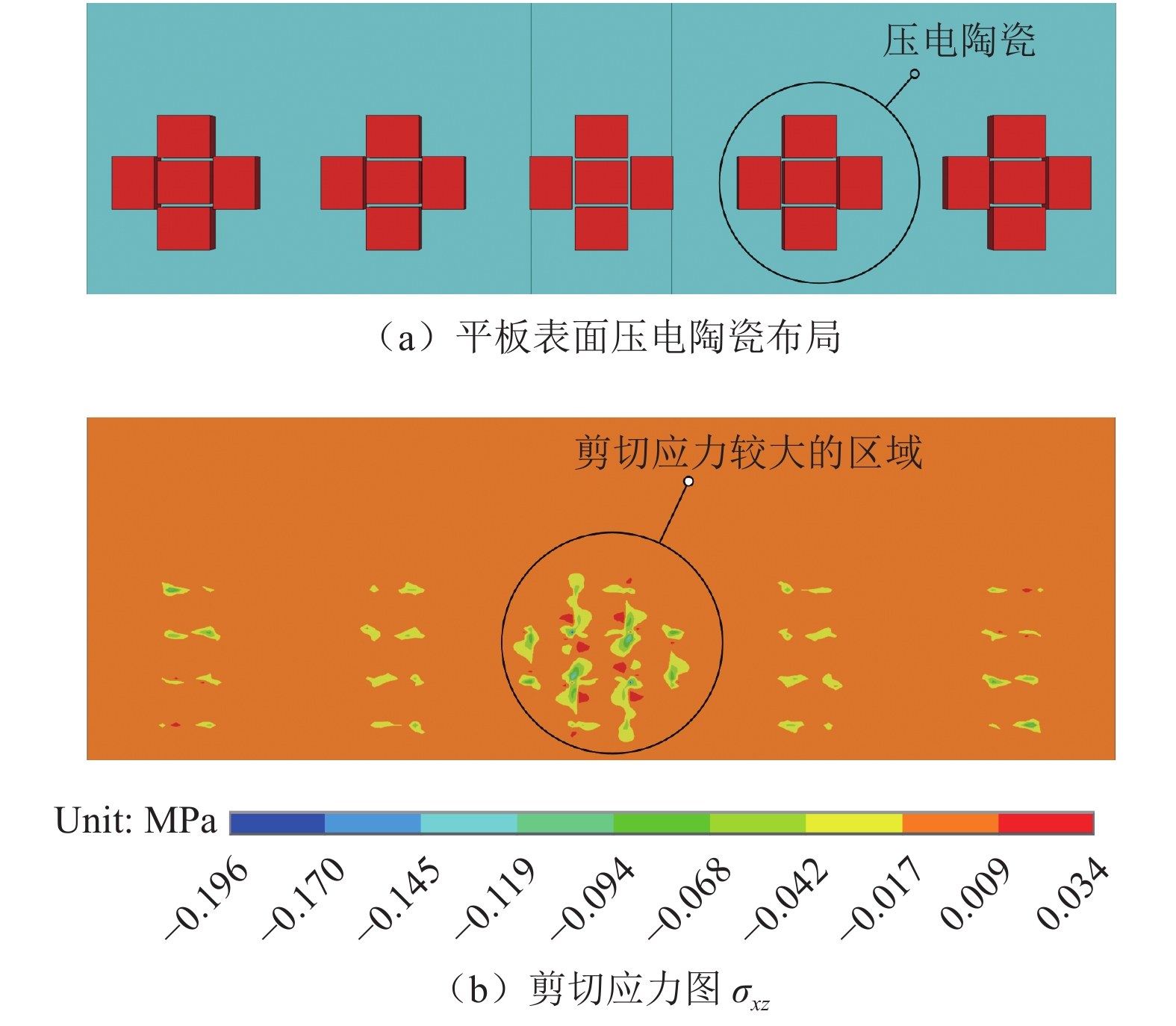
在平板五阶振型的5个波峰/波谷上，按单个压电陶瓷有效面积为180.0 mm2的方式布置了5个压电陶瓷，其间距为1 mm，输入电压为300 V。压电陶瓷在复合材料平板上的布局方式及频率为0.955 kHz时的剪切应力云图如图9所示。
![]()
图 9 5个波峰/波谷上的压电陶瓷布局及剪切应力（0.955 kHz）Fig. 9 Layout of piezoelectric ceramics on five peaks /valleys and shear stress (0.955 kHz)图9（a）中，红色部分为压电陶瓷，蓝色部分为平板结构。剪切应力最大值σshear = 0.330 MPa。
根据引言中所述，大气中的水结的冰与结构间的黏附强度在0.05～0.50 MPa之间，文献[20]也表明冰与复合材料之间的黏附强度为0.24 MPa，由此可知，在低频条件下，利用本文所述的压电陶瓷布局方式理论上可以满足除冰需求。由式（3）可以求得此时的压电陶瓷功率为53.75 W/m2。由图9（b）还可以看出振动产生的剪切应力最大值都分布在压电陶瓷所对应的位置，这说明应将压电陶瓷安置在平板内侧与冰层正对的位置。
3.1.2 高频下的除冰效果验证
当压电陶瓷的激振频率为其谐振频率时，阻抗最小，将最大限度发挥压电陶瓷的激振能力[27]，因此，在压电陶瓷谐振频率范围内进行谐响应分析。以阻抗分析仪测得本文所使用的压电陶瓷的谐振频率为140.000 kHz。压电陶瓷的布置方式仍然如图9（a）所示。剪切应力如图10所示，最佳除冰频率为139.800 kHz。
从图10可以看出，剪切应力σxz的最大值为0.488 MPa，出现在冰层的边缘位置；剪切应力σyz的最大值为1.430 MPa，出现在冰层的中间位置。从图10（a）还可以看出，冰层中间位置剪切应力σxz的值为0.276 MPa。根据式（4），冰层中间位置的总剪切应力为1.450 MPa，大于冰层与复合材料结构间的黏附强度，因此在139.800 kHz的振动频率下，可以达到除冰的目的。由式（3）求得此时压电陶瓷的总功率为7.870 kW/m2。
对比低频下的谐响应分析结果可知，在其他条件不变的前提下，将激振频率由低频提高到高频可以有效增大交界面的剪切应力，从而增强除冰效果。这是因为压电陶瓷振动频率增大后，功率也相应增大；但提高振动频率同时也意味着压电陶瓷能耗的增加。对于复合材料表面而言，振动产生的剪切应力达到0.500 MPa左右就可以达到除冰目的，并不需要高达1.450 MPa。因此，除冰模态与振动频率应该匹配，尽量减少除冰能耗。
3.2 长宽比4.3的平板除冰效果验证
3.2.1 平板模态分析
在一块长宽比较大的复合材料平板上进行了对比验证。平板尺寸为300 mm×70 mm×2 mm。对平板进行了高频与低频下的模态分析，得到其五阶固有频率为932.64 Hz，其最接近压电陶瓷谐振频率（140.000 kHz）的一阶固有频率为139.966 kHz。平板的位移振型如图11所示。
3.2.2 长宽比4.3的平板谐响应分析结果对比
分别在平板的五阶固有频率范围内和压电陶瓷的谐振频率范围内进行谐响应分析。如图12所示，由于待防护结构的尺寸较小，所以仅在平板的中间位置布置5块压电陶瓷。谐响应分析的参数设置与1.2节相同，每块压电陶瓷的尺寸为15 mm×12 mm×2 mm，输入电压为200 V，布局方式如图12所示。不同频率下，交界面剪切应力值如表3所示。
![]()
图 12 长宽比4.3的平板上的压电陶瓷布局Fig. 12 The layout of actuators on the plate with aspect ratio of 4.3表 3 不同激振频率下的剪切应力Table 3 Shear stresses in different vibration frequenciesCase Frequency/kHz Voltage/V Total shear stress/MPa Power /（kW·m–2） 1 0.932 200 0.160 0.010 2 140.000 200 0.890 2.000 3 139.966 200 1.720 1.990 由表3可知，在激振频率为0.932 kHz（平板五阶固有频率）时，压电陶瓷功率为0.010 kW/m2，振动产生的剪切应力为0.160 MPa，未达到冰层与平板黏附强度。因此，在振动频率较小时，为了达到除冰效果，应布置较多的压电陶瓷或提高输入电压值。
在激振频率为140.000 kHz（压电陶瓷的谐振频率）时，总的剪切应力为0.890 MPa，压电陶瓷功率为2.000 kW/m2。此时的剪切应力大于黏附强度，理论上可以达到除冰效果。
当其他条件不变而激振频率为平板的固有频率139.966 kHz时，冰层与复合材料平板交界面上总的剪切应力为1.720 MPa，压电陶瓷功率为1.990 kW/m2，与激振频率为140.000 kHz时的功率基本一致，而产生的交界面剪切应力却将近前者的2倍。这说明合理选择除冰模态可以增大剪切应力，最终起到降低能耗的作用。
3.3 除冰效果验证过程中的能耗分析
为了对比3.1节与3.2节中验证的除冰效果，对压电陶瓷功率进行了分析。剪切应力-能耗曲线如图13所示，由于两个平板的尺寸不同，因此考虑了平板单位面积上的功率。图中U、f分别为电压峰值和频率。由图可见：点5对应的功耗远大于点3，但最终产生的交界面剪切应力却比点3处的小；点4对应的功耗与点3基本相等，产生的交界面剪切应力却约为点3处的一半。这是由于点4与点5对应的激振频率为压电陶瓷谐振频率，而点3对应的激振频率为接近谐振频率的平板固有频率。
这表明在高频范围内选择除冰模态时，可以选择最接近压电陶瓷谐振频率的那一阶模态，因为这个频率既是平板的固有频率，振动效果更好，又接近压电陶瓷的谐振频率，可以较好地发挥压电陶瓷的激振能力。
3.4 复合材料平板失效分析
为了检验除冰过程中振动对复合材料平板本身造成的影响，进行了失效分析。失效分析中的材料强度采用如表4所示的文献[28]中的参数。其中XT
、YT 、ZT分别表示沿x、y、z方向的抗拉强度，XC 、 YC、 ZC 分别表示沿x 、 y 、 z方向的抗压强度，Sxy 、Syz 、Sxz分别为 x-y、y-z、x-z面内的剪切强度，单位均为MPa。 表 4 平板强度参数（MPa）[28]Table 4 The strength parameters of the plate (MPa)[28]XT XC YT YC ZT ZC Sxy Syz Sxz 1100 670 1100 670 35 120 80.0 80 46.1 针对长宽比不同的两块复合材料平板，在图13中剪切应力最大（点3）和压电陶瓷能耗最大（点5）两种极限情况下进行了有限元失效分析。
图14为两平板的Tsai-Wu失效准则破坏因子云图。由图可见，长宽比较小的平板，破坏因子最小值与最大值分别为–0.057、0.026；长宽比较大的平板，破坏因子最小值与最大值分别是–0.008、0.034。根据Tsai-Wu失效准则，破坏因子在（–1.000，1.000）之间时说明结构安全。因此，采用本文所述的压电除冰方法，不会对复合材料平板本身造成损伤。
![]()
图 14 平板Tsai-Wu失效准则破坏因子云图Fig. 14 Destory factors of Tsai-Wu failure criteria of two plates4 除冰实验验证
仿真结果表明，当激振频率为压电陶瓷的谐振频率（140.000 kHz）时，在长宽比1.5的平板上布置5处压电陶瓷产生的剪切应力（1.450 MPa）比长宽比4.3的平板上布置1处压电陶瓷产生的剪切应力（0.890 MPa）大。长宽比4.3的平板上压电陶瓷功率（2.000 kW/m2）比长宽比1.5的平板上压电陶瓷功率（7.870 kW/m2）低。因此，对长宽比为4.3的复合材料平板压电除冰进行了实验验证。实验主要分两部分：除冰效果验证实验，压电陶瓷布局规律验证实验。实验中，为了确保冰层脱黏后在重力作用下掉落以记录除冰所需时间，采用了在平板上粘接块状冰层的结冰方式。
4.1 除冰效果验证实验
除冰效果验证实验中的平板及紧固装置如图15（a）所示，压电陶瓷布局如图15（b）所示，实验环境温度为–25 ℃的冷环境。为了观察到冰层的直接掉落，采用的结冰形式为块状冰层。通过信号发生器与功率放大器改变压电陶瓷的输入功率与电压（输入功率可以由显示的电压值与电流值求得）。除冰结果如图16所示。图16（a）中的输入功率为1.190 kW/m2，当通电72 s后，附着的冰层发生第一次脱落；提高输入功率至1.905 kW/m2时，通电后经过38 s，冰层发生第一次脱落，如图16（b）所示。
平板的数值模拟结果显示：压电陶瓷按照3.2.2小节所述的布局方式，在振动频率为140.000 kHz时，理论上可以使冰层脱落。相应的实验结果也验证了数值模拟结果的准确性，在所有参数与仿真一致时，实验中观察到了冰层的脱落。仿真结果说明压电陶瓷附近的区域有最大剪切应力，实验中也是压电陶瓷附近的冰层最先脱落。当压电陶瓷的输入功率提高60%时，冰层脱落时间减少了47%。这说明提高输入功率（电压）可以较大程度地增强除冰效果、缩短除冰时间。
4.2 压电陶瓷布局规律验证实验
为了验证将尺寸较大的压电陶瓷分成尺寸较小的若干小块时除冰效果会增强、小块压电陶瓷间距越小除冰效果越好这两个结论，针对尺寸为300 mm×70 mm×2 mm的复合材料平板进行了压电除冰实验。
如图17所示，实验采用的较大的压电陶瓷尺寸为40 mm×40 mm×1 mm，较小的压电陶瓷尺寸为20 mm×20 mm×1 mm。压电陶瓷布局规律验证实验分为如图17所示的3组，分别为完整大尺寸压电陶瓷、间距为4 mm的小尺寸压电陶瓷和间距为12 mm的小尺寸压电陶瓷。每组实验分别在1.000 kHz、20.000 kHz及100.000 kHz范围内验证对应布局的除冰效果。在实验温度（–20 ℃）、块状冰层形成时间（5 h）及平板表面结冰时间（10 min）都相同的前提下，通过比较从压电陶瓷通电至第1块冰层掉落的时间长短来衡量除冰效果的强弱。最终实验结果如表5所示。表中“De-bonding”一列中，“Yes”表示通电3 min 之内观察到了冰层掉落，此时“Time”表示从通电到第1块冰层掉落所经过的时间；“No”则表示3 min内未观察到冰层掉落。
由表5中的数据可知：在压电陶瓷功率接近的前提下，压电陶瓷布局为完整一块时，除冰所需时间最长，在频率较低时，采用该种布局未能在3 min内达到除冰效果；而将压电陶瓷分为尺寸较小的多个时，在能耗接近甚至减小的前提下除冰时间有较大程度缩短，这说明将尺寸较大的压电陶瓷分成尺寸较小的小块，可以减弱压电陶瓷对结构振动的抑制，从而增强除冰效果。实验4、5、6中压电陶瓷布局如图17中布局2所示，实验7、8、9中压电陶瓷布局如图17中布局3所示。在振动频率、输入电压及压电陶瓷功率接近的前提下，布局2的除冰时间明显小于布局3，这说明小块压电陶瓷的间距越小，最终除冰效果越好。
表 5 实验结果数据Table 5 Experimental datasNumber Dimension of the
piezoelectric ceramics/mm3Space between the
piezoelectric ceramics/mmFrequency
/kHzVoltage
/VPower
/（kW·m–2）De-bonding Time/s 1 40×40×1 0 0.932 300 0.047 No 2 40×40×1 0 20.000 300 1.017 Yes 120 3 40×40×1 0 134.370 300 6.831 Yes 65 4 20×20×1 4 1.080 300 0.055 Yes 87 5 20×20×1 4 18.000 300 0.915 Yes 40 6 20×20×1 4 110.000 100 5.592 Yes 38 7 20×20×1 12 1.080 300 0.055 Yes 100 8 20×20×1 12 18.000 300 0.915 Yes 48 9 20×20×1 12 113.500 100 5.770 Yes 53 5 结 论
1）在压电陶瓷总的尺寸不变的前提下，合理改变陶瓷片数量可以提高激振产生的剪切应力，从而增强除冰效果。
2）在平板振型的1个波峰/波谷处布置多个压电陶瓷时，压电陶瓷间距越小，除冰效果越佳。
3）实验中，将压电陶瓷按照最佳布局方式，在较小的功耗下达到了除冰效果；随着输入功率的增大，除冰时间有较大程度缩短。将尺寸较大的压电陶瓷分成尺寸较小的多个后，相同能耗下除冰效果有所增强；减小压电陶瓷的间距后，除冰时间进一步缩短。
-
![]()
图 5 节点最大位移随单个压电陶瓷有效面积的变化曲线
Fig. 5 The curve of the maximum displacements of nodes varying with the effective area of single piezoelectric ceramic
![]()
图 9 5个波峰/波谷上的压电陶瓷布局及剪切应力（0.955 kHz）
Fig. 9 Layout of piezoelectric ceramics on five peaks /valleys and shear stress (0.955 kHz)
![]()
图 12 长宽比4.3的平板上的压电陶瓷布局
Fig. 12 The layout of actuators on the plate with aspect ratio of 4.3
![]()
图 14 平板Tsai-Wu失效准则破坏因子云图
Fig. 14 Destory factors of Tsai-Wu failure criteria of two plates
表 1 复合材料的物理参数
Table 1 Physical parameters of composite materials
Density/（kg·m–3） Ex /Pa Ey /Pa Ez /Pa νxy νxz νyz Gxy /Pa Gxz /Pa Gyz /Pa 2000 5.00×1010 8.00×109 8.00×109 0.30 0.30 0.40 5.00×109 5.00×109 3.85×109 
下载: 导出CSV
表 2 不同数目的压电陶瓷的尺寸表（厚度为2 mm）
Table 2 Dimensions of different numbers of piezoelectric ceramics （thickness is 2 mm）
Number of
piezoelectric ceramicsLength/
mmWidth/
mmEffective area of
single piezoelectric ceramic/mm2Total effective
area/mm21 30.0 30.0 900.0 900.0 2 25.0 18.0 450.0 900.0 3 20.0 15.0 300.0 900.0 4 15.0 15.0 225.0 900.0 5 15.0 12.0 180.0 900.0 6 15.0 10.0 150.0 900.0 8 15.0 7.5 112.5 900.0 9 10.0 10.0 100.0 900.0 10 10.0 9.0 90.0 900.0
下载: 导出CSV
表 3 不同激振频率下的剪切应力
Table 3 Shear stresses in different vibration frequencies
Case Frequency/kHz Voltage/V Total shear stress/MPa Power /（kW·m–2） 1 0.932 200 0.160 0.010 2 140.000 200 0.890 2.000 3 139.966 200 1.720 1.990
下载: 导出CSV
表 4 平板强度参数（MPa）[28]
Table 4 The strength parameters of the plate (MPa)[28]
XT XC YT YC ZT ZC Sxy Syz Sxz 1100 670 1100 670 35 120 80.0 80 46.1
下载: 导出CSV
表 5 实验结果数据
Table 5 Experimental datas
Number Dimension of the
piezoelectric ceramics/mm3Space between the
piezoelectric ceramics/mmFrequency
/kHzVoltage
/VPower
/（kW·m–2）De-bonding Time/s 1 40×40×1 0 0.932 300 0.047 No 2 40×40×1 0 20.000 300 1.017 Yes 120 3 40×40×1 0 134.370 300 6.831 Yes 65 4 20×20×1 4 1.080 300 0.055 Yes 87 5 20×20×1 4 18.000 300 0.915 Yes 40 6 20×20×1 4 110.000 100 5.592 Yes 38 7 20×20×1 12 1.080 300 0.055 Yes 100 8 20×20×1 12 18.000 300 0.915 Yes 48 9 20×20×1 12 113.500 100 5.770 Yes 53
下载: 导出CSV
-
[1] CAO Y H,WU Z L,SU Y,et al. Aircraft flight characteristics in icing conditions[J]. Progress in Aerospace Sciences,2015,74:62-80. doi: 10.1016/j.paerosci.2014.12.001
[2] POLITOVICH M K. Aircraft icing caused by large supercooled droplets[J]. Journal of Applied Meteorology,1989,28(9):856-868. doi: 10.1175/1520-0450(1989)028<0856:aicbls>2.0.co;2
[3] ZHU Y, PALACIOS J, ROSE J, et al. De-icing of multi-layer composite plates using ultrasonic guided waves[C]//Proc of the 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference 16th AIAA/ASME/AHS Adaptive Structures Conference. 2008. doi: 10.2514/6.2008-1862
[4] LI Q Y,BAI T,ZHU C L. Numerical simulation and experiment of traveling wave piezoelectric de-icing technique[J]. Applied Mecha-nics and Materials,2014,680:154-159. doi: 10.4028/www.scientific.net/amm.680.154
[5] BUDINGER M,POMMIER-BUDINGER V,BENNANI L,et al. Electromechanical resonant ice protection systems: analysis of fracture propagation mechanisms[J]. AIAA Journal,2018,56(11):4412-4422. doi: 10.2514/1.J056663
[6] VILLENEUVE E,HARVEY D,ZIMCIK D,et al. Piezoelectric deicing system for rotorcraft[J]. Journal of the American Helicopter Society,2015,60(4):1-12. doi: 10.4050/jahs.60.042001
[7] THOMAS S K,CASSONI R P,MACARTHUR C D. Aircraft anti-icing and de-icing techniques and modeling[J]. Journal of Aircraft,1996,33(5):841-854. doi: 10.2514/3.47027
[8] BUDINGER M,POMMIER-BUDINGER V,NAPIAS G,et al. Ultrasonic ice protection systems: analytical and numerical models for architecture tradeoff[J]. Journal of Aircraft,2016,53(3):680-690. doi: 10.2514/1.C033625
[9] JAFFE B, COOK W R, JAFFE H. Piezoelectric ceramics[M]. New York: Academic Press, 1971.
[10] JAFFE B,ROTH R S,MARZULLO S. Piezoelectric properties of lead zirconate-lead titanate solid-solution ceramics[J]. Journal of Applied Physics,1954,25(6):809-810. doi: 10.1063/1.1721741
[11] DANILIUK V,XU Y M,LIU R B,et al. Ultrasonic de-icing of wind turbine blades: Performance comparison of perspective transducers[J]. Renewable Energy,2020,145:2005-2018. doi: 10.1016/j.renene.2019.07.102
[12] POMMIER-BUDINGER V,BUDINGER M,ROUSET P,et al. Electromechanical resonant ice protection systems: initiation of fractures with piezoelectric actuators[J]. AIAA Journal,2018,56(11):4400-4411. doi: 10.2514/1.J056662
[13] HABIBI H,EDWARDS G,SANNASSY C,et al. Modelling and empirical development of an anti/de-icing approach for wind turbine blades through superposition of different types of vibration[J]. Cold Regions Science and Technology,2016,128:1-12. doi: 10.1016/j.coldregions.2016.04.012
[14] 朱永久,李清英,苗波,等. 飞机压电除冰技术的数值模拟与实验[J]. 机电信息,2015(9):102-103. doi: 10.19514/j.cnki.cn32-1628/tm.2015.09.065 [15] 王绍龙. 基于超声波法的风力机叶片翼型防除冰研究[D]. 哈尔滨: 东北农业大学, 2014. WANG S L. The research of wind turbine blade airfoil controlling ice based on ultrasonic method[D]. Harbin: Northeast Agricultural Univer-sity, 2014.
[16] 韩龙伸. 超声波除冰方法与试验研究[D]. 杭州: 杭州电子科技大学, 2013. HAN L S. Research on ultrasonic deicing method and its experi-ment[D]. Hangzhou: Hangzhou Dianzi University, 2013.
[17] ZENG J,SONG B L. Research on experiment and numerical simulation of ultrasonic de-icing for wind turbine blades[J]. Renewable Energy,2017,113:706-712. doi: 10.1016/j.renene.2017.06.045
[18] 谭海辉,李录平,靳攀科,等. 风力机叶片超声波除冰理论与方法[J]. 中国电机工程学报,2010,30(35):112-117. TAN H H,LI L P,JIN P K,et al. Ultrasonic de-icing theory and method for wind turbine blades[J]. Proceedings of the CSEE,2010,30(35):112-117.
[19] 谭海辉. 风力机桨叶超声波防除冰理论与技术研究[D]. 长沙: 长沙理工大学, 2011. TAN H H. Research on ultrasonic wave anti-icing and de-icing theory and technology for wind turbine blades[D]. Changsha: Changsha University of Science & Technology, 2011.
[20] WANG Z J,XU Y M,SU F,et al. A light lithium niobate transducer for the ultrasonic de-icing of wind turbine blades[J]. Renewable Energy,2016,99:1299-1305. doi: 10.1016/j.renene.2016.05.020
[21] 苗波,朱春玲,朱程香,等. 翼型曲面的压电振动除冰方法研究[J]. 实验流体力学,2016,30(2):46-53. DOI: 10.11729/syltlx20160010 MIAO B,ZHU C L,ZHU C X,et al. Vibration de-icing method with piezoelectric actuators on airfoil surface[J]. Journal of Experiments in Fluid Mechanics,2016,30(2):46-53. doi: 10.11729/syltlx20160010
[22] BAI T,ZHU C,MIAO B,et al. Vibration de-icing method with piezoelectric actuators[J]. Journal of Vibroengineering,2015,17(1):61-73.
[23] DUTTON S, KELLY D, BAKER A. Composite materials for aircraft structures, second edition[M]. Reston: American Institute of Aeronau-tics and Astronautics, 2004. doi: 10.2514/4.861680
[24] 孟光, 瞿叶高. 复合材料结构振动与声学[M]. 北京: 国防工业出版社, 2017. MENG G, QU Y G. Vibration and acoustics of composite structures[M]. Beijing: National Defense Industry Press, 2017.
[25] 苗波,朱春玲,朱程香. 平板压电除冰系统中压电元件排布规律研究[J]. 空气动力学学报,2016,34(6):732-737. DOI: 10.7638/kqdlxxb-2015.0216 MIAO B,ZHU C L,ZHU C X. Research on placement of piezoelectric actuators in plate piezoelectric de-icing system[J]. Acta Aerodynamica Sinica,2016,34(6):732-737. doi: 10.7638/kqdlxxb-2015.0216
[26] 苗波. 翼型压电振动除冰理论和实验研究[D]. 南京: 南京航空航天大学, 2016. MIAO B. Research on theories and experiments of airfoil piezo-actuated vibratory de-icing method[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016.
[27] HABIBI H,CHENG L,ZHENG H T,et al. A dual de-icing system for wind turbine blades combining high-power ultrasonic guided waves and low-frequency forced vibrations[J]. Renewable Energy,2015,83:859-870. doi: 10.1016/j.renene.2015.05.025
[28] 钱若力,穆晓光,王轩,等. 含褶皱缺陷玻璃纤维增强复合材料层合板拉伸渐进失效分析[J]. 复合材料科学与工程,2020(7):13-19, 52. DOI: 10.3969/j.issn.1003-0999.2020.07.002 QIAN R L,MU X G,WANG X,et al. Progressive failure analysis of tensile strength of glass fiber reinforced composite laminates with wrinkle defects[J]. Composites Science and Engineering,2020(7):13-19, 52. doi: 10.3969/j.issn.1003-0999.2020.07.002
-
期刊类型引用(2)
1. 邵苛苛，宋孟杰，沈俊，蔡标华，甄泽康，石含，张旋，张龙. 极地低温环境结冰预探测方法与防除破冰技术研究进展. 哈尔滨工业大学学报. 2025(02): 1-16 . 
百度学术
2. 张海波，罗江海，徐志强，周鑫翊，马伟刚，王传民，姜胜林，谭划. 基于压电陶瓷及其复合材料的飞机除冰技术研究现状及发展趋势. 航空制造技术. 2025(03): 32-40+66 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 780
- HTML全文浏览量: 304
- PDF下载量: 40
- 被引次数: 3
