水滴变形及其对阻力特性影响的实验研究

郭龙; 刘森云; 王桥; 赵献礼; 易贤

doi:10.11729/syltlx20200076

水滴变形及其对阻力特性影响的实验研究

郭龙^1,,
刘森云^2, ,,
王桥²,
赵献礼²,
易贤²

1.
西北工业大学航空学院, 西安 710072
2.
中国空气动力研究与发展中心结冰与防除冰重点实验室, 四川绵阳 621000

基金项目:

空气动力学国家重点实验室研究基金 SKL2019020401

详细信息

作者简介:
郭龙(1980-), 男, 陕西淳化人, 高级工程师。研究方向:结冰与防除冰研究。通信地址:四川省绵阳市二环路南段6号(621000)。E-mail:lgguo@163.com

通讯作者:
刘森云 E-mail: cardclsy@163.com

中图分类号: V211.79
计量
- 文章访问数: 389
- HTML全文浏览量: 163
- PDF下载量: 27
出版历程
- 收稿日期: 2020-06-17
- 修回日期: 2020-07-28
- 刊出日期: 2020-10-24

Experimental investigation of water droplet deformation and the effect on its drag characteristic

1.
School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China
2.
Key Laboratory of Icing and Anti/De-icing, China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China

摘要

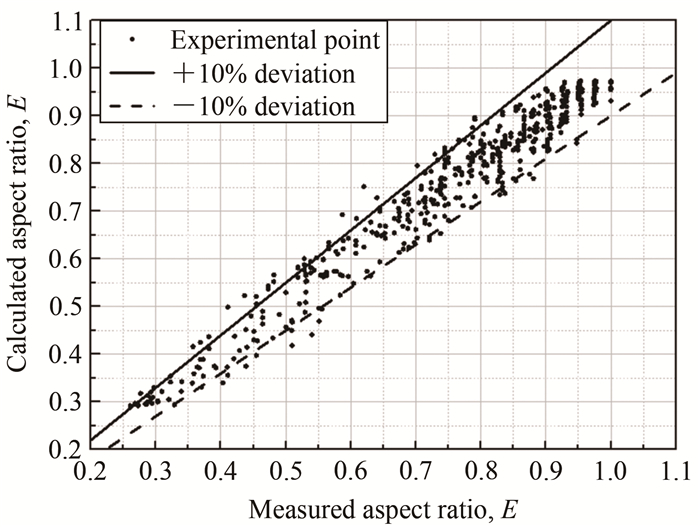
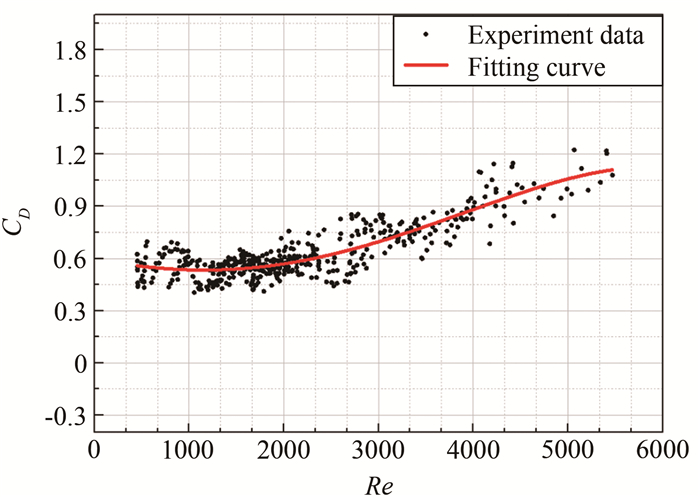
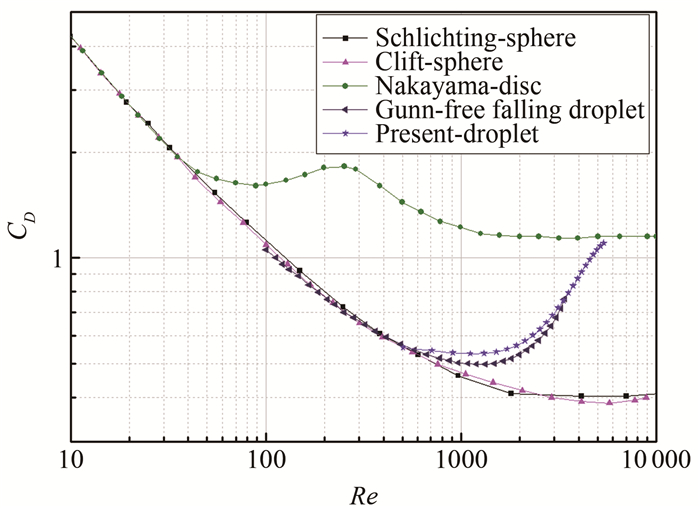
摘要: 为了探索飞机结冰研究中水滴撞击过程的变形行为发生机理和本质特征，提高结冰数值模拟的精准度，利用高速相机对水滴加速运动过程的变形现象进行了实验研究。通过研究，定义了水滴变形过程的4个典型形态，分析了水滴变形与各无量纲量的关系，拟合了水滴变形后的阻力系数曲线和计算式。研究表明：水滴在气动力作用下会发生显著的变形现象，依次历经圆球形、椭球形、半球形、圆盘形4种典型形状；水滴的纵横比随韦伯数(We)的增大呈线性减小，随邦德数(Bo)的增大呈双曲线减小；水滴变形会导致其阻力系数增大，在Re=500左右时，水滴阻力系数曲线开始脱离球形阻力系数曲线，逐渐增大至接近圆盘形阻力系数曲线，这与其变形过程一致。
- 飞机结冰 /
- 水滴变形 /
- 实验研究 /
- 高速摄影 /
- 纵横比 /
- 阻力系数
Abstract: In order to explore the dynamic behavior mechanism and essential feature for water droplets in the process of impact in aircraft icing, and improve the precision of numerical simulation of icing, an experimental investigation of the water droplet deformation and its effect on the drag coefficient in the acceleration was conducted by high-speed camera. Four typical forms of the droplet deformation were defined. The relationship between the deformation water and the dimensionless was also analyzed. The coefficient curve and calculation formula of the deformation droplet were also fitted. The results show that the droplet will distort under aerodynamic force, and the shape of the droplet changes from sphere, ellipsoid and saucer to disc. The aspect ratio of the water droplet linearly decreases with the increase of Weber number(We), and hyperbola decreases along with the increase of Bond number(Bo). The deformation of the water droplet will cause the increase of the drag coefficient, and the increase of the drag coefficient is consistent with the deformation process of the droplet.
- aircraft icing /
- water droplet deformation /
- experimental study /
- high-speed photography /
- aspect ratio /
- drag coefficient

HTML全文

图 1 实验系统图

Fig. 1 Diagram of experimental system

下载: 全尺寸图片幻灯片

图 2 压电式等径离散水滴发生器

Fig. 2 Piezoelectric mono-dispersed droplet generator

下载: 全尺寸图片幻灯片

图 3 等径离散水滴

Fig. 3 Mono-dispersed droplets

下载: 全尺寸图片幻灯片

图 4 水滴图像处理

Fig. 4 Droplets image processing

下载: 全尺寸图片幻灯片

图 5 收缩段和实验段中心线气流速度

Fig. 5 Velocity at the center line of contraction section and experimental section

下载: 全尺寸图片幻灯片

图 6 收缩段出口气流速度计算值与实测值对比图

Fig. 6 Comparison between the calculated value and the measured value of the air velocity at the outlet of the contraction section

下载: 全尺寸图片幻灯片

图 7 稳定球形水滴受力

Fig. 7 The force of the stabilized spherical droplets

下载: 全尺寸图片幻灯片

图 8 水滴变形演化过程

Fig. 8 The evolution of the droplet deformation

下载: 全尺寸图片幻灯片

图 9 水滴变形形状

Fig. 9 The shape of the distorted droplets

下载: 全尺寸图片幻灯片

图 10 水滴纵横比与We的关系

Fig. 10 The relationship between the droplet′s aspect ratio and We

下载: 全尺寸图片幻灯片

图 11 水滴纵横比与Bo的关系

Fig. 11 The relationship between the droplet′s aspect ratio and Bo

下载: 全尺寸图片幻灯片

图 12 水滴纵横比与Sn的关系

Fig. 12 The relationship between the droplet′s aspect ratio and Sn

下载: 全尺寸图片幻灯片

图 13 水滴纵横比的实验测量值与计算值对比

Fig. 13 Comparison of the measured results and calculated values of the droplet′s aspect ratio

下载: 全尺寸图片幻灯片

图 14 水滴阻力系数随Re变化

Fig. 14 The drag coefficient of droplets varies with Re

下载: 全尺寸图片幻灯片

图 15 水滴阻力系数与圆球形、圆盘形阻力系数对比

Fig. 15 Comparison of the drag coefficient among the droplets, spheres and disks

下载: 全尺寸图片幻灯片

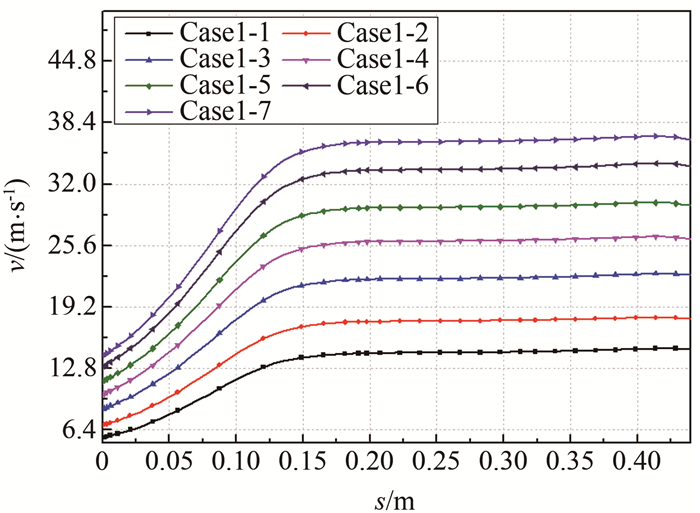
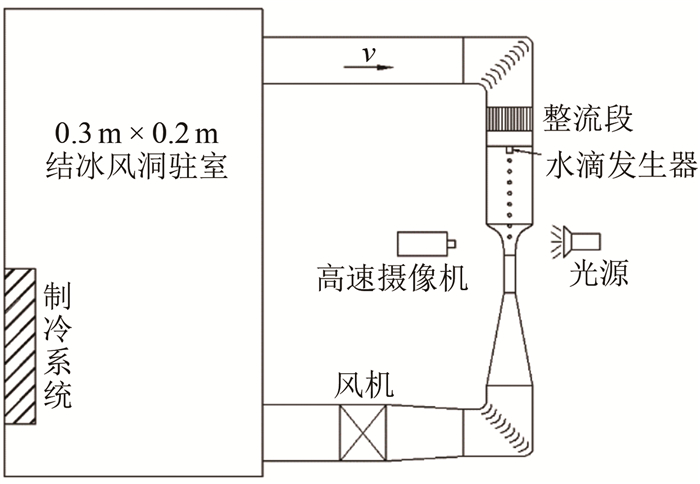
表 1 不同转速下收缩段入口与出口气流速度

Table 1 The air velocity at the inlet and outlet of the contraction section at different rotating speeds

Case	n/(r·min^-1)	v_in/(m·s^-1)	v_out/(m·s^-1)
Case1-1	1100	3.47	13.90
Case1-2	1400	4.28	17.70
Case1-3	1700	5.36	21.70
Case1-4	2000	6.31	25.40
Case1-5	2300	7.17	29.40
Case1-6	2600	8.13	33.40
Case1-7	2800	8.84	35.90

下载: 导出CSV

参考文献(16)

[1]	裘燮纲, 韩凤华.飞机防冰系统[M].北京:航空专业教材编审组, 1985.
[2]	PEREIRA C M. Status of NTSB aircraft icing certification-related safety recommendations issued as a result of the 1994 ATR-72 accident at Roselawn, IN[R]. AIAA 97-0410, 1997.
[3]	MILLER D, RATVASKY T, BERNSTEIN B, et al. NASA/FAA/NCAR supercooled large droplet icing flight research - Summary of winter 96-97 flight operations[R]. AIAA-98-0577, 1998.
[4]	TAN J, PAPADAKIS M, SAMPATH M K. Computational study of large droplet breakup in the vicinity of an airfoil[R]. DOT/FAA/AR-05/42, 2005.
[5]	TAN S C, BARTLETT P G. An experimental study of droplet break-up using a wind tunnel[R]. AIAA 2003-391, 2003.
[6]	LUXFORD G, HAMMOND D, IVEY P. Modelling, imaging and measurement of distortion, drag and break-up of aircraft-icing droplets[R]. AIAA 2005-71, 2005.
[7]	HAMMOND D, QUERO M, IVEY P, et al. Analysis and experimental aspects of the impact of supercooled water droplets into thin water films[R]. AIAA 2005-77, 2005.
[8]	孙志国, 朱程香, 付斌, 等.二维翼型结冰数值计算[J].航空动力学报, 2010, 25(7):1485-1490. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkdlxb201007006 SUN Z G, ZHU C X, FU B, et al. Numerical research of ice accretion on two-dimensional airfoils[J]. Journal of Aerospace Power, 2010, 25(7):1485-1490. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkdlxb201007006
[9]	LUXFORD G. Experimental and modelling investigation of the deformation, drag and break-up of drizzle droplets subjected to strong aerodynamics forces in relation to SLD aircraft icing[D]. England: Cranfield University, 2005.
[10]	GUNN R, KINZER G D. The terminal velocity of fall for water droplets in stagnant air[J]. Journal of Meteorology, 1949, 6(4):243-248. DOI: 10.1175/1520-0469(1949)006<0243:TTVOFF>2.0.CO;2
[11]	TAN C, PAPADAKIS M, MILLER D, et al. Experimental study of large droplet splashing and breakup[R]. AIAA 2007-904, 2007.
[12]	CLIFT R, GRACE J R, WEBER M E. Bubbles, drops and particles[M]. New York:Academic Press, 1978.
[13]	LANE W R, GREEN H L. The mechanics of drops and bubbles[M]. England:Cambridge University Press, 1956.
[14]	MAGARVEY R H, TAYLOR B W. Free fall breakup of large drops[J]. Journal of Applied Physics, 1956, 27(10):1129-1135. DOI: 10.1063/1.1722216
[15]	SCHLICHTING H. Boundary-layer theory[M]. USA: McGraw-Hill Book Company, 1987.
[16]	NAKAYAMA Y, BOUCHER R F. Introduction to fluid mechanics[M]. England: Reed Educational and Professional Publishing Ltd., 1999.

施引文献(7)

期刊类型引用(3)

1.	陈勇，孔维梁，刘洪. 飞机过冷大水滴结冰气象条件运行设计挑战. 航空学报. 2023(01): 7-21 . 百度学术
2.	唐扬刚，吴敬涛，邓文亮. 过冷大水滴撞击结冰特性实验研究. 低温工程. 2022(04): 42-48 . 百度学术
3.	徐弘，孔维梁，王福新，刘洪. 过冷大水滴相继撞壁对结冰影响的实验研究. 实验流体力学. 2018(02): 28-34 . 本站查看