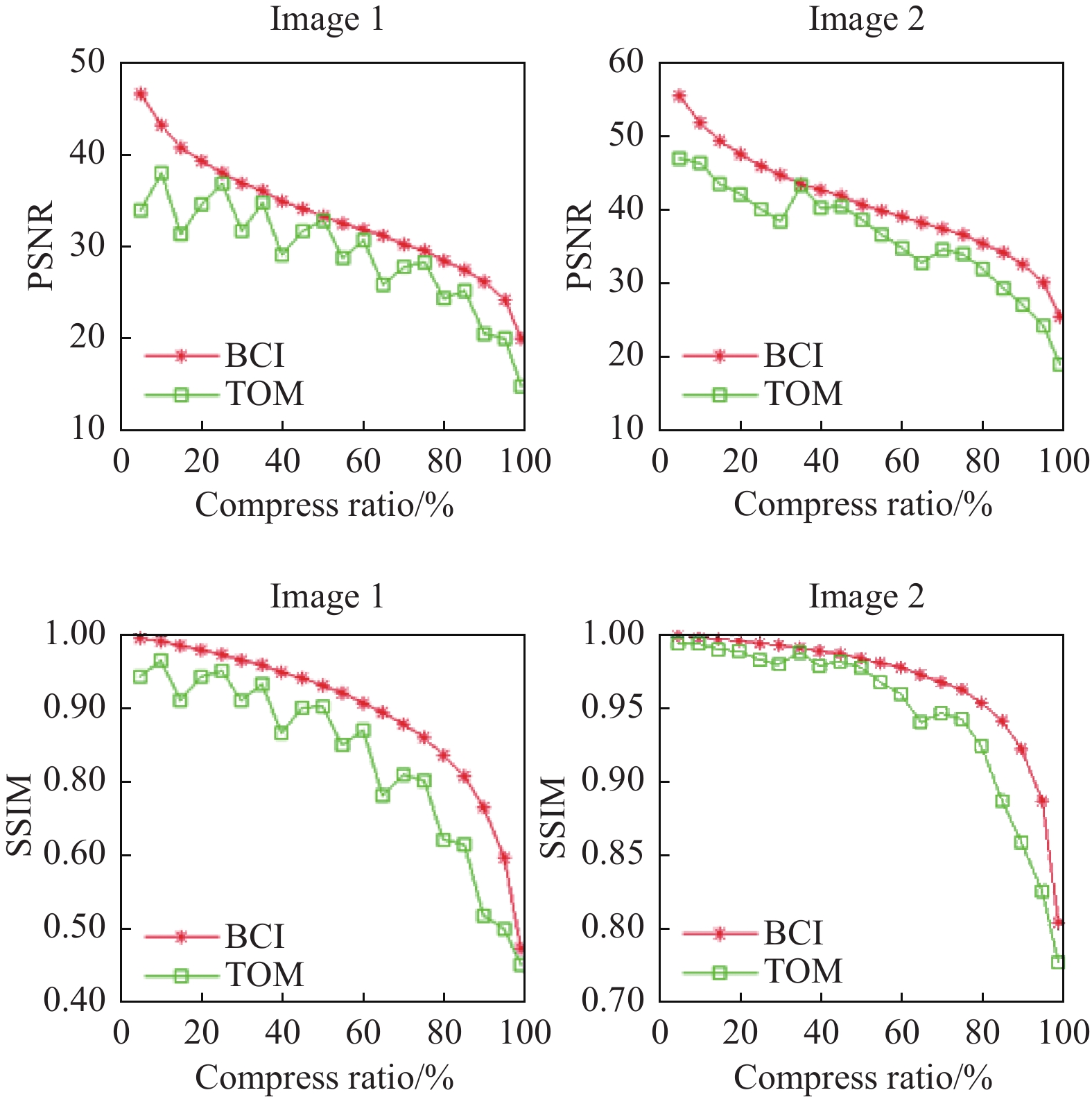
Abstract: High-speed cameras are widely used in explosive mechanics, hydrodynamics, trajectory observation and other scientific research experiments. Due to massive data and the limit of storage and bandwidth of electronic system, high-speed cameras cannot shoot for long periods of time. Compression of captured images is an effective way to extend the recording time of the high-speed cameras. However, the existing image compression methods can not solve high-speed camera mass image compression task caused by the large calculation complexity and long calculation time. In this paper, a low hardware cost, real-time image compression method with Bernoulli sampling is developed. The method randomly samples the pixels with Bernoulli distribution directly in the process of CCD or CMOS image acquisition. Then in usage, the raw image is reconstructed with the unknown pixel estimating method. The simulation results show that the main visual information of the image can still be observed from the reconstruction image, even when the image compression rate reaches 99%, which is superior to the super-resolution enhancement result of the TOM (Thin Out Mode) with interpolation.