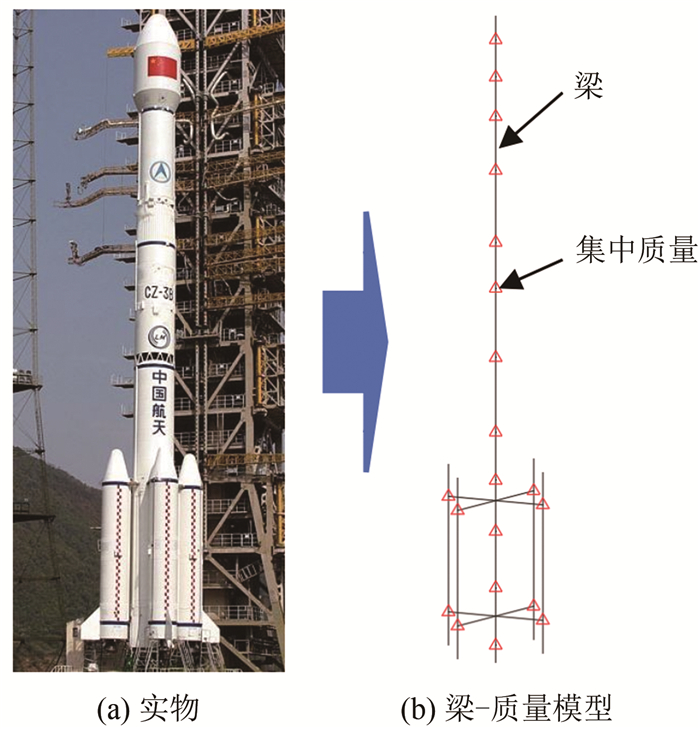
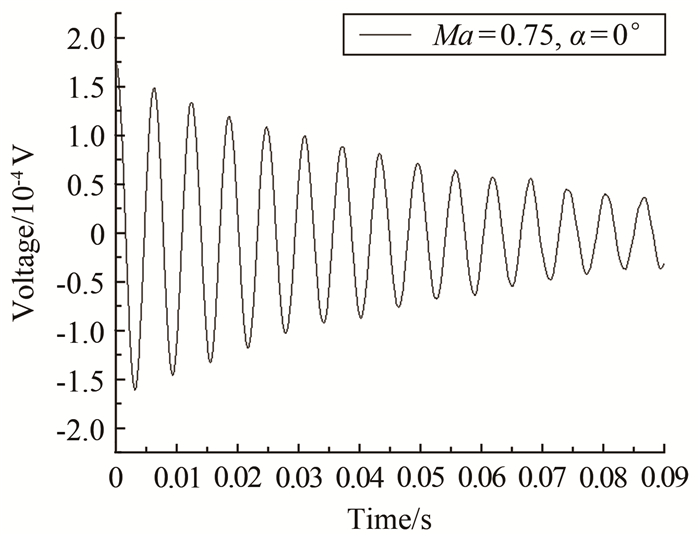
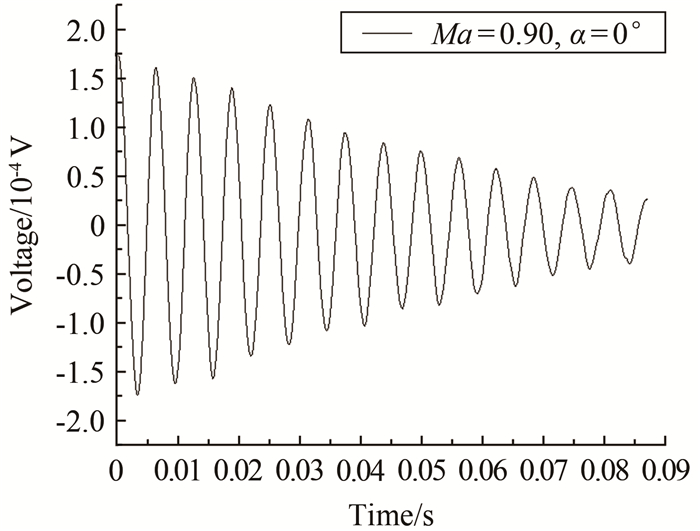
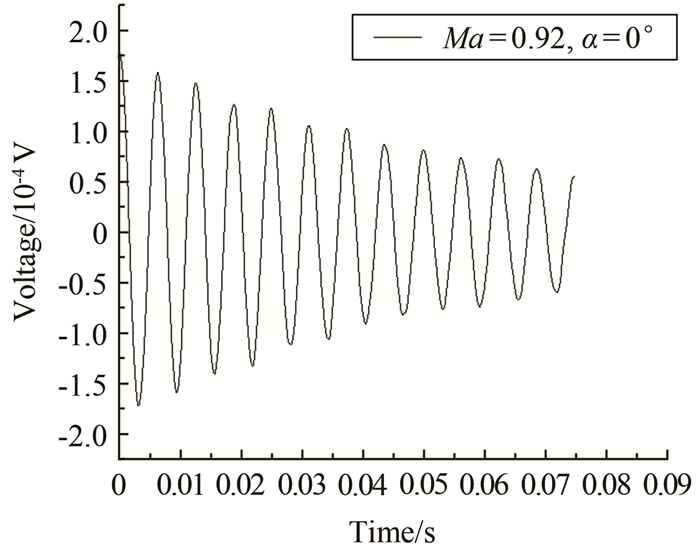
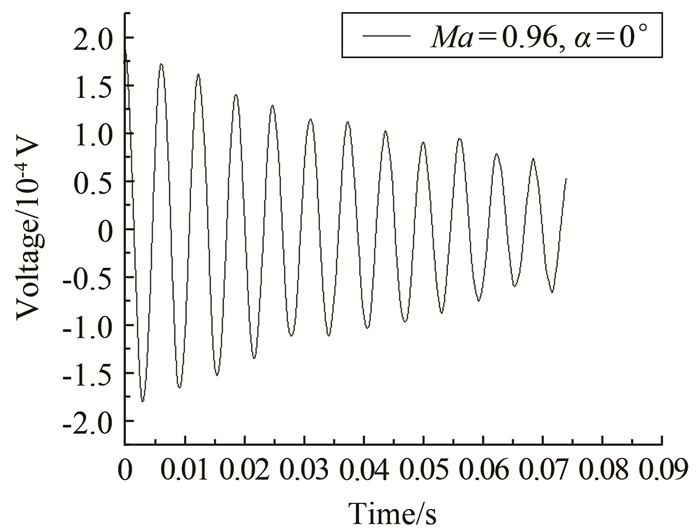
Experimental study of aerodynamic damping characteristics of a launch vehicle with boosters in transonic flow
-
摘要: 以某带助推的捆绑式运载火箭模型为研究对象,通过试验研究了该带助推的细长体弹性模型在不同马赫数和迎角下的一阶自由-自由弯曲气动阻尼特性和频率变化特性,并采用振型类似、频率降低的模型研究了减缩频率变化对气动阻尼的影响。试验马赫数范围0.70~1.05,试验迎角范围0°~10°。研究表明:迎角对火箭一阶自由-自由弯曲模态的气动阻尼和频率有影响,但规律并不明显;一阶自由-自由弯曲模态的气动阻尼受马赫数影响,并在马赫数0.90附近出现跨声速凹坑现象;一阶模态频率随马赫数增加呈下降趋势,但下降数值较小;减缩频率对气动阻尼有影响,在马赫数0.70~0.90范围内和马赫数1.00之后,气动阻尼随着减缩频率的增加而降低,在马赫数0.92~0.98范围内,气动阻尼随着减缩频率的增加而增加。Abstract: The aerodynamic-damping and frequency characteristics of a launch vehicle with boosters vibrating in the first free-free bending mode, and the influence of the reduced frequency on aerodynamic damping were experimentally studied in a transonic wind tunnel. The test Mach number ranged from 0.70 to 1.05, and the angle of attack ranged from 0° to 10°. The result shows that for the elastic model with boosters, the aerodynamic damping and modal frequency are affected by the angle of attack while the trend is not obvious. The aerodynamic damping changes with the Mach number. The transonic dip appears near the Mach number of 0.90. The modal frequency of the first mode decreases with the increase of the Mach number. The reduced frequency has some effect on the aerodynamic damping that when Mach number ranged from 0.70 to 0.90 and after 1.00, the aerodynamic damping decreases with the increase of the reduced frequency, while Mach number ranged from 0.92 to 0.98, the aerodynamic damping increases with the increase of the reduced frequency.
-
Keywords:
- aerodynamic damping /
- transonic /
- wind tunnel test /
- aeroelasticity /
- reduced frequency
-
0 引言
对于某些质量轻、阻尼低的钝体细长结构,在横向来流作用下容易发生所谓的“软驰振”现象,即:当风速超过临界风速时,由于自激力的非线性特性,驰振位移幅值不会无限制发散,而是会收敛到一个稳态幅值、发生极限环振动现象,表现出自限幅特性[1]。软驰振实际发生临界风速Uc一般低于按准定常理论估算的临界风速Ug,且接近涡振理论起振风速UVIV,其极限环振动的稳态振幅会随着风速的增加而近乎线性增加,表现出明显的非线性和非定常特点[1-3]。
从力学原理来看,驰振和颤振本质上都是非定常自激振动,其区别主要在于振动方向或自由度,即:驰振是横风向单自由度弯曲自激振动,而颤振是扭转单自由度或扭转与横风向弯曲两自由度耦合的自激振动。考虑到颤振研究非定常方法的提出和成功应用已有半个多世纪[4-6],因此,直观上看,驰振也应采用非定常方法来研究。然而,至今驰振的研究大多还是停留在准定常层面,或者没有完全跳出准定常理论的框架[7-9]。Parkinson[10]曾指出经典的驰振准定常理论不仅会高估软驰振发生风速,还会低估响应幅值,在准定常框架下无法对驰振进行合理的解释和估计,这说明了从非定常角度研究驰振的重要性。针对矩形断面在中低Scruton数情况下常出现不能明确区分驰振与涡振的现象,许多学者将其视为经典驰振和涡振2种振动的相互耦合,相应地提出了一些“准定常驰振力+涡激力”的混合自激力模型(Corless[11],Tamura[12],Mannini[13])。但是,这类自激力模型或者缺乏明确的物理意义以及风洞试验的验证,或者无法准确对软驰振现象进行再现和预估,普适性较差。
虽然涡激共振通常被认为具有自激振动和强迫振动的双重特性,但朱乐东等[14-15]的研究表明涡激力主要以自激力为主,其中的纯涡脱力占比很小,对涡振振幅的影响可以忽略不计,因此可以忽略涡激振动强迫特性,把其看作是一种自激振动。有鉴于此,对于大Scruton数的情况,驰振临界折减风速往往明显高于涡振起振折减风速,驰振和涡振现象明显相互分离[1, 16],此时可以把驰振和涡振分别看成是高折减风速和低折减风速范围内的2种非定常自激振动;对于中低Scruton数的情况,驰振往往发生在中低折减风速范围,很难与涡振区分[1, 16],此时应该把驰振和涡振理解为一种统一的非定常自激振动,而不是理解为一种驰振和涡振相互耦合或相互作用的振动,避免采用前述显然重复计算了自激力的“准定常驰振力+非定常涡激力”这类不合理的混合模型。为此,为了正确研究非定常非线性驰振和涡振的发展和自限幅的内在机理,有必要建立一套适用于驰振和涡振的统一纯非定常自激力数学模型。
由于驰振和涡振及其自激力具有复杂的非线性和非定常特性,因此通过风洞试验直接测量作用在钝体结构上的自激力时程是研究反映结构振动和气流相互作用(即气动弹性效应)规律的自激力数学模型的最佳方法。然而,由于在天平测得的动态力中,惯性力一般占主要成分,自激力所占比例很小,而对软驰振和涡振发展过程和稳态振幅起关键作用的气动阻尼力又在自激力中占比很小,因此在振动模型上高精度测量自激力是一件非常困难的事。为此,大多数学者都是通过对振动位移的测量来间接识别自激力[13, 17],导致至今对非定常驰振的非线性自限幅特性的机理和非定常非线性自激力数学模型的研究进展不大。本文以3:2矩形断面为例,介绍作者所开展的基于弹簧悬挂节段模型同步测力测振试验的驰振自激力高精度测量和验证工作,探讨影响自激力高精度测量和验证结果可靠性的若干重要问题,如:节段模型振动与周围“静止”空气之间相互作用而产生的非风致附加自激力及节段模型振动与来流相互作用而产生的风致自激力在动态力中的占比关系,非风致附加自激力的非线性特性对驰振自激力测量精度的影响,在通过比较驰振位移时程重构和试验结果来间接验证自激力测量可靠性时考虑弹簧悬挂节段模型系统等效阻尼和刚度参数的非线性特性的重要性。
1 风洞试验概况
1.1 模型结构及天平安装
试验在同济大学TJ-2边界层风洞中进行,风洞试验段长15m,宽3m,高2.5m。图 1为悬挂于TJ-2风洞中两面内支架导流墙之间的节段模型,模型的悬挂系统(弹簧、吊臂等)均位于整流墙内。图 2为弹簧悬挂节段模型系统示意图。模型断面顺风向宽度B=0.15m、横风向高度D=0.1m,全长L=1.5m,总质量Ms= 10.573kg(含弹簧的等效质量)。模型顺风向自由度用上下游共4根限位钢丝进行约束,限位钢丝长度足够大以保证在模型做竖向振动时其倾角足够小,从而可以忽略其张力的竖向分量及由此产生的附加竖向刚度。
为了减小作用在天平上的惯性力、提高自激力测量精度,本次试验采用内置天平进行测力。为此,模型采用“内部金属骨架+木板外衣+高密度泡沫塑料内衬”的结构。如图 1~3所示,木板外衣分成3段,段间留约1mm缝隙;中间测力段长l=0.7m,质量Mc=0.466kg;两边设置补偿段,以消除测力段模型端部三维流动,提高试验精度。内部金属骨架不分段,为一整体结构,由2根铝合金方管、2块端面和若干横隔板焊接而成(见图 3)。中间测力段两端各安装一个专门研制的内置小型三分量动态测力天平[18],天平位于骨架2个铝方管之间并支撑在骨架横隔板上。中间测力段外衣支撑在2个天平上,并与内部构架保持严格不接触状态。天平极限承载力约70N,本试验中用该天平的y方向分量来测试模型的竖向动态力,其动态力量程Fy=12N,测量误差小于被测值的3%。
为了观测不同Scruton数下模型的驰振响应,试验中分别通过在模型两侧整流墙内的吊臂上附加质量和设置简易箱式硅油阻尼器(见图 4)来调整系统的质量和结构阻尼。经试验证明此种简易硅油阻尼器刚度很小、且其阻尼力具有良好的线性特性,相比传统的钢丝圈阻尼器不会引入明显的额外阻尼非线性[18],从而减少了问题的复杂性。
1.2 软驰振现象
本次试验在均匀流场(背景紊流度小于0.5%)中进行,风速范围2.0~18.0m/s,试验工况和相应参数如表 1所示,模型振动位移采用激光位移计测量。
表 1 宽高比3:2矩形断面节段模型风洞试验工况表Table 1 Cases of sectional model wind tunnel test of rectangular cross section with a width-to-height ratio of 3:2
图 5为试验所得的各工况下风致振动无量纲稳态振幅(β=Ay/D)随折减风速(U*=U/fD)变化关系,这里U是风速,Ay是稳态振幅,f是振动频率。各工况在各级风速下的振动均经历如图 6所示的“起振-发展-稳态振动”过程,属于一种非线性自限幅自激振动,且稳态振幅随风速增加而近乎线性增加。由此可见,此宽高比3:2的矩形断面发生了明显的“软驰振”,而且所有工况的驰振起振风速均与涡振起振风速UVIV基本一致,即在折减风速U*=9.17附近,这与按驰振准定常理论估计的驰振临界风速Ug(见表 1)相去甚远,说明驰振的非定常特性不容忽视。此外,对于Scruton数Sc大于30的6个工况(A3、A4、B3、B4、C4和C5),在U*分别达到20.55、14.37、16.73、13.62、15.72和13.85时,驰振突然消失。对于其它7个Sc数小于30的工况,当U*达到大约21时,振幅接近了试验允许值。
以如图 6所示的#C1工况在折减风速U*=U/(f0D)=20.97情况下的振动响应为例,对软驰振发展段3个典型时段和稳态振动段的位移时程分别做频谱分析,结果如图 7所示。结果显示,发展段频谱中除了在模型固有频率f0=3.54Hz处有显著峰值外,还在fvs=StU/D≈7.9Hz处存在纯涡脱力强迫振动响应成分,但所占比例很小,并随振幅增加而迅速降低。强迫振动成分在发展阶段前期(0~25s)只约占自激振动成分的0.14%,在发展阶段中期(25~50s)只占约0.0048%,到发展阶段后期(50~75s)几乎为0,进入稳态阶段后更是消失了,这表明除了在发展的最初阶段外,驰振基本是一个纯自激振动。此外,从发展阶段后期开始振动频谱图中出现了若干高阶倍频成分,并随着振幅的增加而增加,但与基频成分相比显得非常小,可以忽略。这表明驰振的位移响应具有一定的非线性特性,但总体上仍可认为是按基频的简谐振动。
2 自激力的测量原理
如图 8所示,模型振动时,中央测力段外衣上所受的力包括:外衣的惯性力FIc,与加速度方向相反;模型运动与周围空气(不是来流)之间相互作用所产生的气动弹性自激力Fsec0[14, 19-20],也称为非风致附加自激力;模型运动与来流相互作用所产生气动弹性自激力Fsec,即风致自激力,只有在有风的情况下存在;左右两端天平的支反力FR1c、FR2c,与天平受到的作用力大小相等、方向相反。
根据达朗贝尔原理可得到以下力的动平衡方程:

(1) 
(2) 
(3) 式中:上标c表示中央测力段外衣;上标0表示零风速(即无风)状态;下标se表示气动弹性自激力;下标I表示惯性力;下标R表示支反力;下标m表示试验中实测结果;大写F变量表示集中力或分布力总和;FRc为中央测力段外衣两端天平支反力总和;Fmc为天平测得的作用在中央测力段外衣上的竖向动态力总和,沿竖向坐标轴y的正方向为正;


(4) 假定模型所受风致自激力沿模型跨向均匀分布,则作用在模型外衣上的每延米风致自激力fse可由下式确定:

(5) 这里,每延米分布力用f表示;l为测力外衣段长度,mc为中央测量段每延米质量,fse0为作用在模型每延米上的非风致附加自激力;fmc=Fmc/l为通过天平测到的作用在每延米测力段外衣上的总动态力。
从式(5) 可以看出,发生软驰振时自激力的直接测定与天平自身精度以及测力段外衣惯性力大小有关,因此,在天平不变的前提下,采用内置天平、只测量中央测力段外衣上的动态力,可大大降低作用在天平上动态力中的惯性力比重,从而提高自激力的占比,提高测量精度。
3 非风致附加自激力及其确定
3.1 非风致附加自激力的概念
非风致附加自激力反映了模型运动与周边空气之间相互作用程度,也是一种气弹效应,在无风和有风情况下都存在,并且与风洞试验段尺寸及模型的尺寸有关,尤其与风洞高度和模型宽度之比有很大关系。其产生的机理为:当风洞中的模型往下振动时,模型正下方空气被迫往下运动,并受风洞底板的约束而转向模型的上下游运动,从而进一步推动模型上下游空气的运动;与此同时,模型上方的空气受模型向下运动的吸引而向下运动,但受风洞顶板的限制,模型正上方空气有限,无法大量补充而使模型上方形成低压区,从而进一步吸引模型上下游空气向模型上方中央区域运动。当模型向上运动时,情况正好反过来。这样,模型的振动就会带动其四周的空气做受迫振荡,从而反过来对模型产生与模型振动(速度、加速度、频率等)有关的气动弹性力,即自激力。这种自激力与由来流(风)引起的常规自激力是不同的。后者只在有风的情况下存在,虽然常简称“自激力”,但其实质是风致自激力;而前者则在无风和有风情况下均存在,为了区别,这里称之为“非风致附加自激力”。
非风致附加自激力可以表示为附加气动阻尼力和附加气动惯性力之和[14],或者附加气动阻尼力和附加气动恢复(刚度)力之和[19-20],即:

(6) 
(7) 这里,ma0、ca0和ka0分别表示模型每延米长度对应的非风致附加气动质量、附加气动阻尼系数和附加气动刚度系数,一般是振动位移和速度的非线性函数;


显然,对于同一个模型,风洞试验段尺寸、甚至整个风洞流道结构(如回流风洞、直流风洞、扩散段扩散比、收缩段的收缩比等)的改变都会影响上述由于模型振动引起的风洞中空气受迫振荡的范围和形态,从而影响附加自激力的大小和非线性特性。一般来讲,风洞高度与模型宽度之比越小,模型上下方空气受风洞顶板和底板的约束越强,带动上下游受迫振荡空气的范围也越大,附加自激力(附加气动阻尼和附加气动质量)也就越大。此外,在同一个风洞中,不同的桥梁断面,附加自激力也是不一样的,比如:开槽梁模型的非风致附加自激力要小于同样宽度整体梁的非风致附加自激力;窄模型的非风致附加自激力要小于宽模型的非风致附加自激力,甚至出现负的非风致附加阻尼,如1:1矩形断面[20]。
事实上,这种非风致附加自激力在实桥上也是存在的。但是,对于实桥,除了地表外,其周边空气是没有边界的,而且一般桥面离地面也较高,因此,考虑缩尺比换算后实桥周边受迫振荡空气的范围要显著小于风洞中模型周边受迫振荡空气的范围,受迫振荡形态也与风洞中的不相似,引起的附加自激力也要比模型的小很多,除了桥面非常贴近地表的情况外,一般可以忽略不计。对于实桥的非风致附加气动阻尼,一方面由于上述原因其数值一般很小;另一方面,实桥阻尼一般只能利用振动加速度响应的测试数据、采用各种系统参数识别方法来识别[21-23],是无法分离非风致附加气动阻尼和结构阻尼的,因此可以认为:实桥阻尼参数的测试结果或者规范规定数值中已经包含了这种附加气动阻尼,在实桥的风致振动分析中,只需要考虑风致自激力即可。有鉴于此,在风洞试验中,为了精确测量风致自激力,必须排除包含在所测动态力中的这种非风致附加自激力。
虽然,在有风的情况下,上述由于模型振动引起的周围空气受迫振荡的形态与无风时会有一定的区别,但是为了简化处理方法,在本研究中把这种由于来流对周边空气受迫振荡形态的影响而引起的自激力改变归入到风致自激力中,从而近似假设非风致附加气动阻尼和质量(或刚度)在有风和无风情况下是相同的。这样,就可以先通过在无风条件下的节段模型初激励自由衰减振动同步测力测振试验来确定非风致附加自激力参数,即附加气动阻尼和质量(或刚度),然后根据公式(6) 或(7) 确定有风条件下的非风致附加自激力,再代入到公式(5) 中即可获得风致自激力。
3.2 非风致自激力的提取
在无风条件下使节段模型做初激励自由衰减振动,此时风致自激力fse等于0,则由式(5) 可得每延米非风致自激力:

(8) 式中:fse0表示无风时每延米模型外衣上非风致附加自激力;Fmc0为无风时2个天平测得的中央测力段外衣上的竖向动态力总和,沿竖向坐标轴y的正方向为正;fmc0为相应的中央测力段外衣上每延米总动态力;

作为例子,图 9显示了#C1工况对应的节段模型系统在无风情况下做自由衰减振动时测到的每延米总动态力fmc0、每延米外衣惯性力

3.3 线性非风致附加自激力参数识别
如果不考虑非风致附加阻尼系数ca0和附加质量ma0的非线性,即假设非风致附加参数不随运动状态变化,则在获取非风致自激力时程后,可直接根据式(7) 采用最小二乘法拟合识别常数非风致附加阻尼系数ca0和附加质量ma0 2个参数,其中位移时程采用同步测量的信号,速度和加速度时程可由位移信号差分得到。
3.4 非线性非风致附加自激力参数识别
从前述非风致附加自激力的概念和产生机理可知,在模型的振动过程中ma0和ca0(或ka0)一般是振动速度和位移







(9) 由此可知,为了精确识别各级风速下作用在模型上的风致自激力,首先需要识别非风致附加气动阻尼和质量(或刚度)参数与瞬时振幅at(t)的非线性关系,即确定非风致附加瞬幅阻尼系数ca0(at)和附加瞬幅质量ma0(at)或附加瞬幅刚度系数ka0(at)。
(1) 非线性非风致附加气动阻尼系数
如式(6) 和(7) 所示,由于非风致自激力包含1项阻尼力项和1项惯性力项(或恢复力项),那么,根据能量等效原理,即每个完整振动周期内惯性力(或恢复力)做功为0,而非风致自激力做功仅由其中的阻尼力做功产生,因此可以利用自激力中气动阻尼力作功与总自激力做功等效的原理识别非线性非风致附加阻尼系数。文献[20]详细推导了基于能量等效原理的非线性非风致附加阻尼系数识别方法,计算公式如下:

(10) 
(11) 
(12) 
(13) 
(14) 式中:ξa0(at)为非风致附加瞬幅阻尼比;ms=Ms/L为节段模型系统每延米平均质量;E(at)为每延米结构振动的瞬时机械能;PaD0(t)无风时作用在振动模型上的每延米非风致附加气动阻尼力的瞬时功率;WaD0(t)为无风时作用在振动模型上的每延米非风致附加气动阻尼力在时刻t的瞬时累积做功;Wse0(t)为无风时实测到的作用在振动模型上的每延米非风致附加自激力在时刻t的瞬时累积做功,由于气动惯性力(或者气动恢复力)在非完整周期时间点上的累积做功都具有周期性(在所有完整周期时间点上的累积做工等于0),因此Wse0(t)含有由附加气动惯性力(或者恢复力)做功产生的振荡成分,振荡频率与模型振动频率一致;Wse0(t)为通过多项式拟合消除振荡成分后的每延米非风致附加自激力瞬时累积功,为Wse0(t)中由附加气动阻尼力累计做功所贡献的缓变趋势项,理论上等于WaD0(t)。
由公式(11) 可知,公式(10) 中的附加气动阻尼力的功率PaD0(t)是累积Wse0(t)的导数,即曲线的斜率。由于Wse0(t)的振荡成分一般较小,是缓变函数,所以其拟合后的缓变趋势相Wse0(t)的斜率与其振荡曲线波峰和波谷的包络线斜率均非常接近。因此,为了提高拟合效率,PaD0(t)可以近似取Wse0(t)振荡曲线波峰或波谷的拟合包络线的斜率。
作为例子,图 10给出了在#C1工况某次试验测得的每延米非风致自激力(见图 9)的累积做功时程,图中“○”数据点为按式(13) 计算的Wse0(t),可见明显的振荡成分;图中实线表示对W0(t)的波谷进行多项式拟合后得到的缓变趋势项


(a) #C1工况非风致附加阻尼呈现负阻尼特点,附加气动阻尼比的绝对值随振幅增加而缓慢增加,变化趋势呈现一定非线性;
(b)采用基于线性理论拟合得到的常数附加阻尼比相当于实际瞬幅阻尼比的一个平均值,其绝对值在小振幅阶段高于实际附加阻尼比绝对值,而在大振幅阶段则小于附加阻尼比绝对值。
采用同样方法对C组其余工况进行识别,结果如图 12所示。由此可见,不同工况得到的附加气动阻尼比的离散程度很小,随振幅变化的趋势以及非线性特点基本相同。此外,在A组和B组试验当中也得出相近的结果,说明改变结构阻尼比并不影响非风致附加气动阻尼比ξa0,即:对于同种断面以及相同振动频率,作为反映结构-空气相互作用的一个气动参数,ξa0(at)随瞬态振幅的变化规律具有确定性。
(2) 非线性非风致附加质量
对于单自由度振动模型,由运动关系可知,当加速度(或位移)达到峰值点时,振动速度为0,则根据式(6) 和(7) 可知,此时非风致附加自激力等于附加气动惯性力或附加气动恢复力,即:

(15) 
(16) 式中:ti表示振动周期中的加速度峰值点对应的时刻。
由此关系,可以构建

本文仅讨论附加气动质量ma0,并采用上述第二种方法求解。图 13为#C1工况某次试验fse0(t)-

从图 13和14可见:(a) #C1工况非风致附加质量呈现随瞬态振幅增加而缓慢增加的特点,变化趋势呈现一定非线性;(b)基于线性理论拟合的常数附加气动质量相当于瞬幅附加气动质量的一个平均值,其在小振幅阶段高于实际附加气动质量,而在大振幅阶段则小于实际附加气动质量,这主要是因为相对于小振幅情况,大振幅时周围受迫振荡的空气范围更大,受风洞边界的约束作用也更大。
图 15给出了#C1~#C4工况的ma0(at)识别结果比较,从图中可以看到各工况结果之间存在少许的离散性,从#C1~#C4工况ma0(at)逐渐增加,但是离散程度并不大,最大约2%,同时各工况的ma0(at)随振幅缓慢增加的特点以及非线性变化规律是基本一致的。
从表 1可以看到:C组各工况参数的区别仅仅是零风速系统平均阻尼(含非风致附加气动阻尼),从工况#C1至#C4,零风速系统阻尼比从0.11%增加到0.45%,也就是说自由振动的衰减速度越来越快,加速度响应越来越小。在应用前述基于

A组和B组的试验结果也显示了与C组试验结果相似的情况。考虑到各组不同工况识别的ma0(at)值之间离散性不大,故可以认为同组试验(振动频率f0相同,阻尼比ξ0不同)识别的ma0(at)基本相同。
3.5 振动频率对非风致附加气动阻尼和质量的影响
图 16和17分别给出了通过具有不同振动频率的B组和C组试验识别得到的瞬幅非风致附加气动阻尼比ξa0(at)和附加气动质量ma0(at)之间的比较。结果显示:(1) 2组试验得到的ξa0(at)均为负值,ma0(at)均为正值,|ξa0(at)|和ma0(at)随瞬态振幅at(t)的变化规律相似,均随at(t)的增加而缓慢非线性增加;(2) 模型振动频率的增加会使|ξa0(at)|有所下降,ma0(at)有所增加。
3.6 非风致附加气动阻尼比和质量识别结果验证
以C组试验为例,采用识别到的ξa0(at)和ma0(at)以及任意工况实测振动位移信号按照式(6) 重构出非风致附加自激力时程,然后再与该工况实测非风致自激力时程比较,由此来验证前述非风致附加气动参数ξa0(a)和ma0(a)识别方法和识别结果的可靠性。
图 18和19分别为基于非线性瞬幅附加气动阻尼、质量和基于常数附加气动阻尼、质量重构的#C1工况附加自激力时程与试验结果的比较图。从图中可见:采用2套附加气动参数重构的非风致附加自激力时程在幅值和相位上均与试验实测值吻合得较好,说明前述非风致附加气动参数的识别方法和识别结果是可靠的,也说明非风致附加自激力的非线性整体上较弱。这主要是因为:在附加自激力中附加气动惯性力(faI0)占据了大部分、附加气动阻尼力faD0只占据了约3.86%~9.93%(见图 20),因此附加自激力的非线性特性主要取决于附加气动惯性力的非线性特性;而根据3.4节的结果可知,相对于附加气动阻尼力,附加气动惯性力的非线性较弱。
考虑到附加气动惯性力相对于结构的惯性力是小量,而附加气动阻尼力与结构阻尼力却处于同一量级,再考虑到结构响应对阻尼非常敏感,因此,在后续的分析中仍将采用非线性瞬幅附加阻尼比。
4 节段模型系统参数非线性特性
由于没有真实的自激力可以用来检验自激力的测量精度,因此只能通过比较基于测得的自激力重构的位移响应和试验实测位移响应来间接验证自激力测量结果的可靠性。显然,在重构节段模型系统驰振响应时必然要用到节段模型系统的结构阻尼和刚度参数,同时弹簧悬挂节段模型系统一般都具有一定的非线性特性,因此,有必要先讨论弹簧悬挂节段模型系统结构阻尼和刚度参数的非线性特性对位移响应时程重构精度的影响,以确保验证结果本身的可靠性。
4.1 系统自由衰减振动控制方程
在气动导数识别时,传统上一般都是把节段模型系统看成是一个线性系统,假设其阻尼系数或阻尼比以及刚度系数为常数,因此,其初激励自由衰减振动的控制方程可以表示为:

(17) 式中:f0和ξ0分别为节段模型系统在零风速时的无阻尼固有频率和阻尼比,均为常数,并包含了第3节所述的非风致附加气动阻尼和气动刚度或质量的影响,可通过对自由衰减振动实测位移响应进行曲线拟合获得,也可以分别通过频谱分析和振幅的对数衰减法求得。
方程(17) 的解可表示为:

(18) 式中:a0和φ0初始位移和初始相位;f0d=

然而,朱乐东和高广中等[14, 19-20, 24]的研究结果表明:实际的弹簧悬挂节段模型试验系统具有一定的非线性特性,其阻尼和刚度参数是模型振动速度和位移的函数,其中阻尼的非线性特性尤为明显。因此,无风时节段模型系统自由衰减振动方程应修改为如下非线性形式:

(19) 
(20) 
(21) 
(22) 
(23) 式中:ξe0(at)为节段模型与周围空气组成的振动系统的等效瞬幅阻尼比;fe0(at)为振动系统的等效瞬幅频率;ke0(at)为振动系统的等效瞬幅刚度系数。上述3个参数都随瞬时振幅

4.2 系统等效刚度参数的非线性特性
系统等效刚度可以用等效刚度系数ke0(at)来表示,也可以用等效频率fe0(at)来表示,两者存在如式(23) 所示的关系,本文采用后者来讨论系统刚度的非线性特性。文献[19]介绍了一种由零风速自由衰减振动识别低阻尼节段模型系统瞬时等效频率fe0(at)的时域方法,其识别公式如下:

(24) 
(25) 但需说明的是:直接采用式(25) 中第二等式计算瞬时等效频率fe0(t),需要利用实测的位移离散数据通过一阶和二阶差分计算速度和加速度,这会因为试验数据含有噪声干扰而引入显著求导误差,使得计算得到的瞬时等效频率会含有振荡成分(见图 22“○”数据点),离散度较大。为此,可以先采用多项式函数拟合瞬时相位φ(t),然后再对拟合得到的多项式函数求导计算瞬时等效频率(见图 22“□”数据点),这样得到的瞬时等效频率效果比较好。为方便应用,还需要拟合瞬时等效频率fe0(at)与等效瞬时振幅at(t)之间的关系。
以#C1工况(f0=3.5495Hz,ξ0=0.111%)为例,位移衰减时程以及按式(19) 计算的瞬时等效振幅a(t)如图 21所示。图 22给出了根据测得的响应离散数据按公式(25) 第二等式计算的瞬时等效频率以及按公式(25) 第一等式通过对瞬时相位拟合函数求导得到的瞬幅等效频率。对后者进行再次拟合可以得到如图 23所示的瞬幅等效频率fe0(at)随等效瞬时幅值的变化曲线,图中点划线代表对多次识别结果采用最小二乘拟合的函数曲线,虚线代表按对数衰减法识别得到的常数频率f0。
从这些图中可以看到:(1) 瞬幅等效频率随瞬时振幅的变化具有一定的非线性特性;(2) 瞬时等效频率随振幅的增加而缓慢减小,且变化幅度非常小,在0.05D~0.35D幅值范围内,其变化幅度只有大约0.07%f0;(3) 在小振幅下,实际频率略高于常数频率f0,而在大振幅下则是略低于常数频率f0。
采用同样方法对C组其余工况(各工况之间只有结构阻尼不同,结构质量和刚度保持不变)的瞬幅等效频率进行识别和拟合,结果如图 24所示。各工况之间识别结果的差异主要源于更换阻尼元件带来的质量上的差异。结果显示不同工况瞬幅等效频率fe0(at)的非线性特性(即其随瞬时幅值的变化形态或规律)与#C1工况的基本一致,说明采用的硅油阻尼器具有很好线性特性、且刚度很小,不会明显影响系统的非线性特性。
4.3 系统等效阻尼的非线性特性
对于如式(19) 所示的缓变非线性系统运动方程,其等效线性化解的形式为:

(26) 其中,

对瞬时振幅


(27) 式中:

(28) 
(29) 如前所述,瞬幅频率fe0(at)随振幅缓慢变化,且变化幅度很小,因此这里可近似地将A0视为常数,则A(t)的缓变斜率即为瞬时阻尼比ξe0(at):

(30) 求得不同时刻瞬时等效阻尼比ξe0(at)后,即可以通过最小二乘拟合得到其与瞬时振幅at(t)之间的关系,建立瞬幅阻尼比ξe0(at)的计算公式。以#C1工况为例,通过上述方法得到的瞬幅阻尼比ξe0(at)与瞬时振幅之间的关系如图 25所示,图中点划线代表对多次识别结果采用最小二乘拟合的函数曲线,虚线代表按对数衰减法识别得到的常数阻尼比ξ0。从图中可以看到,瞬幅阻尼比ξe0(a)具有明显的非线性,随振幅的增加而缓慢增大,变化幅度约104%ξ0。
采用同样方法对C组其余工况瞬幅阻尼比进行了识别与拟合,结果如图 26所示。结果显示:各工况系统瞬幅阻尼比表现出的非线性规律与#C1工况基本一致,再次说明附加硅油阻尼器的阻尼特性是线性的,基本不影响系统阻尼的变化规律。
4.4 系统非线性参数识别结果的验证
将识别得到的瞬幅频率fe0(at)和瞬幅阻尼比ξe0(at)代入式(19),并利用NewMark-β法进行求解,可以得到节段模型系统自由衰减振动位移时程的重构结果。通过与试验实测结果比较,可以检验非线性参数识别结果的精度、验证其可靠性。
以#C1工况1个衰减振动为例,计算结果与试验值比较如图 27所示,结果显示:无论是对短期响应还是长期响应,计算位移时程与实验结果均符合得很好,两者的幅值和相位完全一致,说明用前述方法识别得到的节段模型系统瞬幅等效刚度和等效阻尼比是精确、可靠的。
4.5 考虑系统参数非线性的必要性
为了说明考虑节段模型系统参数非线性的必要性,这里以与4.4节中所用的#C1工况同一次自由衰减振动试验为例,采用常数阻尼和刚度参数重构了其位移响应时程。重构与试验位移时程的比较如图 28所示,结果显示:采用常数参数计算的位移时程与试验结果之间存在明显差异;对于大振幅阶段的短期响应,重构振幅大于试验结果,而对于小振幅阶段的长期响应,重构振幅明显小于试验结果;同时,随着时间的进展,两者之间的相位偏差越来越大,甚至会达到180°。显然,采用不考虑非线性的常数阻尼比和刚度系数无法保证重构位移响应的精度,从而也会影响自激力验证结论的可靠性,因此,在采用比较重构和试验中实测位移的方法间接验证自激力测量精度时非常有必要考虑节段模型系统阻尼和刚度参数的非线性特性。
5 非定常驰振自激力测量结果及验证
5.1 自激力测量结果
每延米自激力可以根据天平测到的作用在每延米测力段外衣上的总动态力fmc、速度



作为例子,图 29给出了#C1工况在折减风速U*=20.39时非线性软驰振过程中的自激力时程,从图中可见:在驰振起振开始阶段,自激力较小且幅值波动大;进入发展阶段后,自激力幅值快速变大;进入稳态振动后,自激力幅值波动较小且较为稳定。
图 30给出了上述工况驰振稳定阶段每延米测力段外衣所受动态力中不同成份比较,其中,“□”符号为总动态力fmc,实线即为驰振自激力fse,“○”为惯性力fIc,“△”为非风致附加自激力fse0。从图中可见:(1) 驰振自激力信号明显偏离简谐信号,说明其具有显著的非线性特性;(2) 由于内置天平测力方法显著降低了惯性力成分,测得的自激力占到了天平总动态力的12%左右,为提高自激力的测量精度创造了条件;(3) 虽然如此,惯性力仍然是动态力的主要成分,约占62.3%,而非风致附加自激力所占比重也不少,约为22.3%,超过了风致自激力所占比重,因此在自激力测量时必须要扣除其影响。
图 31给出了上述工况软驰振在起振、发展和稳态3个阶段中4个典型时段动态气动力的幅值谱,由此可见:(1) 在驰振发展阶段,振动幅度较小,气动力中存在明显的7.7Hz左右纯涡脱强迫力成分,且在发展前期和中期占主导地位,但随着驰振振幅的发展,由于自激力成分迅速增加,纯涡脱力所占比重迅速降低,并在稳态振动阶段基本消失,动态气动力随之基本上仅体现出自激特性;(2) 在发展阶段后期和稳态阶段,实测动态气动力频谱中存在明显的高次倍频成分,并随振幅的增加而增大;对于稳定阶段,2~6次倍频成分的幅值谱峰值分别是基频成分幅值谱峰值的0.68%、4.36%、0.03%、0.05%和0.01%。由于奇次项自激力非线性成分也会对1次倍频成分做出贡献,比如:因为sin3(ωt)=0.75sin(ωt)-0.25 sin(3ωt),因此,速度三次非线性项对幅值谱中基频成分的贡献是其对3次倍频成分贡献的3倍,即:在基频幅值谱峰值中速度三次非线性项的贡献占了约13%,因此,在稳定阶段自激力的非线性特性是比较明显的。
5.2 自激力测量结果可靠性验证
为检验上述非线性自激力测量结果的可靠性,可将测得的自激力时程fse(t)直接作用于节段模型系统振动方程式(19) 的右端,构建如下驰振运动方程:

(31) 然后采用NewMark-β法按与fse(t)离散数据序列相同的时间步长逐步迭代求解该运动方程,重构出节段模型系统的软驰振位移响应时程。迭代计算中每一步都需要先根据当前时刻的位移和速度按式(9) 计算等效瞬时振幅at(ti),然后再根据在第4节中确定的节段模型系统等效阻尼和刚度参数与等效振幅的非线性关系计算当前时刻的fe0(at)和ξe0(at),再进行下一时刻位移响应计算。最后比较重构的位移时程与对应的实测位移时程,以检验风致自激力识别结果的可靠性。
以#C1工况为例,图 32给出了U*=20.39时基于实测自激力重构的节段模型系统软驰振位移响应时程和实测结果的比较,其中风致自激力采用了扣除非线性非风致附加自激力(按非线性瞬幅附加气动阻尼系数和气动质量计算)的结果,节段模型系统参数也采用了考虑非风致附加气弹效应的非线性瞬幅等效阻尼系数和刚度系数。结果显示无论是幅值还是相位两者都吻合的很好,稳态阶段幅值误差小于1%。其余工况在各级风速下的驰振位移时程重构结果也都与相应的实测结果吻合得很好,表明采用本文方法和试验技术识别的非线性驰振自激力具有足够的可靠性,可以精确地再现软驰振“起振-发散-稳态振动”的整个过程。
![]() 图 32 基于瞬幅等效系统参数和瞬幅非风致附加自激力参数重构的驰振位移时程与试验结果对比(#C1工况,U*=20.39)Fig. 32 Comparison of galloping time history reconstructed by using amplitude-dependent equivalent system parameters and amplitude-dependent parameters of non-wind-induced additional self-excited force with the tested one (Case #C1, U*=20.39)
图 32 基于瞬幅等效系统参数和瞬幅非风致附加自激力参数重构的驰振位移时程与试验结果对比(#C1工况,U*=20.39)Fig. 32 Comparison of galloping time history reconstructed by using amplitude-dependent equivalent system parameters and amplitude-dependent parameters of non-wind-induced additional self-excited force with the tested one (Case #C1, U*=20.39)5.3 非风致附加自激力非线性的影响
图 33给出了分别基于瞬幅非线性和常数非风致附加自激力参数提取的风致自激力时程的比较,前者用蓝色实线表示,后者用红色虚线表示。结果显示:在软驰振起振阶段,由于起主导作用的是纯涡脱力成分,非风致附加自激力很小,所以是否考虑非风致附加阻尼系数和质量随瞬时振幅的变化特性对提取的驰振自激力几乎没有影响;但是在稳态振动阶段,纯涡脱力成分可以忽略不计,此时是否考虑非风致附加自激力参数随瞬时振幅变化的特性对驰振自激力的提取结果有一定影响。采用常数非风致附加自激力参数会使提取的自激力峰值偏小5%~8%,同时自激力时程曲线在某些局部位置的形态也会受到影响,即自激力的高次倍频成分比重会发生一定程度的变化。
图 34给出了基于瞬幅非线性结构参数和常数非风致附加自激力参数重构的位移时程与实测结果对比,以进一步考察非风致附加自激力参数的非线性对位移响应的影响。结果显示:忽略非风致附加自激力参数的非线性特性会使重构的位移响应略偏小于实测值,最大误差在3%左右。因此,为了尽可能提高自激力的测量精度,考虑非风致附加自激力参数的非线性特性还是有一定的价值。
5.4 节段模型系统等效阻尼和刚度参数非线性的影响
图 35给出了忽略节段模型系统等效阻尼和刚度参数非线性时重构的位移时程与实测结果的比较,从中可以看到,忽略系统等效阻尼和刚度参数的非线性会导致重构的位移响应明显大于试验值,稳态振动阶段(如图 35所示振动幅值仍有小幅波动)计算和试验结果的最大误差可达到13%。因此,为了保证自激力间接验证方法本身的可靠性,提高验证结论的置信度,在基于自激力识别结果重构节段模型系统驰振位移响应时必须考虑模型等效阻尼和刚度参数的非线性特性。
6 结论
以3:2矩形断面为例,对影响矩形断面非线性驰振自激力测量及间接验证的精度和可靠性的若干关键问题进行了研究和探讨,获得了以下主要结论:
(1) 在弹簧悬挂节段模型风洞试验中,采用内置天平测力法可以显著提高自激力在总动态力中的比重,但非风致附加自激力在总动态力中的比中仍可能超过风致自激力,因此从测得的总动态力中提取自激力时必须予以扣除。
(2) 非风致附加气动阻尼力和惯性力的非线性对驰振自激力测量精度有一定影响,虽然其影响程度不算大,但为尽可能提高自激力的测量精度,还是值得考虑。
(3) 在采用比较基于实测自激力重构的驰振位移时程和试验实测位移时程的方法来间接验证自激力测量精度时,节段模型系统等效阻尼和刚度参数的非线性对驰振位移响应的重构精度有明显影响,因此在重构驰振位移时程时必须加以考虑。
-
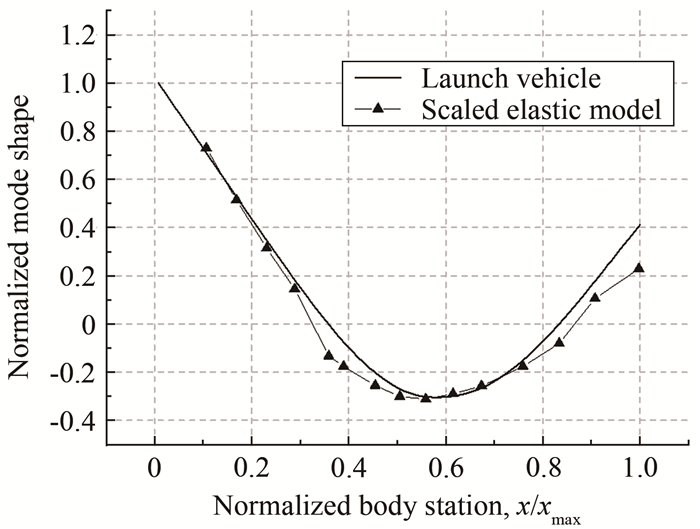
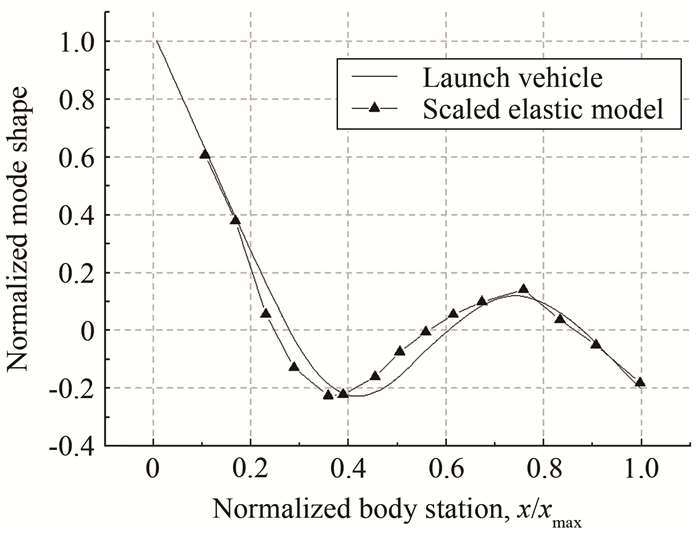
表 1 一阶自由-自由弯曲模态参数
Table 1 Structural dynamic properties of the 1st free-free bending mode
Model Modal frequency/Hz Structural damping ratio Basic model 163.4 0.0165 Model "L" 112.8 0.0125 -
[1] 倪嘉敏.我国运载火箭气动设计回顾[C]//近代空气动力学研讨会论文集. 2005. NI J M. Review of aerodynamic design of China's launch vehicle[C]//Proceedings of the Modern Aerodynamics Symposium. 2005.
[2] 崔尔杰.流固耦合力学研究与应用进展[C]//钱学森科学贡献暨学术思想研讨会论文集. 2001. CUI E J. Research and application progress of fluid-structure interaction mechanics[C]//Proceedings of Seminar of Qian Xuesen Scientific Contributions and Academic Thoughts. 2001.
[3] 程镇煌.宇航飞行器跨音速气动弹性问题探讨[J].上海航天, 1997, (6):16-21. https://www.cnki.com.cn/Article/CJFDTOTAL-SHHT706.003.htm CHENG Z H. Discussion on transonic pneumatic elasticity of spacecraft[J]. Aerospace Shanghai, 1997, (6):16-21. https://www.cnki.com.cn/Article/CJFDTOTAL-SHHT706.003.htm
[4] REDING J P, ERICSSON L E. Effect of aeroelastic considerations on seasat-A payload shroud design[J]. Journal of Spacecraft and Rockets, 1981, 18(3):241-247. DOI: 10.2514/3.57810
[5] COLE H A. Dynamic response of hammerhead launch vehicles to transonic buffeting[R]. NASA TN D-1982, 1963.
[6] BARTELS R E, WIESEMAN C D, MINECK R E. Computational aeroelastic analysis of the ares launch vehicle during ascent[R]. AIAA 2010-4374, 2010.
[7] AZEVEDO J L F. Aeroelastic analysis of launch vehicles in transonic flight[J]. Journal of Spacecraft and Rockets, 1989, 26(1):14-23. DOI: 10.2514/3.26027
[8] SINCLAIR A J, FLOWERS G T. Low-order aeroelastic model of launch-vehicle dynamics[R]. AIAA 2010-7725, 2010.
[9] DOTSON K W. Transient coupling of launch vehicle bending responses with aerodynamic flow state variations[J]. Journal of Spacecraft and Rockets, 2001, 38(1):97-104. DOI: 10.2514/2.3660
[10] COLE S R, HENNING T L. Buffet response of a hammerhead launch vehicle wind-tunnel model[J]. Journal of Spacecraft and Rockets, 1992, 29(3):379-385. DOI: 10.2514/3.26362
[11] 冯明溪, 王志安.火箭跨音速动导数和抖振实验[J].宇航学报, 1987(1):55-62. https://www.cnki.com.cn/Article/CJFDTOTAL-YHXB198701007.htm FENG M X, WANG Z A. Experiments of transonic derivatives and buffeting of rocket[J]. Journal of Astronautics, 1987(1):55-62. https://www.cnki.com.cn/Article/CJFDTOTAL-YHXB198701007.htm
[12] 冉景洪, 刘子强, 胡静, 等.减阻杆气动阻尼研究[J].力学学报, 2014, 46(4):636-641. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201404019.htm RAN J H, LIU Z Q, HU J, et al. Research of aero-damping for blunt with spike[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(4):636-641. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB201404019.htm
[13] 白葵, 冯明溪.弹性模型实验技术[J].流体力学实验与测量, 1999, 13(1):38-42. DOI: 10.3969/j.issn.1672-9897.1999.01.006 BAI K, FENG M X. Aeroelastic model and the buffet experimental technique[J]. Experiments and Measurements in Fluid Mechanics, 1999, 13(1):38-42. DOI: 10.3969/j.issn.1672-9897.1999.01.006
[14] JI C, RAN J H, LI F, et al. The aerodynamic damping test of elastic launch vehicle model in transonic flow[C]//Proc of the 64th International Astronautical Congress. 2013.
[15] 季辰, 吴彦森, 何岗, 等.运载火箭气动阻尼风洞试验研究[C]//第十二届全国空气弹性学术交流会论文集. 2011. JI C, WU Y S, HE G, et al. Experimental study on aerodynamic damping wind tunnel of launch vehicle[C]//Proceedings of the 12th National Aeroelasticity Conference. 2011.
[16] 季辰, 刘子强, 李锋.钝前缘梯形翼高超声速风洞颤振试验[J].气体物理, 2018, 3(1):54-63. https://www.cnki.com.cn/Article/CJFDTOTAL-QTWL201801008.htm JI C, LIU Z Q, LI F. Hypersonic wind tunnel flutter test for a blunt-leading-edge delta wing[J]. Physics of Gases, 2018, 3(1):54-63. https://www.cnki.com.cn/Article/CJFDTOTAL-QTWL201801008.htm
[17] 刘子强, 白葵, 毛国良, 等.锤头体弹性振动跨音速气动阻尼系数的确定[J].宇航学报, 2002, 23(6):1-7. DOI: 10.3321/j.issn:1000-1328.2002.06.001 LIU Z Q, BAI K, MAO G L, et al. The determination of aerodynamic damping on hammerhead launch vehicles at transonic speeds[J]. Journal of Astronautics, 2002, 23(6):1-7. DOI: 10.3321/j.issn:1000-1328.2002.06.001
[18] 朱剑, 冉景洪, 吴彦森, 等.捆绑式运载火箭的气动阻尼数值计算方法[C]//第十三届全国空气弹性学术交流会论文集. 2013. ZHU J, RAN J H, WU Y S, et al. Numerical calculation method for aerodynamic damping of bundle launch vehicles[C]//Proceedings of the 13rd National Aeroelasticity Conference. 2013.
[19] JONES G W Jr, FOUGHNER J T Jr. Investigation of buffet pressures on models of large manned launch vehicle configurations[R]. NASA TN D-1633, 1963.
[20] CF COE. Surface pressure fluctuations associated with aerodynamic noise[R]. NASA SP-207, 1969.
[21] BISPLINGHOFF R L, ASHLEY H, HALFMAN R L. Aeroelasticity[M]. Cambridge:Addison-Wesley Publishing Company Incorporated, 1955.
[22] 曹树谦, 张文德, 萧龙翔.振动结构模态分析——理论、实验与应用[M].天津:天津大学出版社, 2014. -
期刊类型引用(7)
1. 谢斌,王超,徐志伟,廖晓林. 马氏体时效钢18Ni(250)超细晶化锻造工艺. 特殊钢. 2025(02): 82-87 .  百度学术
百度学术
2. 焦林虎,任宗金,张军,李小刚,王碧玲. 六维压电风洞盒式天平研究. 传感器与微系统. 2024(10): 31-34 .  百度学术
百度学术
3. 成垒,段丕轩,康洪铭,陈丹. 一种风洞天平信号电磁干扰补偿方法. 兵工自动化. 2021(03): 32-35 .  百度学术
百度学术
4. 倪章松,张军,符澄,王邦毅,李宇. 磁浮飞行风洞试验技术及应用需求分析. 空气动力学学报. 2021(05): 95-110 .  百度学术
百度学术
5. 袁媛,孙增玉,王杏,高越,刘柯. 基于三维数字图像相关法应力测量技术. 宇航计测技术. 2020(06): 31-36 .  百度学术
百度学术
6. 崔智强,李勇,王世红,赵长辉. 一台大载荷比Φ32mm六分量天平的研制. 弹道学报. 2018(04): 92-96 .  百度学术
百度学术
7. 刘凤华. 高速列车气动性能低温风洞试验. 交通运输工程学报. 2018(06): 93-100 .  百度学术
百度学术
其他类型引用(2)







 下载:
下载: