Research on semiconductor strain gage balance technology applied in shock tunnel
-
摘要: 对于有效试验时间仅有十至几十毫秒的激波风洞,常规应变天平和压电天平无法满足高精度气动力测量要求。半导体应变计的应变灵敏度远大于常用的金属电阻应变计,但其温度系数比金属电阻应变计高出2个数量级。针对此问题,设计了温度自补偿的半导体应变计并应用于等强度梁试验,结果表明:温度自补偿能够有效改善半导体应变计的温度效应,可将温度漂移降低至0.2% FS。在此基础上,设计了一杆高频响六分量半导体应变天平,通过天平、支杆一体化等设计,将测力试验系统的一阶固有频率提升至100 Hz以上。天平静态校准结果表明:该天平的综合加载误差达到国军标合格指标,综合加载重复性达到国军标先进指标。激波风洞B-2标模测力验证试验结果表明:在有效试验时间内,该天平可获得一个周期以上的输出信号,风洞试验结果与气动手册参考值、CFD计算值吻合较好。Abstract: The conventional strain balance or piezoelectric balance cannot meet the requirements of high precision aerodynamic measurement in the shock tunnel, as the effective test time is very short. The strain sensitivity of the semiconductor strain gage is much higher than that of the foil strain gage, but its temperature coefficient is two orders of magnitude greater than that of the foil strain gage. This paper designed a temperature-self-compensation semiconductor strain gage, and applied it on equal strength beam experiments. The results show that the temperature self-compensation technology can effectively improve the temperature effect of the semiconductor strain gage, and the temperature drift of the semiconductor strain gage is reduced down to 0.2% FS after temperature compensation. In this paper, a six-components balance with high frequency response is designed for the shock tunnel, and the results of calibration show that the combining loading repeatability and combining loading error of the balance meet the requirements of the national military standards. The balance can acquire more than one signal during effective test time as the inherent frequency of the test system is more than 100 Hz, and the results of the shock tunnel test are in good agreement with reference values of the aerodynamic manual and CFD results.
-
0 引言
高超声速飞行器具有较强的机动性、突防能力以及较大的作战半径,目前已经成为21世纪各航天大国争相发展的关键技术[1]。高超声速风洞地面测力试验是获得各种高超声速飞行器气动力特性数据、评估其气动性能的主要手段之一。激波风洞能够模拟的总温、总压、焓值等参数值更高,在该类参数的模拟方面优于其他高超声速风洞[2];但激波风洞的有效试验时间很短,在很短的试验时间内准确测量飞行器模型的气动力,是极具挑战性的研究。
激波风洞自20世纪50年代出现以来,其测力试验方法不断完善,从最初的应变天平,逐渐发展至压电天平、加速度天平和应力波天平等。受敏感栅材料灵敏度的影响,应变天平的频响较低,大多应用于有效试验时间较长的激波风洞。中国科学院刘云峰[3]、汪运鹏[4-5]、孟宝清[6]等在百毫秒量级的激波风洞中开展了大量应变天平测力试验研究,在约100 ms的有效试验时间内,天平可获得3~4个信号周期,避免了惯性力补偿,纵向气动力测量误差可优于1%。压电天平出现于20世纪50年代末[7],具有较高的频响,能够满足试验时间较短的激波风洞试验。中国空气动力研究与发展中心吕治国等[8]发展了多种压电天平测试技术,采用“5+1”天平结构,在有效试验时间仅有几至几十毫秒的激波风洞中测量了飞船返回舱等外形的气动力,纵向气动力测量误差优于4%,并实现了较小滚转力矩的测量。加速度天平诞生于20世纪60年代[9],其响应时间约为0.15 ms。Menezes[10]、Singh[11]、Sahoo[12]等对加速度计天平的结构和试验方法进行了深入研究,获得了较好的试验结果,纵向气动力测量误差在6%左右。应力波天平最早由Sanderson和Simmons于1991年提出[13],其响应时间为0.1 ms。昆士兰大学Robinson和Mee等[14-15]发展了多分量应力波天平;中国空气动力研究与发展中心刘施然等[16]实现了激波风洞应力波天平测力试验,单分量测量误差优于10%。
在众多激波风洞测力试验方法中,应力波天平和加速度计天平响应时间最短,但数据处理方法和试验装置较常规天平复杂;压电天平刚度较高,但受压电陶瓷片经时稳定性的影响,天平校准和试验的精准度比应变天平低;应变天平的测量误差最小,但受天平刚度的影响,需要的有效风洞试验时间较长。
制约应变天平刚度的因素主要为敏感栅材料的灵敏度。为提升敏感栅灵敏度,半导体应变计(以机械、化学等方法将单晶硅加工为丝状或其他形状作为敏感栅)于20世纪50年代末问世。与金属电阻应变计相比,半导体应变计具有灵敏度系数高、机械滞后小、体积小、耗电小等优点,但其电阻温度系数比金属电阻应变计高出约2个数量级,大大限制了其应用环境[17-19]。随着半导体工艺的发展,传统体型半导体应变计温度性能差的缺点有了改善的可能[20]。此外,利用半导体应变计灵敏度系数高的优点,可以将应变天平的设计应变降低1~2个数量级,从而提高应变天平刚度,实现在激波风洞上的应用。
本文研制了一种新型半导体应变计,改善了常规半导体应变计的温度特性;在此基础上,设计了一杆高频响六分量半导体应变天平,提升了整个测力试验系统的固有频率。开展了天平静态校准和激波风洞B-2标模测力验证试验,考核了天平的静、动态性能。
1 半导体应变计
1.1 全桥半导体应变计
半导体应变计是利用半导体材料的“压阻效应”来实现测量的:对半导体材料的某一轴施加载荷时,材料发生变形,电阻率变化,导致其电阻发生变化,通过恒流或恒压供电,可将变形引起的电阻变化量转换为电压信号,从而实现测量。
常用的半导体应变计为体型应变计,采用栅状半导体硅作为敏感栅材料。制作工艺如图 1所示:(1)制作敏感栅。以切片、研磨、切小片等方法将半导体单晶硅材料按照一定的晶向加工成栅体状。(2)腐蚀压焊。用腐蚀液刻蚀敏感栅上的电极并焊接引出导线。(3)粘贴成形。将基底胶粘剂涂覆在敏感栅材料上,并加热固化。
由表 1可知,半导体应变计的灵敏度系数比金属电阻应变计高很多,但电阻温度系数也比金属电阻应变计高很多。
表 1 应变计主要性能对比Table 1 Characteristics of different strain gages应变计类型 金属电阻应变计 常规半导体应变计 应变灵敏度系数 1.8~2.2 80~210 电阻温度系数/(℃-1) 2.0×10-5 (70~700)×10-5 温度范围/℃ -270~650 -30~150 常规半导体应变计由单个硅栅构成。为降低温度效应,设计了一种新型半导体应变计,在单片应变计上利用4个阻值接近的硅栅组成Wheatstone全桥,如图 2所示。4个硅栅间距很小,能减小温度梯度引起的温差,从而达到温度自补偿的效果。
1.2 应变灵敏度
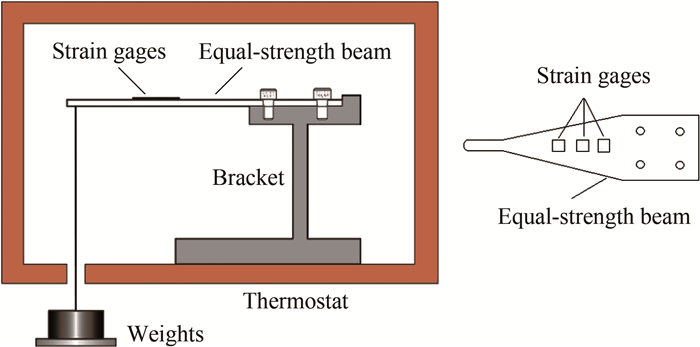
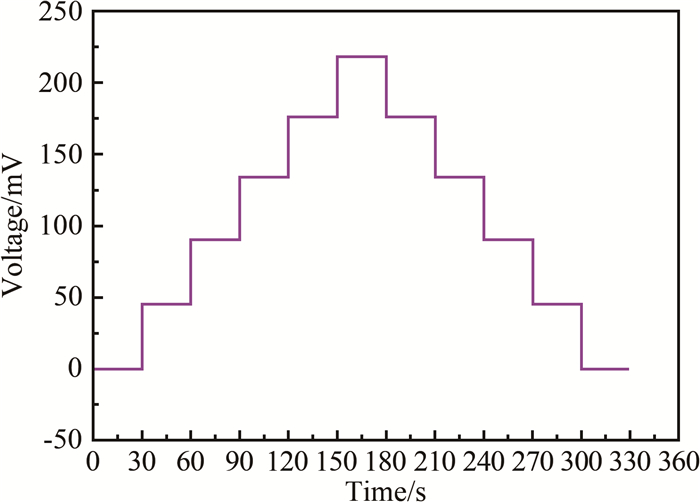
应变计静态性能测试在等强度梁上进行,如图 3所示。本文采用的等强度梁每悬挂1 kg砝码将产生200 με的应变。在等强度梁上分别粘贴全桥金属电阻应变计、常规半导体应变计和全桥半导体应变计,将等强度梁固定于温控箱内,在温控箱外利用细线或金属丝将砝码悬挂于等强度梁前端。
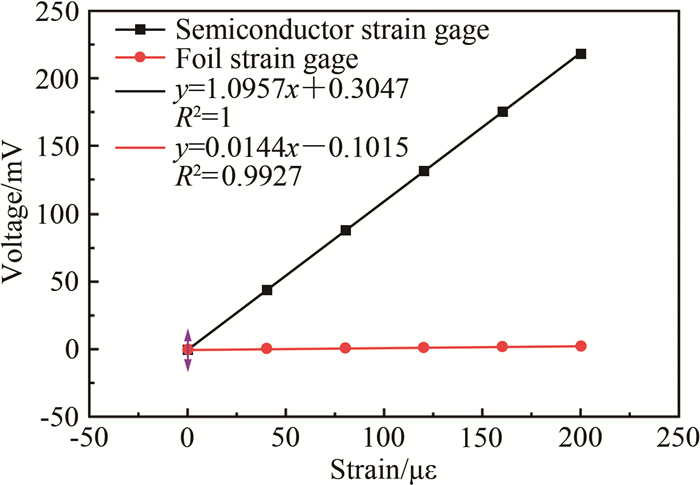
图 4为阶梯加载情况下全桥半导体应变计和全桥金属电阻应变计的输出结果对比(图中将加载换算为相应的应变)。可以看出:半导体应变计的输出变化量远大于金属电阻应变计,前者的应变灵敏度系数(K=(ΔR/R)/ε)高达109,而后者仅为1.4;同时,半导体应变计的输出结果具有很好的线性度。因此,对于相同结构的天平本体,采用半导体应变计作为天平敏感元件可以大幅降低天平的设计应变。
1.3 温度特性
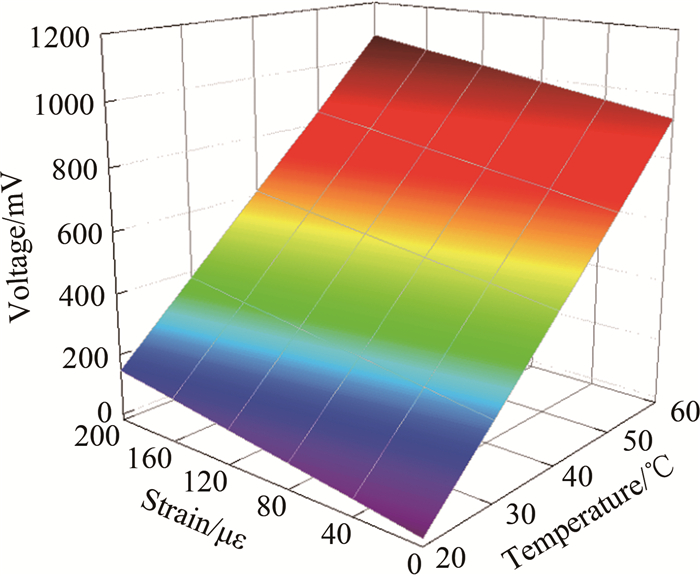
通过等强度梁试验可知:在20~60℃范围内,单个半导体应变计在零载荷条件下的温度漂移高达921.6 mV,零载荷条件下的温漂为621.3% FS,电阻温度系数为230×10-5/℃,如图 5所示;进行全桥半导体应变计设计后,其全温区的温度漂移如图 6所示,零载荷条件下的温漂为5.4% FS,电阻温度系数为3×10-5/℃,与金属电阻应变计相当。
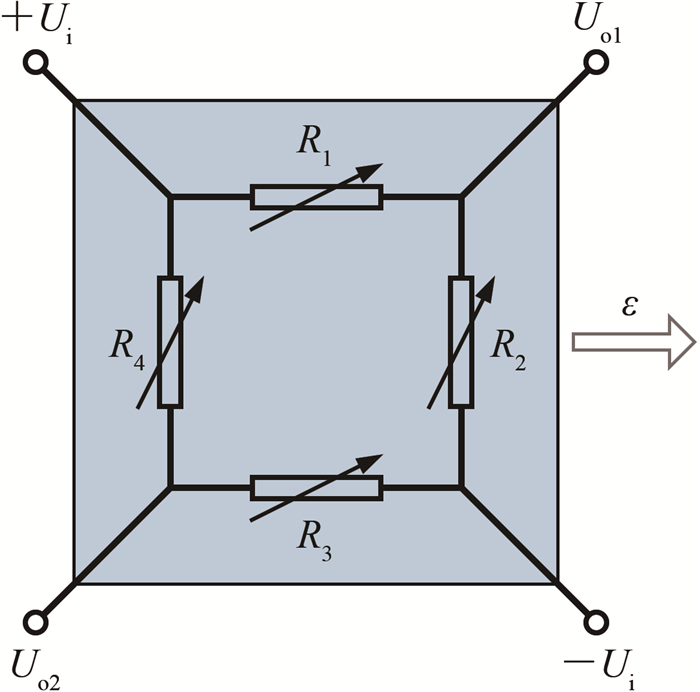
为进一步降低温度漂移,对全桥半导体应变计进行温度补偿,其原理如图 7所示。图中,电阻R1、R2、R3和R4为半导体应变计的桥臂电阻,电阻R0为温度补偿电阻,电阻R01、R02为零点补偿电阻,补偿电阻采用贴片电阻或色环电阻。
温度补偿后的全桥半导体应变计的全温区温度漂移如图 8所示。零载荷条件下的温漂为0.2% FS,电阻温度系数为0.1×10-5/℃,小载荷下半导体应变计的温度特性进一步改善。温度补偿后的全桥半导体应变计在室温条件下的加、卸载输出如图 9所示。在加、卸载过程中,应变计最大滞后为-0.5636 mV,占最大载荷输出的0.3%,零点漂移为-0.4761 mV,占最大载荷输出的0.2%,均满足应变天平使用要求。
2 天平设计
利用半导体应变计灵敏度系数高的优点,可将应变天平的设计应变降低1~2个数量级。考虑信噪比等因素的影响,将天平的设计应变设为常规高超声速风洞应变天平的1/10,如表 2所示。
表 2 天平设计载荷与设计应变Table 2 The range and strain design of balance天平分量 轴向力分量A 法向力分量N 侧向力分量C 滚转力矩分量L 偏航力矩分量Nb 俯仰力矩分量M 设计载荷/(N;N·m) 30 200 40 2 5 15 设计应变/με 10~50 10~50 10~50 10~50 10~50 10~50 为保证天平在激波风洞有效试验时间内能够获得一个以上周期的完整信号,要求整个测力试验系统的一阶固有频率高于100 Hz。
天平元件采用常规应变天平结构,轴向力梁采用“T”型梁结构,组合梁采用五柱梁结构。以设计应变为约束条件,以变形最小为设计目标,采用最优刚度法对天平结构进行设计。天平敏感梁长86 mm,直径38 mm。天平结构如图 10所示。
天平六分量气动力组合形式与常规应变天平有所区别。天平六分量气动力组合如下:

(1) 式中:UA、UN、UC分别为轴向力分量、法向力分量、侧向力分量的电压输出;UL、UNb、UM分别为滚转力矩分量、偏航力矩分量、俯仰力矩分量的电压输出。
2.1 有限元分析
为在有效试验时间仅为十至几十毫秒的激波风洞上实现应用,要求整个测力试验系统具有很大的刚度。以往测力试验系统一般由模型、天平、支杆、耳片、迎角机构等组成,为提升其刚度,将天平和支杆设计为一个整体,天平直接与固定迎角的支撑平台连接,减少中间连接环节,并改耳片支撑为平台支撑。
利用MATLAB、ANSYS等工程软件对天平结构进行有限元分析。天平材料为马氏体时效钢,其密度ρ=7.98 g/cm3,弹性模量E=1.8725×1011 Pa,屈服强度σs=1750 MPa,泊松比μ=0.3。试验系统的模态分析如图 11所示;前六阶固有频率见表 3,其中,一阶固有频率为100 Hz,能够确保天平在十至几十毫秒内的输出信号具有一个以上完整周期,便于数据的后处理。
表 3 试验系统前六阶固有频率Table 3 The first six mode frequencies of system模态 一阶 二阶 三阶 四阶 五阶 六阶 频率/Hz 100 119 200 308 407 558 振型 侧向 法向 侧向 法向 滚转 侧向 2.2 天平校准
在六分量天平静校系统上对天平进行校准:通过单元校准获得天平校准公式,通过多元校准获得天平的综合加载重复性及误差。天平六分量校准结果见表 4,天平综合加载重复性达到国军标先进指标,综合加载误差达到国军标合格指标,满足应变天平设计标准[21]。
表 4 天平多元校准结果Table 4 The results of multi-component calibration天平分量 轴向力分量A 法向力分量N 侧向力分量C 滚转力矩分量L 偏航力矩分量Nb 俯仰力矩分量M 综合加载重复性/(% FS) 0.08 0.04 0.05 0.04 0.02 0.03 综合加载误差/(% FS) 0.15 0.22 0.34 0.48 0.16 0.04 3 风洞试验
3.1 试验装置
风洞试验在中国空气动力研究与发展中心的FD-14激波风洞上进行。该风洞是由激波管(内径80 mm,高压段、低压段长度分别为7.5和12.5 m)以及相应的喷管、试验段、充气系统、液压及控制系统和真空系统组成,如图 12所示。
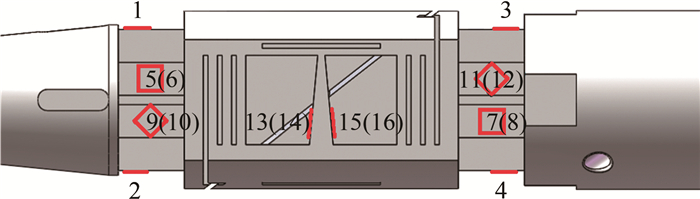
试验模型采用B-2标模(见图 13)。该模型具有大量的试验和计算结果[22],因此常被作为标准模型用于新建或改造风洞的流场校测。模型总长340.65 mm,底部直径为120 mm;材质为铝合金,可以减少模型重量,提升试验系统的固有频率。模型试验迎角为8°、10°和14°,侧滑角为0°,每个状态重复3车次。试验流场主要参数见表 5。
表 5 试验流场参数表Table 5 Parameters of flow field流场参数 数值 单位 来流马赫数Ma∞ 10.5 自由流动压q∞ 13 747 Pa 自由流单位雷诺数Re/L 5.97×106 m-1 自由流静压p∞ 174.56 Pa 自由流静温T∞ 46.73 K 3.2 试验结果
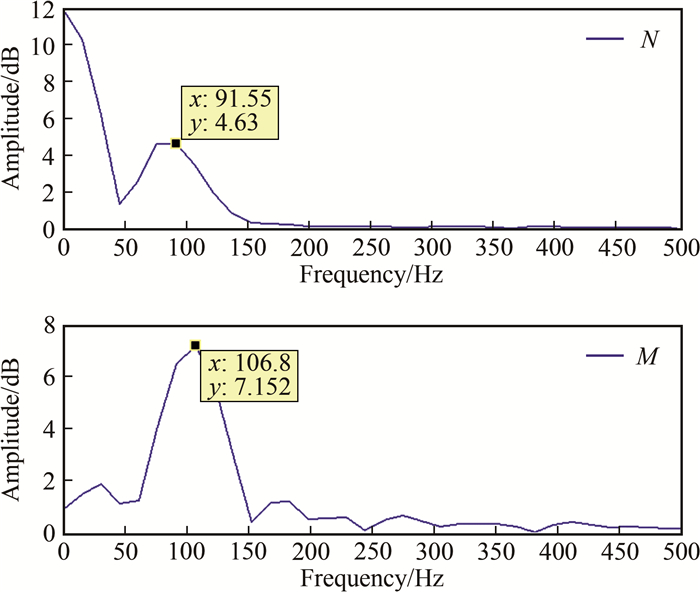
以10°迎角为例,天平输出信号如图 14所示(图中Pitot为皮托压力传感器信号;风洞试验有效时间约为11 ms)。从图中可以看出:天平输出信号与皮托压力传感器输出信号跟随性较好,且在有效试验时间内,天平轴向力、法向力和俯仰力矩分量都能够获得一个以上的完整信号周期。天平法向信号的频谱分析如图 15所示,法向力的低频振动频率约为91.5 Hz,俯仰力矩的低频振动频率约为106.8 Hz,与模态分析的结果基本相符,天平的频响满足要求。
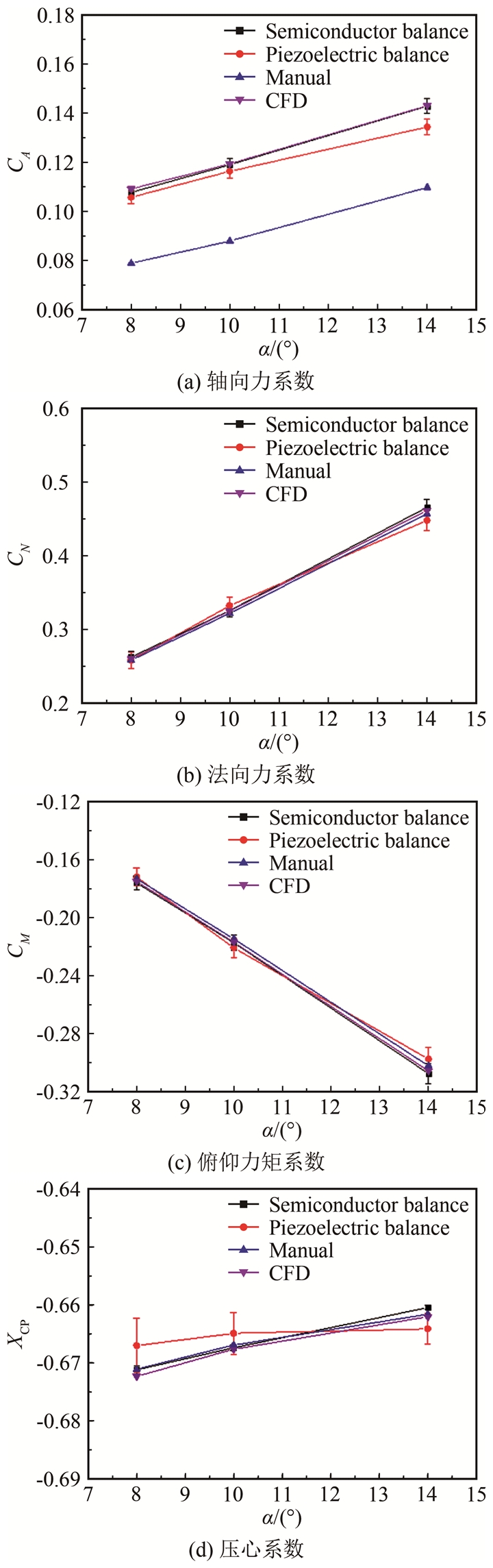
图 16给出了半导体应变天平和压电天平的激波风洞测力试验结果和数值计算结果。可以看出,半导体应变天平试验结果与压电天平试验结果以及数值计算结果吻合较好,说明半导体应变天平能够真实反映试验模型所受到的气动力载荷,可以用于激波风洞气动力测量。需要说明的是:图中气动手册[22]的结果为无黏计算结果,数值计算结果为层流计算结果。
由图 16还可以看出,在0°侧滑角状态下,半导体应变天平试验结果与压电天平试验结果、气动手册的规律性一致,半导体应变天平轴向力系数和压心系数的规律性略优于压电天平。半导体应变天平轴向力系数、法向力系数、俯仰力矩系数和压心系数试验结果与气动手册的最大偏差分别为36.60%、1.99%、1.81%和-0.17%;压电天平轴向力系数、法向力系数、俯仰力矩系数和压心系数试验结果与气动手册的最大偏差分别为34.14%、3.20%、2.89%和-0.61%。半导体应变天平轴向力系数、法向力系数和俯仰力矩系数的不确定度与压电天平相当,压心系数的不确定度优于压电天平。
试验结果的重复性精度如表 6所示。从表中可见,半导体应变天平试验结果的重复性精度优于压电天平,采用半导体应变天平有助于提升试验结果精度。
表 6 试验结果重复性精度Table 6 The repeatability accuracy of results天平分量 轴向力分量A 法向力分量N 俯仰力矩分量M 纵向压心系数Xcp 半导体应变天平/% 0.92 0.88 0.85 0.16 压电天平/% 4.01 1.51 1.60 0.58 4 结论
在研制全桥半导体应变计天平的基础上,在激波风洞中开展了半导体应变天平测力试验,得到以下结论:
(1) 对于试验时间很短的激波风洞,半导体应变计可以很好地发挥其灵敏度系数高的优势;
(2) 在激波风洞有效试验时间内,半导体应变天平能够获得一个周期以上的输出信号,有利于数据的后处理;
(3) 与压电天平相比,半导体应变天平在试验结果的重复性上具有一定优势,且轴向力系数和压心系数的规律性略好。
-
表 1 应变计主要性能对比
Table 1 Characteristics of different strain gages
应变计类型 金属电阻应变计 常规半导体应变计 应变灵敏度系数 1.8~2.2 80~210 电阻温度系数/(℃-1) 2.0×10-5 (70~700)×10-5 温度范围/℃ -270~650 -30~150 表 2 天平设计载荷与设计应变
Table 2 The range and strain design of balance
天平分量 轴向力分量A 法向力分量N 侧向力分量C 滚转力矩分量L 偏航力矩分量Nb 俯仰力矩分量M 设计载荷/(N;N·m) 30 200 40 2 5 15 设计应变/με 10~50 10~50 10~50 10~50 10~50 10~50 表 3 试验系统前六阶固有频率
Table 3 The first six mode frequencies of system
模态 一阶 二阶 三阶 四阶 五阶 六阶 频率/Hz 100 119 200 308 407 558 振型 侧向 法向 侧向 法向 滚转 侧向 表 4 天平多元校准结果
Table 4 The results of multi-component calibration
天平分量 轴向力分量A 法向力分量N 侧向力分量C 滚转力矩分量L 偏航力矩分量Nb 俯仰力矩分量M 综合加载重复性/(% FS) 0.08 0.04 0.05 0.04 0.02 0.03 综合加载误差/(% FS) 0.15 0.22 0.34 0.48 0.16 0.04 表 5 试验流场参数表
Table 5 Parameters of flow field
流场参数 数值 单位 来流马赫数Ma∞ 10.5 自由流动压q∞ 13 747 Pa 自由流单位雷诺数Re/L 5.97×106 m-1 自由流静压p∞ 174.56 Pa 自由流静温T∞ 46.73 K 表 6 试验结果重复性精度
Table 6 The repeatability accuracy of results
天平分量 轴向力分量A 法向力分量N 俯仰力矩分量M 纵向压心系数Xcp 半导体应变天平/% 0.92 0.88 0.85 0.16 压电天平/% 4.01 1.51 1.60 0.58 -
[1] 小约翰·D.安德森.空气动力学基础[M].杨永, 宋文萍, 张正科, 等译注. 5版.北京: 航空工业出版社, 2014. [2] 唐志共, 许晓斌, 杨彦广, 等.高超声速风洞气动力试验技术进展[J].航空学报, 2015, 36(1):86-97. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201501007.htm TANG Z G, XU X B, YANG Y G, et al. Research progress on hypersonic wind tunnel aerodynamic testing techniques[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1):86-97. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXB201501007.htm
[3] LIU Y F, WANG Y P, YUAN C K, et al. Aerodynamic force and moment measurement of 10° half-angle cone in JF12 shock tunnel[J]. Chinese Journal of Aeronautics, 2017, 30(3):983-987. DOI: 10.1016/j.cja.2017.02.008
[4] WANG Y P, LIU Y F, LUO C T, et al. Force test in a large-scale shock tunnel[C]//Proc of the 55th AIAA Aerospace Sciences Meeting. 2017.
[5] WANG Y P, LIU Y F, JIANG Z L. Design of a pulse-type strain gauge balance for a long-test-duration hypersonic shock tunnel[J]. Shock Waves, 2016, 26(6):835-844. DOI: 10.1007/s00193-015-0616-x
[6] MENG B Q, HAN G L, ZHANG D L, et al. Aerodynamic measurement of a large aircraft model in hypersonic flow[J]. Chinese Physics B, 2017, 26(11):114702. DOI: 10.1088/1674-1056/26/11/114702
[7] DURYEA G R, MARTIN J F. An improved piezoelectric balance for aerodynamic force[J]. IEEE Transactions on Aerospace and Electronic Systems, 1968, AES-4(3):351-359. DOI: 10.1109/TAES.1968.5408988
[8] 吕治国, 刘洪山, 齐学群, 等.飞船返回舱再入阶段高超声速六分量测力试验研究[J].空气动力学学报, 2003, 21(3):282-287. DOI: 10.3969/j.issn.0258-1825.2003.03.004 LYU Z G, LIU H S, QI X Q, et al. Experiment study of hypersonic six-component force measurement for re-entry module in shock tunnel[J]. Acta Aerodynamica Sinica, 2003, 21(3):282-287. DOI: 10.3969/j.issn.0258-1825.2003.03.004
[9] SHEERAN W J, DURYEA G R. The application of the accelerometer force balance in short-duration testing[C]//Proc of the 4th Aerodynamic Testing Conference. 1969.
[10] MENEZES V, KUMAR S, MARUTA K, et al. Hypersonic flow over a multi-step afterbody[J]. Shock Waves, 2005, 14(5-6):421-424. DOI: 10.1007/s00193-005-0281-6
[11] SINGH P, MENEZES V, IRIMPAN K J, et al. Impulse force balance for ultrashort duration hypersonic test facilities[J]. Shock and Vibration, 2015, 2015:803253.
[12] SAHOO N, MAHAPATRA D R, JAGADEESH G, et al. An accelerometer balance system for measurement of aerodynamic force coefficients over blunt bodies in a hypersonic shock tunnel[J]. Measurement Science and Technology, 2003, 14(3):260-272. DOI: 10.1088/0957-0233/14/3/303
[13] SANDERSON S R, SIMMONS J M. Drag balance for hypervelocity impulse facilities[J]. AIAA Journal, 1991, 29(12):2185-2191. DOI: 10.2514/3.10858
[14] ROBINSON M J, MEE D J, TSAI C Y, et al. Three-component force measurements on a large scramjet in a shock tunnel[J]. Journal of Spacecraft and Rockets, 2004, 41(3):416-425. DOI: 10.2514/1.10699
[15] MEE D J, DANIEL W J T, SIMMONS J M. Three-component force balance for flows of millisecond duration[J]. AIAA Journal, 1996, 34(3):590-595. DOI: 10.2514/3.13108
[16] 刘施然, 杨赟秀, 胡守超, 等.脉冲风洞单分量应力波天平测力技术[J].宇航学报, 2016, 37(12):1419-1424. DOI: 10.3873/j.issn.1000-1328.2016.12.003 LIU S R, YANG Y X, HU S C, et al. Stress wave force balance for use in hypersonic impulse facilities[J]. Journal of Astronautics, 2016, 37(12):1419-1424. DOI: 10.3873/j.issn.1000-1328.2016.12.003
[17] WACKER N, RICHTER H. Piezoresistive effect in MOSFETS[M]//BURGHARTZ J N. Ultra-thin chip technology and applications. New York: Springer Science + Business Media, 2011.
[18] WATSON R B. Bonded electrical resistance strain gages[M]//SHARPE W N Jr. Springer handbook of experimental solid mechanics. Boston: Springer-Verlag, 2008.
[19] DOLL J C, PRUITT B L. Piezoresistor design and applications[M]. New York:Springer Science+Business Media, 2013.
[20] BARLIAN A A, PARK W T, MALLON J R, et al. Review:semiconductor piezoresistance for microsystems[J]. Proceed-ings of the IEEE, 2009, 97(3):513-552. DOI: 10.1109/JPROC.2009.2013612
[21] 国防科学技术工业委员会. GJB2244A-94风洞应变天平规范[S]. 1994. [22] 航天部第十四研究所.无粘气动力手册[M].北京:航天部第十四研究所, 1984. -
期刊类型引用(3)
1. 王奔,杨晓强,李小刚,王碧玲. 温度梯度对天平轴向力测量精度影响分析. 弹箭与制导学报. 2024(02): 7-12 .  百度学术
百度学术
2. 罗闽燕,时浩天,张涛. 旋转轴天平高精度数据采集及无线传输系统的设计. 机电技术. 2024(03): 69-72 .  百度学术
百度学术
3. 赵荣娟,刘施然,周正,吴里银,吕治国. 激波风洞超燃冲压发动机推力测量技术研究. 实验流体力学. 2022(04): 103-108 .  本站查看
本站查看
其他类型引用(4)







 下载:
下载: