0   引言

进气道是飞机动力装置的重要部件。进气道性能的优劣，对飞机发动机的工作效率、发动机能否正常工作以及推力的大小等起到至关重要的作用^[1]。进气道风洞试验目的就是在模拟进气道内、外部流场条件下，测量进气道的静态和动态特性，研究进气道设计的合理性和改进措施。进气道的动态特性主要用湍流度来表示，湍流度越大表示进气道内部动态畸变越严重，越不利于发动机的正常工作，甚至可能会引起发动机喘振。因此精确测量进气道出口截面的湍流度对进气道的设计与选型至关重要。

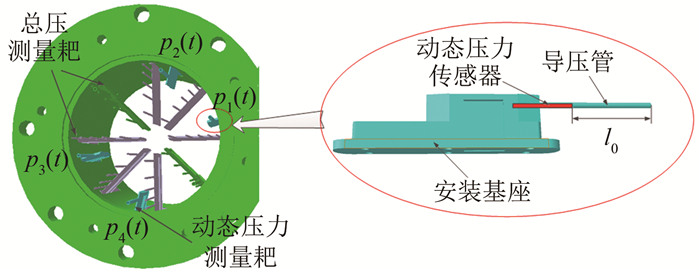
进气道试验中，进气道出口处的湍流度主要由动态压力计算得到，而动态压力由安装在进气道测量段内的动态压力传感器测量。图 1是进气道试验中典型的动态压力测量耙示意图。动态压力测量耙主要由安装基座和测压管组成，动态压力传感器安装在测压管内。一般情况下，动态压力传感器的信号感受端面与测压管前端平齐，但在某些风洞试验中，由于各种原因，比如传感器未固定住，导致试验过程中滑入管道内部，或者动态压力传感器难以安装到测量管前端，使动态压力传感器的信号感受端面与测压管前端存在一段长为l₀，内半径为r₀的圆柱形导压通道。导压通道的存在使动态压力测量过程中引入管道效应，导致动态压力的测量存在较大误差，因此需要研究管道效应对动态压力和湍流度的影响，以便判断试验数据是否需要修正, 并为进气道测量段和动态压力测量耙的设计与安装提供指导。

图  1  进气道试验中典型动态压力测量耙示意图

Fig.  1  The schematic of fluctuating pressure rake in inlet test

下载: 全尺寸图片 幻灯片

测压管前端的动态压力信号经过导压通道到达动态压力传感器的信号感受端面时会发生畸变(平均压力不会发生改变，发生畸变的主要是脉动部分)，使动态压力传感器测量得到的动态压力不能真实的反映导压通道前端的动态压力^[2]。动态压力信号的畸变可以通过频响函数进行衡量，频响函数是测压管道信号输出端和输入端在频域上的比值。国外对管道效应做了系统的研究，Bergh和Tijdeman^[2]基于流体动力学微分方程，并根据流体管道的传输特性推导了管道系统频响函数的理论公式；Irwin等^[3]首先采用了在测压管道中加限制器的方法来改善测压管路系统的频响函数；Gumley^[4-5]在风工程测压中使用Bergh-Tijdeman理论对管道效应进行了分析；Holmes等^[6-8]利用Bergh-Tijdeman理论对测压管道系统进行了优化；Gerstoft等^[9]将电路模拟理论运用于风洞管路测压系统，取代了从前对流体动力方程直接求解的方法。国内苏而皇^[10]及蔡亦钢^[11]对管道动态分析进行了进一步研究，基于电路传输线理论提出了流体管道的耗散模型，并用矩阵传递关系来表达管路输入与输出端的压力及流量关系，较递归式的Bergh-Tijdeman方程，矩阵式的耗散模型运用起来更加方便。另外，谢壮宁等^[12-13]对脉动风压测压管路系统的动态特性进行了分析，并发展了相关的通用分析程序；周晅毅等^[14]基于耗散模型对单通道测压管路系统进行了优化；马文勇等^[15]使用耗散模型以及试验方法对测压管路信号的畸变及修正进行了研究；王学等^[16]系统研究了导压通道长度、内径、材质以及弯曲度等因素对动态压力测量的影响并提出了修正方法。

目前对管道效应的影响研究主要集中在飞行器或建筑表面动态压力的测量，表面测压所关注的动态压力频率较低，只有较长的导压通道测量系统才会对所关注频域内的动态压力造成较大影响。而在进气道风洞试验中，动态压力传感器的采样频率达到10 000 Hz以上，动态压力的低通截止频率也达到5000 Hz，即使存在较短的导压通道，其管道效应也会对湍流度的测量产生较大影响。现阶段关于进气道试验中管道效应的影响研究仍然没有相关报道。因此，研究进气道试验中管道效应对动态压力和湍流度测量的影响非常必要。本文基于耗散模型对进气道试验中管道效应对湍流度测量的影响进行理论分析，并通过进气道风洞试验进行了验证。

1   管道效应的理论分析

1.1   管道效应的耗散模型理论

湍流度通过动态压力计算得到，进气道出口截面某点的湍流度定义为^[1]:

其中, Tu为湍流度；p_N(t)为随时间变化的动态压力，由动态压力传感器测量得到；N为动态压力信号采集点数，T为采样时间；p_N为时间平均压力，可以表示为：

可见，进气道内某点的湍流度本质上反映的是此点动态压力的均方根。动态压力的脉动幅值越大，均方根就越大，湍流度也越大。因此动态压力脉动幅值能否精确测量，将直接影响到湍流度的精确度。

图 2是导压通道内动态压力传播示意图。动态压力从导压通道前端A点传播到动态压力传感器信号感受端面B点的过程中，由于波动方程是非线性的，波形在传播过程中会发生改变；另外，管道内流体黏性和热传导等耗散效应的存在，也会使压力波形发生改变；还有，管道内流体自身存在一定频率，当动态压力脉动频率与管道内流体自身频率一致时会产生共振效应，导致动态压力信号发生改变。这些因素导致动态压力传感器测量得到的动态压力和导压通道前端A处的动态压力有一定的差异。

图  2  动态压力传播示意图

Fig.  2  The schematic of the spread of fluctuating pressure in tube

下载: 全尺寸图片 幻灯片

管道内流体动力学耗散模型^[11]考虑了流体的黏性和热传导效应，能够较准确地分析流体管道频率特性。通过耗散模型可以给出A点和B点动态压力以及流量的信号关系^[11]：

式中，p_B(ω)和Q_B(ω)表示传感器信号感受端面B点的压力和流量在频域上的脉动量；Γ(ω)称为传播算子；Z₀(ω)为特征阻抗。在动态压力传感器测量点B处，流体不发生流动，因此流量为0，即Q_B(ω)=0，则A和B点动态压力在频域上可以表示为：

H(ω)为测压管道系统的频响函数，通过频响函数，可以得到管道输出端和输入端压力信号的关系。其中H(ω)的实数部分表示在圆频率为ω时，B处压力脉动幅值与A处压力脉动幅值之比。传播算子Γ(ω)可以表示为^[11]：

Y(ω)和Z(ω)可以表示为^[11]：

其中, 圆频率ω=2πf，f为频率，ρ₀为通道内流体密度，l₀为测量通道的长度，即A点到B点距离，r₀为通道内半径，ν₀为流体运动黏性系数，a₀为通道内流体声速，γ为内流比热比，σ₀为普朗特数的时间平均值，I₀和I₁为表示零阶和一阶贝塞尔函数，i为复数的虚部符号。通过式(4)可以得到频域上B处动态压力的测量值与A处动态压力真实值之比。

1.2   管道效应对压力脉动幅值的影响

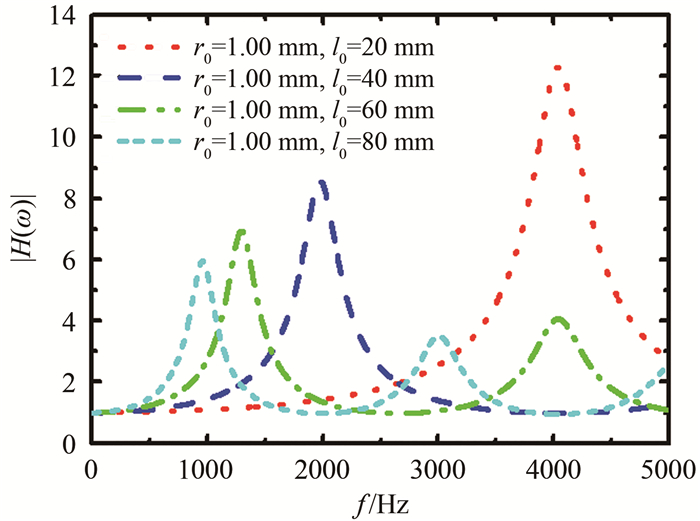
式(4)较复杂, 无法直接计算。本文使用MATLAB编程对式(4)进行计算，在相同的条件下，本文计算结果和文献中的结果^[15]完全吻合，验证了本文所编程序的正确性。下面利用所编程序对动态压力脉动幅值的放大倍数进行理论分析。以温度为15 ℃，压强为95 000 Pa的空气为例，空气密度为1.28 kg/m³，运动黏性系数ν₀为1.42 Pa·s，绝热指数γ取1.4，声速a₀为340.3 m/s，普朗特数为0.704。图 3为导压通道半径r₀=1.00 mm、长度l₀分别取20、40、60和80 mm时，动态压力幅值放大倍数|H(ω)|=|p_B(ω)/p_A(ω)|在频域上的值。从图 3可以看出，|H(ω)|在0~5000 Hz的频域上大于或等于1，而且在某些频率上存在明显的峰值；随着l₀的增加，|H(ω)|峰值减小，而且峰值对应的频率减小。随着导压通道长度的增加，黏性和热传导等耗散因素使压力波的能量减小，从而导致脉动量减小，尤其在脉动量较大时，脉动量减小得更明显。|H(ω)|峰值是由共振效应导致的，随着导压通道长度的增加，导压通道内流体的固有频率减小，动态压力与其共振的频率也减小，因此|H(ω)|峰值所对应的频率减小。

图  3  不同通道长度l₀时|H(ω)|在频域上的曲线

Fig.  3  The curves of |H(ω)| in frequency domain for different l₀

下载: 全尺寸图片 幻灯片

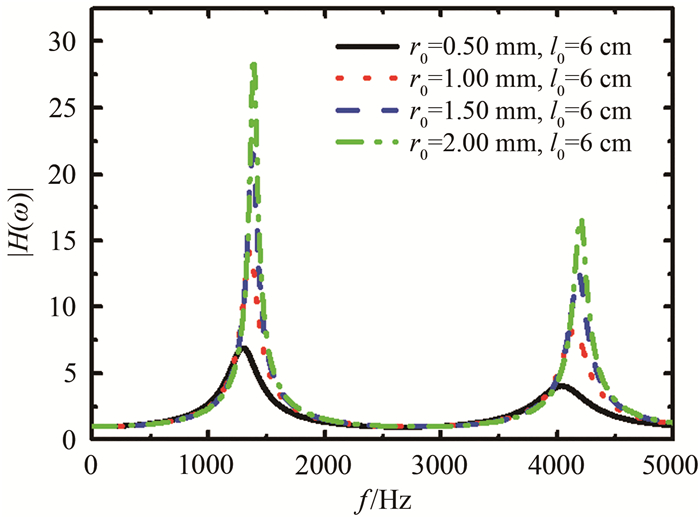
图 4是导压通道长度l₀为60 mm、半径r₀分别取0.50、1.00、1.50和2.00 mm时，|H(ω)|在频域上的值。导压通道长度l₀不变，导压通道取不同内半径时，|H(ω)|峰值所对应的频率变化较小，说明共振频率主要由导压通道长度l₀决定。另外，随着导压通道内半径r₀的减小，|H(ω)|峰值减小；导压通道内径减小，黏性和热传导等耗散作用越明显，从而导致|H(ω)|减小。在进气道试验中，导压通道的内半径一般在0.20~1.50 mm之间；从图 3和4中可以看出，对l₀ < 80 mm，进气道试验中管道效应的影响主要在高频区域，而且对动态压力的脉动幅值主要起放大作用。

图  4  不同通道半径r₀时|H(ω)|在频域上的曲线

Fig.  4  The curves of |H(ω)| in frequency domain for different r₀

下载: 全尺寸图片 幻灯片

1.3   管道效应对湍流度测量的影响

通过前面的理论分析，发现导压通道的管道效应对动态压力的脉动幅值有较大影响。进气道试验中主要以湍流度来表征进气道出口截面的动态特性，下面以中国空气动力研究与发展中心Ф3.2 m风洞中的某次试验数据结果为例，理论分析导压通道的管道效应对湍流度的影响。使用湍流度放大倍数Tu_B/Tu_A，即传感器信号感受端面处的湍流度除以导压通道前端的湍流度来表征管道效应的影响程度，Tu_B/Tu_A越接近于1，说明管道效应的影响越弱；而Tu_B/Tu_A越偏离1，说明管道效应的影响越强。Tu_B/Tu_A可以通过以下方法计算得到：(1)已知导压通道长度l₀=0时的动态压力时域信号p_A(t)，使用式(1)计算得到湍流度Tu_A；(2) p_A(t)经过傅里叶变换后可以得到频域上的动态压力值p_A(ω)；(3)通过式(4)得到加入管道效应后的理论上的动态压力值p_B(ω)；(4)再经过傅里叶逆变换得到时域上的动态压力值p_B(t)；(5)然后再利用式(1)得到理论上存在管道效应时的湍流度Tu_B；(6)最后得到加入管道效应后湍流度的放大倍数Tu_B/Tu_A。

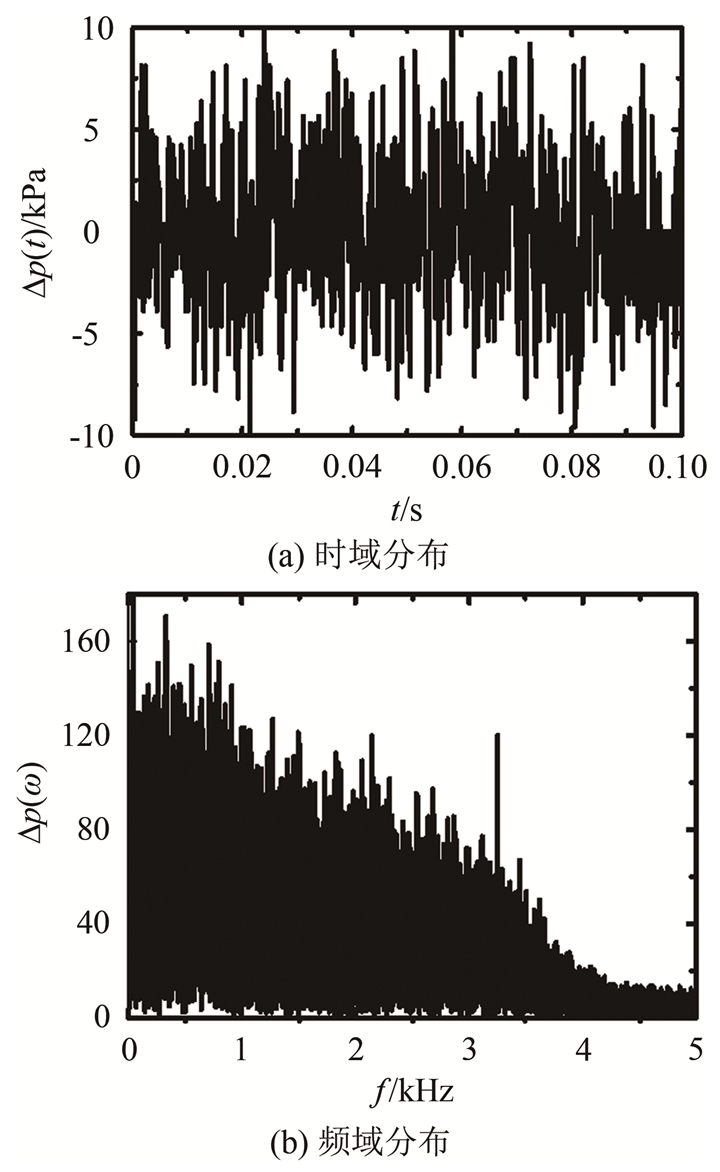
以Ф3.2 m风洞中某次进气道试验的动态压力数据为例，空气温度为15 ℃，密度为1.28 kg/m³, ν₀为1.42 Pa·s，绝热指数γ取1.4，声速a₀为340.3 m/s，普朗特数为0.704。动态压力传感器信号采集频率为10 000 Hz，低通截止频率为5000 Hz，采集时间为3 s，导压通道内半径为0.85 mm。图 5为Ф3.2 m风洞中某次进气道试验某点所采集的动态压力脉动幅值分别在时域和频域上的分布；利用式(1)可计算得到此点湍流度Tu_A为0.0368。假设动态压力传感器前方存在半径为0.85 mm的导压通道，图 6给出了湍流度放大倍数Tu_B/Tu_A与通道长度l₀之间的关系。从图 6可以看出，测量湍流度Tu_B在通道长度l₀=30 mm时放大到真实湍流度的4倍。要使湍流度测量误差控制在10%以内，则动态压力传感器前方所留通道长度l₀不能超过5 mm。

图  5  动态压力脉动幅值

Fig.  5  The curve of fluctuating value for pressure

下载: 全尺寸图片 幻灯片

图  6  r₀=0.85 mm时，湍流度放大倍数随通道长度的变化曲线

Fig.  6  The curve of Tu_B/Tu_A in inlet test for r₀=0.85 mm and different l₀

下载: 全尺寸图片 幻灯片

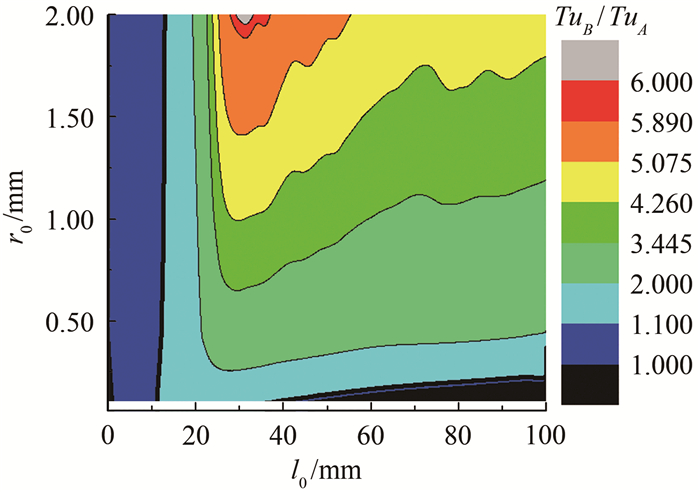
图 7为动态传感器前方通道取不同长度l₀和不同半径r₀时，湍流度放大倍数云图。从图中可以看出，在存在管道效应的大部分区域，湍流度放大倍数大于1，说明管道效应对湍流度测量的影响主要起放大作用；而对于通道长度l₀>40 mm，半径r₀ < 0.10 mm时，由于通道半径较小，耗散效应的影响较大，测量湍流度反而减小。进气道试验中，导压通道的内半径r₀的范围一般在0.20~2.00 mm，因此进气道试验中的管道效应会放大湍流度。另外，湍流度的放大倍数和测量点所处的流场相关，对于不同的动态压力测量点，甚至流速不同时的同一测量点，管道效应对湍流度的影响程度也会有所差异。在进气道试验中，进气道内流马赫数范围0~1.0内，脉动压力传感器前方出现的管道一般不会太长(l₀ < 100 mm), 管道效应对湍流度起放大效应；至于具体的放大量，与所测流场有一定关系。

图  7  不同导压通道长度和内半径r₀时, 湍流度放大倍数云图

Fig.  7  The contour of Tu_B/Tu_A for different r₀ and l₀

下载: 全尺寸图片 幻灯片

2   管道效应的试验验证和修正方法

2.1   管道效应的试验验证

在Ф3.2 m风洞某期进气道试验中，对管道效应的影响进行验证。试验中使用某飞机进气道模型，通过引射器的引射作用模拟进气流量。由于使用引射器的引射效应进行流量模拟，在某些动态压力的某些频域内可能会引入一些误差。本试验的湍流度重复性精度 < 0.0005，因此系统带来的误差在本次试验验证过程中可以忽略。试验测量段的动态压力传感器安装位置如图 1所示，图中p₁(t)~p₄(t)分别表示4个动态压力传感器测量的动态压力。动态压力传感器量程为30 PSI(约为207 000 Pa)，测量精度为±0.08% FS；试验中动态数据采样频率为20 kHz，采集时间1.5 s，滤波器低通截止频率为5 kHz，试验所使用的管道内半径为1.30 mm。试验分2组，第一组试验中4个动态压力传感器前方导压通道的长度l₀均为0。第二组试验中动态压力传感器前方导压通道的长度l₀分别为0、8、18和28 mm。2组试验中，风洞内的来流风速均为0。进气道出口截面处的流量系数分别为0.88和0.89，进气道出口截面的平均马赫数分别为0.58和0.59，忽视流量系数的差别对2次试验湍流度的影响。试验时，采集4个动态压力传感器的动态压力数据p₁(t)~p₄(t)，然后通过式(1)得到进气道出口4个采集点处的湍流度Tu₁~Tu₄。

图 8给出了2组试验动态压力脉动量的频域值。从图 8(a)中可以看出，2组试验在动态压力传感器前方都没有导压通道时，压力的脉动幅值在频域上差别不明显，脉动幅值大体上随着频率的增加而逐渐减小。而从图 8(b)~(d)可以明显看出，在某些频域范围内，动态压力传感器前方存在导压通道时，动态压力脉动幅值明显大于无导压通道时的脉动幅值。而且随着导压通道l₀的增加，动态压力的脉动峰值所对应的频率减小，此变化趋势和1.2节中的耗散理论结果相吻合。

图  8  试验中4个位置动态压力脉动幅值Δp₁(ω)~Δp₄(ω)的频域值

Fig.  8  The value of Δp₁(ω)~Δp₄(ω) in frequency domain for the four sensors

下载: 全尺寸图片 幻灯片

表 1给出了2组试验结果的湍流度值，以及它们之间的比值。2次试验在都没有使用导压通道的情况下，湍流度只相差了0.0003，相差不到1%，因此前面流量系数差别0.01对湍流度影响较小的假设成立。从表 1中可以看出，管道效应对湍流度测量的影响比较明显。导压通道长度l₀在0~28 mm范围内时，湍流度的放大倍数都增大，在l₀=28 mm时，湍流度甚至放大到3.5倍。

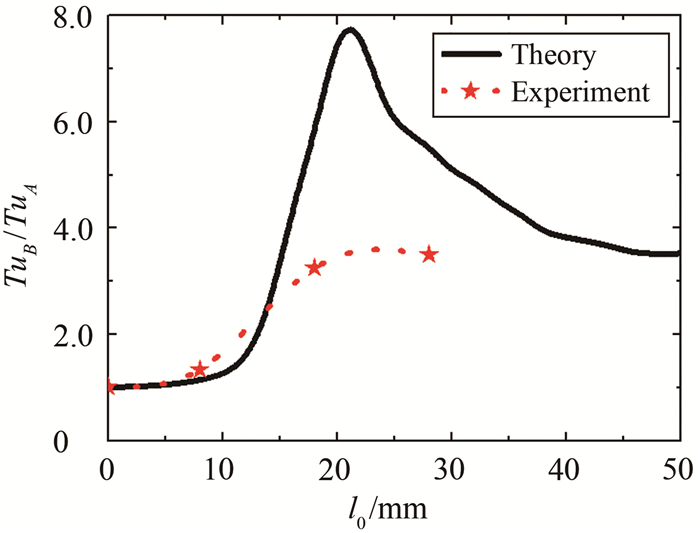
表  1  2组试验湍流度结果

Table  1  The value of turbulivity for the two inlet tests

湍流度	第一组试验	第二组试验				放大倍数TuB/TuA
	l0=0 mm	l0=0 mm	l0=8 mm	l0=18 mm	l0=28 mm
Tu1	0.0226	0.0229	-	-	-	1.01
Tu2	0.0260	-	0.0348	-	-	1.34
Tu3	0.0226	-	-	0.0733	-	3.25
Tu4	0.0187	-	-	-	0.0653	3.50

下载: 导出CSV 

| 显示表格

图 9给出了湍流度放大倍数的理论和试验结果。从图中可以看出，在l₀ < 5 mm时，理论和试验结果差别不大，湍流度放大都小于1.1。而在l₀>5 mm时，理论结果大于试验结果，其中在l₀=28 mm时，试验结果湍流度放大到3.50倍，而理论结果放大到5.54倍。导致理论耗散模型湍流度放大倍数较大的具体原因还需要进一步探索和研究。

图  9  湍流度放大倍数的理论和试验结果

Fig.  9  The curves of Tu_B/Tu_A for the results of theory and the experiment

下载: 全尺寸图片 幻灯片

2.2   管道效应的修正方法

在进气道试验中，由于管道效应放大湍流度，因此试验过程中应尽量保证动态压力传感器端面与测压管前端平齐，以减小管道效应带来的测量误差。如果不能保证动态压力传感器端面和测压管前端平齐，则需要评估管道效应对湍流度带来的影响。如果管道效应的影响量过大，则需要对湍流度试验结果进行修正。在已知导压管道的频响函数下，可以通过式(4)对动态压力进行修正。获得某种尺寸导压通道在某个流速下的频响函数主要有试验方法和理论方法。

试验方法就是同一流场条件下，使用不同长度与内径的管道分别测量脉动压力，并在频域上进行相除，从而得到某种流场速度和某种管道尺寸下的频响函数。试验方法实施起来比较困难。首先，难以保证2次测量的流场完全一致。即使2次试验在同一位置测量，或者同一试验2处相近位置进行测量，都难以保证测量位置处的流场完全一致；其次，使用试验方法获得频响函数成本非常高。不同流场速度、不同长度、不同内径、不同来流介质、甚至不同温度条件下，管道效应所产生的频响函数也会不同。如果只考虑流速、管道长度、管道内径等3个参数，试验量也非常大。例如，把速度Ma从0~2.0划分20个间隔，管道长度从1~10 mm划分10个间隔，内径从0.2~2.0 mm划分10个间隔，要得到Ma为0~2.0、管道内径和长度范围分别为0.20~2.00 mm和1~10 mm管道效应产生的频响函数，需要进行2000次试验，可见试验方法的工作量很大，且试验成本也非常高。

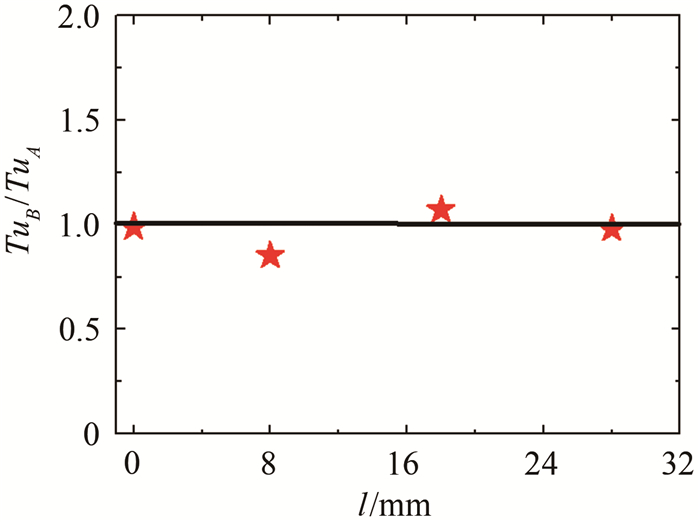
现有的耗散理论给出的频响函数在所测流场流速较低的条件下(Ma < 0.2)，结果比较准确；而在所测流场流速度较高的情况下(Ma>0.2), 结果误差太大。本文人为地减小管道半径参数, 对管道效应试验结果进行修正。图 10给出了带管道效应的试验结果使用耗散理论修正后的湍流度放大倍数(试验中使用的管道内径为1.30 mm，耗散理论模型使用0.80 mm管道内径参数进行修正)。由图 10可见，理论模型使用较小的内径参数后，可以把湍流度放大倍数修正到1附近。管道内半径主要决定动态压力在管道内传播过程中的黏性耗散量，人为地减小管道半径，意味着增加耗散模型中的耗散量。使用较小的内径参数，能够使修正结果接近于无管道效应时的结果，说明耗散模型结果误差过大，可能是模型所考虑的黏性耗散较小导致。使用耗散模型理论方法进行修正时，先通过少量试验方法对理论模型内径参数进行标定，然后通过试验所标定的内径参数使用式(4)获得频响函数，进而对存在管道效应的试验结果进行修正。

图  10  管道效应理论修正后的湍流度放大倍数

Fig.  10  The correcting value of Tu_B/Tu_A for the results of experiments with tubing effect

下载: 全尺寸图片 幻灯片

3   结论

本文通过理论分析和进气道试验研究了导压通道管道效应对进气道试验中湍流度的影响。研究结果表明：进气道试验中导压通道的管道效应对动态压力和湍流度的测量有较大影响，会导致测量湍流度大于真实湍流度。在本文研究条件下，管道长度为28 mm时，湍流度被放大到3.5倍。建议在进气道风洞试验中，应避免使用管路导压的方式进行动态压力的测量。如果在试验中不可避免的存在导压通道时，导压通道长度也须小于5 mm，以便使湍流度的测量误差控制在10%以内。