Experimental research progress of hydrofoil tip vortex cavitation
-
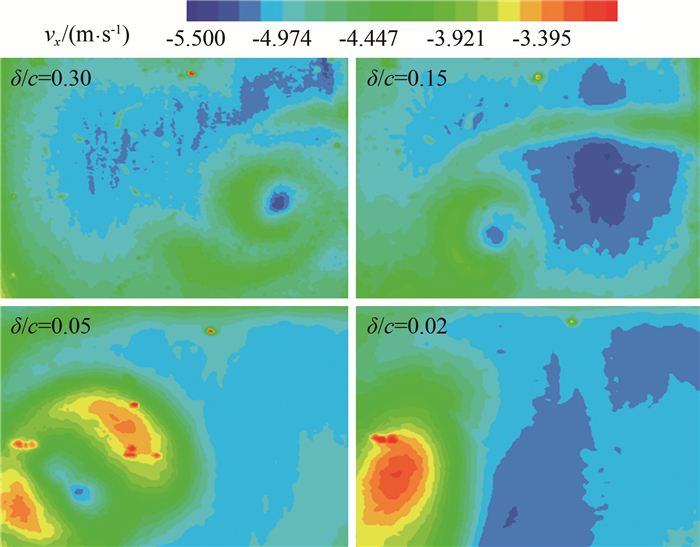
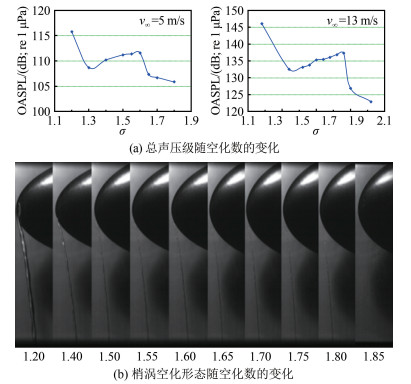
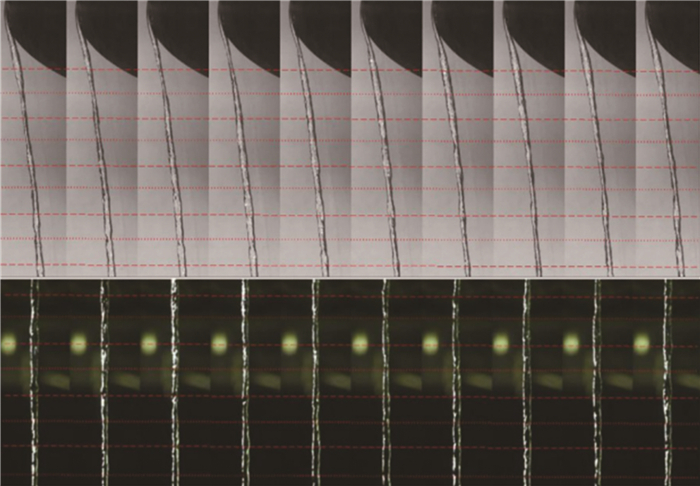
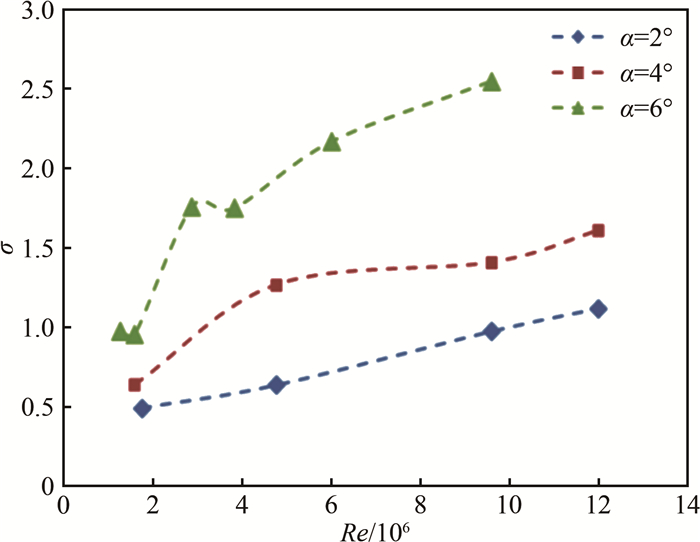
摘要: 针对螺旋桨、水轮机以及导管桨等叶片的梢涡空化现象，国内外学者开展了一系列相关实验研究。本文对梢涡空化起始(或初生)、发展与溃灭(或消失)等3个阶段的实验研究进展及成果进行综述，梳理未来的研究方向及关键问题，为梢涡空化研究提供参考。关于梢涡空化初生问题，基于旋涡理论模型及流场测量技术，对不同翼型的梢涡结构特征进行分析，根据空化发生的相变条件(即气核、低压以及低压作用时间)，初步认识了梢涡空化发生机理；关于梢涡空化发展问题，以辐射噪声骤增为典型特征，借助空泡图像的高速摄影及声学信号同步采集技术，研究梢涡空化形态及对应的辐射噪声特征，通过进一步解释"涡唱"现象，深入认识了梢涡空化发生机理；关于梢涡空化溃灭问题，溃灭发生位置一般远离桨叶等水力机械，对结构物的振动与剥蚀影响很小，本文不作详细阐述。此外，对梢涡空化初生的准确预报，一直是相关理论研究成果应用于工程实际所面临的一个重要问题。归根结底，主要是影响梢涡空化关键参数(比如载荷、雷诺数和水质等)的尺度效应问题和梢涡空化初生预报公式逐渐完善的问题。Abstract: As a typical vortex cavitation phenomenon, Tip Vortex Cavitation (TVC) occurring on the propellers (or duct propellers) and hydro-turbines has been widely investigated in experiments. To figure out the research orientations and the key problems in the near future, experimental research progress and results about the three stages of TVC, that are inception, development and collapse, are summarized to provide reference for further studies. On the inception of TVC, analysis of vortex dynamics of the tip flow field is conducted to get preliminary acquaintance with mechanics of its inception under various phase transformation conditions of bubble nuclei, low pressure and action time of low pressure, based on vortex theoretical models and experimental measurement technology. On the development of TVC characteristiced by a sharp increase of the radiation noise, research on the morphology of TVC and characteristics of the corresponding radiation noise is carried out for a better understanding of the mechanism of the development and radiation noise of TVC, in combination of high-speed photography of the morphology and acoustic signal acquisition of TVC. The collapse of TVC is only mentioned briefly, because few attention is paid to this issue as it can hardly cause vibration and erosion on hull structures. An accurate prediction of the inception of TVC in practice is still an open question though some progress is made in the fundamental research of TVC. How to quantify the scale effect of the vital parameters, such as load, Reynolds number and water quality, and how to improve the incipient prediction formula of TVC are problems still to be solved.
-
Keywords:
- hydrofoil /
- tip vortex /
- cavitation /
- radiation noise /
- flow visualization
-
0 引言
流体推力矢量技术是指针对喷气推进方式，在不采用喷口机械偏转前提下，通过流动控制手段改变和控制发动机主喷流方向，以此改变发动机的推力方向，获得飞行控制所需的控制力和控制力矩。推力矢量技术由发动机推力分量产生直接控制力，可以直接对飞行器姿态进行控制或者取代部分原有舵面的控制功能，实现原有飞机无法做到的机动或大迎角飞行能力。大量研究表明，在航空推进系统中采用流体推力矢量控制在技术上是可行的，它通过气流间的相互作用实现矢量偏转和喉道调节，结构简单、重量和造价大大降低，因此有望取代现有复杂的机械推力转向装置，带来推力矢量技术的革命性变化。
传统推力矢量技术的实现主要采用机械偏转的方式，主要包括折流板[1]、二元矢量喷管和轴对称矢量喷管[2](AVEN)几种方案。推力矢量技术在高性能飞机上有着很大的应用潜力，包括提高飞机的机动性、飞行性能、生存能力以及隐身性能等各个方面。不过，对最新一代飞机来说这些优势还没有得到充分的体现，主要原因是额外增加的推力转向装置显著增加了飞机重量、机构复杂程度以及造价。机械系统的过于复杂一定程度上阻碍了这项技术在飞机上的应用。另一方面，由于具有更好的气动效率，飞翼/无尾布局可能成为未来飞行器的一种主要布局方式，这种布局取消了平尾、垂尾等控制舵面，设计师希望推力矢量能够成为一种高效的控制方式，在推力损失不大、控制响应不降的情况下，补充一种新的稳定和操控手段。流体推力矢量具有达到这一目标的潜在能力，理想设计状况下这种方式具有较高的运动、控制可靠性，不仅可以为高机动飞机提供足够的俯仰控制力矩，也可以为无尾/飞翼布局飞机的飞行安定性，提供频繁工作的三轴稳定性控制力矩。
本文对目前发展的主要流体推力矢量方法进行了回顾，分别介绍了各方法的控制原理和适用范围，在同一评价指标下对推力矢量的矢量效率和推力损失进行了比较，探讨了实现工程应用还需要解决的问题。在此基础上，介绍了3种目前还处于实验室阶段的新概念流体推力矢量方法，讨论了这些方法的潜在优势和存在的问题挑战，为下一步流体推力矢量研究提供借鉴。
1 主要流体推力矢量方法
文献[3-5]对几种流体推力矢量的发展历程进行了很好的综述，这里主要对比分析几种方法的优劣。20世纪80年代末，美国航空航天局兰利研究中心(NASA LaRC)发起了固定形状喷管的流体推力矢量技术研究，前后提出了3种不同的推力矢量控制方法，分别是激波矢量法、喉道偏斜法和逆流方法。3种方式的控制原理如图 1所示，分别利用了激波、喉道声速线和抽吸负压的原理实现偏转。同向流控制在欧洲国家进行了较多研究，是一种利用Coanda效应实现偏转的控制方法，适用于对低速主流进行控制。以上控制技术按控制位置不同又可以分为3类，分别是对喉道施加控制、对喷管扩张段的控制和对喷流出口下游进行控制。
1.1 激波矢量法
激波矢量法[6-10](SVC：Shock Vectoring Control)利用了流体经过斜激波后方向发生偏转的原理，如图 1(a)所示，通过注入二次流动与喷管超声速气流干扰形成激波，激波越强，偏转角度越大。
NASA兰利中心(LaRC)从20世纪80年代开始开展激波矢量法控制技术研究，首先是在二维收敛-扩张型喷管上进行试验，实现了俯仰方向的单轴推力矢量控制。随后又通过在横侧方向上增加科恩达效应吹气控制，实现俯仰和偏航方向的推力矢量控制[6]。NASA LaRC联合普惠公司开展了多轴推力矢量喷管(MATV)研究[8]，将二次射流缝布置在喷管扩张段的上下壁面和侧壁上，分别对射流产生俯仰和偏航方向的控制。试验采用高压冷气源的方式，二次流总压与主流总压的比值变化范围在0~1之间，二次流流量与主流的比值为0~0.12之间，试验获得了俯仰或偏航单个方向上15°的偏角，俯仰和偏航同时偏转的情况下获得了10°的偏角。其他尝试还包括轴对称收敛-扩张喷管[9]的多轴推力矢量控制研究，目的是实现更好的推力矢量和喷管内流性能。
在激波矢量法中，二次流压比作为输入控制参数，理论上二次流压比越大得到的推力矢量角就越大。在流动形态上，随二次流压比增大，二次流注入位置后侧的流动分离类型从闭式分离向开式分离过渡。当二次流压比增大到一定值以后，所产生的诱导激波会碰到另一侧壁面后发生反射，起到减小推力矢量角的反向作用。激波矢量法的主要特点是可以产生较大的矢量角和较高的矢量效率(设计状态下引射量为1%时矢量偏角3.3°)，但是在超声速区使气流发生偏转，产生大的矢量角时要求喷管工作在过膨胀的状态，因此SVC不仅有激波损失，还存在过膨胀损失，其推力系数一般在0.86~0.94之间。文献[9]提出为解决激波矢量方法的过膨胀流动问题，利用流体注入方法改变喉道面积和喷管膨胀比，减少因过膨胀流动带来的推力损失，但必然会带来控制系统的复杂性。
1.2 喉道偏斜法
喉道偏斜法[11]采用在喷管喉道注入二次流的方法控制气流偏转，避免了激波矢量法由于产生激波带来的流动损失，典型条件下具有更大的推力系数，但获得的推力矢量角小于激波矢量法。2003年Deere等提出的双喉道喷管DTN(Dual Throat Nozzle)的概念[12]，如图 1(b)所示，NASA随后开展了比较广泛的数值计算和地面试验研究[13-16]，喷管形状涉及到二维平面和轴对称外形，结果表明双喉道方法可以在较大压比范围内实现推力矢量。经过对双喉道之间区域流道的优化设计后，获得了比原来喉道偏移法更大的推力矢量效率(引射量为1%时矢量偏角约4°), 并且推力系数也较高(0.92~0.96之间), 实现了较好的综合性能。Deere[12]研究后认为，双喉道方法主流偏转与声速线偏离并无直接关系，对上下游喉道之间的分离区进行控制才是产生大的矢量偏转的真正原因。为了产生大的推力矢量角，应当使二次流的入射角度尽量与主流反向，保持上下游喉道面积相等，同时增大空腔收缩段的角度。为了提高矢量喷管的效率，文献[17]对二维双喉道射流推力矢量喷管的静特性进行了参数化数值研究，比较了双喉道喷管的空腔长度、空腔扩张角、空腔收敛角、上游喉道高度等设计参数对双喉道射流矢量喷管的影响。文献[18]采用径向基神经网络(RBF)和粒子群算法(PSO)对设计参数进行寻优，找出了更好的双喉道气动矢量喷管设计参数组合。在主流压比NPR=4，二次流流量3%条件下，经过优化设计以后的喷管的矢量效率从4.039提高到5.147，同时推力损失系数基本保持不变。
双喉道方法的成功之处在于在喷管喉道处进行二次流控制，减少了激波流动损失；同时去掉了喷管扩张段，让气流膨胀发生在管外，减少了过膨胀流动带来的损失。双喉道方法在提高推力系数的同时也带来了新的问题，由于在喷管喉道引入二次流，减小了喉道面积，造成流动出现壅塞而流量系数减小。文献数据表明，双喉道喷管在典型控制状态下流量系数仅为控制前的84%，这就意味着，在施加推力矢量控制以后，由于流量减小导致发动机推力损失，同时为了维持发动机工作稳定，还必须考虑如何处理多余流量的问题。
1.3 逆流控制方法
如图 1(c)所示，逆流控制方法[19-24]在喷管出口截面的下游加一个外套，形成反向流动的通道，在需要主流偏转时，启动真空泵抽吸系统形成负压，使主气流偏转产生侧向力。逆流方法在出口下游增加固壁延伸面，抽吸喷管主流与固壁面之间的气体形成低压区，使主流发生偏转。由于是对射流在切向上进行控制，具有推力损失小的特点，推力系数约在0.92~0.97之间，被认为是一种有前途的控制方法。Strykowski[21]提出，当逆流速度与主流速度的比值超过临界值时(即U2/U1＜-0.14)，逆流剪切层由对流不稳定转变为绝对不稳定，剪切层内的涡结构和湍动特性增强，是射流偏转的内在机制。Hunter[24]在研究中认为，不管剪切流是同向还是逆向，只要注入的动量通量相等，所产生的推力矢量效果就应该是一样的，Hunter认为套筒壁在吸气侧上的压力分布是驱动推力转向的关键因素，与二次流的方向无关。Flamm[20]的实验细致地测量了矢量角和二次流率的关系，证明同向和逆向二次流都能获得推力转向。
文献[22]对逆流推力矢量的外流影响进行了试验，其中喷管落压比对应的完全膨胀马赫数为Ma=1.4，来流马赫数对应了Ma=0.3、0.5和0.7这3种条件。试验表明，在来流条件下，逆流推力矢量方法可以比较容易地实现矢量角22°的偏转，在相同控制条件下，随来流马赫数的升高，喷管的推力矢量有微弱的减小。逆流推力矢量的工程应用还有许多问题亟待解决，比如采用什么样的吸气装置、流动迟滞效应、大尺寸的后缘板与机身难以融合等，更为严重的是，主流在偏角较大时容易附着于控制面上，导致推力方向的突然变化，给飞行控制带来风险。
1.4 同向二次流控制方法
为了寻找新的控制途径，英国曼彻斯特大学Mason等[25]开展了同向二次流控制的射流推力矢量研究。如图 1(d)所示，该方法利用与主流方向平行的二次射流与壁面Coanda效应，使主流方向发生偏转，在主流马赫数Ma=0.33条件下，获得了推力矢量控制效果，研究认为该方案在主流速度为低亚声速时可以取得很好的控制效率。Banazadeh等[26]在小型涡喷发动机上开展试验研究，在发动机低转速下(5.8×104~7.8×104r/min)实现了推力矢量性能，试验喷管为轴对称外形，具有多轴推力矢量的功能，但随发动机转速升高，射流速度增加，该喷管的矢量控制能力迅速下降。该控制技术被应用到英国无尾飞行器创新研究项目FLAVIIR[27-29](Flapless Air Vehicle Integrated Industrial Research)中，在该项目中Gill[30]探讨了从发动机中引气的方式，作为机翼环量控制和流体推力矢量控制的二次流气源。后来这些技术都集成在验证飞行器Demon上，在2010年进行了演示飞行，但是对流体推力矢量的实际控制能力缺少报道。同向二次流也被用来尝试对高速射流进行控制，Heo[31]通过在喷管下游设置更大的产生Coanda效应的壁面，采用同向二次流的射流控制方法，实现了对超声速主流的射流偏转控制。
2 矢量能力与效率
评价一种流体推力矢量方法包括了喷管的单轴/多轴控制能力、最大矢量角、引气量、推力损失大小等多个方面，在控制效率上主要用以下3个指标进行衡量，一是推力比，即实际推力与理想等熵推力的比值；二是推力矢量效率，即单位引气量所产生的推力矢量角大小；三是流量系数，即实际流量与理想等熵流量的比值。上述指标的理论公式如下所示。
(1) 推力系数[32]：
其中Fr为实际推力，Fi, p与Fi, s分别是主流和次流的等熵推力。
(2) 流量系数[16]：
其中wp和ws分别为主流和次流的质量流量，wi, p为理想主流流量。理想质量流率由喷管喉道面积和总压、总温等参数决定的。
(3) 推力矢量的效率:
单位为°/比流量，其中俯仰矢量偏角δp=
图 2对比了不同流体推力矢量控制方法的推力系数，其中数据来源于公开发表的试验数据[3, 7-9, 15-16, 20]。由于同向二次流控制方法主要适用于控制低速主流，与其他几种方法的适用范围不同，这里没有列入图中进行比较。可以看到，双喉道喷管在低落压比的时候推力系数较高，而激波矢量法和逆流控制方法在落压比较大的时候效率较高。就双喉道喷管来说，喷管设计压比为1.89，出口速度为声速，在大落压比的情况下流动欠膨胀造成推力损失。对于激波矢量法来说，为了使主流能够偏转，喷管的设计压比大于实际流动压比，喷流处于过膨胀流动，流动压比越小过膨胀程度就越大，造成较大的推力损失。
图 3显示的是不同推力矢量方法的矢量效率比较，其中逆流矢量法主要利用真空泵抽吸原理，不同于二次流注入方法，此处不便于进行横向比较。这里矢量效率用吹气量占主流1%时得到的矢量角表示，可以看到双喉道方法具有较高的矢量效率，在压比NPR=1.89~10范围内，矢量效率在3.4°/1%~5.2°/1%之间变化。激波矢量法的矢量效率要整体低于双喉道喷管，从文献收集的数据显示矢量效率覆盖0.8°/1%~3.3°/1%这个区间。图 4给出的是双喉道方法与激波矢量法的流量系数比较，从图中可以看到，激波矢量法的流量系数在0.96以上，远远高于双喉道方法。其中原因是激波矢量法在喷管扩张段进行控制，不改变喷管的喉道面积，对流量的影响较小；相反双喉道法是在喷管喉道位置注入二次流，减小了喷管的最小流通面面积，导致流量减小。由此可见，双喉道方法实现推力矢量是以改变喉道面积为代价，越是要获得大的矢量偏角，二次流注入越强，喷管的实际流量就越小，发动机产生的实际推力也就越小。
![]()
图 3 双喉道方法与激波矢量法的推力矢量效率比较Fig. 3 Comparison of thrust vectoring efficiencies between DTN and SVC![]()
图 4 双喉道方法与激波矢量法的流量系数比较Fig. 4 Comparison of discharge coefficients between DTN and SVC表 1给出了3种流体推力矢量喷管的性能比较，可以看到，3种方法中激波矢量法存在较大的推力损失，矢量效率较低，但是流量系数较大；双喉道方法获得了较大的矢量效率和推力比，唯一存在的不足是流量系数受到很大的限制，对发动机主流的影响很大；逆流方法在3个方面都有较高的指标，但存在抽吸系统过于复杂的不足。
表 1 3种流体推力矢量控制方法的比较Table 1 Comparison of three fluidic thrust vectoring methods控制方法 矢量效率 推力系数 流量系数 缺点 激波法 ＜3.3°/1% 0.86~0.94 ＞0.95 推力损失大 双喉道法 (3.4~5.2)°/1% 0.92~0.96 0.78~0.88 流量系数低 逆流方法 ＞5°/1% 0.92~0.97 ＞0.95 系统复杂 流体推力矢量不同于机械偏转的另一个特点是，实际外流条件下的推力矢量角小于静态条件下测得的矢量角。文献[7]开展了激波矢量法的外流计算，自由来流马赫数Ma=0.3~1.2，喷管的落压比NPR=3.6~7.2，二次流的压比pS/pt=0.6~1.0，结果表明，来流影响会减弱推力矢量性能，减少量从Ma=0.9(NPR=6) 的1.5°到Ma=0.7(NPR=5.2) 的2.9°，推力系数损失则从4%(对应压比3.6) 到0.8%(对应压比7.2)。解决从哪里引气是流体推力矢量面临的另一难题，一个比较可行的办法是从发动机的压缩机段引气。WANG[10]采用三维CFD方法模拟了激波矢量喷管航空发动机耦合的气动性能，结果表明采用风扇出口引气的方式优于从一级压力机引气，后者对发动机性能影响严重，前者从风扇出口引气，当推力矢量角达到19°时，推力减少量在17%以内。
3 新概念流体推力矢量方法
传统流体推力矢量方法目前还存在一些难以解决的瓶颈问题，导致该技术未能在工程实践中推广使用。下面介绍几种完全不同于传统方法的流体推力矢量控制技术，作为流体推力矢量的一种新的尝试，可以为下一步推力矢量发展提供借鉴。
3.1 合成射流控制方法
合成射流技术是一种基于小尺度扰动引起大的宏观效应的主动流动控制技术。Smith和Glezer[33]在1998年用合成射流控制了喷口直径是自身25倍的喷流转向，研究中合成射流方向与喷流方向平行，在合成射流不作用时，喷流沿喷口中心线对称分布，在合成射流作用时，射流致动器所产生的涡环引起主喷流上方的压力降低，导致主喷流向这一侧发生偏转。本文对合成射流控制主流偏转进行了非定常数值模拟，图 5显示的是合成射流控制的涡量云图，其中时间t=0~T/2区间为射流的喷出阶段，可以看到射流在经过特殊设计的喷口喷出以后，右侧涡量分布非常集中，左侧涡量发展受到抑制，在诱导速度作用下绕右侧旋涡旋转。图 6显示的是合成射流控制射流偏转的瞬时速度云图，其中主流速度7m/s，零质量射流的峰值速度34m/s，动量比值为1:10，获得的射流转向角约为30°。文献[34-35]对不同出口构型合成射流激励器开展的射流矢量控制进行了研究，认为低压、合成射流动量以及合成射流对主流流体的卷吸是控制主流偏转的主要原因。
为了提高合成射流控制射流偏转的效果，Park等[36]对出口带有扩张段的圆管流进行了实验研究，其中激励器安装在圆管出口与扩张段的交接位置。实验结果表明，出口下游扩张段可以起到增强掺混的作用，同时有控制射流转向的效果，但是实验仅限于对低速主流进行控制。合成射流控制射流转向试验向人们展示了合成射流控制的奇妙之处，但是将这一技术应用于推力转向还有很远的距离，目前成功的射流转向试验还局限于小速度尺度和低雷诺数情形，要实现对更大尺度的发动机高速尾喷流的控制还存在很大的难度。
3.2 Coanda效应喷管
Coanda效应喷管在喷管出口下游进行矢量偏转控制，通常作法是在喷管出口增加后缘板，利用流体自身的附壁效应，在较小输入能量的前提下实现高速大动量射流的偏转，也可以简称这种方式为后缘板控制。2013年欧盟资助开展了空气柯恩达效应高效射流矢量喷管计划ACHEON(Aerial Coanda High Efficiency Orienting-jet Nozzle project)[37-39]，该研究计划提出利用高速射流在凸表面的Coanda效应和等离子体加速流体延迟分离的作用，提高矢量喷管的偏转效率。研究内容包括对3种物理效应进行研究，分别是高速射流的混合效应、Coanda效应和静电场控制。文献[38]设计了一种双主流的合成射流喷管，如图 7所示，2股主流在喷管喉道前进行汇合并经过收缩-扩张喷管排出，当2股主流存在速度差的时候，合成射流将向速度高的一侧偏转。
在后缘Coanda壁面采用等离子体控制被认为是未来流动控制的一项关键技术，未来有可能用于推力矢量控制。吴云等人[40]对等离子体激励器种类及流动控制应用进行了综述，指出了等离子体气动激励在抑制流动分离、激波控制、管道流动方面的诸多应用，等离子体产生气动激励的物理作用原理包括了动力效应、冲击效应和物性改变。Samimy研究组[41]开展了等离子体对高速高雷诺数管道射流控制的研究，表明等离子体可以在有效促进流动掺混，增大管道出口流动的湍动能，缩短主流核心区长度，降低排气噪声等方面发挥作用。
3.3 引射效应矢量喷管
对高速射流而言，一个重要的特点是具有很强的引射效应，射流速度越大，对周围气体的引射作用越强。基于射流的这种特性，本文提出了一种利用引射效应的推力矢量控制方法[42]。如图 8所示，在主喷管出口下游设置有2块对称的后缘板，在主喷流的引射作用下，两侧气体被不断抽走，同时又从下游以回流形式得到补充。此时主流存在一个非常不稳定的状态，既可能保持中立状态，射流方向保持轴线方向不变，又可能因扰动而发生向上或者向下的偏转，我们把射流的这种行为描述为具有双稳特性[42-44]。在把射流变得十分敏感以后，加入人为扰动可以很容易地实现射流偏转。文献[42]采用改变通气量的方式实现了射流的上下偏转控制，但是不足是射流容易附着到固体壁面，导致射流方向的突然变化。
该控制技术被用于对低速主流进行控制[44]，通过改变控制缝入口面积实现了对主射流偏转的比例控制，在测试条件下主射流最大偏转角可达19°。控制曲线分为了2个区域，敏感区和迟钝区。敏感区的控制曲线近似线性，斜率较大，范围约为±15°；在迟钝区射流靠近壁面，射流方向对控制的响应比较迟缓。由于该方法采用的是被动控制手段，不需要任何能量输入，相对其他方法而言具有自己独特的优势。
上述3种新概念流体推力矢量方法都试图从喷管出口下游进行控制，对主流或者说发动机的干扰较小，代表了流体推力矢量研究的一个新方向。目前这些方法还仅限于在设计条件下进行使用，不能胜任大范围变化压比等复杂流动条件，因此这些方法在走向实际应用之前还有许多障碍需要克服。
4 结束语
流体推力矢量技术由于其潜在的应用价值得到了国内外研究机构的重视，目前这项技术还没有得到工程应用，主要原因是制约喷管性能的影响参数较多，这些参数之间的相互作用关系复杂，控制难度较大。未来随着微型传感器技术、自动控制技术的发展，流体推力矢量也一定会走上前台，在工程实践中发挥作用。本文主要结论如下：
(1) 未来流体推力矢量的发展不仅面临解决飞行器的机动问题，实现单轴(俯仰或偏航方向)或多轴推力矢量控制，还要面临解决无尾布局飞行器的安定性问题，为飞行稳定提供频繁工作的三轴稳定性控制力矩，为实现真正的高气动效率飞行器布局设计提供技术支撑。
(2) 流体推力矢量控制受多种因素影响，除形状参数外，还包括喷管落压比，二次流流量，外流速度等流动参数，这些参数影响喷管的推力比、矢量效率、流量系数大小。流体推力矢量走向工程应用是一个与发动机、与飞行控制相结合的过程，需要解决各项系统参数之间的匹配与衔接问题，而计算机技术、先进传感器与飞行控制技术的发展将有助于解决这些问题。
(3) 机械偏转喷管在改变内流道的同时也改变了喷管周围外流的流动方向。目前流体推力矢量研究主要集中解决内流的偏转问题，对外流影响的研究较少，缺乏减少外流影响的措施。对目前所有流体推力矢量控制来说，都面临外流速度增加导致喷管矢量效率下降的问题，如何解决这一问题也应得到重视。
-
![]()
![]()
![]()
![]()
![]()
![]()
图 10 高速摄像获得的梢涡空化初生位置
Fig. 10 Incipient position of tip vortex cavitation captured by high speed camera
![]()
图 13 总声压级、梢涡空化形态随空化数的变化
Fig. 13 Over all sound pressure level and tip vortex cavity for different cavitation indices
![]()
图 14 涡唱中的单周期梢涡空化形态变化图
Fig. 14 Tip vortex cavity variation during one period in vortex sing
![]()
图 15 梢涡空化涡唱前后的噪声频谱
Fig. 15 The frequency spectrum of cavitation noise with and without vortex sing
![]()
![]()
![]()
![]()
-
[1] ARNDT R E A. Cavitation in fluid machinery and hydraulic structures[J]. Annual Review of Fluid Mechanics, 1981, 13(1):273-326. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=294b4bafb6ef7b32fe609e80fcbf07ae
[2] ARNDT R E A. Cavitation in vertical flows[J]. Annual Review of Fluid Mechanics, 2002, 34(1):143-175.
[3] 潘森森, 彭晓星.空化机理[M].北京:国防工业出版社, 2013:30-89. PAN S S, PENG X X. Physical mechanism of cavitation[M]. Beijing:National Defense Industry Press, 2013:30-89.
[4] KORKUT E, ATLAR M. On the importance of the effect of turbulence in cavitation inception tests of marine propellers[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences, 2002, 458(2017):29-48. DOI: 10.1098/rspa.2001.0852
[5] ZHANG L X, ZHANG N, PENG X X, et al. A review of studies of mechanism and prediction of tip vortex cavitation inception[J]. Journal of Hydrodynamics, 2015, 27(4):488-495. DOI: 10.1016/S1001-6058(15)60508-X
[6] ARNDT R E A, KELLER A P. Water quality effects on cavitation inception in a trailing vortex[J]. Journal of Fluids Engineering, 1992, 114(3):430-438. http://ci.nii.ac.jp/naid/30037587761
[7] ARNDT R E A, MAINES B H. Nucleation and bubble dynamics in vortical flows[J]. Journal of Fluids Engineering, 2000, 122(3):488-493. DOI: 10.1115/1.1286994
[8] ARNDT R E A, MAINES B H. Viscous effects in tip vortex cavitation and nucleation[R]. SAFL Technical Paper 397-Series A, 1994.
[9] UBEROI M S, SHIVAMOGGI B K, CHEN S S. Axial flow in trailing line vortices[J]. Physics of Fluids, 1979, 22(2):214-217. DOI: 10.1063/1.862570
[10] BATCHELOR G K. Axial flow in trailing line vortices[J]. Journal of Fluid Mechanics, 1964, 20(4):645-658. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=35361a04e6a04bd013831039e8749bc8
[11] FRUMAN D H, CERRUTTI P, PICHON T, et al. Effect of hydrofoil planform on tip vortex roll-up and cavitation[J]. Journal of Fluids Engineering, 1995, 117(1):162-169. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=fbdf5a62b4ebb97e7517cd50aa6637ee
[12] FRUMAN D H. Recent progress in the understanding and prediction of tip vortex on a rectangular hydrofoil[C]//Proc of the 2nd International Symposium on Cavitation. 1994.
[13] FRUMAN D H, DUGUE C, PAUCHET A, et al. Tip vortex roll-up and cavitation[C]//Proc of the 19th Symposium on Naval Hydrodynamic. 1992.
[14] FRUMAN D H, PICHON T, CERRUTTI P. Effect of a drag-reducing polymer solution ejection on tip vortex cavitation[J]. Journal of Marine Science and Technology, 1995, 1(1):13-23. DOI: 10.1007/BF01240009
[15] BOULON O, CALLENAERE M, FRANC J, et al. An experimental insight into the effect of confinement on tip vortex cavitation of an elliptical hydrofoil[J]. Journal of Fluid Mechanics, 1999, 390:1-23. DOI: 10.1017/S002211209900525X
[16] KATZ J, GALDO J B. Effect of roughness on rollup of tip vortices on a rectangular hydrofoil[J]. Journal of Aircraft, 1989, 26(3):247-253. DOI: 10.2514/3.45753
[17] STINEBRING D R, FARRELL K J, BILLET M L. The structure of a three-dimensional tip vortex at high Reynolds numbers[J]. Journal of Fluids Engineering, 1991, 113(3):496-503. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=JFEGA4000113000003000496000001&idtype=cvips&gifs=Yes
[18] RAN B, KATZ J. Pressure fluctuations and their effect on cavitation inception within water jets[J]. Journal of Fluid Mechanics, 1994, 262:223-263. DOI: 10.1017/S0022112094000492
[19] SOUDERS W G, PLATZER G P. Tip vortex cavitation characteristics and delay of inception on a three-dimensional hydrofoil[R]. DTNSRDC-81/007, 1981.
[20] BRIANÇON-MARJOLLET L, MERLE L. Inception, develop-ment, and noise of a tip vortex cavitation[C]//Proc of the 21st Symposium on Naval Hydrodynamic. 1996.
[21] MAINES B H, ARNDT R E A. Tip vortex formation and cavitation[J]. Journal of Fluids Engineering, 1997, 119(2):413. http://www.researchgate.net/publication/277499680_Tip_Vortex_Formation_and_Cavitation
[22] FRANC J P, MICHEL J M. Fundmentals of cavitation[M]. Dordrecht, Netherlands: Fluwer Academic Publishers, 2004.
[23] 姜树海.含气量对梢涡初生空化的影响[J].水利水运科学研究, 1989(2):53-62. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000002790038 JIANG S H. Influence of gas content on tip vortex cavitation inception[J]. Scientific Research on Water Conservancy and Transportation, 1989(2):53-62. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000002790038
[24] 彭晓星, 王力, 潘森森.水中空气含量对旋涡空化的影响[J].水动力学研究与进展, 1989, 4(4):60-68. http://www.cqvip.com/QK/94099X/19894/140627.html PENG X X, WANG L, PAN S S. Air content effect on the vortex cavitation[J]. Journal of Hydrodynamics, 1989, 4(4):60-68. http://www.cqvip.com/QK/94099X/19894/140627.html
[25] ZHANG L X, CHEN L Y, SHAO X M. The migration and growth of nuclei in an ideal vortex flow[J]. Physics of Fluids, 2016, 28(12):123305. DOI: 10.1063/1.4972275
[26] PENG X X, XU L H, CAO Y T. The study of tip vortex flow and cavitation inception on an elliptical hydrofoil[C]//Proc of the 5th International Symposium on Marine Propulsion. 2017: 590-595.
[27] PENG X X, XU L H, LIU Y W, et al. Experimental measurement of tip vortex flow field with/without cavitation in an elliptic hydrofoil[J]. Journal of Hydrodynamics, 2017, 29(6):939-953. DOI: 10.1016/S1001-6058(16)60808-9
[28] 刘玉文.梢隙流动及梢隙空化的实验研究[D].无锡: 中国船舶科学研究中心, 2017. LIU Y W. Experimental research of tip leakage flow and cavitation[D]. Wuxi: China Ship Scientific Research Center, 2017.
[29] 潘森森.空化核与空化起始[J].中国造船, 1989, 30(3):3-16. http://www.cnki.com.cn/Article/CJFDTotal-ZGZC198903000.htm PAN S S. Cavitation nuclei and cavitation inception[J]. Ship Building of China, 1989, 30(3):3-16. http://www.cnki.com.cn/Article/CJFDTotal-ZGZC198903000.htm
[30] CHAHINE G L. Nuclei effects on cavitation inception and noise[C]//Proc of the 25th Symposium on Naval Hydrodynamics. 2004.
[31] BOULON O, FRANC J P, MICHEL J M. Tip vortex cavitation on an oscillating hydrofoil[J]. Journal of Fluids Engineering, 1997, 119(4):752-758. DOI: 10.1115/1.2819494
[32] ARAKERI V H, HIGUCHI H, ARNDT R E A. A model for predicting tip vortex cavitation characteristics[J]. Journal of Fluids Engineering, 1988, 110(2):190-193. DOI: 10.1115/1.3243533
[33] ARNDT R E A, ARAKERI V H, HIGUCHI H. Some observations of tip-vortex cavitation[J]. Journal of Fluid Mechanics, 1991, 229:269-289. DOI: 10.1017/S0022112091003026
[34] 刘玉文, 徐良浩, 张国平, 等.梢隙流动空化初生及空化形态观测研究[J].水动力学研究与进展:A辑, 2017, 32(6):671-679. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sdlxyjyjz201706002 LIU Y W, XU L H, ZHANG G P, et al. Observation andresearch onthe cavitation inception and cavitation structure of tip leakage flow[J]. Journal of Hydrodynamics, 2017, 32(6):671-679. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sdlxyjyjz201706002
[35] SONG M T, XU L H, PENG X X, et al. An acoustic approach to determine tip vortex cavitation inception for an elliptical hydrofoil considering nuclei-seeding[J]. International Journal of Multiphase Flow, 2017, 90:79-87. DOI: 10.1016/j.ijmultiphaseflow.2016.12.008
[36] HIGUCHI H, ARNDT R E A, ROGERS M F. Characteristics of tip vortex cavitation noise[J]. Journal of Fluids Engineering, 1989, 111(4):495-501. DOI: 10.1115/1.3243674
[37] MAINES B H, ARNDT R E A. The case of the singing vortex[J]. Journal of Fluids Engineering, 1997, 119(2):271-276. DOI: 10.1115/1.2819130
[38] 姜树海.梢涡的初生空化及其发生位置[J].水动力学研究与进展, 1989, 4(1):13-22. http://www.cnki.com.cn/Article/CJFDTotal-SDLJ198901002.htm JIANG S H. Estimation of tip vortex cavitation inception and its location[J]. Journal of Hydrodynamics, 1989, 4(1):13-22. http://www.cnki.com.cn/Article/CJFDTotal-SDLJ198901002.htm
[39] HSIAO C T, CHAHINE G L. Scaling of tip vortex cavitation inception for a marine open propeller[C]//Proc of the 27th Symposium on Naval Hydrodynamics. 2008.
[40] STROBL T, HUBER R, KELLER A P. Cavitation scale effects and case studies on cavitation model tests[J]. International Journal on Hydropower & Dams, 2005, 12(1):86-90. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=103ac74bef1d51b89e9a0ff591967ecb
[41] KUIPER G, VAN TERWISGA T J C, ZONDERVAN G J, et al. Cavitation inception tests on a systematic series of two-bladed propellers[C]//Proc of the 26th Symposium on Naval Hydrodynamics. 2006.
[42] SONG M T, XU L H, PENG X X, et al. Acoustic modeling of the singing vortex and its sound signatures[J]. International Journal of Multiphase Flow, 2018, 99:205-212. DOI: 10.1016/j.ijmultiphaseflow.2017.10.007
[43] 顾湘男, 曾志波, 彭晓星, 等.三维水翼梢涡空泡和片空泡的雷诺数影响试验研究[J].中国造船, 2017, 58(1):28-37. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgzc201701004 GU X N, ZENG Z B, PENG X X, et al. Experimental investigation of the scale effect of Reynolds number for tip vortex cavitation and sheet cavitation around a three-dimensional hydrofoil[J]. Ship Building of China, 2017, 58(1):28-37. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgzc201701004
-
期刊类型引用(16)
1. 王海峰. 高性能战斗机与发动机协同设计关键技术. 航空学报. 2024(05): 33-54 . 
百度学术
2. 王新恺，项坤，田晶，赵建策，李文灏，庞博文. 轴对称矢量喷管平移控制系统运动学建模仿真. 机械科学与技术. 2024(04): 729-736 . 百度学术
3. 陈家兴，姬永超，白云，王刚，武锐，展杰，赵猛. 基于喷管二次流控制的推力矢量特性研究. 固体火箭技术. 2024(03): 321-330 . 百度学术
4. 何敬玉，杨志晨，梁温馨，欧平，董金刚. 双喉道推力矢量喷管内外流特性. 气体物理. 2024(05): 54-64 . 百度学术
5. 王旭飞，杨青真，贺榆波，向惠敏，张赛乐. S弯D形矢量喷管参数化设计及气动特性研究. 推进技术. 2023(09): 45-57 . 百度学术
6. 仇梓豪，李子焱，周楷文，王士奇，刘应征，温新. 振荡射流控制方法在无舵面飞行控制中的应用. 实验流体力学. 2023(04): 116-125 . 本站查看
7. 舒博文，黄江涛，高正红，何成军，夏露. 引气位置对旁路式二元激波矢量喷管性能影响. 气体物理. 2023(05): 19-27 . 百度学术
8. 刘沛聪，周楷文，王士奇，温新. 振荡射流气动矢量喷管参数影响特性的试验研究. 航空科学技术. 2023(10): 9-16 . 百度学术
9. 张鉴予，杜海，范嘉康，王天宇，王可心，李婧，胡佳玉. 基于双级二次流射流的流体推力矢量偏转控制. 西华大学学报(自然科学版). 2023(06): 43-50+67 . 百度学术
10. 许奇，权晓波，魏海鹏，鲍文春. 水下推力矢量控制技术研究现状及进展. 兵器装备工程学报. 2022(01): 27-34 . 百度学术
11. 佟川，李昂贤，王启材，张琦祥，许兰迪，王炫. 基于Coanda效应的无源流体推力矢量喷管研究. 科技资讯. 2021(09): 94-96 . 百度学术
12. 瞿丽霞，李岩，白香君. 流体推力矢量技术的应用验证研究进展. 航空科学技术. 2020(05): 64-72 . 百度学术
13. 王杰. 射流推力矢量技术的研究现状与发展. 科技与创新. 2020(10): 81-83+85 . 百度学术
14. 王海峰. 战斗机推力矢量关键技术及应用展望. 航空学报. 2020(06): 20-43+3 . 百度学术
15. 龚东升，顾蕴松，周宇航，史楠星. 基于微型涡喷发动机热喷流的无源流体推力矢量喷管的控制规律. 航空学报. 2020(10): 106-117 . 百度学术
16. 林泳辰，徐惊雷，韩杰星，黄帅，汪阳生. 气动推力矢量无舵面飞翼的飞行实验. 航空动力学报. 2019(03): 701-707 . 百度学术
其他类型引用(23)
下载:
计量
- 文章访问数: 259
- HTML全文浏览量: 168
- PDF下载量: 45
- 被引次数: 39
