Mach number sensitivity analysis of cavity noise
-
摘要: 敏感度分析在评估参数的重要程度以及计算不确定度方面具有重要作用。通过风洞试验开展了亚跨超声速下的空腔噪声马赫数敏感性研究。亚跨声速下,通过调节调压阀的开度改变马赫数,马赫数名义增量为0.010。超声速下,通过改变模型迎角实现马赫数的连续变化,迎角增量为1°。利用总压耙测量空腔入口马赫数。结果表明:空腔后部测点脉动压力系数在亚跨声速下随着马赫数的增加而增加,而在超声速下随着马赫数的增加而减小。跨声速下,脉动压力系数对马赫数的敏感性导数最大。不考虑模态切换的情况下,不同速域的主导声模态St对马赫数的敏感性导数均为负数。主导声模态谱峰在亚声速下随着马赫数的增加而增加,而在超声速下随着马赫数的增加而降低。敏感度研究结果不仅可用于内埋武器舱气动噪声载荷的不确定度评估,也有助于更好地认识空腔噪声特性。Abstract: Sensitivity analysis plays an important role in assessing the importance of parameters and calculating the uncertainty. Mach number sensitivity analysis of cavity noise at subsonic, transonic and supersonic speed has been investigated by wind tunnel experiments in this study. At subsonic speed, the Mach number is changed by adjusting the opening of the valve, and the nominal increment of the Mach number is 0.01.At supersonic speed, the continuous change of the Mach number is achieved by changing the angle of attack of the model, and the increment of angle of attack is 1 degree. The experimental results show that the fluctuating pressure coefficient at the rear of the cavity increases with the increase of the Mach number at the subsonic speed, while decreases with the increase of the Mach number at the supersonic speed. At transonic speed, the fluctuating pressure coefficient has the largest sensitivity derivative to the Mach number. In the case of modal switching, the derivative of St to Mach number for the dominant acoustic mode is negative. The peak value of the dominant acoustic mode's power spectral density increases with the increase of Mach number at subsonic speed, while decreases at supersonic speed. The obtained sensitivity results can be used not only for the uncertainty assessment of the aerodynamic noise load in the embedded weapon bay, but also for a better understanding of the cavity noise characteristics.
-
Keywords:
- cavity flows /
- noise /
- Mach number /
- sensitivity analysis /
- wind-tunnel experiments
-
0 引言
敏感性分析是一种研究模型中参数的小量变化对其他指标影响程度的分析方法。通过敏感性分析可以定量得到参数的敏感性导数,从而用于评估各参数的重要程度以及计算不确定度。该方法在武器装备性能评估[1-2]、工程结构设计[3-4]、石油开采[5]和气动外形优化[6-7]等方面应用较为广泛。
罗鹏程等[8]指出武器装备敏感性分析可用于评估武器装备的重要程度,是确定武器装备发展建设重点的依据。金镭等[9]通过敏感性分析获得了战斗机性能指标与国外先进飞机之间的差距,为战斗机的改型优化指明了方向。唐冕等[10]针对大跨度自锚式悬索桥结构,建立了基于桥梁多振型耦合的气动参数敏感性分析理论和方法。西北工业大学的徐林程等[11-12]采用自动微分方法获得了翼型压力系数对迎角、马赫数、雷诺数和几何外形的敏感性导数,其中,马赫数的敏感性导数明显高于其他参数。Albring等[13]利用开源代码SU2计算了M6机翼的阻力系数敏感度分布,计算结果显示激波附近区域对阻力的贡献最大。Yang等[14]基于翼型的敏感度信息和梯度算法对NACA0012翼型进行了优化,使阻力降低83%。Liu等[15]采用随机配置法对高超声速飞行器进气道流场计算结果进行了分析,得到了迎角、马赫数、雷诺数、来流温度和壁面温度等参数对压力场的不确定度和敏感度的影响,为进气道性能评估提供了可靠的数据支撑。
尽管数值计算在稳态流动的敏感性分析方面取得了巨大的进步,但是对于非定常流动,数值计算仍面临计算量难以承受、收敛性差等问题。因此,发展基于风洞试验的非定常流动敏感性分析方法显得尤为重要。
空腔流动是一种典型的大分离非定常流动,开展空腔流动的敏感性分析试验对内埋武器舱气动噪声载荷的不确定度评估具有重要的应用价值。近年来,人们在空腔流动参数影响研究方面开展了大量的工作。Plentovich等[16]通过在平板上粘贴金刚砂来改变空腔入口湍流边界层厚度,分析了边界层厚度变化对空腔流动特性的影响。Thangamani等[17]通过改变模型尺寸研究了雷诺数对空腔噪声的影响。Merrick[18]开展了马赫数为1.43、1.84和2.22的超声速空腔流动风洞试验,分析了马赫数对峰值噪声频率的影响。这些研究工作主要通过离散地改变试验参数(试验参数的相对变化量大于10%)来研究空腔流动参数影响,尚未发展出可连续改变试验参数(试验参数的相对变化量在1%左右)的敏感性试验方法。
本文综合采用调节调压阀的开度和变模型迎角的方法实现了亚、跨、超声速下马赫数的连续变化。开展了0.6、0.9和2.0等3个典型马赫数下的空腔噪声敏感性分析,计算了脉动压力系数、主导声模态St和谱峰对马赫数的敏感性导数。敏感度研究结果不仅可用于内埋武器舱气动噪声载荷的不确定度评估,也有助于更好地认识空腔噪声特性。
1 试验方法
1.1 风洞设备
试验在中国空气动力研究与发展中心FL-32直流暂冲式跨超声速风洞中完成。该风洞马赫数范围为0.3~4.0,雷诺数范围为(3.3~89.0)×106 m-1,试验段截面为0.6 m×0.6 m的矩形。超声速下,试验段四周均为实壁;亚跨声速下,将试验段上下壁板更换为槽壁。
1.2 空腔试验模型
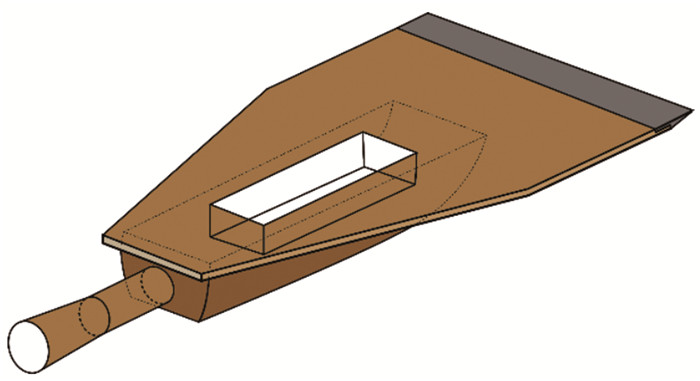
试验模型采用中国空气动力研究与发展中心设计的C201标准空腔模型[19-20],如图 1所示。该模型由平板、腔体和盖板三部分组成。空腔模型前缘为可更换的安装块,在亚跨声速条件下采用椭圆形前缘以消除前缘流动分离,在超声速条件下采用尖劈外形以避免形成头部激波,从而有效避免了前缘分离和脱体激波等对下游空腔流动的干扰。试验过程中,模型通过支杆与试验段迎角机构连接,可实现迎角的连续变化。
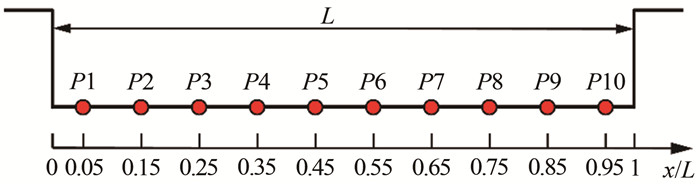
C201空腔模型总长514 mm,宽320 mm。腔体长度、深度和宽度分别为200.0、33.3和66.7 mm。空腔几何长深比为6,属于典型的开式空腔流动。为了获取腔内噪声特性,在空腔底部中轴线上等距离布置了10个脉动压力传感器,如图 2所示。传感器型号为Kulite公司生产的XCE-062压阻式传感器,其量程为30 psi,传感器采样频率为50 kHz。试验过程中,采样持续时间设为10 s。
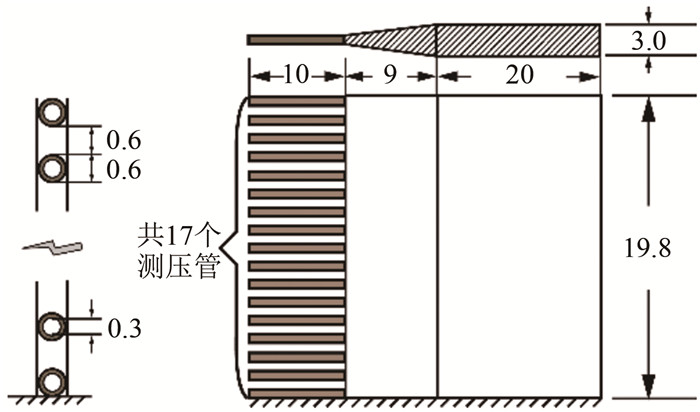
亚跨超声速下,利用总压耙(见图 3)测量空腔入口马赫数。总压耙是一种用于测量湍流边界层内速度分布的试验装置,安装在空腔上游5 mm处。总压耙的高度为19.8 mm,共17个总压测孔,测压管外径为0.6 mm,内径为0.3 mm, 为了降低激波干扰,孔与孔之间间隔一个孔的距离。静压测点布置在平板上,用于测量边界层静压。静压测点的流向位置与总压耙相同,展向距离总压耙约5 mm,以减小总压耙对边界层内静压分布的干扰。
1.3 马赫数敏感性试验方法
亚跨声速下,FL-32风洞采用收缩喷管,可通过调节上游调压阀的开度,连续改变试验段入口总压和马赫数。超声速下,FL-32风洞采用收缩-扩张喷管,试验段入口马赫数完全由喷管型面确定。喷管型面的调试需要花费大量的人力物力,且维护使用成本高,因此超声速风洞可供使用的喷管数量十分有限,通过更换喷管难以做到马赫数的连续变化。本文从C201空腔模型的特点出发,提出了一种通过改变模型迎角实现空腔入口马赫数连续变化的方法。试验中通过调节模型迎角,在平板前缘形成不同扩张(或压缩)角的膨胀(或弱压缩)波,气流经过平板前缘的膨胀(或弱压缩)波后,马赫数将升高(或降低)。
由于马赫数测量装置会对空腔流动产生干扰,因此马赫数测量试验和脉动压力测量试验分开进行。亚跨声速下,采用连续变马赫数的吹风方式开展试验,马赫数名义增量为0.010。超声速下,通过连续变迎角的方式改变马赫数,迎角增量为1°。
2 数据处理方法
2.1 马赫数计算方法
根据亚声速的等熵关系式和超声速的激波关系式,求解式(1)的非线性方程,可计算得到总压耙第i测点处的马赫数Mai。

(1) 式中,pi为总压耙第i测点处的总压,ps为边界层静压。
前期边界层测量试验结果[20]表明,不同马赫数下入口边界层厚度一般在5 mm以内,第6测点以上的测压管处于自由来流均匀区域。本次试验选择远离物面10个测点的平均值作为空腔入口马赫数Ma。

(2) 2.2 噪声数据处理方法
首先,滤除压力时序数据p(n)中的平均成分p,得到脉动压力序列p′(n):

(3) 其中,p为p(n)的算术平均值,N为样本总量。压力的脉动程度一般用压力脉动量的均方根来表示:

(4) 其无量纲形式为:

(5) 其中,ρ∞为空腔入口处来流密度,U∞为空腔入口处来流速度。
然后,通过Burg方法计算脉动压力信号的功率谱密度函数PSD(f)。其中f为频率,其无量纲形式为:

(6) 其中,St为斯特劳哈尔数,L为空腔长度。脉动压力功率谱密度无量纲形式psd(St)为:

(7) 2.3 敏感性导数计算方法
采用最小二乘法计算敏感性导数,变量y对变量x的敏感性导数为:

(8) 其中,(xi, yi)为第i个样本点。
3 试验结果分析
3.1 马赫数测量结果
在亚声速(Ma=0.6)、跨声速(Ma=0.9)和超声速(Ma=2.0)下开展了空腔噪声的马赫数敏感性研究试验。亚跨声速下采用连续变马赫数吹风,超声速下采用连续变迎角吹风,通过总压耙实际测量得到的马赫数序列如表 1所示。亚跨声速下,马赫数增量约为0.010;超声速下,马赫数增量约为0.037。
表 1 马赫数测量结果Table 1 Mach numbers measured by boundary layer probesMa1 Ma2 Ma3 Ma4 亚声速 0.5785 0.5899 0.5992 0.6087 跨声速 0.8802 0.8905 0.9000 0.9106 超声速 1.9740 2.0102 2.0471 2.0843 3.2 脉动压力系数的敏感性分析
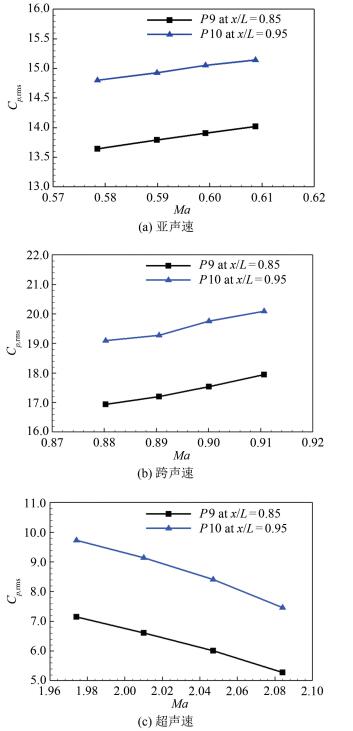
图 4展示了亚跨超声速下空腔脉动压力系数随马赫数的变化曲线。2条曲线分别对应图 2中的P9和P10测点。这2个测点位于压力脉动剧烈的空腔后部,具有一定的代表性。从图 4可以看出,在亚声速和跨声速下,P9和P10测点脉动压力系数随着马赫数的增加而增加,而超声速下,脉动压力系数随马赫数的增加而减小。Hankey等[21]开展了空腔流动的线性稳定性分析,获得了不同马赫数下的扰动增长率曲线。分析结果表明,马赫数从0增长至1左右时,扰动增长率逐渐升高,而马赫数从1增长至2.5时,扰动增长率逐渐降低。本文试验得到的腔内脉动压力变化趋势与Hankey等得到的扰动增长率曲线一致。线性不稳定性对空腔前缘剪切层内扰动的发展起着重要作用,从而对空腔压力脉动产生重要影响,因此扰动增长率和腔内脉动压力的变化趋势往往保持一致。在低马赫数下,剪切层中低速运动的大尺度旋涡与空腔后壁碰撞产生的声波强度较弱,从而导致以声波为主要载体的反馈回路难以建立,腔内噪声水平低,脉动压力系数小。随着马赫数的增加,在空腔后缘产生的声波强度逐渐增强,声反馈回路越来越稳固,流声耦合使得空腔噪声明显升高,脉动压力系数也随之升高。然而,随着马赫数的进一步增加,可压缩性随之增大,大尺度拟序涡结构逐步消失,三维小尺度涡结构逐渐增多[22],剪切层与空腔后壁撞击产生的声波强度逐渐下降,空腔噪声和脉动压力系数也随之降低。
图 5展示了亚跨超声速下空腔内不同测点脉动压力系数对马赫数的敏感性导数。通过对比可以看到,空腔后部的敏感性导数更大,主要原因在于剪切层与空腔的碰撞发生在空腔尾缘,空腔后部区域的噪声声压级最大,对流场参数的变化也最敏感。在亚跨声速下,脉动压力系数对马赫数的敏感导数有正也有负,不同测点对马赫数变化的响应并不完全相同。而超声速下,脉动压力系数对马赫数的敏感导数全部为负数,各位置测点脉动压力系数随马赫数的增加而一致减小。此外,跨声速下,脉动压力系数对马赫数的敏感性导数最大,这也表明空腔流动在跨声速区域对马赫数的变化最为敏感。
3.3 主导声模态St的敏感性分析
随着马赫数的变化,空腔内声模态的分布也会随之调整。空腔流动一般含有多种模态,而其中的主导模态蕴含的能量最大,也是人们最为关心的模态。下面,对主导声模态St开展马赫数敏感性分析。
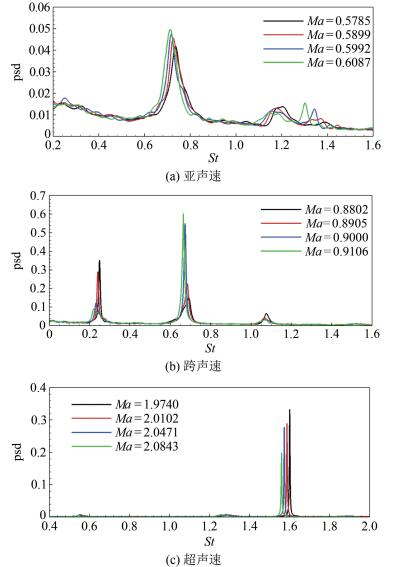
图 6展示了亚跨超声速下空腔后部测点(P10)脉动压力功率谱随马赫数的变化趋势。亚声速和超声速下,空腔主导声模态分别为2阶和5阶Rossiter模态。而跨声速下,空腔主导声模态随着马赫数的变化从1阶切换到2阶。从图 7和表 2可以看出,在不考虑模态切换的情况,不同速域下,随着马赫数的增加,主导声模态St均随之减小,主导模态St对马赫数的敏感性导数均为负数。Rossiter[23]提出的空腔声模态频率预估公式(
 表 2 主导模态St对马赫数的敏感性导数Table 2 Sensitivity of St numbers to Mach numbers
表 2 主导模态St对马赫数的敏感性导数Table 2 Sensitivity of St numbers to Mach numbers∂St/∂Ma 亚声速(Ma=0.60) -0.794 跨声速(Ma=0.90) -1.011(Mode 1), -0.889(Mode 2) 超声速(Ma=2.00) -0.369 其他研究中也发现了类似的主导模态的切换现象。Chandra等[24]在其超声速空腔试验中首次发现了这种主导模态频率的“突跳”现象。Wang等[25]进一步指出, 在一定的条件下,连续改变来流速度或空腔长度,均可能引起空腔主导模态频率的跳跃式变化。
3.4 主导声模态谱峰的敏感性分析
马赫数不仅影响声模态频率,也会影响各阶模态的能量分布。下面开展主导声模态谱峰的马赫数敏感性分析,研究马赫数变化对声模态能量的影响。
图 8为亚跨超声速下空腔底部P10测点的主导声模态谱峰随马赫数的变化曲线。其中,跨声速下, 由于主导声模态发生了切换,因此针对切换前后的2种模态都绘制了曲线。可以看到, 亚声速下,随着马赫数的增加,主导声模态谱峰升高;而超声速下,随着马赫数的增加,主导声模态谱峰降低,这一规律与脉动压力系数的变化趋势一致;跨声速下,随着马赫数的增加,1阶模态谱峰降低,而2阶模态谱峰升高,能量在不同模态之间发生了迁移。
表 3列举了亚跨超声速下,不同模态谱峰对马赫数的敏感性导数。亚跨声速下,谱峰对马赫数的敏感导数有正也有负,表明不同模态在发生竞争,随着马赫数的变化,能量在不同模态之间重新分配;而超声速下,谱峰对马赫数的敏感导数全部为负数,表明全部模态的能量随着马赫数的增加而降低,这一现象对开展超声速空腔噪声控制有一定的启发意义,可以考虑通过增大入口马赫数的方法来抑制峰值噪声。
表 3 主导声模态谱峰对马赫数的敏感性导数Table 3 Sensitivity of peak value of normalized pressure spectral density to Mach numbersMode 1 Mode 2 Mode 3 Mode 4 Mode 5 亚声速 — 0.252 -0.092 0.308 — 跨声速 -9.467 16.449 -0.844 — — 超声速 -0.014 -0.020 -0.008 -0.029 -1.129 4 结论
本文针对亚跨超声速下特定马赫数区间内的空腔噪声特性开展了马赫数敏感性研究试验。在当前研究的马赫数区间内,结论如下:
(1) 空腔后部测点脉动压力系数在亚跨声速下随着马赫数的增加而增加,而超声速下随着马赫数的增加而减小。跨声速下,脉动压力系数对马赫数的敏感性导数最大,表明空腔流动在跨声速区域对马赫数的变化最为敏感。
(2) 不考虑模态切换的情况下,不同速域的主导声模态St对马赫数的敏感性导数均为负数。
(3) 主导声模态谱峰在亚声速下随着马赫数的增加而增加,而超声速下随着马赫数的增加而降低。
(4) 超声速下,各阶模态谱峰对马赫数的敏感导数均为负数,表明马赫数的增加将导致各阶声模态能量降低。
-
表 1 马赫数测量结果
Table 1 Mach numbers measured by boundary layer probes
Ma1 Ma2 Ma3 Ma4 亚声速 0.5785 0.5899 0.5992 0.6087 跨声速 0.8802 0.8905 0.9000 0.9106 超声速 1.9740 2.0102 2.0471 2.0843 表 2 主导模态St对马赫数的敏感性导数
Table 2 Sensitivity of St numbers to Mach numbers
∂St/∂Ma 亚声速(Ma=0.60) -0.794 跨声速(Ma=0.90) -1.011(Mode 1), -0.889(Mode 2) 超声速(Ma=2.00) -0.369 表 3 主导声模态谱峰对马赫数的敏感性导数
Table 3 Sensitivity of peak value of normalized pressure spectral density to Mach numbers
Mode 1 Mode 2 Mode 3 Mode 4 Mode 5 亚声速 — 0.252 -0.092 0.308 — 跨声速 -9.467 16.449 -0.844 — — 超声速 -0.014 -0.020 -0.008 -0.029 -1.129 -
[1] 董雪, 张德平.基于极限学习机的武器装备作战效能全局敏感性分析[J].计算机与现代化, 2018(5):86-92. DOI: 10.3969/j.issn.1006-2475.2018.05.018 DONG X, ZHANG D P. Global sensitivity analysis and optimization of submarine combat effectiveness based on extreme learning machine[J]. Computer and Modernization, 2018(5):86-92. DOI: 10.3969/j.issn.1006-2475.2018.05.018
[2] 周智超.面向武器装备系统效能的敏感性分析[J].火力与指挥控制, 2013, 38(2):98-102. DOI: 10.3969/j.issn.1002-0640.2013.02.026 ZHOU Z C. Sensitivity analysis of oriented to system effectiveness of weapons and equipment[J]. Fire Control & Command Control, 2013, 38(2):98-102. DOI: 10.3969/j.issn.1002-0640.2013.02.026
[3] 李永乐, 苏茂材, 王士刚, 等.大跨度钢桁梁铁路斜拉桥刚度参数敏感性分析[J].振动与冲击, 2015, 34(2):166-170. http://d.old.wanfangdata.com.cn/Periodical/zdycj201502030 LI Y L, SU M C, WANG S G, et al. Sensitivity of structural stiffness parameters of long-span steel truss cable-stayed railway bridge[J]. Journal of Vibration and Shock, 2015, 34(2):166-170. http://d.old.wanfangdata.com.cn/Periodical/zdycj201502030
[4] 李加武, 方成, 侯利明, 等.大跨径桥梁静风稳定参数的敏感性分析[J].振动与冲击, 2014, 33(4):124-130. DOI: 10.3969/j.issn.1000-3835.2014.04.023 LI J W, FANG C, HOU L M, et al. Sensitivity analysis for aerostatic stability parameter of a long-span bridge[J]. Journal of Vibration and Shock, 2014, 33(4):124-130. DOI: 10.3969/j.issn.1000-3835.2014.04.023
[5] 李宪文, 刘锦, 郭钢, 等.致密砂岩储层渗吸数学模型及应用研究[J].特种油气藏, 2017, 24(6):79-83. DOI: 10.3969/j.issn.1006-6535.2017.06.015 LI X W, LIU J, GUO G, et al. Mathematical model of imbibition and its application in tight sandstone reservoir[J]. Special Oil & Gas Reservoirs, 2017, 24(6):79-83. DOI: 10.3969/j.issn.1006-6535.2017.06.015
[6] 杨旭东, 乔志德, 朱兵.升力系数不变时跨音速机翼阻力优化设计[J].计算物理, 2003, 20(3):233-238. DOI: 10.3969/j.issn.1001-246X.2003.03.009 YANG X D, QIAO Z D, ZHU B. Optimization design of transonic wings with drag reduction and constant lift coefficients[J]. Chinese Journal of Computation Physics, 2003, 20(3):233-238. DOI: 10.3969/j.issn.1001-246X.2003.03.009
[7] 江奕廷, 白俊强, 孙智伟.基于参数敏感性分析的反设计方法[J].航空计算技术, 2012, 42(6):65-69. DOI: 10.3969/j.issn.1671-654X.2012.06.017 JIANG Y T, BAI J Q, SUN Z W. Inverse airfoil design based on sensitive analysis of parameterized methods[J]. Aeronautical Computing Technique, 2012, 42(6):65-69. DOI: 10.3969/j.issn.1671-654X.2012.06.017
[8] 罗鹏程, 傅攀峰.武器装备敏感性分析方法综述[J].计算机工程与设计, 2008, 29(21):5546-5549. http://d.old.wanfangdata.com.cn/Periodical/jsjgcysj200821042 LUO P C, FU P F. Review on weapons and equipment sensitivity analysis methods[J]. Computer Engineering and Design, 2008, 29(21):5546-5549. http://d.old.wanfangdata.com.cn/Periodical/jsjgcysj200821042
[9] 金镭, 张曙光, 孙金标.现代战斗机空战能力评估及敏感性分析[J].北京航空航天大学学报, 2009, 35(1):82-86. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bjhkhtdxxb200901020 JIN L, ZHANG S G, SUN J B. Air-combat ability and sensitivity analysis of modern fighter aircraft[J]. Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(1):82-86. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bjhkhtdxxb200901020
[10] 唐冕, 陈政清.大跨径自锚式悬索桥气动参数的敏感性分析[J].湖南科技大学学报(自然科学版), 2008, 23(1):55-59. http://d.old.wanfangdata.com.cn/Periodical/xtkyxyxb200801013 TANG M, CHEN Z Q. Sensitivity analysis of aerodynamic parameter for long-span self-anchored suspension bridges[J]. Journal of Hunan University of Science & Technology, 2008, 23(1):55-59. http://d.old.wanfangdata.com.cn/Periodical/xtkyxyxb200801013
[11] 徐林程, 王刚, 武洁, 等.翼型模型几何误差对气动性能影响的自动微分分析方法[J].空气动力学学报, 2014, 32(4):551-556. DOI: 10.7638/kqdlxxb-2013.0097 XU L C, WANG G, WU J, et al. An automatic differentiation method for uncertainty analysis due to airfoil configuration variation[J]. Acta Aerodynamica Sinica, 2014, 32(4):551-556. DOI: 10.7638/kqdlxxb-2013.0097
[12] 徐林程, 王刚, 武洁, 等.翼型风洞试验中不确定性分析的自动微分方法[J].航空学报, 2014, 35(8):2102-2111. http://d.old.wanfangdata.com.cn/Periodical/hkxb201408003 XU L C, WANG G, WU J, et al. Uncertainty analysis of airfoil wind tunnel tests with automatic differentiation[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(8):2102-2111. http://d.old.wanfangdata.com.cn/Periodical/hkxb201408003
[13] ALBRING T A, SAGEBAUM M, GAUGER N R. Efficient aerodynamic design using the discreteadjoint method in SU2[R]. AIAA-2016-3518, 2016.
[14] YANG G D, RONCH A D. Aerodynamic shape optimisation of benchmark problems using SU2[R]. AIAA-2018-0412, 2018.
[15] LIU H K, YAN C, ZHAO Y T, et al. Uncertainty and sensitivity analysis of flow parameters on aerodynamics of a hypersonic inlet[J].Acta Astronautica, 2018, 151:703-716. DOI: 10.1016/j.actaastro.2018.07.011
[16] PLENTOVICH E B. Three-dimensional cavity flow fields at subsonic and transonic speeds[R]. NASA-TM-4209, 1990.
[17] THANGAMANI V, KNOWLES K, SADDINGTON A J. The effects of scaling on high subsonic cavity flow oscillations and control[R]. AIAA-2012-2052, 2012.
[18] MERRICK J D. Influence of Mach number and dynamic pressure on cavity tones and freedrop trajectories[D]. Ohio: Air Force Air University, 2014.
[19] 王显圣, 杨党国, 刘俊, 等.弹性空腔流致噪声/结构振动特性试验[J].航空学报, 2017, 38(7):182-191. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkxb201707015 WANG X S, YANG D G, LIU J, et al. Test on interactions between aeroacoustic noise and structural vibration in elastic cavity flow[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(7):182-191. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=hkxb201707015
[20] 周方奇, 杨党国, 王显圣, 等.前缘直板扰流对高速空腔的降噪效果分析[J].航空学报, 2018, 39(4):133-143. http://d.old.wanfangdata.com.cn/Periodical/hkxb201804011 ZHOU F Q, YANG D G, WANG X S, et al. Effect of leading edge plate on high speed cavity noise control[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(4):133-143. http://d.old.wanfangdata.com.cn/Periodical/hkxb201804011
[21] HANKEY W L, SHANG J S. Analyses of pressure oscillations in an open cavity[J]. AIAA Journal, 1980, 18(8):892-898. DOI: 10.2514/3.50831
[22] 熊红亮, 袁格, 李潜, 等.可压缩自由剪切层纹影试验研究[J].流体力学实验与测量, 2003, 17(2):74-77, 83. DOI: 10.3969/j.issn.1672-9897.2003.02.015 XIONG H L, YUAN G, LI Q, et al. Flow visualization about a compressible shear flow[J]. Experiments and Measurements in Fluid Mechanics, 2003, 17(2):74-77, 83. DOI: 10.3969/j.issn.1672-9897.2003.02.015
[23] ROSSITER J E.Wind-tunnel experiments on the flow over rectangular cavities at subsonic and transonic speeds: 64037[R]. RAE Technical Report No.64037, 1964.
[24] CHANDRA B U, CHAKRAVARTHY S R. Experimental investigation of cavity-induced acoustic oscillations in confined supersonic flow[J]. Journal of Fluids Engineering, 2005, 127(4):761-769. DOI: 10.1115/1.1949642
[25] WANG Y C, TAN L, WANG B B, et al. Numerical investigation on frequency jump of flow over a cavity using large eddy simulation[J]. Journal of Fluids Engineering, 2015, 137(8):081203. DOI: 10.1115/1.4030002
-
期刊类型引用(1)
1. 刘俊,罗新福,王显圣. 前缘形状对空腔模型气动特性影响试验. 航空学报. 2022(07): 78-88 .  百度学术
百度学术
其他类型引用(1)






 下载:
下载: